Condensates, massive gauge fields and confinement in the SU(3) gauge theory
Abstract
SU(3) gauge theory in the nonlinear gauge of the Curci–Ferrari type is studied. In the low-energy region, ghost condensation and subsequent gauge field condensation can happen. The latter condensation makes classical gauge fields massive. If the color electric potential with string is chosen as the classical gauge field, it produces the static potential with the linear potential. We apply this static potential to the three-quark system, and show, different from the -type potential, infrared divergence remains in the -type potential. The color electric flux is also studied, and show that the current which plays the role of the magnetic current appears.
B0,B3,B6
1 Introduction
In the dual superconductor picture of quark confinement, it is expected that monopole condensation appears in the low energy region. This condensation produces a mass of gauge fields, and confinement happens. To describe this scenario, the dual Ginzburg–Landau model has been considered (See, e.g., Ref. rip ).
Based on the SU(2) gauge theory in a nonlinear gauge, we considered another possibility to give a mass for gauge fields hs17 . In the low-energy region below , which is the QCD scale parameter, the ghost condensation happens. Although this condensation gives rise to a tachyonic gluon mass, a gauge field condensate can remove the tachyonic mass. If there is a classical U(1) gauge field, this classical field becomes massive by this condensate.
In Ref. hs19 , referring to the Zwanziger’s formalism zwa , the electric potential and its dual potential were introduced as a classical field. Due to the string structure of these classical fields, the linear potential was obtained.
In this paper, we extend the previous approach to the SU(3) case. In the next section, the ghost condensation is studied at the one-loop level. In Sect. 3, under the ghost condensation, tachyonic gluon masses and the gluon condensates are calculated in the low momentum limit. The Lagrangian of the massive classical gauge fields is also presented. In Sect. 4, as the classical fields, the color electric potential and its dual potential are introduced, and the static potential between two charges is calculated. Using the result of Sect. 4, the mesonic potential and the baryonic potential are discussed in Sect. 5. Different from the dual Ginzburg–Landau model, there is no magnetic current originally. The Maxwell’s equations in the present model are studied in Sect. 6. The behavior of the color flux tube is also considered. Section 7 is devoted to summary and comment. In Appendix A, the relation between the ghost condensation and is derived. Tachyonic gluon masses are calculated in Appendix B. To make the article self-contained, an example of the electric potential and its dual potential for a color charge is presented in Appendix C. In Appendix D, the static potential between two charges is calculated in detail. Based on a phenomenological Lagrangian for order parameters, the type of the dual superconductivity in the present model is considered in Appendix E.
2 Ghost condensation
2.1 Notation
We consider the SU(3) gauge theory with structure constants in the Minkowski space. The Lagrangian in the nonlinear gauge of the Curci–Ferrari type cf is given by hs03
where is the Nakanishi–Lautrup field, is the ghost (antighost), , and are gauge parameters, and is a constant to keep the BRS symmetry. The Lagrangian is rewritten as
where the auxiliary field represents .
Let us expand the gauge field as
| (2.1) |
where the diagonal components are
and . The off-diagonal components are given by
Using the root vectors of the SU(3) group
| (2.2) |
the above matrices satisfy
and
In the same way, and are expressed as
| (2.3) |
where
and are defined as well.
2.2 Ghost condensation
To obtain the one-loop effective potential of , we diagonalize as . Then, using the expressions (2.1) and (2.3), the Lagrangian becomes
| (2.4) |
Next, as in the SU(2) case hs07 , we integrate out and with the momentum . After the Wick rotation, we obtain the potential
Since we can rewrite as
the one-loop effective potential of becomes ks
| (2.5) |
To study minimum points of , we consider
The explicit forms of are
and leads to . So, the equation has the solution . Now we assume is a minimum point. Since the potential is invariant under the interchange , and has the symmetry , there are six minimum points 111These minimum points were found in Ref. ks . It also contains the three-dimensional figure of .
| (2.6) |
To determine the value of , we consider the case . The condition with becomes
| (2.7) |
If we set at , is obtained. When the cut-off is large enough, Eq.(2.7) gives in the limit .
In Appendix A, we show is the ultraviolet fixed point of , where with is the first coefficient of the function. Substituting this value into , we find
where is the QCD scale parameter. Thus we obtain the ghost condensate that behaves as
3 Gluon mass
3.1 Tachyonic gluon mass
In the SU(2) gauge theory, ghost loops with produce the tachyonic gluon mass terms hs03 ; dv . To study the SU(3) case, we choose the vacuum in Eq.(2.6), and write , where is the quantum part. Neglecting , the Lagrangian (2.4) becomes
and it leads to the ghost propagators
| (3.1) |
Using Eqs.(2.1) and (2.3), the vertex in is rewritten as
| (3.2) |
where is the sign of , and implies the sum for the permutations of and .
Now we consider the two-point function
| (3.3) |
at the one-loop level. As in the SU(2) case, using the ghost propagators (3.1) and the interactions (3.2), the ghost loop in Fig.1(b) gives rise to tachyonic masses in the low momentum limit . The details are presented in Appendix B. From Eqs.(B.3) and (B.7), we find the tachyonic mass terms are
| (3.4) |

3.2 Condensate
To remove the tachyonic masses, we consider the condensate hs17 ; hs19 . Let us introduce the source terms
Although the sources may depend on the momentum scale, for simplicity, the constant sources
are considered. The interaction in contains the terms
| (3.5) |
So, at , the diagram in Fig.1(c) gives the condensate , where is the free propagator with the mass or . If the other divergent diagrams of are subtracted by the terms with or , the condensate is determined to remove the tachyonic masses in Eq.(3.4).
As an example, we consider the self-energy of in the limit . The diagram Fig.1(c) with the first interaction in Eq.(3.5) gives . Similarly, from the second term in Eq.(3.5), we obtain . Since , the third term in Eq.(3.5) gives . So, Fig.1(c) for leads to
where and . The condition that these condensates remove the tachyonic mass of becomes
In the same way, we find the conditions
| (3.6) | |||
| (3.7) | |||
| (3.8) |
for , , and , respectively.
3.3 Inclusion of classical solutions
To incorporate U(1)3 and U(1)8 classical solutions into the above scheme, we divide into the classical part and the quantum fluctuation as
and divide the gauge transformation as
| (3.10) |
where , and is obtained by removing from , i.e., . Using the gauge-fixing function , the transformation (3.10) gives the ghost Lagrangian
So, after the ghost condensation, the tachyonic mass terms are obtained by replacing with and as 222We can use the background covariant gauge. In this case, as the ghost Lagrangian is , and couple with . However, this ghost Lagrangian has the symmetry , and . Therefore, as in the SU(2) case hs17 , this symmetry prevents from getting tachyonic mass terms, and Eq.(3.11) is obtained.
| (3.11) |
The above tachyonic mass terms are removed by the condensates and in Eq.(3.9). When , the interaction
in Eq.(3.5) leads to the mass terms
Since the classical part has no tachyonic mass, the equations (3.7) and (3.8) imply that these mass terms become
| (3.12) |
Thus, after integrating out and , we obtain the low-energy effective Lagrangian
| (3.13) |
where .
We ignored the momentum dependence of the sources and , and applied the expansion. Because it is difficult to modify this treatment, we use as the first approximation of the low energy Lagrangian.
4 Classical fields and static potential
4.1 The classical electric potential and its dual potential
It is expected that the Abelian component of the gauge field dominates in confinement ei . Based on the previous works hs18 ; hs19 , we choose the dual electric potential as the classical field . It describes the electric monopole solution hs19 . The color electric current is incorporated by the replacement
where the space-like vector zwa is chosen as with , and . We note this is the Zwanziger’s dual field strength in Ref. zwa . Then the Lagrangian .(3.13) becomes
| (4.1) |
The equation of motion for is
| (4.2) |
and is solved as
| (4.3) |
If we use Eq.(4.3), Eq.(4.1) becomes
| (4.4) |
Although we used the dual electric potential above, we can use the electric potential . The relation between and is hs19
| (4.5) | ||||
The dual potential has the electric correspondent of the Dirac string, which we call the electric string. The term represents this string. 333 In Appendix C, as an example, we present the massless fields and for a point charge, and show that describes the electric string. The relation (4.5) is also used to consider the color electric flux in Sect. 6. The field satisfies the equation of motion
and the Lagrangian that is equivalent to Eq.(4.1) is hs19
The last term comes from the electric string. Substituting into , we can obtain in Eq.(4.4).
4.2 Potential between static charges
We consider the static charges at and at . Substituting the static current
| (4.6) |
into , we get the potential
| (4.7) | ||||
| (4.8) |
where , and . The first (second) term in leads to (). Historically, these potentials were obtained by using the dual Ginzburg–Landau model suz ; mts ; sst ; sst2 . These potentials are calculated in Appendix D. Assuming that disappears above the scale , Eq.(4.7) gives hs21
| (4.9) |
The first term in is the usual Coulomb potential, which is the main term for small .
Under the same assumption that above , Eq.(4.8) gives
| (4.10) | ||||
| (4.11) |
where the functions and are defined in Eq.(D.11). We have chosen as , and . The vector satisfies , and . The term has infrared divergence , where the infrared cut-off satisfies . To remove this divergence, since the direction of the electric string is arbitrary, we choose sst2 ; hs19 ; hs21 . In this case, as , Eq.(4.10) becomes
| (4.12) | ||||
| (4.13) |
where and are presented in Eq.(D.12). Eq.(4.13) shows that vanishes if . Therefore, the conditions to remove the infrared divergence are
| (4.14) |
When Eq.(4.14) holds, the leading term of Eq.(4.12) is the linear potential , which is the main term for large .
We note the infrared divergence implies the existence of the electric string with infinite length and the mass . The relation between the conditions in Eq.(4.14) and the length of the electric string are depicted in Fig. 2.

In the SU(2) case, comparing the potential with and , we tried to determine the values of parameters, and reproduce the Coulomb plus linear type potential hs21 . However, in the SU(3) case, there are many parameters like and . In addition, since , we are not sure whether a single cut-off is usable or not. So we don’t try to determine the parameters in this paper. Instead, we study the consequences derived from the Lagrangian (4.1) and the potentials (4.9) and (4.12), below.
5 Mesonic and baryonic potentials
5.1 Notation
Corresponding to the three types of the color charge red, blue and green, we use , and , respectively. The quark field is , and the current is written as
where the weight vectors are
| (5.1) |
5.2 Mesonic potential
If a static quark (an antiquark) exists at (), a meson is expressed by
We set , and . Then the two conditions in Eq.(4.14) are satisfied, and vanishes. Using the relation
Eqs.(4.9) and (4.12) give the mesonic potential
| (5.3) |
where and .

5.3 -type potential
Let us study the potential for the configuration in Fig. 3(a), which is called the -ansatz cw . To apply Eqs.(4.9) and (4.12), we replace with , and with which satisfies . When static quarks are placed at , a baryonic state is
If we set and with , and use the relation
| (5.4) |
We make two comments. First, from Eqs.(5.3) and (5.4), we obtain the relation afj
| (5.5) |
Second, by the choice , the first condition is satisfied. However, except for , the second condition does not hold. So, using
we find the infrared divergent term
| (5.6) |
remains. In the -ansatz, there are electric strings with infinite length. When , they give rise to the infrared divergence.
5.4 -type potential
For large , the potential in has the infrared divergence. On the other hand, based on the strong coupling argument, the -shaped baryon depicted in Fig. 3(b) was proposed ckp . The point S at , where the sum of the length becomes minimum, is the Steiner point. The color electric flux lines emanating from the three quarks meet and disappear there. Since the state at this point is color singlet, corresponding to the state , the state at is . So, when is large, the potential is the sum of the three potentials for large . Thus we obtain
| (5.7) |
where .
We note, when is large, Eq.(5.4) gives
| (5.8) |
where and . From Eqs.(5.3), (5.7) and (5.8), the relations , and
| (5.9) |
are obtained at this level afj . As , the inequality holds. However, different from , is free from the infrared divergence.

5.5 Comparison with the lattice results
In the present model, the classical Abelian potentials lead to the linear potential. The -type potential is preferable to the -type potential, because the former has no infrared divergence. The string tension of the -type potential satisfies .
In the lattice simulation, the baryon has been studied, and the -type potential is obtained bi ; sasu ; kk . In Ref. sasu , using the maximal Abelian gauge, it is shown that the three quark string tension satisfies . In addition, the string tensions and , which are obtained from the Abelian part, satisfy and within a few percent deviation. These results show that the potential is -type, and the Abelian dominance is realized.
In Ref. kk , using the Polyakov loop correlation function, the cases with and are simulated, where represents the maximum inner angle of a triangle. In the latter case, the Steiner point is the point in Fig. 4. As in this case, the length is reduced to . When , they found that the long-range potential satisfies , and holds. On the other hand, when , they obtained the -type relation .
In our approach, when , the -type potential is calculable by setting and . The result is
| (5.10) |
When , Fig. 4(b) shows and . As , we find Eq.(5.10) becomes
| (5.11) |
Namely, if , the -type relation Eq.(5.10) coincides with the -type relation (5.11), which is expected from Eq.(5.9). Therefore we can say that the long-range potential is -type for .
6 Color electric flux
6.1 Extended Maxwell’s equations
In Sect. 4, we introduced the electric potential and its dual potential that are related by the Eq.(4.5). We also used the Zwanziger’s dual field strength zwa in the presence of the current . In this subsection, we study the Maxwell’s equations.
Using and , the dual field strength is expressed by
and the field strength is
The electric field and the magnetic field are
| (6.1) | ||||
| (6.2) | ||||
where has been used. From these expressions, it is easy to show the two Maxwell’s equations
| (6.3) |
Next we consider the remaining two Maxwell’s equations. Using , Eq.(6.2) gives
Since the classical fields satisfies the equation of motion
| (6.4) |
the above equation becomes
| (6.5) |
In the same way, we obtain
| (6.6) |
Namely, because of the term , the remaining two Maxwell’s equations are modified.
If we consider a model with the magnetic current , and will appear in the right hand side of Eqs.(6.5) and (6.6), respectively. In the dual superconductor model, there is the monopole field, and the static equation is often discussed rip ; kst . In the present model, there is no monopole field and no magnetic current originally. However, like the London equation in superconductivity, the relation appears.
6.2 Color flux tube
It is expected that the color flux tube connects color charges. In Ref. kst , using the dual superconductor model, the color flux is studied. From this flux and the equation , the magnetic current is also investigated. In this subsection, we consider the color flux tube.
Let us consider the electric flux between the charges at and at . We set , and assume that the mass is approximately constant for , where are the cylindrical coordinates. To study the static flux tube solution, we set and
| (6.7) |
where the unit vectors are
Substituting Eq.(6.7) into Eq.(6.4), we obtain
| (6.8) |
Since holds for , if we assume in the interval , Eq.(6.8) reduces to the equation
in the region . The solution of this equation with is no
where is a constant, and is the modified Bessel function. So, we obtain
| (6.9) |
Using Eq.(6.9) and the equality , the color electric field becomes
| (6.10) |
In the same way, if we apply the relations and , we get
From this equation and Eq.(6.10), we obtain
| (6.11) |
In the interval , is assumed, and Eq.(6.11) becomes Eq.(6.6) with .
6.3 Flux tube represented by
Next, we restudy the flux tube by using the electric potential . In the static case, Eq.(6.1) becomes
| (6.12) |
From the equation of motion
satisfies
If we can write approximately, this equation becomes
| (6.13) |
As in the previous subsection, we set for , and assume in the interval . Then Eq.(6.13) becomes
Using the constant , the solution of this equation is
Since we choose , gives
| (6.14) |
and Eq.(6.12) becomes
| (6.15) |
Comparing Eqs.(6.10) and (6.15), we can identify 444The minus sign comes from the choice that the electric string is in the negative -direction. See Eq.(C.4).
So, and can be approximated by
where is the unit step function.
Thus, the electric potential
| (6.16) |
produces the color electric flux
| (6.17) |
in the region . The string part (6.14) is responsible for this flux tube. The corresponding dual potential is
| (6.18) |
which also gives the flux (6.17). This flux satisfies the extended Maxwell’s equation
| (6.19) |
where the magnetic current is .
We make a comment. The lattice simulation shows that the baryon is -shaped bi ; sasu ; kk and the solenoidal magnetic current exists bi . In the present approach, the -type baryonic potential is free from infrared divergence, and it consists of three potentials. So, although the flux tube of is considered here, we can apply it to the -type baryon. The flux tube of can exist between and . The current with (6.18), which has the solenoidal form, also appears. .
7 Summary and comment
In the dual superconductor picture of the quark confinement, the monopole condensation produces the gluon mass. To realize this scenario, the dual Ginzburg–Landau model introduces the monopole field, and its condensation, the gluon mass and the static potential have been studied.
In Ref. hs19 , we considered another possibility to make Abelian component of the gluon massive in the SU(2) gauge theory. The static potential was also studied hs21 . In this paper, we extended this approach to the SU(3) gauge theory. In the nonlinear gauge of the Curci–Ferrari type, quartic ghost interaction generates the ghost condensate below the scale . The ghost loop with gives rise to the tachyonic mass to the quantum part of the gluon. This tachyonic mass is removable by the gluon condensate . Since the classical part of the gluon has no tachyonic mass, the condensate gives the mass to this part. To study the color confinement, the dual color electric potential , which is equivalent to the color electric potential with the string part , was chosen as . Thus, the classical Lagrangian we use is in Eq.(4.1).
This Lagrangian becomes in Eq.(4.4), and it gives the static potential between the charges and with distance . When is small, the leading term is in Eq.(4.9). For large , in Eq.(4.10) is the main term. However, contains the infrared divergence , which comes from the mass and the electric string with infinite length. If the conditions and in Eq.(4.14) are fulfilled, vanishes. In this case, becomes the linear potential in Eq.(4.12).
We stress the derivation of the Lagrangian is based on the one-loop calculation. In addition, the constant sources and are assumed. The mass in Eq.(4.1) was also assumed to be constant below the cut-off and vanish above . These quantities must be determined. However, different from the SU(2) case, there are many parameters in SU(3). We skipped the determination in this paper, and studied the consequences of the Lagrangian and the potential .
In the case, the two conditions in Eq.(4.14) are satisfied, and the static potential in Eq.(5.3) is obtained. In the case, if the -ansatz holds, the potential is given by Eq.(5.4). However, since the second condition of Eq.(4.14) is not fulfilled, the infrared divergence (5.6) remains. Contrary to the -ansatz, the -ansatz satisfies the two conditions. The potential in Eq.(5.7), which is free from the infrared divergence, is expected for large .
Using the color electric potential and its dual potential , the color electric field and the magnetic field were investigated. Although they satisfy the two Maxwell’s equations (6.3), because of the mass , the remaining two equations are modified as Eqs.(6.5) and (6.6). In the static case, Eq.(6.6) becomes . In the dual Ginzburg–Landau model, which contains the monopole field, the equation has been discussed. In our model, although there is no monopole field, the current plays the role of the magnetic current .
It is expected that the color flux tube exists between color charges. The dual electric potential in Eq.(6.18) produces the electric flux in Eq.(6.17), and they satisfy Eq.(6.19). Namely, without the monopole field, the flux tube leads to the magnetic current . The corresponding electric potential is presented in Eq.(6.16). The string part (6.14) is the origin of the flux tube (6.17).
Comparing the SU(3) case with the SU(2) case in Ref. hs19 , there are some differences. For example, as we stated in Sect. 3, although the condensate of the diagonal component vanishes in SU(2), the condensates () exist in SU(3). Eq.(3.11) shows there are two different mass scales and , and the classical electric potentials and have different masses, whereas the tachyonic mass term in SU(2) has one scale .
Since we have not determined the parameters yet, it is difficult to study differences between SU(2) and SU(3) concretely. In Ref. ks2 , the differences are discussed. One of the issues is the type of the dual superconductivity. Investigating the electric flux, it is concluded that the SU(3) theory is type-I, whereas the SU(2) theory is weak type-I or the border between type-I and type-II. In Appendix E, assuming the phenomenological Lagrangian for the order parameters and , we consider the type of dual superconductivity in the present model. Because of the condensate and the two mass scales and , the value of the Ginzburg-Landau parameter for SU(3) may become smaller than that for SU(2).
Appendix A and
In the momentum region , as the effective potential in Eq.(2.5) gives , we consider the Wilsonian effective action
| (A.1) |
If and represent the quantities at the scale , Eq.(A.1) implies
| (A.2) |
From Eq.(A.2), we obtain .
| (A.3) |
Since satisfies
| (A.4) |
at the one-loop level, Eqs.(A.3) and (A.4) leads to the equation
Namely is the ultraviolet fixed point hs07 ; ks , i.e.,
Appendix B Tachyonic gluon masses
B.1
We consider the diagrams in Fig. B1(a) in the limit , where is the external momentum. The ghost propagators in Eq.(3.1) and the interaction
in Eq.(3.2) gives the integral
| (B.1) |
Performing the Wick rotation and neglecting -independent terms, we obtain the formula
| (B.2) |
If we apply this formula, we find Eq.(B.1) becomes
Using the values of in Eq. (2.2), we obtain
| (B.3) |
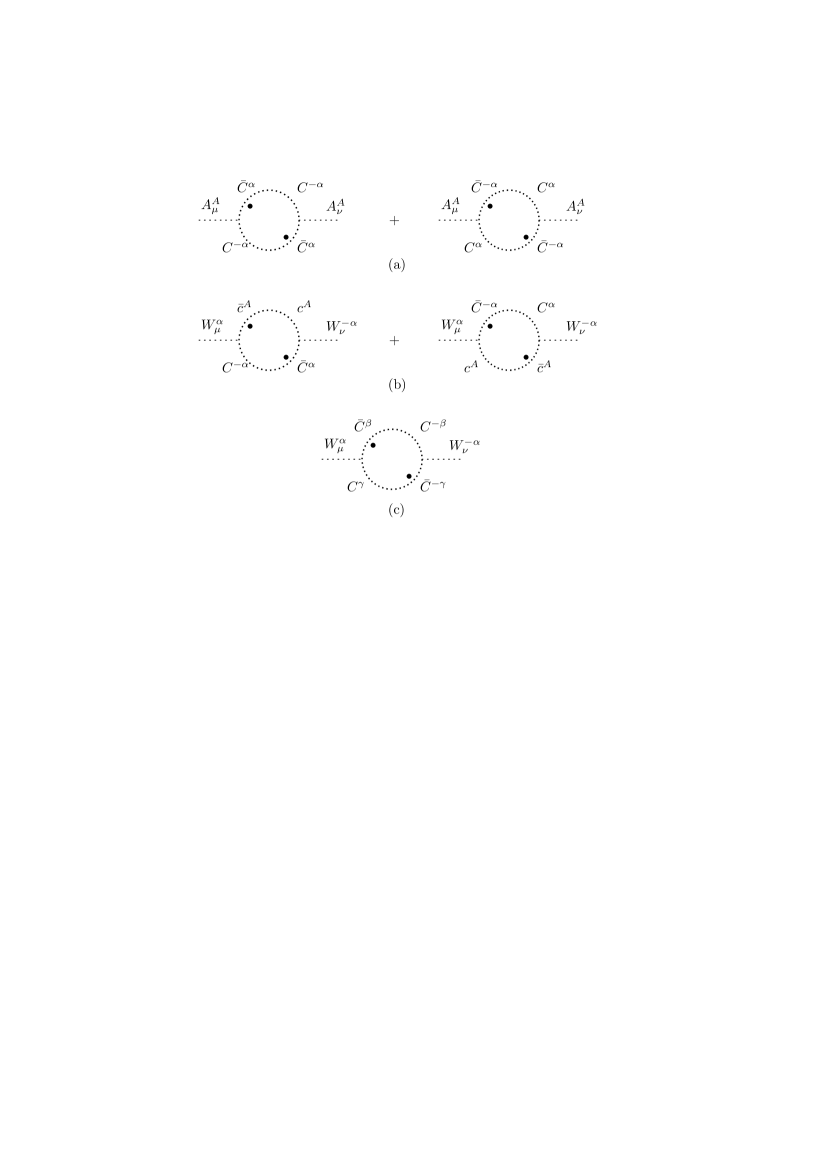
B.2
The diagrams in Fig. B1(b), which come from the interaction
give the integral
Using the values of in Eq.(2.2), we obtain
| (B.4) |
Appendix C Example of the electric potential and its dual potential
In this appendix, we present an example of the massless electric potential and its dual potential for a color electric charge . The color electric current is
and the electric potential
| (C.1) |
satisfies the equation of motion
The dual electric potential that corresponds to (C.1) is
| (C.2) |
This field fulfills the equation of motion
and gives the color electric field
| (C.3) |
where is the unit step function, and has been used.
Appendix D The potentials and
D.1
By subtracting -independent terms, which contain ultraviolet divergence, in Eq.(4.7) becomes
If the mass disappears above some scale , this potential can be written as
The first term on the right hand side gives the Coulomb potential, which contributes mainly in the small region. When becomes large, the second term weakens the effect of the first term. After performing the integration, we obtain hs21
| (D.1) |
We note this potential satisfies
| (D.2) |
In the usual approach suz ; mts ; sst ; hs17 , the cut-off is not taken into account, and becomes the Yukawa potential (D.2).
D.2
When , the potential in Eq.(4.8) vanishes. So, different from , the momentum region contributes to . Let us write , and choose as . The vector satisfies , and . Similarly, we write , and use the spherical coordinates
| (D.3) |
where is chosen to satisfy .
Now we consider the integral
| (D.4) |
in . It becomes
| (D.5) |
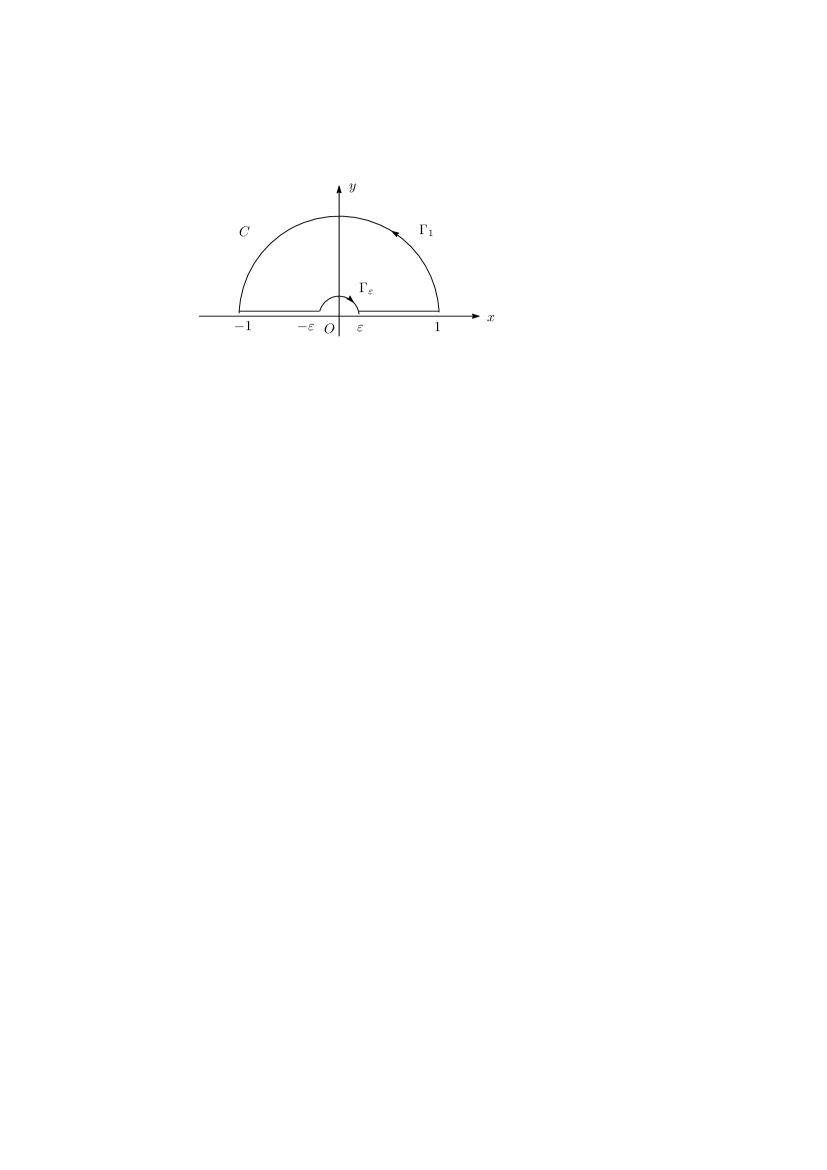
By changing the variable to , we get
which diverges at . If we choose the path in Fig. D1, the integral
leads to
| (D.6) | |||
where means the Cauchy principal value. To calculate , we use the variable , and take the limit . Then it becomes
| (D.7) |
If we substitute Eqs. (D.6), (D.7) and (D.8) into Eq.(D.5), we find
| (D.10) | ||||
where, using the Bessel function , and are defined by
| (D.11) | ||||
These functions satisfy
| (D.12) | ||||
where is the modified Bessel function. The term in Eq.(D.10) has the properties
| (D.13) | ||||
| (D.14) |
We note the first term has the infrared divergence , and the second term leads to the linear potential. When , as Eq.(D.14) shows, the last term does not depend on so much. Therefore, in Sect. 4, we study the potential based on the first and the second terms in Eq.(D.15).
We make a comment. Usually, the ultraviolet cut-off is introduced as suz ; mts ; sst ; hs19 . The domain of integration is and . The infrared divergence and the linear potential come from the region with . In this article, as above , the domain of integration is . The infrared divergence and the linear potential result from . Although the linear potential in these references coincides with that in this article, the coefficient of the infrared divergent term is different. From , we find is related to as . By using this relation, the infrared divergence in Ref. hs19 becomes (D.16).
Appendix E Type of the dual superconductivity
In the Ginzburg-Landau (GL) theory of the superconductivity, the space dependence of an order parameter is considered (See, e.g., Ref. nk ). To see the coherence length, the -dependence is introduced as with and . From the phenomenological Lagrangian for , the function satisfies the equation
| (E.1) |
The solution is , and is the coherence length. The penetration depth is determined by the mass of the magnetic field, and the parameter is called the GL parameter. When (, the superconductor is called type-I (type-II).
In the following subsections, under some assumptions, we consider the coherence length and the GL parameter in the present model.
E.1 SU(2) case
First, we consider the SU(2) case. In Refs. hs17 ; hs19 , we showed that the tachyonic mass term for the off-diagonal component is , and the interaction in contains the term . From these terms, we obtain the gauge field condensate at the one-loop level. This condensate makes the classical U(1) field massive. As its mass term becomes , the penetration depth of is .
Now we consider the spatial behavior of the condensate . Since has the mass dimension 2, we assume its -dependence is expressed by with and . As depends on , we introduce the kinetic energy in the form of . Thus, using this kinetic term, the above tachyonic mass term and the interaction, we assume the following phenomenological Lagrangian for :
where is a parameter to adjust the effect of the assumed kinetic term. This Lagrangian leads to the equation
where has been used. This equation implies . From and , we find . If , it implies the border between type-I and type-II.
E.2 SU(3) case
As in the SU(2) case, we assume the -dependent order parameters and . Using the tachyonic mass terms (3.4), the interaction terms (3.5) and the assumed kinetic terms with the same parameter , we consider the phenomenological Lagrangian
From , we obtain the equations for and given by
| (E.2) | ||||
| (E.3) |
If we assume the relation , these equations become
| (E.4) | ||||
| (E.5) |
where Eqs.(3.6) and (3.8) have been used. In the same way, we find and also satisfy Eq.(E.4). Therefore, comparing these equations with Eq.(E.1), we find
| (E.6) |
Eq.(E.6) shows that we have to modify Eqs.(E.4) and (E.5) to satisfy the relation . If we use this relation, Eqs.(E.2) and (E.3) become
| (E.7) | ||||
| (E.8) |
where Eqs.(3.6) and (3.8) have been used again. Now we use Eq.(3.9), and rewrite the second terms on the right hand side as
Then Eqs.(E.7) and(E.8) become
| (E.9) | ||||
| (E.10) |
We note, as and , and satisfy .
Since and depend on , it is difficult to solve Eqs.(E.9) and (E.10). However, Eq.(E.5) becomes Eq.(E.10), if we replace with . Therefore, it is expected that the coherence length obtained from Eq.(E.10) is longer than . From the masses for the classical fields in Eq.(3.12), the corresponding penetration depth is . If we can use and , the GL parameter becomes . If , we can expect type-I.
References
- (1) G. Ripka, arXiv:hep-ph/0310102.
- (2) H. Sawayanagi, Prog. Theor. Exp. Phys. 2017, 113B02 (2017).
- (3) H. Sawayanagi, Prog. Theor. Exp. Phys. 2019, 033B03 (2019).
- (4) D. Zwanziger, Phys. Rev. D 3, 880 (1971).
- (5) G. Curci and R. Ferrari, Phys. Lett. B63, 91 (1976).
- (6) H. Sawayanagi, Phys. Rev. D 67, 045002 (2003).
- (7) H. Sawayanagi, Prog. Theor. Phys. 117, 305 (2007).
- (8) K. -I. Kondo and T. Shinohara, Phys. Lett. B491, 263 (2000).
- (9) D. Dudal and H. Verschelde, J. Phys. A 36, 8507 (2003).
- (10) Z. F. Ezawa and A. Iwazaki, Phys. Rev. D 25, 2681 (1982).
- (11) H. Sawayanagi, Prog. Theor. Exp. Phys. 2018, 093B01 (2018).
- (12) T. Suzuki, Prog. Theor. Phys. 80, 929 (1988).
- (13) S. Maedan and T. Suzuki, Prog. Theor. Phys. 81, 229 (1989).
- (14) S. Sasaki, H. Suganuma and H. Toki, Prog. Theor. Phys. 94, 373 (1995).
- (15) H. Suganuma, S. Sasaki and H. Toki, Nucl. Phys. B 435, 207 (1995).
- (16) H. Sawayanagi, Prog. Theor. Exp. Phys. 2021, 023B07 (2021).
- (17) J. M. Cornwall, Phys. Rev. D 54, 6527 (1996).
- (18) J. Carlson, J. Kogut and V. R. Pandharipande, Phys. Rev. D 27, 233 (1983).
- (19) C. Alexandrou, Ph. de Forcrand and O. Jahn, Nucl. Phys. B (Proc. Suppl.) 119, 667 (2003).
- (20) V. G. Bornyakov et al., Phys. Rev. D 70, 054506 (2004).
- (21) N. Sakumichi and H. Suganuma, Phys. Rev. D 92, 034511 (2015).
- (22) Y. Koma and M. Koma, Phys. Rev. D 95, 094513 (2017).
- (23) Y. Koma et al., Phys. Rev. D 64, 014015 (2001).
- (24) H. B. Nielsen and P. Olesen, Nucl. Phys. B 61, 45 (1973).
- (25) K. -I. Kondo et al., Phys. Rep. 579, 1 (2015).
- (26) S. Nakajima, Introduction to Superconductivity, (Baifukan, Tokyo, 1971) (in Japanese).