Computer-assisted proofs of Hopf bubbles and degenerate Hopf bifurcations
Abstract
We present a computer-assisted approach to prove the existence of Hopf bubbles and degenerate Hopf bifurcations in ordinary and delay differential equations. We apply the method to rigorously investigate these nonlocal bifurcation structures in the FitzHugh-Nagumo equation, the extended Lorenz-84 model and a time-delay SI model.
1 Introduction
The Hopf bifurcation is a classical mechanism leading to the birth of a periodic orbit in a dynamical system. In the simplest setting of an ordinary differential equation (ODE), a Hopf bifurcation generically occurs when the linearization at a fixed point has a single pair of complex-conjugate imaginary eigenvalues. In this case, a perturbation by way of a scalar parameter would be expected, but not guaranteed, to result in a Hopf bifurcation. To prove the existence of the Hopf bifurcation, some non-degeneracy conditions must be checked. One such non-degeneracy condition pertains to the eigenvalues at the linearization: on variation of the distinguished scalar parameter, they must cross the imaginary axis transversally. We refer the reader to the papers [6, 9, 13, 19, 25] for some classical (and more recent) background concerning the Hopf bifurcation in the context of infinite-dimensional dynamical systems. A standard reference for the ODE case is the book of Marsden & McCracken [21].
1.1 Hopf bubbles
The Hopf bifurcation is generic in one-parameter vector fields of ODEs. Roughly speaking, this means it is prevalent in a topological sense among all vector fields that possess an equilibrium point with a pair of complex-conjugate imaginary eigenvalues. In the world of two-parameter vector fields, the richness of possible bifurcations is much greater. In this paper, we are primarily interested in a type of degenerate Hopf bifurcation that results from a particular failure of the eigenvalue transversality condition. The failure we are interested in is where the curve of eigenvalues has a quadratic tangency with the imaginary axis, so the eigenvalues do not cross transversally and, importantly, do not cross the imaginary axis at all.
Before surveying some literature about this bifurcation pattern, let us construct a minimal working example. Consider the ODE system
| (1) | ||||
| (2) |
The reader familiar with the normal form of the Hopf bifurcation should find this familiar, but might be be unnerved by the term, which is not present in the typical normal form. The linearization at the equilibrium , produces the matrix
which has the pair of complex-conjugate eigenvalues . Treating as being a fixed constant, we have a supercritical Hopf bifurcation as passes through . Conversely, if is fixed and we interpret as the parameter, there are two supercritical Hopf bifurcations: as passes through . However, something problematic happens if : the eigenvalue branches are tangent to the imaginary axis at and do not cross at all, so the non-degeneracy condition of the Hopf bifurcation fails.
More information can be gleaned by transforming to polar coordinates. Setting and results in the equation for the radial component
while . There is a nontrivial periodic orbit (in fact, limit cycle) if , with amplitude . Alternatively, there is a surface of periodic orbits described by the graph of . For fixed , the amplitude of the periodic orbit, as a function of , is , whose graph is half of an ellipse with semi-major axis and semi-minor axis .
This non-local bifurcation structure, characterized by the connection of two Hopf bifurcations by a one-parameter branch of periodic orbits, has been given several names in different scientific fields. In intracellular calcium, it is frequently called a Hopf bubble [7, 16, 22, 27]. In infectious-disease modelling, where the bifurcation typically occurs at an endemic equilibrium, the accepted term is endemic bubble [8, 17, 18, 23, 26]. A more general definition of a (parametrically) non-local structure called bubbling is given in [15]. In the present work, we will refer to the structure as a Hopf bubble, since that name is descriptive of the geometric picture, the bifurcation involved, and is sufficiently general to apply in different scenarios in a model-independent way.
Hopf bubbles can, in many instances, be understood as being generated by a codimension-two bifurcation; see Section 1.3. However, this is not to say that they are rare. Aside from the applications in calcium dynamics and infectious-disease modelling in the previous paragraph, they have been observed numerically in models of neurons [1], condensed-phase combustion [20], predator-prey models [3], enzyme-catalyzed reactions [12], and a plant-water ecosystem model [31]. A recent computer-assisted proof also established the existence of a Hopf bubble in the Lorenz-84 model [30]. We will later refer to the degenerate Hopf bifurcation that gives rise to Hopf bubbles as a bubble bifurcation. The literature seems to not have an accepted name for this bifurcation, so we have elected to give it one here.
1.2 Bautin bifurcation
Bubble bifurcations are one type of dgenerate Hopf bifurcation. Another is the Bautin bifurcation, which occurs at a Hopf bifurcation whose first Lyapunov coefficient vanishes [14]. Like the bubble bifurcation, the Bautin bifurcation is a codimension-two bifurcation of periodic orbits. To illustrate this bifurcation, consider the planar normal form
| (3) | ||||
| (4) |
Transforming to polar coordinates, the angular component decouples producing , while the radial component gives
Nontrivial periodic orbits are therefore determined by the zero set of , which defines a two-dimensional smooth manifold. See later Figure 15 for a triangulation of (part of) this manifold.
1.3 Degenerate Hopf bifurcations and multi-parameter continuation
The bubble bifurcation has been fully characterized by LeBlanc [17], using the center manifold reduction and normal form theory for functional differential equations [9] and a prior classification of degenerate Hopf bifurcations for ODEs by Golubitsky and Langford [11]. The study of the Bautin bifurcation goes back to 1949 with the work of Bautin [2], and a more modern derivation based on normal form theory appears in the textbook of Kuznetsov [14].
Normal form theory and centre manifold reduction are incredibly powerful, providing both the direction of the bifurcation and criticality of bifurcating periodic orbits. The drawback is that they are computationally intricate and inherently local. In the present work, we advocate for an analysis of degenerate Hopf bifurcations in ODE and delay differential equations (DDE) by way of two-parameter continuation, desingularization and computer-assited proofs. We will discuss the latter topics in the next section.
The intuition behind our continuation idea can be pictorially seen in Figure 1, and understood analytically by way of our minimal working example, (1)–(2), and its surface of periodic orbits described by the equation . There is an implicit relationship between two scalar parameters ( and ) and the set of periodic orbits of the dynamical system. At a Hopf bifurcation, one of these periodic orbits should retract onto a steady state. In other words, their amplitudes (relative to steady state) should become zero. Using a desingularization technique to topologically separate periodic orbits from steady states that they bifurcate from, we can use two-parameter continuation to numerically compute and continue periodic orbits as they pass through a degenerate Hopf bifurcation. With computer-assisted proof techniques, we can prove that the numerically-computed objects are close to true periodic orbits, with explicit error bounds. Further a posteriori analysis can then be used to prove the existence of a degenerate Hopf bifurcation based on the output of the computer-assisted proof of the continuation.

1.4 Rigorous numerics
Computer-assisted proofs of Hopf bifurcations have been completed in [30] using a desingularization (sometimes called blow-up) approach, in conjunction with an a posteriori Newton-Kantorvich-like theorem. We lean heavily on these ideas in the present work. The former desingularization idea, which we adapt to delay equations in Section 3.1, is used to resolve the fact that, at the level of a Fourier series, a periodic orbit that limits (as a parameter varies) to a fixed point at a Hopf bifurcation is, itself, indistinguishable from that fixed point. Our methods of computer-assisted proof are based on contraction mappings, and it is critical that the objects we prove are isolated as fixed points. The desingularization idea exploits the fact that an amplitude-based change of variables can be used to develop an equivalent problem where the representative of a periodic orbit consists of a Fourier series, a fixed point and a real number. The latter real number represents a signed amplitude. This reformulation results in fixed points being spatially islolated from periodic orbits, thereby allowing contraction-based computer-assisted proofs to succeed.
The other big point of inspiration in this work is validated multi-parameter continuation. The technique was developed in [10] for continuation in general Banach spaces, and applied to some steady state problems for PDEs. We will overview this method in Section 2. It is based on a combination of a two-dimensional analogue of pseudo-arclength continuation and a posteriori, uniform validation of zeroes of nonlinear maps by a Newton-Kantorovich-like theorem applied to a Newton-like operator.
1.5 Contributions and applications
The main contribution of the present work is a general-purpose code for computing and proving two-parameter families of periodic orbits in polynomial delay differential equations. Equations of advanced or mixed-type can similarly be handled; there is no restriction whether delays are positive or negative. Ordinary differential equations can also be handled as a special case. Orbits can be proven in the vicinity of (and at) Hopf bifurcations, whether these are non-degenerate or degenerate. The first major release of the library BiValVe (Bifurcation Validation Venture, [4]) is being made in conjunction with the present work, and builds on an earlier version of the code associated to the work [29, 30]. Some non-polynomial delay differential equations can be handled using the polynomial embedding technique. The existence of Hopf bifurcation curves and degenerate Hopf bifurcations can then be completed by post-processing of the output of the computer-assisted proof.
To explore the applicability of our validated numerical methods, we explore Hopf bifurcations and degenerate Hopf bifurcations in
-
•
the extended Lorenz-84 model (ODE)
-
•
a time-delay SI model (DDE)
-
•
the FitzHugh-Nagumo equation (ODE)
-
•
an ODE with complicated branches of periodic orbits (ODE)
The first two examples replicate and extend some of the analysis appearing in [17, 30] using our computational scheme. The third examples provides, to our knowledge, the first analytically verified results on degenerate Hopf bifurcations and Hopf bubbles in that equation. The final example is a carefully designed ODE that exhibits the degenerate Hopf bifurcation in addition to folding and pinching in some projections of the manifold.
1.6 Overview of the paper
Section 2 serves as an overview of two-parameter continuation, both in the finite-dimensional and infinite-dimensional case. We introduce the continuation scheme for periodic orbits near Hopf bifurcations in Section 3 in the general case of delay differential equations. Some technical bounds for the computer-assisted proofs in Section 4. A specification to ordinary differential equations is presented in Section 5. In Section 6, we connect the computer-assisted proofs of the manifold of periodic orbits to analytical proofs of Hopf bifurcation curves, Hopf bubbles, and degenerate Hopf bifurcations. Our examples are presented in Section 7, and we complete a discussion and comment on future research directions in Section 8.
1.7 Notation
Given , denote the vector space of -indexed sequences of elements of Denote the proper subspace of consisting of symmetric sequences; if and only if and for all . For any subspace closed under (componentwise) complex conjugation, denote . We will sometimes drop the subscript on when the context is clear.
Given , we denote the subspace of whose elements satisfy . will always be taken to be the norm on induced by the standard inner product. Denote the subspace of whose elements satisfy Introduce a bilinear form on on as follows:
For , define their convolution by
| (5) |
whenever this series converges. Convolution is commutative and associative for sequences in . In this case, we define multiple convolutions (e.g. triple convolutions ) inductively, by associativity.
A function is a convlution polynomial of degree if
for , where denotes the set of -element multisets of , and each multiset is identified with the unique tuple such that for all . Analogously, is a convolution polynomial of degree if is a convolution polynomial of degree , for .
If is a vector space, will denote the zero vector in that space. If is a metric space and , we denote its interior, its boundary, and its closure.
An interval vector in for some is a subset of the form for real scalars , . If is equipped with a norm we define . Similarly, an interval vector in is a product , where each is a closed disc in . We define the norm of a complex interval vector as whenever is a norm on . In each case, be it real or comlex, the unit interval vector is the unique interval vector with the property that , and for any other interval vector with , the inclusion is satisfied.
2 Validated two-parameter continuation
In this section, we review validated two-parameter continuation. Our presentation will loosely follow [10]. Some noteworthy changes compared to the references are that we work in a complexified (as opposed to strictly real) vector space, which causes some minor difficulties at the level of implementation.
We first review the continuation algorithm as it applies to finite-dimensional vector spaces in Section 2.1. We make comments concerning implementation in Section 2.2. We then describe how it is extended to general Banach spaces in Section 2.3. Validated continuation (i.e. computer-assisted proof) is discussed in Section 2.4.
2.1 Continuation in a finite-dimensional space
Let and be finite-dimensional vector spaces over the field , with , and consider a map . We are interested in the zero set of . Given the codimension of , we expect zeroes to be in a two-dimensional manifold in . In what follows, equality with zero should be understood in the sense of numerical precision. For example, if we write , what we mean is that is machine precision small.
Let satisfy , and suppose has two-dimensional kernel. This property is generic. Let span the kernel. The tangent plane at of the two-dimensional solution manifold is therefore spanned by . If are small, we have
by Taylor’s theorem, provided is differentiable at , and is any Euclidean norm of . If is twice continuously differentiable, the error is improved to . Therefore, new candidate zeroes of can be computed using and a basis for the tangent space. This idea is at the heart of the continuation.
The continuation from is done by way of iterative triangulation of the manifold . First, we compute an orthonormal basis of by applying the Gram-Schmidt process to ; see Section 2.2 for some technical details. Using this orthonormal basis to define a local coordinate system, six vertices of a regular hexagon are computed around at a specified distance from ; see Figure 2. Let these vertices be denoted through , arranged in counterclockwise order (relative to the local coordinate system) around . Note that this means
for some small , which means that for . Each of these candidate zeroes are then refined by applying Newton’s method to the map
| (9) |
The two added inner product equations ensure isolation of the solution (hence quadratic convergence of the Newton iterates) and that the Newton correction is perpendicular to the tangent plane. This map can similarly be used to refine the original zero .
This initial hexagonal “patch” is itself formed by six triangles; see Figure 2. The continuation algorithm proceeds by selecting one of the boundary vertices (i.e. one of the vertices through ) and attempting to “grow” the manifold further. We describe this “growth” phase below. However, first, some terminology. The vertices will now be referred to as nodes. An edge is a line segment connecting two nodes, and they will be denoted by pairs of nodes: for node connected to . Two nodes are incident if they are connected by an edge. A simplex is the convex hull of three edges that form a triangle. Once the hexagonal patch is created, the data consists of:
-
•
the nodes ;
-
•
the “boundary edges” ;
-
•
the six simplices formed by triangles with as one of the nodes.
Two simplices are adjacent if they share an edge. An internal simplex is a simplex that is adjacent to three other simplices, and it is a boundary simplex otherwise. Therefore, the six simplices of the initial patch are all considered boundary since they are adjacent to exactly two others. Similarly, an edge of a simplex can be declared boundary or internal; internal edges are those that are shared with another simplex, and boundary edges are not. A boundary node is any node on a boundary edge, a frontal node is a boundary node on an edge shared by two simplices, and an internal node is a node that is not a boundary node.

Let be a chosen frontal node (see Section 2.2.3 for a general discussion on frontal node selection). By construction, is part of (at least) three distinct edges, two of which connect to boundary nodes, and at least one that connects to an internal node. The algorithm to grow a simplex is as follows. See Figure 3 for a visualization.
-
1.
Compute an orthonormal basis for the tangent space .
-
2.
Compute the (average) gap complement direction. Let denote the list of internal nodes nodes incident to . The gap complement direction is .
-
3.
Let and denote the boundary nodes incident to ; form the edge directions and .
-
4.
Orthogonally project , and onto the tangent plane . Let these projections be denoted , and . Introduce a two-dimensional coordinate system on by way of a “unitary” (see Section 2.2) transformation to . Let , and denote the representatives in .
-
5.
In the local two-dimensional coordinate system, compute the counter-clockwise (positive) angle required to complete a rotation from to , and the counter-clockwise (positive) angle required for rotation from to . The gap angle and orientation is
-
6.
If then close the gap: add the the triangle formed by the nodes to the list of simplices, flag it as a boundary simplex, flag as an internal node, and conclude the growth step. Otherwise, proceed to step 7.
-
7.
Generate the predictor “fan” in : let and define the predictors
for the counterclockwise rotation matrix through angle .
-
8.
Invert the unitary transformation and map into the tangent plane ; let the result be the vectors , .
-
9.
Define predictors for , where is a user-specified step size. Refine them using Newton’s method applied to (9), where and are now the orthonormal basis for .
-
10.
Add the triangles formed by nodes , , , . To the list of simplices, flag them as boundary simplices, and flag as an internal node. Do the same with the triangles formed by and , where denotes ones of and , depending on orientation .

At the end of the simplex growth algorithm, one or more boundary simplices is added to the dictionary, and one additional node will be flagged as internal. The structure of this algorithm ensures that each simplex added to the dictionary will be adjacent to exactly two others, indicating that our convention of internal vs. boundary simplices is effective. Once the growth algorithm is complete, another frontal node is selected and the growth phase is repeated. This continues until a sufficient portion of the manifold has been computed (i.e. a user-specified exit condition is reached), or until a Newton’s method correction fails.
2.2 Comments on implementation
Here we collect some remarks concerning implementation of the finite-dimensional continuation. These comments may be applicable for general continuation problems, but we will often emphasize our specific situation which is continuation of periodic orbits in delay differential equations.
2.2.1 Complex rotations for the kernel of
First, generating the kernel elements of for an approximate must be handled in a way that is appropriate to the space . In our problem, has additional structure: it is a subset of a complexified real vector space equipped with a discrete symmetry. However, in our implementation (that is, in the environment of MATLAB) we work on a generic complex vector space without this symmetry, so when we compute kernel elements using QR decomposition, the computed vectors are not necessarily in . We fix this by performing a complex rotation to put the kernel back into . This can always be done because and , as computed using QR, are always -linearly independent.
2.2.2 Orthonormal basis for the tangent space
The next point concerns the “orthonormal basis” of . Let us be a bit more precise. In our problem, is a product of the form , where is characterized by satisfies , where . Consider the standard inner product on . Once a basis of has been computed, these basis vectors can be interpreted as being elements of , and we say that they are orthogonal if . It is straightforward to verify that the Gram-Schmidt process applied to this basis produces yet another basis of (that is, it does not break the symmetry), and that the new basis is orthonormal with respect to .
2.2.3 Node prioritization for the simplex growth algorithm
A suitable selection of a frontal node for simplex growth might not be obvious. First, nodes that are more re-entrant (i.e. have many edges incident to them) are generally given higher priority. This is because such nodes are more likely to have the simplex growth algorithm perform the close the gap sub-routine. We want to avoid having thin simplices, so prioritizing the closing off of re-entrant nodes takes priority. After this, typically grow from the “oldest” boundary node.
2.2.4 Local coordinate system in for the tangent space
Finally, we must discuss the generation of a two-dimensional coordinate system for . If and are an orthonormal basis for the tangent space, then the map
is invertible, where denotes the conjugate transpose of . Writing for , one can verify that is the unique solution of
In particular, the range of this map is (that is, each of and is real) for our specific problem, where the space is , with having the symmetry described two paragraphs prior. The inverse map is
Moreover, this map is unitary in the sense that for , where on the left-hand side we take the standard inner product on . It is for these reasons that rotations on performed after the action of are consistent with rotations in the tangent space relative to the gap complement direction.
2.3 Continuation in a Banach space
Two-parameter continuation can be introduced generally in a Banach space, but here we take the perspective that of Section 2.1 is a projection of a nonlinear map , and we are actually interested in computing the zeroes of , rather than those of . That is to say, there exist projection operators , , and associated embeddings , , such that .
While the zeroes of are what we want, we will still use the approximate zeroes of to rigorously enclose them. Abstractly, let be the three nodes of a simplex. Then we may introduce a coordinate system on this simplex as follows: write each element of this simplex as a unique linear combination
| (10) |
for . Let for denote an orthonormal basis for the kernel of . We can then form the interpolated kernels
for . We introduce a nonlinear map ,
| (14) |
The objective is to prove that has a unique zero close to for each . If this can be proven, and in fact is for some , then one can prove [10] that the the zero set of is a , two-dimensional manifold. If this same can be proven for a collection of simplices, then the zero set is globally (i.e. on the union of the cobordant simplicial patches) a manifold over all patches that can be proven; that is, the transition maps between patches are .
Remark 1.
There is a subtle point concerning the relative orientations of the individual kernel elements , and that are used to define the interpolation . The validated continuation is unstable (and can even fail outright) if the interpolated kernels vary too much over . If these vectors all lived in the exact same two-dimensional tangent space, this would be very straightforward; we could simply (real) rotate and/or reflect each basis for so that they matched exactly. However, these vectors live in different tangent spaces, so it is not as easy. The more consistent differential-geometric way to solve the problem would be to parallel transport the tangent basis to the other two nodes and use these as bases for the tangent spaces there. We do nothing so sophisticated. We merely perform (real) rotations or reflections of the orthonormal bases in their respective tangent spaces (two-dimensional) for in such a way that, in norm, these are as close as possible to . In practice, this has the effect of promoting enough alignment of the bases that proofs are feasible. We emphasize that this alignment process is only needed for the validated continuation; using misaligned tangent bases is not a problem for the steps described in Section 2.1.
2.4 Validated continuation and the radii polynomial approach
The radii polynomial approach is essentially a Newton-Kantorovich theorem with an approximate derivative, approximate inverse, and domain parametrization. It will be used to connect the approximate zeroes of with exact zeroes of from the previous section. We state it generally for a family of -dependent maps . We include a short proof for completeness.
Theorem 1.
Suppose is differentiable for each , where and are Banach spaces. Let for all . Suppose there exist for each a bounded linear operator , a bounded and injective linear operator , and non-negative reals , , and such that
| (15) | ||||
| (16) | ||||
| (17) | ||||
| (18) |
for all , where is the closed ball of radius centered at , and denotes the induced operator norm on . Suppose there exists such that the radii polynomial
satisfies . Then for each , there is a unique such that . If and are , then the same is true of .
Proof.
Define the Newton-like operator . We will show that is a contraction on , uniformly for . First, write in the form for some . Then
Now, using the triangle inequality and the mean-value inequality,
Choosing , the radii polynomial implies that , so is a self-map on with its range in the interior. Moreover, since , we get that , which proves that is a contraction (uniformly in ). By the Banach fixed point theorem, has a unique fixed point for each , and is provided the same is true of . Since is injective, has a unique zero in if and only if has a unique fixed point there. ∎
For our problem, injectivity of will always follow from a successful verification of . See Lemma 4.
Let be the convex combination defined by (10) for the simplex nodes , and . We will say this simplex has been validated if we successfully find a radius such that the conditions of the radii polynomial theorem are successful for the nonlinear map .
In our implementation, we generate simplices “offline” first. This allows the workload to be distributed across several computers, since the validation step can be restricted to only a subset of the computed simplices. We do not implement a typical refinement procedure, where simplices that fail to validated are split, with more nodes added and corrected with Newton. Rather, we implement an adaptive refinement step, which can help with the validation if failure is primarily a result of interval over-estimation. See Section 4.2.1.
Remark 2.
The operators and have standard interpretations in terms of the nonlinear map . The operator is expected to be an approximation of , which means that is a measure of the quality of the approximation. Conversely, is expected to be an approximation of the inverse of , so that measures the quality of this approximation. Indirectly, acts as an appoximation of .
2.5 Globalizing the manifold
Theorem 1 guarantees that the map from the standard simplex to the zero set of is . There is then a natural question as to the smoothness of the manifold obtained by gluing together the images of the maps. This is answered in the affirmative in [10], and is primarily a consequence of the numerical data being equal on cobordant simplices.
3 Continuation of periodic orbits through (degenerate) Hopf bifurcations
In this section, we construct a nonlinear map whose zeroes will encode periodic solutions of a delay differential equation
| (19) |
for , with some (positive, negative or zero) constant delays , and distinguished systems parameters . We will briefly consider ordinary differential equations in Section 5 as a special case. We assume that is sufficiently smooth to permit further partial derivative computations.
Following [30], we use the desingularization approach to isolate periodic orbits from (potentially) nearby steady states. This approach allows us to put a large distance (in the sense of a suitable Banach space) between steady states and periodic orbits that arise from Hopf bifurcations. This is exposited in Section 3.1, where we also discuss some details concerning non-polynomial nonlinearities.
The next Section 3.2 is devoted to the development of a nonlinear map whose zeroes encode periodic orbits of our delay differential equation. In this map, periodic orbits are isolated from fixed points. We present the map abstractly at the level of a function space, and then with respect to a more concrete sequence space.
In Section 3.3, we lift the map of the previous section into the scope of two-parameter continuation. We develop an abstract template for the map on a relevant Banach space, define an approximate Fréchet derivative near a candidate zero of this map, and investigate some properties of the Newton-like operator. Specifically, we verify that numerical data corresponding to an approximate real periodic orbit, under conditional contraction of the Newton-like operator, will converge to a real periodic orbit.
3.1 Desingularization, polynomial embedding and phase isolation
We begin by doing a “blowup” around the periodic orbit. Write , for a candidate equilibrium point. Then we get the rescaled vector field
The interpretation is that , so that behaves like the relative norm-amplitude of the periodic orbit. The vector field above is provided the original function is and is an equilibrium point; that is, . At this stage we can summarize by saying that our goal is to find a pair such
where is -periodic for an unknown period ; equivalently, the frequency of is .
Remark 3.
It is a common strategy in rigorous numerics, especially for periodic orbits, that time is re-scaled so that the period appears as a parameter in the differential equation. We do not do that here, since this would have the effect of dividing every delay by the period. This causes its own set of problems.
In what follows, it will be beneficial for the vector field to be polynomial. This is because we will make use of a Fourier spectral method, and polynomial nonlinearities in the function space translate directly to convolution-type nonlinearities on the sequence space of Fourier coefficients. While we can make due with non-polynomial nonlinearities, it is greatly simplifies the computer-assisted proof if they are polynomial. To fix this, we generally advocate the use of the polynomial embedding technique. The idea is that many analytic, non-polynomial functions are themselves solutions of polynomial ordinary differential equations. The reader may consult [van den Berg, Groothedde, Lessard] for a brief survey of this idea in the context of delay differential equations. See Section 7.2 for a specific example.
Applying the polynomial embedding procedure always introduces additional scalar differential equations. If we need to introduce extra scalar equations to get a polynomial vector field, this will also introduce natural boundary conditions that fix the initial conditions of the new components. As a consequence, we need to bring in unfolding parameters to balance the system. This is accomplished in a problem-specific way; see [van den Berg, Groothedde, Lessard] for some general guidelines and a discussion for the need of these extra unfolding parameters. By an abuse of notation, we assume is polynomial (that is, the embedding has already been performed), and we write it as
where is a vector representing the unfolding parameter, and we now interpret . We then write the natural boundary condition corresponding to the polynomial embedding as
It can also be useful to eliminate non-polynomial parameter dependence from the vector field, especially if the latter has high-order polynomial terms with respect to the state variable . This can often be accomplished by introducing extra scalar variables. For example, if is
and we want to eliminate the non-polynomial term from the vector field, then we can introduce a new variable and impose the equality constraint . The result is that the vector field becomes
Since this operation introduces new variables and additional constraints, we incorporate the constraints as extra components in the natural boundary condition function of the polynomial embedding. Since this type of operation will introduce an equal number of additional scalar variables and boundary conditions, we will neglect them from the dimension counting.
Remark 4.
If we want to formalize the embedding process for parameters, we can introduce differential equations for them. Indeed, in the example above, we have , and this differential equation can be added to the list of differential equations that result from polynomial embeddings of the original state variable . In this way, we can understand as the total embedding dimension. It should be remarked, however, that in numerical implementation, objects like really are treated as scalar quantities.
The final thing we need to take into account is that every periodic orbit is equivalent to a one-dimensional continuum by way of phase shifts. Since our computer-assisted approach to proving periodic orbits is based on Newton’s method and contraction maps, we need to handle this lack of isolation. This can be done by including a phase condition. In this paper we will make use of an anchor condition; we select a periodic function having the same period as , and we require that
3.2 Zero-finding problem
We are ready to write down a zero-finding problem for our rescaled periodic orbits. First, combining the work of the previous sections, we must simultaneously solve the equations
| (20) |
At this stage, the period of the periodic orbit is implicit. In passing to the spectral representation, we will make it explicit. Define the frequency and expand in Fourier series:
| (21) |
Recall that for a real (as opposed to complex-valued) periodic orbit, will satisfy the symmetry . To substitute (21) into the differential equation in (20), we must examine how time delays transform under Fourier series. Observe
which means that at the level of Fourier coefficients, a delay of corresponds to a complex rotation
| (22) |
Note that this operator is linear on and bounded on . To densify our notation somewhat, we define by
As for the derivative, we make use of the operator . Since is polynomial, subsituting (21) into the first equation of (20) will result in an equation of the form
for a function being a (formal) vector polynomial with respect to Fourier convolution, in the arguments . Observe that we have abused notation and identified the function in (21) with its sequence of Fourier coefficients. As an example, the nonlinearity is transformed in Fourier to the nonlinearity
Now, let be an approximate periodic orbit. We can define new amplitude and phase conditions as functions of and the numerical data ; see [30]. Then, define a map , with , and , by
| (28) |
Let be equipped with the norm
| (29) |
where all Euclidean space norms are selected a priori and could be distinct. That is, we allow for the possibility of a refined weighting111It becomes notationally cubmersome to include references to weights, or to explicitly label the different norms, so we will refrain from doing so unless absolutely necessary. In these cases, footnotes will be used to emphasize any particular subtleties. Weighted max norms can make it easier to obtain computer assisted proofs, especially in continuation problem, which is why we have included this option. of the norms being used. Then is a Banach space, and the same is true for when equipped with an analogous norm, replacing with . If the vector field is twice continuously differentiable, then is continuously differentiable. This is because the polynomial embedding results in polynomial ordinary differential equations, while the blow-up procedure only results in one derivaive being lost. However, is generally not twice continuously differentiable; see later Section 4.3.
It will sometimes be convenient to compute norms on the -projection of . In this case, if and is represented (ismorphically) as , then we define , where any weighting is, again, implicit. Then .
Introduce . Any zero of in the space uniquely corresponds to a real periodic orbit of (19) by way of the Fourier expansion (21) and the blow-up coordinates . Moreover, the restriction of to has range in . Each of and are Banach spaces over the reals, and so from this point on we work with the restriction .
3.3 Finite-dimensional projection
To set up the rigorous numerics and the continuation, we need to define projections of and onto suitable finite-dimensional vector spaces. Let denote the projection operator
and its complementary projector. Consider the finite-dimensional vector space
and extend the projection to a map as follows:
Now define a map
| (30) |
is well-defined and smooth, and we have , where is the natural inclusion map. Therefore, this definition of the projection of is consistent with the abstract set-up of Section 2.3.
3.4 A reformulation of the continuation map
It will be convenient to identify and respectively with isomorphic spaces
There is then the natural embedding of into . The isomorphism of with is given by
is finite-dimensional, and as such our language will sometimes reinforce this by describing matrices whose columns are elements of . This should be understood “up to isomorphism”. The purpose of the isomorphism of with is to symbolically group all of the finite-dimensional objects together.
Given for , let be a matrix whose columns are a basis for the kernel of , and are therefore elements of . For , let and be the usual interpolations of the elements and bases for .
The continuation map of (14) could now be defined for our periodic orbit function . However, it will be convenient in our subsequent discussions concerning the radii polynomial approach to re-interpret the codomain of as being
Specifically, this will make it a bit easier to define an approximate inverse of . The codomain of is
where the isomorphisms can be realized by permuting the relevant components of and splitting the Fourier space into direct sums. For , a suitable isomorphic representation of is given by ,
| (37) | ||||
| (46) |
where , and the for are interpolations
| (47) |
Remark 5.
Strictly speaking, the final two components of are not the “standard” ones from (14). The inner product in the latter results in quadratic terms in , while the ones in (46) are -linear. The impact of this change is that, theoretically, the Newton correction is not strictly in the direction orthogonal to the interpolation of the tangent planes. This change has no theoretical bearing on the validated continuation, and is done only foe ease of computation: it is easier to compute derivatives of linear functions than nonlinear ones.
Remark 6.
We have abused notation somewhat, since now we interpret as a map
It acts trivially with respect to the variable . Also, we emphasize that depends on the numerical interpolants and .
Since Theorem 1 is stated with respect to general Banach spaces, the validated continuation approach applies equally to the representation of . The only thing we need to do is specify a compatible norm on . This is straightforward: for and , a suitable norm is
where the Euclidean norms on the components of are the same222Including any weighting, which we recall is implicit. as the ones appearing in (29). With this choice, is equivalent to the induced max norm on , with equipped with the norm (29) and the -norm.
3.5 Construction of and
Write , for . Denote the three vertices of as , and . Introduce an approximation of as follows:
| (54) |
Formally, approximates in the Fourier tail by neglecting the nonlinear terms, leaving only the part coming from the differentiation operator.
Proposition 2.
has the representation
| (58) |
Proof.
Since does not depend on , the upper-right block of is the zero map. Similarly, does not depend on either or , so the finite-dimensional blocks in the (bottom) row are zero. ∎
The upper left block is equivalent to a finite-dimensional matrix operator. In particular, is real. Also,
is invertible, with
where for . Suppose we can explicitly compute and complex matrices for such that
| (63) |
We can then prove the following lemma.
Lemma 3.
For , define matrix interpolants , and analogously define interpolants , and . Introduce a family of operators as follows:
| (67) |
Suppose for , is real and, as maps, , and are equivalent to
Then is well-defined.
Proof.
One can show is well-defined using the fact that each of , and is a real convex combination of maps to/from appropriate symmetric spaces, and noticing that (and hence its inverse) satisfy the symmetry ∎
The point here is that, due to (63), we have
for , and if the interpolation points are close together, we expect to be invertible for all , and .
Remark 7.
Checking the conditions of Lemma 3 amounts to verifying conjugate symmetries of the matrices , and . Numerical rounding makes this a nontrivial task, so we generally post-process the numerically computed matrices to impose these symmetry conditions.
4 Technical bounds for validated continuation of periodic orbits
Based on the previous section, we define a Newton-like operator
| (68) |
for . As described in Section 2.4, our goal is to prove that is a uniform (for ) contraction in a closed ball centered at using Theorem 1. If can be proven (uniformly in ) injective, this will prove the existence of a unique zero of close to , thereby validating the simplex and proving the smooth patch of our manifold.
In Section 4.1, we will demonstrate how the bound of the radii polynomial approach can be used to obtain a proof of uniform (in ) injectivity of the operator . We then provide some detailed discussion concerning general-purpose implementation of the bounds and in Section 4.2 through to Section 4.5.
4.1 Injectivity of
The injectivity of is a consequence of the successful identification of bounds of Theorem 1 and the negativity of the radii polynomial. In particular,
Lemma 4.
Suppose for all , with the operators and of Section 3.5. If , then is injective for .
Proof.
First, observe has non-trivial kernel if and only if there exists such that . This is a consequence of the structure of the operator and injectivity of . Therefore, it suffices to verify the injectivity of the restriction . Define . By definition of the norm on , we have for all . By Neumann series, it follows that is boundedly invertible, which implies is surjective. Since is finite-dimensional, is also injective. ∎
Corollary 5.
If the radii polynomial satisfies for some , then is injective for .
4.2 The bound
To begin, expand the product . We get
Remark that has range in a finite-dimensional subspace of ; specifically, it will be in the part of such that the components in with index (in absolute value) greater than are zero, where is the maximum degree of the (convolution) polynomial . As such, is explicitly computable.
In practice, we must compute an enclosure of the norm for all . This is slightly less trivial. We accomplish this using a first-order Taylor expansion with remainder. For the function , denote by the Fréchet derivative with respect to , and the derivative with respect to . Given the interpolants and , let and denote their Fréchet derivatives with respect to . Also, denote , for defined in (47). Note that these derivatives are constant, since the interpolants are linear in . Then
where the remainder term will be elaborated upon momentarily. The product of the linear-order terms with results in a function that is componentwise quadratic in , for which we can efficiently compute an upper bound on the norm. The derivative is implementable, and will be further discussed in Section 4.3. As for the term,
where and .
As for the remainder , it is bounded by the norm of the second Fréchet derivative of , uniformly over . For each , let this second derivative be denoted . Then
| (69) | ||||
where and denote the first and second (factor) projection maps on . The derivative will be discussed in Section 4.3. At this stage, we need only mention that it acts bilinearly on , and the latter is proportional in norm to the step size of the continuation scheme, so the term will be order . As for the derivatives involving , most of the components are zero as evidenced by the previous calculation of , and it suffices to compute the relevant derivatives of . We have
with , . In terms of the step size, is order , while is order . However, in (69), the latter term is multiplied by . Therefore, as expected, the remainder is quadratic with respect to step size. We therefore compute
Since , the bound can be tempered quadratically by reducing the step size. The caveat is that if and/or has large quadratic terms, it might still be necessary to take small steps.
Remark 8.
Directly computing the norm would require a general-purpose implementation of the second derivative ; see (69). As we have stated previously, such an implementation would be rather complicated. Therefore, in practice, we perform another level of splitting; namely, we use the bound
The first term on the right of the inequality is explicitly implementable using only the derivatives of and the finite blocks of . For the second term, we use the bound which, while not optimal, is implementable and good enough for our purposes.
4.2.1 Adaptive refinement
In continuation, the size of the bound is severely limited by the step size. To distribute computations, we often want to compute the manifold first and then validate patches a posteriori. However, once the manifold has been computed, adjusting and re-computing patches of the manifold with smaller step sizes becomes complicated due to the need to ensure that cobordant simplices have matched data, as discussed in Section 2.5. When the bound is too large due to interval arithmetic over-estimation, we can circumvent this by using adaptive refinement on the relevant simplex. Formally, we subdivide the simplex into four, using the interpolated zeroes at the nodes of the original simplex to define the data at the nodes of the four new ones. The result is that cobordant data still matches, allowing for globalization of the manifold. The advantage of this approach is that it can be safely done in a distributed manner; adaptively refining one simplex does not require re-validating any of its neighbours.
4.2.2 The bound
The product is block diagonal. Indeed, , whereas
Therefore, to compute it suffices to find an upper bound, uniformly in , for the norm of the above expression as a linear map from . Interpreted as matrix operators, , , and are interpolants of other explicit matrices. However, the derivatives , while evaluated at interpolants, are themselves “nonlinear” in .
Remark 9.
The implementation of is influenced by the way in which the dependence on is handled. For example, can be treated as a vector interval and the norm can be computed “in one step” using interval arithmeic, then we take the interval supremum to get a bound. This can result in some wrapping (over-estimation). One way to control the wrapping is to cover in a mesh of balls, compute the norm for replaced with each of these interval balls, and take the maximum. Still another way is to carefully compute a Taylor expansion with respect to , although this task has a few technical issues due to the fact that is generally only . We therefore only consider the “in one step” approach in our implementation.
4.3 A detour: derivatives of convolution-type delay polynomials
In our implementation of the and bounds, we will need to represent various partial derivatives of the map , where . This can quickly become notationally cumbersome. Therefore, in this section we will elaborate on the structure of the derivatives of convolution terms of the following -valued map:
| (70) |
for and . That is . Here, denotes the frequency component of . In this section, will be indexed with the convention , where for . The objects (70) can be interpreted as individual terms of through , which each have codomain . The product symbol indicates iterated convolution, while . Here, is the (polynomial power) order of the term, the indices specify which factors of are involved in the multiplication, while indicates which delays are associated to each of them. Finally, there is a multi-index for multi-index power . Importantly, the multi-index is trivial in the frequency () component, and the latter only enters in the form of the delay mapping . The following lemma can then be proven by means of some rather tedious bookkeeping and the commutativity of the convolution product.
Lemma 6.
If , then for and ,
Also, . If is band-limited, exists and
Finally, if and , then
Remark 10.
The requirement that be band-limited really is necessary for the existence of . Indeed, if , then but is not, and the latter terms appear in the second derivative. This is precisely why is not twice differentiable.
4.4 The bound
To have a hope at deriving a bound, we will first determine the structure of the operator . Represented as an “infinite block matrix”, most blocks are zero. One can verify that
| (74) |
with the individual terms being the operators
and once again denoting the frequency component projection. Computing requires precomposing (74) with , which has the structure (67).
4.4.1 Virtual padding
For with , denote
| (75) |
Computing is equivalent to a uniform (in ) bound for . The tightness of this bound is determined by two levels of computation:
-
•
some finite norm computations that are done on the computer;
-
•
theoretical bounds, which are inversely proportional to the dimension of the object on which the finite norm computations are done.
By default, the size of the finite computation is linear in , the number of modes. This might suggest that explicitly increasing – that is, padding our solution with extra zeros and re-computing everything with more modes – is the only way to improve the bounds. Thankfully, this is not the case.
Intuitively, is an “infinite matrix”, for which we have a canonical numerical center determined by the pre- and post- composition with the projection operator onto . This is determined by the number of modes we have specified in our numerical zero. However, there is no reason to only compute this much of the infinite matrix explicitly; we could instead choose and compute the representation of this operator on . The result is that a larger portion of is stored in the computer’s memory. The advantage of doing this is that the explicit computations of norms are generally much tighter than theoretically guaranteed estimates, while the theoretical bounds related to the tail will be proportional to . See Figure 4 for a visual representation.

To exploit these observations, we decompose (and hence the symmetric subspace) as a direct sum
where , and is now interpreted as the complementary projector to . In the subsections that follow, will be the virtual padding dimension. We therefore re-interpret and as being in the product space
which remains (isometrically) isomorphic to . Remark that the finite blocks and coming from must now be re-interpreted as linear maps involving , as appropriate. Similarly, the blocks can be replaced by
In our implementation, this virtual padding is implemented automatically on an as-needed basis.
4.4.2 Some notation
Let be defined according to
Let denote the interval sequence
where is the unit interval vector333Subject to any weighting of norms; that is, the components of should be scaled so that its norm is equal to 1 in . in . Let denote the unit interval vector444In case the euclidean norms associated to the scalar variables are not homogeneous and different weighting is used, each component of should be scaled so that the norm of is equal to 1 in the induced max norm. in . Finally, we will occasionally require the use of
for . Also, given , define by , and for . By construction, .
4.4.3 The norm
In this section, the norm on is identified with .
Lemma 7.
Let be a convolution polynomial of degree . Let555The absolute value of is precisely the weight attributed to the frequency component, relative to the absolute value norm on . . Then
where the finitely-supported interval sequences are defined according to
Proof.
Explicitly, the sum is
Since is a convolution polynomial of degree , we have for all whenever . It follows that the support of is contained in the range of . Restricting to the range of ,
Next, the range of is contained in that of (recall that while we have used a different padding dimension for the computation of norms, our data is still band-limited to modes). We have
Using these bounds/inclusions, the fact that is supported on the zeroth Fourier index, and the properties of the map , we get
Combining the previous bounds, we get the result claimed in the lemma. ∎
Remark 11.
While perhaps symbolically intimidating, all of the quantities appearing in the statement of Lemma 7 are explicitly machine-computable, so a rigorous uniform (in and ) bound for can indeed be computed.
4.4.4 The norm
In this section, the norm on is identified with . The bound for bears a lot of similarity to the one for , and its derivation is similar. We omit the proof of the following lemma.
Lemma 8.
With the same notation as in Lemma 7, we have the bound
4.4.5 Summary of the bound
Combining the results of Lemma 7 and Lemma 8, it follows that if we choose such that
for all , then will satisfy the bound (17) for our validated continuation problem. In the above bound, one must remember that the norms are actually restrictions of the norm to various subspaces; see the preamble before Lemma 7 and Lemma 8.
4.5 The bound
It is beneficial to perform a further splitting of the expression that defines the bound. Recall that should satisfy
| (76) |
uniformly for and . From Remark 10, is not itself differentiable, so appealing to a “typical” second derivative estimate for this bound is not going to work. To handle this, we use the strategy of [28] and split the norm to be computed using a triangle inequality. Given , split it as , where the components of are all zero except for the frequency component, , and has zero for its frequency component. This decomposition is uniquely defined. Then, consider two new bounds to be computed:
uniformly for and . If we define , then (76) will be satisfied. It turns out that this decomposition is effective. We will elaborate on this now.
4.5.1 The bound
The partial derivative exists and is continuous. This is a consequence of Lemma 6 (n.b. the inputs are band-limited) and the structure of ; see (37). As is bounded, we can use the fundamental theorem of calculus (in Banach space) to obtain
| (77) |
for any , . Due to the structure of , the derivative term in the large parentheses will have
-
•
in the components: convolution polynomials of the form (70) involving Fourier components coming from the set
with coefficients in ;
-
•
in the scalar components: finite-dimensional range functions of and .
To obtain the tightest possible upper bound for (77), one would want to exploit as much structure of (and the directional derivative in the frequency direction) as possible. However, to get a general-purpose implementable bound, we can apply the following operations to .
-
1.
Replace all instances of with the interval ;
-
2.
replace the component of in with the unit interval vector666Note that the components of this “unit” interval vector might be uneven due to weighting. in ;
-
3.
replace all other variables777Note that if the norm on associated to is itself weighted, this must be taken into account. described in the bulleted list above with bounds for their norms, multiplied by the zero-supported basis element of the relevant space (e.g. for elements, the identity of the Banach algebra; for , the vectorized version of ), multiplied by the interval ;
-
4.
compute operator norms of the blocks of in (67);
-
5.
complete block multiplications, taking the norm of the result, followed by an interval supremum (note, is also replaced by an interval).
We emphasize in the algorithm above, every object is a finite-dimensional quantity, so operations can indeed be performed in a suitable complex vector space on the computer. This strategy produces a true bound for (77) largely because of the Banach algebra and the interval arithmetic. For example, consider the impact of this computation on the quantity
in . From the Banach algebra, if , then a triangle inequality produces
where , , , and is the identity element in the Banach algebra . Now, define and compare the result to
The support of this sequence is the zeroth index, and we can explicitly compute the resulting interval. It is precisely . The supremum of this interval is , which matches the analytical triangle inequality / Banach algebra bound computed previously.
Remark 12.
The bound obtained by applying the strategy above is incredibly crude; in effect, we use the triangle inequality for everything. However, producing fully general code to compute the second derivatives for this class of problems (polynomial delay differential equations with arbitrary numbers of delays) would be a messy programming task. Even with the present implementation, where we need only compute second derivatives evaluated at sequences that are supported on the zeroth Fourier mode, the implementation was far from trivial. Long term, it would be beneficial to implement second derivatives, as this would also allow for improvements to the bound; see Section 4.2. The good news is that, theoretically, the computed bound will be for small enough, due to the linear multiplication of appearing in (77).
4.5.2 The bound
Let denote the Gateaux derivative of in the direction . We claim
exists and is continuous for . To see why, observe that that is continuously differentiable, so we need only worry about the part in , namely the components and that come from the vector field. The result now follows from Lemma 6. Indeed, a band-limited input is only required for the double derivative with respect to the frequency variable, and has zero for its frequency component. By the fundamental theorem of calculus,
| (78) |
where we take , .
To bound (78), we make use of a very similar strategy to the one from Section 4.5.1 for . The difference here is that the convolution polynomials in the part of the Gateaux derivative have a more difficult structure. The main problem is in the mixed derivatives with respect to frequency and Fourier space; see the derivatives in Lemma 6. These derivatives involve the action of the derivative operator on the sequence part of , which is not necessarily band-limited. If for , and this sequence is not band-limited, then generally will not have a finite -norm. To combat this problem, we remark that only one such term can appear in any given convolution polynomial. This can be exploited as follows.
To begin, we factor as follows.
Note that is obtained from by multiplying (on the right) the first “column” by , and the last “column” by . The following lemma is a specific case of a lemma of van den Berg, Groothedde and Lessard [28].
Lemma 9.
Define an operator on . Let . Then
Now consider the product . The part in of the Gateaux derivative will be multiplied by the diagonal operator . So consider how we might bound a term of the form
| (79) |
in a given convolution polynomial that contains a factor , for and . Here, is a scalar that could depend on , the scalar components of , and the delays, while is the part of in . Note that by permutation invariance of the convolution, we may assume that appears as the first term on the left, as we have done here. By Lemma 9, the above is bounded above by
We can achieve the same effect by replacing in (79) with , for being the identity in the convolution algebra, and taking the -norm. When is multiplied by a polynomial term that does not contain a factor , then a straightforward calculation shows that . The net result is that the impact on the norm of the polynomial term is a scaling by . Therefore, adapting the algorithm from the bound calculation, it suffices to do perform the following operations to .
-
1.
Multiply the part of in by ;
-
2.
replace all instances of with the interval ;
-
3.
replace all (remaining) instances of with ;
-
4.
replace the component of in with the unit interval vector888Note that the components of this “unit” interval vector might be uneven due to weighting. in ;
-
5.
replace all other variables (, , , , the part of in , and their relevant projections999See footnote 7 concerning the projections of in .) with bounds for their norms, multiplied by the zero-supported basis element of the relevant space, multiplied by the interval ;
-
6.
compute operator norms of the blocks of ;
-
7.
complete block multiplication of on the left, take the -norm of the result, followed by an interval supremum (note: is also replaced by an interval).
The result is a (crude) upper bound of for . This bound is expected to be for small, since the Gateaux derivative is for small.
Remark 13.
In step 3, the variable replacement negates (by multilinearity of the convolution) the multiplication of the relevant polynomial term by that was done in step 1, while propagating forward the correct bound that results from the interaction between and the polynomial term. This somewhat roundabout way of introducing the bound in the correct locations is done in order to make the process implementable in generality.
5 Specification to ordinary differential equations
In Section 3, we demonstrated how rigorous two-parameter continuation of periodic orbits in delay differential equations can be accomplished in such a way that the continuation can pass through degenerate Hopf bifurcations. As ordinary differential equations are a special case – that is, where any delays are identically zero – the theory of the previous sections naturally applies equally to them. However, the formulation of the map (28) can be greatly simplified. Indeed, the reader familiar with numerical methods for periodic orbits has likely noticed that we have not performed the “usual” scaling out by the frequency, so that the period can be abstractly considered as . With delay differential equations, this is not beneficial because it merely moves the frequency dependence into the delayed variables. Additionally, it is the presence of the delays that requires a more subtle analysis of the bound; see Section 4.5.
To compare, with ordinary differential equations without delays, the technicalities with the bound are absent. At the level of implementation, computing second and even third derivatives of the vector field in the Fourier representation is also much easier. In this section, we will present an alternative version of the zero-finding problem of Section 3.2 and analogous map from (28). However, we will not discuss the general implementation of the technical bounds and , since they are both simpler than the ones we have previously presented for the delay differential equations case, and can be obtained by fairly minor modifications of the bounds from [30]. We have implemented them in general in the codes at [4].
5.1 Desingularization, polynomial embedding and phase isolation
The set-up now starts with an ordinary differential equation
| (80) |
again depending on two real parameters and . Performing the same blowup procecure as we did for the delay equations, we define
The goal is therefore to find a pair such that
where is -periodic for an unknown period ; equivalently, the frequency of is . Let denote the reciprocal frequency. Define . Then is -periodic. Substituting this into the differential equation above and dropping the tildes, we obtain the modified vector field
where now the scope is that should be -periodic.
If a polynomial embedding is necessary to eliminate non-polynomial nonlinearities, we allow the inclusion of additional scalar equations that must be simultaneously solved, where we introduce an appropriate number of unfolding parameters, , to balance them. We again use the symbol to function that defines these boundary conditions, with the equation being . We use the same anchor condition to handle the lack of isolation from phase shifts.
5.2 Zero-finding problem
Abusing notation and assuming now that is polynomial after the embedding has been taken into account, the zero-finding problem is
| (81) |
where is understood to be a candidate numerical solution. Expanding as a Fourier series with period , we have for some complex vectors obeying the symmetry . If we now allow to be the representation of as a convolution polynomial in the coefficients , then an analogous derivativation to the delay differential equations case produces the map
defined on the same Banach spaces, with the same codomain. However, this time, one can show that if is , then really is .
6 Proving bifurcations and bubbles
Modulo non-resonance conditions, we would generically expect Hopf bifurcations to occur on the level curve at amplitude zero of the computed 2-manifolds of Section 3. Hopf bubbles are equivalent to curves in the manifold that intersect the amplitude zero surface at two distinct points. As for bubble bifurcations, we can describe these in terms of a the existence of a relative local minimum of a projection of the computed 2-manifold, represented as the graph over amplitude and a distinguished parameter. We develop these points in this section, demonstrating how post-processing of data from the computer-assisted proofs can be used to prove the existence of Hopf bifurcations, bubbles, and degenerate bifurcations.
We should emphasize that to prove the existence of a single Hopf bubble, it suffices to identify a curve connecting two points at amplitude zero in the projection of the proven manifold in space, for one of or being fixed. While this does require verifying two Hopf bifurcations, the rest of the proof of an isolated bubble is fairly trivial, requiring only determining a sequence of simplices that enclose the curve. Therefore, we will only discuss how to prove bubble bifurcations in this section, since this can require a bit more analysis. We will not analyze Bautin bifurcations.
To simplify the presentation, we will assume throughout this section that the norm on is such that . That is, the amplitude component is unit weighted relative to the absolute value.
6.1 Hopf bifurcation curves
In delay differential equations, the sufficient conditions for the existence of a Hopf bifurcation include the non-resonance check, which involves counting all eigenvalues all eigenvalues of the lienarization on the imaginary axis. This is somewhat beyond the scope of our work here, although there is literature on how this can be done using computer-assisted proofs [5, 24]. In this paper, we will consider the following related notion.
Definition 1.
The delay differential equation (3) has a Hopf bifurcation curve if there exists a parametrization such that is a steady state solution and is a periodic orbit at parameters , such that:
-
•
and are on the boundary of , and is in the interior of for .
-
•
; in other words, is a steady state on restriction to the image of .
-
•
For , is not a steady state.
Contrary to the usual Hopf bifurcation, we do not reference the direction of the bifurcation, even along one-dimensional curves in the manifold of periodic orbits.
The existence of a Hopf bifurcation curve can be proven using post-processing of a validated contiuation on given simplex on which one expects a Hopf bifurcation to occur. The idea is that on a simplex that encloses a Hopf bifurcation, the amplitude in the blown-up variables (see Section 3.1) is expected to cross through zero. Since we are working in two-parameter continuation, such a crossing point should persist as a curve. A geometric construction based on the partial derivatives of the amplitude with respect to the simplex paramaterization can be used to construct this curve. See Figure 5 for a visualization.
To establish a more constructive proof, we need to introduce a few projection maps. Let , . Denote the projection to the amplitude component, and the projection onto the parameters. Similarly, write . Denote the three vertices of the standard simplex as , and .

Proposition 10.
Suppose a simplex containing the interpolated numerical data has been validated, for Let be an associated validation radius from the radii polynomial. Let . Suppose the following are satisfied.
-
•
For ,
where the multiplication is in the sense of interval arithmetic.
-
•
The sign of the interval is constant for on the edge of not incident with ; that is, on the edge connecting with .
-
•
Let denote the Fréchet derivative operator with respect to the variable . For , define
(82) where . That is, is a real interval and is an inteval in . Let . The components of have the same sign for .
Then there is a unique (up to parameterizaztion) Hopf bifurcation curve , and each of and lie on the edges of that are incident with .
Proof.
Suppose the radii polynomial proves the existence of such that . The parametrization of the steady state (), periodic orbit () and amplitude parametrization is a consequence of the computer-assisted proof. exists, and . We claim is boundedly invertible for . First,
whose norm is bounded above by . Since the radii polynomial has validated , it follows that . By the Neumann series, is boundedly invertible, with norm bounded by . Since is boundedly invertible by its construction, the same is true of .
It follows that . Observe that
By previous estimates, the above is bounded in norm by . Since — see Section 4.2 — we have
| (83) |
Note that is precisely the amplitude component of .
Consider the line , where is any point on the edge connecting to in . Consider the function . By the assumptions of the proposition and the inclusion (83), we have and for . By the mean-value theorem, there is a unique such that . Moreover, depends continuously on . Letting be a parametrization of the edge connecting to , it follows by the definition of the map that is a Hopf bifurcation curve. ∎
Remark 14.
Proposition 10 is stated in such a way that we assume and the edge connecting to lie on the opposite sides of Hopf curve . This is done almost without loss of generality. First, if the Hopf curve should bisect the simplex in such a way that or is separated from its opposing edge, a suitable re-labeling of the nodes transforms the problem into the form of the proposition. Second, a problem can arise if the Hopf curve intersects one of the vertices , . Similarly, numerical difficulties can arise with the method of computer-assisted proof if the intersections of with the edges of occur very close to the vertices. These problems can be alleviated by a careful selection of numerical data.
Remark 15.
We emphasize that most of the sufficient conditions of Proposition 10 can be checked using the output of the validation of a simplex. We also mention specifically that in the second point, the sign of need only be verified to match at and , due to linearity of . The exception is the computation of and . The former is a finite computation, and the latter can be bounded in a straightforward manner; see Section 4.2 for details concerning the structure of .
Remark 16.
A Hopf bifurcation curve necessarily generates continua of Hopf bifurcations. These can be constructed by selecting curves in that are transversal to .
6.2 Degenerate Hopf bifurcations
In this section, we consider how one might prove the existence of a degenerate Hopf bifurcation, be it a bubble bifurcation or otherwise. For a first definition, we consider the bubble bifurcation.
Definition 2.
A bubble bifurcation (with quadratic fold) occurs at in (19) if there exists a Hopf curve with for some , such that
-
•
the projection of into the plane can be realized as a graph .
-
•
, , and .
-
•
there is a diffeomorphism defined on a neighbourhood of , such that , and the periodic orbit (see Definition 1) is a steady state if and only if , where is the projection onto the second factor. Also, the projection onto the first factor satisfies for all .
-
•
is a strict local extremum of the map .
Our perspective is that a bubble bifurcation is characterized by the existence of a manifold of periodic orbits, parameterized in terms of amplitude and a parameter, such that at an isolated critical point, the projection of the manifold onto the other parameter has a local extremum. The parametrization of near and the local minimum condition reflects the observation that a fold in the curve of Hopf bifurcations is sufficient condition for the birth of the bubble. That is, we have a family of bubbles (loops of Hopf bifurcations) that can be parameterized by in an interval of the form or , for small. This is a consequence of the -parametrization of the simplex.
Remark 17.
We include the adjective “quadratic” to describe the fold in the Hopf curve to contrast with a related definition in Section 6.2.3, where the condition will be weakened.
6.2.1 Preparations
It will facilitate the presentation of the bubble bifurcation if we are able to construct the first and second derivatives of , the zeroes of (37), with respect to the simplex parameter . This was partially done in the proof of Proposition 10, but we will elaborate further here.
To compute the derivatives, the idea is to formally differentiate with respect to twice, allowing for the introduction of and . The result is a system of three nonlinear equations, and solving for amounts to computing zeroes of a map
| (84) |
Remark 18.
It may be unclear whether the second derivative of can be given meaning. Indeed, as we have previously explained in Remark 10, the second Fréchet derivative of does not, in general, exist. The (formal) second derivative of both sides of produces
and we can see that it is in fact possible to interpret as the Gateaux derivative of , at and in the direction . However, even this may not exist as an element of , since the Fourier components of are generally not band-limited. It is therefore necessary to specify the codomain of (84) a bit more carefully. We will not elaborate on this subtlety here; the ramifications of this will be the topic of some of our future work. However, in the case of ordinary differential equations, there is no major complication. When there are no delays (or when they are all zero), is twice continuously differentiable provided the same is true of .
Regardless how the partial derivatives are enclosed, the following equivalent version of Proposition 10 is available.
Proposition 11.
Assume the existence of a family of zeroes of (84) parameterized by and close to a numerical interpolant has been proven, in the sense that we have identified such that there is a unique zero of (84), for each , in the ball . Assume the topolgy on this ball is such that the components satisfy
for , and . Suppose
-
•
For , , where the multiplication is in the sense of interval arithmetic.
-
•
The sign of is constant for on the edge of not incident with ; that is, on the edge connecting to .
-
•
The components of the interval vector in has the same sign for .
Then there exists a Hopf bifurcation curve , each of and lie on the edges of that are incident with , and is .
Comments analogous to those appearing in Remark 14 apply here as well. Note that Proposition 11 requires only the first derivatives, which can be enclosed using (83). However, if the existence of the second derivatives are in question, then can at best be proven to be .
Definition 3.
A triple of line segments in is -oriented if there exist points on the edge , such that
-
•
is a subset of the line connecting to ;
-
•
is a subset of the line connecting to ;
-
•
is a subset of the line connecting to ;
-
•
under the total order on the edge defined by , we have .
In this case the associated wedge cover is the simplex in with vertices and , and it is denoted .
These -oriented line segments will be used to enclose potential bubble bifurcation points. Some finer control can be specified with the following.
Definition 4.
Let be an -oriented triple in . Let be a Hopf curve in associated to a family of zeroes of . A Hopf-bounding trapezoid in is a trapezoid contained in whose edges include both and , and such that the other edges, denoted and , satisfy for , and for .
It is straightforward to verify that, under the assumptions of Proposition 11 , a trapezoid in is Hopf-bounding provided two of its edges match and , while
6.2.2 Enclosure of a bubble bifurcation
The following proposition provides verifiable conditions for the existence of a bubble bifurcation. Some are more explicit than others.
Proposition 12.
Let the hypotheses of Proposition 11 be satisfied. Let be an -oriented triple of line segments in . Suppose the topology on is such that the components , , satisfy
for -tuples , and . With the empty tuple (), the norm reduces to absolute value on . Let , for be interval vectors in such that , for . Finally, given , denote by the set
Suppose the following are satisfied.
-
1.
is bounded away from zero, for all and all .
-
2.
for .
-
3.
.
-
4.
for .
-
5.
The components of are bounded away from zero for all .
-
6.
The determinant of the interval matrix
(87) is bounded away from zero for .
-
7.
Defining
(88) it holds that the interval is bounded away from zero for all and .
-
8.
The matrix
(91) is uniformly (for ) definite, where defining by , the partial derivatives in the matrix above are
Then, there exists a bubble bifurcation with quadratic fold at some in the projection of onto the plane.
Proof.
By a suitable reparametrization, we may assume that for all . Denote . The definition of the Hopf curve is that or all . As consequence, , so that is dual to the orthogonal complement of . That is, . Now,
which is bounded away from zero by assumption (condition 1 of the proposition). It follows that is monotone, so can be parameterized by , for in the monotone range of . Consequently, the projection of the Hopf curve in the plane can be represented as a graph .
Conditions 2–4 of the proposition guarantee that each of the segments , and enjoy the following properties:
-
•
as one-dimensional manifolds, they enclose an intersection with the Hopf curve;
-
•
the -components of and are strictly greater than those of .
As consequence, possesses an internal (to its domain, relative to the previously-computed range) critical point which is a global minimizer. Let this point be , so . Let the associated point on the simplex be .
We wish to show that is a strict, isolated minimum of . We will do that by proving . It is enough to prove that whenever . If the latter is satisfied, then we have simultaneously
Since , it must be the case that and are colinear. By assumption 5, is bounded away from zero, so the quantity of (88) is well-defined and
| (92) |
On its own, (92) might not seem particular useful. However, consider that
where the second equation comes from taking a second derivative of the definition of the Hopf curve. Using the second equation together with (92), we can get the inclusion
thereby removing the dependence on the second derivative of the Hopf curve. Substituting into the expression for the second derivative of , we get
which is bounded away from zero by condition 7. Therefore, .
Next, we need to verify the local parametrization of the simplex near in terms of . This is a fairly direct consequence of the inverse function theorem, using the condition 6 of the proposition. This shows that the function defined in condition 8 of the proposition defines a local diffeomorphism near . The Hessian of can be computed by implicit differentiation; if , then the Hessian is precisely the matrix of condition 8. Since this matrix is uniformly definite on the simplex , every critical point must be a local extremum. We already know that . The other partial derivative is zero due to the amplitude symmetry of periodic orbits. Therefore, is a strict local extremum of the map . ∎
Remark 19.
Checking conditions 2–6 of the proposition is fairly routine. Conditions 1 and 7, however, deserve some extra attention. If the step size is small, we should expect the derivatives of the solution to be close to constant. In this way, the set should not vary too much (in a Hausdorff sense). geometrically consists of two arcs on the unit circle, and we expect the angles defining these arcs to be nearly constant over the simplex. Consequently, the interval computations of conditions 1 and 7 are, indeed, implementable, but the feasibility of the checks — that these intervals are bounded away from zero — will be strongly influenced by the size of the radius, , and any weighting in the norm. As for condition 8, we have not included all of the associated radii, but since all of the intermediary derivatives appearing in the matrix (91) admit (by assumption) rigorous enclosures, the matrix is implementable. Therefore, condition 8 can be checked using a suitable package to compute eigenvalues of interval matrices.
Remark 20.
Condition 4 is formulated in such a way that is a local minimum of the curve . This condition can be reformulated in a straightforward way to allow it instead to be a local maximum. Also, comments analogous to those appearing in Remark 14 apply here as well.
Corollary 13.
It suffices to verify the conditions 6,7,8 of Proposition 12 for all in a given Hopf-bounding trapezoid in .
6.2.3 A degenerate Hopf bifurcation without second derivatives
In Remark 18, we pointed out that, unfortunately, the lack of second-differentiability of the map is a serious obstruction to computing second derivatives and, consequently, checking all the conditions of Proposition 12. While it is not a problem when all of the delays are zero (i.e. an ODE), we would like to provide a constructive result for delay equations. Along these lines, let us slightly weaken Definition 2.
Definition 5.
A degenerate Hopf bifurcation occurs at in (19) if there exists a Hopf curve with for some , such that
-
•
the projection of into the plane can be realized as a graph ;
-
•
and ;
-
•
there is a diffeomorphism defined on a neighbourhood of , such that , and the periodic orbit (see Definition 1) is a steady state if and only if , where is the projection onto the second factor. Also, the projection onto the first factor satisfies and for all .
The main difference between the above and Definition 2 is we no longer require that is an extremum of . We also do not make any specifications concerning the geometry of the implicit map near the Hopf bifurcation curve. Clearly, a bubble bifurcation with quadratic fold satisfies the conditions of the above definition. However, the new definition permits other types of degenerate Hopf bifurcations, including Bautin bifurcations. The following proposition can now be proven using the same ideas as Proposition 12.
Proposition 14.
Assume a family of zeroes of the map has been proven, in addition to the first derivatives , close to a numerical interpolant , in the sense that we have identified such that there is a unique zero of (84), for each , in the ball . Suppose the topology on is such that the components , , satisfy
for -tuples , and . With the empty tuple (), the norm reduces to absolute value on . Let be an -oriented triple of line segments in . Suppose conditions 1–3, 5 and 6 of Proposition 12 are satisfied. Then, there exists a degenerate Hopf bifurcation at some in the projection of onto the plane.
Corollary 15.
It suffices to verify condition 6 of Proposition 14 for all in a Hopf-bounding trapezoid in .
7 Examples
7.1 Extended Lorenz-84 system
The extended Lorenz-84 system is the following system of four coupled ODEs:
We consider the parameters , , , , to be fixed, while and are treated as parameters.
We started the continuation at , close to a Hopf bifurcation. Using a step size of , we generated an approximate triangulation of the manifold with 11928 simplices (including simplices created by adaptive refinement needed for proofs). We used Fourier modes. To capture a “wider” section of the manifold, we restricted the simplex growth to amplitude in the interval . Figure 6 is a plot of the triangulation, projected into amplitude and parameter space, while we restricted to the zero amplitude plane in Figure 7 to generate a plot of the Hopf bifurcation curve. The former figure allows for visualization of the traditional square-root amplitude curvature near the Hopf bifurcation curve. Interesting, far from the bifurcation curve, there appears to be a near-circular “hole” in the manifold. We have not studied its structure in detail, and have no insight into its significance. The restriction of the amplitude to results in the top and bottom edges appearing “ragged”, since simplices can not organically grow to produce hexagon patches. The latter Figure 7 indicates the presence of three bubble bifurcations.

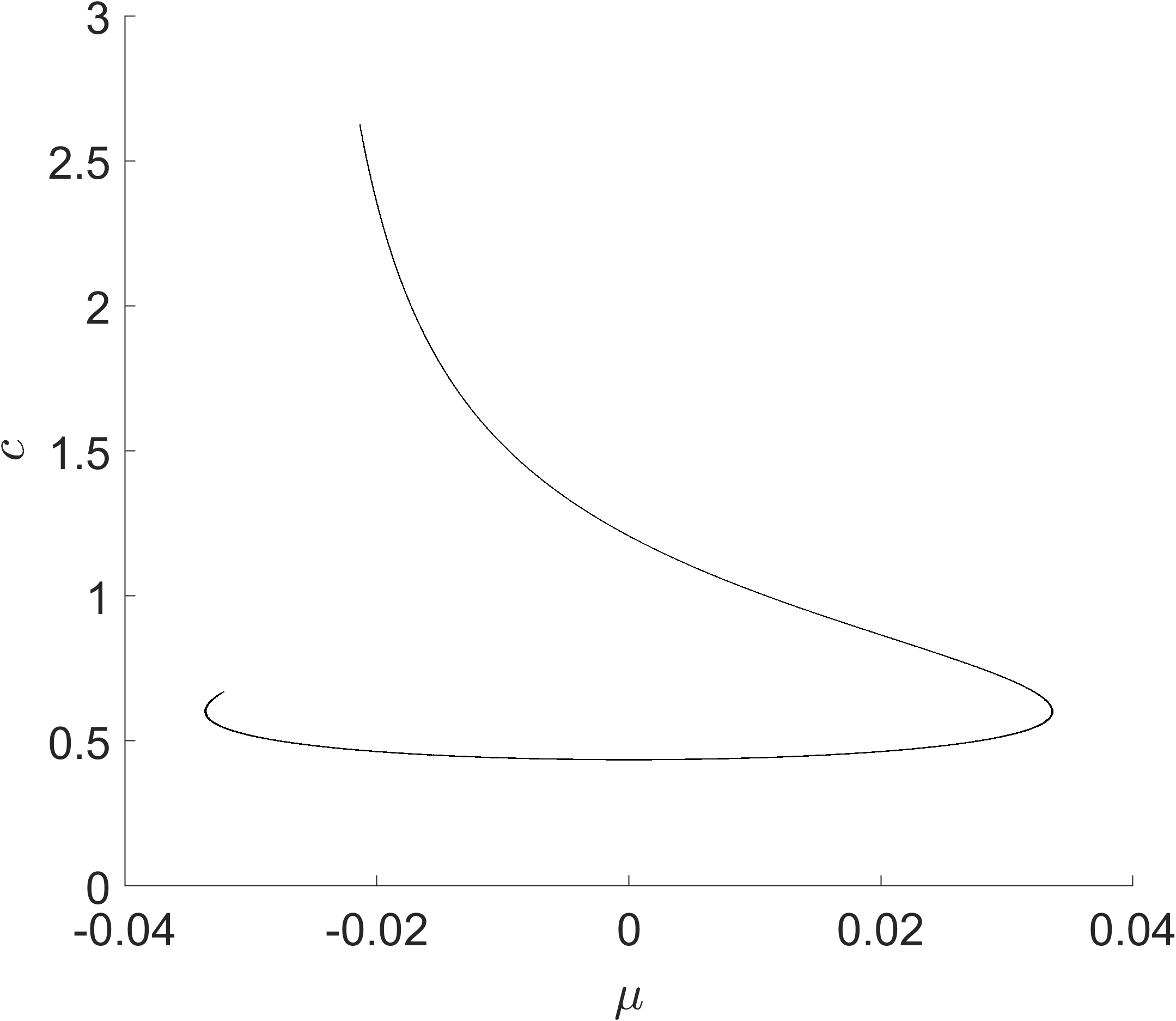
7.2 Time-delay SI model
We consider the time-delay SI model
for which there is an analytical proof of a bubble bifurcation [17] near , for delay . We will replicate this analysis using our rigorous two-parameter continuation.
7.2.1 Set-up
We begin by desingularizing the vector field. Writing , for being a steady state, we get, dropping the tilde,
where , and is defined by
Observe, and
is indeed analytic. Whenever (or its derivatives) must be rigorously evaluated, we construct Taylor polynomials of sufficiently high order and propagate error from the remainder accordingly.
Now we polynomialize. Define and . Then
They can be more compactly written as and . We also have the implied boundary conditions
where . We need two unfolding parameters to compensate for the two extra boundary conditions.
Lemma 16.
If is a periodic solution of
for some , and satisfies and , then .
Proof.
First, suppose . Then necessarily, has constant sign because the differential equation for is affine-linear and . Since , we must have . But this means that
a contradiction, since the left side is periodic and . We may therefore assume that . Then , and it follows again that . But this means
and since the left-hand side is periodic, it follows that . ∎
To complete the polynomial embedding, we further polynomialize the parameters. This is done to ensure compatibility with the numerical implementation. We define , so that the complete polynomialized vector field is
The complete set of boundary conditions is
In the terminology of Remark 4, the embedding dimension is . The steady-state equation is scalar, and is given by
7.2.2 Results
We validated a patch of manifold initially with 406 simplices at a step size of . In the validation of nearly every simplex, three layers of adaptive refinement were needed to keep the bound under control. We have plotted the manifold in Figure 8 without the refinements included. The projection into the plane is provided in Figure 9. The results are consistent with the analysis of Leblanc [17].


7.3 FitzHugh-Nagumo equation
The FitzHugh-Nagumo ODE is
for scalar parameters . It is a cubic vector field in the state variables, and numerical simulations suggest the existence of Hopf bubbles (see Section 5.8 of [7]). We fix , while leaving and as parameters for the continuation. We start the continuation near and compute a triangulation of the manifold with 9006 simplices (including those needed for adaptive refinement) at step size 0.01. For this example, we used Fourier modes. A plot of the proven simplices from the manifold is provided in Figure 10. The Hopf bifurcation curve appears in Figure 11.


7.4 An ODE with a periodic orbit 2-manifold resembling a fish
Consider the three-dimensional ODE system
| (93) | ||||
| (94) | ||||
| (95) |
for parameters , and a real control parameter . When , a change of variables to cylindrical coordinates shows that periodic orbits are in one-to-one correspondence with solutions of the set of algebraic equations
When , the radial symmetry in is broken and this change of variables is no longer informative. We set in (93)–(95) and used our validated continuation scheme to rigorously compute a 2-manifold of periodic orbits. In the projection of amplitude and parameters , the result is a figure that qualitatively resembles an angelfish. See Figure 12. In this projection, the manifold has several folds and appears to exhibit a singularity where it pinches onto a single point. Plotting the manifold in a different projection more clearly allows us to see that this singularity is merely an artifact of the projection; see Figure 13. The Hopf bifurcation curve is plotted in Figure 14. For this example, we used Fourier modes and a step size 0.01. We computed a comparatively small portion of the manifold, since the interesting geometry was localized close to . We computed and validated 1007 simplices. This example did not require any adaptive refinement.





8 Discussion
We have proposed validated continuation as an alternative way of exploring degenerate Hopf bifurcations. In combination with rigorous numerics and additional a posteriori post-processing, one can prove the existence of Hopf bifurcation curves and bubble bifurcations. The library BiValVe is rather flexible, and with the additions of the present paper, can handle multiparameter continuation problems for periodic orbits in ordinary and delay differential equations, near and far from Hopf bifurcations.
Without access to second derivatives of solutions of the zero-finding problem (37), it is difficult to prove bubble bifurcations with quadratic folds. That is, we are only able to prove the weaker characterization of Definition 5. This is a major barrier in applying the method to delay equations. We believe that a suitable re-formulation of the zero-finding problem, taking into account the additional unbounded operators that result from derivatives with respect to frequency, could resolve the issue.
Another way to prove the “quadratic fold” part of the bubble bifurcation, would be to compute the second derivatives of Hopf bifurcation curves without using the machinery of sequences spaces. Along these lines, it would be interesting to use pseudo-arclength continuation to continue Hopf bifurcation curves directly. Computer-assisted proofs of isolated Hopf bifurcations in delay differential equations are completed in [5], and with minimal changes, pseudo-arclength continuation could be used to do continuation of Hopf bifurcations. The map from [5] is finite-dimensional and as smooth as the delay vector field, so the derivatives of the Hopf curve could be rigorously computed that way instead. However, this trick can not be used to prove that has a strict local extremum at the bifurcation point. Indeed, the latter map is defined in terms of the periodic orbits themselves, rather than the algebraic properties of the vector field and the eigenvalues of the linearization.
As remarked in [28], the bound associated to delay periodic orbit validation suffers from a fundamental limitation: it scales linearly with respect to the number of Fourier modes. Therefore, while we have not needed to use many Fourier modes in our examples, it would be very costly (or infeasible) to do continuation of a periodic orbit that required many modes to represent. This is because the bound is naturally dependent on step size, so even if an isolated solution has an exceptionally good numerical defect, a very small step size might be needed to hedge against a large . In this way, while we can compute manifolds of periodic orbits with delay near (degenerate) Hopf bifurcations, we expect that in large-amplitude regimes or for complicated orbits, completing a validation would be difficult. To compare, the situation is far better for ordinary differential equations. The bound is generally unharmed by having many Fourier modes, and second derivatives of the solutions can be computed by solving an auxiliary zero-finding problem using similar techniques from rigorous numerics.
There are other codimension-2+ bifurcations that could be studied from the point of view of validated multi-parameter continuation. For example, the cusp bifurcation should be amenable to this type of analysis, and is simpler than the present work because it involves only bifurcations of fixed points rather than periodic orbits. There is also the Bautin bifurcation, for which the analysis of Section 6 could be replicated. In fact, our continuation scheme is able to validate manifolds of periodic orbits passing through Bautin points. As a very brief final example, recall the normal form (3)–(4), which has a Bautin bifurcation at at the parameters . Periodic orbits in this ODE are equivalent (by a change of variables to polar coordinates) to scalar solutions of
| (96) |
Agnostic to this particular representation of the zeroes, our code is able to validate a large section of the manifold of periodic orbits directly from the ODEs. See Figure 15. As expected, we were able to validated this manifold using very few Fourier modes: three, in this case.

Hopf bubbles have been observed in the Mackey-Glass equation [15] at the classical parameters, and some of our preliminary investigations suggest that the equation possesses a bubble bifurcation. It would be interesting to use a combination of polynomial embedding and blow-up to investigate this bifurcation. However, the added complexity of using both blow-up and polynomial embedding presents a challenge; the resulting (polynomial) delay vector field ends up being high-order with dozens of distinct nonlinear terms.
Acknowledgments
Kevin E. M. Church is supported by a CRM-Simons Postdoctoral Fellowship. Elena Queirolo is supported by Walter Benjamin Programme DFG-Antrag QU579/1-1.
References
- [1] Peter Ashwin, Stephen Coombes, and Rachel Nicks. Mathematical Frameworks for Oscillatory Network Dynamics in Neuroscience. The Journal of Mathematical Neuroscience, 6(1):2, dec 2016.
- [2] N. Bautin. Behaviour of dynamical systems near the boundaries of stability regions. OGIZ GOSTEXIZDAT. Leningrad. In Russian. 1949.
- [3] Peter A. Braza. The Bifurcation Structure of the Holling–Tanner Model for Predator-Prey Interactions Using Two-Timing. SIAM Journal on Applied Mathematics, 63(3):889–904, jan 2003.
- [4] Kevin E.M. Church and Elena Queirolo. BiValVe: Bifurcation Validation Venture. https://github.com/elenaquei/bubbles/releases/tag/v1
- [5] Kevin E.M. Church and Jean-Philippe Lessard. Rigorous verification of Hopf bifurcations in functional differential equations of mixed type. Physica D: Nonlinear Phenomena, 429:133072, jan 2022.
- [6] Michael G. Crandall and Paul H. Rabinowitz. The Hopf Bifurcation Theorem in infinite dimensions. Archive for Rational Mechanics and Analysis, 67(1):53–72, 1977.
- [7] Geneviève Dupont, Martin Falcke, Vivien Kirk, and James Sneyd. Models of Calcium Signalling, volume 43 of Interdisciplinary Applied Mathematics. Springer International Publishing, Cham, 2016.
- [8] Hassan A. El-Morshedy and Alfonso Ruiz-Herrera. Asymptotic convergence in delay differential equations arising in epidemiology and physiology. SIAM Journal on Applied Mathematics, 81(4):1781–1798, 2021.
- [9] Teresa Faria and Luis T. Magalhães. Normal forms for retarded functional differential equations with parameters and applications to hopf bifurcation, 1995.
- [10] Marcio Gameiro, Jean Philippe Lessard, and Alessandro Pugliese. Computation of Smooth Manifolds Via Rigorous Multi-parameter Continuation in Infinite Dimensions. Foundations of Computational Mathematics, 16(2), 2016.
- [11] Martin Golubitsky and William F. Langford. Classification and unfoldings of degenerate Hopf bifurcations. Journal of Differential Equations, 41(3):375–415, 1981.
- [12] Brian Hassard and Katie Jiang. Degenerate Hopf bifurcation and isolas of periodic solutions in an enzyme-catalyzed reaction model. Journal of Mathematical Analysis and Applications, 177:170–189, 1993.
- [13] Weihua Jiang, Qi An, and Junping Shi. Formulation of the normal form of Turing-Hopf bifurcation in partial functional differential equations. Journal of Differential Equations, 268(10):6067–6102, 2020.
- [14] Yuri A Kuznetsov. Elements of Applied Bifurcation Theory. Springer New York, 2004.
- [15] Tibor Krisztin and Eduardo Liz. Bubbles for a Class of Delay Differential Equations. Qualitative Theory of Dynamical Systems, 10(2):169–196, oct 2011.
- [16] Joe Latulippe, Derek Lotito, and Donovan Murby. A mathematical model for the effects of amyloid beta on intracellular calcium. PLOS ONE, 13(8):e0202503, aug 2018.
- [17] Victor G. LeBlanc. A Degenerate Hopf Bifurcation in Retarded Functional Differential Equations, and Applications to Endemic Bubbles. Journal of Nonlinear Science, 26(1):1–25, 2016.
- [18] Maoxing Liu, Eduardo Liz, and Gergely Röst. Endemic bubbles generated by delayed behavioral response: Global stability and bifurcation switches in an sis model. SIAM Journal on Applied Mathematics, 75(1):75–91, 2015.
- [19] Zhihua Liu, Pierre Magal, and Shigui Ruan. Hopf bifurcation for non-densely defined Cauchy problems. Zeitschrift fur Angewandte Mathematik und Physik, 62(2):191–222, 2011.
- [20] Stephen B. Margolis and Bernard J. Matkowsky. New Modes of Quasi-Periodic Combustion Near a Degenerate Hopf Bifurcation Point. SIAM Journal on Applied Mathematics, 48(4):828–853, aug 1988.
- [21] J. E. Marsden and M. McCracken. The Hopf Bifurcation and Its Applications, volume 19 of Applied Mathematical Sciences. Springer New York, New York, NY, 1976.
- [22] Joseph Minicucci, Molly Alfond, Angelo Demuro, David Gerberry, and Joe Latulippe. Quantifying the dose-dependent impact of intracellular amyloid beta in a mathematical model of calcium regulation in xenopus oocyte. PLOS ONE, 16(1):e0246116, jan 2021.
- [23] Richmond Opoku-sarkodie and Ferenc A Bartha. Dynamics of an SIRWS model with waning of immunity and varying immune boosting period. pages 1–26, 2022.
- [24] J. P. Lessard and J. D. Mireles James. A functional analytic approach to validated numerics for eigenvalues of delay equations. Journal of Computational Dynamics, 7(1):123–158, 2020.
- [25] Aldo Rustichini. Hopf bifurcation for functional differential equations of mixed type. Journal of Dynamics and Differential Equations, 1(2):145–177, apr 1989.
- [26] N. Sherborne, K. B. Blyuss, and I. Z. Kiss. Bursting endemic bubbles in an adaptive network. Physical Review E, 97(4):042306, apr 2018.
- [27] James Sneyd, Shawn Means, Di Zhu, John Rugis, Jong Hak Won, and David I. Yule. Modeling calcium waves in an anatomically accurate three-dimensional parotid acinar cell. Journal of Theoretical Biology, 419:383–393, apr 2017.
- [28] Jan Bouwe van den Berg, Chris Groothedde, and Jean Philippe Lessard. A General Method for Computer-Assisted Proofs of Periodic Solutions in Delay Differential Problems. Journal of Dynamics and Differential Equations, 2020.
- [29] Jan Bouwe van den Berg Elena Queirolo. A general framework for validated continuation of periodic orbits in systems of polynomial ODEs. Journal of Computational Dynamics. 8(1):59, 2021.
- [30] Jan Bouwe van den Berg, Jean-Philippe Lessard, and Elena Queirolo. Rigorous Verification of Hopf Bifurcations via Desingularization and Continuation. SIAM Journal on Applied Dynamical Systems, 20(2):573–607, jan 2021.
- [31] Xiaoli Wang, Junping Shi, and Guohong Zhang. Interaction between water and plants: Rich dynamics in a simple model. Discrete & Continuous Dynamical Systems - B, 22(7):2971–3006, 2017.