Computational-Statistical Trade-off in Kernel Two-Sample Testing with Random Fourier Features
Computational-Statistical Trade-off in Kernel Two-Sample Testing with Random Fourier Features
Abstract
Recent years have seen a surge in methods for two-sample testing, among which the Maximum Mean Discrepancy (MMD) test has emerged as an effective tool for handling complex and high-dimensional data. Despite its success and widespread adoption, the primary limitation of the MMD test has been its quadratic-time complexity, which poses challenges for large-scale analysis. While various approaches have been proposed to expedite the procedure, it has been unclear whether it is possible to attain the same power guarantee as the MMD test at sub-quadratic time cost. To fill this gap, we revisit the approximated MMD test using random Fourier features, and investigate its computational-statistical trade-off. We start by revealing that the approximated MMD test is pointwise consistent in power only when the number of random features approaches infinity. We then consider the uniform power of the test and study the time-power trade-off under the minimax testing framework. Our result shows that, by carefully choosing the number of random features, it is possible to attain the same minimax separation rates as the MMD test within sub-quadratic time. We demonstrate this point under different distributional assumptions such as densities in a Sobolev ball. Our theoretical findings are corroborated by simulation studies.
Keywords: Maximum mean discrepancy, Minimax power, Permutation tests, Random Fourier features, Two-sample testing
1 Introduction
The problem of two-sample testing stands as a fundamental topic in statistics, concerned with comparing two distributions to determine their equivalence. Classical techniques, such as the -test and Wilcoxon rank-sum test, have been widely used to tackle this problem, and their theoretical and empirical properties have been well-investigated. However, these classical approaches often require parametric or strong moment assumptions to fully ensure their soundness, and their power is limited to specific directions of alternative hypotheses, such as location shifts. While these classical approaches are effective in well-structured and simple scenarios, their limitations in handling the increasing complexity of modern statistical problems has consistently prompted the need for new developments (Stolte et al.,, 2023, for a recent review). Among various advancements made to address this issue, the kernel two-sample test based on the maximum mean discrepancy (MMD, Gretton et al., 2012a, ) has garnered significant attention over the years, due to its nonparametric nature and flexibility. It can be applied in diverse scenarios without requiring distributional assumptions and offers robust theoretical underpinnings. With its empirical success and popularity, various research endeavors have been dedicated to enhancing their performance and deepening our understanding of their theoretical properties.
Broadly, there are two main branches of research regarding the kernel test: (i) kernel selection and (ii) computational time-power trade-off. Regarding kernel selection, significant advancements have been made in the last decade, aiming to identify the kernel that best captures the difference between two distributions. A common approach involves sample splitting where one-half of the data is used for kernel selection and the other half of data is used for the actual test (e.g., Gretton et al., 2012b, ; Sutherland et al.,, 2017; Liu et al.,, 2020). However, an inefficient use of the data from sample splitting often results in a loss of power, which has been the main criticism. Another approach for kernel selection involves aggregating multiple kernels, which avoids sample splitting but requires a careful selection of kernels in advance (e.g., Schrab et al.,, 2023, 2022; Biggs et al.,, 2023; Chatterjee and Bhattacharya,, 2023).
Regarding the time-power trade-off, much effort has concentrated on constructing a time-efficient test statistic with competitive power. The standard estimator of MMD via U-statistics or V-statistics demands quadratic-time complexity, which hinders the use of kernel tests for large-scale analyses. To mitigate this computational challenge, various methods have been proposed by using linear-time statistics (Gretton et al., 2012a, ; Gretton et al., 2012b, ), block-based statistics (Zaremba et al.,, 2013) and more generally incomplete U-statistics (Yamada et al.,, 2019; Schrab et al.,, 2022). However, these methods typically sacrifice statistical power for computational efficiency. Another approach that aims to balance this time-power trade-off is based on random Fourier features (RFF, Rahimi and Recht,, 2007). The idea is to approximate a kernel function using a finite dimensional random feature mapping, which can be computed efficiently. The use of RFF in a kernel test was initially considered by Zhao and Meng, (2015) and explored further by follow-up studies (e.g., Cevid et al.,, 2022). It is intuitively clear that the performance of an RFF-MMD test crucially depends on the number of random features. While there is a line of work studying theoretical aspects of RFFs (Liu et al.,, 2022, for a survey), their focus is mainly on the approximation quality of RFFs (Liu et al.,, 2022, for a survey), and the optimal choice of the number of random features that balances between computational costs and statistical power remains largely unexplored.
Motivated by this gap, we consider kernel two-sample tests using random Fourier features and aim to establish theoretical foundations for their power properties. Our tests are based on a permutation procedure, which is practically relevant but introduces additional technical challenges. As mentioned earlier, both the quality and the computational complexity of the RFF-MMD test heavily depend on the number of random features. Our primary focus therefore is to determine the number of random features that strikes an optimal balance. It is worth highlighting that the challenge in our analysis lies in managing the interplay of three distinct randomness sources: the data itself, the random Fourier features, and the permutations employed in our approach. All of these random sources are intertwined within the testing process, which makes our analysis non-trivial and unique. To effectively manage this complexity, we systematically decompose and analyze each layer of randomness in the test procedure, transitioning them into forms that are more amenable for analysis. This approach allows us to build on existing results from the literature that specifically address each of the three aspects of randomness.
In the next subsection, we present a brief review of prior work that is most relevant to our paper.
1.1 Related work
In recent years, there has been a growing body of literature aimed at investigating the power of MMD-based tests and enhancing their performance. For example, the work of Li and Yuan, (2019); Balasubramanian et al., (2021) demonstrated that MMD tests equipped with a fine-tuned kernel can achieve minimax optimality with respect to the separation in an asymptotic sense. To establish a similar but non-asymptotic guarantee, Schrab et al., (2023) introduced a MMD aggregated test calibrated by using either permutations or a wild bootstrap. It is also worth noting that the minimax optimality of MMD two-sample tests has been established for separations other than the distance, such as MMD distance (Kim and Schrab,, 2023), and Hellinger distance (Hagrass et al.,, 2022). In addition to these works, several other MMD-based minimax tests have been proposed using techniques such as aggregation (Fromont et al.,, 2013; Chatterjee and Bhattacharya,, 2023; Biggs et al.,, 2023) and studentization (Kim and Ramdas,, 2024; Shekhar et al.,, 2023). Despite significant recent advancements made in this field, the quadratic time complexity of these methods remains a barrier in large-scale applications, which highlights the need for more efficient yet powerful testing approaches.
To address the computational concern of quadratic-time MMD tests, several time-efficient approaches have emerged, which leverage subsampled estimation techniques, such as linear-time statistics (Gretton et al., 2012a, ; Gretton et al., 2012b, ), block-based statistics (Zaremba et al.,, 2013) and incomplete U-statistics (Yamada et al.,, 2019; Schrab et al.,, 2022). However, in terms of power, these methods are either sub-optimal or ultimately require quadratic time complexity to achieve optimality (Domingo-Enrich et al.,, 2023, Proposition 2). Other advancements in accelerating two-sample tests have involved techniques, such as Nyström approximations (Chatalic et al.,, 2022), analytic mean embeddings and smoothed characteristic functions (Chwialkowski et al.,, 2015; Jitkrittum et al.,, 2016), deep linear kernels (Kirchler et al.,, 2020), as well as random Fourier features (Zhao and Meng,, 2015). These tests can also run in sub-quadratic time, while their theoretical guarantees on power remain largely unknown. We also mention the recent method using kernel thinning (Dwivedi and Mackey,, 2021; Domingo-Enrich et al.,, 2023), which achieves the same MMD separation rate as the quadratic-time test but with sub-quadratic running time. However, this guarantee is valid under specific distributional assumptions that differ from those we consider. Moreover, their result focuses solely on alternatives that deviate from the null in terms of the MMD metric.
With this context in mind, we revisit the RFF-MMD test (Zhao and Meng,, 2015) and delve into its time-power trade-off concerning the number of random features. Despite an extensive body of literature on random features for kernel approximation, prior work has mainly focused on the estimation quality of kernel approximation (Rahimi and Recht,, 2007; Zhao and Meng,, 2015; Sriperumbudur and Szabo,, 2015; Sutherland and Schneider,, 2015; Yao et al.,, 2023), and a theoretical guarantee on the power of the RFF-MMD test has not been explored. In this work, we seek to bridge this gap by thoroughly analyzing the trade-off between computation time and statistical power in the context of the RFF-MMD test.
1.2 Our contributions
Having reviewed the prior work, we now summarize the key contributions of this paper.
-
•
Inconsistency result for RFF-MMD (Section 3). We first investigate the setting where the number of random Fourier features is fixed, and demonstrate that the RFF-MMD test fails to achieve pointwise consistency (Theorem 3 and Corollary 4). Concretely, we prove that there exist infinitely many pairs of distinct distributions for which the power of the RFF-MMD test using a fixed number of random Fourier features is almost equal to the size even asymptotically.
-
•
Sufficient conditions for consistency (Section 4). Our previous negative result clearly indicates that increasing the number of random Fourier features is necessary to achieve pointwise consistency. In Theorem 5, we show that it is indeed sufficient to increase the number of Fourier features to infinity to achieve pointwise consistency, even at an arbitrarily slow rate.
-
•
Time-power trade-off (Section 4). As mentioned before, there exists a clear trade-off between computational efficiency and statistical power in terms of the number of random Fourier features. To balance this trade-off, we adopt the non-asymptotic minimax testing framework and analyze how changes in the number of random Fourier features impact both computational efficiency and separation rates in terms of the metric (Theorem 6) and the MMD metric (Theorem 7).
-
•
Achieving optimality in sub-quadratic time (Section 4). We firmly demonstrate in Theorem 6 that it is possible to achieve the minimax separation rate against alternatives in sub-quadratic time when the underlying distributions are sufficiently smooth. Similarly, we establish in Proposition 8 that a parametric separation rate against MMD alternatives can be achieved in linear time for certain classes of distributions including Gaussian distributions.
Our theoretical results are validated through simulation studies under various scenarios and the code that reproduces our numerical results can be found at https://github.com/ikjunchoi/rff-mmd.
Organization.
The remainder of this paper is organized as follows. We set up the problem and present relevant background information in Section 2. Section 3 provides an inconsistency result of the RFF-MMD test and highlights the important role of the number of random features in the power performance. Moving forward to Section 4, we investigate the time-power trade-off in terms of the number of random features denoted as , and discuss an optimal choice of under minimax frameworks. We present simulation results in Section 5 that confirm our theoretical findings. Finally, in Section 6, we discuss the implications of our findings and suggest directions for future research. All technical proofs are collected in the appendix.
2 Background
In this section, we set up the problem and lay out some background for this work. Specifically, Section 2.1 explains the two-sample problem that we tackle, and specifies the desired error guarantees. We then present a brief overview of the MMD in Section 2.2 and its estimators using random Fourier features in Section 2.3. Lastly, in Section 2.4, we review the permutation method for evaluating the significance of a two-sample test statistic.
2.1 Two-sample problem
Let be i.i.d. random samples from the distribution , and be i.i.d. random samples from the distribution where . Based on these mutually independent samples, the problem of two-sample testing is concerned with determining whether and agree or not. More formally, let be a class of all possible pairs of distributions on some generic space , and consider two disjoint subsets in , namely and . Then, the null hypothesis and the alternative hypothesis of two-sample testing can be formulated as follows:
In order to decide whether to reject or not, we devise a test function , and reject the null hypothesis if and only if . This decision-making process naturally leads to two types of errors, which we would like to minimize. The first error, called the type I error, occurs by rejecting the null hypothesis despite being true. Conversely, the second error, called the type II error, arises when the null hypothesis is accepted despite being false. One common approach to design an ideal test is to first bound the probability of the type I error uniformly over as
where denotes the probability operator over and . We say that such a test is a level- test. Next, our focus shifts to controlling the type II error. Given a fixed pair in and a level- test , suppose that the probability of the type II error is upper bounded by some constant . Equivalently, the probability of correctly rejecting the null, referred to as the power, is lower bounded by . Ideally, we expect that the power of the test against any fixed alternative converges to one as we increase the data size and . More formally, we desire a test to be pointwise consistent, satisfying
| (1) |
A stronger notion of the power is uniform consistency, guaranteeing that the power converges to one uniformly over a class of alternative distributions. See Section 4 for a discussion. For simplicity, in the rest of this paper, we consider to be the -dimensional Euclidean space denoted as .
2.2 Maximum Mean Discrepancy
As an example of integral probability metrics, the MMD measures the discrepancy between two distributions in a nonparametric manner. Specifically, given a reproducing kernel Hilbert space (RKHS) equipped with a positive definite kernel , the MMD between and is defined as
It can also be represented as the RKHS distance between two mean embeddings of and , i.e., where and . For a characteristic kernel , the mean embedding of the kernel is injective (Sriperumbudur et al.,, 2010), which means that if and only if . Among several ways to estimate the MMD, one straightforward way is to substitute the population mean embeddings and with the empirical counterparts and . This plug-in approach results in a biased quadratic-time estimator of the squared MMD, also referred to as the V-statistic, given as
| (2) | ||||
Denoting , this plug-in estimator requires a quadratic-time cost of in terms of the sample size as it involves evaluating pairwise kernel similarities between samples. Another common approach to estimate is using the U-statistic (e.g., Gretton et al., 2012a, , Lemma 6), which is given as
This estimator is an unbiased estimator of the squared MMD and also requires quadratic-time computational costs.
2.3 Random Fourier features
Numerous approaches have been introduced to mitigate the computational cost of quadratic-time statistics often at the cost of sacrificing power performance. As reviewed in Section 1.1, some notable approaches include incomplete U-statistics (Gretton et al., 2012a, ; Zaremba et al.,, 2013; Schrab et al.,, 2022), Nyström approximations (Chatalic et al.,, 2022), kernel thinning (Dwivedi and Mackey,, 2021; Domingo-Enrich et al.,, 2023) and random Fourier features (Rahimi and Recht,, 2007; Zhao and Meng,, 2015). This work focuses on the method utilizing random Fourier features and investigates the effect of the number of random features on the power of a test. At the heart of this method is Bochner’s theorem (Lemma 9), which offers a means to approximate the kernel using a low-dimensional feature mapping , satisfying . If a bounded continuous positive definite kernel is translation invariant on , that is, , Bochner’s theorem guarantees the existence of a nonnegative Borel measure . It can be shown that is the inverse Fourier transform of and meets
where the equality is obtained by the fact that is both real and symmetric. Without loss of generality, we assume that is a probability measure, allowing the last integral to be expressed as with . If not, we instead work with the scaled versions of and , given as and . In this case, can be represented as .
Now, by drawing a sequence of i.i.d. random frequencies from , we construct an unbiased estimator of defined as an inner product of random feature maps:
| (3) |
where and . Let us define the vector in representing the difference in sample means of random feature maps as follows:
Also, denote the quadratic form of as . When we replace the kernel in Equation (2) with the estimated , we obtain a RFF-MMD estimator of that can run with a time complexity of :
| (4) |
Notably, this estimator can be computed in linear time in terms of the pooled sample size , and this computational benefit has motivated the prior work, such as Zhao and Meng, (2015), Sutherland and Schneider, (2015) and Cevid et al., (2022), that consider RFF-MMD statistics.
One may also consider an unbiased RFF-MMD statistic, given as
| (5) | ||||
which also involves computational time (Zhao and Meng,, 2015, Appendix A.1). In this work, we consider both and to demonstrate statistical and computational trade-offs in RFF-based two-sample testing.
2.4 Permutation tests
There have been several methods proposed for determining the threshold for MMD tests, which ensures (asymptotic or non-asymptotic) type I error control. These methods include those using limiting distributions or concentration inequalities, Gamma approximations, and bootstrap/permutation methods (e.g., Gretton et al., 2012a, ; Schrab et al.,, 2023). Among these, permutation tests stand out for their unique strength: they maintain level for any finite sample size and often achieve optimal power (e.g., Kim et al.,, 2022). This advantage has made permutation tests a popular choice in real-world applications despite extra computational costs. Given their practical relevance, this work focuses on permutation-based MMD tests and establishes their theoretical guarantees.
To explain the procedure, let us write the pooled sample as , and denote the collection of all possible permutations of as . Given a permutation we denote the permuted pooled samples as Then, for a generic test statistic the permutation distribution of is defined as
The permutation test rejects the null hypothesis when where denotes the quantile of given as
It is well-known that the resulting permutation test maintains non-asymptotic type I error control under the exchangeability of random vectors (e.g., Hemerik and Goeman,, 2018, Theorem 1). This exchangeability condition is satisfied under the null hypothesis of two-sample testing where are assumed to be i.i.d. random vectors.
A more computationally efficient permutation test is defined through Monte Carlo simulations. Let be permutation vectors randomly drawn from with replacement. We let denote the test statistics computed based on . Let be the quantile of the empirical distribution of , and reject the null when . The resulting Monte Carlo-based test is also valid in finite samples (Hemerik and Goeman,, 2018, Theorem 2) and has almost equivalent power behavior as the full permutation test for sufficiently large .
3 Lack of consistency
In this section, we show that the RFF-MMD test, employing a finite number of random Fourier features, lacks pointwise consistency — i.e., it fails to fulfill the guarantee in Equation (1) — even when the underlying kernel is characteristic. We establish this inconsistency result by focusing on a permutation test based on the test statistic in Equation (4) or that in Equation (5), while our main idea is not limited to these specific tests. We start by explaining the intuition behind this negative result in Section 3.1 and then present the main results in Section 3.2.
3.1 Preliminaries and intuition
An alternative formulation of in Equation (4) is in terms of the characteristic functions of and . This reformulation provides a key insight into our negative result in Section 3.2. To fix ideas, the squared MMD with a translation-invariant kernel can be represented as where and are the characteristic functions of and , respectively (e.g., Sriperumbudur et al.,, 2010, Corollary 4). Letting and , we may represent the plug-in estimator in Equation (2) as
With this identity in place, the RFF-MMD statistic can be regarded as an approximation of the above plug-in estimator via Monte Carlo simulations with random frequencies . Specifically, the RFF-MMD statistic can be written in terms of the empirical characteristic functions as:
As it is well-known, the characteristic function uniquely determines the distribution of a random vector. Therefore, when the support of is the entire Euclidean space, the population MMD becomes zero if and only if and coincide. However, the empirical MMD evaluated on a finite number of random points is unable to capture an arbitrary difference between and , even asymptotically. At a high-level, this happens due to a combination of two factors. First of all, it is possible that two distinct characteristic functions can be equal in an interval (e.g., Romano and Siegel,, 1986, page 74). Moreover, if random evaluation points fall within such interval with high probability, then the RFF-MMD statistic would behave similarly to the null case, resulting in a test that is inconsistent with a fixed number of random features. This observation was partly made in Chwialkowski et al., (2015, Proposition 1), which we generalize to as below.
Lemma 1 (Chwialkowski et al., 2015).
Let be a fixed number and let be a sequence of real-valued i.i.d. random vectors from a probability distribution on which is absolutely continuous with respect to the Lebesgue measure. For arbitrary , there exists an uncountable set of mutually distinct probability distributions on such that for any distinct pair and their corresponding random vectors and , it holds that .
The above lemma implies that there exists a certain pair of under the alternative such that the expectation of the RFF-MMD statistic (4) is approximately zero with high probability. Given that the same test statistic has an expectation approximately equal to zero under the null, one may argue that the power of an RFF-MMD test would be strictly less than one against that specific alternative. However, this argument is insufficient to correctly claim the lack of consistency. An instructive example would be the case where a test statistic is either or with probability and , respectively, under the null, whereas it takes the value with probability one. In this case, it is clear to see that the expectation of remains the same under and , converging to zero as . Nevertheless, if we reject the null when , the resulting test has size and power one for any value of . This toy example suggests that Lemma 1 is insufficient to formally prove the inconsistency result and we indeed need a distribution-level understanding of the RFF-MMD statistic. Moreover, when the critical value is determined via the permutation procedure (Section 2.4), we further need to take care of random sources arising from permutations, which adds an additional layer of technical challenges. With this context in place, we next develop inconsistency results by carefully studying the limiting distribution of the RFF-MMD statistic and its permuted counterpart.
3.2 Main results
Consider a permutation test based on the test statistic in Equation (4) defined as follows:
| (6) |
where and . Building on the intuition laid out in Section 3.1, we aim to prove that the asymptotic power of the test is strictly less than one with a fixed number of against certain fixed alternatives. To formally achieve this, let be defined similarly as by replacing with . Based on Euler’s formula, the event is equivalent to where
| (7) |
We call as the first moment equivalence (1-ME) condition, which holds with high probability, say , for some fixed according to Lemma 1. As mentioned earlier, the 1-ME condition alone is insufficient to formally prove the inconsistency result, which prompts an extension of the 1-ME condition to include higher-order moments. Specifically, consider a subset where implies equivalence up to the -th moment, i.e., with denoting
for and . We refer as the first moments equivalence (k-ME) condition. In the following proposition, we prove a generalized version of Lemma 1 demonstrating that the -ME condition holds with high probability for some fixed . The proof of this result can be found in Section B.1.
Proposition 2.
Let be a fixed number and let be a sequence of real-valued i.i.d. random vectors from a probability distribution on which is absolutely continuous with respect to the Lebesgue measure. For arbitrary , there exists an uncountable set of mutually distinct probability distributions on such that for any distinct pair and their corresponding random vectors and , it holds that .
Suppose that , specified in Proposition 2. The power of the considered test against this specific alternative is then upper bounded as
| (8) | ||||
Given this bound, our proof for inconsistency revolves around showing that is sufficiently small. This in turn requires understanding the limiting behavior of the test statistic and the permutation critical value under the -ME condition. On the one hand, the limiting distribution of the test statistic can be derived using the standard asymptotic tools such as the central limit theorem. On the other hand, we leverage asymptotic results for permutation distributions in Chung and Romano, (2016) to show that the critical value converges to the quantile of a continuous distribution. We point out that both limiting and permutation distributions of are determined by the first two moments of and . Furthermore, both distributions become asymptotically identical when those moments are the same, implying the coincidence of both distributions under the 2-ME condition. Consequently, the power of the test under the 2-ME condition remains small even asymptotically, which together with inequality (8), leads to the inconsistency result. This negative result is formally stated in the following theorem and the proof can be found in Section B.2.
Theorem 3.
Let be a bounded continuous positive definite kernel whose inverse Fourier transform is absolutely continuous with respect to the Lebesgue measure. Then, given any , for the test defined in Equation (6) with a fixed number and the limiting sample-ratio , there exist uncountably many pairs of distinct probability distributions on that satisfies
The underlying idea of the proof for Theorem 3 can be applied to the unbiased RFF-MMD statistic in Equation (5) as well. In particular, consider a permutation test
| (9) |
where and is the corresponding critical value. Building on the observation that the difference between and is asymptotically negligible, we derive a result analogous to Theorem 3, demonstrating that fails to be pointwise consistent.
Corollary 4.
The proof of Corollary 4 can be found in Section B.3. Our findings so far indicate that RFF-MMD tests with a fixed number of random features fail to be pointwise consistent. To address this issue, we naturally consider increasing with the sample size and show that the tests then become pointwise consistent. Moreover, in some cases, the RFF-MMD test can attain comparable power to the quadratic-time MMD test but in strictly less than quadratic time. These are the topics of the next section.
4 Optimal choice of the number of random features
We now turn to scenarios where the number of random Fourier features grows with the sample size, and examine computational and statistical trade-offs in selecting these random features. The first result of this section complements the previous inconsistency results, indicating that the RFF-MMD tests are pointwise consistent as long as the number of random Fourier features increases to infinity even at an arbitrarily slow rate.
Theorem 5.
The proof of Theorem 5 is given in Section B.4. It is worth noting that increasing the number of random features comes with an increase in computational cost. On the other hand, using a small number of random features may lead to suboptimal power performance compared to the quadratic-time MMD test. Therefore, achieving a balance between computational costs and statistical power is crucial from a practical standpoint. To determine the number of random features that balance this time-power trade-off, we adopt the minimax testing framework pioneered by Ingster, (1987, 1993) explained below.
Minimax two-sample testing framework.
While pointwise consistency in Equation (1) is an important property, it only provides a guarantee against a fixed pair of alternative distributions, which may be regarded as a weak property. Given some constant , one might instead aim to build a test that also uniformly bounds the probability of type II error in a non-asymptotic sense:
In general, however, achieving this uniform guarantee is not feasible unless the two classes and are sufficiently distant. Therefore it is common to introduce a gap between and , and analyze the minimum gap for which the testing error is uniformly controlled. In detail, we define a class of alternative pairs where is a metric of interest, is a predefined class of distribution pairs (if not stated otherwise, ), and is a separation parameter. Then the uniform separation rate that measures the performance of the test is defined (e.g., Baraud,, 2002; Schrab et al.,, 2023) as
Among all possible level- tests, it is reasonable to consider a test that achieves the smallest uniform separation as an optimal test. More formally, we define the minimax separation as
where the infimum is taken over all level- tests, and we refer to the test satisfying as a minimax optimal test. However, except for a few parametric problems, it is generally infeasible to devise an optimal test that precisely achieves the minimax separation. As a compromise, it is now conventional to seek a minimax rate optimal test, which achieves the minimax separation, up to a constant. It has been shown that the quadratic-time MMD test is minimax rate optimal against the metric (Schrab et al.,, 2023; Li and Yuan,, 2019) and against the MMD metric (Kim,, 2021; Kim and Schrab,, 2023). Our aim is to determine the minimum number of random features for which the RFF-MMD test attains the same optimality property as the quadratic-time MMD.
4.1 Uniform consistency in metric
We start by examining the uniform separation rate of the RFF-MMD test over the Sobolev ball with respect to the distance. Let us denote as the th order Sobolev ball in with radius that is
where is the smoothness parameter, and is the Fourier transform of . Furthermore, each of and denotes a set of functions that are integrable in absolute value and square integrable, respectively. Let be the collection of distribution pairs on where each pair of distributions admits the probability density functions with respect to the Lebesgue measure. Defining the class of distribution pairs with some constant given as
Schrab et al., (2023) demonstrated that the minimax rate in terms of the distance is , where indicates for some positive constants . They further showed that the MMD test using a translation-invariant kernel is minimax rate optimal in a non-asymptotic sense. A similar but asymptotic result was obtained by Li and Yuan, (2019), focusing specifically on the Gaussian kernel.111Both Schrab et al., (2023) and Li and Yuan, (2019) assume that under which the minimax rate against the alternative is given as . Without this balanced sample size assumption, however, the minimax rate is dominated by the minimum sample size i.e., . It is intuitively clear that when the number of random features is sufficiently large, the RFF-MMD test will also attain the same minimax optimality as the law of large numbers guarantees that the approximated kernel converges to the underlying kernel almost surely. Our next question is then to ask how rapidly should be increased to ensure the same minimax guarantee and whether it is possible to attain the same optimality in sub-quadratic time. We answer these questions in the affirmative.
Similarly to Schrab et al., (2023), our analysis assumes that the kernel can be represented as a product of one-dimensional translation-invariant characteristic kernels with a given bandwidth . More specifically, we assume that the kernel can be decomposed as
for where are some non-negative functions in satisfying for . We note that is indeed a characteristic kernel on , and we treat the bandwidth as a tuning parameter that varies with the sample size. In order to highlight the dependence on , we let (resp. ) denote the test (resp. ) equipped with the kernel . Given a constant , let us now consider a subset of where the support of individual distributions lies within the -dimensional hypercube . In other words, we define
Recalling and , the following theorem discusses the choice of and that allows and to achieve the minimax separation rate against the class of alternatives defined on .
Theorem 6.
Consider the tests and with , and for . Then there exists some positive constant such that the uniform separation of satisfies
The same guarantee also holds for . Moreover, the computational cost of the corresponding test statistics and is .
Theorem 6, proven in Section B.5, has several interesting aspects worth highlighting. First of all, it indicates that the RFF-MMD tests can achieve the optimal separation rate when is larger than . This in turn suggests that this optimality can be attained in sub-quadratic time when the underlying distributions are sufficiently smooth (i.e., ). Indeed, the computational time becomes linear in as . On the other hand, the computational complexity may need to exceed quadratic-time to achieve the minimax separation rate in non-smooth cases.
An astute reader may have realized that Theorem 6 is established for distributions on the bounded domain, which differs from the unbounded setting in the prior work (Schrab et al.,, 2023). We impose this additional constraint for analytical tractability, and in fact, the bounded domain is frequently assumed in minimax analysis (e.g., Ingster,, 1987, 1993; Arias-Castro et al.,, 2018). Nevertheless, it is important to point out that the worst-case instance used for deriving the minimax lower bound is defined on a bounded domain, say . Therefore the minimax rate remains unchanged for the bounded distributions that we consider.
4.2 Uniform consistency in MMD metric
In the previous subsection, we demonstrated that the RFF-MMD tests can achieve the minimax separation rate in sub-quadratic time complexity. It is worth pointing out that this result is presented against the Sobolev smooth alternatives, and optimal choices of the bandwidth , which parameterizes the kernel , and that balances between computational and statistical trade-offs may vary depending on classes of alternatives. To illustrate this point, we now turn to studying the uniform separation rate of the RFF-MMD test with respect to the MMD metric equipped with a generic kernel , and discuss the choice of that strikes the aforementioned trade-offs. Given a kernel , consider the alternative with a class of distribution pairs, , and a MMD metric, As formally shown in Kim and Schrab, (2023), the minimax rate of testing against the MMD metric satisfies where . The next theorem demonstrates that the number of random features required to achieve the minimax separation rate in terms of the MMD metric is of order where recall ; thereby the overall runtime becomes in the sample size. The proof can be found in Section B.6.
Theorem 7.
Consider the tests and with kernel which is bounded as for all . Then, the test with achieves the minimax separation rate, satisfying
for some positive constant The same guarantee also holds for . Moreover, the computational cost of the corresponding test statistics and is
It has been commonly believed that the RFF-MMD test requires at least cubic-time complexity to match the power of a standard MMD test (e.g., Domingo-Enrich et al.,, 2023). However, Theorem 7 refutes this common belief, claiming that the RFF-MMD test can attain the same minimax separation rate with quadratic-time complexity. Indeed, we can further improve this point: when properly carving out the distributions of interest, it becomes possible to achieve the same separation rate of in sub-quadratic or even linear-time complexity. To demonstrate this point, denote the U-statistic in Equation (5) with a single random Fourier feature (i.e., ) as . One of the crucial steps in the proof of Theorem 7 involves finding an upper bound for the expectation . Since the kernel is uniformly bounded and , the previous expectation is bounded above by , up to a constant. Our analysis utilizes this somewhat crude, but not universally improvable, upper bound, which is the place where the quadratic-time complexity arises.
Now let us consider a subclass of distribution pairs . Suppose that there exist some universal constants and such that the following inequality
| (10) |
holds for all (see Remark 17.1 of the appendix for a discussion on the range of ). Against this class of alternatives , our proof shows that the RFF-MMD test achieves -separation rate within sub-quadratic time. Specifically, the time complexity depends on the value of in Equation (10) with a precise computational cost of for . As a concrete example, consider the class of pairs of Gaussian distributions with a common fixed covariance , denoted as
| (11) |
and set . For this Gaussian subclass and a generic Gaussian kernel given as
with bandwidth , we prove that the inequality in Equation (10) holds with the constant . This main building block allows us to show the following proposition, indicating that the RFF-MMD test achieves the uniform separation rate of in linear-time complexity.
Proposition 8.
For the class of distribution pairs and the Gaussian kernel with any fixed bandwidth , there exist some positive constants and such that with the choice of satisfies
and the computational cost of the corresponding estimator is This result also holds for the test with the same choice of and its corresponding estimator
Proposition 8, proven in Section B.7, states that the RFF-MMD test requires only a fixed number of random features to match the uniform separation rate of the original MMD test. At first glance, this appears to contradict Theorem 3, which demonstrates the pointwise inconsistency of the test when the number of random features is fixed. However, this is not a contradiction as Proposition 8 assumes a smaller, specific class of distributions, whereas Theorem 3 considers all possible distributions. Notably, the distributions that lead to the inconsistency demonstrated in Theorem 3 do not fall within the class .
While we focus on the class of Gaussian distributions for technical tractability, we believe that Proposition 8 holds for a broader class of distributions as evidenced by our empirical studies. It would be of great interest to further explore classes of distributions for which the RFF-MMD test offers significant computational gains over the original MMD test, while maintaining nearly the same power. We leave this topic for future work.
5 Numerical studies
In this section, we compare the empirical power and computational time of RFF-MMD tests with other computationally efficient methods such as linear-time statistics (lMMD; Gretton et al., 2012a, ; Gretton et al., 2012b, ), block-based statistics (bMMD; Zaremba et al.,, 2013), incomplete U-statistics (incMMD; Yamada et al.,, 2019; Schrab et al.,, 2022) under several different scenarios. Within each scenario, we run RFF-MMD tests with varying numbers of random features , and also run the quadratic time MMD test (Gretton et al., 2012b, ) as a benchmark for comparison. In our simulations, all kernel tests employ a Gaussian kernel with the bandwidth selected using the median heuristic. The significance level is set at and the critical value of each test is determined by using permutation or bootstrap methods with Monte Carlo iterations. The power of each test is approximated by averaging the results over repetitions.
The specific scenarios that we consider in our simulation studies are described as follows.
-
•
Scenario 1: Univariate Gaussians. Our first experiment is concerned with comparing two Gaussian distributions on with a mean difference or a variance difference. Specifically, we first evaluate the performance of the methods in distinguishing from by (i) varying from to and (ii) varying the sample sizes with a fixed mean difference of . We conducted a similar experiment to evaluate the performance of the methods in distinguishing from by (i) varying from to and (ii) varying the sample sizes with fixed variance .
-
•
Scenario 2: High-dimensional Gaussians. We also compared the power of the tests for distinguishing two Gaussian distributions with different mean vectors or variance matrices in high-dimensional settings. For location alternatives, we let be a vector whose first coordinates are and the others are 0. We set and and also report the test powers by varying from to or the sample sizes with fixed . For scale alternatives, we set and and vary from 0.95 to 1.1 or the sample sizes while fixing .
-
•
Scenario 3: Perturbed uniforms. Motivated by the experiments conducted in Schrab et al., (2022, 2023); Biggs et al., (2023), we investigate the test powers for capturing perturbations in uniform distributions on or . Specifically, for we set the density of the null distribution as and that of the alternative as where is perturbation amplitude and is the -dimensional perturbation function of size , defined as with The perturbation shape function is given by:
We set as an one-dimensional alternative and as a two-dimensional alternative. In this case, the perturbation amplitude implies the null hypothesis and we consider different scenarios by varying from to . Additionally, we fix the perturbation amplitude at for and for and vary the sample sizes .
-
•
Scenario 4: MNIST. To evaluate the performance of the methods in real-world settings, we consider a task of distinguishing between the distribution of even-number images and the distribution of odd-number images in the MNIST dataset. Each data point is an image with dimension (without downsampling) or (with downsampling), with labels . We collect the images of even numbers to define a distribution and collect the images of odd numbers to define another distribution . Given a mixing rate , we set and . Accordingly, we regard the case as the null hypothesis and vary from to to evaluate the power performance. When we vary the sample sizes , we fix the mixing rate at .

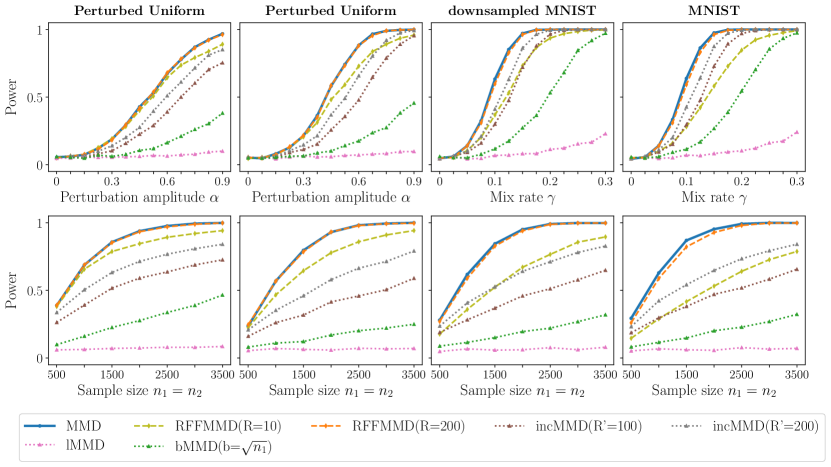
The simulation results for the first two scenarios are displayed in Figure 1, whereas the simulation results for the last two scenarios can be found in Figure 2. We first note that the test power of RFF-MMD test increases monotonically with , converging to the power of the quadratic-time MMD test. This empirically illustrates that the RFF-MMD test approximates the quadratic time MMD test as increases. Also, the empirical results demonstrate that different values of are required depending on the underlying distribution to match the power of the RFF-MMD test with that of the quadratic-time MMD test. Specifically, the RFF-MMD test matched the power of the original MMD test in all cases when , except in Scenario 2, where it matched when . It is also worth noting that the RFF-MMD test outperforms other efficient methods in Scenarios 1 and 3, even with as small as 10.
In Scenario 2, which involves a high-dimensional Gaussian setting, we observed that the power of the RFF-MMD test drops more sharply than that of the incMMD test when the sample size is fixed and the dimension increases. Conversely, when the dimension is fixed and the sample size increases, the power of the RFF-MMD test converges to that of the quadratic time MMD test more quickly than the incMMD test. A similar phenomenon was observed in Scenario 4: as the dimension increases from downsampled MNIST to MNIST data, the power curve of the RFF-MMD test shifts downward, while the power curves of other methods show little variation for the same mixing rate. However, when fixing the mixing rate and varying the sample size, the power of the RFF-MMD test increases faster than that of the incMMD test. This can be explained by the fact that the RFF-MMD test involves kernel approximation. As the dimension increases while the number of random features remains fixed, the accuracy of the kernel approximation decreases, leading to a relatively faster decline in power compared to the incMMD test. Conversely, when the dimension is fixed and the sample size varies, the incMMD test considers only a subset of the samples for computing the test statistic, resulting in a relatively slower increase in power compared to the RFF-MMD test.
We empirically measured the computational time of the considered methods under Scenario 1, as recorded in Table 1. In the experiments, we varied the sample size from to , with a mean difference of . To ensure the efficiency of the experiments, we measured the time taken to compute the test statistic once, rather than the time taken to perform the permutation test. The results were approximated by averaging over repetitions. From Table 1, we experimentally confirmed that while the computational time of the conventional MMD increases quadratically with the sample size, the computational times of RFF-MMD and incMMD increase linearly. Additionally, the last row of Table 1 demonstrates that the time increases linearly with the number of features, which aligns with the theoretical computational time of for RFF-MMD. We also note that similar patterns were observed in other simulation scenarios.
|
MMD |
|
|
|
|
|
lMMD |
|
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 250 | 0.0088 | 0.0002 | 0.0009 | 0.0070 | 0.0057 | 0.0084 | 0.0001 | 0.0006 | ||||||||||||||
| 500 | 0.0411 | 0.0003 | 0.0017 | 0.0130 | 0.0140 | 0.0251 | 0.0001 | 0.0019 | ||||||||||||||
| 1000 | 0.1946 | 0.0004 | 0.0051 | 0.0254 | 0.0325 | 0.0681 | 0.0002 | 0.0053 | ||||||||||||||
| 2000 | 0.7983 | 0.0006 | 0.0097 | 0.0485 | 0.0744 | 0.1497 | 0.0004 | 0.0155 | ||||||||||||||
| 4000 | 3.2662 | 0.0010 | 0.0192 | 0.0966 | 0.1567 | 0.3128 | 0.0007 | 0.0439 | ||||||||||||||
| 8000 | 13.247 | 0.0020 | 0.0371 | 0.1933 | 0.3189 | 0.6391 | 0.0015 | 0.1426 |
6 Discussion
In this work, we laid the theoretical foundations for kernel MMD tests using random Fourier features. Firstly, we proved that pointwise consistency is attainable if and only if the number of random Fourier features tends to infinity with the sample size. This observation naturally motivates an investigation into the optimal choice of the number of random Fourier features that strikes a balance between computational efficiency and statistical power. We explored this time-power trade-off under the minimax testing framework, and showed that it is possible to attain minimax separation rates within sub-quadratic time under certain distributional assumptions. We also validated these theoretical findings through numerical studies.
Our work opens up several promising avenues for future work. A natural extension of our work is to adapt our techniques to other kernel-based inference methods, such as the Hilbert–Schmidt independence criterion, and investigate fundamental time-power trade-offs in different applications. From a technical standpoint, it remains open whether a similar result to Theorem 6 can be obtained for distributions with unbounded supports. Future work can also attempt to extend our results in Section 4 to other metrics such as the Hellinger distance (e.g., Hagrass et al.,, 2022) and explore further improvements under other smoothness conditions. Finally, it would be of interest to consider deterministic Fourier features, which are shown to better approximate a kernel than random Fourier features (e.g., Wesel and Batselier,, 2021), and apply those in our application. We leave all these intriguing yet challenging problems to future work.
Acknowledgments
We acknowledge support from the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2022R1A4A1033384), and the Korea government (MSIT) RS-2023-00211073. We are grateful to Yongho Jeon and Gyumin Lee for their careful proofreading and helpful discussion.
References
- Arias-Castro et al., (2018) Arias-Castro, E., Pelletier, B., and Saligrama, V. (2018). Remember the curse of dimensionality: The case of goodness-of-fit testing in arbitrary dimension. Journal of Nonparametric Statistics, 30(2):448–471.
- Balasubramanian et al., (2021) Balasubramanian, K., Li, T., and Yuan, M. (2021). On the optimality of kernel-embedding based goodness-of-fit tests. Journal of Machine Learning Research, 22(1):1–45.
- Baraud, (2002) Baraud, Y. (2002). Non-asymptotic minimax rates of testing in signal detection. Bernoulli, 8(5):577–606.
- Biggs et al., (2023) Biggs, F., Schrab, A., and Gretton, A. (2023). MMD-FUSE: Learning and combining kernels for two-sample testing without data splitting. In Advances in Neural Information Processing Systems, volume 36, pages 75151–75188.
- Bochner, (1933) Bochner, S. (1933). Monotone Funktionen, Stieltjessche Integrale und harmonische Analyse. Mathematische Annalen, 108(1):378–410.
- Bogachev, (2007) Bogachev, V. I. (2007). Measure Theory. Springer Berlin Heidelberg.
- Cevid et al., (2022) Cevid, D., Michel, L., Näf, J., Bühlmann, P., and Meinshausen, N. (2022). Distributional random forests: Heterogeneity adjustment and multivariate distributional regression. Journal of Machine Learning Research, 23(333):1–79.
- Chatalic et al., (2022) Chatalic, A., Schreuder, N., Rosasco, L., and Rudi, A. (2022). Nyström kernel mean embeddings. In Proceedings of the 39th International Conference on Machine Learning, volume 162 of Proceedings of Machine Learning Research, pages 3006–3024.
- Chatterjee and Bhattacharya, (2023) Chatterjee, A. and Bhattacharya, B. B. (2023). Boosting the power of kernel two-sample tests. arXiv preprint arXiv:2302.10687.
- Chung and Romano, (2016) Chung, E. and Romano, J. P. (2016). Multivariate and multiple permutation tests. Journal of Econometrics, 193(1):76–91.
- Chwialkowski et al., (2015) Chwialkowski, K. P., Ramdas, A., Sejdinovic, D., and Gretton, A. (2015). Fast two-sample testing with analytic representations of probability measures. In Advances in Neural Information Processing Systems, volume 28, pages 1981–1989.
- Domingo-Enrich et al., (2023) Domingo-Enrich, C., Dwivedi, R., and Mackey, L. (2023). Compress then test: Powerful kernel testing in near-linear time. In International Conference on Artificial Intelligence and Statistics, volume 206 of Proceedings of Machine Learning Research, pages 1174–1218.
- Dwivedi and Mackey, (2021) Dwivedi, R. and Mackey, L. (2021). Kernel thinning. In Proceedings of Thirty Fourth Conference on Learning Theory, volume 134 of Proceedings of Machine Learning Research, pages 1753–1753.
- Fromont et al., (2013) Fromont, M., Laurent, B., and Reynaud-Bouret, P. (2013). The two-sample problem for Poisson processes: Adaptive tests with a nonasymptotic wild bootstrap approach. The Annals of Statistics, 41(3):1431–1461.
- (15) Gretton, A., Borgwardt, K. M., Rasch, M. J., Schölkopf, B., and Smola, A. (2012a). A kernel two-sample test. Journal of Machine Learning Research, 13(25):723–773.
- (16) Gretton, A., Sejdinovic, D., Strathmann, H., Balakrishnan, S., Pontil, M., Fukumizu, K., and Sriperumbudur, B. K. (2012b). Optimal kernel choice for large-scale two-sample tests. In Advances in Neural Information Processing Systems, volume 25, pages 1214–1222.
- Guo and Shah, (2024) Guo, F. R. and Shah, R. D. (2024). Rank-transformed subsampling: inference for multiple data splitting and exchangeable p-values. arXiv preprint arXiv:2301.02739.
- Hagrass et al., (2022) Hagrass, O., Sriperumbudur, B. K., and Li, B. (2022). Spectral regularized kernel two-sample tests. arXiv preprint arXiv:2212.09201.
- Hemerik and Goeman, (2018) Hemerik, J. and Goeman, J. (2018). Exact testing with random permutations. Test, 27(4):811–825.
- Ingster, (1987) Ingster, Y. I. (1987). Minimax testing of nonparametric hypotheses on a distribution density in the metrics. Theory of Probability & Its Applications, 31(2):333–337.
- Ingster, (1993) Ingster, Y. I. (1993). Asymptotically minimax hypothesis testing for nonparametric alternatives. i, ii, iii. Mathematical Methods of Statistics, 2(2):85–114.
- Jitkrittum et al., (2016) Jitkrittum, W., Szabó, Z., Chwialkowski, K. P., and Gretton, A. (2016). Interpretable distribution features with maximum testing power. In Advances in Neural Information Processing Systems, volume 29, pages 181–189.
- Kim, (2021) Kim, I. (2021). Comparing a large number of multivariate distributions. Bernoulli, 27(1):419–441.
- Kim et al., (2022) Kim, I., Balakrishnan, S., and Wasserman, L. (2022). Minimax optimality of permutation tests. The Annals of Statistics, 50(1):225–251.
- Kim and Ramdas, (2024) Kim, I. and Ramdas, A. (2024). Dimension-agnostic inference using cross U-statistics. Bernoulli, 30(1):683–711.
- Kim and Schrab, (2023) Kim, I. and Schrab, A. (2023). Differentially private permutation tests: Applications to kernel methods. arXiv preprint arXiv:2310.19043.
- Kirchler et al., (2020) Kirchler, M., Khorasani, S., Kloft, M., and Lippert, C. (2020). Two-sample testing using deep learning. In Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics, volume 108 of Proceedings of Machine Learning Research, pages 1387–1398.
- Lee, (1990) Lee, J. (1990). U-statistics: Theory and Practice. CRC Press.
- Lehmann and Romano, (2006) Lehmann, E. and Romano, J. (2006). Testing Statistical Hypotheses. Springer New York.
- Li and Yuan, (2019) Li, T. and Yuan, M. (2019). On the optimality of gaussian kernel based nonparametric tests against smooth alternatives. arXiv preprint arXiv:1909.03302.
- Liu et al., (2022) Liu, F., Huang, X., Chen, Y., and Suykens, J. A. K. (2022). Random Features for Kernel Approximation: A Survey on Algorithms, Theory, and Beyond. IEEE Transactions on Pattern Analysis and Machine Intelligence, 44(10):7128–7148.
- Liu et al., (2020) Liu, F., Xu, W., Lu, J., Zhang, G., Gretton, A., and Sutherland, D. J. (2020). Learning deep kernels for non-parametric two-sample tests. In Proceedings of the 37th International Conference on Machine Learning, volume 119 of Proceedings of Machine Learning Research, pages 6316–6326.
- Pólya, (1949) Pólya, G. (1949). Remarks on characteristic functions. In Proceedings of the Berkeley Symposium on Mathematical Statistics and Probability, pages 115–123.
- Rahimi and Recht, (2007) Rahimi, A. and Recht, B. (2007). Random features for large-scale kernel machines. In Advances in Neural Information Processing Systems, volume 20, pages 1177–1184.
- Ramdas et al., (2015) Ramdas, A., Jakkam Reddi, S., Poczos, B., Singh, A., and Wasserman, L. (2015). On the decreasing power of kernel and distance based nonparametric hypothesis tests in high dimensions. Proceedings of the AAAI Conference on Artificial Intelligence, 29(1):3571–3577.
- Romano and Siegel, (1986) Romano, J. P. and Siegel, A. F. (1986). Counterexamples in Probability and Statistics. CRC Press.
- Schrab et al., (2023) Schrab, A., Kim, I., Albert, M., Laurent, B., Guedj, B., and Gretton, A. (2023). MMD aggregated two-sample test. Journal of Machine Learning Research, 24(194):1–81.
- Schrab et al., (2022) Schrab, A., Kim, I., Guedj, B., and Gretton, A. (2022). Efficient Aggregated Kernel Tests using Incomplete U-statistics. In Advances in Neural Information Processing Systems, volume 35, pages 18793–18807.
- Shekhar et al., (2023) Shekhar, S., Kim, I., and Ramdas, A. (2023). A permutation-free kernel independence test. Journal of Machine Learning Research, 24(369):1–68.
- Sriperumbudur and Szabo, (2015) Sriperumbudur, B. and Szabo, Z. (2015). Optimal rates for random fourier features. In Advances in Neural Information Processing Systems, volume 28, page 1144–1152.
- Sriperumbudur et al., (2010) Sriperumbudur, B. K., Gretton, A., Fukumizu, K., Schölkopf, B., and Lanckriet, G. R. (2010). Hilbert space embeddings and metrics on probability measures. Journal of Machine Learning Research, 11(50):1517–1561.
- Stolte et al., (2023) Stolte, M., Bommert, A., and Rahnenführer, J. (2023). A Review and Taxonomy of Methods for Quantifying Dataset Similarity. arXiv preprint arXiv:2312.04078.
- Sutherland and Schneider, (2015) Sutherland, D. J. and Schneider, J. (2015). On the error of random fourier features. In Proceedings of the Thirty-First Conference on Uncertainty in Artificial Intelligence, page 862–871.
- Sutherland et al., (2017) Sutherland, D. J., Tung, H.-Y., Strathmann, H., De, S., Ramdas, A., Smola, A., and Gretton, A. (2017). Generative models and model criticism via optimized maximum mean discrepancy. In International Conference on Learning Representations.
- Wesel and Batselier, (2021) Wesel, F. and Batselier, K. (2021). Large-scale learning with fourier features and tensor decompositions. In Advances in Neural Information Processing Systems, volume 34, pages 17543–17554.
- Yamada et al., (2019) Yamada, M., Wu, D., Tsai, Y. H., Ohta, H., Salakhutdinov, R., Takeuchi, I., and Fukumizu, K. (2019). Post selection inference with incomplete maximum mean discrepancy estimator. In International Conference on Learning Representations.
- Yao et al., (2023) Yao, J., Erichson, N. B., and Lopes, M. E. (2023). Error estimation for random fourier features. In Proceedings of The 26th International Conference on Artificial Intelligence and Statistics, volume 206 of Proceedings of Machine Learning Research, pages 2348–2364.
- Zaremba et al., (2013) Zaremba, W., Gretton, A., and Blaschko, M. (2013). B-test: A non-parametric, low variance kernel two-sample test. In Advances in Neural Information Processing Systems, volume 26, page 755–763.
- Zhao and Meng, (2015) Zhao, J. and Meng, D. (2015). FastMMD: Ensemble of circular discrepancy for efficient two-sample test. Neural Computation, 27(6):1345–1372.
Appendix A Technical lemmas
In this section, we collect technical lemmas used in the main proofs of our results.
Lemma 9 (Bochner,, 1933, Bochner’s theorem,).
A translation-invariant bounded continuous kernel on is positive definite if and only if there exists a finite non-negative Borel measure on such that
The following result is commonly known as Young’s convolution inequality.
Lemma 10 (Bogachev,, 2007, Theorem 3.9.4).
Let and be real numbers such that Then, for any functions and ,
We next collect useful asymptotic tools from Chung and Romano, (2016) to analyze the limiting behavior of permutation distributions.
Lemma 11 (Chung and Romano, 2016, Lemma A.2).
Suppose has distribution in and is a finite group of transformations of onto itself. Also, let be a random variable that is uniform on . Assume and are mutually independent. For a -dimensional test statistic let denote the randomization distributions of a -dimensional random vector defined by
| (12) |
Suppose, under
| (13) |
for a constant Then under
where denotes the distribution function corresponding to the point mass function at
Lemma 12 (Chung and Romano, 2016, Lemma A.3).
Let and be sequences of -dimensional random variables satisfying Equation (13) and
where and are independent, each with common -variate cumulative distribution function Let (t) denote the randomization distribution of defined in Equation (12) with replaced by Then, converges to the cumulative distribution function of in probability. In other words,
if is continuous at where denotes the corresponding -variate cumulative distribution function of
Lemma 13 (Chung and Romano, 2016, Lemma A.6).
Suppose the randomization distribution of a test statistic converges to in probability. In other words,
if is continuous at where denotes the corresponding cumulative distribution function of . Let be a measurable map from to Let be the set of points in for which is continuous. If then the randomization distribution of converges in probability.
Lemma 14 (Chung and Romano, 2016, Theorem 2.1).
Suppose that are i.i.d. random samples from the -dimensional distribution , where for with mean vector and covariance matrix , and inedpendently, be i.i.d. random samples from the -dimensional distribution , where for with the common mean vector and covariance matrix Let and write Consider a test statistic and its permutation distribution
where denotes the permutations of and . Assume and for all and Let and assume that is positive definite. Then,
where denotes the -variate normal distribution with mean and variance
The following result is a slight modification of Ramdas et al., (2015, Proposition 1) tailored to our kernel setting.
Lemma 15 (Ramdas et al., 2015, Proposition 1).
Suppose and . The squared MMD between and using a Gaussian kernel has the following explicit form:
where
The next lemma facilitates the calculation of . The proof can be found in Appendix B.8.
Lemma 16.
Let and be the independent copies of and , respectively. Then, the following two equations hold:
The next lemma serve as a main block in the proof of Propositions 8. The proof can be found in Appendix B.9.
Lemma 17.
Remark 17.1.
Regarding the range of in Equation (10), note that when , the inequality in Equation (10) yields and this is not of our interest (in fact, this condition becomes vacuous since using a bounded kernel is bounded above by a constant). More specifically, by Jensen’s inequality, we have and then the inequality in Equation (10) implies
Therefore we may see some computational gain when but it is only possible when the minimum separation is of constant order as .
Appendix B Proofs
Notation and terminology.
We start by organizing the notation and the terminology we use throughout this appendix. Unless explicitly stated otherwise, the symbol denotes the probability measure that takes into account all inherent uncertainties. In addition, we represent constants as , which may depend on “fixed” parameters such as that do not vary with the sample sizes and . The specific values of these constants may vary in different places. We use the notation to denote that the sequence of the random variables converges in probability to a random variable We also introduce a terminology for the convergence of permutation distributions. For a given generic test statistic and a continuous random variable , denote the permutation distribution of as and the cumulative distribution function (CDF) of as . Suppose that
or equivalently, for any given
In this case, we say that converges weakly in probability to , as in Chung and Romano, (2016). Also, if a sequence of random variables converges in distribution to a continuous random variable , we use the expression that aligns with the above:
instead of Note that Pólya’s theorem can be generalized into the multivariate case (Guo and Shah,, 2024, Lemma C.7) and thus guarantees the equivalence between those two expressions under the assumption that is continuous.
B.1 Proof of Proposition 2
For simplicity, we consider the case where , as the scenario with can be extended naturally by taking the Cartesian product of the one-dimensional cases. Also, we consider the case , since the case is identical to Lemma 1, and the logic used for can be extended to prove the cases for .
Now, suppose that . Given frequencies recall that the feature mapping is defined as
and can be written as
Then, the components of the second moment matrix of should be one of the following terms:
Similarly, the same argument holds true for . Hence, to show that holds, it is enough to show that the following identities are satisfied simultaneously:
for all By trigonometric identities, these identities are equivalent to
for all Hence, if we show that the following identities
hold for all given the second moment matrices of and become identical. Also, note that satisfying the first two identities is equivalent to the coincidence of characteristic functions and at the point and the last two identities imply the coincidence of and at the point Let us denote and as and , respectively, for all , and then, a sufficient condition for is for all Now, observe that all random variables have continuous probability distributions, and thus, for any , we can find satisfying for all Then,
Here, according to Pólya’s criterion (Pólya,, 1949, Theorem 1), we can find uncountably many characteristic functions that vanish outside the interval and let us denote this set as A representative example of these functions (see e.g., Chwialkowski et al.,, 2015, Proposition 1) is a set where
Then, for any distribution pair we have
and this completes the proof.
B.2 Proof of Theorem 3
Recall that we use a permutation test defined as follows:
We first note that the permutation test is invariant under multiplying a positive constant to the test statistic. Therefore, throughout the proof of Theorem 3, we consider as a test statistic and its permutation quantile instead of and , respectively. Now, note that both the test statistic and the permutation quantile are random variables. Our strategy to prove Theorem 3 is to first assume the ME condition (7), , which holds for any distribution pair with high probability by Lemma 1. For such fixed , we analyze the asymptotic behavior of and show that the test power is strictly smaller than one for an uncountable number of pairs of distributions and .
Asymptotic behavior of the unconditional distribution
Let us start by investigating the test statistic with a fixed . For the sake of notation, we denote the covariances of and as and , respectively. Note that and are trigonometric functions, having finite variance. Hence the central limit theorem guarantees that the unconditional distribution of converges in distribution to where . Letting , consider an eigendecomposition of :
Here, is a diagonal matrix formed from the non-zero eigenvalues of , and is an orthogonal matrix with columns corresponding to the eigenvectors of . Then, a Gaussian random vector can be decomposed as where . Therefore, the distribution of can be derived as follows:
Based on the fact that converges in distribution to , the continuous mapping theorem guarantees
| (14) |
for fixed , where is the CDF of If , then the limiting distribution becomes . Even when is strictly less than , we note that the distribution can also be regarded as the distribution of instead of since we can extend the eigenvalue set to by including zero eigenvalues.
Asymptotic behavior of the permutation distribution
We now examine the asymptotic behavior of the permutation distribution of and for fixed . First, let where , and consider an eigendecomposition
where is a diagonal matrix composed of and zeros, is a diagonal matrix formed from the non-zero eigenvalues of . In addition denotes an orthogonal matrix whose columns are the eigenvectors of and denotes an orthogonal matrix that makes also orthogonal. Note that can be decomposed as
| (15) | ||||
For the first term, note that and for . Furthermore, we observe that
Since is positive definite, we apply Lemma 14 to and conclude that the permutation distribution of converges weakly in probability to for fixed . Therefore, the continuous mapping theorem for permutation distribution (Chung and Romano,, 2016, Lemma A.6) guarantees that the permutation distribution of converges weakly in probability to for . More formally, if we denote the permutation distribution of as , for any we have
for each fixed , where denotes the CDF of
For the second term in Equation (15), we note that the null space of the sum of two positive semidefinite matrices is the intersection of the null spaces of each of them. Since is the null space of and is positive semidefinite, the columns of are in the null space of and . This implies that and . Hence, for any permutation , we have
and we conclude that the permutation distribution of is degenerate at zero. Combining the results, Equation (15) implies , thus for any
for each fixed . Similar to Equation (14), we can include zero eigenvalues and can be seen as the distribution of , instead of
When a sequence of “random” distribution functions converges weakly in probability to a fixed distribution function, it ensures convergence in its quantile (Lehmann and Romano,, 2006, Lemma 11.2.1 (ii)). Hence, the critical value of converges in probability to , where is the -quantile of under the ME condition. In other words, for any
| (16) |
for each fixed .
Constructing and
We start by summarizing the analysis we have done so far. For the permutation test with , which implies that the 1-ME condition holds, we have shown that the unconditional distribution of the test statistic , denoted as , converges in distribution to and the critical value of permtation distribution converges in probability to , that is, the -quantile of . Since and are the eigenvalues of and , the asymptotic power depends on the difference between these matrices. Note that they are given as
which involves the second moments of the feature mappings.
Here, given , suppose that the matrices and coincide for some distribution pair . This implies that the permutation distribution and the unconditional distribution become asymptotically identical for such fixed , and thus we can expect that the test fails to distinguish those distributions and in this case. To formalize this scenario, consider an extension of the 1-ME condition to include second moments. Recall that the 1-ME condition is meaning that the first moments of the feature mappings are identical. Now, consider the 2-ME condition, which implies the coincidence up to the second moments of the feature mappings. i.e.,
Then, note that Proposition 2 guarantees that the 2-ME condition holds for any distribution pair with arbitrarily high probability . Also, observe that if then the covariance matrices of the feature mapping and are the same, and this indicates that the matrices and coincide. We again emphasize that and become asymptotically identical in this case. Therefore, for such the critical value converges in probability to the -quantile of the unconditional distribution, and combining this fact with Equation (14) and Equation (16), Slutsky’s theorem yields the convergence
| (17) |
for fixed . For a given , let and be distinct distributions in defined in Proposition 2. Then, we obtain the following result:
Since the probability is bounded by 1, by taking limits on both sides and applying the dominated convergence theorem, we get the desired result:
where the last inequality follows from Equation 17.
B.3 Proof of Corollary 4
As shown by Zhao and Meng, (2015, Appendix A.1), the unbiased estimator of MMD can be written as
where . By replacing the kernel with , we get
| (18) | ||||
Recall that we use the test statistics given as and in the permutation tests defined in Theorem 3 and Corollary 4, respectively. Also, throughout the proof of Theorem 4, we assume , which can be done without loss of generality as mentioned earlier in Section 2.3. Then, multiplying on both sides of Equation (18), we get
| (19) |
Our aim is to show that the unconditional distribution of the second and third terms and their permutation distribution are asymptotically the same under the ME condition. To start with, recall that the ME condition is implying Let us denote the exact value of this expectation as for such fixed . Then, as and are the sample means of and with finite variance, the law of large numbers ensures that
Therefore, by applying the continuous mapping theorem and Slutsky’s theorem, it can be shown that
| (20) |
where denotes the unconditional distribution of and denotes the asymptotic unconditional distribution of . Note that we derived the asymptotic unconditional distribution of in Equation (14).
For the case of the permutation distribution, we reformulate the -dimensional vectors as follows:
where . Then, we observe that and in Equation (19) can be written as and Let denote the permutation distribution of , defined by
and let denote the permutation distribution of defined similarly. Let be a random variable that is uniformly distributed over . If we can show and , then the desired results and are followed by Lemma 11. Since is a fixed number, it suffices to show that each component of converges to the corresponding component of in probability.
For , let us denote the -th component of , and as , and , respectively. Note that
where uses the the fact that for , and holds since is uniformly distributed over .
Furthermore, we note that
and also
Based on these observations, we have
Therefore, we now have for each , and this implies
Similarly, we can get
For the final step, letting denote the permutation distribution function of , and we apply the continuous mapping theorem for permutation distributions (Lemma 13) and Slutsky’s theorem extended for permutation distributions (Lemma 12) to conclude that
where is the asymptotic permutation distribution of under the ME condition. Therefore, in the same manner as Equation (16), we have
for fixed where denotes the -quantile of the distribution of Combining the result with Equation (20), Slutsky’s theorem yields
for fixed Hence, the lack of consistency of the test follows from Theorem 3.
B.4 Proof of Theorem 5
Recall that we use a permutation test defined as follows:
For pointwise consistency, our strategy is to find a sequence such that
is true for and , where and are constants depending on a given with . Similarly, if we use the test instead of , our goal is to show that To achieve this goal, we use the approach that replaces a random permutation quantile with a deterministic quantity (see Fromont et al.,, 2013; Kim et al.,, 2022; Schrab et al.,, 2023). First, we start by integrating frameworks to analyze tests and in a unified manner. Let us define four events,
and
| (21) | |||
| (22) |
Observe that implies and similarly implies Then, for an event we claim that implies and To see this, observe that Chebyshev’s inequality yields
Then we have
and we can get a similar result with Therefore, our focus is on carefully identifying an event and demonstrating that for sufficiently large and . To obtain such , we take a lower bound on the left-hand side and upper bound on the right-hand side in Equation (21) and Equation (22). Note that, as shown in Equation (18), the test statistic can be decomposed as
| (23) |
where
and for all
| (24) |
Therefore, and are less than or equal to , and this implies that satisfies Now, as a lower bound for and , we observe that
On the other hand, we note that and are both upper bounded by
where the inequality (a) follows the fact that the variance of bounded variable is also bounded, (b) follows from the fact that for all . For the critical value term, recall that the critical value is and if we substitute the test statistic with then the critical value is We claim that and are both upper bounded by
To see this, note that we have from Equation (23). Based on this fact, for given and , if a permutation satisfies then we also have This yields the desired result and further, we also get using for all
Combining the above results, we define an event
| (25) |
then it is straightforward to see that Now, our strategy is to show that the probability becomes 1 with sufficiently large , and . To start with, similar to Corollary 4, we can assume throughout the proof. Then the event becomes
and now we examine the three terms in the above event.
Expectation of
For we note that the test statistic is an unbiased estimator, and hence
| (26) | ||||
Upper bound for the variance of
For consider the decomposition of as follows:
| (27) | ||||
For the first term in the last equation, recall that the statistic is
Here, we emphasize that the inner product and similar terms are actually the sample means. To be specific, observe that
We note that as shown in Equation (29) when the samples and are given, then the statistic can be seen as a mean of observations of , functions of i.i.d. random variables defined as
| (28) | ||||
Hence, the conditional variance of in Equation (27) can be written as
| (29) |
Also, since for all , we note that Therefore, since its variance is also bounded, we conclude that the first term in Equation (27) is bounded by
| (30) | ||||
For the second term in Equation (27), we leverage the result of Kim et al., (2022, Appendix F). Let Then, there exists some positive constant such that the variance of the unbiased estimator of MMD can be bounded as
for
where is an independent copy of , and is an independent copy of We note that the kernel is bounded and Bochner’s theorem (Lemma 9) guarantees the existence of the nonnegative Borel measure that satisfies
Since for all and the measure is nonnegative, we have
| (31) |
for all Therefore, the kernel is bounded by and the term is bounded by . This yields
Now, we conclude that the second term in Equation (27) is bounded by
| (32) |
Upper bound for the critical value
In order to derive an upper bound for we use the property of U-statistics as done by Kim et al., (2022, Appendix E, F). First, observe that Chebyshev’s inequality yields
and by the definition of quantile, we have an upper bound of :
For the first term of the right-hand side, since the U-statistic is centered at zero under the permutation law (see e.g., Kim et al.,, 2022, Appendix F), we can deduce that Similarly, for the second term, observe that
Here, we note that this statistic has been carefully studied in Kim et al., (2022, Appendix F), and the following result holds true:
| (34) | ||||
where is a kernel defined as , and is a set of index defined as Here denotes the cardinality of a set , and implies Recall that is the approximated kernel defined in Equation (3), and we have a bound for all , in Equation (24). This implies and thus Using this observation and counting the number of (Kim et al.,, 2022, Appendix F) yields
for some positive constant regardless of the realized values of and Therefore, we get
and we conclude that
| (35) | ||||
for
Finding
Based on Equations (33) and (35) that we obtained so far, we can derive the result as follows:
for a constant Here, we consider a sequence that converges to zero, Then we get
Since and , there exist and such that and implies
Then we can deduce that
for and . Note that the sequence converges to 0 and this completes the proof.
B.5 Proof of Theorem 6
To begin with, we introduce some assumptions and useful facts for ease of analysis. Note that we use a translation invariant kernel which can be decomposed as
for Here, without loss of generality, we assume that If not, this can be done by scaling the bandwidth and with a constant while the kernel remains unchanged. To be specific,
holds where and then Now, note that our assumption yields Also, let us denote be a constant that satisfies
| (36) |
and
| (37) |
respectively.
For the proof of Theorem 6, we follow a similar approach taken in Schrab et al., (2023) to derive an upper bound for the uniform separation rate. First, as in the proof of Theorem 5, we define an event that can be utilized concurrently for analyzing both tests and . Consider the following two events
and suppose that there exists an event and . Also, for the following two events,
recall that implies and similarly implies Then Chebyshev’s inequality yields the desired result as
and similarly we can get
Therefore, our strategy is to identify such event To begin with, we carefully analyze the difference between the statistics and , following the logic similar to Kim and Schrab, (2023, Appendix E.11). From Equation (23), the statistic can be decomposed as
Here, we claim that the event
with a positive constant defined in Equation 37 satisfies To see this, we would first show and then show Now, note that the nonnegativity of the kernel guarantees that the inequality
Based on this observation, it can be shown that the right-hand side in the event is an upper bound for the right-hand side in the event , i.e.,
and this implies
For the inequality observe that
and plugging this equality into the event yields
Here, note that we have
and
for the constant defined in Equation 37. These two facts guarantee that the right-hand side in the event is an upper bound for the right-hand side in the event , i.e.,
and we conclude that
Now, we move our focus to find a sufficient condition for Observe that Chebyshev’s inequality yields
and by the definition of a quantile, we have an upper bound for :
For the first term of the right-hand side, since the U-statistic is centered at zero under the permutation law (see e.g., Kim et al.,, 2022, Appendix F), we can deduce that Then, since Markov’s inequality yields
we conclude that
| (38) |
is a sufficient condition for Therefore, our goal is to analyze the above equation and to find a proper rate of and the bandwidth in terms of and to uniformly control both types of errors.
Lower bound for
We first note that , and can be written in sense (Schrab et al.,, 2023, Appendix E.5):
where for denotes convoluton, and is an inner product defined on i.e., for Hence,
Now, we want to upper bound , and recall that we assumed the difference of the densities lying in a Sobolev ball . In this setting, as shown in Schrab et al., (2023, Appendix E.6), we have
for some fixed constant and positive constant Therefore, we conclude that
| (39) | ||||
for
Upper bound for
Recall the statistic that estimates the squared MMD with a single random feature, defined in Equation (28). Note that as shown in Equation (29), when the samples and are given, then the statistic can be seen as the expectation of observations of , functions of i.i.d. random variables Hence, we can decompose the variance of as follows:
Therefore, we have
| (40) | ||||
We start by analyzing the first term of the right hand side, . When is fixed, we note that is a two-sample U-statistic. We use the exact variance formula of the two-sample U-statistic (see e.g., page 38 of Lee,, 1990). To do so, let us define a kernel for a two-sample U-statistic,
where for a given , and write the symmetrized kernel as
Also, let
and
for Then, the variance of the two-sample U-statistic is
| (41) |
Here, note that we have for all , since for all Also, denote and , and observe that
| (42) | ||||
where inequality (a) is by the Cauchy–Schwarz inequality and inequality (b) is by the fact that for all Similarly, we can get Now, followed by (41) and for all , we can show that there exist universal constants such that
Then, observe
| (43) | ||||
where (a) is according to the equality and (b) follows from the fact that Young’s convolution inequality (Lemma 10) yields Since we have and for all Hence, using for all we can conclude that
| (44) |
for and
Now, we analyze the second term in the right hand side of Equation (40), . Note that can be written as
Therefore, for some positive constant we have
where uses Jensen’s inequality since the supports of both density and are uniformly bounded. Hence, we can get
| (45) | ||||
for
Upper bound for
Since the U-statistic is centered at zero under the permutation law, we have
Recall Equation (34) and note that the following result holds true (Kim et al.,, 2022, Appendix F):
Also, it can be shown that there exists some positive constant such that for any
where
Observe that
Therefore, we have
where the last inequality follows from the fact that for all and where , as shown in Schrab et al., (2023, Appendix E.3). A similar calculation shows that and are also upper bounded by the bound in the above inequality, thus we get
Using this observation and counting the number of (Kim et al.,, 2022, Appendix F) yields
for some positive constant Therefore, using for all we get
| (48) |
for some positive constants .
Upper bound for
Recall that is defined as
and its expectation is
Here we observe that
and similarly we have Therefore, we conclude that
| (49) | ||||
for some constant .
Upper bound for
We note that the variance of can be upper bounded as
Moreover, recall And then, for some positive constant , we also have
where the first inequality follows from for all and the last inequality follows from the result in Kim and Schrab, (2023, Appendix E.11). In a similar manner, we can get
Therefore, using for all we conclude that
| (50) | ||||
for some positive constants
Sufficient condition for Equation (38)
Recall that Equation (38),
is a sufficient condition for So far, in Equations (39), (47), (48), (49) and (50), we derived a lower bound for the left-hand side of the inequality, and upper bounds for the terms in the right-hand side of the inequality as follows:
Recall that and suppose that This assumption does not compromise our analysis, as ultimately we choose later satisfies this assumption. Now, observe that implies Also note that for . Then, by grouping similar terms, a sufficient condition for the above inequality is
We observe that the simultaneous satisfaction of the following four inequalities is a sufficient condition for the above inequality:
Now, we simplify the above inequalities to facilitate our discussion. Note that the inequality (i) is equivalent to the inequality denoted as :
where Also, observe that the inequality (ii) is equivalent to
Since and , a sufficient condition, denoted as (b), for simultaneously satisfying the inequalities (ii) and (iii) is
for For the inequality (iv), we note that we would like to assume This is because if not, the term in the inequality (iv) becomes larger than one, having the test become worthless. Under the assumption, observe that the term is dominated by the term . Therefore, the following inequality, denoting (c), is sufficient to show that the inequality (iv) holds:
| (51) |
where
In summary, a sufficient condition for satisfying the inequalities (i), (ii), (iii) and (iv) at once is the simultaneous satisfaction of the following three inequalities:
Then by the definition of uniform separation rate, for both tests or , we have
for and For the smallest order of possible, we choose the bandwidth for , and in this case, the condition on becomes Plugging these values into the above inequality, we get
for We note that our choice satisfies the condition for Equation (46) and the condition for Equation 51. By letting we conclude that
holds and this completes the proof.
B.6 Proof of Theorem 7
We start by recalling the event defined in Equation (25), equipped with the kernel :
As shown in the proof of Theorem 5, to control the probability of type II error of both tests and simultaneously, it is sufficient to show that Similar to the proof of Theorem 6, we analyze the terms in the event and derive a sufficient condition for the event . To start with, note that we have
for some positive constant from Equation (26) and (35). This gives
for some positive constant . Therefore, a sufficient condition for is the following inequality:
| (52) |
Upper bound for
Now we analyze the square root of the variance term. Recall the decomposition of the variance of in Equation (40):
We aim to analyze each term on the right-hand side and derive an upper bound for them. First, recall the result in Equation (43) and the assumption that the kernel is uniformly bounded by Then we have
| (53) |
for some positive constants
For the term , recall the statistic defined in Equation 28 and let us denote the statistic V with a single random feature as , i.e.,
Also, let be the difference between and Then, observe
where (a) follows from the inequality for all , (b) follows from , (c), (d) is according to and the last inequality holds with a constant Using for all , we conclude that
| (54) |
for some positive constants
For we follow a similar logic to Equation (40) through Equation (44). The difference is that instead of using , we use the following kernel for a two-sample U-statistic:
where Note that we have for all as shown in Equation (31). This fact corresponds to the condition for the inequality (b) in Equation 42. Also note that holds. This is the condition for the inequality (a) in Equation 43; therefore, we can follow the same logic to the previous analysis with kernel and we have a similar result to the first line in Equation 43:
for some positive constants We apply for all here and get the following result:
| (55) |
where are some positive constants. In summary, given Equations (53),(54) and (55), a valid upper bound for is
Sufficient condition for Equation 52
Recall that Equation 52,
is a sufficient condition for Utilizing an upper bound for the variance of we derived, a sufficient condition for Equation 52 to hold is
Note that for Then, by merging similar terms, a sufficient condition for the above inequality is
for some positive constants Now the satisfaction of the following four inequalities at once is a sufficient condition for the above inequality:
Here we note that the inequalities (i) and (ii) are equivalent to the following inequalities (a) and (b), respectively:
Considering the inequalities (a),(b),(iii) and (iv), for both tests or , we have
for some positive constant For the smallest order of possible, choose and then we have
By letting we conclude that
holds and this completes the proof.
B.7 Proof of Proposition 8
Recall the event defined in Equation (25):
and note that when , both tests and uniformly control the probability of type II error. Also, with in place, Equation 52 implies that a sufficient condition for is the following inequality:
| (56) |
where is some positive constant. Similar to the proof of Theorem 7, our objective is to find an upper bound for the right-hand side of the above inequality.
Upper bound for
Recall the decomposition in Equation (40)
Also, as previously noted in Equation 53 and (55), we derived upper bounds for the first term and the last term on the right-hand side of the above inequality, respectively:
We now analyze and derive an upper bound for the remaining term, We emphasize that, unlike the result in Equation (54) we stated in the proof of Theorem 7, a stronger upper bound can be established here since we assumed a smaller class of distribution pairs, specifically a class of Gaussian distribution with a common fixed variance, This favorable setting allows us to explicitly calculate the term and upper bound it with to a higher power than the general case. In detail, Lemma 17 yields
for some positive constant . Therefore, it holds that
We point out that there are two improvements on this upper bound, compared to the previous bound in Equation 54 that induces quadratic computational cost. Firstly, the power of in this upper bound is two, whereas it is one in the previous. Also, note that there is no additional term in the current bound such as that exists in the previous bound.
To sum up, a valid upper bound for the square root of the variance of satisfies
for some positive constants where the inequality follows from for , and .
Sufficient condition for Equation 56
Note that our objective is to find a sufficient condition for Equation 56,
Plugging the upper bound we derive in the preceding section into the above inequality, observe that a sufficient condition for Equation 56 to hold is
Now the simultaneous satisfaction of the following three inequalities is a sufficient condition for the above inequality:
where Observe that the inequalities (i) and (ii) are equivalent to the following inequalities (a) and (b), respectively:
| (a) | |||
| (b) |
Considering the inequalities (a), (b) and (iii) above, for both tests or , we have
for some positive constant and Therefore, we conclude that
with and .
B.8 Proof of Lemma 16
Recall that the statistic in Equation 28 is defined as
By taking conditional expectation with respect to and given we get
Our strategy is to decompose the term explicitly and simplify it with trigonometric identities. First, let be the independent copies of , and be the independent copies of . And, let us drop the subscripts with respect to on if the context is clear. Now, observe that the term the term can be expressed as
where
| (i) | |||
| (ii) | |||
| (iii) | |||
| (iv) | |||
| (v) | |||
| (vi) |
Here, observe that
| (i) | |||
where the last equality follows from . A similar calculation guarantees that the term can be written as
where
Now, note that the symmetry of the cosine function allows different representations of the above terms. For example, combined with the symmetry of () can also be written as
Then, observe that
and therefore,
where are independent copies of . Similarly, we can show that
where are independent copies of . Since
we can conclude that
Additionally, note that the second statement in the lemma can be proven in a similar manner, thereby completing the proof.
B.9 Proof of Lemma 17
Recall the class of Gaussian distributions with a common fixed variance :
Here we claim that the following inequality
| (57) |
holds for any distribution pair , with and some positive constant To prove the claim, one important observation is that the exact calculation of is feasible when we use the Gaussian kernel. To be specific, consider a Gaussian kernel with bandwidth ,
There have been several existing results on calculating MMD with a Gaussian kernel for Gaussian distributions. Among them, we leverage the result from Ramdas et al., (2015, Proposition 1), which is displayed on Lemma 15:
for a constant and We are now ready to analyze the two terms in Equation 57.
Exact value of
Recall Lemma 16 and observe that can be expressed with several terms:
To simplify the above equation, let us define Gaussian random variables such that
Then, observe that and , and these equivalences in distribution yield
We apply the calculation formula in Lemma 15 here and obtain
where we denote , and
Exact value of
Existence of constant
Our goal now is to show the existence of that satisfies
Plugging our previous results in the above equation, it is equivalent to
Note that the last term can be written as
Since and for we have for Also, observe that for , and for all thus we get Therefore, we can derive
and this implies that there exists some positive constant satisfying
This completes the proof of Lemma 17.