Computation and data driven discovery of topological phononic materials

Over the past decade, topological concepts have made far-reaching impacts on the theory of electronic band structures in condensed matters physics and materials sciences Kane and Mele (2005); Bernevig et al. (2006); Fu and Kane (2007). Thousands of topological electronic materials König et al. (2007); Hsieh et al. (2008); Xia et al. (2009) were theoretically proposed Vergniory et al. (2019); Zhang et al. (2019a); Tang et al. (2019) and some of them were experimentally verified, such as, topological insulators König et al. (2007); Hsieh et al. (2008); Xia et al. (2009), Dirac/Weyl semimetals Young et al. (2012); Wang et al. (2012); Wan et al. (2011); Weng et al. (2015); Huang et al. (2015), and nodal line semimetals Li et al. (2016); Schoop et al. (2016); Wu et al. (2016); Bian et al. (2016); Li et al. (2019). As the counterpart of electrons, phonons Ozawa et al. (2019) are energy quanta of lattice vibrations. They make crucial contributions to many physical properties, such as, thermal conductivity, superconductivity and thermoelectricity as well as specific heat. Similar to topological electronic nature, the crucial theorems and concepts of topology can be introduced to the field of phonons, called topological phononics (TPs) Li et al. (2018); Zhang et al. (2018); Xie et al. (2019); Liu et al. (2019a); Xia et al. (2019); Jin et al. (2018a); Wang et al. (2020); Jin et al. (2018b); Liu et al. (2019b); Li et al. (2020a, b); Zhang et al. (2019b, 2010a); Zhang and Niu (2015); Liu et al. (2017a, b); Wang and Zhao (2018); Miao et al. (2018); Liu et al. (2019c). In particular, TPs in solid materials are also correlated to some specified atomic lattice vibrations generally within a scale of THz frequency, thereby providing a rich platform for the investigation of various quasi-particles related with Bosons.

TPs have been theoretically or experimentally investigated in the materials. Several theoretical models, including monolayer hexagonal lattices Zhang et al. (2010a); Zhang and Niu (2015), Kekul$\acute{e}$ lattice Liu et al. (2017a, b) and one-dimensional (1D) chains Wang and Zhao (2018), were discussed. More recently, a number of real materials were predicted to host the Weyl TPs Li et al. (2018); Xie et al. (2019); Zhang et al. (2018); Liu et al. (2019a); Xia et al. (2019); Jin et al. (2018a); Wang et al. (2020); Li et al. (2020b), nodal-line TPs  Jin et al. (2018b); Liu et al. (2019b); Li et al. (2020a, b); Zhang et al. (2019b) and nodal-ring phonons Li et al. (2020a). Single Weyl TPs were predicted in noncentrosymmetric WC-type materials Li et al. (2018); Xie et al. (2019), exhibiting two-fold degenerate Weyl points with the $\pm 1$ topological charges. In FeSi-type materials, double Weyl TPs were predicted and then experimentally confirmed Zhang et al. (2018); Miao et al. (2018). In SiO₂, the coexisted single/double Weyl TPs was suggested Wang et al. (2020). In addition to occupying the discrete sites in the reciprocal space as Weyl points, these band crossing points can also continuously form nodal-line (e.g., in MgB₂ Liu et al. (2019b) and Rb₂Sn₂O₃ Li et al. (2020b)) or nodal-ring TPs (e.g., in graphene Li et al. (2020a), bcc C₈ Jin et al. (2018b) and MoB₂ Zhang et al. (2019b)). TPs exhibit the typical features of bulk-surface (edge) correspondence, which are rooted in different geometry phases of Hamiltonian. The existence of multiple critical physical phenomena, such as phononic valley Hall effect Zhang and Niu (2015), phononic quantum anomalous Hall-like effect, and phononic quantum spin Hall-like effect controlled by multiple-valued degrees of freedom Liu et al. (2017a), are beneficial to TPs’ applications. Because the topologically protected states are immune to backscattering Kane and Mele (2005); Bernevig et al. (2006); Fu and Kane (2007), TPs would be very promising for applications in the abnormal heat transport, solid-state refrigeration, and phonon wave-guides, and so on.

Unlike the topological electronic materials in which one only needs to focus on energy states near the Fermi level, phonons exhibit several distinct properties. First, there are no limits of Pauli exclusion principle. Second, each phonon mode, following Bose-Einstein statistics, can become practically active, due to thermal excitation. Third, phonons are charge neutral and spinless Bosons, which can not be directly influenced by the electric and magnetic fields. Hence, a full frequency analysis for all phononic branches is needed for the study of TPs. To date, a large-scale identification of TP materials remains challenging, because it is far more expensive to compute the phonon band dispersions than to calculate the electronic band structures. Hence, it is certainly more difficult to seek feasible TP materials in a high-throughput (HT) computational manner, as compared with the recent works in topological electronic materials Vergniory et al. (2019); Zhang et al. (2019a); Tang et al. (2019). In this work, we present an efficient and fully automated workflow that can screen the TP crossings in a large number of solid materials. Our results reveal that TPs extensively exist in phonon spectra of many known materials, which can be classified into single Weyl, high degenerate Weyl, and nodal-line (ring) TPs.

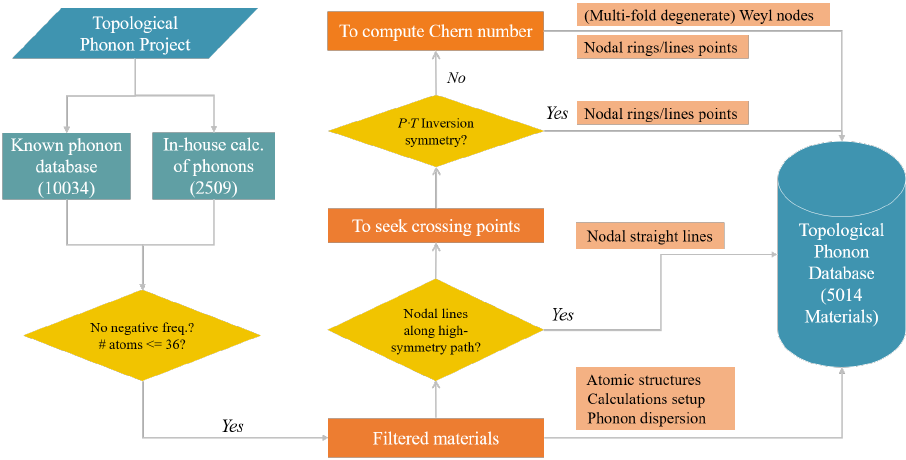
As shown in several prototypical materials Zhang et al. (2018); Li et al. (2018); Xie et al. (2019); Liu et al. (2019a); Xia et al. (2019); Jin et al. (2018a); Wang et al. (2020); Jin et al. (2018b); Liu et al. (2019b); Li et al. (2020a, b); Zhang et al. (2019b, 2010a); Liu et al. (2019c); Zhang and Niu (2015); Liu et al. (2017a, b); Wang and Zhao (2018); Miao et al. (2018); Liu et al. (2019c), identifying TPs requires several stages of manual selection and subjective human decisions. To enable the TPs discovery in an automatic manner, we present a high-throughput (HT) screening and data-driven approach to discover and categorize TPs, as described in Fig. 1 including the following four steps.

(1) Phonon data collection. To obtain phonon spectra for a large volume of known materials, our approach collects the force constant data from public phonon database pho (2018); Petretto et al. (2018), which includes about 10,000 materials. The data set was further augmented by our in-house computations for over 2000 materials possessing 58 common structural prototypes. It is well known that the calculated force constants are numerically sensitive to the choices of several parameters, e.g., the supercell size, K-point mesh and energy cutoff. To guarantee that the predictions are reliable, we filtered out the materials with notable imaginary frequencies ($<$ -0.5 THz) in the whole phononic momentum space.

(2) Nodal straight lines identification. We computed their band dispersions on the automatically generated high symmetry band paths Hinuma et al. (2017). If there exist degenerate phononic bands along high-symmetry paths, we will compute the Berry phases, by an integral of Berry connection ($\mathcal{A}_{n}(q)=i<\mu_{n,q}|\nabla_{q}|\mu_{n,q}>$) over a closed $q$ path Berry (1984)), for 20 consecutive points on each of these bands. The bands possessing continuous points with Berry phase values, $\pm$$\pi$, will be marked as the topologically non-trivial nodal straight lines.

(3) Crossing points identification. For the rest band paths in the phonon spectra, we systematically scan 50 consecutive points on each band path. In the entire frequency range, we considered the points possessing two adjacent eigenfrequencies less than 0.5 THz. For each point, we performed a minimization based on the conjugate gradient algorithm to obtain the local minimum of the frequency difference ($\Delta_{\textrm{freq}}$). The points with $\Delta_{\textrm{freq}}$ less than 0.2 THz were stored for further evaluation. After optimization, the identified inversion points may go anywhere in the entire reciprocal space. Therefore, we also checked if the points are at or off the high-symmetry paths.

(4) Crossing points assignment. The identified phononic crossing points were then divided into two groups based on the presence of both inversion ($P$) and time reversal ($T$) symmetries for each material. In a three-dimensional (3D) system with $PT$ symmetries, the Berry curvatures of non-degenerate phononic bands are forced to be zero because of the monopole feature of Berry curvature, and thus, the Weyl TPs would not occur in such system. Once the phononic bands at a degenerate point has an opposite non-zero Berry curvature along one direction, such topological non-trivial degenerate point has to occur continuously by forming nodal-line (ring) TPs, due to the continuity of phonon wave function in the 3D momentum space. As a result, we only looked for nodal-line (ring) TPs in materials with PT symmetries.

In noncentrosymmetic materials, the phonon dispersions possibly form single Weyl or high degenerate Weyl TPs, in addition to nodal-line (ring) TPs. In order to clarify these three types of TPs, we introduced another formula of Chern number, which can be derived by integrating Berry curvatures of a close surface Berry (1984) according to $n=\frac{1}{2\pi}\int_{\textbf{\emph{S}}}d\textbf{\emph{S}}\cdot\Omega(\textbf{\emph{q}}).$ Here, S is a closed surface which wraps the target crossing point, and the $\Omega(\textbf{\emph{q}})$ is the Berry curvature at the phonon momentum q on the selected closed surface. For the isolated crossing points at the high-symmetry band paths, we marked the points with nonzero integer Chern numbers (e.g., $\pm$1, $\pm$2) as single or high degenerate Weyl points. Otherwise, they would be labeled as nodal-ring points, given the fact that the nodal-line points were already extracted in step (2). Of course, it needs to be emphasized that many materials may yield many crossing bands along off-high-symmetry paths, which can be separate Weyl TPs or nodal-line (ring) TPs. In principles, this approach can be easily extended to investigate these crossing points.

In total, our approach revealed that 5014 materials exhibit TPs states (supplementary Table S1). Among them, we have identified three main categories of single Weyl, and high degenerate Weyl, and nodal-line (ring) TP materials. Although people have suggested several possible routes to break the time-reversal symmetry (TRS), such as, Lorentz force for ionic lattices Zhang et al. (2010b) and spin-lattice interactions for magnetic lattice  Sheng et al. (2006), it is impossible to break the TRS for phonon without any tunable external field. Therefore, we did not attempt to identify the intrinsic topological phonon insulators in our data. Here, we present three typical cases for each group, including half-Heusler LiCaAs alloy (single Weyl TPs), superconducting BeAu (high degenerate Weyl TPs), and ScZn with the PT symmetries (nodal-line/ring TPs).

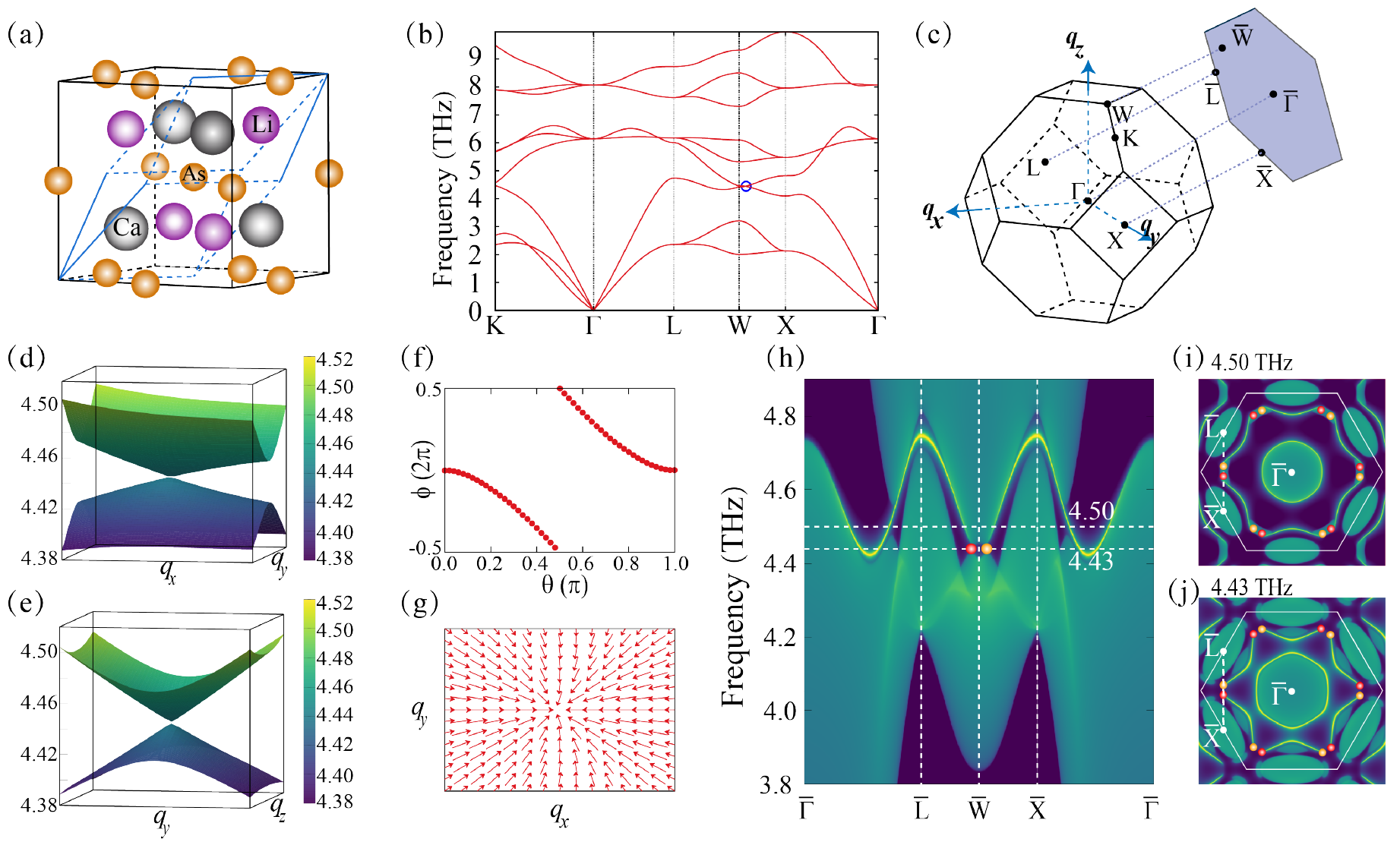
Half-Heusler compounds $ABX$ ($A$ = Li, Na, K, Rb, Cs; $B$ = Mg, Ca, Zn; $X$ = P, As) exhibit similar phonon spectra and here we use LiCaAs as an example (Fig. 2 a). At the frequency of 4.590 THz, the highest longitudinal acoustic and the lowest transverse optical branches cross at the (0.5000, 0.2175, 0.5175) point along the W-X high-symmetry path (Fig 2 b). This double degenerate point is protected by $C_{2}$ symmetry at the BZ boundary. The phononic dispersions around this crossing point holds the Weyl nodal feature, as shown in the 3D phononic dispersions in q_xy and q_yz in Fig 2 d and  2e. To further confirm its topological nature, the Wannier centers evolution has been derived for the 3rd phononic band (Fig 2 f). It gives a negative topological charge of -1 and this crossing acts like the sink of Berry curvature distributions in Fig 2 g. These results indicate that the crossing along the $X$-$W$ path is a single type-I Weyl TP. The nontrivial surface states of the (111) surface along the high-symmetry line have been derived in Fig 2 h and the opening arcs connecting two projected Weyl nodes with opposite topological charges can be observed at 4.43 and 4.50 THz (Fig 2 i-j), respectively.

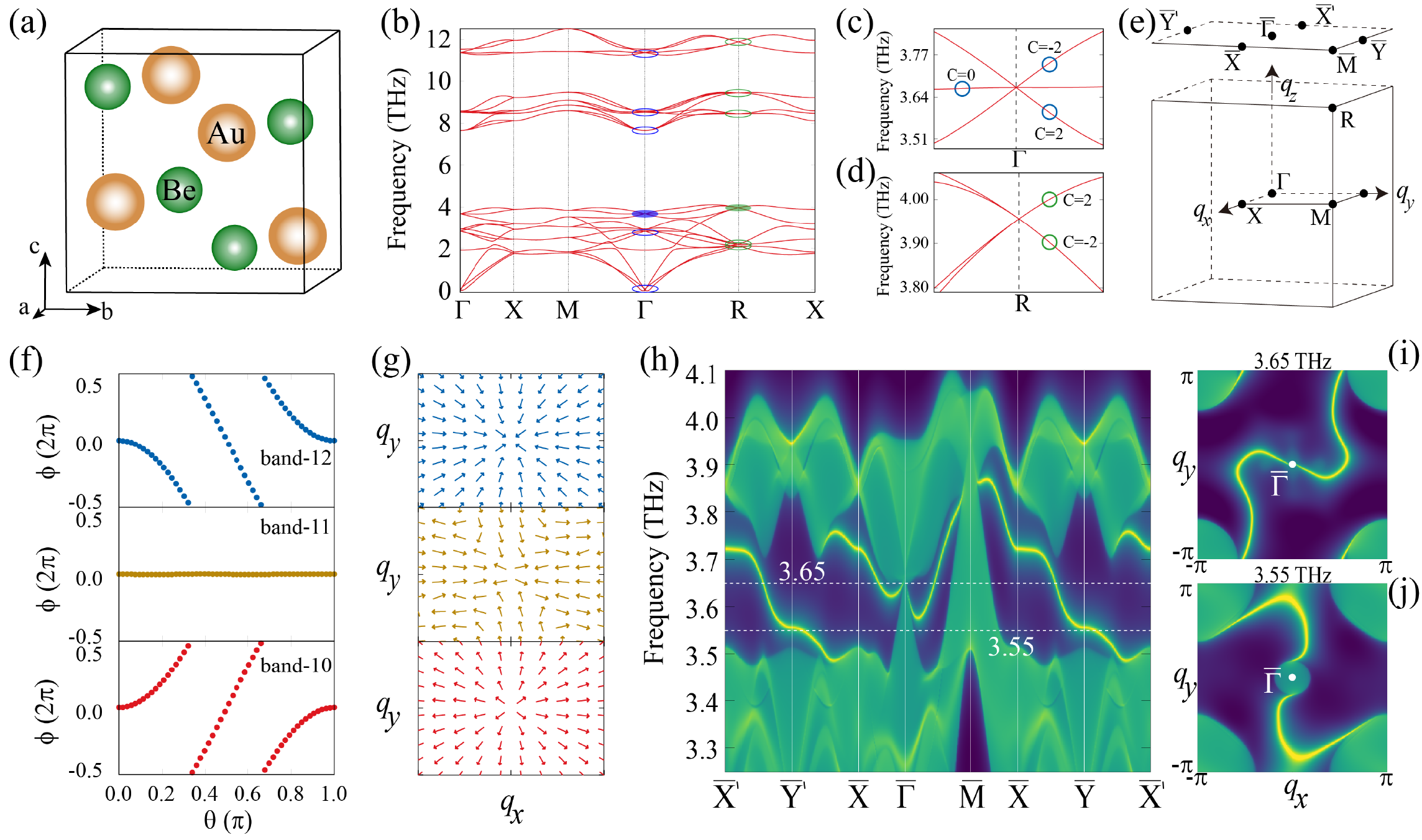
BeAu is a typical non-centrosymmetric superconductor with a transition temperature of 3.2 K Singh et al. (2019) and its structure crystallizes in a cubic symmetry with a space group of No. 198 ($P2_{1}3$, Fig. 3 a). In it phonon dispersion (Fig. 3 b), there exists two kinds of high degenerate Weyl points. At the $\Gamma$ point, the Hamiltonian of six threefold degenerate Weyl TPs (see blue circles in Fig. 3 b and c) and can be written as $\mathbf{H_{3}(k)\varpropto q\cdot C}$, where $\mathbf{q}$ is a wavevector and $\mathbf{C_{i}}$ are the rotation generators for spin-1 bosons  Zhang et al. (2018). As shown in Fig. 3c, each high degenerate Weyl node has three degenerate bands with respective Chern numbers of +2, 0 and -2. As illustrated in Fig. 3(f-h), the Wannier center evaluations for three phononic branches of the $\Gamma$ point with the frequency of 3.669 THz confirm that their nontrivial topological charges and their corresponding Berry curvatures show the sink and source behaviors. At the R point, the phonon spectrum exhibits six nontrivial fourfold degenerate Weyl points in Fig. 3 b and d. For each Weyl point, the Hamiltonian can be written as $\mathbf{H_{4}(k)\thicksim I_{2}\bigotimes(q\cdot\sigma)}$ where $\mathbf{I_{2}}$ are the $2$-order identity matrix and $\mathbf{\sigma_{i}}(i=x,y,z)$ are the three Pauli matrices. These high degenerate Weyl nodes induce the topological non-trivial surface states in Fig. 3 h, indicating that the two long non-trivial arcs connect two projected high degenerate Weyl points at $\bar{\Gamma}$ and $\bar{M}$.

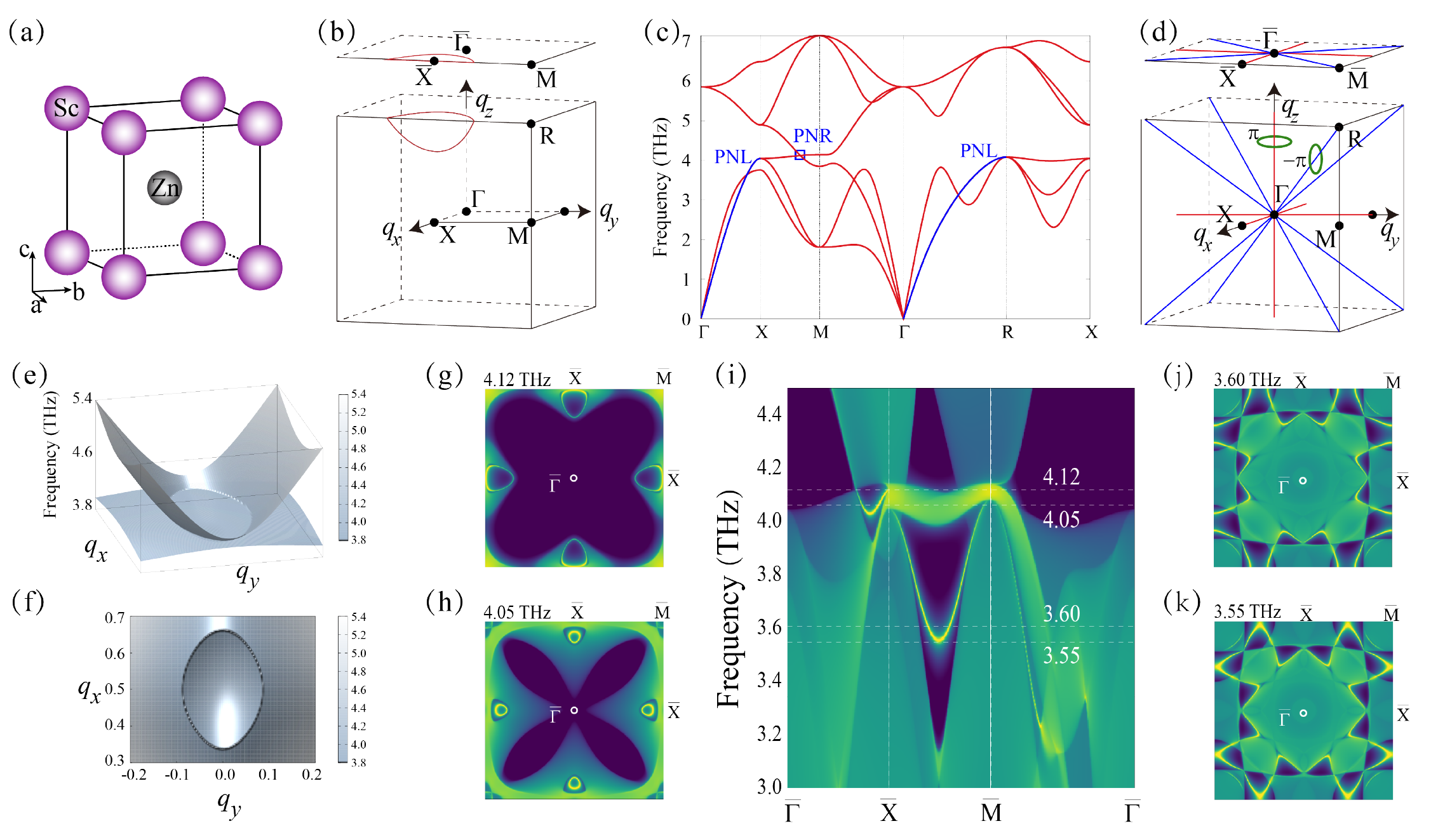
ScZn (Fig. 4a) is a well-known Zintle compound MX Palenzona and Manfrinetti (1997) (M = Sc, Y, La; X = Zn, Cd, Hg). In its phononic dispersion, there exist six nodal-ring TPs (Fig. 4e and 4f), surrounding the $M$ point on the BZ boundary (Fig. 4 b). ScZn also host phononic nodal straight lines along both $\Gamma$-X and the $\Gamma$-R directions (Fig. 4c and d). Both the nodal-ring and nodal straight line TPs exhibit the topological nontrivial feature with nonzero Berry phases. Their occurrences are protected by the mirror symmetry of ScZn. We have further derived the nontrivial surface TPs in Fig. 4 i. Two types of the drumhead-like nontrivial surface TP states can be observed, one is the nodal-ring TP induced closed loops around the $\bar{X}$ point (Fig. 4 g-h) and the other is the straight nodal line induced special pattern with fourfold symmetry on the (001) surface (see Fig. 4(j-k)).

Furthermore, in order to be experimentally observable, a candidate material is expected to possess distinct Weyl or nodal-line (ring) TPs and possible clean nontrivial surface TPs. For this purpose, we mathematically define the clean TP states for the nontrivial crossing points satisfying two conditions in bulk phonon spectra, (i) the crossing points have to be located at local minima with negligible or zero phononic density of states (DOS) ($<$ 0.01 states/atom/THz) and (ii) the dispersion at the local minima is sufficiently large ($\partial E/\partial q>$ 3 THz$\cdot$Å). On basis of these two criteria, we have filtered 322 clean TP materials (supplementary Table S5). For instance, The single type-I Weyl TPs in LiCaAs are clean, because they do not overlap with the other bulk phonon branches and have a zero phonon density at the frequency of 4.590 THz (Fig. 2 i and j). Among those 5014 TP materials 34 materials only have single Weyl TPs (supplementary Table S2) and 463 materials host mixed single Weyl TPs and nodal-line (ring) TPs as well as 268 materials host mixed single Weyl, high degenerate Weyl and nodal-line (ring) TPs (supplementary Table S4). In addition, we have found 449 materials host high degenerate Weyl TPs ( supplementary Table S4) and 4977 materials for topological nodal-line (ring) TPs (in supplementary Tables S3, S4 and S5).

In summary, we have developed a HT and data-driven approach to evaluate TPs over 10,000 materials using the existing phononic database and our in-house calculations. Our screening suggest that TP states are universally present in many materials, highlighting extensive possibilities for investigation of TPs and their potential applications in many fields.