Compression of M♮-convex Functions — Flag Matroids and Valuated Permutohedra
Abstract
Murota (1998) and Murota and Shioura (1999) introduced concepts of M-convex function and M♮-convex function as discrete convex functions, which are generalizations of valuated matroids due to Dress and Wenzel (1992). In the present paper we consider a new operation defined by a convolution of sections of an M♮-convex function that transforms the given M♮-convex function to an M-convex function, which we call a compression of an M♮-convex function. For the class of valuated generalized matroids, which are special M♮-convex functions, the compression induces a valuated permutohedron together with a decomposition of the valuated generalized matroid into flag-matroid strips, each corresponding to a maximal linearity domain of the induced valuated permutohedron. We examine the details of the structure of flag-matroid strips and the induced valuated permutohedron by means of discrete convex analysis of Murota.
Keywords: Discrete convex functions, compression,
flag matroids, permutohedra
MSC: 90C27 52B40
1 Introduction
Murota (1998) and Murota and Shioura (1999) introduced the concepts of M-convex function [12] and M♮-convex function [16], as discrete convex functions. Their original ideas can be traced back to Dress and Wenzel’s valuated matroids [3] introduced in 1992. See [13, 14, 15] for details about the theory of discrete convex analysis and its applications developed by Murota and others (also see [9, Chapter VII]).
In the present paper we consider a new operation defined by a convolution of sections of an M♮-convex function that transforms the given M♮-convex function to an M-convex function, which we call a compression of an M♮-convex function. For the class of valuated generalized matroids, which is a special class of M♮-convex functions, the compression induces a valuated permutohedron together with a decomposition of the valuated generalized matroid into flag-matroid strips, each corresponding to a maximal linearity domain of the valuated permutohedron. We examine the details of the structure of flag-matroid strips and the induced valuated permutohedron. We investigate the structures of the strip decomposition of valuated generalized-matroids, special M♮-convex functions by means of discrete convex analysis of Murota ([13]). The strip decomposition of a valuated generalized-matroid uniquely determines a valuated permutohedron, identified with a special M-convex function.
The present paper is organized as follows. In Section 2 we give some definitions and preliminaries about (i) submodular/supermodular functions and related polyhedra such as base polyhedra, submodular/supermodular polyhedra, and generalized polymatroids, and (ii) M-/M♮-convex functions and L-/L♮-convex functions. In Section 3 we introduce a new operation called a compression of M♮-convex functions, which leads us to the concepts of flag-matroid strips and a strip decomposition of M♮-convex functions in Section 4. In Section 5 we consider valuated generalized matroids, which are special M♮-convex functions, and examine implications of our results in valuated generalized matroids. The strip decomposition of a valuated generalized matroid gives a collection of strips of flag matroids [2], each inducing a sub-permutohedra. The compression of a valuated generalized matroid induces a valuated permutohedron whose maximal linearity domains corresponds to flag-matroid strips of the valuated generalized matroid. Section 6 gives some concluding remarks.
2 Definitions and Preliminaries
Let for a positive integer . For any and define , where . For any subset its characteristic vector in is defined by if and if . We also write instead of for .
2.1 Basics of submodular/supermodular functions
A function is called a submodular function if it satisfies
| (2.1) |
We assume that for any set function in the sequel. A negative of a submodular function is called a supermodular function. (Also see [4, 9].)
For a submodular function define
| (2.2) |
which is called the submodular polyhedron associated with submodular function . Also define
| (2.3) |
which is called the base polyhedron associated with submodular function . As is well known (see [9]), the base polyhedron is always nonempty (and is a face of ).
For a supermodular function we define in a dual manner the supermodular polyhedron
| (2.4) |
and the base polyhedron
| (2.5) |
For a submodular function define a supermodular function by
| (2.6) |
which is called the dual supermodular function of . Then we have . For more details about submodular/supermodular functions and associated polyhedra see [9, Chapter II], where submodular/supermodular functions defined on distributive lattices are also investigated and their base polyhedra are unbounded unless .
Define for any set . Also denote by the convex hull of in . When , we identify with .
When a submodular function is integer-valued, its submodular polyhedron and base polyhedron are integral (i.e., every vertex of the polyhedra is an integral vector). Moreover, we have
| (2.7) |
Most of the following arguments are valid even if we regard in place of as the underlying totally ordered additive group. When is integer-valued, we call and the submodular polyhedron and the base polyhedron, respectively, associated with as well. (This is the approach taken in [9], indeed.)
For a submodular function and a nonempty proper subset of define functions and by
| (2.8) |
We also define . We call the restriction of on and the contraction of by . Similarly we define the restriction and contraction for supermodular functions.
2.2 Permutohedra and sub-permutohedra
For a permutation we identify with the permutation vector in , which we denote by (or simply by when there is no possibility of confusion). Suppose that an integer-valued submodular function is given by for all . Then the base polyhedron has the extreme points, each being a permutation vector identified with a permutation of , which is called the permutohedron (or permutahedron) in .
For any permutation of we have a unique complete flag
| (2.9) |
such that for each is the set of the first elements of , i.e.,
-
1.
for each and
-
2.
, where is the characteristic vector of a set .
Denote the flag in (2.9) by .
Let us consider a polyhedron satisfying the following two:
-
(P1)
is the convex hull of a set of some permutation vectors.
-
(P2)
is a base polyhedron.
We call such a polyhedron a sub-permutohedron.333 We may call the sub-permutohedron a permutohedron, and an ordinary permutohedron a complete permutohedron, but we resist the temptation. A sub-permutohedron is precisely the Coxeter matroid polytope associated with a flag matroid of complete flag (see [2] and the discussions to be made in Section 5). A recent interesting appearance of a sub-permutohedron is from the theory of Bruhat order ([1]), due to Tsukerman and Williams [19], that every Bruhat interval polytope is a sub-permutohedron.
2.3 Base polyhedra, generalized polymatroids, and strong maps
Suppose that a submodular function and a supermodular function with satisfy the following inequalities
| (2.10) |
Then the polyhedron
| (2.11) |
is called a generalized polymatroid ([6, 10]). There exists a one-to-one correspondence between base polyhedra and generalized polymatroids up to translation along a coordinate axis as follows (see [9, Figure 3.7]).
Theorem 2.1 ([8, 9])
For the base polyhedron associated with a submodular function the projection of along an axis on the coordinate subspace given by the hyperplane is a generalized polymatroid in with , where is the restriction of on and is the restriction of on .
Conversely, every generalized polymatroid in is obtained in this way.
When a generalized polymatroid is a convex hull of -valued points (vertices), then it is called a generalized-matroid polytope, which can be identified with the family of subsets such that are vertices of the generalized-matroid polytope. The family is called a generalized matroid (see [7]).
An ordered pair of submodular functions is called a weak map if we have
| (2.12) |
Moreover, the ordered pair is called a strong map if we have
| (2.13) |
i.e., every ordered pair of contractions of and by is a weak map. The concept of strong map was originally considered for matroids (see [17, 18, 20]), and we adopt it to any submodular functions (or submodular systems).
We also have the following theorem.
Theorem 2.2
is a generalized polymatroid if and only if
is a strong map.
(Proof)
Relation (2.13) is equivalent to the following inequalities
| (2.14) |
Putting , (2.14) is rewritten in terms of the dual supermodular function of as
| (2.15) |
with . Because of the supermodularity of (2.15) is equivalent to
| (2.16) |
for all with , which is equivalent to (2.10).
A sequence of submodular functions is called a strong map sequence if for each the pair is a strong map. It follows from Theorem 2.2 that
-
(F1)
Given a strong map sequence , we have a sequence of generalized polymatroids for .
We also have the following.
-
(F2)
For a generalized polymatroid and such that the intersection of and the hyperplane is a base polyhedron (we call such a base polyhedron a section of and denote it by ). When is integral and is an integer, the section is integral. Moreover, letting be a section of with a submodular function , we have a strong map sequence , i.e., and are generalized polymatroids.
A strong map sequence with being matroid rank functions is called a flag matroid (see [2]).
2.4 M♮-convex functions and L♮-convex functions
Let be a polyhedral convex function such that
-
1.
its effective domain, , is a generalized polymatroid (hence nonempty) and
-
2.
every linearity domain of is a generalized polymatroid,
where a linearity domain (or affinity domain) of is for a linear function with some . Then is called an M♮-convex function444Here we employ another equivalent definition of M♮-convexity, instead of the original definition by means of the exchange axiom introduced by Murota and Shioura [16, 13]., which is due to Murota and Shioura [16, 13] (also see [9, Section 17]). The negative of an M♮-convex function is called an M♮-concave function (see Figure 1).

When of an M♮-convex function is a base polyhedron, is called an M-convex function (see [13]).555 M-convex functions were introduced earlier than M♮-convex functions by Murota (see [12, 13]). There is a one-to-one correspondence between M-convex functions and M♮-convex convex functions because of Theorem 2.1. Any concept related to M-/M♮-concave functions is defined in a natural way from that defined for M-/M♮-convex functions.
Now let be an M♮-convex function satisfying the following (a) and (b):
-
(a)
The effective domain of is an integral generalized polymatroid.
-
(b)
Every linearity domain of is also an integral generalized polymatroid.
Such an M♮-convex function can be identified with being restricted on the integer lattice . So we can consider an M♮-convex function . An integer-valued M-concave function with its effective domain being a matroid base polytope coincides with a valuated matroid due to Dress and Wenzel [3]. Also, if an M♮-convex function has an effective domain whose convex hull is a permutohedron, we call a valuated permutohedron.
For any M♮-convex function define the Legendre-Fenchel transform (or convex conjugate) of by
| (2.17) |
where . The function is called an L♮-convex function ([13]), which is equivalent to submodular integrally convex function due to Favati and Tardella [5]. The original is recovered from by taking another Legendre-Fenchel transform as follows.
| (2.18) |
(See [13, 14].) Hence there exists a one-to-one correspondence between M♮-convex functions and L♮-convex functions. Furthermore, Murota [13] showed the integrality property that (2.17) and (2.18) with being replaced by hold for any M♮-convex function . When is an M-convex function, its Legendre-Fenchel transform is what is called an L-convex function ([13]).
For any the subdifferential of at , denoted by , is defined by
| (2.19) |
The subdifferential of is defined similarly as
| (2.20) |
Then we have the following.
Lemma 2.3
We have if and only if .
(Proof) Note that both statements, and
, are equivalent to that
.
Remark: When is an M♮-convex function, subdifferentials for all are generalized polymatroids (or M♮-convex sets). Furthermore, if is defined on integer lattice , then for all are integral generalized polymatroids (restricted on ).
3 Compression of M♮-convex Functions
In this section we introduce a new transformation, called compression, of M♮-convex functions defined on the integer lattice . The compression of an M♮-convex function is a transformation of the M♮-convex function to an M-convex function .
Consider any M♮-convex function . We suppose the following:
-
•
The effective domain is bounded and full-dimensional. That is, is a full-dimensional generalized polymatroid (with finite ).
For each integer such that let be the M-convex function defined by
| (3.1) |
(cf. [13, 14, 15]). We call the -section of . Then put
| (3.2) |
and consider the convolution of all the sections , which is given by
| (3.3) |
where note that only if . The convolution of M-convex functions is an M-convex function ([13, 14, 15]). We call the compression of .
Theorem 3.1
For the compression of an M♮-convex function the Legendre-Fenchel transform of is given by
| (3.4) |
We also have
| (3.5) |
where the right-hand side is the Minkowski sum of the effective domains
for all .
(Proof)
For any we have from (3.3)
| (3.6) | |||||
This implies (3.4) and (3.5) because of the definition of the Legendre-Fenchel transform.
4 M♮-convex Functions and Strip Decomposition
Now, we introduce a concept of the strip decomposition of an M♮-convex function defined on the integer lattice . Let be an M♮-convex function with a full-dimensional and bounded effective domain .
4.1 Strip decomposition of M♮-convex functions
For the compression of and for any let us define and by
| (4.1) |
| (4.2) |
where recall (3.2) for the definition of . We call and linearity domains of and , respectively, associated with . We see from Lemma 2.3 that for every we have
| (4.3) |
This means that the linearity domains of are exactly the subdifferentials of .
Let be the collection of all maximal linearity domains of (or maximal subdifferentials of ). Then gives a polyhedral division of into generalized polymatroids. Since is full-dimensional, the dimension of is equal to .
For each maximal linearity domain of let be a vector in such that and put , which are independent of the choice of satisfying . Define and let be the restriction of on . Then we call a strip of associated with , where is the restriction of on . (See Figure 2 for an example of a strip of an M♮-concave function.) The collection of the strips for all is called the strip decomposition of .
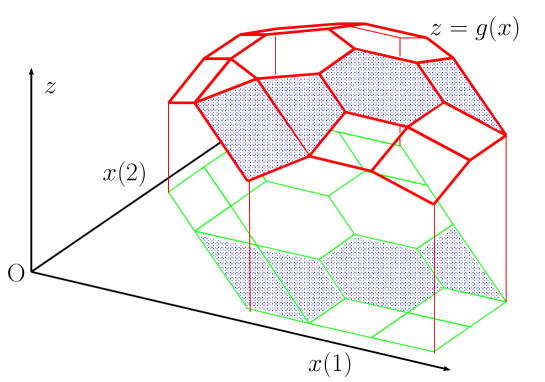
4.2 Strips viewed from parametric optimization
For any strip of an M♮-convex function associated with let be a vector in such that . Then consider a parametric optimization problem with a parameter described as follows.
| (4.4) |
where is the -dimensional vector of all ones. We then have the following theorem.
Theorem 4.1
For chosen as above there exist a finite sequence of values and that of integers such that the set of optimal solutions of for each is given by
| (4.5) |
(Proof) Because of the discrete structure of the M♮-convex function and the assumption that is bounded, there exists a finite sequence of values such that
-
1.
for each Problems for all have one and the same optimal solution set, and
-
2.
the set of optimal solutions of for each consists of more than one optimal solution and we have for each and .
Hence the optimal solution sets are expressed as (4.5) for a sequence of some integers that gives a division of the interval .
Here it should be noted that values depend on the choice of , while the vectors are uniquely determined by and , because of the assumptions that is full-dimensional and is a maximal linearity domain of .
5 Valuated Generalized Matroids
In this section we further investigate the structures of strips and their compressions for a class of valuated generalized matroids, which are special M♮-convex functions defined on the unit hypercube , in more details.
Let be an M♮-convex function such that , which is called a valuated generalized matroid. For any we often write as and regard as a function on in the sequel.
5.1 Compression of valuated generalized matroids and valuated permutohedra
For a valuated generalized matroid the compression of given by (3.3) becomes
| (5.1) |
where for , and we define if the minimum on the right-hand side does not exist for . Then the effective domain of the compression given by (3.6) is expressed by the following Minkowski sum:
| (5.2) |
Recall that .
Theorem 5.1
The effective domain of the compression
is a permutohedron.
Hence the compression is a valuated permutohedron, whose linearity
domains are sub-permutohedra.
(Proof) The right-hand side of (5.2) is the Minkowski
sum of the sets of the characteristic vectors of bases of uniform matroids
of rank for . Hence it is a base polyhedron
whose every extreme point
(a greedy solution in the sense of Edmonds [4]) is a permutation
of and vice versa.
It follows that (the convex hull of)
is a permutohedron and is
a valuated permutohedron.
Moreover, for any generic and every ,
in
(4.2) is a singlton, say. Then,
for each we have and
for some
with . Hence sets for form a complete flag
| (5.3) |
and it determines a permutation of with the permutation vector . It follows that every linearity domain of the compression is a sub-permutohedron.
5.2 Strips of valuated generalized matroids and flag matroids
For every we have the strip of associated with , which is characterized as follows. We identify with for any .
Theorem 5.2
For each we have a base family of
a matroid with a rank
function satisfying .
Moreover, the sequence of is that of
strong maps, i.e., a flag matroid.
(Proof) The present theorem follows from the definition of the strip
and
the assumption that is a valuated generalized matroid.
We call the flag matroid the flag matroid associated with a strip (or a flag-matroid strip) of the valuated generalized matroid . We see from Theorems 5.1 and 5.2 the following.
Theorem 5.3
Every valuated generalized matroid induces a valuated permutohedron by its compression and each flag-matroid strip of corresponds to a maximal linearity domain, a sub-permutohedron, of the induced valuated permutohedron.
Every valuated generalized matroid is regarded as a valuated permutohedron endowed with valuated flag-matroid strips, one for each maximal linearity domain of it.
6 Concluding Remarks
We have introduced the concepts of strip decomposition and compression of M♮-convex functions. We have examined the structures of valuated generalized-matroids by considering the strip decomposition of a valuated generalized-matroid into flag-matroid strips. The compression of a valuated generalized matroid induces a valuated permutohedron, a special M-convex function of Murota [13]. We thus have a new transformation, which we call the compression, of a valuated generalized-matroid (an M♮-convex function) to a valuated permutohedron (a special M-convex function). Every Bruhat interval polytope is known to be a sub-permutohedron, due to Tsukerman and Williams [19]. It is interesting to investigate Bruhat interval polytopes from a point of view of the strip decomposition of valuated generalized-matroids and also from a point of view of valuated permutohedra.
Acknowledgments
Satoru Fujishige’s work is supported by JSPS KAKENHI Grant Number 19K11839 and Hiroshi Hirai’s work is supported by JSPS KAKENHI Grant Number JP17K00029 and JST PRESTO Grant Number JPMJPR192A, Japan.
References
- [1] A. Björner and F. Brenti: Combinatorics of Coxeter Groups (Graduate Texts in Mathematics 231), Springer, 2005.
- [2] A. V. Borovik, I. M. Gelfand and N. White: Coxeter Matroids (Progress in Mathematics, Vol. 216) (Birkhäuser, Boston, 2003).
- [3] A. W. M. Dress and W. Wenzel: Valuated matroids. Advances in Mathematics 93 (1992) 214–250.
- [4] J. Edmonds: Submodular functions, matroids, and certain polyhedra. Proceedings of the Calgary International Conference on Combinatorial Structures and Their Applications (R. Guy, H. Hanani, N. Sauer and J. Schönheim, eds., Gordon and Breach, New York, 1970), pp. 69–87; also in: Combinatorial Optimization—Eureka, You Shrink! (M. Jünger, G. Reinelt and G. Rinaldi, eds., Lecture Notes in Computer Science 2570, Springer, Berlin, 2003), pp. 11–26.
- [5] P. Favati and F. Tardella: Convexity in nonlinear integer programming. Ricerca Operativa 53 (1990) 3–44.
- [6] A. Frank: Generalized polymatroids. Proceedings of the Sixth Hungarian Combinatorial Colloquium (Eger, 1981); also, Finite and Infinite Sets, I (A. Hajnal, L. Lovász and V. T. Sós, eds., Colloquia Mathematica Societatis János Bolyai 37, North-Holland, Amsterdam, 1984), pp. 285–294.
- [7] A. Frank and É. Tardos: Generalized polymatroids and submodular flows. Mathematical Programming 42 (1988) 489–563.
- [8] S. Fujishige: A note on Frank’s generalized polymatroids. Discrete Applied Mathematics 7 (1984) 105–109.
- [9] S. Fujishige: Submodular Functions and Optimization (North-Holland, 1991), Second Edition (Elsevier, 2005).
- [10] R. Hassin: Minimum cost flow with set-constraints. Networks 12 (1982) 1–21.
- [11] K. Murota: Matroid valuation on independent sets. Journal of Combinatorial Theory 69B (1997) 59–78.
- [12] K. Murota: Discrete convex analysis. Mathematical Programming, Ser. A 83 (1998) 313–371.
- [13] K. Murota: Discrete Convex Analysis (SIAM Monographs on Discrete Mathematics and Applications 10, SIAM, 2003).
- [14] K. Murota: Discrete convex analysis: A tool for economics and game theory, Journal of Mechanism and Institution Design, 1 (2016) 151–273.
-
[15]
K. Murota: A survey of fundamental operations on discrete
convex functions of various kinds. Optimization Methods and Software (to appear)
DOI: 10.1080/10556788.2019.1692345 - [16] K. Murota and A. Shioura: M-convex function on generalized polymatroid. Mathematics of Operations Research 24 (1999) 95–105.
- [17] J. Oxley: Matroid Theory (Oxford University Press, Oxford, 1992).
- [18] A. Schrijver: Combinatorial Optimization—Polyhedra and Efficiency (Springer, Heidelberg, 2003).
- [19] E. Tsukerman and L. Williams: Bruhat interval polytopes. Advances in Mathematics 285 (2015) 766–810.
- [20] D. J. A. Welsh: Matroid Theory (Academic Press, London, 1976).