Comprehensive Performance Analysis of
Homomorphic Cryptosystems for
Practical Data Processing

Oblivious data processing can solve a spectrum of security issues, mitigate a wide range of business risks, facilitate migration to the cloud for the companies that are still on the fence, and help with compliance in the view of new data protection regulations such as GDPR, PDPA or CCPA. Cryptography is an obvious candidate on how to achieve obliviousness; however, typically cryptosystems do have the capability for any meaningful manipulations with the encrypted data.

Homomorphic encryption is a type of encryption that is capable of carrying out specific types of computations directly on ciphertext and generates an encrypted result which, when decrypted, matches the result of operations would they have been performed on the plaintexts [1]. Typically, homomorphic cryptosystems possess a homomorphic property with respect to one or several arithmetic operations, i.e., allowing for encrypted addition, multiplication, etc. However, there also are some other types of homomorphic cryptosystems, e.g., Goldwasser-Micali probabilistic cryptosystem that allows for encrypted XOR (addition modulo 2) [2].

Strictly speaking, a homomorphic cryptosystem could be defined as follows. Assume $e(\cdot)$ and $d(\cdot)$ to be the encryption and decryption functions, $v_{1},\ldots,v_{n}$ to be plaintext values, and $f(\cdot)$ to be an $n$-ary plaintext operation. Then, if there exists an operation $g(\cdot)$ such that for any $v_{1},\ldots,v_{n}$: $f(v_{1},\ldots,v_{n})=d(g(e(v_{1}),\ldots,e(v_{n})))$, then the encryption scheme is said to have a property of homomorphism, i.e., it preserves operation $f(\cdot)$.

For arithmetic homomorphic cryptosystems (ones that preserve arithmetic operations), we can distinguish two groups: partially and fully homomorphic cryptosystems. Using partially homomorphic encryption, it is possible to perform only one operation on encrypted data—multiplication or addition—but not both [3]. There are numerous ciphers capable of performing partially homomorphic encryption, but determining a feasible cipher for real world applications can be exceedingly challenging, primarily due to functional requirements and efficiency concerns. A cryptosystem that is capable of performing both addition and multiplication over ciphertexts is called a fully homomorphic cryptosystem.

This work seeks to examine the practicality of homomorphic cryptography in the light of computing resources that are available today. For this work we have chosen five implementations of homomorphic cryptosystems; namely, three fully homomorphic cryptosystems: Homomorphic Encryption Library (HElib), Simple Encrypted Arithmetic Library (SEAL), and an implementation of the somewhat¹¹1Somewhat fully homomorphic scheme is a scheme that enables both addition and multiplication but exposes limits to the number of operations that can be executed. Typically, this refers to a scheme that can perform many additions and a small amount (sometimes, just one) multiplications. Some fully homomorphic schemes overcome this by executing a procedure called bootstrapping — an operation of “refreshing” the ciphertext. Bootstrapping is usually a very expensive operation. Unlike PyAono, both HElib and SEAL implement bootstrapping, which makes them fully homomorphic. homomorphic encryption scheme by Y. Aono et al. (PyAono); and our own implementations of Paillier (additive) and ElGamal (multiplicative) partially homomorphic cryptosystems.

This choice was influenced by several factors. First, we were looking for solutions that reached a certain level of maturity and recognition in the research community, as an indication that both the underlying cryptographic scheme and the implementation can be considered thoroughly reviewed. Cryptographic analysis of the schemes and analysis of implementation fidelity were not in the scope of this work. In addition to that, we only considered implementations that had their license indicate that it is allowed to carry out research on them. Furthermore, after extensive attempts we were still unable to get some of the available implementations to work due to compilation errors, lack of documentation, runtime errors, etc. Those were eventually removed from the experiments.

The examination presented in this paper arose from our research on practicality of emulating fully homomorphic computations using partially homomorphic cryptosystems and a trusted re-encryption agent equipped with a smart computation scheduler that enables re-encryptions between the partial schemes to be done while other portions of homomorphic computation are carried out. In this research, our own implementations of Paillier and ElGamal are used as partially homomorphic cryptosystems in the emulation; thus, they were also selected for the final list of contenders. The work presented in this paper is a continuation of our earlier short analysis on the topic [4].

For each cipher, we obtained the source code and applied minor tweaks to measure precisely the computation time with the execution of each operation. We additionally tested the performance of each cipher under a full spectrum of cryptosystem initialization parameters; the data collected from these tests is presented in charts in the annex of the paper.

The rest of the paper is structured as follows: Section II reviews some of the previous works in a similar direction; Section III discusses details of the comparative testing that was carried out; Section IV presents the findings and a short commentary; Section V presents a concluding discussion of the results and indicates directions of future work; performance charts are appended at the end of the paper.

There is a multitude of homomorphic schemes: unpadded RSA [5] and ElGamal [6] schemes are multiplicative homomorphic; Benaloh [7], Paillier [8], and Boneh-Goh-Nissim [9] schemes are additive homomorphic. However, a fully homomorphic scheme, i.e., a scheme that supports both addition and multiplication, remained undiscovered for a long time and was referred to by some researchers as a “holy grail of cryptography” [10]. A breakthrough in the area was made in 2009 when Dr. Craig Gentry has published his work on the first fully homomorphic encryption scheme [11].

Most researchers agree that currently the Gentry’s scheme is impractical for general-purpose computations due to its poor performance. There have been multiple studies of its performance as well as attempts to improve it [12, 13, 14], but it is still considered to be far from being practical.

Although several researchers have approached the issue of measuring the performance of homomorphic computations and comparing it to plaintext computations, there are not many empirical results in that direction. Certain insights could be gathered from the work by Gentry et al. that covers implementation details of his scheme and how its behavior in practice [14]. An attempt to secure third-party applications by amending the binaries to work over homomorphically encrypted data was done by Tople et al. [15]. Performance analysis done in their project AutoCrypt could provide an approximate understanding of performance drop after switching from plaintext to homomorphic computations. Thorough performance analysis of Gentry’s scheme was done by Liu et al. [16]. However, the work omits to compare homomorphic computation performance to the plaintext alternative and focuses on the relation between the computation time and key length.

Preliminary research was carried out to select the candidates for comparison. Five solutions were identified based on existing use cases, code availability, license, and implementation stability.

Due to the irregular range of data values collected, charts were plotted using a logarithmic scale. Please note that differences in bar length are not linearly proportional to differences in computation time.

Tests were run on the three basic operations, namely addition, subtraction, and multiplication. Division was left out due to SEAL, PyAono and Paillier not supporting division, whereas for ElGamal division is completely equivalent to multiplication. We considered applying our number encoding scheme to support division in SEAL and PyAono, but eventually decided that the results are more informative if the implementations are tested in their “vanilla” form.

Results were obtained using operations on ciphertexts from all five ciphers, as well as on plaintext for scale. All tests were conducted without bootstrapping (where applicable), as the strategy on deciding when to execute this computationally expensive procedure is non-trivial and varies from one use-case to another. All three plain text operations ran at the same efficiency, which was on average $\approx 1.8\times 10^{-9}$ seconds per one execution, which is also $\approx 10^{4}$ times as fast as the fastest homomorphic operation, which appeared to be multiplication by ElGamal.

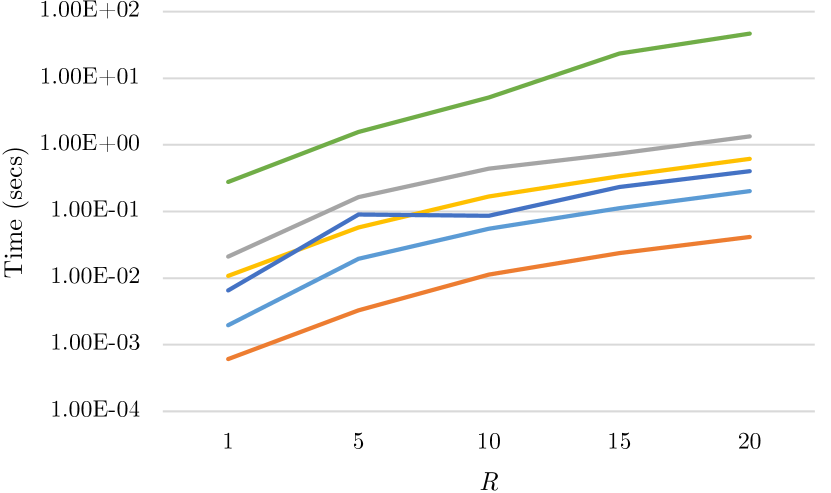
All tests conducted were ran on 1000 pairs of 2-digit plaintext numbers. Each test was repeated 5 times and the mean result was tabulated for each operation. Aggregated results are presented in Figure 1. Paillier possesses the fastest addition, subtraction, and key generation operations, ElGamal — the fastest multiplication operation, HElib demonstrates the fastest encryption, and SEAL has the fastest decryption. PyAono was least efficient in four operations, namely multiplication, encryption, decryption, and key generation. Its addition and subtraction operations are also relatively inefficient, topping only that of HElib. During the research period, PyAono was declared deprecated, so it is unlikely to be optimized in the future. We still include the empirical numbers for PyAono for reference, but we will not focus on it in discussing the results.

Results clearly suggest that partially homomorphic cryptosystems are significantly faster at homomorphic operations and relatively on par in en-/decryption times with HElib and SEAL. Paillier and ElGamal are consistently about 20–30k times slower than plaintext. At the same time, HElib is 500k times slower for subtraction, 1.6M times slower for addition, and almost 19M times slower for multiplication. SEAL shows relatively acceptable performance on addition and subtraction: 60–100k times slower than plaintext; but 15M times slower for multiplication (not to forget that it doesn’t support division). PyAono takes the middle ground performing around 235k times slower than plaintext addition/subtraction; however, it absolutely breaks records in all other measurements: 2.2B (sic!) times slower in multiplication, 4.5 seconds for en-/decryption and over 700 seconds (sic!) for key generation.

Let us imagine that we use an emulation of fully homomorphic properties based on Paillier and ElGamal and a trusted re-encryption agent. Re-encryption agent uses a serialized strategy of executing a computation: it performs all operations that are possible with current encryptions, then re-encrypts intermediate values into a different encryption scheme, and continues (see Algorithm 2 for an example). Note that this strategy does not involve any parallelization; e.g., step 2 does not need to wait for the agent to finish encryption of $c$ and $d$, and the agent can start the decryption of $p$ in step 4 while step 3 is not yet complete. We also do not take into account network latency and speed between the compute engine and the agent.

Using the numbers that are presented in Figure 1, we can estimate the comparative efficiency of SEAL and HElib and the emulation described above on some sample tasks. E.g., on a simple task of computing $r=(a\times b)+(c\times d)$, the emulation works with the same speed as SEAL and 1.46 times slower than HElib.

A slightly more complex task of computing a weighted sum of a large number of elements $\left(a_{1}\times w_{1}+\cdots+a_{n}\times w_{n}\right)$ is emulated at 0.9 the time of SEAL and is 1.35 times slower than HElib. However, if we assume that the numbers were pre-encrypted (therefore eliminating the initial encryption), emulation finishes in 0.63 the time of SEAL and 0.75 the time of HElib. Somewhere in between these two scenarios is such task as secure linear regression: the weights $w_{i}$ of the model are pre-encrypted, but the values $a_{i}$ that we are applying the model to are coming in online; in this case, the emulation performs the computation in 0.81 the time of SEAL and 1.1 the time of HElib.

As we can see, on more complex tasks, the emulation can be on par or even better than fully homomorphic schemes. It is important to notice that in reality, these theoretical numbers will be significantly corrected in favor of the emulation due to 1) bootstrapping in fully homomorphic schemes, that will happen on more complex tasks and is a very expensive operation ($\approx$600 ms bootstrapping a single ciphertext in HElib as compared to 1–20 ms for a homomorphic operation [24]); 2) parallelization of work between the agent and the compute engine, which can significantly improve overall timings for the emulation.

It is also clear that due to the requirement in re-encryption under the emulation protocol, the en-/decryption efficiency of the partially homomorphic scheme becomes crucial for the overall performance. We plan to continue our work on optimizing Paillier and ElGamal en-/decryption procedures and investigate other partially and fully homomorphic cryptosystems that could provide better overall performance.