Complexity classification of counting graph homomorphisms modulo a prime number

Andrei A.Bulatov and Amirhossein Kazeminia

Abstract

Counting graph homomorphisms and its generalizations such as the Counting Constraint Satisfaction Problem (CSP), its variations, and counting problems in general have been intensively studied since the pioneering work of Valiant. While the complexity of exact counting of graph homomorphisms (Dyer and Greenhill, 2000) and the counting CSP (Bulatov, 2013, and Dyer and Richerby, 2013) is well understood, counting modulo some natural number has attracted considerable interest as well. In their 2015 paper Faben and Jerrum suggested a conjecture stating that counting homomorphisms to a fixed graph $\mathcal{H}$ modulo a prime number is hard whenever it is hard to count exactly, unless $\mathcal{H}$ has automorphisms of certain kind. In this paper we confirm this conjecture. As a part of this investigation we develop techniques that widen the spectrum of reductions available for modular counting and apply to the general CSP rather than being limited to graph homomorphisms.

1 Introduction

Counting problems have been intensively studied since the pioneering work by Valiant [Val79b, Val79a]. For a problem from NP the corresponding counting problem asks about the number of accepting paths of a nondeterministic Turing machine that solves the problem. In many cases this may be a more tangible number. For example, in the Constraint Satisfaction Problem (CSP) the question is to decide the existence of an assignment of values to variables subject to a given collection of constraints. Thus, in the Counting CSP the objective is to find the number of such assignments. The counting CSP also allows for generalizations such as partition functions [Bar16, BG05] that yield connections with areas such as statistical physics, see, e.g. [JS93, LS81].

Counting CSP.

While the general Counting CSP is of course #P-complete, certain restrictions of the problem, first, allow us to model specific combinatorial problems, and, second, give rise to counting problems of lower complexity. One of the most natural ways to restrict a CSP is to require that the constraints allowed in instances belong to a certain set $\Gamma$ , often called a constraint language. The resulting decision problem is then denoted by $\mathsf{CSP}(\Gamma)$ and the corresponding counting problem by $\mathsf{\#CSP}(\Gamma)$ . As was noticed by Feder and Vardi [FV98], the CSP can also be reformulated in terms of homomorphisms of relational structures. It means that problems of the form $\mathsf{CSP}(\Gamma),\mathsf{\#CSP}(\Gamma)$ can also be defined as $\mathsf{CSP}(\mathcal{H}),\mathsf{\#CSP}(\mathcal{H})$ for some relational structure $\mathcal{H}$ , in which the question is, given a relational structure $\mathcal{G}$ , decide the existence (find the the number) of a homomorphism from $\mathcal{G}$ to $\mathcal{H}$ . In particular, if $\mathcal{H}$ is a graph, we obtain the $\mathcal{H}$ -Coloring problem concerning graph homomorphisms [HN04]. Its counting variant is called the $\#\mathcal{H}$ -Coloring problem.

The complexity of the $\#\mathcal{H}$ -Coloring problem was characterized by Dyer and Greehill [DG00]. It turns out that this problem can be solved in polynomial time if and only if every connected component of $\mathcal{H}$ is either an isolated vertex, or a complete graph with all loops present, or a complete bipartite graph. Otherwise $\#\mathcal{H}$ -Coloring is #P-complete. This theorem was generalized through a sequence of intermediate results [DGP07, CH96, BD07, BG05] to a complexity classification of $\mathsf{\#CSP}(\mathcal{H})$ for arbitrary finite relational structures $\mathcal{H}$ by Bulatov [Bul13] and Dyer and Richerby [DR13].

Modular counting.

In this paper we study the problem of counting solutions to a CSP modulo a prime number. If a constraint language $\Gamma$ or a relational structure $\mathcal{H}$ is fixed, this problem is denoted $\#_{p}\mathsf{CSP}(\Gamma)$ or $\#_{p}\mathsf{CSP}(\mathcal{H})$ . More precisely, in $\#_{p}\mathsf{CSP}(\mathcal{H})$ the objective is, given a relational structure $\mathcal{G}$ , to find the number of homomorphisms from $\mathcal{G}$ to $\mathcal{H}$ modulo $p$ . Problems of this form naturally belong to the class $\mathsf{Mod}_{p}P$ [CH89, Her90], in particular, to $\oplus$ P if $p=2$ . A priori the relationship of the complexity of such problems with that of regular counting problems is unclear, except modular counting cannot be harder than exact counting. Later we will see examples when modular counting problems are much easier than their exact counterparts.

Since we are not aware of any study of the general modular Counting CSP, we discuss here counting graph homomorphisms modulo $p$ . A systematic study of this problem was initiated by Faben and Jerrum [FJ13]. One of the first observations they made concerns the cases where exact and modular counting clearly deviate from each other. As Faben and Jerrum observed, the automorphism group $\mathsf{Aut}(\mathcal{H})$ of graph $\mathcal{H}$ plays a very important role in solving the $\#_{p}\mathsf{CSP}(\mathcal{H})$ problem. Let $\varphi$ be a homomorphism from a graph $\mathcal{G}$ to $\mathcal{H}$ . Then composing $\varphi$ with an element from $\mathsf{Aut}(\mathcal{H})$ we again obtain a homomorphism from $\mathcal{G}$ to $\mathcal{H}$ . Thus, $\mathsf{Aut}(\mathcal{H})$ acts on the set $\mathsf{Hom}(\mathcal{G},\mathcal{H})$ of all homomorphisms from $\mathcal{G}$ to $\mathcal{H}$ . If $\mathsf{Aut}(\mathcal{H})$ contains an automorphism $\pi$ of order $p$ (that is $p$ is the smallest number such that $\pi^{p}$ is the identity permutation), the cardinality of the orbit of $\varphi$ is divisible by $p$ , unless $\pi\circ\varphi=\varphi$ , that is, the range of $\varphi$ is the set of fixed points $\mathsf{Fix}(\pi)$ of $\pi$ ( $a\in V(\mathcal{H})$ is a fixed point of $\pi$ if $\pi(a)=a$ ). Let $\mathcal{H}^{\pi}$ denote the subgraph of $\mathcal{H}$ induced by $\mathsf{Fix}(\pi)$ . We write $\mathcal{H}\rightarrow_{p}\mathcal{H}^{\prime}$ if there is $\pi\in\mathsf{Aut}(\mathcal{H})$ such that $\mathcal{H}^{\prime}$ is isomorphic to $\mathcal{H}^{\pi}$ . We also write $\mathcal{H}\rightarrow^{*}_{p}\mathcal{H}^{\prime}$ if there are graphs $\mathcal{H}_{1},\dots,\mathcal{H}_{k}$ such that $\mathcal{H}$ is isomorphic to $\mathcal{H}_{1}$ , $\mathcal{H}^{\prime}$ is isomorphic to $\mathcal{H}_{k}$ , and $\mathcal{H}_{1}\rightarrow_{p}\mathcal{H}_{2}\rightarrow_{p}\dots\rightarrow_{p}\mathcal{H}_{k}$ .

Lemma 1.1 ([FJ13]).

Let $\mathcal{H}$ be a graph and $p$ a prime. Up to an isomorphism there is a unique smallest (in terms of the number of vertices) graph $\mathcal{H}^{*p}$ such that $\mathcal{H}\rightarrow_{p}^{*}\mathcal{H}^{*p}$ , and for any graph $\mathcal{G}$ it holds

\mathsf{hom}(\mathcal{G},\mathcal{H})\equiv\mathsf{hom}(\mathcal{G},\mathcal{H}^{*p})\pmod{p}.

Moreover, $\mathcal{H}^{*p}$ does not have automorphisms of order $p$ .

Often Lemma 1.1 helps to reduce the complexity of modular counting.

Example 1.2.

Consider the 3-Coloring problem. Since permuting colors in a proper coloring produces another proper coloring, the number of 3-colorings of a graph is always $0\pmod{3}$ , that is, counting 3-colorings modulo 3 is trivial. From a more formal perspective, the $\#_{3}3$ -Coloring problem is equivalent to $\#_{3}\mathsf{CSP}(K_{3})$ , where $K_{3}$ is a complete graph with 3 vertices. Any permutation of the vertices of $K_{3}$ is an automorphism, and the cyclic permutation of all vertices has order $3$ . Therefore by Lemma 1.1 $\#_{3}\mathsf{CSP}(K_{3})$ is equivalent to counting homomorphisms to an empty graph.

Graphs in Lemma 1.1 can be replaced with relational structures without changing the result, see Lemma 2.2 in Section 2. We will call relational structures without order $p$ automorphisms $p$ -rigid. By Lemmas 1.1, 2.2, and 2.3 it suffices to determine the complexity of $\#_{p}\mathsf{CSP}(\mathcal{H})$ for $p$ -rigid structures $\mathcal{H}$ .

Faben and Jerrum [FJ13] proposed the following conjecture that we slightly rephrase and generalize.

Conjecture 1.3 (Faben and Jerrum, [FJ13]).

For a $p$ -rigid structure $\mathcal{H}$ the problem $\#_{p}\mathsf{CSP}(\mathcal{H})$ is $\mathsf{Mod}_{p}$ P-complete (solvable in polynomial time) if and only if $\mathsf{\#CSP}(\mathcal{H})$ is #P-complete (solvable in polynomial time.

The existing results.

The research in modular counting has mostly been aimed at verifying Conjecture 1.3. In [FJ13] Faben and Jerrum proved their conjecture in the case when $\mathcal{H}$ is a tree and $p=2$ . This result has been extended by Göbel et al. first to the class of cactus graphs [GGR14] and then to the class of square-free graphs [GGR16] (a graph is square-free if it does not contain a 4-cycle), still for $p=2$ . Next, the same authors confirmed Conjecture 1.3 for trees and arbitrary prime $p$ [GLS18]. Kazeminia and Bulatov [KB19] confirmed the conjecture in the case of square-free graphs and arbitrary prime $p$ . Focke et al. [FGRZ20, FGRZ21] used some techniques from [KB19] to prove the conjecture for $K_{4}$ -minor-free graph and $p=2$ . Finally, Lagodzinski et al. [LGCF21] considered quantum graphs and quantum homomorphisms, where quantum graphs are simply formal sums of graphs, and quantum homomorphisms are homomorphism-like constructions for quantum graphs defined in an appropriate way. They proved that $\#_{p}\mathsf{CSP}(\mathcal{H})$ for a quantum graph is $\mathsf{Mod}_{p}$ P-complete whenever it is hard for any of its component graphs. Also, they showed that $\#_{p}\mathsf{CSP}(\mathcal{H})$ is polynomial time interreducible with $\#_{p}\mathsf{CSP}(\mathcal{H}^{\prime})$ , where $\mathcal{H}^{\prime}$ is a certain bipartite graph. Finally, they confirmed Conjecture 1.3 for bipartite graphs that do not contain $K_{3,3}$ without an edge or a domino as an induced subgraph (a domino is a bipartite graph obtained from $K_{3,3}$ by removing two non-incident edges). The last two results use intricate structural properties of graphs and a massive case analysis.

In this paper we confirm Conjecture 1.3 for arbitrary graphs.

Methodology.

In order to avoid extensive case analysis we employ the technique that has been very successful in the study of the decision CSP [Jea98, BJK05] and the exact Counting CSP [BD07]. This technique identifies what relations can be added to a constraint language without changing the complexity of the corresponding problem. Two of the constructions used in the papers mentioned above are also used here. They are primitive positive definitions and adding constants.

A relation or a predicate $R$ is said to be primitive-positive definable or pp-definable in a constraint language $\Gamma$ or a relational structure $\mathcal{H}$ , if it can be expressed by a first order formula that only allows existential quantifiers, conjunctions, predicates from $\Gamma$ or $\mathcal{H}$ , and the equality relation. Such formulas are called primitive-positive (pp-)formulas. It was proved in [Jea98], [BD07] that if $R$ is pp-definable in a language $\Gamma$ then $\mathsf{CSP}(\Gamma\cup\{R\})$ is polynomial time reducible to $\mathsf{CSP}(\Gamma)$ and $\mathsf{\#CSP}(\Gamma\cup\{R\})$ is polynomial time reducible to $\mathsf{\#CSP}(\Gamma)$ .

For modular counting it is possible to strengthen pp-definitions. For a prime $p$ we say that $R$ is $p$ -mpp-definable (pp-definable modulo $p$ ) in $\Gamma$ if there exists a pp-formula as above

R(x_{1},\dots,x_{k})=\exists y_{1},\dots,y_{s}\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s})

such that $R(a_{1},\dots,a_{k})=1$ if and only if the number of assignments to $y_{1},\dots,y_{s}$ such that $\Phi(a_{1},\dots,a_{k},y_{1},\dots,y_{s})$ is true is not divisible by $p$ . The first part of the following theorem is fairly straightforward, but this is the second part that enables our study.

Theorem 1.4.

Let $p$ be a prime, $\Gamma$ a constraint language. Then

(1)

if $R$ is $p$ -mpp-definable in $\Gamma$ , then $\#_{p}\mathsf{CSP}(\Gamma\cup\{R\})$ is polynomial time reducible to $\#_{p}\mathsf{CSP}(\Gamma)$ ;
(2)

if the relational structure whose predicates are the predicates from $\Gamma$ is $p$ -rigid, and $R$ is pp-definable in $\Gamma$ , then $R$ is $p$ -mpp-definable in $\Gamma$ .

While the analogous reduction in [Jea98, BJK05] is straightforward and that in [BD07] uses interpolation techniques, the main tool in proving Theorem 1.4 is careful counting homomorphism numbers showing that the non-existence of the right pp-formula contradicts $p$ -rigidity by using Möbius inversion formula.

The second way to expand a constraint language is to add constant relations. Let $\Gamma$ be a constraint language whose relations are on a set $H$ . Then $C_{a}=\{(a)\}$ , $a\in H$ , denotes the unary relation containing only one tuple. Such relations are called constant relations. Let $\Gamma^{*}=\Gamma\cup\{C_{a}\mid a\in H\}$ . It was proved in [BD07] that $\mathsf{\#CSP}(\Gamma^{*})$ is polynomial time reducible to $\mathsf{\#CSP}(\Gamma)$ , and in [BJK05] it was proved that under certain conditions $\mathsf{CSP}(\Gamma^{*})$ is polynomial time reducible to $\mathsf{CSP}(\Gamma)$ . The next theorem was first proved in [FJ13] for graphs.

Theorem 1.5.

If $\Gamma$ is $p$ -rigid, then $\#_{p}\mathsf{CSP}(\Gamma^{*})$ is polynomial time reducible to $\#_{p}\mathsf{CSP}(\Gamma)$ .

We emphasise that Theorems 1.4 and 1.5 are true not only for graphs, but for general relational structures as well.

Modular counting of graph homomorphisms.

The following is the main result of the paper.

Theorem 1.6.

Let $p$ be prime and $\mathcal{H}$ a $p$ -rigid graph. Then $\#_{p}\mathsf{CSP}(\mathcal{H})$ is solvable in polynomial time if and only if every connected component of $\mathcal{H}$ is either an isolated vertex, or a complete graph with all loops present, or a complete bipartite graph. (Note that $p$ -rigidity implies the the number of vertices in each complete component is less than $p$ and the number of vertices on each side of the bipartition in bipartite components is at most $p-1$ .) Otherwise it is $\mathsf{Mod}_{p}$ P-complete.

In order to prove Theorem 1.6 we first prove a generalization (Theorem 5.17) of Theorem 8.15 from [HIK11] to bipartite graphs. Theorem 5.17 severely restricts the possible form of automorphisms of direct products of graphs. It again allows us to prove that certain relations are pp-definable by showing that the non-existence of such relations contradicts $p$ -rigidity. Interestingly, Theorem 5.17 does not hold for general relational structures.

The results of [LGCF21] show that it suffices to prove Theorem 1.6 only for bipartite graphs $\mathcal{H}$ . To explain how the argument goes in the case of bipartite graphs we need to introduce another counting problem and a special type of bipartite graphs.

Let $\alpha,\beta\not\equiv 0\pmod{p}$ . Then $\#_{p}\mathsf{BIS}(\alpha,\beta)$ is the problem defined as follows: given a bipartite graph $\mathcal{G}$ with bipartition $L_{\mathcal{G}},R_{\mathcal{G}}$ , find the value

\mathcal{Z}_{\alpha,\beta}(\mathcal{G})=\sum_{I\in\mathsf{IS}(\mathcal{G})}\alpha^{|I\cap L_{\mathcal{G}}|}\cdot\beta^{|I\cap R_{\mathcal{G}}|}

modulo $p$ . The problem of computing the function $\mathcal{Z}_{\alpha,\beta}(\mathcal{G})$ is proven to be $\mathsf{Mod}_{p}$ P-hard in [GLS18].

The special type of bipartite graphs we need is shown in Figure 1. More precisely, a bipartite graph $\mathcal{G}=(V,E)$ is said to be a thick Z-graph if its vertices can be partitioned into four sets $A,B,C,D$ , where $A,C\subseteq L_{\mathcal{G}},B,D\subseteq R_{\mathcal{G}}$ , such that the sets $A\cup B,C\cup B,C\cup D$ induce complete bipartite subgraphs of $\mathcal{G}$ , and there are no edges between vertices from $A\cup D$ .

If $|A|,|B|,|C|,|D|\not\equiv 0\pmod{p}$ then $\#_{p}\mathsf{BIS}(\alpha,\beta)$ for appropriate $\alpha,\beta$ can be reduced to $\#_{p}\mathsf{CSP}(\mathcal{G})$ . Next, we prove, Theorem 6.5, that such a reduction is still possible if there is an induced subgraph $\mathcal{G}$ that is a thick Z-graph and we can simulate the conditions $|A|,|B|,|C|,|D|\not\equiv 0\pmod{p}$ using $p$ -mpp-definitions in the language of $\mathcal{H}$ . This last step is done through a careful analysis of the unary relations $p$ -mpp-definable in $\mathcal{H}$ . Due to some limitations of Theorem 5.17 we need to consider cases $p=2$ and $p>2$ separately. However, in both cases the the argument uses Lemma 3.2(1)

Organization.

The paper is organized as follows. In Section 2 we introduce the basic definitions and results. Then in Section 3 we prove several auxiliary results that concern the existence of homomorphisms with special properties. In Section 4 we prove reductions for pp- and $p$ -mpp-definitions, and for adding constant relations. It also contains an important auxiliary result. The structure of automorphisms of direct products of graphs is analysed in Section 5. A proof of Theorem 1.6 is given in two steps. After some helpful preparations in Section 6.1 we start in Section 6.2 with identifying the requirements to induced thick Z-subgraphs of $\mathcal{H}$ sufficient for hardness. Then we prove that a required thick Z-subgraph always exists. The cases $p=2$ and $p>2$ are considered separately. The case $p>2$ is considered in Section 6.3, and the case $p=2$ in Section 6.4. Section 7 contains proof omitted from the previous sections due to similarity with the existing results.

2 Preliminaries

2.1 Constraint Satisfaction Problem

Structures and Homomorphisms

We use $[n]$ to denote the set $\{1,...,n\}$ . A relational signature $\sigma$ is a collection of relational symbols each with assigned positive integer, the arity of the symbol. A relational structure $\mathcal{H}$ with signature $\sigma$ is a set $H$ and an interpretation $R^{\mathcal{H}}$ of each $R\in\sigma$ , where $R^{\mathcal{H}}$ is a relation or a predicate on $H$ whose arity equals that of $R$ . The set $H$ is said to be the base set or the universe of $\mathcal{H}$ . We will use for the base set the same letter as for the structure, only in the regular font. A structure with signature $\sigma$ is often called a $\sigma$ -structure. Structures with the same signature are called similar.

Let $\mathcal{G},\mathcal{H}$ be similar structures. A homomorphism from $\mathcal{G}$ to $\mathcal{H}$ is a mapping $\varphi:G\to H$ such that for any $R\in\sigma$ , say, of arity $r$ , if $R^{\mathcal{G}}(a_{1},\dots,a_{r})$ , $a_{1},\dots,a_{r}\in H$ , is true then $R^{\mathcal{H}}(\varphi(a_{1}),\dots,\varphi(a_{r}))$ is true. The set of all homomorphisms from $\mathcal{G}$ to $\mathcal{H}$ is denoted $\mathsf{Hom}(\mathcal{G},\mathcal{H})$ . The cardinality of $\mathsf{Hom}(\mathcal{G},\mathcal{H})$ is denoted by $\mathsf{hom}(\mathcal{G},\mathcal{H})$ . A homomorphism $\varphi$ is an isomorphism if it is bijective and the inverse mapping $\varphi^{-1}$ is a homomorphism from $\mathcal{H}$ to $\mathcal{G}$ . If $\mathcal{H},\mathcal{G}$ are isomorphic, we write $\mathcal{H}\cong\mathcal{G}$ .

Automorphism group

For a relational structure $\mathcal{H}$ , an automorphism is an injective homomorphism into itself. The automorphisms of $\mathcal{H}$ form a group with respect to composition denoted $\mathsf{Aut}(\mathcal{H})$ . The set of all automorphisms with $a\in H$ as a fixed point is the stabilizer of $a$ denoted $\mathsf{Stab}_{\mathcal{H}}(a)$ . It is always a subgroup of $\mathsf{Aut}(\mathcal{H})$ .

We will use two basic facts from group theory. First, for any prime $p$ , if $G$ is a group and $|G|\equiv 0\pmod{p}$ , then $G$ contains an element of order $p$ . In particular, if $|\mathsf{Aut}(G)|\equiv 0\pmod{p}$ , then $\mathcal{H}$ has an automorphism of order $p$ . We call such automorphisms $p$ -automorphisms.

Second, if $H$ is a subgroup of a group $G$ then $G:H$ denotes the set of cosets of $G$ modulo $H$ . In this case Lagrange’s theorem holds claiming $|G|=|H|\cdot|G:H|$ .

Two views on the CSP

The simplest way to define the Constraint Satisfaction Problem is as follows: Given similar relational structures $\mathcal{G},\mathcal{H}$ , decide whether there is a homomorphism from $\mathcal{G}$ to $\mathcal{H}$ . The CSP is often restricted in certain ways. The most widely studied way to restrict the CSP, and the one we use here, is to fix the target structure $\mathcal{H}$ . By $\mathsf{CSP}(\mathcal{H})$ we denote the problem, in which given a structure $\mathcal{G}$ similar to $\mathcal{H}$ , the goal is to decide whether there is a homomorphism from $\mathcal{G}$ to $\mathcal{H}$ . In the counting version of $\mathsf{CSP}(\mathcal{H})$ denoted $\mathsf{\#CSP}(\mathcal{H})$ the goal is to find $\mathsf{hom}(\mathcal{G},\mathcal{H})$ for a given structure $\mathcal{G}$ .

There is another view on the CSP that is widely used in the literature and that will be very useful from the technical perspective. Firstly, note that for a $\sigma$ -structure $\mathcal{H}$ the collection of interpretations $R^{\mathcal{H}}$ , $R\in\sigma$ , is just a set of relations. We call a set of relations over some set $H$ a constraint language over $H$ . Thus, for every relational structure $\mathcal{H}$ there is an associated constraint language $\Gamma_{\mathcal{H}}$ . Conversely, every (finite) constraint language $\Gamma$ can be converted into a relational structure $\mathcal{H}_{\Gamma}$ such that $\Gamma_{\mathcal{H}_{\Gamma}}=\Gamma$ in a straightforward way, although in this case there is much room for the choice of a signature.

Definition 2.1.

Let $\Gamma$ be a constraint language on a set $H$ , called the domain. The Constraint Satisfaction Problem $\mathsf{CSP}(\Gamma)$ is the combinatorial function problem with:
Instance: a pair $\mathcal{P}=(V,\mathcal{C})$ where $V$ is a finite set of variables and $\mathcal{C}$ is a finite set of constraints. Each constraint $C\in\mathcal{C}$ is a pair $\langle\mathbf{s},R\rangle$ where

•

$\mathbf{s}=(v_{1},v_{2},...,v_{m})$ is a tuple of variables from $V$ of length $m$ , called the constraint scope;
•

$R\in\Gamma$ is an $m$ -ary relation, called the constraint relation.

Objective: Decide whether there is a solution of $\mathcal{P}$ , that is, a mapping $\varphi:V\to H$ such that for each constraint $\langle\mathbf{s},R\rangle\in\mathcal{C}$ with $\mathbf{s}=(v_{1},\dots,v_{m})$ the tuple $(\varphi(v_{1}),\dots,\varphi(v_{m}))$ belongs to $R$ .

In the counting version of $\mathsf{CSP}(\Gamma)$ denoted $\mathsf{\#CSP}(\Gamma)$ the objective is to find the number of solutions of instance $\mathcal{P}$ .

It is well known, see e.g. [FV98] and [BKW17] that problems $\mathsf{CSP}(\mathcal{H})$ and $\mathsf{CSP}(\Gamma_{\mathcal{H}})$ can be easily translated into each other. The same is true for $\mathsf{\#CSP}(\mathcal{H})$ and $\mathsf{\#CSP}(\Gamma_{\mathcal{H}})$ . Thus, we use the two forms of the CSP interchangeably.

2.2 Modular counting

In this paper we study modular counting CSPs, where the objective is to find the number of homomorphisms (solutions) modulo a prime number $p$ . We fix $p$ throughout the paper. More precisely, for a structure $\mathcal{H}$ or a constraint language $\Gamma$ in $\#_{p}\mathsf{CSP}(\mathcal{H})$ , $\#_{p}\mathsf{CSP}(\Gamma)$ the objective is to find the number of homomorphisms or solutions for a given instance modulo $p$ .

As is mentioned in the introduction, a major complication when studying the complexity of modular counting $\#_{p}\mathsf{CSP}(\mathcal{H})$ are $p$ -automorphisms of $\mathcal{H}$ . We call a structure $\mathcal{H}$ $p$ -rigid if it does not have $p$ -automorphisms. Also, we call a language $\Gamma$ $p$ -rigid if $\mathcal{H}_{\Gamma}$ is $p$ -rigid.

As was mentioned, $p$ -automorphisms allow for a reduction of $\#_{p}\mathsf{CSP}(\mathcal{H})$ as follows. Let $\pi$ be a $p$ -automorphism of $\mathcal{H}$ . By $\pi^{(\ell)}$ we denote the composition $\pi\circ\dots\circ\pi$ of $\ell$ applications of $\pi$ . For an instance $\mathcal{G}$ and any homomorphism $\varphi$ from $\mathcal{G}$ to $\mathcal{H}$ the mappings $\pi^{(\ell)}\circ\varphi$ , $\ell\in[p]$ , are also homomorphisms. This means that the homomorphism $\varphi$ makes a contribution into $\mathsf{hom}(\mathcal{G},\mathcal{H})$ other than $0\pmod{p}$ only if $\pi\circ\varphi=\varphi$ . This happens only if $\varphi$ maps $\mathcal{G}$ to the set of fixed points $\mathsf{Fix}(\pi)$ of $\pi$ , that is, $\mathsf{Fix}(\pi)=\{a\in H\mid\pi(a)=a\}$ . By $\mathcal{H}^{\pi}$ we denote the relational structure obtained by restricting $\mathcal{H}$ to $\mathsf{Fix}(\pi)$ .

Lemma 2.2.

If $\mathcal{H}$ is relational structure, and $\pi$ an $p$ -automorphism of $\mathcal{H}$ , then for any structure $\mathcal{G}$

\mathsf{hom}(\mathcal{G},\mathcal{H})\equiv\mathsf{hom}(\mathcal{G},\mathcal{H}^{\pi})\pmod{p}

Proof.

Let $H$ and $H^{\pi}$ denote the universe of $\mathcal{H}$ and $\mathcal{H}^{\pi}$ respectively. For a similar structure $\mathcal{G}$ with universe $G$ , we show that the number of homomoprhisms which use at least one element of $H-H^{\pi}$ is $0\pmod{p}$ .

Given any homomorphism $\varphi:\mathcal{G}\rightarrow\mathcal{H}$ , consider the homomorphism $\pi\circ\varphi$ . This is still a homomorphism which is different from $\varphi$ as there is some element $v\in G$ such that $\varphi(v)\in H-H^{\pi}$ , and so $\pi(\varphi(v))\neq\varphi(v)$ . On the other hand $\pi^{(p)}\circ\varphi$ is just $\varphi$ , as $\pi$ is an $p$ -automorphism. So $\pi$ acts as a $p$ -automorphism on the set of homomorphisms from $\mathsf{Hom}(\mathcal{G},\mathcal{H})$ that use at least one element from $H\setminus H^{\pi}$ . Since this automorphism has no fixed points, the size of this set must be 0 $\pmod{p}$ . ∎

The binary relation $\rightarrow_{p}$ on relational structures is defined as follows. For relational structures $\mathcal{H}$ and $\mathcal{K}$ , we have $\mathcal{H}\rightarrow_{p}\mathcal{K}$ if and only if there exists an automorphism $\pi$ of $\mathcal{H}$ , of order $p$ , such that $\mathcal{H}^{\pi}=\mathcal{K}$ . If there exists a sequence of structures $\mathcal{H}_{1},\mathcal{H}_{2},\dots,\mathcal{H}_{\ell}$ such that $\mathcal{H}=\mathcal{H}_{1}\rightarrow_{p}\mathcal{H}_{2}\rightarrow_{p}\dots\rightarrow_{p}\mathcal{H}_{\ell}=\mathcal{K}$ , we write $\mathcal{H}\rightarrow_{p}^{*}\mathcal{K}$ and say that $\mathcal{H}$ $p$ -reduces to $\mathcal{K}$ . If $\mathcal{K}$ is $p$ -rigid, it is called a $p$ -reduced form associated with $\mathcal{H}$ . The following lemma is proved by a light modification of the proof in [FJ13].

Lemma 2.3 ([FJ13]).

For a relational structure $\mathcal{H}$ there is (up to isomorphism) exactly one $p$ -rigid structure $\mathcal{H}^{\star p}$ such that $\mathcal{H}\rightarrow_{p}\mathcal{H}^{\star p}$ .

2.3 Factors, products and homomorphisms

We will need several concepts related to homomorphisms. Recall that a $\sigma$ -structure $\mathcal{H}$ is a said to be an expansion of a $\sigma^{\prime}$ -structure $\mathcal{G}$ if $H=G$ , $\sigma^{\prime}\subseteq\sigma$ (with arities of predicate symbols in $\sigma^{\prime}$ being equal in $\sigma,\sigma^{\prime}$ ), and $R^{\mathcal{H}}=R^{\mathcal{G}}$ for any $R\in\sigma^{\prime}$ .

A pair $(\mathcal{H},\mathbf{a})$ , where $\mathbf{a}=(a_{1},\dots,a_{k})\in H^{k}$ for some $k$ , will be called a relational structure $\mathcal{H}$ with distinguished vertices $\mathbf{a}$ . For structures with distinguished vertices $(\mathcal{G},\mathbf{a}),(\mathcal{H},\mathbf{b})$ such that $\mathcal{G},\mathcal{H}$ are similar, a homomorphism from $(\mathcal{G},\mathbf{a})$ to $(\mathcal{H},\mathbf{b})$ is a homomorphism $\varphi$ from $\mathcal{G}$ to $\mathcal{H}$ that maps $a_{i}$ to $b_{i}$ , $i\in[k]$ . The set of all homomorphisms from $(\mathcal{G},\mathbf{a})$ to $(\mathcal{H},\mathbf{b})$ is denoted by $\mathsf{Hom}((\mathcal{G},\mathbf{a}),(\mathcal{H},\mathbf{b}))$ . Also, $\mathsf{hom}((\mathcal{G},\mathbf{a}),(\mathcal{H},\mathbf{b}))=|\mathsf{Hom}((\mathcal{G},\mathbf{a}),(\mathcal{H},\mathbf{b}))|$ .

This notion can be slightly generalized replacing $\mathbf{b}$ with a sequence $B_{1},\dots,B_{k}\subseteq H$ :

	$\displaystyle\mathsf{Hom}((\mathcal{G},\mathbf{a}),(\mathcal{H},B_{1},\dots,B_{k}))$	$\displaystyle=\bigcup_{b_{i}\in B_{i},i\in[k]}\mathsf{Hom}((\mathcal{G},\mathbf{a}),(\mathcal{H},\mathbf{b}))\qquad\text{and}$
	$\displaystyle\mathsf{hom}((\mathcal{G},\mathbf{a}),(\mathcal{H},B_{1},\dots,B_{k}))$	$\displaystyle=\sum_{b_{i}\in B_{i},i\in[k]}\mathsf{hom}((\mathcal{G},\mathbf{a}),(\mathcal{H},\mathbf{b}))$

Note that a relational structure $(\mathcal{G},\mathbf{a})$ with distinguished vertices can be viewed as an expansion of $\mathcal{G}$ with $k$ additional unary symbols, one for each distinguished vertex. In such an interpretation a homomorphism of structures with distinguished vertices is just a homomorphism between the corresponding expansions.

Next we introduce two types of products of structures. The direct product of $\sigma$ -structures $\mathcal{H},\mathcal{G}$ , denoted $\mathcal{H}\times\mathcal{G}$ is the $\sigma$ -structure with the base set $H\times G$ and such that the interpretation of $R\in\sigma$ is given by $R^{\mathcal{H}\times\mathcal{G}}((a_{1},b_{1}),\dots,(a_{k},b_{k}))=1$ if and only if $R^{\mathcal{H}}(a_{1},\dots,a_{k})=1$ and $R^{\mathcal{G}}(b_{1},\dots,b_{k})=1$ . By $\mathcal{H}^{\ell}$ we will denote the $\ell$ th power of $\mathcal{H}$ , that is, the direct product of $\ell$ copies of $\mathcal{H}$ . The direct product $(\mathcal{G},\mathbf{x})\times(\mathcal{H},\mathbf{y})$ of structures $(\mathcal{G},\mathbf{x}),(\mathcal{H},\mathbf{y})$ is defined to be $(\mathcal{H}\times\mathcal{G},(x_{1},y_{1}),\dots,(x_{r},y_{r}))$ .

Two $r$ -tuples $\mathbf{x}$ and $\mathbf{y}$ have the same equality type if $x_{i}=x_{j}$ if and only if $y_{i}=y_{j}$ for $i,j\in[r]$ . Let $(\mathcal{G},\mathbf{x})$ and $(\mathcal{H},\mathbf{y})$ be structure with $r$ distinguished vertices and such that $\mathbf{x}$ and $\mathbf{y}$ have the same equality type. Then $(\mathcal{G},\mathbf{x})\odot(\mathcal{H},\mathbf{y})$ denotes the structure that is obtained by taking the disjoint union of $\mathcal{G}$ and $\mathcal{H}$ and identifying every $x_{i}$ with $y_{i}$ , $i\in[r]$ . The distinguished vertices of the new structure are $x_{1},\dots,x_{r}$ .

The following statement is straightforward.

Proposition 2.4.

Let $(\mathcal{G},\mathbf{x}),(\mathcal{H},\mathbf{y}),(\mathcal{K},\mathbf{z})$ be similar relational structures with $r$ distinguished vertices. Then

	$\displaystyle\mathsf{hom}((\mathcal{G},\mathbf{x})\odot(\mathcal{H},\mathbf{y}),(\mathcal{K},\mathbf{z}))$	$\displaystyle=\mathsf{hom}((\mathcal{G},\mathbf{x}),(\mathcal{K},\mathbf{z}))\cdot\mathsf{hom}((\mathcal{H},\mathbf{y}),(\mathcal{K},\mathbf{z}));$
	$\displaystyle\mathsf{hom}((\mathcal{K},\mathbf{z}),((\mathcal{G},\mathbf{x})\times(\mathcal{H},\mathbf{y}))$	$\displaystyle=\mathsf{hom}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))\cdot\mathsf{hom}((\mathcal{K},\mathbf{z}),(\mathcal{H},\mathbf{y})).$

We will also need another simple observation. By $\mathsf{inj}((\mathcal{G},\mathbf{x}),(\mathcal{H},\mathbf{y}))$ we denote the number of injective homomorphisms from $(\mathcal{G},\mathbf{x})$ to $(\mathcal{H},\mathbf{y})$ .

Lemma 2.5.

Let $(\mathcal{G},\mathbf{y})$ and $(\mathcal{H},\mathbf{y})$ be relational structures with $r$ distinguished vertices. If $\mathbf{x},\mathbf{y}$ do not have the same equality type, then $\mathsf{inj}((\mathcal{G},\mathbf{x}),(\mathcal{H},\mathbf{y}))=0$ .

Finally, we will use factor structures. Let $\mathcal{H}$ be a $\sigma$ -structure and $\theta$ an equivalence relation on $H$ . By $\mathcal{H}/_{\theta}$ we denote the factor structure defined as follows.

•

$\mathcal{H}/_{\theta}$ is a $\sigma$ -structure.
•

The base set of $\mathcal{H}/_{\theta}$ is $H/_{\theta}=\{a/_{\theta}\mid a\in H\}$ , where $a/_{\theta}$ denotes the $\theta$ -class containing $a$ .
•

For any $R\in\sigma$ , say, $k$ -ary, $R^{\mathcal{H}/_{\theta}}=\{(a_{1}/_{\theta},\dots,a_{k}/_{\theta})\mid(a_{1},\dots,a_{k})\in R^{\mathcal{H}}\}$ .

Factor structures often appear in relation with homomorphisms. If $\varphi$ is a homomorphism from a structure $\mathcal{H}$ to a structure $\mathcal{G}$ , then the kernel $\theta$ of $\varphi$ is the equivalence relation on $H$ given by

(a,b)\in\theta\text{ if and only if }\varphi(u)=\varphi(v).

Homomorphism $\varphi$ gives rise to a homomorphism $\varphi/_{\theta}$ from $\mathcal{H}/_{\theta}$ to $\mathcal{G}$ , where $\varphi/_{\theta}(a/_{\theta})=\varphi(a)$ , $a\in H$ . Homomorphism $\varphi/_{\theta}$ is always injective.

We also define factor structures for structures with distinguished vertices as follows. Let $(\mathcal{H},\mathbf{a})$ be a structure with $k$ distinguished vertices and $\theta$ an equivalence relation on $H$ . Then $(\mathcal{H},\mathbf{a})/_{\theta}=(\mathcal{H}/_{\theta},(a_{1}/_{\theta},\dots,a_{k}/_{\theta}))$ .

2.4 Primitive-positive definitions

The reader is referred to [BKW17] for details about primitive positive definitions and their use in the study of the CSP.

Primitive positive definitions allow to add predicates to a constraint language without changing the complexity of the CSP. Let $=_{H}$ denote the relation of equality on the set $H$ .

Let $\Gamma$ be a constraint language on a set $H$ . A primitive positive formula in $\Gamma$ is a first-order formula $\exists y_{1},\dots,y_{s}\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s})$ , where $\Phi$ is a conjunction of atomic formulas of the form $z_{1}=_{H}z_{2}$ or $R(z_{1},\dots,z_{\ell})$ , $z_{1},\dots,z_{\ell}\in\{x_{1},\dots,x_{k},y_{1},\dots,y_{s}\}$ , and $R\in\Gamma$ . We say that $\Gamma$ pp-defines a predicate $R$ if there exists a pp-formula $\exists y_{1},\dots,y_{s}\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s})$ such that $R(x_{1},\dots,x_{k})=\exists y_{1},\dots,y_{s}\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s})$ . A relational structure pp-defines $R$ if so does $\Gamma_{\mathcal{H}}$ .

Jeavons et al. [Jea98] and Bulatov and Dalmau [BD07] proved that if $\Gamma$ pp-defines $R$ then $\mathsf{CSP}(\Gamma\cup\{R\})$ (respectively, $\mathsf{\#CSP}(\Gamma\cup\{R\})$ ) is polynomial time reducible to $\mathsf{CSP}(\Gamma)$ (respectively, to $\mathsf{\#CSP}(\Gamma)$ ). Later we will prove a similar result for modular counting.

Primitive positive definitions have close connections to homomorphisms, see [FV98, Kol04].

Lemma 2.6.

A predicate $R(x_{1},\dots,x_{k})$ is pp-definable in a $\sigma$ -structure $\mathcal{H}$ if and only if there exists a $\sigma$ -structure $(\mathcal{G},(x_{1},\dots,x_{k}))$ such that

\mathsf{hom}((\mathcal{G},(x_{1},\dots,x_{k}),(\mathcal{H},(a_{1},\dots,a_{k}))\neq 0\qquad\text{if and only if}\qquad(a_{1},\dots,a_{k})\in R.

Proof.

It suffices to demonstrate the connection between pp-formulas and structures. Then the lemma follows straightforwardly.

Let $\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s})$ be the quantifier free part of a pp-formula, and assume that the equality predicates are eliminated from $\Phi$ by identifying equated variables. In other words, $\Phi$ is a conjunction of atomic formulas of the form $Q(z_{1},\dots,z_{\ell})$ , where $Q\in\sigma$ and $z_{1},\dots,z_{\ell}\in\{x_{1},\dots,x_{k},y_{1},\dots,y_{s}\}$ . The corresponding $\sigma$ -structure $\mathcal{H}_{\Phi}$ is constructed as follows. Its base set is $H_{\Phi}=\{x_{1},\dots,x_{k},y_{1},\dots,y_{s}\}$ . Then for any $Q\in\sigma$ , say, $\ell$ -ary, $(z_{1},\dots,z_{\ell})\in Q^{\mathcal{H}_{\Phi}}$ if and only if $Q(z_{1},\dots,z_{\ell})$ is an atom in $\Phi$ . The transition from a structure $(\mathcal{G},(x_{1},\dots,x_{k}))$ to a formula is defined in the reverse way. The result now follows from the observation that every satisfying assignment of $\Phi$ is also a homomorphism from $\mathcal{H}_{\Phi}$ to $\mathcal{H}$ . ∎

3 Gadgets and automorphisms

In this section we prove several results that claim the existence of certain well behaved pp-definitions and homomorphisms for $p$ -rigid relational structures.

3.1 Möbius inversion

We will use Möbius inversion formula. Let $H$ be a set, $\mathsf{Part}(H)$ denote the poset of partitions of $H$ , where ${\underline{1}}$ denotes the single class partition, ${\underline{0}}$ the partition into 1-element classes, and $\eta\leq\theta$ means that $\eta$ is the finer partition of the two. Let also $M,N:\mathsf{Part}(H)\rightarrow\mathbb{Z}$ be some functions satisfying

M(\theta)=\sum_{\eta\geq\theta}N(\eta).

Then

N({\underline{0}})=\sum_{\theta\in\mathsf{Part}(H)}w(\theta)M(\theta),

where the function $w:\mathsf{Part}(H)\rightarrow\mathbb{Z}$ is given by:

•

$w({\underline{1}})=1$ ,
•

for any partition $\theta<{\underline{1}}$ , $w(\theta)=-{\sum}\limits_{\gamma>\theta}w(\gamma)$ .

The Möbius inversion formula will mainly be used as the following lemmas indicate.

Lemma 3.1.

Let $p$ be prime and let $\mathcal{H}$ be a relational structure such that, for any $\mathcal{G}$ , $\mathsf{hom}(\mathcal{G},\mathcal{H})\equiv c\pmod{p}$ , where $c$ does not depend on $\mathcal{G}$ . Then $\mathcal{H}$ has a $p$ -automorphism.

Proof.

We use the following parameters in Möbius inversion formula: the set $H$ is the base set of $\mathcal{H}$ , $M(\theta)=\mathsf{hom}(\mathcal{H}/_{\theta},\mathcal{H})$ , $N(\theta)=\mathsf{inj}(\mathcal{H}/_{\theta},\mathcal{H})$ . Then clearly $N({\underline{0}})=\mathsf{Aut}(\mathcal{H})$ . By the formula we have

N({\underline{0}})=\sum_{\theta\in\mathsf{Part}(H)}w(\theta)M(\theta)=\sum_{\theta\in\mathsf{Part}(H)}w(\theta)\mathsf{hom}(\mathcal{H}/_{\theta},\mathcal{H})\equiv c\cdot\sum_{\theta\in\mathsf{Part}(H)}w(\theta)\equiv 0\pmod{p}.

Therefore $|\mathsf{Aut}(\mathcal{H})|\equiv 0\pmod{p}$ and $\mathcal{H}$ has a $p$ -automorphism. ∎

We call a subset $A\subseteq\mathcal{H}^{r}$ automorphism-stable if there is $\mathbf{a}\in A$ such that the set $\mathsf{Stab}(\mathbf{a},A)=\{\pi\in\mathsf{Aut}(\mathcal{H}^{r})\mid\pi(\mathbf{a})\in A\}$ is a subgroup of $\mathsf{Aut}(\mathcal{H}^{r})$ . Note that $\mathsf{Stab}(\mathbf{a},A)$ is always nonempty, as it contains the identity mapping. Also, by $\mathsf{Stab}(\mathbf{a}_{1},\dots,\mathbf{a}_{k})$ we denote the subset of $\mathsf{Aut}(\mathcal{H}^{r})$ that contains all the automorphisms for which each of $\mathbf{a}_{1},\dots,\mathbf{a}_{k}$ is a fixed point.

Lemma 3.2.

Let $p$ be prime, $\mathcal{H}$ a relational structure.

(1)

Let $A\subseteq H^{r}$ an automorphism-stable set. If for any $\mathcal{G}$ and $\mathbf{x}\in\mathcal{G}$ , $\mathsf{hom}((\mathcal{G},\mathbf{x}),(\mathcal{H},A))\equiv c\pmod{p}$ , where $c$ does not depend on $\mathcal{G}$ and $\mathbf{x}$ , then the structure $\mathcal{H}^{r}$ has a $p$ -automorphism $\pi\in\mathsf{Stab}(\mathbf{a},A)$ for some $\mathbf{a}\in A$ .
(2)

Let $\mathbf{a}_{1},\dots,\mathbf{a}_{k}\in\mathcal{H}^{r}$ . If for any $\mathcal{G}$ and $x_{1},\dots,x_{k}\in\mathcal{G}$ , $\mathsf{hom}((\mathcal{G},x_{1},\dots,x_{k}),(\mathcal{H},\mathbf{a}_{1},\dots,\mathbf{a}_{k}))\equiv c\pmod{p}$ , where $c$ does not depend on $\mathcal{G}$ and $x_{1},\dots,x_{k}$ , then the structure $\mathcal{H}^{r}$ has a $p$ -automorphism $\pi\in\mathsf{Stab}(\mathbf{a}_{1},\dots,\mathbf{a}_{k})$ for some $\mathbf{a}\in A$ .

Proof.

(1) Similar to Lemma 3.1 we use Möbius inversion formula on $\mathsf{Part}(H^{r})$ . Let $\mathbf{a}\in A$ be the element witnessing that $A$ is automorphism stable and set $M(\theta)=\mathsf{hom}((\mathcal{H}^{r}/_{\theta},\mathbf{a}/_{\theta}),(\mathcal{H}^{r},A))$ , $N(\theta)=\mathsf{inj}((\mathcal{H}^{r}/_{\theta},\mathbf{a}/_{\theta}),(\mathcal{H}^{r},A))$ . Then $N({\underline{0}})\neq 0$ , as it includes the identity mapping, and as before we have

	$\displaystyle N({\underline{0}})$	$\displaystyle=\sum_{\theta\in\mathsf{Part}(H^{r})}w(\theta)M(\theta)$
		$\displaystyle=\sum_{\theta\in\mathsf{Part}(H^{r})}w(\theta)\mathsf{hom}((\mathcal{H}^{r}/_{\theta},x/_{\theta}),(\mathcal{H}^{r},A))\equiv c\cdot\sum_{\theta\in\mathsf{Part}(H^{r})}w(\theta)\equiv 0\pmod{p}.$

Note that $N({\underline{0}})=\mathsf{Stab}(\mathbf{a},A)$ and therefore is a subgroup of $\mathsf{Aut}(\mathcal{H}^{r})$ . As it has order that is a multiple of $p$ , it contains a $p$ -automorphism.

(2) In this case the argument is essentially the same. ∎

3.2 Rigidity and the number of extensions

The main goal of this section, Proposition 3.3, is to prove that for a $p$ -rigid relational structure $\mathcal{H}$ there is always a pp-definition that somewhat uniformizes the number of extensions of tuples in predicates pp-definable in $\mathcal{H}$ .

Let $\mathcal{H}$ be a relational structure and $R$ is pp-definable in $\mathcal{H}$ by a pp-formula

R(x_{1},\dots,x_{k})=\exists y_{1},\dots,y_{s}\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s}).

For $\mathbf{a}\in R$ by $\mathsf{\#ext}_{\Phi}(\mathbf{a})$ we denote the number of assignments $\mathbf{b}\in H^{s}$ to $y_{1},\dots,y_{s}$ such that $\Phi(\mathbf{a},\mathbf{b})$ holds.

Proposition 3.3.

Let $\mathcal{H}$ be a $p$ -rigid relational structure and $R$ is pp-definable in $\mathcal{H}$ . Then there exists a pp-definition $\exists y_{1},\dots,y_{s}\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s})$ of $R$ such that for any $\mathbf{a}\in R$ , $\mathsf{\#ext}_{\Phi}(\mathbf{a})\equiv 1\pmod{p}$ .

Proof.

We use the equivalence between pp-definitions and homomorphisms discussed in Section 2.4. Let $R=\{\mathbf{a}_{1},\dots,\mathbf{a}_{\ell}\}\subseteq H^{k}$ . Our goal is to find a relational structure $\mathcal{G}$ similar to $\mathcal{H}$ such that for some $x_{1},\dots,x_{k}\in G^{k}$ and any $\mathbf{a}=(a_{1},\dots,a_{k})\in R$ ,

\mathsf{hom}((\mathcal{G},x_{1},\dots,x_{k}),(\mathcal{H},a_{1},\dots,a_{k}))\equiv 1\pmod{p}.

Note that by Proposition 2.4 and Fermat’s Little Theorem it suffices to prove that such a structure exists satisfying $\mathsf{hom}((\mathcal{G},x_{1},\dots,x_{k}),(\mathcal{H},a_{1},\dots,a_{k}))\not\equiv 0\pmod{p}$ .

Consider $\mathcal{H}^{\ell}=\mathcal{H}\times\dots\times\mathcal{H}$ ( $\ell$ times) with distinguished vertices $\mathbf{a}^{1},\dots,\mathbf{a}^{k}$ , where $\mathbf{a}_{i}=(a_{i1},\dots,a_{ik})$ and $\mathbf{a}^{j}=(a_{1j},\dots,a_{\ell j})$ , $i\in[\ell],j\in[k]$ . By Proposition 2.4

\mathsf{hom}((\mathcal{G},x_{1},\dots,x_{k}),(\mathcal{H}^{\ell},\mathbf{a}^{1},\dots,\mathbf{a}^{k}))=\prod_{i\in[\ell]}\mathsf{hom}((\mathcal{G},x_{1},\dots,x_{k}),(\mathcal{H},\mathbf{a}_{i})).

(1)

If $(\mathcal{H}^{\ell},\mathbf{a}^{1},\dots,\mathbf{a}^{k})$ was $p$ -rigid, we could apply Möbius inversion formula in a way similar to Lemma 3.2(2) to infer the existence of a required $\mathcal{G}$ . However, there is no guarantee this is the case. We need to make one more step.

Note that each of the $\mathbf{a}^{j}$ is a fixed point of any automorphism of $(\mathcal{H}^{\ell},\mathbf{a}^{1},\dots,\mathbf{a}^{k})$ . This means that the $p$ -reduced form $\mathcal{H}^{\star p}$ of $(\mathcal{H}^{\ell},(\mathbf{a}^{1},\dots,\mathbf{a}^{k}))$ contains all the $\mathbf{a}^{j}$ . Thus

\mathsf{hom}((\mathcal{G},x_{1},\dots,x_{k}),(\mathcal{H}^{\ell},\mathbf{a}^{1},\dots,\mathbf{a}^{k}))=\mathsf{hom}((\mathcal{G},x_{1},\dots,x_{k}),(\mathcal{H}^{\star p},\mathbf{a}^{1},\dots,\mathbf{a}^{k})).

(2)

We apply Möbius inversion to $(\mathcal{H}^{\star p},\mathbf{a}^{1},\dots,\mathbf{a}^{k})$ . For $\theta\in\mathsf{Part}(H^{\star p})$ we set

	$\displaystyle M(\theta)$	$\displaystyle=\mathsf{hom}((\mathcal{H}^{\star p}/_{\theta},\mathbf{a}^{1}/_{\theta},\dots,\mathbf{a}^{k}/_{\theta}),(\mathcal{H}^{\star p},\mathbf{a}^{1},\dots,\mathbf{a}^{k})),$
	$\displaystyle N(\theta)$	$\displaystyle=\mathsf{inj}((\mathcal{H}^{\star p}/_{\theta},\mathbf{a}^{1}/_{\theta},\dots,\mathbf{a}^{k}/_{\theta}),(\mathcal{H}^{\star p},\mathbf{a}^{1},\dots,\mathbf{a}^{k})).$

Then we proceed as in the proof of Lemma 3.2 to conclude that if $M(\theta)\equiv 0\pmod{p}$ for all $\theta\in\mathsf{Part}(H^{\star p})$ , then $(\mathcal{H}^{\star p},\mathbf{a}^{1},\dots,\mathbf{a}^{k})$ has a $p$ -automorphism, leading to a contradiction with the construction of $(\mathcal{H}^{\star p},\mathbf{a}^{1},\dots,\mathbf{a}^{k})$ . Therefore, there exists $\theta\in\mathsf{Part}(H^{\star p})$ such that

\mathsf{hom}((\mathcal{H}^{\star p}/_{\theta},\mathbf{a}^{1}/_{\theta},\dots,\mathbf{a}^{k}/_{\theta}),(\mathcal{H}^{\star p},\mathbf{a}^{1},\dots,\mathbf{a}^{k}))\not\equiv 0\pmod{p}.

Observe that since for each $j\in[l]$ it holds that $(a_{j1},\dots,a_{jk})\in R$ , we have

\mathsf{hom}((\mathcal{H}^{\star p}/_{\theta},\mathbf{a}^{1}/_{\theta},\dots,\mathbf{a}^{k}/_{\theta}),(\mathcal{H},b_{1},\dots,b_{k})\not\equiv 0\pmod{p},

unless $(b_{1},\dots,b_{k})\in R$ . By (1),(2) $(\mathcal{H}^{*}/_{\theta},\mathbf{a}^{1}/_{\theta},\dots,\mathbf{a}^{k}/_{\theta})$ satisfies the required conditions. ∎

3.3 Indistinguishability and isomorphism

In this section we prove a variation of Lovasz’s theorem about homomorphism counts and graph isomorphisms [GGR16, GLS18].

Lemma 3.4.

Let $(\mathcal{G},\mathbf{x})$ and $(\mathcal{H},\mathbf{x})$ be $p$ -rigid relational structures with $r$ distinguished vertices. Then, $(\mathcal{G},\mathbf{x})\cong(\mathcal{H},\mathbf{y})$ if and only if

\mathsf{hom}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))\equiv\mathsf{hom}((\mathcal{K},\mathbf{z}),(\mathcal{H},\mathbf{y}))\pmod{p}

(3)

for all relational structures $(\mathcal{K},\mathbf{z})$ with $r$ distinguished vertices.

Proof.

The proof goes along the same lines as that in [GLS18]. If $(\mathcal{G},\mathbf{x})$ and $(\mathcal{H},\mathbf{y})$ are isomorphic, then (3) obviously holds for all relational structures $(\mathcal{K},\mathbf{z})$ .

For the other direction, suppose that (3) is true for all $(\mathcal{K},\mathbf{z})$ .

First, we claim that this implies that $\mathbf{x}$ and $\mathbf{y}$ have the same equality type. Indeed, if they do not, then without loss of generality there are $i,j\in[r]$ such that $x_{i}=x_{j}$ but $y_{i}\neq y_{j}$ . Let $\mathcal{K}$ be the relational structure with the base set $\{z_{1},\dots,z_{r}\}$ such that $z_{i}=z_{j}$ with empty predicates and $(z_{1},\dots,z_{r})$ as distinguished vertices. Then $\mathsf{hom}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))=1\neq 0=\mathsf{hom}((\mathcal{K},\mathbf{z}),(\mathcal{H},\mathbf{y}))$ , a contradiction with the assumption that (3) holds for all $(\mathcal{K},\mathbf{z})$ .

We show by induction on the number of vertices in $\mathcal{K}$ that

\mathsf{inj}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))\equiv\mathsf{inj}((\mathcal{K},\mathbf{z}),(\mathcal{H},\mathbf{y}))\pmod{p}.

(4)

for all $(\mathcal{K},\mathbf{z})$ . Let $n_{0}=|\{x_{1},\dots,x_{r}\}|=|\{y_{1},\dots,y_{r}\}|$ be the number of distinct elements in $\mathbf{x},\mathbf{y}$ . For the base case of the induction, consider a relational structure $(\mathcal{K},\mathbf{z})$ such that $|K|\leq n_{0}$ . If $\mathbf{z}$ does not have the same equality type as $\mathbf{x},\mathbf{y}$ , then $\mathsf{inj}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))=\mathsf{inj}((\mathcal{K},\mathbf{z}),(\mathcal{H},\mathbf{y}))=0$ . If $\mathbf{x}$ has the same equality type as $\mathbf{x},\mathbf{y}$ , the only homomorphisms from $(\mathcal{K},\mathbf{z})$ to $(\mathcal{G},\mathbf{x}),(\mathcal{H},\mathbf{y})$ are the ones that map $z_{i}$ to $x_{i},y_{i}$ , respectively. Therefore, $\mathsf{inj}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))=\mathsf{inj}((\mathcal{K},\mathbf{z}),(\mathcal{H},\mathbf{y}))$ .

For the inductive step, let $n>n_{0}$ and assume that (4) holds for all $(\mathcal{K},\mathbf{z})$ with $|K|<n$ . Let $(\mathcal{K},\mathbf{z})$ be a relational structure with $|K|=n$ , and let $\theta$ be an equivalence relation on $K$ . Then, as is easily seen

\mathsf{hom}_{\theta}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))=\mathsf{inj}((\mathcal{K}/_{\theta},\mathbf{z}/_{\theta}),(\mathcal{G},\mathbf{x}))\quad\text{ and }\quad\mathsf{hom}_{\theta}((\mathcal{K},\mathbf{z}),(\mathcal{H},\mathbf{y}))=\mathsf{inj}((\mathcal{K}/_{\theta},\mathbf{z}/_{\theta}),(\mathcal{H},\mathbf{y})),

where $\mathsf{hom}_{\theta}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x})),\mathsf{hom}_{\theta}((\mathcal{K},\mathbf{z}),(\mathcal{H},\mathbf{y}))$ denote the number of homomorphisms $\varphi$ from $(\mathcal{K},\mathbf{z})$ to $(\mathcal{G},\mathbf{x}),(\mathcal{H},\mathbf{y})$ , respectively, and such that $\ker(\varphi)=\theta$ . Then

	$\displaystyle\mathsf{hom}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))$	$\displaystyle=\mathsf{inj}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))+\sum_{\theta\in\mathsf{Part}(K)-\{{\underline{0}}\}}\mathsf{inj}((\mathcal{K},\mathbf{z})/_{\theta},(\mathcal{G},\mathbf{x}))$
	$\displaystyle\mathsf{hom}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))$	$\displaystyle=\mathsf{inj}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))+\sum_{\theta\in\mathsf{Part}(K)-\{{\underline{0}}\}}\mathsf{inj}((\mathcal{K},\mathbf{z})/_{\theta},(\mathcal{G},\mathbf{x}))$

Since $\mathsf{hom}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))\equiv\mathsf{hom}((\mathcal{K},\mathbf{z}),(\mathcal{H},\mathbf{y}))\pmod{p}$ and $\mathsf{inj}((\mathcal{K},\mathbf{z})/_{\theta},(\mathcal{G},\mathbf{x}))\equiv\mathsf{inj}((\mathcal{K},\mathbf{z})/_{\theta},(\mathcal{H},\mathbf{y}))\pmod{p}$ for all $\theta\in\mathsf{Part}(K)-\{{\underline{0}}\}$ we get $\mathsf{inj}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))\equiv\mathsf{inj}((\mathcal{K},\mathbf{z}),(\mathcal{G},\mathbf{x}))\pmod{p}$ .

Finally, we prove that (4) for $(\mathcal{K},\mathbf{z})=(\mathcal{G},\mathbf{x})$ implies $(\mathcal{G},\mathbf{x})\cong(\mathcal{H},\mathbf{y})$ . An injective homomorphism from a relational structure to itself is an automorphism. Since $(\mathcal{G},\mathbf{x})$ is $p$ -rigid, $|\mathsf{Aut}(\mathcal{G},\mathbf{x})|=\mathsf{inj}((\mathcal{G},\mathbf{x}),(\mathcal{G},\mathbf{x}))\not\equiv 0\pmod{p}$ . Therefore $\mathsf{inj}(\mathcal{G},\mathbf{x}),(\mathcal{H},\mathbf{y}))\not\equiv 0\pmod{p}$ , meaning there is an injective homomorphism from $(\mathcal{G},\mathbf{x})$ to $(\mathcal{H},\mathbf{y})$ . In a similar way, there is an injective homomorphism from $(\mathcal{H},\mathbf{y})$ to $(\mathcal{G},\mathbf{x})$ . Thus, the two structures are isomorphic. ∎

Let $\mathcal{H}$ be a relational structure. Elements $a,b\in H$ are said to be isomorphic if there is $\varphi\in\mathsf{Aut}(H)$ such that $\varphi(a)=b$ . We say that $a,b\in H$ are $(\mathcal{G},x)$ -indistinguishable, for a relational structure $\mathcal{G}$ with a distinguished vertex $x$ , if $\mathsf{hom}((\mathcal{G},x),(\mathcal{H},a))=\mathsf{hom}((\mathcal{G},x),(\mathcal{H},b))$ . Elements $a,b$ are indistiguishable if they are $(\mathcal{G},x)$ -indistinguishable for any $(\mathcal{G},x)$ . We use $a\sim b$ if $a,b$ are indistinguishable.

The following is an easy implication of Lemma 3.4.

Lemma 3.5.

Let $\mathcal{H}$ be a relational structure and $a,b\in H$ . Then $a\sim b$ if and only if $a,b$ are isomorphic.

Proof.

By definition $a\sim b$ if and only if for all $(\mathcal{G},x)$ , $\mathsf{hom}((\mathcal{G},x),(\mathcal{H},a))=\mathsf{hom}((\mathcal{G},x),(\mathcal{H},b))$ . Therefore, by Lemma 3.4, $(\mathcal{H},a)\cong(\mathcal{H},b)$ , which means there is an isomorphism $\varphi:(\mathcal{H},a)\rightarrow(\mathcal{H},b)$ . Hence, $\varphi\in\mathsf{Aut}(\mathcal{H})$ and such that $\varphi(a)=b$ . ∎

4 Expanding constraint languages

In this section we show that the standard methods of expanding constraint languages work for modular counting.

4.1 Primitive-positive definitions

We will use two versions of primitive-positive definitions. The first one, modular, is more natural for counting problems, but its properties are unexplored. The second one is the standard one, and one result we prove is that in $p$ -rigid structures modular pp-definitions are more expressive, a feature we will extensively use.

We start with the $p$ -modular quantifier $\exists^{\oplus p}$ . Its syntax is the same as that of the regular existential quantifier, while the semantics is given a follows: Let $R(x_{1},\dots,x_{k},y)$ be a predicate on a set $H$ . Then $\exists^{\oplus p}y\;R(x_{1},\dots,x_{k},y)$ defines the predicate $Q(x_{1},\dots,x_{k})$ such that $Q(a_{1},\dots,a_{k})=1$ , $a_{1},\dots,a_{k}\in H$ , if and only if $|\{b\in H\mid R(a_{1},\dots,a_{k},b)=1\}|\not\equiv 0\pmod{p}$ .

Modular primitive-positive definitions are the same as the regular ones with the exception of replacing of the regular quantifier with the modular one. Let $\Gamma$ be a constraint language on a set $H$ . A $p$ -modular primitive positive formula in $\Gamma$ is a first-order formula $\exists^{\oplus p}y_{1},\dots,y_{s}\;\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s})$ , where $\Phi$ is a conjunction of atomic formulas of the form $z_{1}=_{H}z_{2}$ or $R(z_{1},\dots,z_{\ell})$ and $R\in\Gamma$ , $z_{1},\dots,z_{\ell}\in\{x_{1},\dots,x_{k},y_{1},\dots,y_{s}\}$ . We say that $\Gamma$ $p$ -mpp-defines a predicate $R$ if there exists a $p$ -modular primitive-positive formula $\exists^{\oplus p}y_{1},\dots,y_{s}\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s})$ such that $R(x_{1},\dots,x_{k})=\exists^{\oplus p}y_{1},\dots,y_{s}\;\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s})$ . A relational structure $p$ -mpp-defines $R$ if so does $\Gamma_{\mathcal{H}}$ . We also call the $p$ -mpp-definition $R(x_{1},\dots,x_{k})=\exists^{\oplus p}y_{1},\dots,y_{s}\;\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s})$ strict if for any $a_{1},\dots,a_{k}\in H$ such that $R(a_{1},\dots,a_{k})=1$ the following condition holds $\mathsf{\#ext}_{\Phi}(a_{1},\dots,a_{k})\equiv 1\pmod{p}$ .

Mpp-definitions have a similar connection to homomorphisms, as pp-definitions, see Lemma 2.6.

Lemma 4.1.

A predicate $R(x_{1},\dots,x_{k})$ is $p$ -mpp-definable (strictly $p$ -mpp-definable) in a relational structure $\mathcal{H}$ if and only if there is a structure $\mathcal{G}$ similar to $\mathcal{H}$ and $x_{1},\dots,x_{k}\in G$ such that $R(a_{1},\dots,a_{k})=1$ for $a_{1},\dots,a_{k}\in H$ exactly when $\mathsf{hom}((\mathcal{G},\mathbf{x}),(\mathcal{H},\mathbf{a}))\not\equiv 0\pmod{p}$ (when $\mathsf{hom}((\mathcal{G},\mathbf{x}),(\mathcal{H},\mathbf{a}))\equiv 1\pmod{p}$ ).

It turns out that $p$ -mpp-definitions and strict $p$ -mpp-definitions are quite similar.

Lemma 4.2.

If $R$ is $p$ -mpp-definable in a relational structure $\mathcal{H}$ , it is also strictly $p$ -mpp-definable in $\mathcal{H}$ .

Proof.

As $R$ is $p$ -mpp-definable in $\mathcal{H}$ , there exists $(\mathcal{G},x_{1},\dots,x_{k})$ such that $\mathsf{hom}((\mathcal{G},\mathbf{x}),(\mathcal{H},\mathbf{a}))\not\equiv 0\pmod{p}$ if and only if $R(a_{1},\dots,a_{k})=1$ . Then by Proposition 2.4 $(\mathcal{G}^{\prime},\mathbf{x})$ given by

(\mathcal{G}^{\prime},\mathbf{x})=\underbrace{(\mathcal{G},\mathbf{x})\odot\dots\odot(\mathcal{G},\mathbf{x})}_{\text{$p-1$ times}}

is such that $R(a_{1},\dots,a_{k})=1$ if and only if $\mathsf{hom}((\mathcal{G}^{\prime},\mathbf{x}),(\mathcal{H},\mathbf{a}))\equiv 1\pmod{p}$ . ∎

Mpp-definitions give rise to reductions between modular counting CSPs.

Proposition 4.3.

Let $\Gamma,\Delta$ be constraint languages over a set $H$ , $\Delta$ finite, and every relation from $\Delta$ is $p$ -mpp-definable in $\Gamma$ . Then $\#_{p}\mathsf{CSP}(\Delta)$ is polynomial time reducible to $\#_{p}\mathsf{CSP}(\Gamma)$ .

Proof.

We show that for any $R$ $p$ -mpp-definable in $\Gamma$ , $\#_{p}\mathsf{CSP}(\Gamma\cup\{R\})$ is polynomial time reducible to $\#_{p}\mathsf{CSP}(\Gamma)$ . We need to consider two cases.

First, suppose that $R$ is $=_{H}$ . Take a $\#_{p}\mathsf{CSP}(\Gamma\cup\{R\})$ instance $\mathcal{P}=(X,\mathcal{C})$ , and for every constraint $x=_{H}y$ replace every occurrence of $y$ in $\mathcal{P}$ with $x$ . Clearly the resulting instance has the same number of solutions, and after eliminating all the equality constraints, it also does not use $=_{H}$ .

Second, suppose that $R$ has a $p$ -mpp-definition in $\Gamma$ that uses only relations from $\Gamma$ . By Lemma 4.2 there exists a strict $p$ -mpp-definition of $R(x_{1},\dots,x_{k})=\exists y_{1},\dots,y_{s}\Phi(x_{1},\dots,x_{k},y_{1},\dots,y_{s})$ such that for any $\mathbf{a}\in R$ , $\mathsf{\#ext}_{\Phi}(\mathbf{a})\equiv 1\pmod{p}$ . Let $\mathcal{P}=(X,\mathcal{C})$ be a $\#_{p}\mathsf{CSP}(\Gamma\cup\{R\})$ instance. Without loss of generality assume that $C_{1},\dots,C_{m}$ are the constraints containing $R$ . Construct a $\#_{p}\mathsf{CSP}(\Gamma)$ instance $\mathcal{P}^{\prime}=(X^{\prime},\mathcal{C}^{\prime})$ as follows:

•

For each $i\in[m]$ introduce new variables $y_{i1},\dots,y_{is}$ and set $X^{\prime}=X\cup\bigcup_{i\in[m]}\{y_{i1},\dots,y_{is}\}$ .
•

The set $\mathcal{C}^{\prime}$ contains every constraint from $\mathcal{C}-\{C_{1},\dots,C_{m}\}$ . Also, we replace each $C_{i}=\langle(x_{i1},\dots,x_{ik}),R\rangle$ with the definition $\Phi(x_{i1},\dots,x_{ik},y_{i1},\dots,y_{is})$ of $R$ .

Next, we find the number of solutions of $\mathcal{P}^{\prime}$ . As is easily seen, for every solution $\varphi$ of $\mathcal{P}$ there are

\prod_{i\in[m]}\mathsf{\#ext}_{\Phi}(\varphi(x_{i_{1}}),\dots,\varphi(x_{ik}))\equiv 1\pmod{p}

solutions of $\mathcal{P}^{\prime}$ . Therefore if $N,N^{\prime}$ denote the number of solutions of $\mathcal{P},\mathcal{P}^{\prime}$ , respectively, we have $N\equiv N^{\prime}\pmod{p}$ . ∎

Primitive-positive definitions have been intensively used in the decision and counting CSPs. They do not appear so naturally in the context of modular counting, but Proposition 3.3 basically proves that they are a special case of modular pp-definitions and give rise to reductions between modular counting CSPs as well.

Theorem 4.4.

Let $\Gamma,\Delta$ be constraint languages on a finite set $H$ such that $\Delta$ is finite, and $\Gamma$ is $p$ -rigid. If $\Delta$ is pp-definable in $\Gamma$ , Then $\#_{p}\mathsf{CSP}(\Delta)$ is polynomial time reducible to $\#_{p}\mathsf{CSP}(\Gamma)$ .

Proof.

We show that for any $R$ pp-definable in $\Gamma$ , $\#_{p}\mathsf{CSP}(\Gamma\cup\{R\})$ is polynomial time reducible to $\#_{p}\mathsf{CSP}(\Gamma)$ . The proof repeats the proof of Proposition 4.3 verbatim, except we use Proposition 3.3 in place of Lemma 4.2. ∎

A unary relation pp-definable in a constraint language or relational structures is said to be a subalgebra of the language or structure. In a similar way let $\mathcal{H}$ be a relational structure. A set $U\subseteq H$ is said to be a $p$ -subalgebra of $\mathcal{H}$ if $U$ is strictly $p$ -mpp-definable in $\mathcal{H}$ . Set $U$ is a $p$ -subalgebra of a constraint language $\Gamma$ if it is a $p$ -subalgebra of $\mathcal{H}_{\Gamma}$ .

4.2 Adding constants

Recall that for a constraint language $\Gamma$ by $\Gamma^{*}$ we denote the language $\Gamma\cup\{C_{a}|a\in H\}$ . Theorem 4.5 was proved for exact counting in [BD07] and for modular counting of graph homomorphisms in [FJ13]. We use a proof similar to that in [BD07].

Theorem 4.5.

Let $\Gamma$ be a $p$ -rigid constraint language on a set $H$ . Then, the problem $\#_{p}\mathsf{CSP}(\Gamma^{*})$ is polynomial time reducible to $\#_{p}\mathsf{CSP}(\Gamma)$ .

Proof.

We follow the same line of argument as the proof of a similar result in [BD07] for exact counting. Let $H=\{a_{1},...,a_{n}\}$ . It is known, see e.g. [JCG99], that the $n$ -ary relation $Q=\{(\varphi(a_{1}),\dots,\varphi(a_{n}))|\text{ $\varphi$ is a homomorphism of $\mathcal{H}_{\Gamma}$ into itself}\}$ is pp-definable in $\Gamma$ .

Let $\mathcal{P}=(V;\mathcal{C})$ be an instance of $\#_{p}\mathsf{CSP}(\Gamma^{*})$ . We construct an instance $\mathcal{P}^{\prime}=(X^{\prime},\mathcal{C}^{\prime})$ of $\#_{p}\mathsf{CSP}(\Gamma\cup\{Q,=_{H}\})$ as follows.

•

$V^{\prime}=V\cup\{v_{a}|a\in H\}$ ;
•

$\mathcal{C}^{\prime}$ consists of three parts: $\{C=\langle\mathbf{x},R\rangle\in\mathcal{C}\mid R\in\Gamma\}$ , $\{\langle(a_{1},\dots,a_{n}),Q\rangle\}$ , and $\{\langle(x,y_{a}),=_{H}\rangle\mid\langle(x),C_{a}\rangle\in\mathcal{C}\}$ .

The number of solutions of $\mathcal{P}$ equals the number of solutions $\varphi$ to $\mathcal{P}^{\prime}$ such that $\varphi(v_{a})=a$ for all $a\in H$ . Let $U$ be the set of all such solutions of $\mathcal{P}^{\prime}$ and $T=|U|$ . Then $T$ can be computed in two stages.

Let again $\mathsf{Part}(H)$ be the poset of partitions of $H$ . For every partition $\theta\in\mathsf{Part}(H)$ we define $\mathcal{P}^{\prime}_{\theta}$ as the instance $(V^{\prime},\mathcal{C}_{\theta})$ , where $\mathcal{C}^{\prime\prime}=\mathcal{C}^{\prime}\cup\{\langle(v_{a},v_{a^{\prime}}),=_{H}\rangle\}\mid a,a^{\prime}$ belong to the same class of $\theta\}$ ). Note that if $\varphi$ is a solution of $\mathcal{P}^{\prime}$ , then $\varphi$ is a solution of $\mathcal{P}^{\prime}_{\theta}$ if and only if $\varphi(v_{a})=\varphi(v_{a^{\prime}})$ for every $a,a^{\prime}$ from the same class of $\theta$ . Let us denote $M(\theta)$ the number of solutions of $\mathcal{P}^{\prime}_{\theta}$ . By Theorem 4.4 the number $M(\theta)$ can be computed using the oracle $\#_{p}\mathsf{CSP}(\Gamma)$ , since $\{=_{H},Q\}$ are pp-definable in $\Gamma$ .

Next we find the number solutions $\varphi$ of $\mathcal{P}^{\prime}$ that assign $v_{a}$ , $a\in A$ , pairwise different values. Let $W$ be the set of all such solutions. Let us denote by $N(\theta)$ the number of all solutions $\varphi$ of $\mathcal{P}^{\prime}_{\theta}$ such that $\varphi(v_{a})=\varphi(v_{b})$ if and only if $a,b$ belong to the same class of $\theta$ . In particular, $N({\underline{0}})=|W|$ . The number $N(\theta)$ can be obtained using Möbius inversion formula for poset $\mathsf{Part}(H)$ . Let $w:\mathsf{Part(H)}\rightarrow\mathbb{Z}$ be defined as in Section 3.1. Also, observe that for any $\theta\in\mathsf{Part}(H)$

M(\theta)=\sum_{\eta\geq\theta}N(\eta).

Therefore,

N({\underline{0}})=\sum_{\theta\in\mathsf{Part}(A)}w(\theta)M(\theta).

Thus $N({\underline{0}})$ can be found through a constant number of calls to $\#_{p}\mathsf{CSP}(\Gamma)$ .

Now, we express $T$ via $N({\underline{0}})$ . Let $G=\mathsf{Aut}(\Gamma)$ be the automorphism group of $\mathcal{H}_{\Gamma}$ . We show that $W=\{g\circ\varphi|g\in G,\varphi\in U\}$ . For every solution $\varphi$ in $U$ and every $g\in G$ , $g\circ\varphi$ is also a solution of $\mathcal{P}^{\prime}$ . Moreover, since $g$ is one-to-one, $g\circ\varphi$ is in $W$ . Conversely, for every $\psi\in W$ , there exists some $g\in G$ such that $g(a)=\psi(v_{a})$ , $a\in H$ . Note that $g^{-1}\in G$ implies $\varphi=g^{-1}\circ\psi\in U$ , which witnesses that $\psi=g\circ\varphi$ is of the required form. Finally, for every $\varphi,\varphi^{\prime}\in U$ and every $g,g^{\prime}\in G$ , if $\varphi\neq\varphi^{\prime}$ or $g\neq g^{\prime}$ then $g\circ\varphi\neq g^{\prime}\circ\varphi^{\prime}$ . Thus, $N({\underline{0}})=|G|\cdot T$ . Since $\Gamma$ is $p$ -rigid, $|G|\not\equiv 0\pmod{p}$ . Therefore $T\equiv|G|^{-1}\cdot N({\underline{0}})\pmod{p}$ . ∎

Remark 4.6.

For any relational structure $\mathcal{H}$ the structure $\mathcal{H}^{*}$ does not have any nontrivial homomorphisms, in particular, it is $p$ -rigid. However, it does not mean that powers of $\mathcal{H}^{*}$ have no nontrivial automorphisms. The reason is that formally speaking if $\mathcal{H}$ is a $\sigma$ -structure then $\mathcal{H}^{*}$ has the signature $\sigma\cup\{C_{a}\mid a\in H\}$ . Therefore, so does, say $(\mathcal{H}^{*})^{2}$ . For the latter structure $(b,c)\in C_{a}^{(\mathcal{H}^{*})^{2}}$ if and only if $b,c\in C_{a}^{\mathcal{H}^{*}}$ , that is, if and only if $b=c=a$ . This means that the involution $(a,b)\mapsto(b,a)$ is an automorphism of $(\mathcal{H}^{*})^{2}$ .

5 Automorphisms of direct powers of bipartite graphs

The goal of this section is to study the structure of automorphisms of $H^{\ell}$ , a direct power of a simple graph $H$ .

If $H$ is non-bipartite, the results we need can be found in Chapter 8 of [HIK11]. Here, we expand the scope of [HIK11] to bipartite graphs by introducing diamond product of graphs. This kind of graph products treats the vertices of a bipartite graph as one of the two sorts, left and right, and when constructing a direct product only forms tuples of vertices of the same sort. Automorphisms of the bipartite graph also preserve the sorts of vertices. An alternative way to view such a sorted bipartite graph $H$ is to consider it as a relational structure with two unary relations representing the left and the right parts of the bipartition, and one binary edge relation.

In this section, we denote the disjoint union of graphs $G$ and $H$ by $G+H$ . It will also be convenient to use the standard graph theory notation, and denote graphs in regular font and use $V(H),E(H)$ for the sets of vertices and edges. The neighborhood of a vertex $v\in V(G)$ or a set $A\subseteq V(G)$ in $G$ is denoted $N_{G}(v),N_{G}(A)$ . However, we will use $\left\langle a,b\right\rangle$ to denote edges, because sometimes vertices will have a complicated structure.

5.1 Graph Products

We will need three types of graph products. For Cartesian product we use the results of Chapter 6 of [HIK11], which are valid for arbitrary graphs.

The Cartesian product of two simple graphs $A,B$ is the graph $A\;\small\Box\;B$ with vertices $V(A)\times V(B)$ and edges $E(A\;\small\Box\;B)=\{\left\langle(a,b),(a^{\prime},b^{\prime})\right\rangle|\left\langle a,a^{\prime}\right\rangle\in E(A)\text{ and }b=b^{\prime},\text{ or }a=a^{\prime}\text{ and }\left\langle b,b^{\prime}\right\rangle\in E(B)\}$ .

A graph $G$ is called prime with respect to Cartesian product if whenever $G=G_{1}\;\small\Box\;G_{2}$ , one of $G_{1},G_{2}$ contains only one vertex.

Theorem 5.1 (Theorem 6.8, [HIK11]).

Let $G,H$ be isomorphic connected graphs $G=G_{1}\;\small\Box\;\dots\;\small\Box\;G_{k}$ and $H=H_{1}\;\small\Box\;\dots\;\small\Box\;H_{l}$ , where each factor $G_{i}$ and $H_{i}$ is prime with respect to Cartesian product. Then $k=l$ , and for any isomorphism $\varphi:G\rightarrow H$ , there is a permutation $\pi$ of $[k]$ and isomorphisms $\varphi_{i}:G_{\pi(i)}\rightarrow H_{i}$ for which

\varphi(x_{1},\dots,x_{k})=(\varphi_{1}(x_{\pi(1)}),,\dots,\varphi_{k}(x_{\pi(k)})).

The direct product of two graphs $A,B$ is defined in the regular way, as the graph $A\times B$ with vertices $V(A)\times V(B)$ and edges $E(A\times B)=\{\left\langle(a,b),(a^{\prime},b^{\prime})\right\rangle|\left\langle a,a^{\prime}\right\rangle\in E(A)\text{ and }\left\langle b,b^{\prime}\right\rangle\in E(B)\}$ .

The diamond product is defined with bipartite graphs in mind. For a bipartite graph $G=(L\cup R,E)$ , we denote the two parts of the bipartition by $L_{G}=L$ and $R_{G}=R$ .

The diamond product of two simple bipartite graphs $G=(L_{G}\cup R_{G},E(G))$ and $H=(L_{H}\cup R_{H},E(H))$ is the graph $G\vec{\diamond}H$ with vertices $(L_{G}\times L_{H})\cup(R_{G}\times R_{H})$ and edges $E(G\vec{\diamond}H)=\{\left\langle(a,b),(a^{\prime},b^{\prime})\right\rangle|\left\langle a,a^{\prime}\right\rangle\in E(G)\text{ and }\left\langle b,b^{\prime}\right\rangle\in E(H)\}$ .

The diamond product of a simple non-bipartite graphs $G=(V(G),E(G))$ and a bipartie graph $H=(L_{H}\cup R_{H},E(H))$ is the graph $H\bar{\diamond}H$ with vertices $(V(G)\times L_{H})\cup(V(G)\times R_{H})$ and edges $E(G\bar{\diamond}H)=\{\left\langle(a,b),(a^{\prime},b^{\prime})\right\rangle|\left\langle a,a^{\prime}\right\rangle\in E(G)\text{ and }\left\langle b,b^{\prime}\right\rangle\in E(H)\}$ .

Definition 5.2.

The diamond product of two simple graphs $G,H$ is defined as follows:

G\diamond H=\left\{\begin{array}[]{cl}G\;\vec{\diamond}\;H&\mbox{if }G,H\mbox{ are bipartite}\\ G\;\bar{\diamond}\;H&\mbox{if }G\mbox{ is bipartite and }H\mbox{ is non-bipartite}\\ G\;\bar{\diamond}\;H&\mbox{if }H\mbox{ is bipartite and }G\mbox{ is non-bipartite}\\ G\times H&\mbox{if }G,H\mbox{ are non-bipartite}\end{array}\right.

Remark 5.3.

The diamond product for simple graphs $G$ and $H$ is commutative and associative up to an isomorphism, meaning $G\diamond H\cong H\diamond G$ , and $(G\diamond H)\diamond K\cong G\diamond(H\diamond K)$

The following statement is straightforward.

Proposition 5.4.

Let $G,H,K$ be simple graphs with $r$ distinguished vertices $\mathbf{x},\mathbf{y},\mathbf{z}$ respectively. Then

	$\displaystyle\mathsf{hom}((K,G\diamond H)$	$\displaystyle=\mathsf{hom}(K,G)\cdot\mathsf{hom}(K,H),$
	$\displaystyle\mathsf{hom}((K,\mathbf{z}),((G,\mathbf{x})\diamond(H,\mathbf{y}))$	$\displaystyle=\mathsf{hom}((K,\mathbf{z}),(G,\mathbf{x}))\cdot\mathsf{hom}((K,\mathbf{z}),(H,\mathbf{y})).$

We denote the $k$ diamond power of $H$ by $H^{\diamond k}$ .

5.2 Automorphisms of products of R-thin graphs

Relation $R_{G}$ on $V(G)$ for a graph $G$ is defined as follows. Vertices $x$ and $x^{\prime}$ are in $R_{G}$ , written $xRx^{\prime}$ , if and only if $N_{G}(x)=N_{G}(x^{\prime})$ . Clearly, $R_{G}$ is an equivalence relation. Normally we will omit the subscript $G$ .

We denote the quotient of $G$ modulo $R$ by $G/_{R}$ . Given $x\in V(G)$ , let $[x]=\{x\in V(G)|N_{G}(x^{\prime})=N_{G}(x)\}$ denote the $R$ -class containing $x$ . Then $V(G/_{R})=\{[x]\mid x\in V(G)\}$ and $E(G/_{R})=\{\left\langle[x],[y]\right\rangle\mid\left\langle x,y\right\rangle\in E(G)\}$ . Since $R_{G}$ is defined entirely in terms of $E(G)$ , it is easy to see that for an isomorphism $\varphi:G\rightarrow H$ , we have $xR_{G}y$ if and only if $\varphi(x)R_{H}\varphi(y)$ . Thus, $\varphi$ maps equivalence classes of $R_{G}$ to equivalence classes of $R_{H}$ , and can be defined to act on $V(G/_{R})$ by $\varphi([x])=[\varphi(x)]$ .

We need the following lemmas from [HIK11].

Lemma 5.5 (Proposition 8.4, [HIK11]).

Suppose $G,H$ are simple graphs. Then $G\cong H$ if and only if $G/_{R}\cong H/_{R}$ and there is an isomorphism $\psi:G/_{R}\rightarrow H/_{R}$ with $|[x]|=|\psi([x])|$ for each $[x]\in V(G/_{R})$ . In fact, given an isomorphism $\varphi:G/_{R}\rightarrow H/_{R}$ , any map $\varphi:V(G)\rightarrow V(H)$ that restricts to a bijection $\varphi:[x]\rightarrow\psi([x])$ for every $[x]\in G/_{R}$ is an isomorphism from $G$ to $H$ .

Lemma 5.6 (Proposition 8.5, [HIK11]).

If graphs $G$ and $H$ are simple graphs and have no isolated vertices, then $V((G\times H)/_{R})=\{X\times Y|X\in V(G/_{R}),Y\in V(H/_{R})\}$ . In particular, $[(x,y)]=[x]\times[y]$ . Furthermore, $(G\times H)/_{R}\cong G/_{R}\times H/_{R}$ , and $\psi:(G\times H)/_{R}\rightarrow G/_{R}\times H/_{R}$ with $\psi([x,y])=([x],[y])$ is an isomorphism.

We prove similar statements for diamond product.

Remark 5.7.

If $G=H\diamond K$ , then $N_{G}((h,k))=N_{H}(h)\times N_{K}(k)$ for any $(h,k)\in V(H\diamond K)$ . Recall however that if $G$ and $H$ are bipartite, then for any $(h,k)\in V(H\diamond K)$ either $h\in L_{G},k\in L_{K}$ or $h\in R_{G},k\in R_{K}$ .

Lemma 5.8.

If graphs G and H are simple graphs and have no isolated vertices, then $(G\diamond H)/_{R}\cong G/_{R}\diamond H/_{R}$ , and $\psi:(G\diamond H)/_{R}\rightarrow G/_{R}\diamond H/_{R}$ with $\psi([x,y])=([x],[y])$ is an isomorphism. Also $[(x,y)]=[x]\times[y]$ .

The proof of Lemma 5.8 is similar to that of Proposition 8.5 of [HIK11] and is moved to Section 7.

A graph $G$ is said to be $R$ -thin if $R$ is the equality relation.

5.2.1 Cartesian Skeleton

In this subsection we introduce several definitions and results from Chapter 8 of [HIK11]. The Boolean square of a graph $G$ is the graph $G^{s}$ with $V(G^{s})=V(G)$ and $E(G^{s})=\{\left\langle x,y\right\rangle|N_{G}(x)\cap N_{G}(y)\not=\emptyset\}$ .

Lemma 5.9.

If $G_{1},\dots,G_{k}$ are graphs, then $(G_{1}\diamond\dots\diamond G_{k})^{s}=G^{s}_{1}\diamond\dots\diamond G^{s}_{k}$ .

Proof.

Observe that $\left\langle(x_{1},\dots,x_{k}),(y_{1},\dots,y_{k})\right\rangle\in E((G_{1}\diamond\dots\diamond G_{k})^{s})$ if and only if there is a walk of length 2 joining $(x_{1},\dots,x_{k})$ and $(y_{1},\dots,y_{k})$ . By definition of $\diamond$ such a walk exists if and only if each $G_{i}$ has a walk of length 2 between $x_{i}$ and $y_{i}$ . The latter is equivalent to $\left\langle x_{i},y_{i}\right\rangle\in E((G_{i})^{s})$ for each $i\in[k]$ , which happens if and only if $\left\langle(x_{1},\dots,x_{k}),(y_{1},\dots,y_{k})\right\rangle$ is an edge of $G^{s}_{1}\diamond\dots\diamond G^{s}_{k}$ . ∎

We now explain how to construct the Cartesian skeleton $S(G)$ of a graph $G$ by removing specific edges from $G^{s}$ .

Given a factorization $G=H\diamond K$ , we say that an edge $\left\langle(h,k),(h^{\prime},k^{\prime})\right\rangle$ of the Boolean square $G^{s}$ is Cartesian relative to the factorization if either $h=h^{\prime}$ and $k\not=k^{\prime}$ , or $h\not=h^{\prime}$ and $k=k^{\prime}$ . An edge $\left\langle x,y\right\rangle$ of the Boolean square $G^{s}$ is dispensable if it is a loop, or if there exists some $z\in V(G)$ for which both of the following statements hold:

1.

$N_{G}(x)\cap NG(y)\subset N_{G}(x)\cap NG(z)$ or $N_{G}(x)\subset N_{G}(z)\subset N_{G}(y)$ ,
2.

$N_{G}(y)\cap NG(x)\subset N_{G}(y)\cap NG(z)$ or $N_{G}(y)\subset N_{G}(z)\subset N_{G}(x)$ .

Definition 5.10.

The Cartesian skeleton $S(G)$ of a graph $G$ is the spanning subgraph of the Boolean square $G^{s}$ obtained by removing all dispensable edges from $G^{s}$ .

The following statements are from [HIK11].

Lemma 5.11 (Proposition 8.11, [HIK11]).

Any isomorphism $\varphi:G\rightarrow H$ , as a map $\varphi:V(G)\rightarrow V(H)$ , is also an isomorphism $\varphi:S(G)\rightarrow S(H)$ .

Lemma 5.12 (Proposition 8.13, [HIK11]).

Suppose a graph G is connected.

1.

If $G$ has an odd cycle, then $S(G)$ is connected.
2.

If $G$ is bipartite, then $S(G)$ has two connected components whose respective vertex sets are the two parts of the bipartition of $G$ .

If $G$ is bipartite, we denote the connected component of the $S(G)$ corresponding to the left part of $G$ by $S_{L}(G)$ and the one corresponding to the right part of $G$ by $S_{R}(G)$ . Note that if $G=H\diamond K$ , by Remark 5.7 $N_{G}((h,k))=N_{H}(h)\times N_{K}(k)$ . This implies the following:

Lemma 5.13 ([HIK11]).

If $G$ is an R-thin graph with an arbitrary factorization $G=H\diamond K$ , then every edge of $S(G)$ is Cartesian relative to this factorization.

Observe that in the case of bipartite graphs the Cartesian skeleton is restricted to the left and right parts of the bipartition of the graph. Hence, we can modify Proposition 8.10 of [HIK11] for the diamond product.

Proposition 5.14.

If $A,B$ are $R$ -thin graphs without isolated vertices, then

S(A\diamond B)=\left\{\begin{array}[]{cl}S_{L}(A)\;\small\Box\;S_{L}(B)+S_{R}(A)\;\small\Box\;S_{R}(B)&\mbox{if }A,B\mbox{ are bipartite}\\ S_{L}(A)\;\small\Box\;S(B)+S_{R}(A)\;\small\Box\;S(B)&\mbox{if }A\mbox{ is bipartite and }B\mbox{ is non-bipartite}\\ S(A)\;\small\Box\;S_{L}(B)+S(A)\;\small\Box\;S_{R}(B)&\mbox{if }B\mbox{ is bipartite and }A\mbox{ is non-bipartite}\\ S(A)\;\small\Box\;S(B)&\mbox{if }G,H\mbox{ are non-bipartite}\end{array}\right.

The proof of Proposition 5.14 is similar to that of Proposition 8.10 of [HIK11] and is moved to Section 7.

5.2.2 Diamond product factorization

A graph $G$ is said to be prime if for any $G\cong H\diamond K$ one of $H,K$ is an edge. The following lemma is the core technical statement of this section.

Lemma 5.15.

Consider any isomorphism $\varphi:G_{1}\diamond\dots\diamond G_{k}\rightarrow H_{1}\diamond\dots\diamond H_{\ell}$ , where $\varphi(x_{1},\dots,x_{k})=(\varphi_{1}(x_{1},\dots,x_{k}),\dots,\varphi_{\ell}(x_{1},\dots,x_{k}))$ (recall that $\varphi$ preserves the left and right parts of the graphs) and all the factors are connected and R-thin. If a factor $G_{i}$ is prime, then exactly one of the functions $\varphi_{1},\varphi_{2},...,\varphi_{\ell}$ depends on $x_{i}$ .

Proof.

By grouping and permuting the factors we may assume that $k=\ell=2$ and $G_{1}$ is prime. If none of $G_{1}$ and $G_{2}$ is bipartite, then Lemma 5.15 is Lemma 8.14 of [HIK11]. We will consider the case when one or both of $G_{1}$ or $G_{2}$ are bipartite. We prove this by showing that if it is not the case that exactly one of $\varphi_{1}$ and $\varphi_{2}$ depends on $x_{1}$ , then $G_{1}$ is not prime. Now, if $G_{1}$ or $G_{2}$ is bipartite, the graph $G_{1}\diamond G_{2}$ is bipartite, hence the graph $H_{1}\diamond H_{2}$ is bipartite. We denote the connected components of $S(G_{1}\diamond G_{2})$ by $S_{L}$ and $S_{R}$ , and the connected components of $S(H_{1}\diamond H_{2})$ by $C_{L}$ and $C_{R}$ which correspond to the left and right parts of the bipartition.

By Lemma 5.11 $\varphi$ is also an isomorphism for Cartesian skeletons:

\varphi:S_{L}+S_{R}\rightarrow C_{L}+C_{R},

(5)

which gives us isomorphisms on each connected component:

\varphi_{L}:S_{L}\rightarrow C_{L},\;\;\varphi_{R}:S_{R}\rightarrow C_{R}

Note that although $G_{1}$ is prime, $S(G_{1})$ as well as $S_{L},S_{R}$ are not necessarily prime. Take prime factorizations of each component, when both $G$ and $H$ are bipartite:

	$\displaystyle S_{L}(G)=A_{1}\;\small\Box\;\dots\;\small\Box\;A_{t}\;$	$\displaystyle,\;\;S_{R}(G)=B_{1}\;\small\Box\;\dots\;\small\Box\;B_{s},$
	$\displaystyle S_{L}(H)=D_{1}\;\small\Box\;\dots\;\small\Box\;D_{w}\;$	$\displaystyle,\;\;S_{R}(H)=E_{1}\;\small\Box\;\dots\;\small\Box\;E_{r},$
	$\displaystyle C_{L}=C_{1}\;\small\Box\;\dots\;\small\Box\;C_{m}\;$	$\displaystyle,\;\;C_{R}=C^{\prime}_{1}\;\small\Box\;\dots\;\small\Box\;C^{\prime}_{n},$

Note that, if both $G_{1}$ and $G_{2}$ are bipartite, then the $A_{i}$ ’s and $B_{i}$ ’s, as well as the $D_{i}$ ’s and $E_{i}$ ’s can be nonisomorphic. If $G_{1}$ is non-bipartite, then $t=s$ and for $i\in[t]$ , $A_{i}\cong B_{i}$ . Similarly, if $G_{2}$ is non-bipartite, then $w=r$ and for $i\in[w]$ , $D_{i}\cong E_{i}$ .

As $\varphi$ is an isomorphism, we have

	$\displaystyle\varphi_{L}:(A_{1}\;\small\Box\;\dots\;\small\Box\;A_{t})\;\small\Box\;(D_{1}\;\small\Box\;\dots\;\small\Box\;D_{w})$	$\displaystyle\rightarrow(C_{1}\;\small\Box\;\dots\;\small\Box\;C_{m})$
	$\displaystyle\varphi_{R}:(B_{1}\;\small\Box\;\dots\;\small\Box\;B_{s})\;\small\Box\;(E_{1}\;\small\Box\;\dots\;\small\Box\;E_{r})$	$\displaystyle\rightarrow(C^{\prime}_{1}\;\small\Box\;\dots\;\small\Box\;C^{\prime}_{n})$

We relabel the vertices of $G_{1}$ with $V((A_{1}\;\small\Box\;\dots\;\small\Box\;A_{t})+(B_{1}\;\small\Box\;\dots\;\small\Box\;B_{s}))$ , and those of $G_{2}$ with $V(D_{1}\;\small\Box\;\dots\;\small\Box\;D_{w}+E_{1}\;\small\Box\;\dots\;\small\Box\;E_{r})$ . We relabel vertices of $H_{1}\diamond H_{2}$ with $V(C_{1}\;\small\Box\;\dots\;\small\Box\;C_{m}+C^{\prime}_{1}\;\small\Box\;\dots\;\small\Box\;C^{\prime}_{n})$ . By Proposition 5.14 the isomorphism $\varphi$ can be represented as follows:

	$\displaystyle\varphi_{L}:(A_{1}\;\small\Box\;\dots\;\small\Box\;A_{t})\;\small\Box\;(D_{1}\;\small\Box\;\dots\;\small\Box\;D_{w})$	$\displaystyle\rightarrow$
	$\displaystyle(A_{1}\;\small\Box\;\dots\;\small\Box\;A_{t^{\prime}}\;\small\Box\;D_{1}\;\small\Box\;\dots\;\small\Box\;D_{w^{\prime}})$	$\displaystyle\;\small\Box\;(A_{t^{\prime}+1}\;\small\Box\;\dots\;\small\Box\;A_{t}\;\small\Box\;D_{w^{\prime}+1}\;\small\Box\;\dots\;\small\Box\;D_{w})$
	$\displaystyle\varphi_{R}:(B_{1}\;\small\Box\;\dots\;\small\Box\;B_{s})\;\small\Box\;(E_{1}\;\small\Box\;\dots\;\small\Box\;E_{r})$	$\displaystyle\rightarrow$
	$\displaystyle(B_{1}\;\small\Box\;\dots\;\small\Box\;B_{s^{\prime}}\;\small\Box\;E_{1}\;\small\Box\;\dots\;\small\Box\;E_{r^{\prime}})$	$\displaystyle\;\small\Box\;(B_{s^{\prime}+1}\;\small\Box\;\dots\;\small\Box\;B_{s}\;\small\Box\;E_{r^{\prime}+1}\;\small\Box\;\dots\;\small\Box\;E_{r})$

To simplify the notation we will denote a left vertex $(a_{1},\dots,a_{t^{\prime}},a_{t^{\prime}+1},\dots,a_{t})$ of $G_{1}$ by $(x_{L},y_{L})$ , where $x_{L}=(a_{1},\dots,a_{t^{\prime}})$ and $y_{L}=(a_{t^{\prime}+1},\dots,a_{t})$ , and right vertex $(b_{1},\dots,b_{s^{\prime}},b_{s^{\prime}+1},\dots,b_{s})$ of $G_{1}$ by $(x_{R},y_{R})$ , where $x_{R}=(b_{1},,\dots,b_{s^{\prime}})$ and $y_{R}=(b_{s^{\prime}+1},\dots,b_{s})$ . Similarly, we denote a left vertex $(d_{1},\dots,d_{w^{\prime}},d_{w^{\prime}+1},\dots,d_{w})$ of $G_{2}$ by $(u_{L},v_{L})$ , where $u_{L}=(d_{1},\dots,d_{w^{\prime}})$ and $v_{L}=(d_{w^{\prime}+1},\dots,d_{w})$ , and a right vertex $(e_{1},\dots,e_{r^{\prime}},e_{r^{\prime}+1},\dots,e_{r})$ of $G_{2}$ by $(u_{R},v_{R})$ , where $u_{R}=(e_{1},\dots,e_{r^{\prime}})$ and $v_{R}=(e_{r^{\prime}+1},\dots,e_{r})$ . By Theorem 5.1, isomorphism $\varphi$ is represented as follows

\varphi_{L}((x_{L},y_{L}),(u_{L},v_{L}))=((x_{L},u_{L}),(y_{L},v_{L})),\;\varphi_{R}((x_{R},y_{R}),(u_{R},v_{R}))=((x_{R},u_{R}),(y_{R},v_{R}))

Since this holds for both left and right parts $G_{1}\diamond G_{2}$ , we can represent the isomorphism like $\varphi((x,y),(u,v))=((x,u),(y,v))$ .

Now we find a nontrivial factorization $G_{1}\cong S\diamond S^{\prime}$ . Define $S$ and $S^{\prime}$ as follows:

	$\displaystyle V(S)$	$\displaystyle=\left\{x_{L}\|\;\Big{(}(x_{L},y_{L}),(u_{L},v_{L})\Big{)}\in V(G_{1}\diamond G_{2})\right\}\cup\left\{x_{R}\|\;\Big{(}(x_{R},y_{R}),(u_{R},v_{R})\Big{)}\in V(G_{1}\diamond G_{2})\right\}$
	$\displaystyle E(S)$	$\displaystyle=\left\{\left\langle x_{L},x_{R}\right\rangle\|\;\left\langle\Big{(}(x_{L},y_{L}),(u_{L},v_{L})\Big{)},\Big{(}(x_{R},y_{R}),(u_{R},v_{R})\Big{)}\right\rangle\in E(G_{1}\diamond G_{2})\right\}$
	and
	$\displaystyle V(S^{\prime})$	$\displaystyle=\left\{y_{L}\|\;\Big{(}(x_{L},y_{L}),(u_{L},v_{L})\Big{)}\in V(G_{1}\diamond G_{2})\right\}\cup\left\{y_{R}\|\;\Big{(}(x_{R},y_{R}),(u_{R},v_{R})\Big{)}\in V(G_{1}\diamond G_{2})\right\}$
	$\displaystyle E(S^{\prime})$	$\displaystyle=\left\{\left\langle y_{L},y_{R}\right\rangle\|\;\left\langle\Big{(}(x_{L},y_{L}),(u_{L},v_{L})\Big{)},\Big{(}(x_{R},y_{R}),(u_{R},v_{R})\Big{)}\right\rangle\in E(G_{1}\diamond G_{2})\right\}$

We need to prove that $\left\langle(x,y),(x^{\prime},y^{\prime})\right\rangle\in E(G_{1})$ if and only of $\left\langle(x,y),(x^{\prime},y^{\prime})\right\rangle\in E(S\diamond S^{\prime})$ . If $\left\langle(x,y),(x^{\prime},y^{\prime})\right\rangle\in E(G_{1})$ , then for some $u,v,u^{\prime},v^{\prime}$ there is an edge $\left\langle\Big{(}(x,y),(u,v)\Big{)},\Big{(}(x^{\prime},y^{\prime}),(u^{\prime},v^{\prime})\Big{)}\right\rangle\in E(G_{1}\diamond G_{2})$ , and hence there is an edge $S\diamond S^{\prime}$ which is $\left\langle(x,y),(x^{\prime},y^{\prime})\right\rangle\in E(S\diamond S^{\prime})$ . Next, suppose that $\left\langle(x,y),(x^{\prime},y^{\prime})\right\rangle\in E(S\diamond S^{\prime})$ . Then, $\left\langle x,x^{\prime}\right\rangle\in E(S)$ and $\left\langle y,y^{\prime}\right\rangle\in E(S^{\prime})$ . By the construction of $S$ and $S^{\prime}$ we have that there exist $a,b,u,v,u^{\prime},v^{\prime}$ such that

\displaystyle\left\langle\Big{(}(x,a),(u,v)\Big{)},\Big{(}(x^{\prime},b),(u^{\prime},v^{\prime})\Big{)}\right\rangle\in E(G_{1}\diamond G_{2})

and there exists $c,d,u^{\prime\prime},v^{\prime\prime},u^{\prime\prime\prime},v^{\prime\prime\prime}$ , such that

\displaystyle\left\langle\Big{(}(c,y),(u^{\prime\prime},v^{\prime\prime\prime})\Big{)},\Big{(}(d,y^{\prime}),(u^{\prime\prime\prime},v^{\prime\prime\prime})\Big{)}\right\rangle\in E(G_{1}\diamond G_{2})

Now, apply the isomorphism $\varphi$

	$\displaystyle\left\langle\Big{(}(x,u),(a,v)\Big{)},\Big{(}(x^{\prime},u^{\prime}),(b,v^{\prime})\Big{)}\right\rangle$	$\displaystyle\in E(H_{1}\diamond H_{2})$
	$\displaystyle\left\langle\Big{(}(c,u^{\prime\prime}),(y,v^{\prime\prime\prime})\Big{)},\Big{(}(d,u^{\prime\prime\prime}),(y^{\prime},v^{\prime\prime\prime})\Big{)}\right\rangle$	$\displaystyle\in E(H_{1}\diamond H_{2})$

Hence, $\left\langle(x,u),(x^{\prime},u^{\prime})\right\rangle\in E(H_{1})$ , $\left\langle(y,v^{\prime\prime\prime}),(y^{\prime},v^{\prime\prime\prime})\right\rangle\in E(H_{2})$ . Therefore, $\left\langle\Big{(}(x,u),(y,v^{\prime\prime\prime})\Big{)},\Big{(}(x^{\prime},u^{\prime}),(y^{\prime},v^{\prime\prime\prime})\Big{)}\right\rangle\in E(H_{1}\diamond H_{2})$ . Applying $\varphi^{-1}$ we get

\left\langle\Big{(}(x,y),(u,v^{\prime\prime\prime})\Big{)},\Big{(}(x^{\prime},y^{\prime}),(u^{\prime},v^{\prime\prime\prime})\Big{)}\right\rangle\in E(G_{1}\diamond G_{2}).

Thus, $\left\langle(x,y),(x^{\prime},y^{\prime})\right\rangle\in E(G_{1})$ . ∎

Corollary 5.16.

Let $\varphi$ be an automorphism of a prime $R$ -thin graph $G^{\diamond\ell}$ , Then there is a permutation $\pi$ of $[k]$ such that

\varphi(x_{1},\dots,x_{\ell})=(\varphi_{1}(x_{\pi(1)}),\dots,\varphi_{\ell}(x_{\pi(\ell)}))

where each $\varphi_{i}$ is an automorphism of $G$ .

5.3 Automorphisms of general graphs

In this section we prove an analog of Corollary 5.16 for graphs that are not necessarily $R$ -thin. An automorphism of a graph $G$ is called local if it is the identity mapping on $G/_{R}$ .

Theorem 5.17.

Suppose $\varphi$ is an automorphism of $G^{\diamond\ell}$ . Let $\psi:G^{\diamond\ell}/_{R}\rightarrow G^{\diamond\ell}/_{R}$ be the automorphism induced by $\varphi$ , and let $G=G_{1}\diamond\dots\diamond G_{k}$ be a prime factorization of $G$ . Then there is a permutation $\pi$ of $[\ell]\times[k]$ such that every automorphism of $G^{\diamond\ell}/_{R}$ can be split into $k\ell$ automorphisms:

	$\displaystyle\psi([v_{1}],\dots,[v_{\ell}])$	$\displaystyle=\Big{(}\big{(}\psi_{1,1}([v_{\pi(1,1)}]),\dots,\psi_{1,k}([v_{\pi(1,k)}])\big{)},$
		$\displaystyle\;\;\;\;\;\;\vdots$
		$\displaystyle\;\;\;\;\;\;\big{(}\psi_{\ell,1}([v_{\pi(\ell,1)}]),\dots,\psi_{\ell,k}([v_{\pi(\ell,k)}])\big{)}\Big{)}.$

We start with two auxiliary lemmas.

Lemma 5.18.

Let $G$ be a simple connected graph such that $G/_{R}\cong H_{1}\diamond H_{2}$ . Then every vertex $(x,y)\in V(H_{1}\diamond H_{2})$ corresponds to a unique $R$ -class of $G$ , denote its cardinality by $|(x,y)|$ . If there are functions $\omega_{1}:V(H_{1})\rightarrow\mathbb{N},\omega_{2}:V(H_{2})\rightarrow\mathbb{N}$ such that $|(x,y)|=\omega_{1}(x)\cdot\omega_{2}(y)$ , then there are graphs $H^{\prime}_{1}$ and $H^{\prime}_{2}$ such that $G\cong H^{\prime}_{1}\diamond H^{\prime}_{2}$ , and $H^{\prime}_{1}/_{R}=H_{1}$ and $H^{\prime}_{2}/_{R}=H_{2}$ .

Proof.

By Lemma 5.8 $H_{1},H_{2}$ are $R$ -thin. Define $H^{\prime}_{1}$ as follows. Take a family $\{A_{x}\mid x\in V(H_{1})\}$ of disjoint sets such that $|A_{x}|=\omega_{1}(x)$ for each $x\in V(H_{1})$ . Set $V(H^{\prime}_{1})=\bigcup_{x\in V(H_{1})}A_{x}$ , and $E(H^{\prime}_{1})=\{\left\langle u,v\right\rangle|a\in A_{x},b\in A_{y}\mbox{ and }\left\langle x,y\right\rangle\in E(H_{1})\}$ . A graph $H^{\prime}_{2}$ is constructed in the same way by choosing sets $B_{x}$ with $|B_{x}|=\omega_{2}(x)$ for each $x\in V(H_{2})$ .

Claim 1. The $R$ -classes of $H^{\prime}_{1},H^{\prime}_{2}$ are the sets $A_{x},B_{x}$ , respectively.

Proof of Claim 1..

It suffices to prove that if $a,b\in A_{x}$ , then $N_{H^{\prime}_{1}}(a)=N_{H^{\prime}_{2}}(b)$ . If there is a $c$ such that $\left\langle a,c\right\rangle\in E(A^{\prime})$ , then there is $z$ such that $c\in A_{z}$ and $\left\langle x,z\right\rangle\in E(H_{1})$ , then by the definition of $E(H^{\prime}_{1})$ we have $\left\langle b,c\right\rangle\in E(H^{\prime}_{1})$ . For $H^{\prime}_{2}$ the proof is analogous. ∎

By Claim 1 there are isomorphisms $\psi_{1}:H_{1}\rightarrow H^{\prime}_{1}/_{R}$ and $\psi_{2}:H_{2}\rightarrow H^{\prime}_{2}/_{R}$ , hence, there is a isomorphism $\psi:H_{1}\diamond H_{2}\rightarrow H^{\prime}_{1}/_{R}\diamond H^{\prime}_{2}/_{R}$ . Therefore, $(H^{\prime}_{1}\diamond H^{\prime}_{2})/_{R}\cong H^{\prime}_{1}/_{R}\diamond H^{\prime}_{2}/_{R}\cong H_{1}\diamond H_{2}\cong G/_{R}$ . By Lemma 5.5 we have $H^{\prime}_{1}\diamond H^{\prime}_{2}\cong G$ . ∎

Lemma 5.19.

Suppose there is an isomorphism $\varphi:G_{1}\diamond\dots\diamond G_{k}\rightarrow H_{1}\diamond\dots\diamond H_{\ell}$ where $\varphi(x_{1},\dots,x_{k})=(\varphi_{1}(x_{1},\dots,x_{k}),\dots,\varphi_{\ell}(x_{1},\dots,x_{k}))$ and all factors are connected and such that $G_{i}/_{R},H_{i}/_{R}$ are nontrivial. Let $\psi:G_{1}/_{R}\diamond\dots\diamond G_{k}/_{R}\rightarrow H_{1}/_{R}\diamond\dots\diamond H_{\ell}/_{R}$ be the induced isomorphism

\psi([x_{1}],\dots,[x_{k}])=(\psi_{1}([x_{1}],\dots,[x_{k}]),...,\psi_{l}([x_{1}],\dots,[x_{k}]))

If some $G_{i}$ is prime, then at most one of the functions $\psi_{j}$ depends on $[x_{i}]$ .

Proof.

Grouping and permuting factors, it suffices only to prove the lemma in the case when $G_{1}$ is prime and $k=l=2$ . We rewrite $\varphi:G_{1}\diamond G_{2}\rightarrow H_{1}\diamond H_{2}$ as $\varphi(x,y)=(\varphi_{1}(x,y),\varphi_{2}(x,y))$ . As a consequence we have $\psi:G_{1}/_{R}\diamond G_{2}/_{R}\rightarrow H_{1}/_{R}\diamond H_{2}/_{R}$ , where $\psi([x],[y])=(\psi_{1}([x],[y]),\psi_{2}([x],[y]))$ . As $G_{1},G_{2},H_{1},H_{2}$ are connected, each of $G_{1}/_{R},G_{2}/_{R},H_{1}/_{R},H_{2}/_{R}$ is connected and $R$ -thin. We prove that if $\psi_{1}$ and $\psi_{2}$ depend on $[x]$ , then $G_{1}$ is not prime, a contradiction with the assumption made.

Lemma 5.15 implies that if both $\psi_{1}$ and $\psi_{2}$ depend on $[x]$ , then $G_{1}/_{R}$ is not prime. Take a prime factorization $G_{1}/_{R}=A_{1}\diamond\dots\diamond A_{n}$ . This gives a labeling $[x]=(a_{1},\dots,a_{n})$ of $R$ -classes of $G_{1}$ with vertices of $A_{1}\diamond\dots\diamond A_{n}$ . Then $\psi$ can be viewed as an isomorphism $\psi:A_{1}\diamond\dots\diamond A_{n}\diamond G_{2}/_{R}\rightarrow H_{1}/_{R}\diamond H_{2}/_{R}$ . By Lemma 5.15 for each $i\in[n]$ , exactly one of $\psi_{1}$ and $\psi_{2}$ depends on $a_{i}$ . We order the factors of $G_{1}/_{R}$ = $A_{1}\diamond\dots\diamond A_{n}$ so that $\psi_{1}$ depends on $a_{1},\dots,a_{s}$ , but not on $a_{s+1},\dots,a_{n}$ , and $\psi_{2}$ depends on $a_{s+1},\dots,a_{n}$ but not on $a_{1},\dots,a_{s}$ . Then we have

\psi(a_{1},\dots,a_{s},a_{s+1},,\dots,a_{n},[y])=(\psi_{1}(a_{1},\dots,a_{s},[y]),\psi_{2}(a_{s+1},\dots,a_{n},[y]).

We know that $(a_{1},\dots,a_{n})=[x]\in V(G_{1}/_{R})$ is an $R$ -class of $G_{1}$ , so it makes sense to speak of its cardinality $|(a_{1},\dots,a_{n})|$ . By Lemma 5.18 graph $G_{1}$ has a nontrivial factorization (i.e., be non-prime) if we can define functions $\omega_{1}:A_{1}\diamond\dots\diamond A_{s}\rightarrow\mathbb{N}$ and $\omega_{2}:A_{s+1}\diamond\dots\diamond A_{n}\rightarrow\mathbb{N}$ , for which $|(a_{1},\dots,a_{s},a_{s+1},\dots,a_{n})|=\omega_{1}(a_{1},\dots,a_{s})\cdot\omega_{2}(a_{s+1},\dots,a_{n})$ . Let $[y]\in V(G_{2}/_{R})$ be an $R$ -class of $G_{2}$ . Observe that the isomorphism $\varphi:G_{1}\diamond G_{2}\rightarrow H_{1}\diamond H_{2}$ maps each $R$ -class $((a_{1},\dots,a_{n},[y])$ of $G_{1}\diamond G_{2}$ bijectively to the $R$ -class $(\psi_{1}(a_{1},\dots,a_{s},[y]),\psi_{2}(a_{s+1},\dots,a_{n},[y]))$ of $H_{1}\diamond H_{2}$ . Therefore

|(a_{1},\dots,a_{s},a_{s+1},\dots,a_{n})|=\frac{|\psi_{1}(a_{1},\dots,a_{s},[y])|\cdot|\psi_{2}(a_{s+1},\dots,a_{n},[y])|}{|[y]|}

Since $|(a_{1},\dots,a_{s},a_{s+1},\dots,a_{n})|$ is an integer, $|[y]|$ divides $|\psi_{1}(a_{1},\dots,a_{s},[y])|\cdot|\psi_{2}(a_{s+1},\dots,a_{n},[y])|$ . So there are $d_{1}$ and $d_{2}$ such that $d_{1}\cdot d_{2}=d$ and $d_{1}$ divides $|\psi_{1}(a_{1},\dots,a_{s},[y])|$ and $d_{2}$ divides $|\psi_{2}(a_{s+1},\dots,a_{n},[y])|$ . Set $\omega_{1}(a_{1},\dots,a_{s})=\frac{|\psi_{1}(a_{1},\dots,a_{s},[y])|}{d_{1}}$ and $\omega_{2}(a_{s+1},\dots,a_{n})=\frac{|\psi_{2}(a_{s+1},\dots,a_{n},[y])|}{d_{2}}$ . It is easy to see that functions $\omega_{1},\omega_{2}$ are as required. ∎

Proof of Theorem 5.17.

Let $G=G_{1}\diamond\dots\diamond G_{k}$ be a factorization of $G$ into prime factors. It will be convenient to represent $G^{\diamond\ell}/_{R}$ as

G^{\diamond\ell}/_{R}=(G_{1,1}/_{R}\diamond\dots\diamond G_{1,k}/_{R})\diamond\dots\diamond(G_{\ell,1}/_{R}\diamond\dots\diamond G_{\ell,k}/_{R}),

(6)

where $G_{i,t}=G_{j,t}$ for all $i,j\in[\ell],t\in[k]$ . Relable each vertex $(v_{1},\dots,v_{\ell})\in V(G^{\diamond\ell})$ as

(v_{1},\dots,v_{\ell})=\big{(}(v_{1,1},\dots,v_{1,k}),\dots,(v_{\ell,1},\dots,v_{\ell,k})\big{)}.

By Lemma 5.19, for any automorphism $\psi$ of $G^{\diamond\ell}/_{R}$ there is a permutaion $\pi$ of $[\ell]\times[k]$ such that $\psi$ can be split into $k\ell$ automorphisms:

	$\displaystyle\psi([v_{1}],\dots,[v_{\ell}])$	$\displaystyle=\psi(([v_{1,1}],\dots,[v_{1,k}]),\dots,([v_{\ell,1}],\dots,[v_{\ell,k}]))$
		$\displaystyle=\Big{(}\big{(}\psi_{1,1}([v_{\pi(1,1)}]),\dots,\psi_{1,k}([v_{\pi(1,k)}])\big{)},$
		$\displaystyle\;\;\;\;\;\;\vdots$
		$\displaystyle\;\;\;\;\;\;\big{(}\psi_{\ell,1}([v_{\pi(\ell,1)}]),\dots,\psi_{\ell,k}([v_{\pi(\ell,k)}])\big{)}\Big{)}$

where the equality follows by putting together all $\psi_{i,j}$ for $j\in[k]$ to obtain the automorphism $\psi_{i}$ on $G_{i}/_{R}$ . ∎

5.4 Reduced form of $H^{\diamond\ell}$

As Faben and Jerum showed in [FJ13], the $p$ -reduced form of $H^{\diamond\ell}$ is obtained by removing from a relational structure or a graph vertices that are not fixed under a $p$ -automorphism. On the other hand, we will often use the $p$ -reduced form of $H^{\diamond\ell}$ , and need to make sure that some vertices remain in that $p$ -reduced form. In this section our goal is to show that if $H$ is $p$ -rigid, then we can guarantee that at least some vertices from certain specified sets are not eliminated when constructing the $p$ -reduced form. Recall the definition of the relation $\sim$ from Section 3.3.

Lemma 5.20.

For a simple graph $H$ , A permutation $\pi$ of its R-class $[a]$ can be transform to an automorphism of $H$ . Therefore for $a,b\in V(H)$ , if $aRb$ then $a\sim b$ .

Proof.

Let $\pi$ be a permutation of $[a]$ . As is easily seen, the following mapping is an automorphism of $H$ .

\varphi(v)=\left\{\begin{array}[]{cl}\pi(v)&v\in[a],\\ v&v\not\in[a].\end{array}\right.

Observe that if $aRb$ , then there is a permutation $\pi$ of $[a]$ such that $\pi(a)=b$ , hence there is a $\phi$ such that $\varphi(a)=b$ . ∎

Let $\widetilde{H^{\diamond\ell}}$ be a subgraph of $H^{\diamond\ell}$ obtained by eliminating local $p$ -automorphisms. Note that $\widetilde{H^{\diamond\ell}}$ is NOT the reduced form of $H^{\diamond\ell}$ , as some $p$ -automorphisms may remain. It means that from an $R$ -class $[x]$ of $H^{\diamond\ell}$ with size $|[x]|=ap+r$ , $0\leq r\leq p$ , we remove $ap$ elements of $[x]$ . Denote the result by $\widetilde{[x]}$ . Note that $\widetilde{[x]}\subseteq[x]$ , and $|[x]-\widetilde{[x]}|\equiv 0\pmod{p}$ . Also, $\left\langle x,y\right\rangle\in E(\widetilde{H^{\diamond\ell}})$ if and only if $\left\langle[x],[y]\right\rangle\in E(H^{\diamond\ell}/_{R})$ . More formally

	$\displaystyle V(\widetilde{H^{\diamond\ell}})$	$\displaystyle=\bigcup_{x\in V(H^{\diamond\ell})}\widetilde{[x]},$
	$\displaystyle E(\widetilde{H^{\diamond\ell}})$	$\displaystyle=\{\left\langle x,y\right\rangle\|\left\langle[x],[y]\right\rangle\in E({H^{\diamond\ell}}/_{R})\}.$

The following lemma is a direct implication of the definition of $\widetilde{H^{\diamond\ell}}$ . Observe that if $|[a]|\geq p$ then by Lemma 5.20 $H$ is not $p$ -rigid.

Lemma 5.21.

If $H$ is a $p$ -rigid graph, then $\widetilde{H^{\diamond\ell}}/_{R}$ is isomoprhic to $H^{\diamond\ell}/_{R}$ .

Proof.

We prove the lemma by the following claims.

Claim 1. The $R$ -classes of $H^{\diamond\ell}$ are the sets $\widetilde{[x]}$ .

Proof of Claim 1..

It suffices to prove that if $a,b\in\widetilde{[x]}$ , then $N_{\widetilde{H^{\diamond\ell}}}(a)=N_{\widetilde{H^{\diamond\ell}}}(b)$ . By the definition, if $a,b\in\widetilde{[x]}$ , then $[a]=[b]$ , Hence

	$\displaystyle c\in N_{\widetilde{H^{\diamond\ell}}}(a)\Leftrightarrow\left\langle a,c\right\rangle\in E({\widetilde{H^{\diamond\ell}}})$	$\displaystyle\Leftrightarrow\left\langle[a],[c]\right\rangle\in E({{H^{\diamond\ell}}}/_{R})$
		$\displaystyle\Leftrightarrow\left\langle[b],[c]\right\rangle\in E({{H^{\diamond\ell}}}/_{R})\Leftrightarrow\left\langle b,c\right\rangle\in E({\widetilde{H^{\diamond\ell}}})\Leftrightarrow c\in N_{\widetilde{H^{\diamond\ell}}}(b).$

∎

Claim 2. The function $\varphi:H^{\diamond\ell}/_{R}\rightarrow\widetilde{H^{\diamond\ell}}/_{R}$ where $\varphi([x])=\widetilde{[x]}$ is an isomrphism.

Proof of Claim 2..

Clearly, the function $\varphi$ in bijective and surjective. We just need to prove that the function $\varphi$ is edge preserving.

Assume $\left\langle[a],[b]\right\rangle\in E({{H^{\diamond\ell}}}/_{R})$ . Then, $\varphi([a])=\widetilde{[a]}\subseteq[a]$ and $\varphi([b])=\widetilde{[b]}\subseteq[b]$ . So, there are $a\in\widetilde{[a]}$ and $b\in\widetilde{[b]}$ such that $\left\langle a,b\right\rangle\in E(H^{\diamond\ell})$ , also, $\left\langle a,b\right\rangle\in E(\widetilde{H^{\diamond\ell}})$ . Hence there are $a\in\widetilde{[a]},b\in\widetilde{[b]}$ such that $\left\langle a,b\right\rangle\in E(\widetilde{H^{\diamond\ell}})$ , therefore, $\left\langle[a],[b]\right\rangle\in E(\widetilde{H^{\diamond\ell}}/_{R})$ . ∎

We have an isomorphism from $\widetilde{H^{\diamond\ell}}$ to $H^{\diamond\ell}$ . The result follows. ∎

Theorem 5.22.

Let $H$ be a $p$ -rigid graph and $A\subseteq V(H^{\diamond\ell})$ a union of $R$ -classes of $H^{\diamond\ell}$ . Then

1.

$\widetilde{A}/_{R}=A/_{R}$ .
2.

For any graph $(G,x)$ , $\mathsf{hom}((G,x),(H^{\diamond\ell},A))\equiv\mathsf{hom}((G,x),(\widetilde{H^{\diamond\ell}},\widetilde{A}))\pmod{p}$ .
3.

If $A$ is a $p$ -subalgebra of $H^{\diamond\ell}$ , then $\widetilde{A}$ is a $p$ -subalgebra of $\widetilde{H^{\diamond\ell}}$ .

Proof.

1.

By the definition of local $p$ -automorphisms $\widetilde{A}/_{R}\subseteq A/_{R}$ . On the other hand, by Lemma 5.21 $\widetilde{H^{\diamond\ell}}$ contains elements of every $R$ -class of $H^{\diamond\ell}$ . The result follows.

Note first that if $\mathbf{a}R\mathbf{b}$ for $\mathbf{a},\mathbf{b}\in H^{\diamond\ell}$ then $\mathbf{a}\sim\mathbf{b}$ , that is, for any graph $(G,x)$ it holds that $\mathsf{hom}((G,x),(H^{\diamond\ell},\mathbf{a}))=\mathsf{hom}((G,x),(H^{\diamond\ell},\mathbf{b}))$ . Let $B$ be an $R$ -class of $H^{\diamond\ell}$ and $\widetilde{B}=B\cap V(H^{\diamond\ell})$ . Then $|B-\widetilde{B}|$ is a multiple of $p$ . Therefore

	$\displaystyle\mathsf{hom}((G,x),(H^{\diamond\ell},B))$	$\displaystyle=\sum_{\mathbf{a}\in B}\mathsf{hom}((G,x),(H^{\diamond\ell},\mathbf{a}))$
		$\displaystyle=\mathsf{hom}((G,x),(H^{\diamond\ell},\widetilde{B}))+\sum_{\mathbf{a}\in B-\widetilde{B}}\mathsf{hom}((G,x),(H^{\diamond\ell},\mathbf{a}))$
		$\displaystyle=\mathsf{hom}((G,x),(H^{\diamond\ell},\widetilde{B})).$

3.

Suppose that $A$ is a $p$ -subalgebra of $H^{\diamond\ell}$ . By Lemma 4.1 there exists $(G,x)$ such that $\mathsf{hom}((G,x),(H^{\diamond\ell},\mathbf{a}))\not\equiv 0\pmod{p}$ if and only if $\mathbf{a}\in A$ . By what is observed above for $\mathbf{a}\in V(\widetilde{H^{\diamond\ell}})$ we have $\mathsf{hom}((G,x),(\widetilde{H^{\diamond\ell}},\mathbf{a}))\not\equiv 0\pmod{p}$ if and only if $\mathbf{a}\in A$ . Therefore $(G,x)$ defines $\widetilde{A}$ .

∎

6 Counting graph homomorphisms

6.1 Reductions for bipartite graphs

In this section we prove the Faben-Jerrum Conjecture. Fix a prime $p$ . Let $\mathcal{H}$ be a graph. By Lemma 2.2 $\mathcal{H}$ can be assumed to be $p$ -rigid. Also, by the results of [LGCF21] it suffices to consider the case when $\mathcal{H}$ is bipartite. Thus, we assume that $\mathcal{H}$ is a $p$ -rigid bipartite graph that is not complete. Here we use the techniques developed in the previous sections to prove that $\#_{p}\mathsf{CSP}(\mathcal{H})$ is $\mathsf{Mod}_{p}$ P-complete.

One of the results we use is Theorem 5.17 about automorphisms of $\diamond$ -powers of $\mathcal{H}$ . However, Theorem 5.17 is proved assuming that $\mathcal{H}$ is prime and has two sorts of vertices, left and right. We first prove that we can use this theorem.

Let $\mathcal{H}^{\mathsf{bip}}$ denote the graph $\mathcal{H}$ viewed as a 2-sorted structure. Note that if $\mathcal{H}$ is $p$ -rigid, so is $\mathcal{H}^{\mathsf{bip}}$ . Also, in this case $\mathcal{H}^{\diamond\ell}=(\mathcal{H}^{\mathsf{bip}})^{\ell}$ .

Lemma 6.1 (Lemma 3.28, [LGCF21], rephrased).

If $\mathcal{H}$ is a $p$ -rigid bipartite graph then $\#_{p}\mathsf{CSP}(\mathcal{H})$ and $\#_{p}\mathsf{CSP}(\mathcal{H}^{\mathsf{bip}})$ are polynomial time interreducible.

Since we only work with $\mathcal{H}^{\mathsf{bip}}$ , to simplify notation we will omit ${\mathsf{bip}}$ from $\mathcal{H}^{\mathsf{bip}}$ .

By Theorem 4.5 $\#_{p}\mathsf{CSP}(\mathcal{H}^{*})$ is polynomial time reducible to $\mathcal{H}$ . Again, to simplify the notation we use $\mathcal{H}$ instead of $\mathcal{H}^{*}$

Proposition 6.2.

Let $\mathcal{H}$ a bipartite graph, and let $\mathcal{H}=\mathcal{H}_{1}\diamond\dots\diamond\mathcal{H}_{k}$ be a prime factorization of $\mathcal{H}$ . Then for every automorphism $\varphi$ of $\mathcal{H}^{\ell}/_{R}$ there are permutations $\pi_{1},\dots,\pi_{k}$ of $[\ell]$ such that

\varphi(a_{1,1},\dots,a_{1,k},\dots,a_{\ell,1},\dots,a_{\ell,k})=(a_{\pi_{1}(1),1},\dots,a_{\pi_{k}(1),k},\dots,a_{\pi_{1}(\ell),1},\dots,a_{\pi_{k}(\ell),k}).

where $(a_{i,1},\dots,a_{i,k})$ is an element of the $i$ th copy of $\mathcal{H}/_{R}$ .

Proof.

By Theorem 5.17 there are isomorphisms $\varphi_{1,1},\dots,\varphi_{\ell,k}$ and a permutation $\pi$ of $[\ell]\times[k]$ such that

\varphi(a_{1,1},\dots,a_{1,k},\dots,a_{\ell,1},\dots,a_{\ell,k})=(\varphi_{1,1}(a_{\pi(1,1)}),\dots,\varphi_{\ell,k}(a_{\pi(\ell,k)})).

Now observe that as $\mathcal{H}/_{R}$ has all the constant relations, for any $(a_{1},\dots,a_{k})\in H/_{R}$ we have

\varphi(a_{1},\dots,a_{k},a_{1},\dots,a_{k},\dots,a_{1},\dots,a_{k})=(a_{1},\dots,a_{k},a_{1},\dots,a_{k},\dots,a_{1},\dots,a_{k}).

(7)

Firstly, this implies that every $\varphi_{i,j}$ is the identity mapping. This means that $\varphi$ is basically the permutation $\pi$ of coordinates. If for some $i\in[\ell],j\in[k]$ , $\pi(i,j)=(i^{\prime},j^{\prime})$ and $j^{\prime}\neq j$ then choosing any $(a_{1},\dots,a_{k})$ such that $a_{i}\neq a_{j}$ we get a contradiction. The result follows. ∎

Proposition 6.2 provides strong restrictions on the possible $p$ -automorphisms of $\mathcal{H}^{\ell}$ .

Corollary 6.3.

If $\ell<p$ then every $p$ -automorphism of $\mathcal{H}^{\ell}$ is local.

Proof.

Let $\psi$ be a non-local $p$ -automorphism of $\mathcal{H}^{\ell}$ and $\varphi$ the corresponding automorphism of $\mathcal{H}^{\ell}/_{R}$ . By Proposition 6.2 there are permutations $\pi_{1},\dots,\pi_{k}$ of $[\ell]$ such that

\varphi(a_{1,1},\dots,a_{1,k},\dots,a_{\ell,1},\dots,a_{\ell,k})=(a_{\pi_{1}(1),1},\dots,a_{\pi_{k}(1),k},\dots,a_{\pi_{1}(\ell),1},\dots,a_{\pi_{k}(\ell),\ell}).

for any $(a_{1,1},\dots,a_{\ell,k})\in\mathcal{H}^{\ell}$ . As $\psi$ is a $p$ -automorphism, so is $\varphi$ . Therefore every $\pi_{i}$ is either the identity mapping or has order $p$ . The latter is impossible as $\ell<p$ , and $\varphi$ has to be the identity mapping. ∎

Lemma 6.4.

1. Let $a\in H$ . Then $N_{\mathcal{H}}(a)$ is a subalgebra of $\mathcal{H}$ .
2. Let $A\subseteq H$ be a $p$ -subalgebra of $\mathcal{H}$ . Then $N_{\mathcal{H}}(A)$ is a $p$ -subalgebra of $\mathcal{H}$ .

Proof.

Let $E$ be the edge relation of $\mathcal{H}$ .
1. Since $\mathcal{H}$ has the constant relation $R_{a}$ , $Q(x)=\exists y(E(x,y)\wedge R_{a}(y)$ pp-defines (and by Theorem 4.4) $p$ -mpp-defines $N_{\mathcal{H}}(a)$ .
2. In this case the argument is similar. Let $A$ is $p$ -mpp-defined by $A(x)=\exists^{\oplus p}y_{1},\dots,y_{s}\Phi(x,y_{1},\dots,y_{s})$ . Then $Q(x)=\exists z\exists^{\oplus p}y_{1},\dots,y_{s}(E(x,z)\wedge\Phi(z,y_{1},\dots,y_{s}))$ defines $N_{\mathcal{H}}(A)$ . ∎

6.2 Weighted $\#\mathsf{BIS}$ and thick $\mathsf{Z}$ -graphs

To prove hardness we reduce the Weighted $\#_{p}\mathsf{BIS}$ problem to $\#_{p}\mathsf{CSP}(H)$ . For a graph $\mathcal{G}$ let $\mathsf{IS}(\mathcal{G})$ denote the set of its independent sets. Also, for a bipartite graph $\mathcal{G}$ let $L_{\mathcal{G}},R_{\mathcal{G}}$ denote the two parts of the bipartition. Let $\alpha,\beta\not\equiv 0\pmod{p}$ . Then $\#_{p}\mathsf{BIS}(\alpha,\beta)$ is the problem defined as follows: given a bipartite graph $\mathcal{G}$ , find the value

\mathcal{Z}_{\alpha,\beta}(\mathcal{G})=\sum_{I\in\mathsf{IS}(\mathcal{G})}\alpha^{|I\cap L_{\mathcal{G}}|}\cdot\beta^{|I\cap R_{\mathcal{G}}|}

modulo $p$ . The problem of computing the function $\mathcal{Z}_{\alpha,\beta}(\mathcal{G})$ is proven to be $\#_{p}P$ -hard in [GLS18].

A bipartite graph $\mathcal{G}$ is said to be a thick Z-graph if its vertices can be partitioned into four sets $A,B,C,D$ , where $A,C\subseteq L_{\mathcal{G}},B,D\subseteq R_{\mathcal{G}}$ , such that the sets $A\cup B,C\cup B,C\cup D$ induce complete bipartite subgraphs of $\mathcal{G}$ , and there are no edges between vertices from $A\cup D$ , see Figure 1.

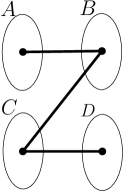
Refer to caption — Figure 1: Thick $\mathsf{Z}$ -graph

An induced subgraph $\mathcal{H}^{\mathsf{Z}}$ of $\mathcal{H}$ that is a thick Z-graph with parts $A,B,C,D$ is said to be non-degenerate if there exist graphs with distinguished vertices $(\mathcal{K}_{L},x),(\mathcal{K}_{R},x)$ such that

\displaystyle\begin{split}\mathsf{hom}((\mathcal{K}_{L},x),(\mathcal{H},A))\equiv\alpha_{1}&\not\equiv 0\pmod{p},\\ \mathsf{hom}((\mathcal{K}_{L},x),(\mathcal{H},C))\equiv\alpha_{2}&\not\equiv 0\pmod{p},\\ \mathsf{hom}((\mathcal{K}_{R},x),(\mathcal{H},D))\equiv\beta_{1}&\not\equiv 0\pmod{p},\\ \mathsf{hom}((\mathcal{K}_{R},x),(\mathcal{H},B))\equiv\beta_{2}&\not\equiv 0\pmod{p},\end{split}

(8)

and

\displaystyle\begin{split}\mathsf{hom}((\mathcal{K}_{L},x),(\mathcal{H},v))&\equiv 0\pmod{p},\qquad\text{for $v\in L_{\mathcal{H}}-(A\cup C)$},\\ \mathsf{hom}((\mathcal{K}_{R},x),(\mathcal{H},v)&\equiv 0\pmod{p}\qquad\text{for $v\in R_{\mathcal{H}}-(B\cup D)$}.\end{split}

(9)

Theorem 6.5.

Let there exist an induced subgraph of $\mathcal{H}$ that is a non-degenerate thick Z-graph with parameters $\alpha_{1},\alpha_{2},\beta_{1},\beta_{2}$ , then $\#_{p}\mathsf{BIS}(\alpha_{1}\alpha_{2}^{-1},\beta_{1}\beta_{2}^{-1})$ (multiplication and inversion here is $\pmod{p}$ ) is polynomial time reducible to $\#_{p}\mathsf{CSP}(\mathcal{H})$ .

Proof.

Let $\mathcal{G}=(L_{\mathcal{G}}\cup R_{\mathcal{G}},E)$ be a bipartite graph, an instance of $\#_{p}\mathsf{BIS}$ . We construct a graph $\mathcal{G}^{\prime}$ , an instance of $\#_{p}\mathsf{CSP}(\mathcal{H})$ as follows:

•

For each vertex $x\in L_{\mathcal{G}}$ and each vertex $y\in R_{\mathcal{G}}$ , we make vertices $l^{x}$ and $r^{y}$ , respectively. If ${xy}\in E$ , then we add an edge between $l^{x}$ and $r^{y}$ in $\mathcal{G}^{\prime}$ .
•

For $x\in L_{\mathcal{G}}$ let $\mathcal{K}_{L}(x)$ denote a copy of $\mathcal{K}_{L}$ attached to $l^{x}$ , that is, $x$ in $(\mathcal{K}_{L},x)$ is identified with $l^{x}$ . For $y\in R_{\mathcal{G}}$ a copy $\mathcal{K}_{R}(y)$ is attached in the same way.

The vertices from $A,D$ will help to encode independent sets of $\mathcal{G}$ . Specifically, with every independent set $I$ of $\mathcal{G}$ we associate a set of homomorphisms $\varphi:\mathcal{G}^{\prime}\to\mathcal{H}$ such that for every vertex $x\in L_{\mathcal{G}}$ , $x\in I$ if and only if $\varphi(l^{x})\in A$ (recall that $x$ is also a vertex of $G^{\prime}$ identified with $l^{x}$ in $(\mathcal{K}_{L}(x),l^{x})$ ); and similarly, for every $y\in R_{\mathcal{G}}$ , $y\in I$ if and only if $\varphi(y)\in D$ . Finally, the structure of $\mathcal{H}^{\mathsf{Z}}$ makes sure that every homomorphism from $\mathcal{G}^{\prime}$ to $\mathcal{H}$ is associated with an independent set. Note that just an association of independent sets with collections of homomorphisms is not enough, the number of homomorphisms in those collections have to allow one to compute the weight of an independent set in $\#_{p}\mathsf{BIS}$ .

Now, we give a formal definition of $G^{\prime}$ :

	$\displaystyle V(\mathcal{G}^{\prime})$	$\displaystyle=\Big{(}\bigcup_{x\in L_{\mathcal{G}}}V(\mathcal{K}_{L}(x))\Big{)}\cup\Big{(}\bigcup_{y\in R_{\mathcal{G}}}V(\mathcal{K}_{R}(y))\Big{)},$
	$\displaystyle E(\mathcal{G}^{\prime})$	$\displaystyle=\Big{(}\bigcup_{x\in L_{\mathcal{G}}}E(\mathcal{K}_{L}(x))\Big{)}\cup\Big{(}\bigcup_{y\in R_{\mathcal{G}}}E(\mathcal{K}_{R}(y))\Big{)}\cup\{{l^{x}r^{y}}\|{xy}\in E\}$

For each $\varphi\in\mathsf{Hom}(\mathcal{G}^{\prime},\mathcal{H})$ , define

I_{\varphi}=\{x\in L_{\mathcal{G}}:\varphi(l^{x})\in A\}\cup\{y\in R_{\mathcal{G}}:\varphi(r^{y})\in D\}.

Claim 1. $I_{\varphi}$ is an independent set.

Proof of Claim 1.

Assume that for some $\varphi\in\mathsf{Hom}(\mathcal{G}^{\prime},\mathcal{H})$ the set $I_{\varphi}$ is not an independent set in $\mathcal{G}$ , i.e. there are two vertices $a,b\in I_{\varphi}$ such that ${ab}\in E(\mathcal{G})$ . Without loss of generality, let $a\in L_{\mathcal{G}}$ and $b\in R_{\mathcal{G}}$ . By the construction of $I_{\varphi}$ , $\varphi(a)\in A$ and $\varphi(b)\in D$ and by definition of $\mathcal{H}^{\mathsf{Z}}$ there is no edge between $A$ and $D$ , that is $\varphi$ is not a homomorphism. A contradiction. ∎

Let $\bumpeq_{I}$ be a relation on $\mathsf{Hom}(G^{\prime},H)$ given by $\varphi\bumpeq_{I}\varphi^{\prime}$ if and only if $I_{\varphi}=I_{\varphi^{\prime}}$ .

Obviously $\bumpeq_{I}$ is an equivalence relation on $\mathsf{Hom}(\mathcal{G}^{\prime},H)$ . We denote the class of $\mathsf{Hom}(\mathcal{G}^{\prime},H)\mathbin{/}_{\bumpeq_{I}}$ containing $\varphi$ by $\varphi/_{\bumpeq_{I}}$ . Clearly, the $\bumpeq_{I}$ -classes correspond to the independent sets of $\mathcal{G}$ . We will need the corresponding mapping

\mathfrak{F}:\mathsf{Hom}(\mathcal{G}^{\prime},\mathcal{H})\mathbin{/}_{\bumpeq_{I}}\to\mathsf{IS}(\mathcal{G}),\quad\text{where}\quad\mathfrak{F}([\varphi])=I_{\varphi}

First, we will prove that $\mathfrak{F}$ is bijective, then compute the cardinalities of classes $\varphi/_{\bumpeq_{I}}$ .

Claim 2. The mapping $\mathfrak{F}$ is bijective.

Proof of Claim 2.

By the definition of $\mathfrak{F}$ , it is injective. To show surjectivity let $I\in\mathsf{IS}(\mathcal{G})$ be an independent set. We construct a homomorphism $\varphi\in\mathsf{Hom}(\mathcal{G}^{\prime},\mathcal{H})$ such that $I_{\varphi}=I$ . Pick arbitrary $a\in A,b\in B,c\in C,d\in D$ , and :

•

For every vertex $x\in I\cap L_{G}$ set $\varphi(l^{x})=a$ .
•

For every vertex $\bar{x}\in L_{G}-I$ set $\varphi(l^{\bar{x}})=c$ .
•

For every vertex $y\in I\cap R_{G}$ set $\varphi(r^{y})=d$ .
•

For every vertex $\bar{y}\in R_{G}-I$ set $\varphi(r^{\bar{y}})=b$ .

By construction of $\varphi$ , if ${xy}\in E(G)$ and $\varphi(l^{x})\in A$ , then $\varphi(r^{y})\in B$ . Similarly, if $\varphi(r^{y})\in D$ , then $\varphi(l^{x})=C$ . If none of the endpoints of an edge ${xy}$ belongs to $I$ then $\varphi(l^{x})\in C$ and $\varphi(r^{y})\in B$ . By the assumption on $(\mathcal{K}_{L},x),(\mathcal{K}_{R},x)$ , mapping $\varphi$ can be extended to a homomorphism from $\mathcal{G}^{\prime}$ to $\mathcal{H}$ . Hence $\mathfrak{F}$ is surjective. ∎

Claim 3. $|\varphi/_{\bumpeq_{I}}|\equiv\alpha_{1}^{|L_{\mathcal{G}}\cap I_{\varphi}|}\;\;\alpha_{2}^{|L_{\mathcal{G}}-I|}\;\;\beta_{1}^{|R_{\mathcal{G}}\cap I_{\varphi}|}\;\;\beta_{2}^{|R_{\mathcal{G}}-I|}\pmod{p}$ .

Proof of Claim 3.

We find the number of homomorphisms $\varphi^{\prime}\in\varphi/_{\bumpeq_{I}}$ . The graph $\mathcal{G}^{\prime}$ consists of copies of $(\mathcal{K}_{L}(x),l^{x})$ and $(\mathcal{K}_{R}(y),r^{y})$ . By Claim 2, and by (9) and (8)

	$\displaystyle\|\varphi/_{\bumpeq_{I}}\|$	$\displaystyle=\Big{(}\prod_{x\in L_{\mathcal{G}}\cap I_{\varphi}}\mathsf{hom}((\mathcal{K}_{L}(x),l^{x}),(\mathcal{H},A))\Big{)}\cdot\Big{(}\prod_{x\in L_{\mathcal{G}}-I_{\varphi}}\mathsf{hom}((\mathcal{K}_{L}(x),l^{x}),(\mathcal{H},C))\Big{)}$
		$\displaystyle\times\Big{(}\prod_{y\in R_{\mathcal{G}}\cap I_{\varphi}}\mathsf{hom}((\mathcal{K}_{R}(y),r^{x}),(\mathcal{H},D))\Big{)}\cdot\Big{(}\prod_{y\in R_{\mathcal{G}}-I_{\varphi}}\mathsf{hom}((\mathcal{K}_{R}(y),r^{x}),(\mathcal{H},B))\Big{)}$
		$\displaystyle\equiv\alpha_{1}^{\|L_{\mathcal{G}}\cap I_{\varphi}\|}\;\;\alpha_{2}^{\|L_{\mathcal{G}}-I_{\varphi}\|}\;\;\beta_{1}^{\|R_{\mathcal{G}}\cap I_{\varphi}\|}\;\;\beta_{2}^{\|R_{\mathcal{G}}-I_{\varphi}\|}\pmod{p}$

∎

Assume that $\bumpeq_{I}$ has $M$ classes and $\varphi_{i}$ is a representative of the $i$ -th class. Let $N^{\prime}$ be the number of homomorphisms $\varphi$ such that $\varphi(l^{x})\not\in A\cup C$ or $\varphi(r^{y})\not\in B\cup D$ . Then

	$\displaystyle\|\mathsf{Hom}(G^{\prime},H)\|=N^{\prime}+\sum_{i=1}^{M}\|\varphi_{i}/_{\bumpeq_{I}}\|$	$\displaystyle\equiv\sum_{i=1}^{M}\alpha_{1}^{\|L_{G}\cap I_{\varphi_{i}}\|}\;\;\alpha_{2}^{\|L_{G}-I_{\varphi_{i}}\|}\;\;\beta_{1}^{\|R_{G}\cap I_{\varphi_{i}}\|}\;\;\beta_{2}^{\|R_{G}-I_{\varphi_{i}}\|}$
		$\displaystyle\equiv N^{\prime}+\sum_{I\in\mathsf{IS}(G)}\alpha_{1}^{\|L_{G}\cap I\|}\;\;\alpha_{2}^{\|L_{G}-I\|}\;\;\beta_{1}^{\|R_{G}\cap I\|}\;\;\beta_{2}^{\|R_{G}-I\|}$
		$\displaystyle\equiv N^{\prime}+\alpha_{2}^{\|L_{G}\|}\beta_{2}^{\|R_{R}\|}\sum_{I\in\mathsf{IS}(G)}\alpha_{1}^{\|L_{G}\cap I\|}\;\;\alpha_{2}^{-\|L_{G}\|}\alpha_{2}^{\|L_{G}-I\|}\;\;\beta_{1}^{\|R_{G}\cap I\|}\;\;\beta_{2}^{-\|R_{G}\|}\beta_{2}^{\|R_{G}-I\|}$
		$\displaystyle\equiv N^{\prime}+\alpha_{2}^{\|L_{G}\|}\beta_{2}^{\|R_{R}\|}\sum_{I\in\mathsf{IS}(G)}(\alpha_{1}\alpha_{2}^{-1})^{\|L_{G}\cap I\|}\;\;(\beta_{1}\beta_{2}^{-1})^{\|R_{G}\cap I\|}$
		$\displaystyle\equiv N^{\prime}+\alpha_{2}^{\|L_{G}\|}\beta_{2}^{\|R_{G}\|}\mathcal{Z}_{(\alpha_{1}\alpha_{2}^{-1}),(\beta_{1}\beta_{2}^{-1})}(G)\pmod{p}.$

Finally, by (9) $N^{\prime}\equiv 0\pmod{p}$ . ∎

6.3 $p>2$

We will consider squares of $\mathcal{H}$ , and so Corollary 6.3 indicates that the cases $p>2$ and $p=2$ have to be considered separately. While Lemma 6.6 below holds for both cases, after it we split the proof into two parts. Let $\mathcal{H}$ be as in Section 6.1. The goal is to prove the existence of a non-degenerate thick Z-subgraph of $\mathcal{H}$ .

We start with showing that there exists a thick Z-subgraph of $\mathcal{H}$ such that both parts of the bipartition are $p$ -subalgebras.

Lemma 6.6.

There are subsets $A,C\subseteq L_{\mathcal{H}},B,D\subseteq R_{\mathcal{H}}$ such that $A\cup C,B\cup D$ are $p$ -subalgebras of $\mathcal{H}$ and the subgraph induced by $A\cup B\cup C\cup D$ is a thick Z-graph. Moreover, $A\cup C,B\cup D$ are unions of $R$ -classes.

Proof.

We prove by induction on the number of vertices in $\mathcal{H}$ . If $|L_{\mathcal{H}}|=|R_{\mathcal{H}}|=2$ , graph $\mathcal{H}$ is either disconnected, or complete, or a Z-graph. Then it suffices to show that if $\mathcal{H}$ is not complete or is a thick Z-graph, then there are $L^{\prime}\subseteq L_{\mathcal{H}},R^{\prime}\subseteq R_{\mathcal{H}}$ such that $L^{\prime},R^{\prime}$ are $p$ -subalgebras of $\mathcal{H}$ , one of the inclusions is strict, and the subgraph induced by $L^{\prime}\cup R^{\prime}$ is not complete. If a connected bipartite graph $\mathcal{H}$ is not complete, then either it is a thick Z-graph, or there are $v,w\in H$ (assume $v,w\in L_{\mathcal{H}}$ ) such that $N_{\mathcal{H}}(v)\neq R_{\mathcal{H}}$ and $\emptyset\neq N_{\mathcal{H}}(v)\cap N_{\mathcal{H}}(w)\neq N_{\mathcal{H}}(v)$ . Then $R^{\prime}=N_{\mathcal{H}}(v)$ , $L^{\prime}=N_{\mathcal{H}}(N_{\mathcal{H}}(v))$ are subalgebras of $\mathcal{H}$ and the subgraph induced by $L^{\prime}\cup R^{\prime}$ is not a complete bipartite graph. ∎

For the rest of Section 6.3 we assume $p>2$ .

Proposition 6.7.

$\mathcal{H}$ contains a non-degenerate thick Z-subgraph.

Proof.

Let $\mathcal{H}^{\prime}$ be the thick Z-subgraph found in Lemma 6.6. In particular, $A,B,C,D$ are such that $A\cup C,B\cup D$ are $p$ -subalgebras of $\mathcal{H}$ and are unions of R-classes. We need to prove the existence of structures $(\mathcal{K}_{L},x),(\mathcal{K}_{R},x)$ from the definition of non-degeneracy. We prove it for $(\mathcal{K}_{L},x)$ , as for $(\mathcal{K}_{R},x)$ a proof is identical.

Set $\mathcal{J}=\mathcal{H}^{2}$ , $M=(A\times C)\cup(C\times A)$ , and $M^{\prime}=(A\cup C)\times(A\cup C)$ . As we demonstrate in Claim 4, it suffices to show that for some $(\mathcal{G},x)$ it holds that $\mathsf{hom}((\mathcal{G},x),(\mathcal{J},M))\not\equiv 0\pmod{p}$ . Indeed, if this is the case, by Proposition 2.4 we would conclude that $2\mathsf{hom}((\mathcal{G},x),(\mathcal{H},A)),2\mathsf{hom}((\mathcal{G},x),(\mathcal{H},C))\not\equiv 0\pmod{p}$ , and $(\mathcal{K}_{L},x)$ with the required properties can be easily constructed from $(\mathcal{G},x)$ . We will apply Lemma 3.2(1) to prove the existence of such a structure. However, in order to to apply Lemma 3.2(1) the set $M$ needs to be automorphism stable, and there must be no $p$ -automorphism $\varphi$ of $\mathcal{J}$ such that $\varphi(a)\in M$ for some $a\in M$ . Unfortunately, $\mathcal{J}$ and $M$ do not satisfy any of these conditions. We will modify them to enforce the conditions.

Firstly, by Theorem 5.22, $\mathcal{J},M$ can be replaced by ${\widetilde{\mathcal{J}}}$ and $\widetilde{M}$ , respectively, obtained by reducing $\mathcal{J}$ using local $p$ -automorphisms, such that $\mathcal{J}/_{R}={\widetilde{\mathcal{J}}}/_{R}$ , $M/_{R}=\widetilde{M}/_{R}$ . Moreover, for any $(\mathcal{G},x)$

\mathsf{hom}((\mathcal{G},x),({\widetilde{\mathcal{J}}},{\widetilde{M}}))\equiv\mathsf{hom}((\mathcal{G},x),(\mathcal{J},M))\pmod{p}.

Claim 1. ${\widetilde{\mathcal{J}}}$ is $p$ -rigid.

Proof of Claim X..

By Corollary 6.3 every $p$ -automorphism of $\mathcal{J}$ is local. As ${\widetilde{\mathcal{J}}}/_{R}=\mathcal{J}/_{R}$ the same holds for ${\widetilde{\mathcal{J}}}$ . By the construction ${\widetilde{\mathcal{J}}}$ does not have local $p$ -automorphisms. The claim follows. ∎

Claim 2. The set ${\widetilde{M}}$ is automorphism stable for ${\widetilde{\mathcal{J}}}$ .

Proof of Claim Y..

We need to show that for some $a\in{\widetilde{M}}$ , $\mathsf{Stab}(a,{\widetilde{M}})$ is a subgroup of $\mathsf{Aut}({\widetilde{\mathcal{J}}})$ . In fact we show that for any $a\in{\widetilde{M}}$ , $\mathsf{Stab}(a,{\widetilde{M}})=\mathsf{Aut}({\widetilde{\mathcal{J}}})$ . In order to do that it suffices to proof that for any $\varphi\in\mathsf{Aut}({\widetilde{\mathcal{J}}})$ it holds $\varphi(a)\in{\widetilde{M}}$ .

We first show that no element of ${\widetilde{M}}$ is isomorphic to an element of ${\widetilde{M}}^{\prime}-{\widetilde{M}}$ . Clearly, for every automorphism of ${\widetilde{\mathcal{J}}}/_{R}$ and every $y\in{\widetilde{M}}^{\prime}/_{R}$ the degree of $v$ in $(B\cup D)^{2}/_{R}$ and that of $\varphi(y)$ are equal. As is easily seen, this degree of $y\in{\widetilde{M}}/_{R}$ equals $|D/_{R}|\cdot(|B/_{R}|+|D/_{R}|)$ , while for $y\in A/_{R}\times A/_{R}$ and $y\in C/_{R}\times C/_{R}$ it is $|D/_{R}|^{2}$ and $(|B/_{R}|+|D/_{R}|)^{2}$ , respectively. It remains to recall that if any $x\in{\widetilde{M}}$ is isomorphic to $y\in{\widetilde{M}}^{\prime}-{\widetilde{M}}$ , then $x/_{R}$ is isomorphic to $y/_{R}$ .

Next, as is easily seen, ${\widetilde{M}}^{\prime}$ is a $p$ -subalgebra of ${\widetilde{\mathcal{J}}}$ . Indeed, since $A\cup C$ is a $p$ -subalgebra of $\mathcal{H}$ , there is $(\mathcal{G},x)$ such that $\mathsf{hom}((\mathcal{G},x),(\mathcal{H},a))\not\equiv 0\pmod{p}$ if and only if $a\in A\cup C$ . Then by Proposition 2.4(2) the same $(\mathcal{G},x)$ witnesses that $M^{\prime}$ is a $p$ -subalgebra of $\mathcal{J}$ . Finally, for any $a\in\widetilde{M}^{\prime}$ it holds

\mathsf{hom}((\mathcal{G},x),({\widetilde{\mathcal{J}}},a))\equiv\mathsf{hom}((\mathcal{G},x),(\mathcal{J},a))\pmod{p},

and so $\mathsf{hom}((\mathcal{G},x),({\widetilde{\mathcal{J}}},a))\not\equiv 0\pmod{p}$ if and only if $a\in{\widetilde{M}}^{\prime}$ .

That ${\widetilde{M}}^{\prime}$ is a $p$ subalgebra means that for no $b\in{\widetilde{M}}^{\prime}$ and no $\varphi\in\mathsf{Aut}({\widetilde{\mathcal{J}}})$ , $\varphi(b)\not\in{\widetilde{M}}^{\prime}$ . Claim 2 follows. ∎

Claim 3. ${\widetilde{M}}$ is a union of $R$ -classes.

Proof of Claim 3..

By the proof of Claim 2, for any $a\in{\widetilde{M}}$ and $\varphi\in\mathsf{Aut}({\widetilde{\mathcal{J}}})$ , $\varphi(a)\in{\widetilde{M}}$ . On the other hand, if $bRa$ then the mapping that swaps $a,b$ leaving all the other vertices in place is an automorphism of ${\widetilde{\mathcal{J}}}$ . ∎

Claim 4. For any $(\mathcal{G},x)$ , $\mathsf{hom}((\mathcal{G},x),({\widetilde{\mathcal{J}}},\widetilde{M}))=2\mathsf{hom}((\mathcal{G},x),(\mathcal{H},A))\cdot\mathsf{hom}((\mathcal{G},x),(\mathcal{H},C))$ .

Proof of Claim 3.

By Theorem 5.22 it suffices to prove the claim for $\mathcal{J}$ and $M$ . By Proposition 2.4 every homomorphism $\varphi:\mathcal{G}\to\mathcal{J}$ can be represented as $\varphi(y)=(\varphi_{1}(y),\varphi_{2}(y))$ , where $\varphi_{1},\varphi_{2}$ are homomorphisms $\mathcal{G}\to\mathcal{H}$ . Conversely, if $\varphi_{1},\varphi_{2}:\mathcal{G}\to\mathcal{H}$ are homomorphisms, then the mapping given by $\varphi(y)=(\varphi_{1}(y),\varphi_{2}(y)$ is a homomorphism from $\mathcal{G}$ to $\mathcal{J}$ . Finally, $\varphi(x)\in M$ if and only if $\varphi_{1}(x)\in A,\varphi_{2}(x)\in C$ or $\varphi_{1}(x)\in C,\varphi_{2}(x)\in A$ . Since swapping coordinates of $\mathcal{J}$ is an automorphism of $\mathcal{K}$ the number of homomorphisms of the two kinds is the same. ∎

By Lemma 3.2(1) there is $(\mathcal{G},x)$ such that $\mathsf{hom}((\mathcal{G},x),({\widetilde{\mathcal{J}}},{\widetilde{M}}))\not\equiv 0\pmod{p}$ . Then by Claim 3 we also have $\mathsf{hom}((\mathcal{G},x),(\mathcal{H},A)),\mathsf{hom}((\mathcal{G},x),(\mathcal{H},C))\not\equiv 0\pmod{p}$ . To obtain a required gadget $(\mathcal{K}_{L},x)$ we need to ensure that $\mathsf{hom}((\mathcal{K}_{L},x),(\mathcal{H},a))\equiv 0\pmod{p}$ whenever $a\not\in A\cup C$ . Since $A\cup C$ is a $p$ -subalgebra, there is $(\mathcal{G}^{\prime},x)$ such that $\mathsf{hom}((\mathcal{G}^{\prime},x),(\mathcal{H},a))\equiv 1\pmod{p}$ whenever $a\in A\cup C$ , and $\mathsf{hom}((\mathcal{G}^{\prime},x),(\mathcal{H},a))\equiv 0\pmod{p}$ otherwise. The structure $(\mathcal{K}_{L},x)=(\mathcal{G},x)\odot(\mathcal{G}^{\prime},x)$ satisfies the required conditions. ∎

6.4 $p=2$

In this subsection we assume $p=2$ and $\mathcal{H}$ is as in Section 6.1. Note that, as the underlying bipartite graph of $\mathcal{H}$ is 2-rigid, $\mathcal{H}$ is R-thin and in any prime factorization $\mathcal{H}$ all the factors are pairwise non-isomorphic. The goal is again to prove the existence of a non-degenerate thick Z-subgraph of $\mathcal{H}$ . By Lemma 6.6 $\mathcal{H}$ has a thick induced Z-subgraph $\mathcal{H}^{\prime}$ . Let the parts of $\mathcal{H}^{\prime}$ are $A,B,C,D$ as before. We only give a proof for $A,C$ and $(\mathcal{K}_{L},x)$ , as the proof for $B,D,(\mathcal{K}_{R},x)$ is identical.

Let $\mathcal{H}=\mathcal{H}_{1}\diamond\dots\diamond\mathcal{H}_{K}$ be a prime factorization of $\mathcal{H}$ . By Proposition 6.2 every automorphism $\varphi$ of $\mathcal{H}^{2}$ has the form

\varphi(a_{1,1},\dots,a_{1,k},a_{2,1},\dots,a_{2,k})=(a_{\pi_{1}(1),1},\dots,a_{\pi_{k}(1),k},a_{\pi_{1}(2),1},\dots,a_{\pi_{k}(2),k}).

where $(a_{i,1},\dots,a_{i,k})$ is an element of the $i$ th copy of $\mathcal{H}$ and $\pi_{1},\dots,\pi_{k}$ are permutations of $[2]$ , that is, either identity mappings or involutions. Let $I_{\varphi}=\{i\in[k]\mid\pi_{i}\text{ is an involution}\}$ .

We plan to use Lemma 3.2(1), and for that we need to find a $\mathbf{a}=(a_{1},\dots,a_{k},c_{1},\dots,c_{k})\in A\times C$ such that $\mathsf{Stab}(\mathbf{a},A\times C)$ is as small as possible. Suppose for some $\mathbf{a}\in A\times C$ and an automorphism $\varphi$ of $\mathcal{H}^{2}$ we have $\varphi(\mathbf{a})\in A\times C$ . If $\varphi$ is not an identity mapping, $I_{\varphi}\neq\emptyset$ . Choose $\mathbf{a}$ and $\varphi$ such that $I_{\varphi}$ is maximal possible. Without loss of generality, $I_{\varphi}=[s]$ , that is,

\varphi(a_{1,1},\dots,a_{1,k},a_{2,1},\dots,a_{2,k})=(a_{2,1},\dots,a_{2,s},a_{1,s+1},\dots,a_{1,k},a_{1,1},\dots,a_{1,s},a_{2,s+1},\dots,a_{2,k}).

Note that $I_{\varphi}\neq[k]$ , because in this case $(a_{1},\dots,a_{k})\in A\cap C$ , which is impossible, as $A$ and $C$ are disjoint.

By the choice of $\mathbf{a},\varphi$ we have $(c_{1},\dots,c_{s},a_{s+1},\dots,a_{k})\in A$ and $(a_{1},\dots,a_{s},c_{s+1},\dots,c_{k})\in C$ . Therefore, $\mathbf{b}=(c_{1},\dots,c_{s},a_{s+1},\dots,a_{k},c_{1},\dots,c_{s},c_{s+1},\dots,c_{k})\in A\times C$ is a fixed point of $\varphi$ . Let $\bar{\mathcal{H}}^{2}$ denote the structure $\mathcal{H}^{2}$ reduced using the automorphism $\varphi$ . In other words, $\bar{\mathcal{H}}^{2}$ is the induced structure on the set $S=\{(a_{1,1},\dots,a_{1,k},a_{2,1},\dots,a_{2,k})\in\mathcal{H}^{2}\mid a_{1,i}=a_{2,i},\ i\in[s]\}$ . Also, let $M=(A\times C)\cap S$ . Note that $M\neq\emptyset$ because $\mathbf{b}\in M$ .

Lemma 6.8.

For any $\mathbf{c}\in M$ , the only automorphism $\psi$ of $\bar{\mathcal{H}}^{2}$ such that $\psi(\mathbf{c})\in M$ is the identity mapping.

Proof.

Any nontrivial homomorphism $\psi$ of $\mathcal{H}^{2}$ has the form

\psi(a_{1,1},\dots,a_{1,k},a_{2,1},\dots,a_{2,k})=(a_{\pi_{1}(1),1},\dots,a_{\pi_{k}(1),k},a_{\pi_{1}(2),1},\dots,a_{\pi_{k}(2),k}).

Suppose that $\pi_{i}$ is an involution for some $i\in\{s+1,\dots,k\}$ and there is $\mathbf{c}\in M$ such that $\psi(\mathbf{c})\in M$ . But then for the automorphism $\psi^{\prime}$ of $\mathcal{H}^{2}$ given by

\psi^{\prime}(a_{1,1},\dots,a_{1,k},a_{2,1},\dots,a_{2,k})=(a_{\pi^{\prime}_{1}(1),1},\dots,a_{\pi^{\prime}_{k}(1),k},a_{\pi^{\prime}_{1}(2),1},\dots,a_{\pi^{\prime}_{k}(2),k}),

where $\pi^{\prime}_{1},\dots,\pi^{\prime}_{s}$ are involutions and $\pi^{\prime}_{i}=\pi_{i}$ for $i\in\{s+1,\dots,k\}$ we have $\psi^{\prime}(\mathbf{c})\in A\times C$ . Since $I_{\varphi}\subset I_{\psi^{\prime}}$ we get a contradiction with the choice of $\mathbf{a},\varphi$ . ∎

Lemma 6.8 implies that $\mathsf{Stab}(\mathbf{c},M)$ contains only the identity mapping, and therefore is a subgroup of $\mathsf{Aut}(\bar{\mathcal{H}}^{2})$ . Therefore $M$ is automorphism stable. By Lemma 3.2(1) there is $(\mathcal{G},x)$ such that $\mathsf{hom}((\mathcal{G},x),(\bar{\mathcal{H}}^{2},M))\equiv 1\pmod{2}$ . Therefore

1\equiv\mathsf{hom}((\mathcal{G},x),(\bar{\mathcal{H}}^{2},M))\equiv\mathsf{hom}((\mathcal{G},x),(\mathcal{H}^{2},A\times C))=\mathsf{hom}((\mathcal{G},x),(\mathcal{H},A))\cdot\mathsf{hom}((\mathcal{G},x),(\mathcal{H},C)).

Since $A\cup C$ is a 2-subalgebra we obtain a structure $(\mathcal{K}_{L},x)$ satisfying the requirements for a non-degenerate thick Z-graph as in the end of Section 6.3

7 Proofs missing from Section 5

7.1 A proof of Lemma 5.8

Lemma 7.1 (Lemma 5.8).

Proof.

Consider a vertex $[(x,y)]$ of $(G\diamond H)/_{R}$ , By Remark 5.7, we have

	$\displaystyle(x^{\prime},y^{\prime})\in[(x,y)]$	$\displaystyle\Leftrightarrow N_{G\diamond H}((x^{\prime},y^{\prime}))=N_{G\diamond H}((x,y))$
		$\displaystyle\Leftrightarrow N_{G}(x^{\prime})\times N_{H}(y^{\prime})=N_{G}(x)\times N_{H}(y)$
		$\displaystyle\Leftrightarrow N_{G}(x^{\prime})=N_{G}(x)\mbox{ and }N_{H}(y^{\prime})=N_{H}(y)$
		$\displaystyle\Leftrightarrow x^{\prime}\in[x]\mbox{ and }y^{\prime}\in[y]$
		$\displaystyle\Leftrightarrow(x^{\prime},y^{\prime})\in[x]\times[y].$

Thus $[(x,y)]=[x]\times[y]$ . To complete the proof, we show that $\psi([(x,y)])=([x],[y])$ is an isomorphism. Using the fact that $\left\langle x,y\right\rangle\in E(G)$ if and only if $[x][y]\in E(G/_{R})$ :

	$\displaystyle\left\langle[(x,y)],[(x^{\prime},y^{\prime})]\right\rangle\in E((G\diamond H)/_{R})$	$\displaystyle\Leftrightarrow\left\langle(x,y),(x^{\prime},y^{\prime})\right\rangle\in E(G\diamond H)$
		$\displaystyle\Leftrightarrow\left\langle x,x^{\prime}\right\rangle\in E(G)\mbox{ and }\left\langle y,y^{\prime}\right\rangle\in E(H)$
		$\displaystyle\Leftrightarrow\left\langle[x],[x^{\prime}]\right\rangle\in E(G/_{R})\mbox{ and }\left\langle[y],[y^{\prime}]\right\rangle\in E(H/_{R})$
		$\displaystyle\Leftrightarrow\left\langle[(x,y)],[(x^{\prime},y^{\prime})]\right\rangle\in E((G\diamond H)/_{R})$

∎

7.2 A proof of Proposition 5.14

Proposition 7.2 (Proposition 5.14).

If $A,B$ are $R$ -thin graphs without isolated vertices, then

S(A\diamond B)=\left\{\begin{array}[]{cl}S_{L}(A)\;\small\Box\;S_{L}(B)+S_{R}(A)\;\small\Box\;S_{R}(B)&\mbox{if }A,B\mbox{ are bipartite}\\ S_{L}(A)\;\small\Box\;S(B)+S_{R}(A)\;\small\Box\;S(B)&\mbox{if }A\mbox{ is bipartite and }B\mbox{ is non-bipartite}\\ S(A)\;\small\Box\;S_{L}(B)+S(A)\;\small\Box\;S_{R}(B)&\mbox{if }B\mbox{ is bipartite and }A\mbox{ is non-bipartite}\\ S(A)\;\small\Box\;S(B)&\mbox{if }G,H\mbox{ are non-bipartite}\end{array}\right.

Proof.

The case when $A$ and $B$ are non-bipartite is proved in Proposition 8.15 [HIK11]. We prove Proposition 5.14 for the following two cases:

(i)

$A$ is bipartite and $B$ is non-bipartite,
(ii)

$A$ and $B$ are bipartite.

Consider Case (i). As is easily seen, $S(A\diamond B)$ is bipartite. We prove that the $L_{S(A\diamond B)}$ is equal to $S_{L}(A)\;\small\Box\;S(B)$ . The proof for the right part is similar.

First, we show $S_{L}(A)\;\small\Box\;S(B)\subseteq L_{S(A\diamond B)}$ . Take an edge in $E(S_{L}(A)\;\small\Box\;S(B))$ , say $\left\langle(a,b),(a^{\prime},b)\right\rangle$ with $\left\langle a,a^{\prime}\right\rangle\in S_{L}(A)$ . We must show that $\left\langle(a,b),(a^{\prime},b)\right\rangle$ is not dispensable in $(A\diamond B)^{s}$ . Suppose it is. Then there would be a vertex $z=(c^{\prime},c^{\prime\prime})$ in $G=L_{A\diamond B}$ such that the dispensability conditions (1) and (2) hold for $x=(a,b),y=(a^{\prime},b)$ , and $z=(c^{\prime},c^{\prime\prime})$ . The various cases are considered below. Each leads to a contradiction.

Suppose $N_{G}(x)\subset N_{G}(z)\subset N_{G}(y)$ . This means $N_{A}(a)\times N_{B}(b)\subset N_{A}(c^{\prime})\times N_{B}(c^{\prime\prime})\subset N_{A}(a^{\prime})\times N_{B}(b)$ , so $N_{B}(c^{\prime\prime})=N_{B}(b)$ . Then the fact that $N_{B}(b)\neq\emptyset$ permits cancellation of the common factor $N_{B}(b)$ , so $N_{A}(a)\subset N_{A}(c^{\prime})\subset N_{A}(a^{\prime})$ , and $\left\langle a,a^{\prime}\right\rangle$ in $L_{A^{s}}$ is dispensable. We will reach the same contradiction if $N_{G}(y)\subset N_{G}(z)\subset N_{G}(x)$ .

Finally, suppose there is a $z=(c^{\prime},c^{\prime\prime})$ for which both $N_{G}(x)\cap N_{G}(y)\subset N_{G}(x)\cap N_{G}(z)$ and $N_{G}(y)\cap N_{G}(x)\subset N_{G}(y)\cap N_{G}(z)$ . Rewrite this as

	$\displaystyle N_{G}((a,b))\cap N_{G}((a^{\prime},b))$	$\displaystyle\subset N_{G}((a,b))\cap N_{G}((c^{\prime},c^{\prime\prime}))$
	$\displaystyle N_{G}((a^{\prime},b))\cap N_{G}((a,b))$	$\displaystyle\subset N_{G}((a^{\prime},b))\cap N_{G}((c^{\prime},c^{\prime\prime})),$

which is the same as

	$\displaystyle(N_{A}(a)\cap N_{A}(a^{\prime}))\times N_{B}(b)$	$\displaystyle\subset(N_{A}(a)\cap N_{A}(c^{\prime}))\times(N_{B}(b)\cap N_{B}(c^{\prime\prime}))$
	$\displaystyle(N_{A}(a^{\prime})\cap N_{A}(a))\times N_{B}(b)$	$\displaystyle\subset(N_{A}(a^{\prime})\cap N_{A}(c^{\prime}))\times(N_{B}(b)\cap N_{B}(c^{\prime\prime}))$

Thus $N_{B}(b)\subset N_{B}(b)\cap N_{B}(c^{\prime\prime})$ , so $N_{B}(B)=N_{B}(b)\cap N_{B}(c^{\prime\prime})$ , whence

	$\displaystyle N_{A}(a)\cap N_{A}(a^{\prime})$	$\displaystyle\subset N_{A}(a)\cap N_{A}(c^{\prime})$
	$\displaystyle N_{A}(a^{\prime})\cap N_{A}(a^{\prime})$	$\displaystyle\subset N_{A}(a^{\prime})\cap N_{A}(c^{\prime})$

Thus $\left\langle a,a^{\prime}\right\rangle$ in $L_{A^{s}}$ is dispensable, a contradiction.

Note that the proof for the Case (ii). where we need to prove that $S_{L}(A)\;\small\Box\;S_{L}(B)\subseteq L_{S(A\diamond B)}$ is exactly the same.

We now show $L_{S(A\diamond B)}\subseteq S_{L}(A)\;\small\Box\;S(B)$ , considering Case (i). By Lemma 5.13, all edges of $L_{S(A\diamond B)}$ are Cartesian, so we just need to show that $\left\langle(a,b),(a^{\prime},b)\right\rangle\in E(L_{S(A\diamond B)})$ implies $\left\langle a,a^{\prime}\right\rangle\in E(S(A))$ (The same argument will work for edges of form $\left\langle(a,b),(a,b^{\prime})\right\rangle$ ).

Suppose for the sake of contradiction that $\left\langle(a,b),(a^{\prime},b)\right\rangle\in E(L_{S(A\diamond B)})$ , but $\left\langle a,a^{\prime}\right\rangle\not\in E(S(A))$ , Thus $\left\langle a,a^{\prime}\right\rangle$ is dispensable in $L_{A^{s}}$ , so there is a $c\in V(A)$ for which both of the following conditions hold:

1.

$N_{A}(a)\cap N_{A}(a^{\prime})\subset N_{A}(a)\cap N_{A}(c)$ or $N_{A}(a)\subset N_{A}(c)\subset N_{A}(a^{\prime})$ ,
2.

$N_{A}(a^{\prime})\cap N_{A}(a)\subset N_{A}(a^{\prime})\cap N_{A}(c)$ or $N_{A}(a^{\prime})\subset N_{A}(c)\subset N_{A}(a)$ ,

There are no isolated vertices, so $N_{B}(d)\neq\emptyset$ . Now, we can multiply each neighborhood $N_{A}(x)$ in Condition 1 and 2 by $N_{B}(d)$ on the right and still preserve the proper inclusions. Then the fact that $N_{(A\diamond B)}((a,b))=N_{A}(a)\times N_{B}(b)$ (where $A$ is bipartite and $B$ is non-bipartite) yields the dispensability conditions (1) and (2), where $x=(a,b)$ and $y=(a^{\prime},b)$ and $z=(c,b)$ . Thus $\left\langle(a,b),(a^{\prime},b)\right\rangle\in E(L_{S(A\diamond B)})$ , a contradiction. Considering Case (ii). we only have the equation $N_{(A\diamond B)}((a,b))=N_{A}(a)\times N_{B}(b)$ when $a\in L_{A}$ and $b\in L_{B}$ , therefore what we will get is again $\left\langle(a,b),(a^{\prime},b)\right\rangle\in E(L_{S(A\diamond B)})$ , which is a contradiction. ∎

References

[Bar16] Alexander I. Barvinok. Combinatorics and Complexity of Partition Functions, volume 30 of Algorithms and combinatorics. Springer, 2016.
[BD07] Andrei A. Bulatov and Víctor Dalmau. Towards a dichotomy theorem for the counting constraint satisfaction problem. Information and Computation, 205(5):651–678, 2007.
[BG05] Andrei A. Bulatov and Martin Grohe. The complexity of partition functions. Theor. Comput. Sci., 348(2-3):148–186, 2005.
[BJK05] Andrei A. Bulatov, Peter Jeavons, and Andrei A. Krokhin. Classifying the complexity of constraints using finite algebras. SIAM J. Comput., 34(3):720–742, 2005.
[BKW17] Libor Barto, Andrei Krokhin, and Ross Willard. Polymorphisms, and how to use them. In Dagstuhl Follow-Ups, volume 7. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2017.
[Bul13] Andrei A. Bulatov. The complexity of the counting constraint satisfaction problem. J. ACM, 60(5):34:1–34:41, 2013.
[CH89] Jin-yi Cai and Lane A. Hemachandra. On the power of parity polynomial time. In Burkhard Monien and Robert Cori, editors, STACS 89, 6th Annual Symposium on Theoretical Aspects of Computer Science, Paderborn, FRG, February 16-18, 1989, Proceedings, volume 349 of Lecture Notes in Computer Science, pages 229–239. Springer, 1989.
[CH96] Nadia Creignou and Miki Hermann. Complexity of generalized satisfiability counting problems. Inf. Comput., 125(1):1–12, 1996.
[DG00] M. Dyer and C. Greenhill. The complexity of counting graph homomorphisms. Random Structures and Algorithms, 17:260–289, 2000.
[DGP07] Martin E. Dyer, Leslie Ann Goldberg, and Mike Paterson. On counting homomorphisms to directed acyclic graphs. J. ACM, 54(6):27, 2007.
[DR13] Martin E. Dyer and David Richerby. An effective dichotomy for the counting constraint satisfaction problem. SIAM J. Comput., 42(3):1245–1274, 2013.
[FGRZ20] Jacob Focke, Leslie Ann Goldberg, Marc Roth, and Stanislav Zivney. Counting homomorphisms to $k_{4}$ -minor-free graphs, modulo 2. CoRR, abs/2006.16632, 2020.
[FGRZ21] Jacob Focke, Leslie Ann Goldberg, Marc Roth, and Stanislav Zivný. Counting homomorphisms to $k_{4}$ -minor-free graphs, modulo 2. In Dániel Marx, editor, Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms, SODA 2021, Virtual Conference, January 10 - 13, 2021, pages 2303–2314. SIAM, 2021.
[FJ13] John Faben and Mark Jerrum. The complexity of parity graph homomorphism: an initial investigation. arXiv preprint arXiv:1309.4033, 2013.
[FV98] Tomás Feder and Moshe Y. Vardi. The computational structure of monotone monadic SNP and constraint satisfaction: A study through datalog and group theory. SIAM J. Comput., 28(1):57–104, 1998.
[GGR14] Andreas Göbel, Leslie Ann Goldberg, and David Richerby. The complexity of counting homomorphisms to cactus graphs modulo 2. ACM Transactions on Computation Theory, 6(4):1–29, Aug 2014.
[GGR16] Andreas Göbel, Leslie Ann Goldberg, and David Richerby. Counting homomorphisms to square-free graphs, modulo 2. ACM Transactions on Computation Theory (TOCT), 8(3):1–29, 2016.
[GLS18] Andreas Göbel, J. A. Gregor Lagodzinski, and Karen Seidel. Counting homomorphisms to trees modulo a prime. In Igor Potapov, Paul Spirakis, and James Worrell, editors, 43rd International Symposium on Mathematical Foundations of Computer Science (MFCS 2018), volume 117 of Leibniz International Proceedings in Informatics (LIPIcs), pages 49:1–49:13, Dagstuhl, Germany, 2018. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik.
[Her90] Ulrich Hertrampf. Relations among mod-classes. Theor. Comput. Sci., 74(3):325–328, 1990.
[HIK11] Richard Hammack, Wilfried Imrich, and Sandi Klavzar. Handbook of Product Graphs, Second Edition. CRC Press, Inc., USA, 2nd edition, 2011.
[HN04] P. Hell and Nešetřil. Graphs and homomorphisms, volume 28 of Oxford Lecture Series in Mathematics and its Applications. Oxford University Press, 2004.
[JCG99] P.G. Jeavons, D.A. Cohen, and M. Gyssens. How to determine the expressive power of constraints. Constraints, 4:113–131, 1999.
[Jea98] Peter Jeavons. On the algebraic structure of combinatorial problems. Theoretical Computer Science, 200(1-2):185–204, 1998.
[JS93] Mark Jerrum and Alistair Sinclair. Polynomial-time approximation algorithms for the Ising model. SIAM J. Comput., 22(5):1087–1116, 1993.
[KB19] Amirhossein Kazeminia and Andrei A Bulatov. Counting homomorphisms modulo a prime number. In 44th International Symposium on Mathematical Foundations of Computer Science (MFCS 2019). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2019.
[Kol04] Phokion G Kolaitis. Constraint satisfaction, complexity, and logic. In Hellenic Conference on Artificial Intelligence, pages 1–2. Springer, 2004.
[LGCF21] J. A. Gregor Lagodzinski, Andreas Göbel, Katrin Casel, and Tobias Friedrich. On counting (quantum-)graph homomorphisms in finite fields of prime order. CoRR, abs/2011.04827, 2021.
[LS81] E.H. Lieb and A.D. Sokal. A general Lee-Yang theorem for one-component and multicomponent ferromagnets. Communications in Mathematical Physics, 80(2):153–179, 1981.
[Val79a] L. Valiant. The complexity of computing the permanent. Theoretical Computing Science, 8:189–201, 1979.
[Val79b] L. Valiant. The complexity of enumeration and reliability problems. SIAM Journal on Computing, 8(3):410–421, 1979.

	$\displaystyle\|\mathsf{Hom}(G^{\prime},H)\|=N^{\prime}+\sum_{i=1}^{M}\|\varphi_{i}/_{\bumpeq_{I}}\|$	$\displaystyle\equiv\sum_{i=1}^{M}\alpha_{1}^{\|L_{G}\cap I_{\varphi_{i}}\|}\;\;\alpha_{2}^{\|L_{G}-I_{\varphi_{i}}\|}\;\;\beta_{1}^{\|R_{G}\cap I_{\varphi_{i}}\|}\;\;\beta_{2}^{\|R_{G}-I_{\varphi_{i}}\|}$
		$\displaystyle\equiv N^{\prime}+\sum_{I\in\mathsf{IS}(G)}\alpha_{1}^{\|L_{G}\cap I\|}\;\;\alpha_{2}^{\|L_{G}-I\|}\;\;\beta_{1}^{\|R_{G}\cap I\|}\;\;\beta_{2}^{\|R_{G}-I\|}$
		$\displaystyle\equiv N^{\prime}+\alpha_{2}^{\|L_{G}\|}\beta_{2}^{\|R_{R}\|}\sum_{I\in\mathsf{IS}(G)}\alpha_{1}^{\|L_{G}\cap I\|}\;\;\alpha_{2}^{-\|L_{G}\|}\alpha_{2}^{\|L_{G}-I\|}\;\;\beta_{1}^{\|R_{G}\cap I\|}\;\;\beta_{2}^{-\|R_{G}\|}\beta_{2}^{\|R_{G}-I\|}$
		$\displaystyle\equiv N^{\prime}+\alpha_{2}^{\|L_{G}\|}\beta_{2}^{\|R_{R}\|}\sum_{I\in\mathsf{IS}(G)}(\alpha_{1}\alpha_{2}^{-1})^{\|L_{G}\cap I\|}\;\;(\beta_{1}\beta_{2}^{-1})^{\|R_{G}\cap I\|}$
		$\displaystyle\equiv N^{\prime}+\alpha_{2}^{\|L_{G}\|}\beta_{2}^{\|R_{G}\|}\mathcal{Z}_{(\alpha_{1}\alpha_{2}^{-1}),(\beta_{1}\beta_{2}^{-1})}(G)\pmod{p}.$