Competing Lattice Instability and Magnetism on the Surface of Kagome Metals
Abstract
Only a few magnetic kagome materials exhibit lattice instabilities among the large kagome material array. In this work, we find that kagome magnets Mn6Sn6 ( = rare-earth elements) and their non-magnetic counterparts V6Sn6 exhibit intriguing interplay between magnetism and lattice dynamics on their surfaces. Notably, V6Sn6 surfaces terminated by kagome layers demonstrate pronounced lattice instabilities, manifesting as and surface charge orders (SCOs). These instabilities are absent on corresponding magnetic materials Mn6Sn6. Here, the SCO is suppressed by magnetism. Otherwise, surface distortions would significantly reduce the spin polarization, elevating the energy via Hund’s rule. Thus, SCOs are energetically unfavorable on magnetic surfaces. The competition of magnetism and lattice instability is further substantiated by observing SCOs on V-substituted Mn6Sn6 kagome surfaces, contrasting with their absence on Mn-substituted V6Sn6 surfaces. Our findings reveal unexpected surface instability and profound spin-lattice coupling in these kagome magnets, highlighting the complex dynamics hidden within magnetic materials.
I Introduction
Kagome materials, characterized by a corner-sharing triangular sublattice, are a fertile playground for various correlated electronic orders Wen et al. (2010); Kiesel and Thomale (2012); Wang et al. (2013); Kiesel et al. (2013). The discovery of charge density wave (CDW) in non-magnetic kagome superconductors Ortiz et al. (2020); Jiang et al. (2021); Tan et al. (2021); Liang et al. (2021); Chen et al. (2021) sparked immediate interest because of its close relationship with the potential time-reversal symmetry breaking and superconductivity. In contrast, magnetic kagome materials showing CDW are rare, primarily due to the lack of lattice instability in most systems and the competition between magnetism and other low-energy scale orders.
The recent discovery of CDW in the magnetic kagome metal FeGe Teng et al. (2022) highlights the intricate interplay between magnetism and lattice instability Teng et al. (2023); Miao et al. (2023); Wang (2023); Chen et al. (2023), enabling the exploration of intertwining between these orders. This FeGe-type structure is derived by excluding the element from the extensively studied magnetic kagome compounds Mn6Sn6 ( = Y, Gd-Lu) Ghimire et al. (2020); Riberolles et al. (2022); Yin et al. (2020); Zhang et al. (2020); Li et al. (2021); Xu et al. (2022); Li et al. (2022); Asaba et al. (2020); Ma et al. (2021); Gao et al. (2021); Zhang et al. (2022a), where no charge instability has been reported. This structural resemblance raises the possibility of an underlying lattice instability in Mn6Sn6, potentially suppressed by magnetism and observable when magnetism is diminished. The observation of CDW transition in the non-magnetic ScV6Sn6 Arachchige et al. (2022); Tan and Yan (2023); Cao et al. (2023); Korshunov et al. (2023), as opposed to its magnetic counterpart ScMn6Sn6 without CDW, suggests such a potential. However, the absence of CDW in other non-magnetic V6Sn6 variants underscores the complexity of these materials. This complexity prompts questions about the existence of competition between lattice instability and magnetism and its manifestation in the wider range. Our recent Scanning Tunneling Microscopy (STM) studies reveal significant distortions on the surface of ScV6Sn6 Cheng et al. (2024), hinting at the possibility of observing this competition in a decreased dimension.
In this study, we elucidate the interplay between lattice instabilities and magnetism in surfaces of V6Sn6 and Mn6Sn6. We reveal that the kagome layer on V6Sn6 surfaces inherently exhibits charge instabilities, manifesting as and surface charge orders (SCOs), driven by phonon softening and characterized by distinct V trimer and clover-like distortions. Introducing magnetic Mn in place of non-magnetic V on these kagome surfaces leads to a significant weakening of Mn spin polarization due to surface distortions, increasing the magnetic energy via Hund’s rule. This energy increase suppresses SCOs, further evidenced by the absence of SCOs in magnetic Mn6Sn6. Remarkably, substituting Mn with V on Mn6Sn6 kagome surfaces allows SCOs to reappear, underlining a potent competition between surface lattice instability and magnetism and highlighting a pathway to potential high-temperature SCOs. Our findings unveil complex dynamics in surfaces of kagome magnets and beyond.
II Results and discussions
Bulk properties of V6Sn6. The crystalline structure of V6Sn6 comprises a Sn honeycomb layer, a Sn triangular layer, and two V-Sn kagome layers in a buckled configuration, as shown in Fig. 1(a). Prior experimental observations have identified a complex ordering of the 4 magnetic moments below 4 K Pokharel et al. (2022); Rosenberg et al. (2022); Zhang et al. (2022b); Lee and Mun (2022). ARPES analysis has revealed the minimal influence of the 4 magnetism on the low energy physics Peng et al. (2021); Hu et al. (2022); Sante et al. (2023). Our calculations demonstrate robust SCOs not only in the ferromagnetic TbV6Sn6 but also in paramagnetic GdV6Sn6 and nonmagnetic YV6Sn6. Consequently, we will omit discussions regarding -electron magnetism. Given the similarity of results across all V6Sn6 compounds, we will primarily illustrate our findings with TbV6Sn6.
The bulk band structure of TbV6Sn6 is depicted in Fig. 1(b), characterized by typical kagome band features, such as van Hove singularities at /, Dirac points at /, and a flat band at approximately 0.3 eV. Notice that all V6Sn6 materials exhibit similar band structures Pokharel et al. (2021); Peng et al. (2021); Hu et al. (2022); Tan and Yan (2023); Ding et al. (2023). In Fig. 1(c), the phonon spectrum of TbV6Sn6 confirms its bulk dynamical stability by showing the absence of imaginary phonon modes. This absence extends to all V6Sn6 compounds (except for ScV6Sn6 Tan and Yan (2023)), indicating all V6Sn6 compounds (except for Sc) are stable in their bulk forms. It’s worth noting that, among these stable compounds, LuV6Sn6 exhibits the softest phonon branch on the plane, which may suggest its susceptibility to structural phase transitions under external influences like strain (see Supplementary II.A SM for additional details).
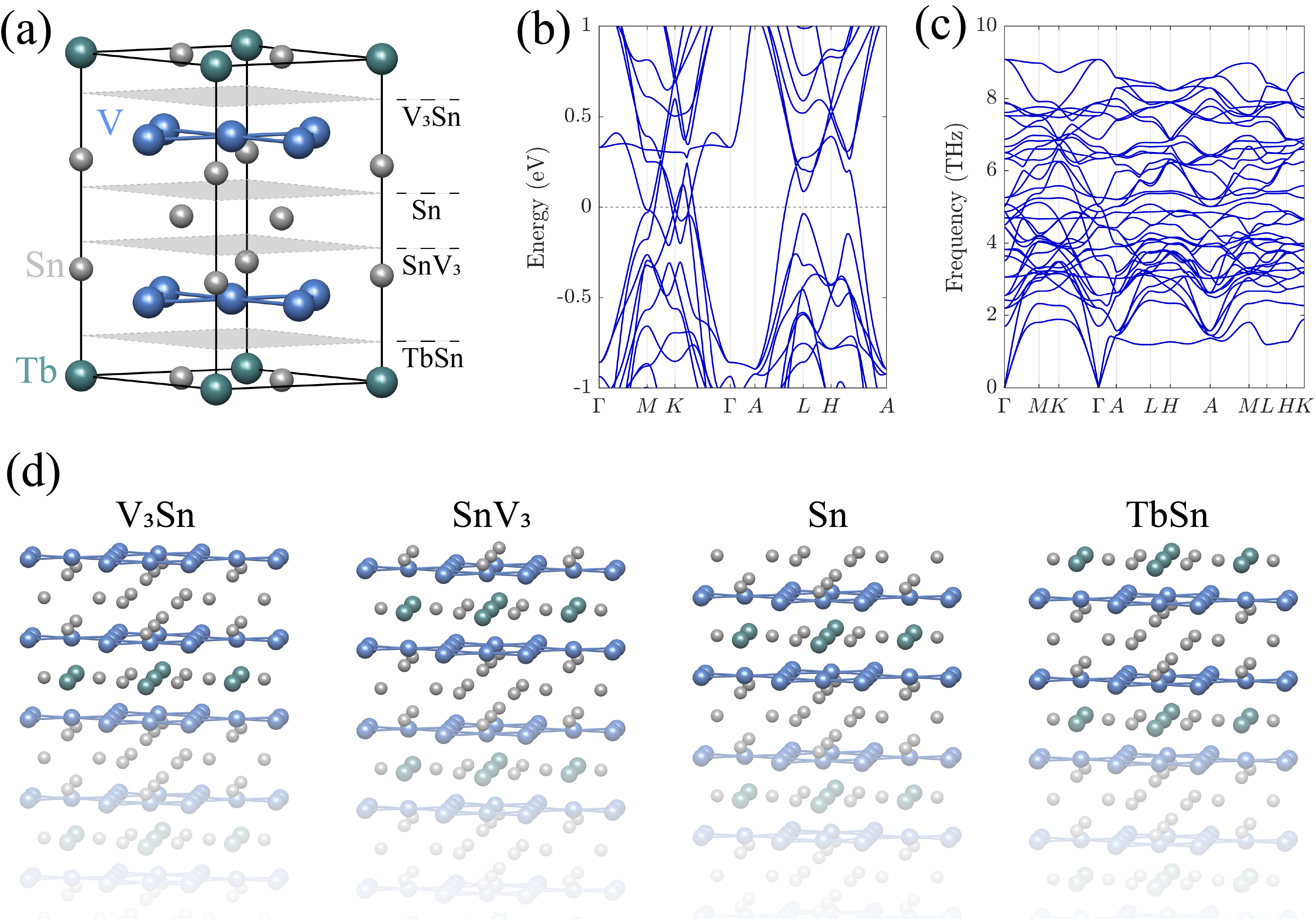
SCOs of V6Sn6. The layered structure of V6Sn6 promises four different terminations, i.e., the Sn triangular surface, Sn honeycomb surface, and two kagome surfaces, V3Sn and SnV3, as shown in Fig. 1(a)&(d), These different surfaces have been observed in various experiments Yin et al. (2020); Cheng et al. (2024); Hu et al. (2022); Peng et al. (2021); Rosenberg et al. (2022); Li et al. (2022). The primary differentiation between the two kagome surfaces arises from the respective chemical configurations underneath. In the V3Sn termination, the V-kagome sublattice is positioned above the closely associated Sn sublattice from the same buckled V-Sn layer, with the subsequent layer being the Sn honeycomb layer not . In contrast, the SnV3 termination situates the V-kagome sublattice below the closely associated Sn sublattice, with the next layer the Sn triangular layer. Both terminations show similar SCOs and are collectively called kagome surfaces within this work.
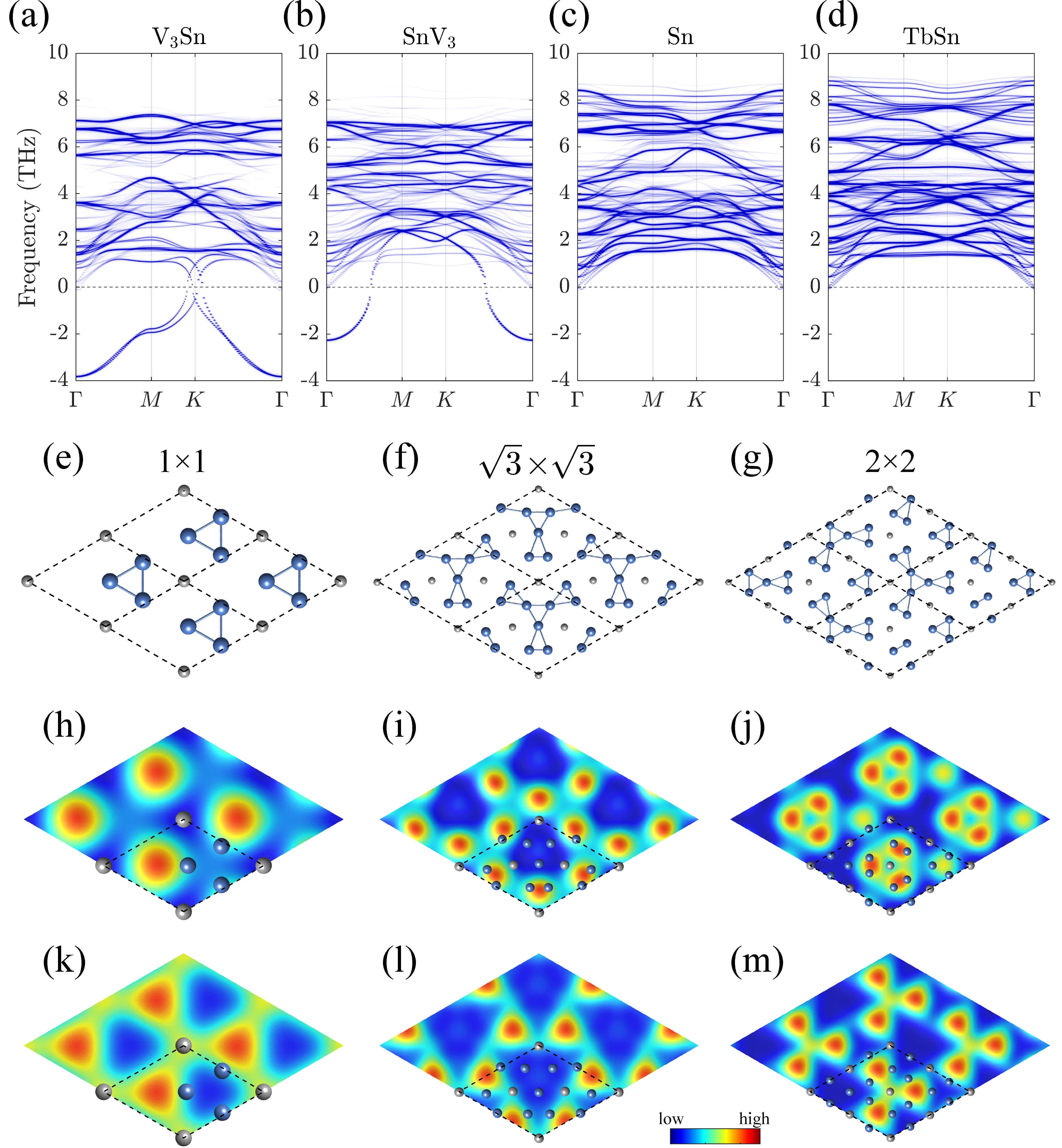
Figures 2(a)-(d) display the surface phonon band structures of the four different terminations of TbV6Sn6, obtained from thick slab model calculations. Notably, the V3Sn surface exhibits imaginary phonon modes across the entire surface Brillouin zone [Fig. 2(a)]. The interpretation of these modes unfolds as follows: i) The imaginary phonon at results in a surface modulation, primarily involving the surface V layer trimerization [Fig. 2(e)]. This modulation reduces the surface’s rotational symmetry from 6-fold to 3-fold while preserving the translational symmetry. However, such a trimerized surface is marked by a significant imaginary phonon at the point (see Supplementary II.C SM ), indicating its instability. ii) The imaginary phonon at induces a SCO, as depicted in Fig. 2(f). In this phase with broken translational symmetry, the surface V-kagome layer transforms into a clover-like pattern, resulting in a total energy decrease of about 307 meV per surface primitive unit cell (u.c.), relative to the pristine surface (see Table 1). iii) The imaginary phonon at drives a SCO, combining V trimers and clovers, as illustrated in Fig. 2(g). This phase exhibits a lower total energy of 394 meV/u.c. The dynamical stability of these two SCOs is confirmed by the absence of imaginary phonon modes in their respective phonon spectra (see Supplementary II.C SM ). Typical scanning tunneling microscopy (STM) images at the charge neutral point are presented in Fig. 2(h)-(j) with additional results available in Supplementary II.H SM .
In Fig. 2(b), the phonon spectrum of the SnV3 termination reveals exclusively imaginary phonons at point. The imaginary phonon instigates the 1 surface modulation with V trimers as illustrated in Fig. 2(e), which reduces the total energy by 17 meV/u.c.. Intriguingly, such a V trimerized SnV3 surface shows a substantial imaginary phonon at , akin to the scenario in V3Sn, as detailed in Supplementary II.C SM . Furthermore, the and SCOs displayed in Fig. 2(f)&(g) elicit more pronounced reductions in the total energy of the SnV3 surface, amounting to 26 and 21 meV/u.c., respectively. An insightful deduction from the phonon band structure is that an imaginary phonon mode at a reciprocal space momentum generally implies the presence of a stable structure modulated by the same momentum. The SnV3 surface, however, presents a paradoxical case by revealing the absence of a stable structure modulated by the imaginary phonon and the unexpected emergence of energy-favored structures driven by the non-imaginary phonons at . This peculiarity might arise from the effective screening of the long-range imaginary phonon to the short-range imaginary phonons, which manifests only after the elimination of the imaginary phonon. Notably, this imaginary phonon screening effect may also apply to the V3Sn surface, exhibiting strong imaginary phonons at and weak ones at . STM images of SCOs for the SnV3 surface at the charge neutral point are presented in Fig. 2(k)-(m), with additional details available in Supplementary II.H SM .
The phonon spectra of the Sn and TbSn terminations in Fig. 2(c)&(d) notably lack any soft modes. The above-established SCOs in kagome terminations are also confirmed to be unstable on both surfaces. It is crucial to emphasize that these two surfaces can be achieved by overlaying one Sn (TbSn) layer atop the SnV3 (V3Sn) surface. Consequently, introducing additional layers effectively mitigates the instabilities observed in the kagome surfaces. This comparison underscores the pivotal role of exposing the kagome layer at the surface in attaining SCOs in V6Sn6. Furthermore, it is worth noting that there are numerous flat phonon bands evident across all surfaces, which could potentially influence the phonon dynamics, as discussed in Hu et al. (2023).
| V3Sn | SnV3 | |||||||
| Gd | 318 | 402 | 214 | 36 | 33 | 26 | ||
| Tb | 307 | 394 | 212 | 26 | 21 | 17 | ||
| Dy | 304 | 392 | 204 | 31 | Unstable | 25 | ||
| Ho | 300 | 391 | 200 | 28 | Unstable | 23 | ||
| Er | 297 | 388 | 196 | 25 | Unstable | 22 | ||
| Tm | 294 | 386 | 192 | 22 | Unstable | 21 | ||
| Lu | 289 | 383 | 186 | 17 | Unstable | 16 | ||
| Y | 305 | 393 | 205 | 33 | Unstable | 27 | ||
| Sc | 251 | 359 | 155 | Unstable | Unstable | 4 | ||
| Sc∗ | 94 | Unstable | ||||||
We apply the above SCOs to the kagome terminations of all other V6Sn6. After adequate surface relaxation, these SCOs consistently reduce the total energy, as summarized in Table 1. Similar to the Tb compound, the SCO consistently exhibits a lower total energy in the V3Sn termination, while the SCO attains a lower total energy in the SnV3 termination across all compounds. Remarkably, while the SCO can be achieved in the SnV3 termination of GdV6Sn6 following surface relaxation, the distorted SnV3 surfaces of Y and Dy-Lu materials spontaneously revert to the trimerized surface configuration after relaxation, effectively restoring the broken translational symmetry. Phonon calculations additionally reveal that the trimerized kagome surfaces of YV6Sn6 exhibit a pronounced imaginary phonon at (resulting in the SCO), notwithstanding the pristine SnV3 surface of the Y compound only manifesting an imaginary phonon at the point (elaborated in Supplementary II.D SM ). Given the resemblance of these materials, we conjecture that the trimerized kagome surfaces exhibit instability across all V6Sn6 compounds (except for Sc). However, their total energies are included in Table 1 for reference and comparative analysis. These SCOs are pure surface effects, which are robust against the slab thickness as comprehensively elucidated in Supplementary II.E SM .
We have also extended our analysis of SCOs to the extensively studied ScV6Sn6. In the pristine bulk phase, while two SCOs reduce the energy of the V3Sn termination, they are unstable in the SnV3 termination, and only the surface trimerization reduces the total energy. This phenomenon may be attributed to the significantly higher in-plane chemical pressure in ScV6Sn6 (see Supplementary II.A SM ). Furthermore, we applied the SCO to kagome terminations of ScV6Sn6 in bulk CDW phase Arachchige et al. (2022), and found it to be only stabilized in the V3Sn termination (Table 1).
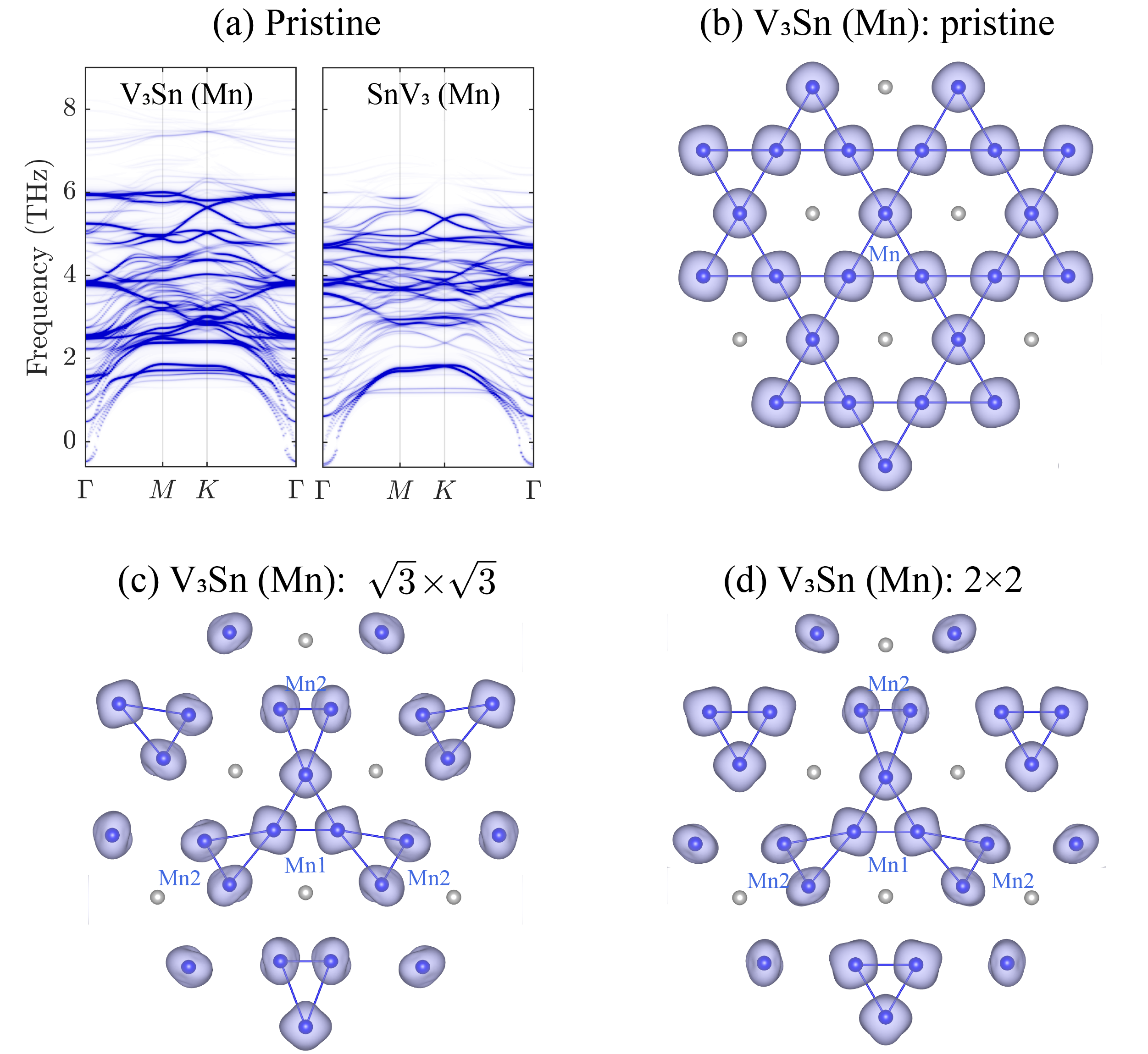
Suppression of SCO by magnetism. Now we explore the impact of magnetism on SCOs by substituting the outermost V kagome layer on TbV6Sn6 kagome terminations with a magnetic Mn kagome layer. Calculations indicate that the local magnetic moments of Mn form a ferromagnetic ordering. This magnetic substitution leads to the disappearance of SCOs, following sufficient surface relaxation. Indeed, such Mn-doped surfaces with frozen SCOs show much higher total energies (Table 2). Moreover, phonon spectra analyses of these Mn-doped kagome surfaces reveal no lattice instabilities, as shown in Figs. 3(a). The interplay between SCOs and magnetism is further elucidated by studying magnetic counterpart TbMn6Sn6. Namely, the absence of imaginary phonon modes on kagome surfaces Mn3Sn and SnMn3 indicates no SCOs (see Supplementary II.G SM ). Conversely, reintroducing V into kagome surfaces of TbMn6Sn6 stabilizes the SCOs. Notably, the cross substitution between V and Mn does not exert a noticeable strain effect, attributed to the similar effective radii of V and Mn ions (V 0.640 Å versus Mn 0.645 Å Shannon and Prewitt (1969)). Thus, the stabilization or destabilization of SCOs in these kagome surfaces is more closely related to magnetic effects rather than mechanical strain. Notice that the -electron magnetism of Tb does not affect SCOs.
| Mn-replaced | Pristine | SCO | SCO | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| kagome surface | Mn up | Mn dn | Mn1 up | Mn1 dn | Mn2 up | Mn2 dn | Mn1 up | Mn1 dn | Mn2 up | Mn2 dn | ||||
| V3Sn | charge () | 5.17 | 1.65 | 4.84 | 2.02 | 4.34 | 2.53 | 4.88 | 1.96 | 4.22 | 2.65 | |||
| () | 3.52 | 2.82 | 1.81 | 2.92 | 1.57 | |||||||||
| (eV/p.c.) | 0 | 1.23 | 1.29 | |||||||||||
| SnV3 | charge () | 5.11 | 1.75 | 5.04 | 1.84 | 5.00 | 1.87 | 5.02 | 1.86 | 4.99 | 1.88 | |||
| () | 3.36 | 3.20 | 3.13 | 3.16 | 3.11 | |||||||||
| (eV/p.c.) | 0 | 0.38 | 0.54 | |||||||||||
These observations highlight the competition between lattice instabilities and magnetism. A detailed Bader charge analysis of Mn atoms of the Mn-doped kagome surfaces of TbV6Sn6 with frozen SCOs is presented in Table 2. It shows that while the total charge of each Mn atom is preserved, SCOs transfer charges from the spin-up channel to the spin-down channel, weakening the spin polarization heavily. For example, on the Mn-doped V3Sn surface, Mn atoms have initial spin-up/down charges of 5.17/1.65, yielding a total charge of 6.82 and magnetization of 3.52. With the frozen SCO, spin-up charges adjust to 4.84 (Mn1) and 4.34 (Mn2, labeled in Fig. 3(c)), and spin-down to 2.02 (Mn1) and 2.53 (Mn2), nearly preserving total charges (6.86 for Mn1, 6.87 for Mn2) but reducing magnetizations to 2.82 (Mn1) and 1.81 (Mn2). Magnetization densities are exemplified with Mn-doped V3Sn in Fig. 3(b)-(d), where the Mn2 atoms have a much smaller magnetization density area under SCOs. Similar behaviors are confirmed for all other surfaces and SCOs (changes are smaller in the SnV3 surface because of its smaller SCO distortion amplitudes). Results of TbMn6Sn6 kagome terminations are found in Supplementary II.G SM . According to Hund’s rule which favors high-spin states in magnetic ions for maximum spin polarization, the reduction in spin polarization leads to increased magnetic energy, which outweighs the kinetic energy loss from structural distortions. As a result, the total energy of the surface is increased, mitigating surface distortions. For TbV6Sn6 and V-doped TbMn6Sn6 kagome terminations, the elimination of surface magnetism ceases its antagonistic effect on SCOs, resulting in SCOs as previously discussed.
This mechanism contrasts the scenario for the CDW formation of the kagome magnet FeGe. In FeGe, structural distortions lead to kinetic energy gains and increased spin polarization, reducing more magnetic energy Miao et al. (2023); Wang (2023); Chen et al. (2023). Moreover, spin-splitting shifts a von Hove singularity into the Fermi level in the spin minority band Teng et al. (2023), enhancing Fermi surface nesting and promoting charge instability. The intricate interplay among spin, lattice, and charge degrees of freedom culminates in the CDW formation in FeGe and SCO suppression in Mn6Sn6, illustrating the complex quantum ground states emergent from the intertwined dynamics of these variables.
Now we address the potential experimental detection of the predicted SCOs. SCOs significantly disrupt the surface kagome layers, obfuscating certain surface states (see Supplementary II.F SM ). ARPES appears as the initial experimental technique to consider. Notably, a limited number of ARPES experiments have been conducted on kagome terminations of V6Sn6 Hu et al. (2022); Peng et al. (2021); Rosenberg et al. (2022); Sante et al. (2023); Cheng et al. (2024); Ding et al. (2023). While experiments observe some distinctive bands, ambiguous states are also present whose origin remains challenging to identify. Consequently, the determination of the presence of SCOs in these experiments, as well as the characterization of their range (long-range or short-range), remains elusive. We propose that microscope techniques such as STM, capable of detecting local atomic structures, could be an optimal approach for SCO detection. Nevertheless, relatively few STM experiments have been conducted on V6Sn6. In the case of ScV6Sn6 within the bulk CDW phase, recent STM experiments on kagome terminations observed a prominent reconstruction Cheng et al. (2024). We do not conclude it the SCO (Table 1) because the bulk CDW also exhibits a in-plane modulation. However, it’s crucial to underscore that the bulk CDW of ScV6Sn6 exclusively involves Sc/Sn out-of-plane movements, with minimal distortion in the V kagome layer Arachchige et al. (2022); Tan and Yan (2023). This contrasts the STM experiment, underscoring the need for more comprehensive studies for V6Sn6.
In the context of Mn6Sn6, intriguing phenomena are anticipated. It is noteworthy to consider the possibility of observing SCOs in Mn6Sn6 at high temperatures when the magnetic order ceases to exist. Confirmation of this phenomenon in experiments would establish Mn6Sn6 as a rare class of symmetry-descending materials when temperature increases Wu et al. (2024). We recommend more STM experiments on Mn6Sn6 at elevated temperatures to explore this intriguing prospect. Furthermore, the sizeable structural distortion accompanying SCOs might also suggest the potential for a significant surface magnetostriction Lee (1955) and piezomagnetic effect, which would benefit the application of antiferromagnetic.
III Conclusion
In conclusion, we have revealed the pervasive and SCOs across kagome terminations in V6Sn6, which are suppressed in Mn6Sn6 by magnetism due to the profound competition between lattice instability and magnetism through Hund’s rule. We call for additional experimental efforts to explore these fascinating surface phenomena. Our findings suggest the existence of undiscovered quantum states in general magnets, potentially accessible through the suppression of magnetism.
IV Acknowledgements
We thank Ilija Zeljkovic for fruitful discussions. H.T. also thanks Yizhou Liu for helpful discussions. B.Y. acknowledges the financial support by the European Research Council (ERC Consolidator Grant “NonlinearTopo”, No. 815869) and the ISF - Personal Research Grant (No. 2932/21) and the DFG (CRC 183, A02).
References
- Wen et al. (2010) Jun Wen, Andreas Rüegg, C.-C. Joseph Wang, and Gregory A. Fiete, “Interaction-driven topological insulators on the kagome and the decorated honeycomb lattices,” Phys. Rev. B 82, 075125 (2010).
- Kiesel and Thomale (2012) Maximilian L. Kiesel and Ronny Thomale, “Sublattice interference in the kagome hubbard model,” Phys. Rev. B 86, 121105 (2012).
- Wang et al. (2013) Wan-Sheng Wang, Zheng-Zhao Li, Yuan-Yuan Xiang, and Qiang-Hua Wang, “Competing electronic orders on kagome lattices at van hove filling,” Phys. Rev. B 87, 115135 (2013).
- Kiesel et al. (2013) Maximilian L. Kiesel, Christian Platt, and Ronny Thomale, “Unconventional fermi surface instabilities in the kagome hubbard model,” Phys. Rev. Lett. 110, 126405 (2013).
- Ortiz et al. (2020) Brenden R. Ortiz, Samuel M. L. Teicher, Yong Hu, Julia L. Zuo, Paul M. Sarte, Emily C. Schueller, A. M. Milinda Abeykoon, Matthew J. Krogstad, Stephan Rosenkranz, Raymond Osborn, Ram Seshadri, Leon Balents, Junfeng He, and Stephen D. Wilson, “: A Topological Kagome Metal with a Superconducting Ground State,” Phys. Rev. Lett. 125, 247002 (2020).
- Jiang et al. (2021) Yu-Xiao Jiang, Jia-Xin Yin, M Michael Denner, Nana Shumiya, Brenden R Ortiz, Gang Xu, Zurab Guguchia, Junyi He, Md Shafayat Hossain, Xiaoxiong Liu, et al., “Unconventional chiral charge order in kagome superconductor KV3Sb5,” Nature Materials 20, 1353–1357 (2021).
- Tan et al. (2021) Hengxin Tan, Yizhou Liu, Ziqiang Wang, and Binghai Yan, “Charge density waves and electronic properties of superconducting kagome metals,” Phys. Rev. Lett. 127, 046401 (2021).
- Liang et al. (2021) Zuowei Liang, Xingyuan Hou, Fan Zhang, Wanru Ma, Ping Wu, Zongyuan Zhang, Fanghang Yu, J.-J. Ying, Kun Jiang, Lei Shan, Zhenyu Wang, and X.-H. Chen, “Three-Dimensional Charge Density Wave and Surface-Dependent Vortex-Core States in a Kagome Superconductor ,” Phys. Rev. X 11, 031026 (2021).
- Chen et al. (2021) Hui Chen, Haitao Yang, Bin Hu, Zhen Zhao, Jie Yuan, Yuqing Xing, Guojian Qian, Zihao Huang, Geng Li, Yuhan Ye, et al., “Roton pair density wave in a strong-coupling kagome superconductor,” Nature 599, 222–228 (2021).
- Teng et al. (2022) Xiaokun Teng, Lebing Chen, Feng Ye, Elliott Rosenberg, Zhaoyu Liu, Jia-Xin Yin, Yu-Xiao Jiang, Ji Seop Oh, M Zahid Hasan, Kelly J Neubauer, et al., “Discovery of charge density wave in a kagome lattice antiferromagnet,” Nature 609, 490–495 (2022).
- Teng et al. (2023) Xiaokun Teng, Ji Seop Oh, Hengxin Tan, Lebing Chen, Jianwei Huang, Bin Gao, Jia-Xin Yin, Jiun-Haw Chu, Makoto Hashimoto, Donghui Lu, et al., “Magnetism and charge density wave order in kagome fege,” Nature Physics 19, 814–822 (2023).
- Miao et al. (2023) H Miao, TT Zhang, HX Li, G Fabbris, AH Said, R Tartaglia, T Yilmaz, E Vescovo, J-X Yin, S Murakami, et al., “Signature of spin-phonon coupling driven charge density wave in a kagome magnet,” Nature Communications 14, 6183 (2023).
- Wang (2023) Yilin Wang, “Enhanced spin-polarization via partial Ge-dimerization as the driving force of the charge density wave in FeGe,” Phys. Rev. Mater. 7, 104006 (2023).
- Chen et al. (2023) Ziyuan Chen, Xueliang Wu, Shiming Zhou, Jiakang Zhang, Ruotong Yin, Yuanji Li, Mingzhe Li, Jiashuo Gong, Mingquan He, Yisheng Chai, Xiaoyuan Zhou, Yilin Wang, Aifeng Wang, Ya-Jun Yan, and Dong-Lai Feng, “Long-ranged charge order conspired by magnetism and lattice in an antiferromagnetic kagome metal,” arXiv:2307.07990 (2023).
- Ghimire et al. (2020) Nirmal J. Ghimire, Rebecca L. Dally, L. Poudel, D. C. Jones, D. Michel, N. Thapa Magar, M. Bleuel, Michael A. McGuire, J. S. Jiang, J. F. Mitchell, Jeffrey W. Lynn, and I. I. Mazin, “Competing magnetic phases and fluctuation-driven scalar spin chirality in the kagome metal YMn6Sn6,” Science Advances 6, eabe2680 (2020).
- Riberolles et al. (2022) S. X. M. Riberolles, Tyler J. Slade, D. L. Abernathy, G. E. Granroth, Bing Li, Y. Lee, P. C. Canfield, B. G. Ueland, Liqin Ke, and R. J. McQueeney, “Low-Temperature Competing Magnetic Energy Scales in the Topological Ferrimagnet ,” Phys. Rev. X 12, 021043 (2022).
- Yin et al. (2020) Jia-Xin Yin, Wenlong Ma, Tyler A Cochran, Xitong Xu, Songtian S Zhang, Hung-Ju Tien, Nana Shumiya, Guangming Cheng, Kun Jiang, Biao Lian, Zhida Song, Guoqing Chang, Ilya Belopolski, Daniel Multer, Maksim Litskevich, Zi-Jia Cheng, Xian P. Yang, Bianca Swidler, Huibin Zhou, Hsin Lin, Titus Neupert, Ziqiang Wang, Nan Yao, Tay-Rong Chang, Shuang Jia, and M. Zahid Hasan, “Quantum-limit Chern topological magnetism in TbMn6Sn6,” Nature 583, 533–536 (2020).
- Zhang et al. (2020) H. Zhang, X. Feng, T. Heitmann, A. I. Kolesnikov, M. B. Stone, Y.-M. Lu, and X. Ke, “Topological magnon bands in a room-temperature kagome magnet,” Phys. Rev. B 101, 100405 (2020).
- Li et al. (2021) Man Li, Qi Wang, Guangwei Wang, Zhihong Yuan, Wenhua Song, Rui Lou, Zhengtai Liu, Yaobo Huang, Zhonghao Liu, Hechang Lei, et al., “Dirac cone, flat band and saddle point in kagome magnet YMn6Sn6,” Nature Communications 12, 3129 (2021).
- Xu et al. (2022) Xitong Xu, Jia-Xin Yin, Wenlong Ma, Hung-Ju Tien, Xiao-Bin Qiang, PV Reddy, Huibin Zhou, Jie Shen, Hai-Zhou Lu, Tay-Rong Chang, et al., “Topological charge-entropy scaling in kagome Chern magnet TbMn6Sn6,” Nature Communications 13, 1197 (2022).
- Li et al. (2022) Hong Li, He Zhao, Kun Jiang, Qi Wang, Qiangwei Yin, Ning-Ning Zhao, Kai Liu, Ziqiang Wang, Hechang Lei, and Ilija Zeljkovic, “Manipulation of Dirac band curvature and momentum-dependent g factor in a kagome magnet,” Nature Physics 18, 644–649 (2022).
- Asaba et al. (2020) T. Asaba, S. M. Thomas, M. Curtis, J. D. Thompson, E. D. Bauer, and F. Ronning, “Anomalous Hall effect in the kagome ferrimagnet ,” Phys. Rev. B 101, 174415 (2020).
- Ma et al. (2021) Wenlong Ma, Xitong Xu, Jia-Xin Yin, Hui Yang, Huibin Zhou, Zi-Jia Cheng, Yuqing Huang, Zhe Qu, Fa Wang, M. Zahid Hasan, and Shuang Jia, “Rare Earth Engineering in (, Lu) Topological Kagome Magnets,” Phys. Rev. Lett. 126, 246602 (2021).
- Gao et al. (2021) Lingling Gao, Shiwei Shen, Qi Wang, Wujun Shi, Yi Zhao, Changhua Li, Weizheng Cao, Cuiying Pei, Jun-Yi Ge, Gang Li, Jun Li, Yulin Chen, Shichao Yan, and Yanpeng Qi, “Anomalous Hall effect in ferrimagnetic metal RMn6Sn6 (R = Tb, Dy, Ho) with clean Mn kagome lattice,” Applied Physics Letters 119, 092405 (2021).
- Zhang et al. (2022a) Heda Zhang, Jahyun Koo, Chunqiang Xu, Milos Sretenovic, Binghai Yan, and Xianglin Ke, “Exchange-biased topological transverse thermoelectric effects in a Kagome ferrimagnet,” Nature Communications 13, 1091 (2022a).
- Arachchige et al. (2022) Hasitha W. Suriya Arachchige, William R. Meier, Madalynn Marshall, Takahiro Matsuoka, Rui Xue, Michael A. McGuire, Raphael P. Hermann, Huibo Cao, and David Mandrus, “Charge Density Wave in Kagome Lattice Intermetallic ,” Phys. Rev. Lett. 129, 216402 (2022).
- Tan and Yan (2023) Hengxin Tan and Binghai Yan, “Abundant Lattice Instability in Kagome Metal ,” Phys. Rev. Lett. 130, 266402 (2023).
- Cao et al. (2023) Saizheng Cao, Chenchao Xu, Hiroshi Fukui, Taishun Manjo, Ming Shi, Yang Liu, Chao Cao, and Yu Song, “Competing charge-density wave instabilities in the kagome metal ScV6Sn6,” Nature Communications 14, 7671 (2023).
- Korshunov et al. (2023) A. Korshunov, H. Hu, D. Subires, Y. Jiang, D. Călugăru, X. Feng, A. Rajapitamahuni, C. Yi, S. Roychowdhury, M. G. Vergniory, J. Strempfer, C. Shekhar, E. Vescovo, D. Chernyshov, A. H. Said, A. Bosak, C. Felser, B. Andrei Bernevig, and S. Blanco-Canosa, “Softening of a flat phonon mode in the kagome ScV6Sn6,” Nature Communications 14, 6646 (2023).
- Cheng et al. (2024) Siyu Cheng, Zheng Ren, Hong Li, Jiseop Oh, Hengxin Tan, Ganesh Pokharel, Jonathan M. DeStefano, Elliott Rosenberg, Yucheng Guo, Yichen Zhang, Ziqin Yue, Yongbin Lee, Sergey Gorovikov, Marta Zonno, Makoto Hashimoto, Donghui Lu, Liqin Ke, Federico Mazzola, Junichiro Kono, R. J. Birgeneau, Jiun-Haw Chu, Stephen D. Wilson, Ziqiang Wang, Binghai Yan, Ming Yi, and Ilija Zeljkovic, “Nanoscale visualization and spectral fingerprints of the charge order in ScV6Sn6 distinct from other kagome metals,” npj Quantum Mater. 9, 14 (2024).
- Pokharel et al. (2022) Ganesh Pokharel, Brenden Ortiz, Juan Chamorro, Paul Sarte, Linus Kautzsch, Guang Wu, Jacob Ruff, and Stephen D. Wilson, “Highly anisotropic magnetism in the vanadium-based kagome metal ,” Phys. Rev. Mater. 6, 104202 (2022).
- Rosenberg et al. (2022) Elliott Rosenberg, Jonathan M. DeStefano, Yucheng Guo, Ji Seop Oh, Makoto Hashimoto, Donghui Lu, Robert J. Birgeneau, Yongbin Lee, Liqin Ke, Ming Yi, and Jiun-Haw Chu, “Uniaxial ferromagnetism in the kagome metal ,” Phys. Rev. B 106, 115139 (2022).
- Zhang et al. (2022b) Xiaoxiao Zhang, Ziyi Liu, Qi Cui, Qi Guo, Ningning Wang, Lifen Shi, Hua Zhang, Weihua Wang, Xiaoli Dong, Jianping Sun, Zhiling Dun, and Jinguang Cheng, “Electronic and magnetic properties of intermetallic kagome magnets ,” Phys. Rev. Mater. 6, 105001 (2022b).
- Lee and Mun (2022) Jeonghun Lee and Eundeok Mun, “Anisotropic magnetic property of single crystals ,” Phys. Rev. Mater. 6, 083401 (2022).
- Peng et al. (2021) Shuting Peng, Yulei Han, Ganesh Pokharel, Jianchang Shen, Zeyu Li, Makoto Hashimoto, Donghui Lu, Brenden R. Ortiz, Yang Luo, Houchen Li, Mingyao Guo, Bingqian Wang, Shengtao Cui, Zhe Sun, Zhenhua Qiao, Stephen D. Wilson, and Junfeng He, “Realizing Kagome Band Structure in Two-Dimensional Kagome Surface States of ( = Gd, Ho),” Phys. Rev. Lett. 127, 266401 (2021).
- Hu et al. (2022) Yong Hu, Xianxin Wu, Yongqi Yang, Shunye Gao, Nicholas C. Plumb, Andreas P. Schnyder, Weiwei Xie, Junzhang Ma, and Ming Shi, “Tunable topological Dirac surface states and van Hove singularities in kagome metal GdV6Sn6,” Science Advances 8, eadd2024 (2022).
- Sante et al. (2023) Domenico Di Sante, Chiara Bigi, Philipp Eck, Stefan Enzner, Armando Consiglio, Ganesh Pokharel, Pietro Carrara, Pasquale Orgiani, Vincent Polewczyk, Jun Fujii, Phil D. C. King, Ivana Vobornik, Giorgio Rossi, Ilija Zeljkovic, Stephen D. Wilson, Ronny Thomale, Giorgio Sangiovanni, Giancarlo Panaccione, and Federico Mazzola, “Flat band separation and robust spin berry curvature in bilayer kagome metals,” Nature Physics 19, 1135–1142 (2023).
- Pokharel et al. (2021) Ganesh Pokharel, Samuel M. L. Teicher, Brenden R. Ortiz, Paul M. Sarte, Guang Wu, Shuting Peng, Junfeng He, Ram Seshadri, and Stephen D. Wilson, “Electronic properties of the topological kagome metals and ,” Phys. Rev. B 104, 235139 (2021).
- Ding et al. (2023) Jianyang Ding, Ningning Zhao, Zicheng Tao, Zhe Huang, Zhicheng Jiang, Yichen Yang, Soohyun Cho, Zhengtai Liu, Jishan Liu, Yanfeng Guo, Kai Liu, Zhonghao Liu, and Dawei Shen, “Kagome surface states and weak electronic correlation in vanadium-kagome metals,” Journal of Physics: Condensed Matter 35, 405502 (2023).
- (40) See the Supplemental Material for methods employed in our calculations and extended results and discussions about the bulk, surfaces, and thin films of TbV6Sn6 and YV6Sn6, and properties of magnetic kagome surfaces (Mn-doped TbV6Sn6, TbMn6Sn6 and V-doped TbMn6Sn6). Refs. Kresse and Furthmüller (1996a, b); Perdew et al. (1996); Wang et al. (2021); Togo and Tanaka (2015); Tan and Yan (2023); Hu et al. (2022, 2024); Arachchige et al. (2022); Ishikawa et al. (2021); Rosenberg et al. (2022); Romaka et al. (2011) are included.
- (41) After structural relaxation, the V-kagome sublattice goes below the closely associated Sn sublattice in the V3Sn termination.
- Hu et al. (2023) Haoyu Hu, Yi Jiang, Dumitru Călugăru, Xiaolong Feng, David Subires, Maia G. Vergniory, Claudia Felser, Santiago Blanco-Canosa, and B. Andrei Bernevig, “Kagome Materials I: SG 191, ScV6Sn6. Flat Phonon Soft Modes and Unconventional CDW Formation: Microscopic and Effective Theory,” arXiv:2305.15469 (2023).
- Shannon and Prewitt (1969) R. D. Shannon and C. T. Prewitt, “Effective ionic radii in oxides and fluorides,” Acta Crystallographica Section B 25, 925–946 (1969).
- Wu et al. (2024) Shangfei Wu, Mason L. Klemm, Jay Shah, Ethan T. Ritz, Chunruo Duan, Xiaokun Teng, Bin Gao, Feng Ye, Masaaki Matsuda, Fankang Li, Xianghan Xu, Ming Yi, Turan Birol, Pengcheng Dai, and Girsh Blumberg, “Symmetry Breaking and Ascending in the Magnetic Kagome Metal FeGe,” Phys. Rev. X 14, 011043 (2024).
- Lee (1955) E. W. Lee, “Magnetostriction and magnetomechanical effects,” Reports on Progress in Physics 18, 184 (1955).
- Kresse and Furthmüller (1996a) G. Kresse and J. Furthmüller, “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set,” Phys. Rev. B 54, 11169 (1996a).
- Kresse and Furthmüller (1996b) Georg Kresse and Jürgen Furthmüller, “Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set,” Comput. Mater. Sci. 6, 15–50 (1996b).
- Perdew et al. (1996) John P. Perdew, Kieron Burke, and Matthias Ernzerhof, “Generalized gradient approximation made simple,” Phys. Rev. Lett. 77, 3865 (1996).
- Wang et al. (2021) Vei Wang, Nan Xu, Jin-Cheng Liu, Gang Tang, and Wen-Tong Geng, “VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code,” Computer Physics Communications 267, 108033 (2021).
- Togo and Tanaka (2015) A Togo and I Tanaka, “First principles phonon calculations in materials science,” Scr. Mater. 108, 1–5 (2015).
- Hu et al. (2024) Yong Hu, Junzhang Ma, Yinxiang Li, Yuxiao Jiang, Dariusz Jakub Gawryluk, Tianchen Hu, Jérémie Teyssier, Volodymyr Multian, Zhouyi Yin, Shuxiang Xu, et al., “Phonon promoted charge density wave in topological kagome metal ScV6Sn6,” Nature Communications 15, 1658 (2024).
- Ishikawa et al. (2021) Hajime Ishikawa, Takeshi Yajima, Mitsuaki Kawamura, Hiroyuki Mitamura, and Koichi Kindo, “GdV6Sn6: A Multi-carrier Metal with Non-magnetic 3d-electron Kagome Bands and 4f-electron Magnetism,” Journal of the Physical Society of Japan 90, 124704 (2021).
- Romaka et al. (2011) L. Romaka, Yu. Stadnyk, V.V. Romaka, P. Demchenko, M. Stadnyshyn, and M. Konyk, “Peculiarities of component interaction in {Gd, Er}–V–Sn Ternary systems at 870 K and crystal structure of V6Sn6 stannides,” Journal of Alloys and Compounds 509, 8862–8869 (2011).