Yuying Chen*[email protected]
\addauthorCongcong Liu*[email protected]
\addauthorBertram [email protected]
\addauthorMing [email protected]
\addinstitution
Robotics Institute
Hong Kong University of Science and Technology
Hong Kong, China
Coherent Motion Aware Trajectory Prediction WITH GCN
CoMoGCN: Coherent Motion Aware Trajectory Prediction with Graph Representation
Abstract
Forecasting human trajectories is critical for tasks such as robot crowd navigation and autonomous driving. Modeling social interactions is of great importance for accurate group-wise motion prediction. However, most existing methods do not consider information about coherence within the crowd, but rather only pairwise interactions. In this work, we propose a novel framework, coherent motion aware graph convolutional network (CoMoGCN), for trajectory prediction in crowded scenes with group constraints. First, we cluster pedestrian trajectories into groups according to motion coherence. Then, we use graph convolutional networks to aggregate crowd information efficiently. The CoMoGCN also takes advantage of variational autoencoders to capture the multimodal nature of the human trajectories by modeling the distribution. Our method achieves state-of-the-art performance on several different trajectory prediction benchmarks, and the best average performance among all benchmarks considered.
1 Introduction
Forecasting human trajectories is of great importance for tasks, such as robot navigation in crowds, autonomous driving, and crowd surveillance. For autonomous robot systems, predicting the human motion enables feasible and efficient planning and control.
However, making accurate trajectory predictions is still a challenging task because pedestrian trajectories can be affected by many factors, such as the topology of the environment, intended goals, and social relationships and interactions [Rudenko et al.(2019)Rudenko, Palmieri, Herman, Kitani, Gavrila, and Arras]. Furthermore, the highly dynamic and multimodal properties inherent in human motion must also be considered.
Multimodality in trajectory prediction has been studied recently [Gupta et al.(2018)Gupta, Johnson, Fei-Fei, Savarese, and Alahi, Sadeghian et al.(2019)Sadeghian, Kosaraju, Sadeghian, Hirose, Rezatofighi, and Savarese, Kosaraju et al.(2019)Kosaraju, Sadeghian, Martín-Martín, Reid, Rezatofighi, and Savarese, Lee et al.(2017)Lee, Choi, Vernaza, Choy, Torr, and Chandraker, Amirian et al.(2019)Amirian, Hayet, and Pettré]. Most past work uses generative adversarial models (GANs) to generate multiple predictions. However, GANs suffer from the instability of adversarial training, which is sensitive to hyperparameters and structure [Wang et al.(2019)Wang, She, and Ward]. As an alternative, variational autoencoder (VAE) is relatively more stable. Lee et al. present a CVAE based framework to predict future object locations [Lee et al.(2017)Lee, Choi, Vernaza, Choy, Torr, and Chandraker]. A recent work adopted CVAE for trajectory prediction [Ivanovic and Pavone(2019)]. This paper takes advantage of the VAE to capture the multimodality of human trajectories.
Recently, some works have proposed to model the dynamic interactions of pedestrians by combining information from pairwise interactions, through pooling mechanisms such as max-pooling [Gupta et al.(2018)Gupta, Johnson, Fei-Fei, Savarese, and Alahi] and self-attention pooling [Sadeghian et al.(2019)Sadeghian, Kosaraju, Sadeghian, Hirose, Rezatofighi, and Savarese]. However, those works do not completely capture important information about the geometric configuration of the crowd. Furthermore, these works rely on some ad-hoc rules to handle varying numbers of agents, such as setting a maximum on the number of agents and using dummy values for non-existing agents [Sadeghian et al.(2019)Sadeghian, Kosaraju, Sadeghian, Hirose, Rezatofighi, and Savarese]. To avoid such ad-hoc assumptions, Chen et al. [Chen et al.(2020)Chen, Liu, Shi, and Liu] propose to use graph convolutional networks (GCN) to aggregate information about neighboring humans for robot crowd navigation tasks. The GCN can handle varying numbers of neighbors naturally, and can be extended to modulate interactions by changing its adjacency matrix. In this paper, we use a similar graph structure for crowd information aggregation in a different task: trajectory prediction.
Most previous work has focused only on the interactions between pairs of humans. Coherent motion patterns of pedestrian groups, which encode rich information about implicit social rules, has rarely been considered. This lack of attention may be due in part to the lack of information about social grouping in current benchmark datasets, such as the commonly used ETH [Pellegrini et al.(2009)Pellegrini, Ess, Schindler, and Van Gool] and UCY [Lerner et al.(2007)Lerner, Chrysanthou, and Lischinski] datasets, for trajectory prediction. To address this unavailability, we add coherent motion cluster labels to trajectory prediction datasets using a coherent filtering method [Zhou et al.(2012)Zhou, Tang, and Wang], and leverage DBSCAN clustering to compensate for the drawbacks of the coherent filtering method in the small group detection. These coherent motion labels provide a mid-level representation of crowd dynamics, which is very useful for crowd analysis. We incorporated the coherent motion constraints into our model by using GCNs for intergroup and intragroup relationship modeling.
There are several main contributions of our work:
-
•
We introduce graph convolutional networks (GCN) to better model social interactions within human crowds. The use of GCNs enables our approach to handle varying crowd sizes in a principled way. Interactions between humans can be controlled easily by modifying the adjacency matrix.
-
•
Unlike past work that considered pairwise interactions between individuals only, we take into account coherent motion constraints inside crowds to better capture social interactions.
-
•
We developed a hybrid labeling method to add coherent motion labels to trajectory prediction datasets. We will release the re-labelled dataset publicly for use by other researchers111https://sites.google.com/view/comogcn.
-
•
We take advantage of the VAE to handle multimodality in trajectory modeling.
-
•
With the above mechanisms, the CoMoGCN achieves state-of-the-art performance on several different trajectory prediction benchmarks, and the best average performance across all datasets considered.
2 Related works
2.1 Crowd Interaction
A pioneering work for crowd interaction modeling, the Social Force Model (SFM) proposed by [Helbing and Molnar(1995)], has been applied successfully to many applications such as abnormal crowd behavior detection[Mehran et al.(2009)Mehran, Oyama, and Shah] and multi-object tracking [Pellegrini et al.(2009)Pellegrini, Ess, Schindler, and Van Gool]. However, as discussed in [Alahi et al.(2016)Alahi, Goel, Ramanathan, Robicquet, Fei-Fei, and Savarese], the social force model can model simple interactions, but fails to model complex crowd interactions. There are also other hand crafted feature based models, such as continuum dynamics [Treuille et al.(2006)Treuille, Cooper, and Popović], discrete choice [Antonini et al.(2006)Antonini, Bierlaire, and Weber] and Gaussian Process models [Wang et al.(2007)Wang, Fleet, and Hertzmann]. However, all the above methods are based on hand-crafted energy functions and specific rules, which limit their performance.
2.2 RNN for Trajectory Prediction
Recently, Recurrent Neural Networks (RNN), such as the Long Short Term Memory (LSTM), have achieved many successes in trajectory prediction tasks [Alahi et al.(2016)Alahi, Goel, Ramanathan, Robicquet, Fei-Fei, and Savarese, Su et al.(2017)Su, Zhu, Dong, and Zhang, Xu et al.(2018)Xu, Piao, and Gao, Zhang et al.(2019)Zhang, Ouyang, Zhang, Xue, and Zheng, Lisotto et al.(2019)Lisotto, Coscia, and Ballan, Hasan et al.(2018)Hasan, Setti, Tsesmelis, Del Bue, Galasso, and Cristani]. Alahi et al. proposed a social pooling layer to model neighboring humans [Alahi et al.(2016)Alahi, Goel, Ramanathan, Robicquet, Fei-Fei, and Savarese]. Gupta et al. proposed a pooling module, which consists of an MLP followed by max-pooling to aggregate information from all other humans [Gupta et al.(2018)Gupta, Johnson, Fei-Fei, Savarese, and Alahi]. Sadeghian et al. [Sadeghian et al.(2019)Sadeghian, Kosaraju, Sadeghian, Hirose, Rezatofighi, and Savarese] adopted a soft attention module to aggregate information across agents. More recent work uses GCNs to aggregate information by treating humans as nodes and modeling interaction through edge strength for robot navigation [Chen et al.(2020)Chen, Liu, Shi, and Liu]. Similarly, a variant of the GCN, the Graph Attention Network (GAT), has been used to model the social interactions [Kosaraju et al.(2019)Kosaraju, Sadeghian, Martín-Martín, Reid, Rezatofighi, and Savarese]. However, the use of multi-head attention in the GAT increases the number of parameters and the computational complexity of the GAT in comparison to the GCN. In this work, we integrate information across humans using GCNs, which enables our method to handle varying crowd sizes.
2.3 Coherent Motion Information for Motion Prediction
Most previous work only pay attention to interactions among pairs of pedestrians. However, the pedestrian trajectories are also influenced by more complex social relations between humans. Coherent motion patterns inside crowds, which encode implicit social information, have been shown to be useful in many applications, such as crowd activity recognition[Wang et al.(2008)Wang, Ma, and Grimson]. Bisagno et al. [Bisagno et al.(2018)Bisagno, Zhang, and Conci] considered intragroup interactions for trajectory predictions, but neglected intergroup interactions. Current benchmark datasets for trajectory prediction do not provide coherent motion labels.
Several works have been done in detecting coherent motions [Zhou et al.(2012)Zhou, Tang, and Wang] and measuring the collectiveness of crowds [Mei et al.(2019)Mei, Lai, Chen, and Xie]. Zhou et al. [Zhou et al.(2012)Zhou, Tang, and Wang] proposed the coherent filtering that detects invariant neighbors of every individual, and measures the velocity correlations for motion clustering. It shows good performance on collective motion benchmark and can detect coherent motions given the crowd trajectories in a short time window. In this paper, we use the coherent filtering method to label trajectory prediction datasets. In addition, we leverage DBSCAN clustering to compensate for the disadvantages of the coherent filtering method in small group detection. Based on the labels, we incorporate the coherent motion information into our model for better interaction modeling.
3 Method

3.1 Problem Definition
The goal of this work is to generate the future trajectories of all humans in a scene at the same time. The trajectory of a person is defined using which denotes the relative position of human at time step to the position at . Consistent with previous works [Gupta et al.(2018)Gupta, Johnson, Fei-Fei, Savarese, and Alahi, Sadeghian et al.(2019)Sadeghian, Kosaraju, Sadeghian, Hirose, Rezatofighi, and Savarese], the observed trajectory of all humans in a scene is defined as for time steps ; the future trajectory to be predicted is defined as for time step , where the number of humans may change dynamically. The model aims to generate trajectories whose distribution matches that of ground truth future trajectories of all humans .
3.2 Overall Model
Figure 1 shows the overall framework of our method for trajectory prediction. Data pre-processing is applied offline to obtain the coherent motion pattern for each human. For feature extraction, we first use a single layer MLP (FC) to encode each pedestrian’s relative displacements as a fixed-length embedding. These embeddings are fed to an LSTM as shown below:
| (1) |
where is the weight of FC layer, and is the weight of the encoding LSTM. On the other hand, for specific person , the relative position of other humans are fed into an FC layer to obtain social information which is similar to the pooling module in Social GAN [Gupta et al.(2018)Gupta, Johnson, Fei-Fei, Savarese, and Alahi].
Then the features from all pedestrians and the interested person’s social information are concatenated together as the input to the two GCNs for intergroup and intragroup interaction aggregation:
| (2) | ||||
| (3) |
where and denote the adjacency matrices as described in more detail in Section. 3.4. and are weight matrices. We extract the feature of node after the final graph convolutional layer as the features and .
The features computed by the outputs of the two GCNs are then concatenated together and input to an MLP, which computes the mean and variance of a distribution over the feature vectors to be input to the decoder:
| (4) |
where is the weight matrix. We sample an input feature vector to the decoder stage, , from this distribution and concatenate it with the embedding computed from an embedding of the last predicted state. The resulting features are fed into the decoder LSTM cell for trajectory prediction:
| (5) |
where is the weight for decoder LSTM and is the weight for decoder MLP.
3.3 Coherent Motion Clustering for Pedestrian Groups
For coherent motion detection, we use the coherent filtering proposed by [Zhou et al.(2012)Zhou, Tang, and Wang]. The process takes the positions of humans from consecutive frames to and generates a clustering index for each human and for each frame. Humans sharing the same index are considered to have coherent motion. The process of coherent filtering mainly includes three steps: a) finding K nearest neighbors b) finding the invariant neighbors of a individual c) measuring the time-averaged velocity correlations of the invariant neighbors to the individual. Among these individual-neighbor pairs, pairs with correlation intensity above a threshold are marked as coherent pairs.
Though this method is effective for crowds with large crowd densities, it performs poorly for sparse crowds and fails to detect small groups. To compensate, we apply an extra clustering step, the DBSCAN method [Ester et al.(1996)Ester, Kriegel, Sander, Xu, et al.], for the unlabeled humans. As a density based clustering method, it relies on the distance to find the neighbors. We account for moving direction and calculate the angular distance of each pair of humans. These differences are used to classify humans into clusters.
Our hybrid labeling method improves the labeling yield and generates better labels than the coherent filtering alone. Figure 1 of the supplementary file shows examples of detection by coherent filtering on each dataset. The quantitative evaluations of the coherent filtering and of our hybrid labeling method are shown in Table 2 and 3 of the supplementary file. Figure 2 of the supplementary file shows a qualitative comparison between the coherent filtering and our method. The parameter settings are shown in Table 1 of the supplementary file.
3.4 Graph Convolutional Networks
Dealing with the large and varied numbers of humans in a scene is one of the main challenges for multi-human trajectory prediction. Previous works adopted ad-hoc solutions such as setting a maximum number of humans[Sadeghian et al.(2019)Sadeghian, Kosaraju, Sadeghian, Hirose, Rezatofighi, and Savarese]. In this work, we address this problem in a simpler and more principled way through graph representations. Nodes in the graph denote humans in the crowd. In the following, we denote the number of humans in the crowd by .
We adopt a two-layer graph convolutional networks (GCNs) [Kipf and Welling(2016)] to aggregate information in crowds. To each node in the network, we associate a feature vector, which contains important information about the node. The graph convolutional layer is the main building block of GCNs. It takes input feature vectors for each node and converts them to output feature vectors for each node by integrating information both within and across nodes. We use to denote the dimension of the input feature vectors and to denote the dimension of the output feature vectors The input feature vectors of layer are represented by matrix . The input feature matrix is converted to output vectors represented by a matrix based on the layer-wise forward rule:
| (6) |
is a trainable weight matrix for layer . is the adjacency matrix of the graph, whose values determine how information from different nodes is aggregated. Each row of is normalized to sum to one. is Relu activation function.
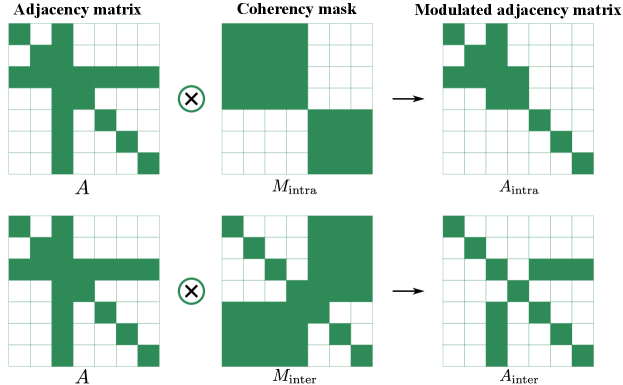
The adjacency matrix reflects the connections between nodes of the graph. The vanilla GCN assumes that the qualitative influence of each human on another (as determined by ) is the same and only the strength of that influence can be modulated (through the adjacency matrix). However, we think that the qualitative effect of humans in the crowd on a particular human’s trajectory are different, based on whether the humans are in the same group or not. A single GCN can not handle this. Thus, we propose to use two GCNs. As shown in Fig.2, for each human, we modulate the adjacency matrix by multiplication with two coherence masks which encodes the intergroup and intragroup labels. Then we obtain two adjacency matrix denoting intergroup connection () and intragroup () connection separately for each human by pixelwise multiplying the adjacency matrix () with the masks. We set the value in the adjacency matrix by first constructing a binary matrix denoting connections between nodes, and then normalizing each row.
By modulating the adjacency matrix of GCNs with coherent motion information, we incorporate implicit social relations into our network for better interaction modeling.
3.5 Implementation Details
We trained the network with Adam optimizer. The mini-batch size is 64 and the learning rate is 1e-4. The models were trained for 200 epochs. The encoder encodes the relative trajectories by a single layer of MLP () with dimension of 16 followed by an LSTM ()with a hidden dimension of 32. The embedding output from LSTM was then concatenated with the features extracted from relative position from other humans by a single MLP with dimension of 16. The concatenated features are then fed into two GCNs for feature integration. Then hidden number for two graph convolutional layer has the dimension of 72 and 8 separately. Then an MLP () was used to take state of humans to create a distribution with mean and variance. Then we sample from this distribution with a dimension of 8, and fed it into an LSTM ()with dimension of 32 and followed by an MLP ()with dimension of 2 for decoding.
4 Experiments
In this section, we evaluate our method in two public datasets ETH [Pellegrini et al.(2009)Pellegrini, Ess, Schindler, and Van Gool] and UCY [Lerner et al.(2007)Lerner, Chrysanthou, and Lischinski]. The ETH datasets contain two scenes (ETH and Hotel) while the UCY datasets contain three scenes (Zara1, Zara2, and Univ). There are five sets of data with four different scenarios and 1536 pedestrians in total.
4.1 Evaluation Methodology
Following the setting in [Gupta et al.(2018)Gupta, Johnson, Fei-Fei, Savarese, and Alahi], we adopt the leave-one-out approach, i.e. train with four sets and test in the remaining set. We take trajectories with 8 time steps as observation and evaluate trajectory predictions over the next 12 time steps.
4.1.1 Metrics
Similar to previous works [Gupta et al.(2018)Gupta, Johnson, Fei-Fei, Savarese, and Alahi, Sadeghian et al.(2019)Sadeghian, Kosaraju, Sadeghian, Hirose, Rezatofighi, and Savarese, Kosaraju et al.(2019)Kosaraju, Sadeghian, Martín-Martín, Reid, Rezatofighi, and Savarese], we adopt two standard metrics including Average Displacement Error (ADE) and Final Displacement Error (FDE) in meter.
ADE: Mean L2 distance between ground truth and predictions of all time steps.
FDE: Mean L2 distance between ground truth and prediction at the final time step.
4.1.2 Baselines
We compare our work with following several recent works based on generative models:
Social GAN (S-GAN) [Gupta et al.(2018)Gupta, Johnson, Fei-Fei, Savarese, and Alahi]: A generative model using GAN to generate multimodal predictions. It utilizes a global pooling module to combine crowd interactions by an MLP followed by a max-pooling layer.
Sophie [Sadeghian et al.(2019)Sadeghian, Kosaraju, Sadeghian, Hirose, Rezatofighi, and Savarese]: A improved GAN based model which considers both social interactions and physical interaction with scene context.
Trajectron [Ivanovic and Pavone(2019)]: A generative model based on CVAE for multimodal predictions with spatiotemporal graphs.
Social-BiGAT [Kosaraju et al.(2019)Kosaraju, Sadeghian, Martín-Martín, Reid, Rezatofighi, and Savarese]: A generative model using Bicycle-GAN for multimodal prediction and GAT for crowd interaction modeling.
4.2 Quantitative results
| Baselines | Ours | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | S-GAN | Sophie | Trajectron | Social-BiGAT | MLP | GCN | GAT |
|
|
||||
| ETH | 0.81/1.52 | 0.70/1.43 | 0.59/1.17 | 0.69/1.29 | 0.73/1.40 | 0.72/1.31 | 0.73/1.36 | 0.71/1.28 | 0.70/1.26 | ||||
| HOTEL | 0.72/1.61 | 0.76/1.67 | 0.42/0.80 | 0.49/1.01 | 0.45/0.93 | 0.41/0.81 | 0.41/0.85 | 0.37/0.76 | 0.37/0.75 | ||||
| UNIV | 0.60/1.26 | 0.54/1.24 | 0.59/1.21 | 0.55/1.32 | 0.61/1.31 | 0.55/1.18 | 0.55/1.19 | 0.55/1.19 | 0.53/1.16 | ||||
| ZARA1 | 0.34/0.69 | 0.30/0.63 | 0.55/1.09 | 0.30/0.62 | 0.34/0.72 | 0.35/0.74 | 0.35/0.74 | 0.34/0.72 | 0.34/0.71 | ||||
| ZARA2 | 0.42/0.84 | 0.38/0.78 | 0.52/1.04 | 0.36/0.75 | 0.33/0.71 | 0.32/0.68 | 0.31/0.68 | 0.32/0.68 | 0.31/0.67 | ||||
| AVG | 0.58/1.18 | 0.54/1.15 | 0.53/1.06 | 0.48/1.00 | 0.49/1.01 | 0.47/0.94 | 0.47/0.96 | 0.46/0.93 | 0.45/0.91 | ||||
4.2.1 Comparison to state-of-the-art methods
As shown in Table 1, we compare our models with various baselines. The average displacement error (ADE) and final displacement error (FDE) were reported across five datasets. Following settings in every baseline, we run 20 samples for evaluation.
It is clear to see that our final model with GCN and coherent motion constraints beat all baselines and obtain more consistent results in both ADE and FDE. Compared to Social GAN, we achieve 22.4% improvement in ADE and 22.9% improvement in FDE on average. Compared to Sophie who use additional scene context information, we achieve 16.7% improvement in ADE and 20.9% improvement in FDE on average. Compared to Trajectron who also uses VAE as backbone network, we achieve 15.1% improvement in ADE and 14.2% improvement in FDE on average. Compare to Social-BiGAT who also considers graph structure for interaction modeling, we achieve 6.3% improvement in ADE and 9.0% improvement in FDE on average.
4.2.2 Ablation study
We conduct several ablation studies to validate the benefits of the use of GCN and coherent motion information.
To show the benefit of the use of GCN, we investigated another model that replaces GCN with MLP (followed by max-pooling, similar to the pooling module in social GAN [Gupta et al.(2018)Gupta, Johnson, Fei-Fei, Savarese, and Alahi]) as shown in Table 1.
When comparing the model using GCN with MLP, we can see that the one with GCN achieves 4.1% improvement in ADE and 6.9% improvement in FDE.
To show the benefit of the incorporation of coherent motion information, we compare our full model with the one without considering coherent information (only using GCN), and GAT (same implementation with [Veličković et al.(2017)Veličković, Cucurull, Casanova, Romero, Lio, and Bengio]).
When compare the full model with the one using GCN only, we can see that our full model with coherent motion information achieves 4.3% improvement in ADE and 3.2% improvement in FDE. When compare the full model with GAT, we can see that the full model achieves 4.3% improvement in ADE and 5.2% improvement in FDE.
The above ablation studies clearly demonstrate the benefits of the use of GCN and the introduction of coherent motion information.
We further investigated trajectory prediction performance of models with different coherent detection method, Coherent Filtering method (CF) [Zhou et al.(2012)Zhou, Tang, and Wang] vs. our hybrid labeling method (hybrid). We can see that model with our hybrid coherent detection method (Coherent Filtering + DBSCAN) outperforms model with Coherent Filtering method by 2.2 % improvement in ADE and 2.2 % improvement in FDE on average. The improvements are consistent over all five datasets.
4.3 Qualitative results

In order to better understanding the benefits of our model in capturing social interactions between humans, we visualize several examples of the generated trajectories across testing sets as shown in Fig.3.
From the four examples, we can see that the predictions of our model generally have lower variance than S-GAN, which means we can generate model in a more efficient way. Also, the examples show that our model better captures the interactions of pedestrians walking in the crowds which obtain more accurate predictions (as shown in (d)). It is clear to see that our model generates more realistic predictions avoiding collisions as shown in example (b). Besides, S-GAN tends to predict slower motion in dataset HOTEL (as shown in (c)).
For qualitative results of the ablation study, please refer to Fig. 3 in supplementary file. We can observe consistent results with the quantitative evaluation. The proposed full model make more accurate and realistic predictions.
5 Conclusion
In this paper, we propose a novel VAE based generative model for trajectory prediction which outperforms state-of-the-art methods. We introduce graph convolutional networks (GCNs) for efficient crowd interaction aggregation. Furthermore, we provided coherent motion information for the trajectory prediction datasets. The coherent motion labels that significantly enrich the social information for the commonly used datasets (ETH and UCY) will be released to the research community later. Then we incorporated the coherent motion information, which contains rich information about implicit social relationship among the humans, into our methods. We show that the introduction of GCNs and coherent motion information significantly improve the performance for accurate trajectory prediction.
References
- [Alahi et al.(2016)Alahi, Goel, Ramanathan, Robicquet, Fei-Fei, and Savarese] Alexandre Alahi, Kratarth Goel, Vignesh Ramanathan, Alexandre Robicquet, Li Fei-Fei, and Silvio Savarese. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 961–971, 2016.
- [Amirian et al.(2019)Amirian, Hayet, and Pettré] Javad Amirian, Jean-Bernard Hayet, and Julien Pettré. Social ways: Learning multi-modal distributions of pedestrian trajectories with gans. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, pages 0–0, 2019.
- [Antonini et al.(2006)Antonini, Bierlaire, and Weber] Gianluca Antonini, Michel Bierlaire, and Mats Weber. Discrete choice models of pedestrian walking behavior. Transportation Research Part B: Methodological, 40(8):667–687, 2006.
- [Bisagno et al.(2018)Bisagno, Zhang, and Conci] Niccolo Bisagno, Bo Zhang, and Nicola Conci. Group lstm: Group trajectory prediction in crowded scenarios. In The European Conference on Computer Vision Workshops, September 2018.
- [Chen et al.(2020)Chen, Liu, Shi, and Liu] Yuying Chen, Congcong Liu, Bertram E Shi, and Ming Liu. Robot navigation in crowds by graph convolutional networks with attention learned from human gaze. IEEE Robotics and Automation Letters, 5(2):2754–2761, 2020.
- [Ester et al.(1996)Ester, Kriegel, Sander, Xu, et al.] Martin Ester, Hans-Peter Kriegel, Jörg Sander, Xiaowei Xu, et al. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, volume 96, pages 226–231, 1996.
- [Gupta et al.(2018)Gupta, Johnson, Fei-Fei, Savarese, and Alahi] Agrim Gupta, Justin Johnson, Li Fei-Fei, Silvio Savarese, and Alexandre Alahi. Social gan: Socially acceptable trajectories with generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2255–2264, 2018.
- [Hasan et al.(2018)Hasan, Setti, Tsesmelis, Del Bue, Galasso, and Cristani] Irtiza Hasan, Francesco Setti, Theodore Tsesmelis, Alessio Del Bue, Fabio Galasso, and Marco Cristani. Mx-lstm: mixing tracklets and vislets to jointly forecast trajectories and head poses. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 6067–6076, 2018.
- [Helbing and Molnar(1995)] Dirk Helbing and Peter Molnar. Social force model for pedestrian dynamics. Physical review E, 51(5):4282, 1995.
- [Ivanovic and Pavone(2019)] Boris Ivanovic and Marco Pavone. The trajectron: Probabilistic multi-agent trajectory modeling with dynamic spatiotemporal graphs. In Proceedings of the IEEE International Conference on Computer Vision, pages 2375–2384, 2019.
- [Kipf and Welling(2016)] Thomas N Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907, 2016.
- [Kosaraju et al.(2019)Kosaraju, Sadeghian, Martín-Martín, Reid, Rezatofighi, and Savarese] Vineet Kosaraju, Amir Sadeghian, Roberto Martín-Martín, Ian Reid, Hamid Rezatofighi, and Silvio Savarese. Social-bigat: Multimodal trajectory forecasting using bicycle-gan and graph attention networks. In Advances in Neural Information Processing Systems, pages 137–146, 2019.
- [Lee et al.(2017)Lee, Choi, Vernaza, Choy, Torr, and Chandraker] Namhoon Lee, Wongun Choi, Paul Vernaza, Christopher B Choy, Philip HS Torr, and Manmohan Chandraker. Desire: Distant future prediction in dynamic scenes with interacting agents. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 336–345, 2017.
- [Lerner et al.(2007)Lerner, Chrysanthou, and Lischinski] Alon Lerner, Yiorgos Chrysanthou, and Dani Lischinski. Crowds by example. In Computer Graphics Forum, volume 26, pages 655–664. Wiley Online Library, 2007.
- [Lisotto et al.(2019)Lisotto, Coscia, and Ballan] Matteo Lisotto, Pasquale Coscia, and Lamberto Ballan. Social and scene-aware trajectory prediction in crowded spaces. In Proceedings of the IEEE International Conference on Computer Vision Workshops, pages 0–0, 2019.
- [Mehran et al.(2009)Mehran, Oyama, and Shah] Ramin Mehran, Alexis Oyama, and Mubarak Shah. Abnormal crowd behavior detection using social force model. In 2009 IEEE Conference on Computer Vision and Pattern Recognition, pages 935–942. IEEE, 2009.
- [Mei et al.(2019)Mei, Lai, Chen, and Xie] Ling Mei, Jianghuang Lai, Zeyu Chen, and Xiaohua Xie. Measuring crowd collectiveness via global motion correlation. In Proceedings of the IEEE International Conference on Computer Vision Workshops, pages 0–0, 2019.
- [Pellegrini et al.(2009)Pellegrini, Ess, Schindler, and Van Gool] Stefano Pellegrini, Andreas Ess, Konrad Schindler, and Luc Van Gool. You’ll never walk alone: Modeling social behavior for multi-target tracking. In 2009 IEEE 12th International Conference on Computer Vision, pages 261–268. IEEE, 2009.
- [Rudenko et al.(2019)Rudenko, Palmieri, Herman, Kitani, Gavrila, and Arras] Andrey Rudenko, Luigi Palmieri, Michael Herman, Kris M Kitani, Dariu M Gavrila, and Kai O Arras. Human motion trajectory prediction: A survey. arXiv preprint arXiv:1905.06113, 2019.
- [Sadeghian et al.(2019)Sadeghian, Kosaraju, Sadeghian, Hirose, Rezatofighi, and Savarese] Amir Sadeghian, Vineet Kosaraju, Ali Sadeghian, Noriaki Hirose, Hamid Rezatofighi, and Silvio Savarese. Sophie: An attentive gan for predicting paths compliant to social and physical constraints. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 1349–1358, 2019.
- [Su et al.(2017)Su, Zhu, Dong, and Zhang] Hang Su, Jun Zhu, Yinpeng Dong, and Bo Zhang. Forecast the plausible paths in crowd scenes. In International Joint Conferences on Artificial Intelligence, volume 1, page 2, 2017.
- [Treuille et al.(2006)Treuille, Cooper, and Popović] Adrien Treuille, Seth Cooper, and Zoran Popović. Continuum crowds. In ACM Transactions on Graphics (TOG), volume 25, pages 1160–1168. ACM, 2006.
- [Veličković et al.(2017)Veličković, Cucurull, Casanova, Romero, Lio, and Bengio] Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. Graph attention networks. arXiv preprint arXiv:1710.10903, 2017.
- [Wang et al.(2007)Wang, Fleet, and Hertzmann] Jack M Wang, David J Fleet, and Aaron Hertzmann. Gaussian process dynamical models for human motion. IEEE Transactions on Pattern Analysis and Machine Intelligence, 30(2):283–298, 2007.
- [Wang et al.(2008)Wang, Ma, and Grimson] Xiaogang Wang, Xiaoxu Ma, and W Eric L Grimson. Unsupervised activity perception in crowded and complicated scenes using hierarchical bayesian models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 31(3):539–555, 2008.
- [Wang et al.(2019)Wang, She, and Ward] Zhengwei Wang, Qi She, and Tomas E Ward. Generative adversarial networks: A survey and taxonomy. arXiv preprint arXiv:1906.01529, 2019.
- [Xu et al.(2018)Xu, Piao, and Gao] Yanyu Xu, Zhixin Piao, and Shenghua Gao. Encoding crowd interaction with deep neural network for pedestrian trajectory prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5275–5284, 2018.
- [Zhang et al.(2019)Zhang, Ouyang, Zhang, Xue, and Zheng] Pu Zhang, Wanli Ouyang, Pengfei Zhang, Jianru Xue, and Nanning Zheng. Sr-lstm: State refinement for lstm towards pedestrian trajectory prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 12085–12094, 2019.
- [Zhou et al.(2012)Zhou, Tang, and Wang] Bolei Zhou, Xiaoou Tang, and Xiaogang Wang. Coherent filtering: Detecting coherent motions from crowd clutters. In European Conference on Computer Vision, pages 857–871. Springer, 2012.