Communication Efficient Distributed Learning for
Kernelized Contextual Bandits
Abstract
We tackle the communication efficiency challenge of learning kernelized contextual bandits in a distributed setting. Despite the recent advances in communication-efficient distributed bandit learning, existing solutions are restricted to simple models like multi-armed bandits and linear bandits, which hamper their practical utility. In this paper, instead of assuming the existence of a linear reward mapping from the features to the expected rewards, we consider non-linear reward mappings, by letting agents collaboratively search in a reproducing kernel Hilbert space (RKHS). This introduces significant challenges in communication efficiency as distributed kernel learning requires the transfer of raw data, leading to a communication cost that grows linearly w.r.t. time horizon . We addresses this issue by equipping all agents to communicate via a common Nyström embedding that gets updated adaptively as more data points are collected. We rigorously proved that our algorithm can attain sub-linear rate in both regret and communication cost.
Keywords: kernelized contextual bandit, distributed learning, communication efficiency
1 Introduction
Contextual bandit algorithms have been widely used for a variety of real-world applications, including recommender systems (Li et al., 2010a), display advertisement (Li et al., 2010b) and clinical trials (Durand et al., 2018). While most existing bandit solutions assume a centralized setting (i.e., all the data reside in and all the actions are taken by a central server), there is increasing research effort on distributed bandit learning lately (Wang et al., 2019; Dubey and Pentland, 2020; Shi and Shen, 2021; Huang et al., 2021; Li and Wang, 2022), where clients, under the coordination of a central server, collaborate to minimize the overall cumulative regret incurred over a finite time horizon . In many distributed application scenarios, communication is the main bottleneck, e.g., communication in a network of mobile devices can be slower than local computation by several orders of magnitude (Huang et al., 2013). Therefore, it is vital for distributed bandit learning algorithms to attain sub-linear rate (w.r.t. time horizon ) in both cumulative regret and communication cost.
However, prior works in this line of research are restricted to linear models (Wang et al., 2019), which could oversimplify the problem and thus leads to inferior performance in practice. In centralized setting, kernelized bandit algorithms, e.g., KernelUCB (Valko et al., 2013) and IGP-UCB (Chowdhury and Gopalan, 2017), are proposed to address this issue by modeling the unknown reward mapping as a non-parametric function lying in a reproducing kernel Hilbert space (RKHS), i.e., the expected reward is linear w.r.t. an action feature map of possibly infinite dimensions. Despite the strong modeling capability of kernel method, collaborative exploration in the RKHS gives rise to additional challenges in designing a communication efficient bandit algorithm. Specifically, unlike distributed linear bandit where the clients can simply communicate the sufficient statistics (Wang et al., 2019), where is the dimension of the input feature vector, the joint kernelized estimation of the unknown reward function requires communicating either 1) the sufficient statistics in the RKHS, where is the dimension of the RKHS that is possibly infinite, or 2) the set of input feature vectors that grows linearly w.r.t. . Neither of them is practical due to the huge communication cost.
In this paper, we propose the first communication efficient algorithm for distributed kernel bandits, which tackles the aforementioned challenge via a low-rank approximation of the empirical kernel matrix. In particular, we extended the Nyström method (Nyström, 1930) to distributed learning for kernelized contextual bandits. In this solution, all clients first project their local data to a finite RKHS spanned by a common dictionary, i.e., a small subset of the original dataset, and then they only need to communicate the embedded statistics for collaborative exploration. To ensure effective regret reduction after each communication round, as well as ensuring the dictionary remains representative for the entire distributed dataset throughout the learning process, the frequency of dictionary update and synchronization of embedded statistics is controlled by measuring the amount of new information each client has gained since last communication. We rigorously prove that the proposed algorithm incurs an communication cost, where is the maximum information gain that is known to be for kernels with exponentially decaying eigenvalues, which includes the most commonly used Gaussian kernel, while attaining the optimal cumulative regret.
2 Related Works
To balance exploration and exploitation in stochastic linear contextual bandits, LinUCB algorithm (Li et al., 2010a; Abbasi-Yadkori et al., 2011) is commonly used, which selects arm optimistically w.r.t. a constructed confidence set on the unknown linear reward function. By using kernels and Gaussian processes, studies in Srinivas et al. (2009); Valko et al. (2013); Chowdhury and Gopalan (2017) further extend UCB algorithms to non-parametric reward functions in RKHS, i.e., the feature map associated with each arm is possibly infinite.
Recent years have witnessed increasing research efforts in distributed bandit learning, i.e., multiple agents collaborate in pure exploration Hillel et al. (2013); Tao et al. (2019); Du et al. (2021), or regret minimization Shi and Shen (2021); Wang et al. (2019); Li and Wang (2022). They mainly differ in the relations of learning problems solved by the agents (i.e., homogeneous vs., heterogeneous) and the type of communication network (i.e., peer-to-peer (P2P) vs., star-shaped). Most of these works assume linear reward functions, and the clients communicate by transferring the sufficient statistics. Korda et al. Korda et al. (2016) considered a peer-to-peer (P2P) communication network and assumed that the clients form clusters, i.e., each cluster is associated with a unique bandit problem. Huang et al. Huang et al. (2021) considered a star-shaped communication network as in our paper, but their proposed phase-based elimination algorithm only works in the fixed arm set setting. The closest works to ours are (Wang et al., 2019; Dubey and Pentland, 2020; Li and Wang, 2022), which proposed event-triggered communication protocols to obtain sub-linear communication cost over time for distributed linear bandits with a time-varying arm set. In comparison, distributed kernelized contextual bandits still remain under-explored. The only existing work in this direction (Dubey et al., 2020) considered heterogeneous agents, where each agent is associated with an additional feature describing the task similarity between agents. However, they assumed a local communication setting, where the agent immediately shares the new raw data point to its neighbors after each interaction, and thus the communication cost is still linear over time.
Another closely related line of works is kernelized bandits with approximation, where Nyström method is adopted to improve computation efficiency in a centralized setting. Calandriello et al. Calandriello et al. (2019) proposed an algorithm named BKB, which uses Ridge Leverage Score sampling (RLS) to re-sample a new dictionary from the updated dataset after each interaction with the environment. A recent work by Zenati et al. Zenati et al. (2022) further improved the computation efficiency of BKB by adopting an online sampling method to update the dictionary. However, both of them updated the dictionary at each time step to ensure the dictionary remains representative w.r.t. the growing dataset, and therefore are not applicable to our problem. This is because the dataset is stored cross clients in a distributed manner, and projecting the dataset to the space spanned by the new dictionary requires communication with all clients, which is prohibitively expensive in terms of communication. Calandriello et al. Calandriello et al. (2020) also proposed a variant of BKB, named BBKB, for batched Gaussian process optimization. BBKB only needs to update the dictionary occasionally according to an adaptive schedule, and thus partially addresses the issue mentioned above. However, as BBKB works in a centralized setting, their adaptive schedule can be computed based on the whole batch of data, while in our decentralized setting, each client can only make the update decision according to the data that is locally available. Moreover, in BBKB, all the interactions are based on a fixed model estimation over the whole batch, which is mentioned in their Appendix A.4 as a result of an inherent technical difficulty. In comparison, our proposed method effectively addresses this difficulty with improved analysis, and thus allows each client to utilize newly collected data to update its model estimation on the fly.
3 Preliminaries
In this section, we first formulate the problem of distributed kernelized contextual bandits. Then, as a starting point, we propose and analyze a naive UCB-type algorithm for distributed kernelized contextual bandit problem, named DisKernelUCB. This demonstrates the challenges in designing a communication efficient algorithm for this problem, and also lays down the foundation for further improvement on communication efficiency in Section 4.
3.1 Distributed Kernelized Contextual Bandit Problem
Consider a learning system with 1) clients that are responsible for taking actions and receiving feedback from the environment, and 2) a central server that coordinates the communication among the clients. The clients cannot directly communicate with each other, but only with the central server, i.e., a star-shaped communication network. Following prior works (Wang et al., 2019; Dubey and Pentland, 2020), we assume the clients interact with the environment in a round-robin manner for a total number of rounds.
Specifically, at round , each client chooses an arm from a candidate set , and then receives the corresponding reward feedback , where the subscript indicates this is the -th interaction between the learning system and the environment, and we refer to it as time step 111The meaning of index is slightly different from prior works, e.g. DisLinUCB in (Wang et al., 2019), but this is only to simplify the use of notation and does not affect the theoretical results. Note that is a time-varying subset of that is possibly infinite, denotes the unknown reward function shared by all the clients, and denotes the noise.
Denote the sequence of indices corresponding to the interactions between client and the environment up to time as (if , then ; otherwise ) for . By definition, , i.e., the clients have equal number of interactions at the end of each round .
Kernelized Reward Function
We consider an unknown reward function that lies in a RKHS, denoted as , such that the reward can be equivalently written as
where is an unknown parameter, and is a known feature map associated with . We assume is zero-mean -sub-Gaussian conditioned on , which denotes the -algebra generated by client ’s previously pulled arms and the corresponding noise. In addition, there exists a positive definite kernel associated with , and we assume that, and for some .
Regret and Communication Cost
The goal of the learning system is to minimize the cumulative (pseudo) regret for all clients, i.e., , where . Meanwhile, the learning system also wants to keep the communication cost low, which is measured by the total number of scalars being transferred across the system up to time step .
3.2 Distributed Kernel UCB
As a starting point to studying the communication efficient algorithm in Section 4 and demonstrate the challenges in designing a communication efficient distributed kernelized contextual bandit algorithm, here we first introduce and analyze a naive algorithm where the clients collaborate on learning the exact parameters of kernel bandit, i.e., the mean and variance of estimated reward. We name this algorithm Distributed Kernel UCB, or DisKernelUCB for short, and its description is given in Algorithm 1.
Arm Selection
For each round , when client interacts with the environment, i.e., the -th interaction between the learning system and the environment where , it chooses arm based on the UCB of the mean estimator (line 5):
| (1) |
where and denote client ’s local estimated mean reward for arm and its variance, and is a carefully chosen scaling factor to balance exploration and exploitation (see Lemma 1 for proper choice).
To facilitate further discussion, for time step , we denote the sequence of time indices for the data points that have been used to update client ’s local estimate as , which include both data points collected locally and those shared by the other clients. If the clients never communicate, ; otherwise, , with recovering the centralized setting, i.e., each new data point collected from the environment immediately becomes available to all the clients in the learning system. The design matrix and reward vector for client at time step are denoted by , respectively. By applying the feature map to each row of , we obtain , where is the dimension of and is possibly infinite. Since the reward function is linear in , client can construct the Ridge regression estimator , where is the regularization coefficient. This gives us the estimated mean reward and variance in primal form for any arm , i.e., and , where and . Then using the kernel trick, we can obtain their equivalence in the dual form that only involves entries of the kernel matrix, and avoids directly working on which is possibly infinite:
where , and .
Communication Protocol
To reduce the regret in future interactions with the environment, the clients need to collaborate via communication, and a carefully designed communication protocol is essential in ensuring the communication efficiency. In prior works like DisLinUCB Wang et al. (2019), after each round of interaction with the environment, client checks whether the event is true, where denotes the time step of last global synchronization. If true, a new global synchronization is triggered, such that the server will require all clients to upload their sufficient statistics since , aggregate them to compute , and then synchronize the aggregated sufficient statistics with all clients, i.e., set .
Using kernel trick, we can obtain an equivalent event-trigger in terms of the kernel matrix,
| (2) |
where denotes the predefined threshold value. If event is true (line 7), a global synchronization is triggered (line 7-10), where the local datasets of all clients are synchronized to . We should note that the transfer of raw data is necessary for the update of the kernel matrix and reward vector in line 6 and line 10, which will be used for arm selection at line 5. This is an inherent disadvantage of kernelized estimation in distributed settings, which, as we mentioned in Section 2, is also true for the existing distributed kernelized bandit algorithm Dubey et al. (2020). Lemma 1 below shows that in order to obtain the optimal order of regret, DisKernelUCB incurs a communication cost linear in (proof given in the appendix), which is expensive for an online learning problem.
Lemma 1 (Regret and Communication Cost of DisKernelUCB)
With threshold , , we have
with probability at least , and
where is the maximum information gain after interactions (Chowdhury and Gopalan, 2017). It is problem-dependent and can be bounded for specific arm set and kernel function . For example, for linear kernel and for Gaussian kernel.
Remark 2
In the distributed linear bandit problem, to attain regret, DisLinUCB (Wang et al., 2019) requires a total number of synchronizations, and DisKernelUCB matches this result under linear kernel, as it requires synchronizations. We should note that the communication cost for each synchronization in DisLinUCB is fixed, i.e., to synchronize the sufficient statistics with all the clients, so in total . However, this is not the case for DisKernelUCB that needs to send raw data, because the communication cost for each synchronization in DisKernelUCB is not fixed, but depends on the number of unshared data points on each client. Even if the total number of synchronizations is small, DisKernelUCB could still incur in the worse case. Consider the extreme case where synchronization only happens once, but it happens near , then we still have . The time when synchronization gets triggered depends on , which is out of the control of the algorithm. Therefore, in the following section, to improve the communication efficiency of DisKernelUCB, we propose to let each client communicate embedded statistics in some small subspace during each global synchronization.
4 Approximated Distributed Kernel UCB
In this section, we propose and analyze a new algorithm that improves the communication efficiency of DisKernelUCB using the Nyström approximation, such that the clients only communicate the embedded statistics during event-triggered synchronizations. We name this algorithm Approximated Distributed Kernel UCB, or Approx-DisKernelUCB for short. Its description is given in Algorithm 2.
4.1 Algorithm
Arm selection
For each round , when client interacts with the environment, i.e., the -th interaction between the learning system and the environment where , instead of using the UCB for the exact estimator in Eq (1), client chooses arm that maximizes the UCB for the approximated estimator (line 5):
| (3) |
where and are approximated using Nyeström method, and the statistics used to compute these approximations are much more efficient to communicate as they scale with the maximum information gain instead of .
Specifically, Nyström method works by projecting some original dataset to the subspace defined by a small representative subset , which is called the dictionary. The orthogonal projection matrix is defined as
We then take eigen-decomposition of to rewrite the orthogonal projection as , and define the Nyström embedding function
which maps the data point from to .
Therefore, we can approximate the Ridge regression estimator in Section 3.2 as , where , and , and thus the approximated mean reward and variance in Eq (3) can be expressed as and , and their kernelized representation are (see appendix for detailed derivation)
where is obtained by applying to each row of , i.e., . We can see that the computation of and only requires the embedded statistics: matrix and vector , which, as we will show later, makes joint kernelized estimation among clients much more efficient in communication.
After obtaining the new data point , client immediately updates both and using the newly collected data point , i.e., by projecting to the finite dimensional RKHS spanned by (line 6). Recall that, we use to denote the sequence of indices for data collected by client , and denote by the sequence of indices for data that has been used to update client ’s model estimation . Therefore, both of them need to be updated to include time step .
Communication Protocol
With the approximated estimator, the size of message being communicated across the learning system is reduced. However, a carefully designed event-trigger is still required to minimize the total number of global synchronizations up to time . Since the clients can no longer evaluate the exact kernel matrices in Eq (2), we instead use the event-trigger in Eq (4), which can be computed using the approximated variance from last global synchronization as,
| (4) |
Similar to Algorithm 1, if Eq (4) is true, global synchronization is triggered, where both the dictionary and the embedded statistics get updated. During synchronization, each client first samples a subset from (line 8) using Ridge Leverage Score sampling (RLS) (Calandriello et al., 2019, 2020), which is given in Algorithm 3, and then sends to the server. The server aggregates the received local subsets to construct a new dictionary , where , and then sends it back to all clients (line 9). Finally, the clients use this updated dictionary to re-compute the embedded statistics of their local data, and then synchronize it with all other clients via the server (line 10-12).
Intuitively, in Algorithm 2, the clients first agree upon a common dictionary that serves as a good representation of the whole dataset at the current time , and then project their local data to the subspace spanned by this dictionary before communication, in order to avoid directly sending the raw data as in Algorithm 1. Then using the event-trigger, each client monitors the amount of new knowledge it has gained through interactions with the environment from last synchronization. When there is a sufficient amount of new knowledge, it will inform all the other clients to perform a synchronization. As we will show in the following section, the size of scales linearly w.r.t. the maximum information gain , and therefore it improves both the local computation efficiency on each client, and the communication efficiency during the global synchronization.
4.2 Theoretical Analysis
Denote the sequence of time steps when global synchronization is performed, i.e., the event in Eq (4) is true, as , where denotes the total number of global synchronizations. Note that in Algorithm 2, the dictionary is only updated during global synchronization, e.g., at time , the dictionary is sampled from the whole dataset in a distributed manner, and remains fixed for all the interactions happened at . Moreover, at time , all the clients synchronize their embedded statistics, so that .
Since Algorithm 2 enables local update on each client, for time step , new data points are collected and added into , such that . This decreases the approximation accuracy of , as new data points may not be well approximated by . For example, in extreme cases, the new data could be orthogonal to the dictionary. To formally analyze the accuracy of the dictionary, we adopt the definition of -accuracy from Calandriello et al. (2017). Denote by a diagonal matrix, with its -th diagonal entry equal to if and otherwise. Then if
we say the dictionary is -accurate w.r.t. dataset .
As shown below, the accuracy of the dictionary for Nyström approximation is essential as it affects the width of the confidence ellipsoid, and thus affects the cumulative regret. Intuitively, in order to ensure its accuracy throughout the learning process, we need to 1) make sure the RLS procedure in line 8 of Algorithm 2 that happens at each global synchronization produces a representative set of data samples, and 2) monitor the extent to which the dictionary obtained in previous global synchronization has degraded over time, and when necessary, trigger a new global synchronization to update it. Compared with prior work that freezes the model in-between consecutive communications Calandriello et al. (2020), the analysis of -accuracy for Approx-DisKernelUCB is unique to our paper and the result is presented below.
Lemma 3
With , for some , and threshold , Algorithm 2 guarantees that the dictionary is accurate with constant , and its size for all .
Based on Lemma 3, we can construct the following confidence ellipsoid for unknown parameter .
Lemma 4 (Confidence Ellipsoid of Approximated Estimator)
Under the condition that , for some , and threshold , with probability at least , we have that
Using Lemma 4, we obtain the regret and communication cost upper bound of Approx-DisKernelUCB, which is given in Theorem 5 below.
Theorem 5 (Regret and Communication Cost of Approx-DisKernelUCB)
Here we provide a proof sketch for Theorem 5, and the complete proof can be found in appendix.
Proof [Proof Sketch] Similar to the analysis of DisKernelUCB in Section 3.2 and DisLinUCB from (Wang et al., 2019), the cumulative regret incurred by Approx-DisKernelUCB can be decomposed in terms of ‘good’ and ‘bad’ epochs, and bounded separately. Here an epoch refers to the time period in-between two consecutive global synchronizations, e.g., the -th epoch refers to . Now consider an imaginary centralized agent that has immediate access to each data point in the learning system, and denote by for the matrix constructed by this centralized agent. We call the -th epoch a good epoch if , otherwise it is a bad epoch. Note that , where the last equality is due to the matrix determinant lemma, and the last inequality is by the definition of the maximum information gain in Lemma 1. Then based on the pigeonhole principle, there can be at most bad epochs.
By combining Lemma 14 and Lemma 4, we can bound the cumulative regret incurred during all good epochs, i.e., , which matches the optimal regret attained by the KernelUCB algorithm in centralized setting. Our analysis deviates from that of DisKernelUCB in the bad epochs, because of the difference in the event-trigger. Previously, the event-trigger of DisKernelUCB directly bounds the cumulative regret each client incurs during a bad epoch, i.e., . However, the event trigger of Approx-DisKernelUCB only bounds part of it, i.e., , which leads to that is slightly worse than that of DisKernelUCB, i.e., a factor in place of the factor. By setting , we have . Note that, to make sure is still well-defined, we can set .
For communication cost analysis, we bound the total number of epochs by upper bounding the total number of summations like , over the time horizon . Using Lemma 14, our event-trigger in Eq (4) provides a lower bound . Then in order to apply the pigeonhole principle, we continue to upper bound the summation over all epochs, by deriving a uniform bound for the ratio in terms of the communication threshold on each client. This leads to the following upper bound about the total number of epochs , and with , we have , which completes the proof.
Remark 6
Compared with DisKernelUCB’s communication cost, Approx-DisKernelUCB removes the linear dependence on , but introduces an additional dependence due to the communication of the embedded statistics. In situations where , DisKernelUCB is preferable. As mentioned in Lemma 1, the value of , which affects how much the data can be compressed, depends on the specific arm set of the problem and the kernel function of the choice. By Mercer’s Theorem, one can represent the kernel using its eigenvalues, and characterizes how fast its eigenvalues decay. Vakili et al. (Vakili et al., 2021) showed that for kernels whose eigenvalues decay exponentially, i.e., , for some , . In this case, Approx-DisKernelUCB is far more efficient than DisKernelUCB. This includes Gaussian kernel, which is widely used for GPs and SVMs. For kernels that have polynomially decaying eigenvalues, i.e., , for some , . Then as long as , Approx-DisKernelUCB still enjoys reduced communication cost.
5 Experiments
In order to evaluate Approx-DisKernelUCB’s effectiveness in reducing communication cost, we performed extensive empirical evaluations on both synthetic and real-world datasets, and the results (averaged over 3 runs) are reported in Figure 1, 2 and 3, respectively. We included DisKernelUCB, DisLinUCB (Wang et al., 2019), OneKernelUCB, and NKernelUCB (Chowdhury and Gopalan, 2017) as baselines, where One-KernelUCB learns a shared bandit model across all clients’ aggregated data where data aggregation happens immediately after each new data point becomes available, and N-KernelUCB learns a separated bandit model for each client with no communication. For all the kernelized algorithms, we used the Gaussian kernel . We did a grid search of for kernelized algorithms, and set for DisLinUCB and DisKernelUCB, for Approx-DisKernelUCB. For all algorithms, instead of using their theoretically derived exploration coefficient , we followed the convention Li et al. (2010a); Zhou et al. (2020) to use grid search for in . Due to space limit, here we only present the experiment results and discussions. Details about the experiment setup are presented in appendix.


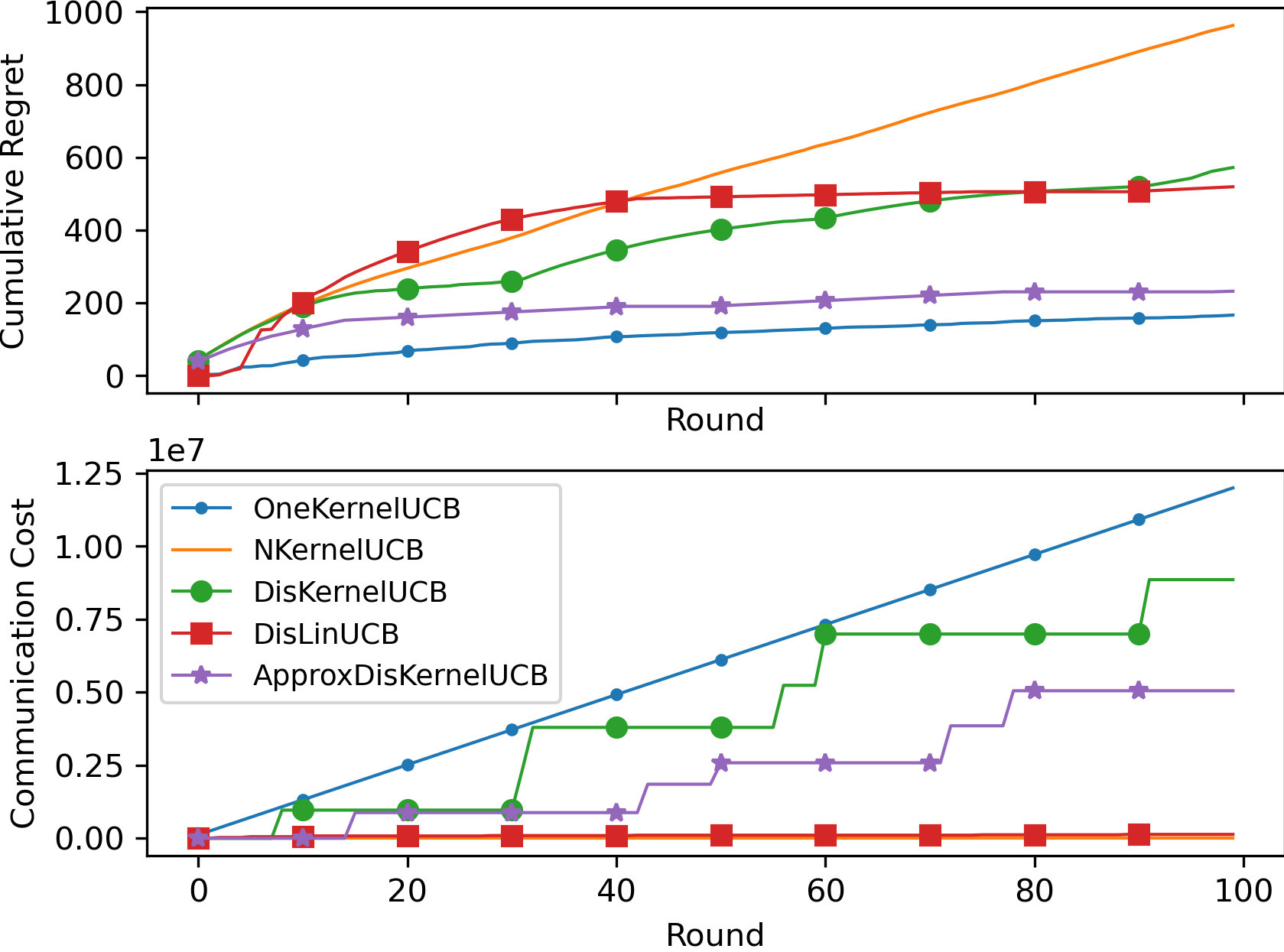




When examining the experiment results presented in Figure 1, 2 and 3, we can first look at the cumulative regret and communication cost of OneKernelUCB and NKernelUCB, which correspond to the two extreme cases where the clients communicate in every time step to learn a shared model, and each client learns its own model independently with no communication, respectively. OneKernelUCB achieves the smallest cumulative regret in all experiments, while also incurring the highest communication cost, i.e., . This demonstrates the need of efficient data aggregation across clients for reducing regret. Second, we can observe that DisKernelUCB incurs the second highest communication cost in all experiments due to the transfer of raw data, as we have discussed in Remark 2, which makes it prohibitively expensive for distributed setting. On the other extreme, we can see that DisLinUCB incurs very small communication cost thanks to its closed-form solution, but fails to capture the complicated reward mappings in most of these datasets, e.g. in Figure 1(a), 2(b) and 3(a), it leads to even worse regret than NKernelUCB that learns a kernelized bandit model independently for each client. In comparison, the proposed Approx-DisKernelUCB algorithm enjoys the best of both worlds in most cases, i.e., it can take advantage of the superior modeling power of kernels to reduce regret, while only requiring a relatively low communication cost for clients to collaborate. On all the datasets, Approx-DisKernelUCB achieved comparable regret with DisKernelUCB that maintains exact kernelized estimators, and sometimes even getting very close to OneKernelUCB, e.g., in Figure 1(b) and 2(a), but its communication cost is only slightly higher than that of DisLinUCB.
6 Conclusion
In this paper, we proposed the first communication efficient algorithm for distributed kernel bandits using Nyström approximation. Clients in the learning system project their local data to a finite RKHS spanned by a shared dictionary, and then communicate the embedded statistics for collaborative exploration. To ensure communication efficiency, the frequency of dictionary update and synchronization of embedded statistics are controlled by an event-trigger. The algorithm is proved to incur communication cost, while attaining the optimal cumulative regret.
We should note that the total number of synchronizations required by Approx-DisKernelUCB is , which is worse than DisKernelUCB. An important future direction of this work is to investigate whether this part can be further improved. It is also interesting to extend the proposed algorithm to P2P setting, at the absence of a central server to coordinate the update of the shared dictionary and the exchange of embedded statistics. Due to the delay in propagating messages, it may be beneficial to utilize possible local structures in the network of clients, and approximate each block of the kernel matrix separately (Si et al., 2014), i.e., each block corresponds to a group of clients, instead of directly approximating the complete matrix.
7 Acknowledgement
This work is supported by NSF grants IIS-2128019, IIS-1838615, IIS-1553568, IIS-2107304, CMMI-1653435, AFOSR grant and ONR grant 1006977.
References
- Abbasi-Yadkori et al. (2011) Yasin Abbasi-Yadkori, Dávid Pál, and Csaba Szepesvári. Improved algorithms for linear stochastic bandits. Advances in neural information processing systems, 24:2312–2320, 2011.
- Ban et al. (2021) Yikun Ban, Yuchen Yan, Arindam Banerjee, and Jingrui He. Ee-net: Exploitation-exploration neural networks in contextual bandits. arXiv preprint arXiv:2110.03177, 2021.
- Calandriello et al. (2017) Daniele Calandriello, Alessandro Lazaric, and Michal Valko. Second-order kernel online convex optimization with adaptive sketching. In International Conference on Machine Learning, pages 645–653. PMLR, 2017.
- Calandriello et al. (2019) Daniele Calandriello, Luigi Carratino, Alessandro Lazaric, Michal Valko, and Lorenzo Rosasco. Gaussian process optimization with adaptive sketching: Scalable and no regret. In Conference on Learning Theory, pages 533–557. PMLR, 2019.
- Calandriello et al. (2020) Daniele Calandriello, Luigi Carratino, Alessandro Lazaric, Michal Valko, and Lorenzo Rosasco. Near-linear time gaussian process optimization with adaptive batching and resparsification. In International Conference on Machine Learning, pages 1295–1305. PMLR, 2020.
- Chowdhury and Gopalan (2017) Sayak Ray Chowdhury and Aditya Gopalan. On kernelized multi-armed bandits. In International Conference on Machine Learning, pages 844–853. PMLR, 2017.
- Du et al. (2021) Yihan Du, Wei Chen, Yuko Yuroki, and Longbo Huang. Collaborative pure exploration in kernel bandit. arXiv preprint arXiv:2110.15771, 2021.
- Dua and Graff (2017) Dheeru Dua and Casey Graff. UCI machine learning repository, 2017. URL http://archive.ics.uci.edu/ml.
- Dubey and Pentland (2020) Abhimanyu Dubey and AlexSandy’ Pentland. Differentially-private federated linear bandits. Advances in Neural Information Processing Systems, 33, 2020.
- Dubey et al. (2020) Abhimanyu Dubey et al. Kernel methods for cooperative multi-agent contextual bandits. In International Conference on Machine Learning, pages 2740–2750. PMLR, 2020.
- Durand et al. (2018) Audrey Durand, Charis Achilleos, Demetris Iacovides, Katerina Strati, Georgios D Mitsis, and Joelle Pineau. Contextual bandits for adapting treatment in a mouse model of de novo carcinogenesis. In Machine learning for healthcare conference, pages 67–82. PMLR, 2018.
- Filippi et al. (2010) Sarah Filippi, Olivier Cappe, Aurélien Garivier, and Csaba Szepesvári. Parametric bandits: The generalized linear case. In NIPS, volume 23, pages 586–594, 2010.
- Harper and Konstan (2015) F Maxwell Harper and Joseph A Konstan. The movielens datasets: History and context. Acm transactions on interactive intelligent systems (tiis), 5(4):1–19, 2015.
- He et al. (2022) Jiafan He, Tianhao Wang, Yifei Min, and Quanquan Gu. A simple and provably efficient algorithm for asynchronous federated contextual linear bandits. arXiv preprint arXiv:2207.03106, 2022.
- Hillel et al. (2013) Eshcar Hillel, Zohar S Karnin, Tomer Koren, Ronny Lempel, and Oren Somekh. Distributed exploration in multi-armed bandits. Advances in Neural Information Processing Systems, 26, 2013.
- Huang et al. (2013) Junxian Huang, Feng Qian, Yihua Guo, Yuanyuan Zhou, Qiang Xu, Z Morley Mao, Subhabrata Sen, and Oliver Spatscheck. An in-depth study of lte: Effect of network protocol and application behavior on performance. ACM SIGCOMM Computer Communication Review, 43(4):363–374, 2013.
- Huang et al. (2021) Ruiquan Huang, Weiqiang Wu, Jing Yang, and Cong Shen. Federated linear contextual bandits. Advances in Neural Information Processing Systems, 34, 2021.
- Korda et al. (2016) Nathan Korda, Balazs Szorenyi, and Shuai Li. Distributed clustering of linear bandits in peer to peer networks. In International conference on machine learning, pages 1301–1309. PMLR, 2016.
- Li and Wang (2022) Chuanhao Li and Hongning Wang. Asynchronous upper confidence bound algorithms for federated linear bandits. In International Conference on Artificial Intelligence and Statistics, pages 6529–6553. PMLR, 2022.
- Li et al. (2010a) Lihong Li, Wei Chu, John Langford, and Robert E Schapire. A contextual-bandit approach to personalized news article recommendation. In Proceedings of the 19th international conference on World wide web, pages 661–670, 2010a.
- Li et al. (2010b) Wei Li, Xuerui Wang, Ruofei Zhang, Ying Cui, Jianchang Mao, and Rong Jin. Exploitation and exploration in a performance based contextual advertising system. In Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining, pages 27–36, 2010b.
- Nyström (1930) Evert J Nyström. Über die praktische auflösung von integralgleichungen mit anwendungen auf randwertaufgaben. Acta Mathematica, 54:185–204, 1930.
- Scarlett et al. (2017) Jonathan Scarlett, Ilija Bogunovic, and Volkan Cevher. Lower bounds on regret for noisy gaussian process bandit optimization. In Conference on Learning Theory, pages 1723–1742. PMLR, 2017.
- Shi and Shen (2021) Chengshuai Shi and Cong Shen. Federated multi-armed bandits. In Proceedings of the 35th AAAI Conference on Artificial Intelligence (AAAI), 2021.
- Si et al. (2014) Si Si, Cho-Jui Hsieh, and Inderjit Dhillon. Memory efficient kernel approximation. In International Conference on Machine Learning, pages 701–709. PMLR, 2014.
- Srinivas et al. (2009) Niranjan Srinivas, Andreas Krause, Sham M Kakade, and Matthias Seeger. Gaussian process optimization in the bandit setting: No regret and experimental design. arXiv preprint arXiv:0912.3995, 2009.
- Tao et al. (2019) Chao Tao, Qin Zhang, and Yuan Zhou. Collaborative learning with limited interaction: Tight bounds for distributed exploration in multi-armed bandits. In 2019 IEEE 60th Annual Symposium on Foundations of Computer Science (FOCS), pages 126–146. IEEE, 2019.
- Vakili et al. (2021) Sattar Vakili, Kia Khezeli, and Victor Picheny. On information gain and regret bounds in gaussian process bandits. In International Conference on Artificial Intelligence and Statistics, pages 82–90. PMLR, 2021.
- Valko et al. (2013) Michal Valko, Nathaniel Korda, Rémi Munos, Ilias Flaounas, and Nelo Cristianini. Finite-time analysis of kernelised contextual bandits. arXiv preprint arXiv:1309.6869, 2013.
- Wang et al. (2019) Yuanhao Wang, Jiachen Hu, Xiaoyu Chen, and Liwei Wang. Distributed bandit learning: Near-optimal regret with efficient communication. In International Conference on Learning Representations, 2019.
- Zenati et al. (2022) Houssam Zenati, Alberto Bietti, Eustache Diemert, Julien Mairal, Matthieu Martin, and Pierre Gaillard. Efficient kernel ucb for contextual bandits. arXiv preprint arXiv:2202.05638, 2022.
- Zhou et al. (2020) Dongruo Zhou, Lihong Li, and Quanquan Gu. Neural contextual bandits with ucb-based exploration. In International Conference on Machine Learning, pages 11492–11502. PMLR, 2020.
A Technical Lemmas
Lemma 7 (Lemma 12 of (Abbasi-Yadkori et al., 2011))
Let , and be positive semi-definite matrices with finite dimension, such that . Then, we have that:
Lemma 8 (Extension of Lemma 7 to kernel matrix)
Define positive definite matrices and , where and is possibly infinite. Then, we have that:
where and .
Proof [Proof of Lemma 8] Similar to the proof of Lemma 12 of (Abbasi-Yadkori et al., 2011), we start from the simple case when , where . Using Cauchy-Schwartz inequality, we have
and thus,
so we have
for any . Then using the kernel trick, e.g., see the derivation of Eq (27) in Zenati et al. (2022), we have
which finishes the proof of this simple case. Now consider the general case where . Let’s define and the corresponding kernel matrix , and note that . Then we can apply the result for the simple case on each term in the product above, which gives us
which finishes the proof.
Lemma 9 (Eq (26) and Eq (27) of Zenati et al. (2022))
Let be a sequence in , a positive definite matrix, where is possibly infinite, and define . Then we have that
where is the kernel matrix corresponding to as defined in Lemma 8.
Lemma 10 (Lemma 4 of (Calandriello et al., 2020))
For , we have for any
B Confidence Ellipsoid for DisKernelUCB
In this section, we construct the confidence ellipsoid for DisKernelUCB as shown in Lemma 11.
Lemma 11 (Confidence Ellipsoid for DisKernelUCB)
Let . With probability at least , for all , we have
The analysis is rooted in (Zenati et al., 2022) for kernelized contextual bandit, but with non-trivial extensions: we adopted the stopping time argument from (Abbasi-Yadkori et al., 2011) to remove a logarithmic factor in (this improvement is hinted in Section 3.3 of (Zenati et al., 2022) as well); and this stopping time argument is based on a special ‘batched filtration’ that is different for each client, which is required to address the dependencies due to the event-triggered distributed communication. This problem also exists in prior works of distributed linear bandit, but was not addressed rigorously (see Lemma H.1. of (Wang et al., 2019)).
Recall that the Ridge regression estimator
and thus, we have
| (5) |
where the first inequality is due to the triangle inequality, and the second is due to the property of Rayleigh quotient, i.e., .
Difference from standard argument
Note that the second term may seem similar to the ones appear in the self-normalized bound in previous works of linear and kernelized bandits (Abbasi-Yadkori et al., 2011; Chowdhury and Gopalan, 2017; Zenati et al., 2022). However, a main difference is that , i.e., the sequence of indices for the data points used to update client , is constructed using the event-trigger as defined in Eq (2) . The event-trigger is data-dependent, and thus it is a delayed and permuted version of the original sequence . It is delayed in the sense that the length unless is the global synchronization step. It is permuted in the sense that every client receives the data in a different order, i.e., before the synchronization, each client first updates using its local new data, and then receives data from other clients at the synchronization. This prevents us from directly applying Lemma 3.1 of (Zenati et al., 2022), and requires a careful construction of the filtration, as shown in the following paragraph.
Construction of filtration
For some client at time step , the sequence of time indices in is arranged in the order that client receives the corresponding data points, which includes both data added during local update in each client, and data received from the server during global synchronization. The former adds one data point at a time, while the latter adds a batch of data points, which, as we will see, break the assumption commonly made in standard self-normalized bound (Abbasi-Yadkori et al., 2011; Chowdhury and Gopalan, 2017; Zenati et al., 2022). Specifically, we denote , for , as the -th element in this sequence, i.e., is the -th data point received by client . Then we denote as the sequence of ’s that marks the end of each batch (a singel data point added by local update is also considered a batch). We can see that if the -th element is in the middle of a batch, i.e., , it has dependency all the way to the ’s element, since this index can only be determined until some client triggers a global synchronization at time step .
Denote by the -algebra generated by the sequence of data points up to the -th element in . As we mentioned, because of the dependency of the index on the future data points, for some -th element that is inside a batch, i.e., , is not -measurable and is not -measurable, which violate the assumption made in standard self-normalized bound (Abbasi-Yadkori et al., 2011; Chowdhury and Gopalan, 2017; Zenati et al., 2022). However, they become measurable if we condition on . In addition, recall that in Section 3.1 we assume is zero-mean -sub-Gaussian conditioned on , which is the -algebra generated by the sequence of local data collected by client . We can see that as , is zero-mean -sub-Gaussian conditioned on . Basically, our assumption of -sub-Gaussianity conditioned on local sequence instead of global sequence of data points, prevents the situation where the noise depends on data points that have not been communicated to the current client yet, i.e., they are not included in .
With our ‘batched filtration’ for each client , we have everything we need to establish a time-uniform self-normalized bound that resembles Lemma 3.1 of (Zenati et al., 2022), but with improved logarithmic factor using the stopping time argument from (Abbasi-Yadkori et al., 2011). Then we can take a union bound over clients to obtain the uniform bound over all clients and time steps.
Super-martingale & self-normalized bound
First, we need the following lemmas adopted from (Zenati et al., 2022) to our ‘batched filtration’.
Lemma 12
Let be arbitrary and consider for any , , we have
is a -super-martingale, and . Let be a stopping time w.r.t. the filtration . Then is almost surely well-defined and .
Proof [Proof of Lemma 12] To show that is a super-martinagle, we denote
with , and as we have showed earlier, is -sub-Gaussian conditioned on . Therefore, . Moreover, and are -measurable. Then we have
which shows is a super-martinagle, with .
Then using the same argument as Lemma 8 of (Abbasi-Yadkori et al., 2011), we have that is almost surely well-defined, and .
Lemma 13
Let be a stopping time w.r.t. the filtration . Then for , we have
Proof of Lemma 11
Now using the stopping time argument as in (Abbasi-Yadkori et al., 2011), and a union bound over clients, we can bound the second term in Eq (5). First, define the bad event
and , which is a stopping time. Moreover, . Then using Lemma 13, we have
Note that is the sequence of indices in when client gets updated. Therefore, the result above is equivalent to
for all , with probability at least . Then by taking a union bound over clients, we finish the proof.
C Proof of Lemma 1: Regret and Communication Cost of DisKernelUCB
Based on Lemma 11 and the arm selection rule in Eq (1), we have
and thus , for all , with probability at least . Then following similar steps as DisLinUCB of (Wang et al., 2019), we can obtain the regret and communication cost upper bound of DisKernelUCB.
C.1 Regret Upper Bound
We call the time period in-between two consecutive global synchronizations as an epoch, i.e., the -th epoch refers to , where and denotes the total number of global synchronizations. Now consider an imaginary centralized agent that has immediate access to each data point in the learning system, and denote by and for the covariance matrix and kernel matrix constructed by this centralized agent. Then similar to (Wang et al., 2019), we call the -th epoch a good epoch if
otherwise it is a bad epoch. Note that by definition of , i.e., the maximum information gain. Since , and due to the pigeonhole principle, there can be at most bad epochs.
If the instantaneous regret is incurred during a good epoch, we have
where the second inequality is due to Lemma 8, and the last inequality is due to the definition of good epoch, i.e., . Define . Then using standard arguments, the cumulative regret incurred in all good epochs can be bounded by,
where the third inequality is due to Cauchy-Schwartz and Lemma 9, and the forth is due to the definition of maximum information gain .
Then we look at the regret incurred during bad epochs. Consider some bad epoch , and the cumulative regret incurred during this epoch can be bounded by
where the last inequality is due to our event-trigger in Eq (2). Since there can be at most bad epochs, the cumulative regret incurred in all bad epochs
Combining cumulative regret incurred during both good and bad epochs, we have
C.2 Communication Upper Bound
For some , there can be at most epochs with length larger than . Based on our event-trigger design, we know that for any epoch , where is the client who triggers the global synchronization at time step . Then if the length of certain epoch is smaller than , i.e., , we have . Since , the total number of such epochs is upper bounded by . Combining the two terms, the total number of epochs can be bounded by,
where the LHS can be minimized using the AM-GM inequality, i.e., . To obtain the optimal order of regret, we set , so that . And the total number of epochs . However, we should note that as DisKernelUCB communicates all the unshared raw data at each global synchronization, the total communication cost mainly depends on when the last global synchronization happens. Since the sequence of candidate sets , which controls the growth of determinant, is an arbitrary subset of , the time of last global synchronization could happen at the last time step . Therefore, in such a worst case.
D Derivation of the Approximated Mean and Variance in Section 4
For simplicity, subscript is omitted in this section. The approximated Ridge regression estimator for dataset is formulated as
where denotes the sequence of time indices for data in the original dataset, denotes the time indices for data in the dictionary, and denotes the orthogonal projection matrix defined by . Then by taking derivative and setting it to zero, we have , and thus , where and .
Hence, the approximated mean reward and variance for some arm are
To obtain their kernelized representation, we rewrite
where . Solving this equation, we get . Note that , since projection matrix is idempotent. Moreover, we have , and . Therefore, we can rewrite the approximated mean for some arm as
To derive the approximated variance, we start from the fact that , so
Then we have
By rearranging terms, we have
E Proof of Lemma 3
In the following, we analyze the -accuracy of the dictionary for all .
At the time steps when global synchronization happens, i.e., for , is sampled from using approximated variance . In this case, the accuracy of the dictionary only depends on the RLS procedure, and Calandriello et al. (Calandriello et al., 2020) have already showed that the following guarantee on the accuracy and size of dictionary holds .
Lemma 14 (Lemma 2 of (Calandriello et al., 2020))
Under the condition that , for some , with probability at least , we have that the dictionary is -accurate w.r.t. , and . Moreover, the size of dictionary , where denotes the effective dimension of the problem, and it is known that (Chowdhury and Gopalan, 2017).
Lemma 14 guarantees that for all , the dictionary has a constant accuracy, i.e., . In addition, since the dictionary is fixed for , its size .
Then for time steps , due to the local update, the accuracy of the dictionary will degrade. However, thanks to our event-trigger in Eq (4), the extent of such degradation can be controlled, i.e., a new dictionary update will be triggered before the previous dictionary becomes completely irrelevant. This is shown in Lemma 15 below.
Lemma 15
Under the condition that is -accurate w.r.t. , , is -accurate w.r.t. .
Proof [Proof of Lemma 15] Similar to (Calandriello et al., 2019), we can rewrite the -accuracy condition of w.r.t. for as
where . Notice that the second term in the norm has weight because the dictionary is fixed after . With triangle inequality, now it suffices to bound
We should note that the first term corresponds to the approximation accuracy of w.r.t. the dataset . And under the condition that it is -accurate w.r.t. , we have . The second term measures the difference between compared with , which is unique to our work. We can bound it as follows.
We can further bound the term using the threshold of the event-trigger in Eq (4). For any ,
where the first inequality is due to Lemma 10, the second is due to Lemma 14, and the third is due to the event-trigger in Eq (4).
Putting everything together, we have that if is -accurate w.r.t. , then it is -accurate w.r.t. dataset , which finishes the proof.
F Proof of Lemma 4
To prove Lemma 4, we need the following lemma.
Lemma 16
We have that
with probability at least .
Proof [Proof of Lemma 16] Recall that the approximated kernel Ridge regression estimator for is defined as
where is the orthogonal projection matrix for the Nyström approximation, and . Then our goal is to bound
Bounding the first term
To bound the first term, we begin with rewriting
and by substituting this into the first term, we have
where the first inequality is due to Cauchy Schwartz, and the last inequality is because .
Bounding the second term
By applying Cauchy-Schwartz inequality to the second term, we have
Note that and , so we have
Then using the self-normalized bound derived for Lemma 13, the term can be bounded by
for , with probability at least .
Combining everything finishes the proof.
Now we are ready to prove Lemma 4 by further bounding the term .
Proof [Proof of Lemma 4] Recall that denotes the diagonal matrix, whose -th diagonal entry equals to , where if and otherwise (note that for , we set , so ). Therefore, , , as the dictionary is fixed after . We can rewrite , where . Then by definition of the spectral norm , and the properties of the projection matrix , we have
| (6) |
Moreover, due to Lemma 15, we know is -accurate w.r.t. for , where , so we have by the property of -accuracy (Proposition 10 of Calandriello et al. (2019)). Therefore, by substituting this back to Eq (6), we have
which finishes the proof.
G Proof of Theorem 5: Regret and Communication Cost of Approx-DisKernelUCB
G.1 Regret Analysis
Consider some time step , where . Due to Lemma 4, i.e., the confidence ellipsoid for approximated estimator, and the fact that , we have
and thus , where
Note that, different from Appendix C, the term now depends on the threshold and accuracy constant , as a result of the approximation error. As we will see in the following paragraphs, their values need to be set properly in order to bound .
We begin the regret analysis of Approx-DisKernelUCB with the same decomposition of good and bad epochs as in Appendix C.1, i.e., we call the -th epoch a good epoch if , otherwise it is a bad epoch. Moreover, due to the pigeon-hold principle, there can be at most bad epochs.
As we will show in the following paragraphs, using Lemma 14, we can obtain a similar bound for the cumulative regret in good epochs as that in Appendix C.1, but with additional dependence on and . The proof mainly differs in the bad epochs, where we need to use the event-trigger in Eq (4) to bound the cumulative regret in each bad epoch. Compared with Eq (2), Eq (4) does not contain the number of local updates on each client since last synchronization., and as mentioned in Section 4.2, this introduces a factor in the regret bound for bad epochs in place of the term in Appendix C.1.
Cumulative Regret in Good Epochs
Let’s first consider some time step in a good epoch , i.e., , and we have the following bound on the instantaneous regret
where the second inequality is because the (approximated) variance is non-decreasing, the third inequality is due to Lemma 14, the forth is due to Lemma 8, and the last is because in a good epoch, we have for .
Therefore, the cumulative regret incurred in all good epochs, denoted by , is upper bounded by
where .
Cumulative Regret in Bad Epochs
The cumulative regret incurred in this bad epoch is
where the third inequality is due to the Cauchy-Schwartz inequality, the forth is due to our event-trigger in Eq (4), the fifth is due to our assumption that clients interact with the environment in a round-robin manner, the sixth is due to the Cauchy-Schwartz inequality again, and the last is due to the fact that there can be at most bad epochs.
Combining cumulative regret incurred during both good and bad epochs, we have
G.2 Communication Cost Analysis
Consider some epoch . We know that for the client who triggers the global synchronization, we have
Then by summing over epochs, we have
Now we need to bound the ratio for .
Note that for the client who triggers the global synchronization, we have , i.e., one time step before it triggers the synchronization at time . Due to the fact that the (approximated) posterior variance cannot exceed , we have . For the other clients, we have . Summing them together, we have
for the -th epoch. By substituting this back, we have
Therefore,
and thus the total number of epochs .
By setting , we have
because . Moreover, to ensure , we need to set the constant . Therefore,
and the total number of global synchronizations . Since for each global synchronization, the communication cost is , we have
H Experiment Setup
Synthetic dataset
We simulated the distributed bandit setting defined in Section 3.1, with ( interactions in total). In each round , each client (denote ) selects an arm from candidate set , where is uniformly sampled from a unit ball, with . Then the corresponding reward is generated using one of the following reward functions:
where the parameter is uniformly sampled from a unit ball.
UCI Datasets
To evaluate Approx-DisKernelUCB’s performance in a more challenging and practical scenario, we performed experiments using real-world datasets: MagicTelescope, Mushroom and Shuttle from the UCI Machine Learning Repository (Dua and Graff, 2017). To convert them to contextual bandit problems, we pre-processed these datasets following the steps in (Filippi et al., 2010). In particular, we partitioned the dataset in to clusters using k-means, and used the centroid of each cluster as the context vector for the arm and the averaged response variable as mean reward (the response variable is binarized by associating one class as , and all the others as ). Then we simulated the distributed bandit learning problem in Section 3.1 with , and ( interactions in total).
MovieLens and Yelp dataset
Yelp dataset, which is released by the Yelp dataset challenge, consists of 4.7 million rating entries for 157 thousand restaurants by 1.18 million users. MovieLens is a dataset consisting of 25 million ratings between 160 thousand users and 60 thousand movies (Harper and Konstan, 2015). Following the pre-processing steps in (Ban et al., 2021), we built the rating matrix by choosing the top 2000 users and top 10000 restaurants/movies and used singular-value decomposition (SVD) to extract a 10-dimension feature vector for each user and restaurant/movie. We treated rating greater than as positive. We simulated the distributed bandit learning problem in Section 3.1 with and ( interactions in total). In each time step, the candidate set (with ) is constructed by sampling an arm with reward and nineteen arms with reward from the arm pool, and the concatenation of user and restaurant/movie feature vector is used as the context vector for the arm (thus ).
I Lower Bound for Distributed Kernelized Contextual Bandits
First, we need the following two lemmas
Lemma 17 (Theorem 1 of Valko et al. (2013))
There exists a constant , such that for any instance of kernelized bandit with , the expected cumulative regret for KernelUCB algorithm is upper bounded by , where the maximum information gain for Squared Exponential kernels.
Lemma 18 (Theorem 2 of Scarlett et al. (2017))
There always exists a set of hard-to-learn instances of kernelized bandit with , such that for any algorithm, for a uniformly random instance in the set, the expected cumulative regret for Squared Exponential kernels, with some constant .
Then we follow a similar procedure as the proof for Theorem 2 of Wang et al. (2019) and Theorem 5.3 of He et al. (2022), to prove the following lower bound results for distributed kernelized bandit with Squared Exponential kernels.
Theorem 19
For any distributed kernelized bandit algorithm with expected communication cost less than , there exists a kernelized bandit instance with Squared Exponential kernel, and , such that the expected cumulative regret for this algorithm is at least .
Proof [Proof of Theorem 19] Here we consider kernelized bandit with Squared Exponential kernels. The proof relies on the construction of a auxiliary algorithm, denoted by AuxAlg, based on the original distributed kernelized bandit algorithm, denoted by DisKernelAlg, as shown below. For each agent , AuxAlg performs DisKernelAlg, until any communication happens between client and the server, in which case, AuxAlg switches to the single-agent optimal algorithm, i.e., the KernelUCB algorithm that attains the rate in Lemma 17. Therefore, AuxAlg is a single-agent bandit algorithm, and the lower bound in Lemma 18 applies: the cumulative regret that AuxAlg incurs for some agent is lower bounded by
and by summing over all clients, we have
For each client , denote the probability that client will communicate with the server as , and . Note that before the communication, the cumulative regret incurred by AuxAlg is the same as DisKernelAlg, and after the communication happens, the regret incurred by AuxAlg is the same as KernelUCB, whose upper bound is given in Lemma 17. Therefore, the cumulative regret that AuxAlg incurs for client can be upper bounded by
and by summing over clients, we have
Combining the upper and lower bounds for , we have
Therefore, for any DisKernelAlg with number of communications , we have