Common Information Belief based Dynamic Programs for Stochastic Zero-sum Games with Competing Teams

Zero-sum games between two individual players with asymmetric information have been extensively studied. In [10, 11, 12, 13, 14, 15], stochastic zero-sum games with varying degrees of generality were considered and dynamic programming characterizations of the value of the game were provided. Various properties of the value functions (such as continuity) were also established and for some specialized information structures, these works also characterize a min-max strategy. Linear programs for computing the values and strategies in certain games were proposed in [16, 17]; and methods based on heuristic search value iteration (HSVI) [18] to compute the value of some games were proposed in [19, 20]. Zero-sum extensive form games in which a team of players competes against an adversary have been studied in [21, 22, 23]. Structured Nash equilibria in general games (i.e. not necessarily zero-sum) were studied in [24, 25, 26] under some assumptions on the system dynamics and players’ information structure. A combination of reinforcement learning and search was used in [27] to solve two-player zero-sum games. While this approach has very strong empirical performance, a better analytical understanding of it is needed. Our work is closely related to [28, 15] and builds on their results. Our novel contributions in this paper over past works are summarized below.

(i) In this paper, we study a general class of stochastic zero-sum games between two competing teams of players. Our general model captures a variety of information structures including many previously considered stochastic team [5, 7, 1] and zero-sum game models [15, 19, 20] as well as game models that have not been studied before. Our results provide a unified framework for analyzing a wide class of game models that satisfy some minimal assumptions. (ii) For our general model, we adapt the techniques in [15] to provide bounds on the upper (min-max) and lower (max-min) values of the game. These bounds provide us with fundamental limits on the performance achievable by either team. Furthermore, if the upper and lower values of the game are identical (i.e., if the game has a value), our bounds coincide with the value of the game. Our bounds are obtained using two dynamic programs (DPs) based on a sufficient statistic known as the common information belief (CIB). (iii) We also identify a subclass of game models in which only one of the teams (say the minimizing team) controls the evolution of the CIB. In these cases, we show that one of our CIB based dynamic programs can be used to find the min-max value as well as a min-max strategy¹¹1Note that this characterization of a min-max strategy is not present in [15]. A similar result for a very specific model with limited applicability exists in [28]. Our result is substantially more general than that in [28].. (iv) Our result reveals that the structure of the CIB based min-max strategy is similar to the structure of team optimal strategies. Such structural results have been successfully used in prior works [7, 27] to design efficient strategies for significantly challenging team problems. (v) Lastly, we discuss an approximate dynamic programming approach along with key structural properties for computing the values (and the strategy when applicable) and illustrate our results with the help of an example.

Random variables are denoted by upper case letters, their realizations by the corresponding lower case letters. In general, subscripts are used as time index while superscripts are used to index decision-making agents. For time indices $t_{1}\leq t_{2}$, ${{X}}_{t_{1}:t_{2}}$ is the short hand notation for the variables $({{X}}_{t_{1}},{{X}}_{t_{1}+1},...,{{X}}_{t_{2}})$. Similarly, ${{X}}^{1:2}$ is the short hand notation for the collection of variables $({{X}}^{1},{{X}}^{2})$. Operators ${\mathbb{P}}(\cdot)$ and ${\mathbb{E}}[\cdot]$ denote the probability of an event, and the expectation of a random variable respectively. For random variables/vectors $X$ and $Y$, ${\mathbb{P}}(\cdot|{{Y}}=y)$, ${\mathbb{E}}[{{X}}|{{Y}}=y]$ and ${\mathbb{P}}({{X}}=x\mid{{Y}}=y)$ are denoted by ${\mathbb{P}}(\cdot|y)$, ${\mathbb{E}}[{{X}}|y]$ and ${\mathbb{P}}(x\mid y)$, respectively. For a strategy $g$, we use ${\mathbb{P}}^{g}(\cdot)$ (resp. ${\mathbb{E}}^{g}[\cdot]$) to indicate that the probability (resp. expectation) depends on the choice of $g$. For any finite set $\mathcal{A}$, $\Delta\mathcal{A}$ denotes the probability simplex over the set $\mathcal{A}$. For any two sets $\mathcal{A}$ and $\mathcal{B}$, $\mathcal{F}(\mathcal{A},\mathcal{B})$ denotes the set of all functions from $\mathcal{A}$ to $\mathcal{B}$. We define rand to be mechanism that given (i) a finite set $\mathcal{A}$, (ii) a distribution $d$ over $\mathcal{A}$ and a random variable $K$ uniformly distributed over the interval $(0,1]$, produces a random variable $X\in\mathcal{A}$ with distribution $d$, i.e.,

At time $t$, Player $j$ in Team $i$ has access to a subset of all observations and actions generated so far. Let $I^{i,j}_{t}$ denote the collection of variables (i.e. observations and actions) available to Player $j$ in team $i$ at time $t$. Then ${{I}}_{t}^{i,j}\subseteq\cup_{i,j}\{{{Y}}^{i,j}_{1:t},{{U}}^{i,j}_{1:t-1}\}$. The set of all possible realizations of ${{I}}_{t}^{i,j}$ is denoted by $\mathcal{I}^{i,j}_{t}$. Examples of such information structures include $I_{t}^{i,j}=\{Y_{1:t}^{i,j},U_{1:t-1}^{i,j}\}$ which corresponds to the information structure in Dec-POMDPs [5] and $I_{t}^{i,j}=\{Y_{1:t}^{i,j},Y^{1:2}_{1:t-d},U_{1:t-1}^{1:2}\}$ wherein each player’s actions are seen by all the players and their observations become public after a delay of $d$ time steps.

Information ${{I}}_{t}^{i,j}$ can be decomposed into common and private information, i.e. ${{I}}_{t}^{i,j}={{C}}_{t}\cup{{P}}_{t}^{i,j}$; common information ${{C}}_{t}$ is the set of variables known to all players at time $t$. The private information $P_{t}^{i,j}$ for Player $j$ in Team $i$ is defined as ${{I}}_{t}^{i,j}\setminus C_{t}$. Let

We will refer to $P_{t}^{i}$ as Team $i$’s private information. Let $\mathcal{C}_{t}$ be the set of all possible realizations of common information at time $t$, $\mathcal{P}_{t}^{i,j}$ be the set of all possible realizations of private information for Player $j$ in Team $i$ at time $t$ and $\mathcal{P}_{t}^{i}$ be the set of all possible realizations of $P^{i}_{t}$. We make the following assumption on the evolution of common and private information. This is similar to Assumption 1 of [24, 15].

As noted in [4, 15], a number of information structures satisfy the above assumption. Our analysis applies to any information structure that satisfies Assumption 1 including, among others, Dec-POMDPs and the delayed sharing information structure discussed above.

Players can use any information available to them to select their actions and we allow behavioral strategies for all players. Thus, at time $t$, Player $j$ in Team $i$ chooses a distribution $\delta{{U}}_{t}^{i,j}$ over its action space using a control law $g_{t}^{i,j}:\mathcal{I}_{t}^{i,j}\rightarrow\Delta\mathcal{U}_{t}^{i,j}$, i.e., $\delta{{U}}_{t}^{i,j}=g_{t}^{i,j}({{I}}_{t}^{i,j})=g_{t}^{i,j}({{C}}_{t},{{P}}_{t}^{i,j}).$ The distrubtion $\delta U^{i,j}_{t}$ is then used to randomly generate the control action $U^{i,j}_{t}$ as follows. We assume that player $j$ of Team $i$ has access to i.i.d. random variables ${{K}}^{i,j}_{1:T}$ that are uniformly distributed over the interval $(0,1]$. These uniformly distributed variables are independent of each other and of the primitive random variables. The action $U^{i,j}_{t}$ is generated using $K^{i,j}_{t}$ and the randomization mechanism described in (1), i.e.,

The collection of control laws used by the players in Team $i$ at time $t$ is denoted by $g_{t}^{i}\doteq(g_{t}^{i,1},\dots,g_{t}^{i,N_{i}})$ and is referred to as the control law of Team $i$ at time $t$. Let the set of all possible control laws for Team $i$ at time $t$ be denoted by $\mathcal{G}_{t}^{i}$. The collection of control laws ${g}^{i}\doteq(g_{1}^{i},\dots,g_{T}^{i})$ is referred to as the control strategy of Team $i$, and the pair of control strategies $({g}^{1},{g}^{2})$ is referred to as a strategy profile. Let the set of all possible control strategies for Team $i$ be $\mathcal{G}^{i}$.

The total expected cost associated with a strategy profile $({g}^{1},{g}^{2})$ is

where $c_{t}:{\mathcal{X}}_{t}\times{\mathcal{U}}_{t}^{1}\times{\mathcal{U}}_{t}^{2}\rightarrow{\mathbb{R}}$ is the cost function at time $t$. Team 1 wants to minimize the total expected cost, while Team 2 wants to maximize it. We refer to this zero-sum game between Team 1 and Team 2 as Game $\mathscr{G}$.

A key objective of this work is to characterize the upper and lower values $S^{u}(\mathscr{G})$ and $S^{l}(\mathscr{G})$ of Game $\mathscr{G}$. To this end, we will define an expanded virtual game $\mathscr{G}_{e}$. This virtual game will be used to obtain bounds on the upper and lower values of the original game $\mathscr{G}$. These bounds happen to be tight when the upper and lower values of game $\mathscr{G}$ are equal. For a sub-class of information structures, we will show that the expanded virtual game $\mathscr{G}_{e}$ can be used to obtain optimal strategies for one of the teams.

We note that if the upper and lower values of game $\mathscr{G}$ are the same, then any pair of optimal strategies $(g^{1*},g^{2*})$ forms a Team Nash Equilibrium⁴⁴4When players in a team randomize independently, Team Nash equilirbia may not exist in general [32]., i.e., for every ${g}^{1}\in\mathcal{G}^{1}$ and ${g}^{2}\in\mathcal{G}^{2}$,

In this case, $J(g^{1*},g^{2*})$ is the value of the game, i.e. $J({g}^{1*},{g}^{2*})=S^{l}(\mathscr{G})=S^{u}(\mathscr{G})=S(\mathscr{G}).$ Conversely, if a Team Nash Equilibrium exists, then the upper and lower values are the same [33].

Consider virtual player $i$ associated with Team $i$, $i=1,2$. At each time $t$ and for each $j=1,\dots,N_{i}$, virtual player $i$ selects a function $\Gamma^{i,j}_{t}$ that maps private information $P^{i,j}_{t}$ to a distribution $\delta{{U}}_{t}^{i,j}$ over the space $\mathcal{U}_{t}^{i,j}$. Thus, $\delta U_{t}^{i,j}=\Gamma_{t}^{i,j}(P_{t}^{i,j})$. The set of all such mappings is denoted by $\mathcal{B}_{t}^{i,j}\doteq\mathcal{F}({\mathcal{P}}_{t}^{i,j},\Delta{\mathcal{U}}_{t}^{i,j})$. We refer to the tuple $\Gamma_{t}^{i}\doteq(\Gamma_{t}^{i,1},\dots,\Gamma_{t}^{i,N_{i}})$ of such mappings as virtual player $i$’s prescription at time $t$. The set of all possible prescriptions for virtual player $i$ at time $t$ is denoted by $\mathcal{B}_{t}^{i}\doteq\mathcal{B}_{t}^{i,1}\times\dots\times\mathcal{B}_{t}^{i,N_{i}}$. Once virtual player $i$ selects its prescription, the action $U^{i,j}_{t}$ is randomly generated according to the distribution $\Gamma_{t}^{i,j}({{P}}_{t}^{i,j})$. More precisely,

where the random variable $K^{i,j}_{t}$ and the mechanism rand are the same as in equation (6).

The virtual players in game $\mathscr{G}_{e}$ have access to the common information ${{C}}_{t}$ and all the past prescriptions of both players, i.e., $\Gamma_{1:t-1}^{1:2}$. Virtual player $i$ selects its prescription at time $t$ using a control law $\tilde{\chi}_{t}^{i}$, i.e., $\Gamma_{t}^{i}=\tilde{\chi}_{t}^{i}({{C}}_{t},\Gamma_{1:t-1}^{1:2}).$ Let $\tilde{\mathcal{H}}_{t}^{i}$ be the set of all such control laws at time $t$ and $\tilde{\mathcal{H}}^{i}\doteq\tilde{\mathcal{H}}_{1}^{i}\times\dots\times\tilde{\mathcal{H}}_{T}^{i}$ be the set of all control strategies for virtual player $i$. The total cost for a strategy profile $(\tilde{{\chi}}^{1},\tilde{{\chi}}^{2})$ is

The upper and lower values in $\mathscr{G}_{e}$ are defined as

The following theorem establishes the relationship between the upper and lower values of the expanded game $\mathscr{G}_{e}$ and the original game $\mathscr{G}$. This result is analogous to Theorem 1 from [15].

We consider a particular example of game $\mathscr{H}$ described above. In this example, there are two entities ($l$ and $r$) that can potentially be attacked and at any given time, exactly one of the entities is vulnerable. Player 1 of Team 1 knows which of the two entities is vulnerable whereas all the other players do not have this information. Player 2 of Team 1 can choose to defend one of the entities. The attacker in Team 2 can either launch a blanket attack on both entities or launch a targeted attack on one of the entities. When the attacker launches a blanket attack, the damage incurred by the system is minimal if Player 2 in Team 1 happens to be defending the vulnerable entity and the damage is substantial otherwise. When the attacker launches a targeted attack on the vulnerable entity, the damage is substantial irrespective of the defender’s position. But if the attacker targets the invulnerable entity, the attacker becomes passive and cannot attack for some time. Thus, launching a targeted attack involves high risk for the attacker. The state of the attacker (active or passive) and all the players’ actions are public information. The system state $X_{t}$ thus has two components, the hidden state ($l$ or $r$) and the state of the attacker ($a$ or $p$). For convenience, we will denote the states $(l,a)$ and $(r,a)$ with 0 and 1 respectively.

The only role of Player 1 in Team 1 in this game is to signal the hidden state using two available actions $\alpha$ and $\beta$. The main challenge is that both the defender and the attacker can see Player 1’s actions. Player 1 needs to signal the hidden state to some extent so that its teammate’s defense is effective under blanket attacks. However, if too much information is revealed, the attacker can exploit it to launch a targeted attack and cause significant damage. In this example, the key is to design a strategy that can balance between these two contrasting goals of signaling and secrecy. A precise description of this model is provided in Appendix J.

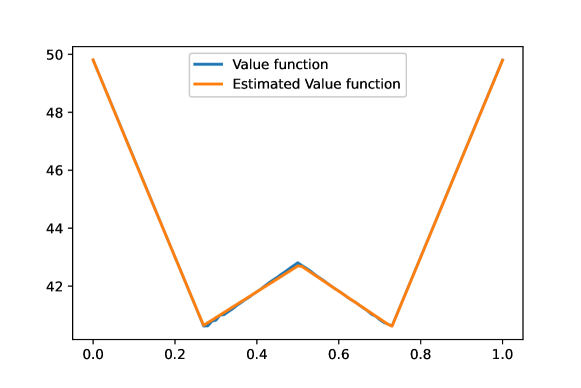
In order to solve this problem, we used the approximate DP approach discussed in Appendix H. The value function $V_{1}^{u}(\cdot)$ thus obtained is shown in Figure 1(a). The tension between signaling and secrecy can be seen in the shape of the value function in Figure 1(a). When the CIB $\pi_{1}(0)=0.5$, the value function is concave in its neighborhood and decreases as we move away from 0.5. This indicates that in these belief states, revealing the hidden state to some extent is preferable. However, as the belief goes further away from 0.5, the value function starts increasing at some point. This indicates that the adversary has too much information and is using it to inflict damage upon the system. Figure 1(b) depicts Player 1’s prescriptions leading to non-trivial signaling patterns at various belief states. Notice that the distributions $\gamma_{1}^{1,1}(0)$ and $\gamma_{1}^{1,1}(1)$ for hidden states 0 and 1 are quite distinct when $\pi_{1}(0)=0.5$ (indicating significant signaling) and are nearly identical when $\pi_{1}(0)=0.72$ (indicating negligible signaling). A more detailed discussion on our experimental results can be found in Appendix J.