Collective excitations of the Chern-insulator states in commensurate double moiré superlattices of twisted bilayer graphene on hexagonal boron nitride
Abstract
We study the collective excitation modes of the Chern insulator states in magic-angle twisted bilayer graphene aligned with hexagonal boron nitride (TBG/BN) at odd integer fillings () of the flat bands. For the commensurate double moiré superlattices in TBG/BN at three twist angles () between BN and graphene, self-consistent Hartree-Fock calculations show that the electron-electron interaction and the broken symmetry lead to the Chern-insulator ground states with valley-spin flavor polarized HF bands at odd . In the active-band approximation, the HF bands in the same flavor of TBG/BN are much more separated than those of the pristine TBG with TBG/BN having a larger intra-flavor band gap so that the energies of the lowest intra-flavor exciton modes of TBG/BN computed within the time-dependent HF method are much higher than those of TBG and reach about 20 meV, and the exciton wavefunctions of TBG/BN become less localized than those of TBG. The inter-flavor valley-wave modes in TBG/BN have excitation energies higher than 2.5 meV which is also much larger than that of TBG, while the spin-wave modes all have zero excitation gap. In contrast to TBG with particle-hole symmetric excitation modes for positive and negative , the excitation spectrums and gaps of TBG/BN at positive are rather different from those at negative . The quantitative behavior of the excitation spectrum of TBG/BN also varies with . Full HF calculations demonstrate that more HF bands besides the two central bands can have rather large contributions from the single-particle flat-band states, then the lowest exciton modes that determine the optical properties of the Chern insulator states in TBG/BN are generally the ones between the remote and flat-like bands, while the valley-wave modes have similar energies as those in the active-band approximation.
I Introduction





Flat bands with vanishing band widths and well separated from other remote bands occur around the Fermi level in magic-angle twisted bilayer graphene (TBG)Bistritzer and MacDonald (2011); Suárez Morell et al. (2010); Lopes dos Santos et al. (2012); Fang and Kaxiras (2016); Carr et al. (2017); Tarnopolsky et al. (2019); Ren et al. (2021), and the experimental realization of such TBG intrigued great interest in exploring various electronic, transport and optical properties associated with the flat bandsCao et al. (2018a, b); Kim et al. (2017); Lu et al. (2019); Xie et al. (2019); Kerelsky et al. (2019); Jiang et al. (2019); Choi et al. (2019); Yankowitz et al. (2019); Uri et al. (2020); Nuckolls et al. (2020); Wong et al. (2020); Zondiner et al. (2020); Saito et al. (2020); Stepanov et al. (2020); Luo et al. (2020); Rozen et al. (2021); Hesp et al. (2021); Ma et al. (2022); Carr et al. (2020); Andrei and MacDonald (2020); Andrei et al. (2021); Liu and Dai (2021a). The emergence of correlated insulator states at integer filling of the flat bands in TBG and the superconductivity in the vicinity of these insulating states have been observed and theoretically comprehendedCao et al. (2018a, b); Kim et al. (2017); Lu et al. (2019); Xie et al. (2019); Kerelsky et al. (2019); Jiang et al. (2019); Choi et al. (2019); Yankowitz et al. (2019); Uri et al. (2020); Nuckolls et al. (2020); Wong et al. (2020); Zondiner et al. (2020); Saito et al. (2020); Stepanov et al. (2020); Rozen et al. (2021); Po et al. (2018); Koshino et al. (2018); Kang and Vafek (2018); Isobe et al. (2018); Liu et al. (2018); Kang and Vafek (2019); Zhang and Senthil (2019); Chittari et al. (2019); Zhang et al. (2019); Repellin et al. (2020); Xie and MacDonald (2020); Bultinck et al. (2020a, b); Zhang et al. (2020); Kang and Vafek (2020); Wu and Das Sarma (2020); Liu and Dai (2021b); Hejazi et al. (2021); Liu et al. (2021); Da Liao et al. (2021); Lin and Ni (2020); Bernevig et al. (2021a); Lian et al. (2021); Bernevig et al. (2021b); Kwan et al. (2021). There are eight single-particle flat bands taking into account the spin and valley degrees in TBG, then the electron filling of the flat bands per moiré supercell relative to charge neutrality point (CNP) is in the range of -4 to 4. At odd , the ground states are Chern insulators with spontaneously broken symmetry in the valley and spin degrees due to the electron-electron (e-e) interaction Bultinck et al. (2020b); Zhang et al. (2019); Repellin et al. (2020); Wu and Das Sarma (2020); Xie and MacDonald (2020); Liu and Dai (2021b); Hejazi et al. (2021); Da Liao et al. (2021); Lin and Ni (2020); Kwan et al. (2021). The alignment of TBG with BN breaks the symmetry in the relaxed atomic structure and the single-particle HamiltonianLin and Ni (2020); Cea et al. (2020); Lin et al. (2021); Shi et al. (2021); Mao and Senthil (2021); Shin et al. (2021); Long et al. (2022) and thus enhances the energy gaps of such Chern insulator statesZhang et al. (2019); Bultinck et al. (2020b); Wu and Das Sarma (2020); Lin and Ni (2020). In particular, the quantum anomalous Hall effect associated with their finite Chern numbers has been experimentally realized in TBG aligned with BN (TBG/BN)Serlin et al. (2020); Tschirhart et al. (2021). For such insulating correlated states, low-energy collective excitation states may appear within the gap due to the Coulomb interaction between the particle and hole states. In experiments, the observed Pomeranchuk effect from the measured electron compressibility in TBG at extremely low temperatures implies the presence of the low-energy collective excitations for the correlated insulator statesRozen et al. (2021). The optical excitations in the infrared regime have also been observed in twisted graphene systems around the integer fillings of the flat bandsHesp et al. (2021); Ma et al. (2022); Luo et al. (2020).
For the pristine TBG or the TBG with a sublattice potential differenceWu and Das Sarma (2020); Lian et al. (2021); Bernevig et al. (2021b); Kumar et al. (2021), theoretical analysis or Hartree-Fock (HF) calculations indeed demonstrated the occurrence of the low-energy collective excitation modes of inter-flavor spin wave, valley wave and intra-flavor exciton at odd . The spin-wave excitation states are Goldstone modes with a zero excitation gapWu and Das Sarma (2020); Lian et al. (2021); Bernevig et al. (2021b); Kumar et al. (2021). The valley-wave modes have an extremely small excitation gap for the pristine TBGKumar et al. (2021), and a sublattice potential difference increases their excitation energiesWu and Das Sarma (2020). For the pristine TBG, low energy exciton states of a few meV also appearKumar et al. (2021). We note that all the previous calculations focused on one odd of -3 or 3 and adopted the active-band approximation that considers only the excitations between flat bandsWu and Das Sarma (2020); Kumar et al. (2021). A full HF calculation of the excitation states at all odd may provide more excitation modes and can influence the excitation energy spectrums. For TBG/BN with enhanced Chern insulator states at odd , previous studies have established that BN induces not only the sublattice potential difference in graphene but also spatially varying effective moiré potentials, and the structural deformation due to the interlayer vdW interaction between BN and graphene also strongly breaks the C2z symmetry of the single-particle HamiltonianLin and Ni (2020); Lin et al. (2021). Moreover, the correlated band structure of TBG/BN changes with the twist angle () between TBG and BNLin and Ni (2020); Cea et al. (2020). Therefore, it is desirable to explore systematically the collective excitation modes at all odd for all the possible commensurate configurations of TBG/BN.
Here, we demonstrate that the energies of the lowest intra-flavor exciton modes of TBG/BN are much higher than those of TBG and reach about 20 meV, the inter-flavor valley-wave modes have excitation energies higher than 2.5 meV which is also much larger than that of TBG, while the spin-wave modes all have zero excitation gap. The excitation spectrums and gaps of TBG/BN at positive are rather different from those at negative , which contrasts with the particle-hole symmetric excitation modes for positive and negative in TBG. Full HF calculations indicate that the lowest exciton modes that determine the optical properties of the Chern insulator states in TBG/BN are generally the ones between the remote and flat-like bands, while the valley-wave modes have similar energies as those in the active-band approximation. Moreover, the quantitative behavior of the excitation spectrum of TBG/BN also varies with .
II HF bands and excitations in the active-band approximation
For TBG with the magic twist angle of aligned with BN, we consider the commensurate supercells of TBG/BN at three twist angles between BN and its adjacent graphene layer of , , , as seen in Fig. 1(a), and their structural parameters are detailed in the Supplemental Material (SM). At the origin of the TBG/BN supercell, both the local stackings between the graphene layers and between graphene and BN are taken to be the AA stacking. The moiré superlattices of TBG/BN and the pristine TBG are fully relaxed based on the continuum elastic theory to obtain their stable atomic structuresLin and Ni (2020); Lin et al. (2021).
For the fully relaxed TBG/BN, an effective single-particle tight-binding model () of the graphene layers can be built taking into account the relaxation effect and the full moiré Hamiltonian induced by BNLin and Ni (2020); Lin et al. (2021). The parameters in and its expression in the planewave-like basis are detailed in the SM. The single-particle flat bands around the Fermi level () in TBG are well separated by the effective moiré potentials induced by BN, as shown in Fig. 1(b). The C2z symmetry in the pristine TBG is broken in TBG/BN. In a rigid TBG/BN, the effective Hamiltonian induced by BN lacks the C2z symmetry as reflected in the in-plane inversion asymmetric terms of the moiré potentials. The structural relaxation of TBG/BN also leads to the in-plane atomic deformation without the C2z symmetry. The strength of the effective moiré potential by BN varies with , giving rising to -dependent flat bands, as shown in Fig. S1(a) of the SM. The widths of the flat bands are much larger at = and than those at , while the valence and conduction bands are more separated at . The system at also has a much smaller energy difference between the flat and remote bands due to the wider flat bands and the larger gap at .
Upon inclusion of the e-e interaction, TBG/BN and TBG become Chern insulators at odd . We employ the self-consistent HF (SCHF) methodXie and MacDonald (2020); Lin and Ni (2020) to obtain the mean-field ground states of the systems at odd , then the time dependent HF (TDHF) approachWu and Das Sarma (2020); Kumar et al. (2021) is adopted to explore the collective excitations of TBG/BN and TBG based on the SCHF ground states as detailed in the Appendix. We first perform the HF calculations in the active-band approximation, and the computationally expensive full HF calculations are then done for further exploration of the collective excitations as presented in the next section. For the active-space approximation, only the two central HF bands of each flavor are updated during the SCHF iterations and they are only expanded in the basis of the single-particle flat bands, and the lower remote bands are kept frozen but still contribute to the mean-field Hartree and Fock operators of the active-band Hamiltonian. In addition, the HF operators contributed by the isolated fixed and rotated graphene layers with at CNP are subtracted from the HF Hamiltonian to avoid double-counting of the e-e interaction.
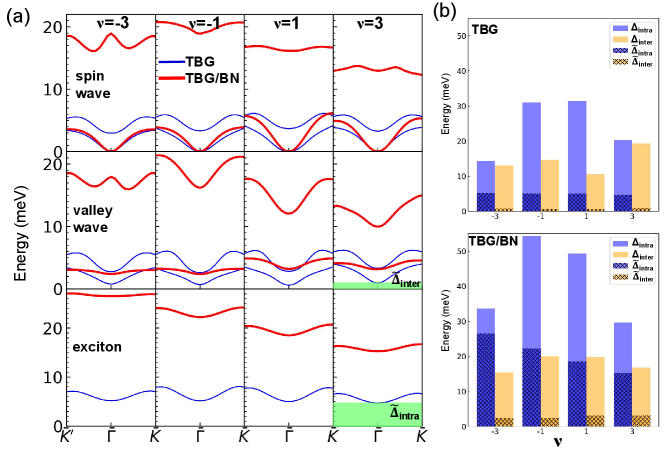
The HF band structures of the Chern-insulator ground states at odd are exhibited in Fig. 1(c) for TBG/BN with and the pristine TBG. In TBG, sublattice polarization within one layer spontaneously occurs at odd . In the valley, the lower band has a Chern number of and the higher band has a Chern number of . The Chern numbers of the bands in the valley are just opposite to those in the valley. At each odd , the ground states of TBG and TBG/BN are Chern insulators with the total Chern numbers of . For each , three of the four flavors have the same quantitative band properties, such as the intra-flavor band gaps and the band widths, and one flavor has different properties, which is taken to be the valley-spin flavor, as shown in Fig. 1(c). At a flavor with the two bands both filled or empty, the two bands of TBG/BN are well separated, while those of the pristine TBG have close energies around the point. For TBG/BN at , the two empty bands in the same flavor are separated by 17 meV. When one flat band is filled and the other one is empty in a flavor, the intra-flavor band gap () between them in TBG/BN is much larger than that in the pristine TBG. Compared to , the inter-favor band gap () between the highest valence band in one flavor and the lowest conduction band in another flavor generally has a smaller value, so the global band gap is just .
The HF bands at and appear to be the particle-hole symmetric correspondences of the bands at and , respectively, while the band gaps can still be quite different between positive and negative , as shown in Figs. 1(c) and 2(b). The of TBG/BN influences the quantitative properties of the HF bands, as seen in Fig. S1(b). At , at is much larger than those at other . The at is the largest for . In addition, when two bands in a flavor are both filled or empty, they have a much larger energy difference at .
We employ the TDHF method to obtain the collective excitation modes based on the HF ground states at odd . We consider the collective modes with the momentum expressed asWu and Das Sarma (2020); Kumar et al. (2021)
| (1) |
where is the HF ground state, represents an excitation process from the occupied band with index to the empty band with the index , and the operator annihilates an electron in the HF band states. A collective mode is characterized by its set of excitation processes, which are labeled in Fig. 1(c) for the inter-flavor spin-wave, valley-wave, and intra-flavor exciton modes.
For the pristine TBG, all the excitation spectrums exhibit approximate particle-hole symmetry and are almost the same for all odd , as shown in Fig. 2(a). The spin-wave mode has a zero excitation gap, the valley-wave mode has an extremely small gap of about 0.5 meV, and the exciton mode has a gap of about 5 meV. Such finite gaps of the valley-wave and exciton modes are slightly larger than those predicted for the TBG described by the Bistritzer-MacDonald modelKumar et al. (2021), which can be attributed to the in-plane structural deformation in the relaxed TBG. For the pristine TBG, both the spin-wave and valley-wave excitations have two low-energy collective modes in the gap at each . In contrast, the excitation spectrum of TBG/BN at positive are rather different from those at negative , and those with the same sign of are quite similar. The lowest spin-wave mode at positive has a larger spectrum width than that at negative but they all have zero excitation gap. For the valley-wave, all the excitation energies are higher than 2.5 meV, which is much larger than that of the pristine TBG. This is consistent with Ref. [Wu and Das Sarma, 2020] for TBG with a sublattice potential difference. The valley wave has a higher excitation gap () at positive . For both the spin wave and the valley wave, the lowest modes become much more apart than those in TBG. The lowest exciton modes of TBG/BN have much higher energies than those of TBG. The exciton gap () decreases with from -3 to 3, with the gap still reaching about 16 meV at .
In comparison to the HF band gaps, the of the valley wave modes are much smaller than the for both TBG and TBG/BN, while the of the exciton modes of TBG/BN reaches about half of the , which is a significant contrast to the much smaller for TBG, as shown in Fig 2(b). For the exciton modes, the two-body exciton wavefunction as a function of the electron () and hole () positions can be calculated as
| (2) |
where and are the HF conduction and valence band states corresponding to the exciton excitation. Figure 3 exhibits the wavefunction of the lowest exciton mode at with at the origin of a supercell where the bilayer graphene is locally AA-stacked. The particle and hole are strongly bound at all the odd for the pristine TBG with the particle localized around the origin. The spatial map of the exciton wavefunctions in TBG/BN spread a much larger range with the particle mainly distributed around the nonzero smallest superlattice vectors. Unlike TBG, TBG/BN at has a quite different exciton wavefunction from that at with the wavefunction at less spatially localized.
The quantitative behavior of the excitation spectrum varies with , as seen in Fig. 4. The systems with the negative of tend to have a smaller valley-wave excitation energy, while their exciton energies are much higher than those at positive for the positive . For the valley-wave modes, the at the two positive have similar values for the negative , while they differ by about 1 meV for the positive . The exciton energy at is higher than that at for the negative but has similar values for the positive .
III Full HF bands and excitations
Since the remote bands are frozen in the active-band approximation of the SCHF calculations, the excitation processes between the remote and flat bands have been ignored, and the quantitative properties of the flat bands can be modified when the remote bands are allowed to be updated in the SCHF calculations. Full SCHF calculations have also been performed to obtain the full HF bands of TBG/BN, and the excitation spectrums are computed by considering the excitation processes between the five highest valence HF bands and the five lowest conduction HF bands. It is noted that the convergent spin-wave spectrum requires the possible excitation processes between all the HF bands, which are beyond our calculation capability, so only the inter-flavor valley-wave and the intra-flavor exciton modes are considered based on the full SCHF ground states.
To compare the active-band approximation with the full SCHF description of the central HF bands, the projection of each HF band state on the single-particle flat bands is computed as with representing the two single-particle flat-band states of flavor and a HF band state. We find that at a k-point rather away from the point, only two low-energy HF band states of a flavor are mainly contributed by the single-particle flat-band states, as shown in Fig. 5 for TBG/BN with . These HF bands are termed as flat-like bands to distinguish them from the single-particle flat bands. In contrast, several other HF bands near the point can have substantial contribution from the flat-band states, especially for the flavor with one flat-like band occupied and the other flat-like band empty. In particular, the flat-band contribution becomes very small for some low-energy HF states at . When the flat-like bands of a flavor are both occupied or empty, they are generally well separated from the remote bands, and the intra-flavor gap around between the remote and flat-like bands is denoted by . The flat-like bands become entangled with the remote bands when lies between them, and the intra-flavor gap between these flat-like bands is denoted by . Similar to the active-band approximation, the inter-flavor gap is also between the flat-like bands. For the full HF bands, the global gap among all flavors is just . has large and similar values for all the negative and positive , which is similar to the active-band approximation. However, the systems at positive have much smaller and than those at negative , which indicates the strong breaking of the particle-hole symmetry for the full HF band structures. At each , there are also three flavors with the same quantitative band properties, as seen in Fig. 5.
We consider the inter-flavor valley-wave excitation modes corresponding to , and the intra-flavor exciton modes corresponding to and , based on the full HF ground states. The excitation spectrum and the excitation gaps of these modes are displayed in Fig. 6 for TBG/BN with . The valley-wave excitation gap becomes slightly higher than that obtained from the active-band approximation and reaches about 3 meV, but is still rather small compared with . The excitation gaps of the exciton modes between the flat-like bands have similar values as those from the active-band approximation and are below half of . In contrast, The gaps () of the exciton modes between the flat-like bands and the remote bands are just slightly smaller than . This indicates that the exciton modes between the flat-like bands and the remote bands are composed of weak-bound particle-hole pairs, while strong binding of the particle-hole pairs occurs in the exciton modes between the flat-like bands. At , is higher than and even the gap . Only at , has a lower value than . In addition, the excitation energies of the lowest modes for the exciton modes between the flat-like bands and the remote bands are much more dispersive as a function of than those of the valley-wave modes and the exciton modes between the flat-like bands, as shown in Fig. 6(b).
The optical properties of the Chern insulators are determined by the intra-flavor exciton modes, and the optical conductivity within the TDHF method is given byKumar et al. (2021)
| (3) | |||||
where is the frequency of the incident light, is the energy of an exciton mode labeled by , is the state vector of the exciton mode, is the element of the current density operator between the empty and occupied states of the excitation process , is a small energy for broadening of the excitation energy, is the area of the moire supercell, and is the number of k-points. So at , the contribution of the exciton mode to is proportional to . We find that the of the lowest exciton mode between the remote and flat-like bands at reaches 0.102 eV Å2 and is even much larger than that of the lowest exciton mode between the flat-like bands, which is just 0.022 eV Å2. Therefore, the lowest-frequency optical properties associated with the intra-flavor excitations are mainly determined by the exciton modes between the remote bands and the flat-like bands at , while they are mainly contributed by the exciton mode between the flat-like bands at .
At the other two of and , from the full SCHF calculations can become larger than , but are all much smaller than , as seen in Figs. S2 and S3 of the SM. For , the system at becomes metallic with the highest occupied band of the flavor slightly overlapping with the lowest empty bands of other flavors. The systems at generally have smaller than those at other . For the exciton modes, the excitation gaps are also much smaller than , and the systems with have the largest , as seen in Fig. S3 of SM. In addition, can even become larger than the indirect gap for some systems with of and . The for the valley-wave modes all have similar values of about 3 meV.
IV Summary and Conclusions
In the commensurate supercells of TBG/BN, the single-particle flat bands around are gaped due to the broken C2z symmetry, and the SCHF ground states at odd are the Chern insulators with flavor-polarized HF bands. In the active-band approximation, the two active HF bands in the same flavor are well separated in TBG/BN when they are both filled or empty, and the intra-flavor gap in TBG/BN is much larger than that in the pristine TBG. The energy spectrums of the collective excitation modes for the Chern insulator states are obtained with the TDHF method. The spin-wave modes in both TBG/BN and TBG have a zero excitation gap, while the gaps of the valley-wave and exciton modes in TBG/BN are much larger than those in TBG. The excitation gap and in TBG/BN reach about 2.5 meV and 20 meV, respectively, with almost a half of the intra-flavor band gap . In contrast to TBG with almost particle-hole symmetric excitation modes for positive and negative , the excitation spectrums and gaps of TBG/BN at positive are rather different from those at negative . The exciton wavefunctions in TBG are also much more spatially localized than those in TBG/BN. Full SCHF calculations show that more HF bands besides the two central bands can have rather large contribution from the single-particle flat-band states in TBG/BN, and the intra-flavor gap between the flat-like bands is much larger than the between the remote and flat-like bands. The excitation gap of the exciton modes between the remote and flat-like bands is just slightly smaller than , but is generally lower than the between the flat-like bands, so the optical properties of the Chern insulator states are mainly determined by the exciton modes between the remote and flat-like bands. The valley-wave modes from full HF calculations have similar energies as those in the active-band approximation. In addition, the quantitative behavior of the excitation spectrums varies with of TBG/BN.
Acknowledgements.
We gratefully acknowledge valuable discussions with D. Tománek, Y. Yin, and X. Xiong. This research was supported by the National Natural Science Foundation of China (Grants No. 11974312 and No. 92270104) and the Open Research Fund of CNMGE Platform & NSCC-TJ.References
- Bistritzer and MacDonald (2011) R. Bistritzer and A. H. MacDonald, “Moiré bands in twisted double-layer graphene,” Proc. Natl. Acad. Sci. U.S.A. 108, 12233 (2011).
- Suárez Morell et al. (2010) E. Suárez Morell, J. D. Correa, P. Vargas, M. Pacheco, and Z. Barticevic, “Flat bands in slightly twisted bilayer graphene: Tight-binding calculations,” Phys. Rev. B 82, 121407 (2010).
- Lopes dos Santos et al. (2012) J. M. B. Lopes dos Santos, N. M. R. Peres, and A. H. Castro Neto, “Continuum model of the twisted graphene bilayer,” Phys. Rev. B 86, 155449 (2012).
- Fang and Kaxiras (2016) S. Fang and E. Kaxiras, “Electronic structure theory of weakly interacting bilayers,” Phys. Rev. B 93, 235153 (2016).
- Carr et al. (2017) S. Carr, D. Massatt, S. Fang, P. Cazeaux, M. Luskin, and E. Kaxiras, “Twistronics: Manipulating the electronic properties of two-dimensional layered structures through their twist angle,” Phys. Rev. B 95, 075420 (2017).
- Tarnopolsky et al. (2019) G. Tarnopolsky, A. Jura Kruchkov, and A. Vishwanath, “Origin of Magic Angles in Twisted Bilayer Graphene,” Phys. Rev. Lett. 122, 106405 (2019).
- Ren et al. (2021) Y. Ren, Q. Gao, A. H. MacDonald, and Q. Niu, “WKB Estimate of Bilayer Graphene’s Magic Twist Angles,” Phys. Rev. Lett. 126, 016404 (2021).
- Cao et al. (2018a) Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori, and P. Jarillo-Herrero, “Correlated insulator behaviour at half-filling in magic-angle graphene superlattices,” Nature 556, 80 (2018a).
- Cao et al. (2018b) Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras, and P. Jarillo-Herrero, “Unconventional superconductivity in magic-angle graphene superlattices,” Nature 556, 43 (2018b).
- Kim et al. (2017) K. Kim, A. DaSilva, S. Huang, B. Fallahazad, S. Larentis, T. Taniguchi, K. Watanabe, B. J. LeRoy, A. H. MacDonald, and E. Tutuc, “Tunable Moiré bands and strong correlations in small-twist-angle bilayer graphene,” Proc. Natl. Acad. Sci. U.S.A 114, 3364 (2017).
- Lu et al. (2019) X. Lu, P. Stepanov, W. Yang, M. Xie, M. A. Aamir, I. Das, C. Urgell, K. Watanabe, T. Taniguchi, G. Zhang, A. Bachtold, A. H. MacDonald, and D. K. Efetov, “Superconductors, orbital magnets, and correlated states in magic angle bilayer graphene,” Nature 574, 653 (2019).
- Xie et al. (2019) Y. Xie, B. Lian, B. Jäck, X. Liu, C.-L. Chiu, K. Watanabe, T. Taniguchi, B. A. Bernevig, and A. Yazdani, “Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene,” Nature 572, 101 (2019).
- Kerelsky et al. (2019) A. Kerelsky, L. J. McGilly, D. M. Kennes, L. Xian, M. Yankowitz, S. Chen, K. Watanabe, T. Taniguchi, J. Hone, C. Dean, A. Rubio, and A. N. Pasupathy, “Maximized electron interactions at the magic angle in twisted bilayer graphene,” Nature 572, 95 (2019).
- Jiang et al. (2019) Y. Jiang, X. Lai, K. Watanabe, T. Taniguchi, K. Haule, J. Mao, and E. Y. Andrei, “Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene,” Nature 573, 91 (2019).
- Choi et al. (2019) Y. Choi, J. Kemmer, Y. Peng, A. Thomson, H. Arora, R. Polski, Y. Zhang, H. Ren, J. Alicea, G. Refael, F. von Oppen, K. Watanabe, T. Taniguchi, and S. Nadj-Perge, “Electronic correlations in twisted bilayer graphene near the magic angle,” Nat. Phys. 15, 1174 (2019).
- Yankowitz et al. (2019) M. Yankowitz, S. Chen, H. Polshyn, Y. Zhang, K. Watanabe, T. Taniguchi, D. Graf, A. F. Young, and C. R. Dean, “Tuning superconductivity in twisted bilayer graphene,” Science 363, 1059 (2019).
- Uri et al. (2020) A. Uri, S. Grover, Y. Cao, J.A. Crosse, K. Bagani, D. Rodan-Legrain, Y. Myasoedov, K. Watanabe, T. Taniguchi, P. Moon, M. Koshino, P. Jarillo-Herrero, and E. Zeldov, “Mapping the twist-angle disorder and Landau levels in magic-angle graphene,” Nature 581, 47 (2020).
- Nuckolls et al. (2020) K. P. Nuckolls, M. Oh, D. Wong, B. Lian, K. Watanabe, T. Taniguchi, B. A. Bernevig, and A. Yazdani, “Strongly correlated Chern insulators in magic-angle twisted bilayer graphene,” Nature 588, 610 (2020).
- Wong et al. (2020) D. Wong, K. P. Nuckolls, M. Oh, B. Lian, Y. Xie, S. Jeon, K. Watanabe, T. Taniguchi, B. A. Bernevig, and A. Yazdani, “Cascade of electronic transitions in magic-angle twisted bilayer graphene,” Nature 582, 198 (2020).
- Zondiner et al. (2020) U. Zondiner, A. Rozen, D. Rodan-Legrain, Y. Cao, R. Queiroz, T. Taniguchi, K. Watanabe, Y. Oreg, F. von Oppen, A. Stern, E. Berg, P. Jarillo-Herrero, and S. Ilani, “Cascade of phase transitions and Dirac revivals in magic-angle graphene,” Nature 582, 203 (2020).
- Saito et al. (2020) Y. Saito, J. Ge, K. Watanabe, T. Taniguchi, and A. F. Young, “Independent superconductors and correlated insulators in twisted bilayer graphene,” Nat. Phys. 16, 926 (2020).
- Stepanov et al. (2020) P. Stepanov, I. Das, X. Lu, A. Fahimniya, K. Watanabe, T. Taniguchi, F. H. L. Koppens, J. Lischner, L. Levitov, and D. K. Efetov, “Untying the insulating and superconducting orders in magic-angle graphene,” Nature 583, 375 (2020).
- Luo et al. (2020) Y. Luo, R. Engelke, M. Mattheakis, M. Tamagnone, S. Carr, K. Watanabe, T. Taniguchi, E. Kaxiras, P. Kim, and W. L. Wilson, “In situ nanoscale imaging of moiré superlattices in twisted van der Waals heterostructures,” Nat. Commun. 11, 4209 (2020).
- Rozen et al. (2021) A. Rozen, J. M. Park, U. Zondiner, Y. Cao, D. Rodan-Legrain, T. Taniguchi, K. Watanabe, Y. Oreg, A. Stern, E. Berg, P. Jarillo-Herrero, and S. Ilani, “Entropic evidence for a Pomeranchuk effect in magic-angle graphene,” Nature 592, 214 (2021).
- Hesp et al. (2021) N. C. H. Hesp, I. Torre, D. Rodan-Legrain, P. Novelli, Y. Cao, S. Carr, S. Fang, P. Stepanov, D. Barcons-Ruiz, H. Herzig Sheinfux, K. Watanabe, T. Taniguchi, D. K. Efetov, E. Kaxiras, P. Jarillo-Herrero, M. Polini, and F. H. L. Koppens, “Observation of interband collective excitations in twisted bilayer graphene,” Nat. Phys. 17, 1162 (2021).
- Ma et al. (2022) C. Ma, S. Yuan, P. Cheung, K. Watanabe, T. Taniguchi, F. Zhang, and F. Xia, “Intelligent infrared sensing enabled by tunable moiré quantum geometry,” Nature 604, 266 (2022).
- Carr et al. (2020) S. Carr, S. Fang, and E. Kaxiras, “Electronic-structure methods for twisted moiré layers,” Nat. Rev. Mater. 5, 748 (2020).
- Andrei and MacDonald (2020) E. Y. Andrei and A. H. MacDonald, “Graphene bilayers with a twist,” Nat. Mater. 19, 1265 (2020).
- Andrei et al. (2021) E. Y. Andrei, D. K. Efetov, P. Jarillo-Herrero, A. H. MacDonald, K. F. Mak, T. Senthil, E. Tutuc, A. Yazdani, and A. F. Young, “The marvels of moiré materials,” Nat. Rev. Mater. 6, 201 (2021).
- Liu and Dai (2021a) J. Liu and X. Dai, “Orbital magnetic states in moiré graphene systems,” Nat. Rev. Phys. 3, 367 (2021a).
- Po et al. (2018) H. C. Po, L. Zou, A. Vishwanath, and T. Senthil, “Origin of Mott Insulating Behavior and Superconductivity in Twisted Bilayer Graphene,” Phys. Rev. X 8, 031089 (2018).
- Koshino et al. (2018) M. Koshino, N. F. Q. Yuan, T. Koretsune, M. Ochi, K. Kuroki, and L. Fu, “Maximally Localized Wannier Orbitals and the Extended Hubbard Model for Twisted Bilayer Graphene,” Phys. Rev. X 8, 031087 (2018).
- Kang and Vafek (2018) J. Kang and O. Vafek, “Symmetry, Maximally Localized Wannier States, and a Low-Energy Model for Twisted Bilayer Graphene Narrow Bands,” Phys. Rev. X 8, 031088 (2018).
- Isobe et al. (2018) H. Isobe, N. F. Q. Yuan, and L. Fu, “Unconventional Superconductivity and Density Waves in Twisted Bilayer Graphene,” Phys. Rev. X 8, 041041 (2018).
- Liu et al. (2018) C.-C. Liu, L.-D. Zhang, W.-Q. Chen, and F. Yang, “Chiral Spin Density Wave and Superconductivity in the Magic-Angle-Twisted Bilayer Graphene,” Phys. Rev. Lett. 121, 217001 (2018).
- Kang and Vafek (2019) J. Kang and O. Vafek, “Strong Coupling Phases of Partially Filled Twisted Bilayer Graphene Narrow Bands,” Phys. Rev. Lett. 122, 246401 (2019).
- Zhang and Senthil (2019) Y.-H. Zhang and T. Senthil, “Bridging Hubbard model physics and quantum Hall physics in trilayer moiré superlattice,” Phys. Rev. B 99, 205150 (2019).
- Chittari et al. (2019) B. L. Chittari, G. Chen, Y. Zhang, F. Wang, and J. Jung, “Gate-Tunable Topological Flat Bands in Trilayer Graphene Boron-Nitride Moiré Superlattices,” Phys. Rev. Lett. 122, 016401 (2019).
- Zhang et al. (2019) Y.-H. Zhang, D. Mao, and T. Senthil, “Twisted bilayer graphene aligned with hexagonal boron nitride: Anomalous Hall effect and a lattice model,” Phys. Rev. Research 1, 033126 (2019).
- Repellin et al. (2020) C. Repellin, Z. Dong, Y.-H. Zhang, and T. Senthil, “Ferromagnetism in Narrow Bands of Moiré Superlattices,” Phys. Rev. Lett. 124, 187601 (2020).
- Xie and MacDonald (2020) M. Xie and A. H. MacDonald, “Nature of the Correlated Insulator States in Twisted Bilayer Graphene,” Phys. Rev. Lett. 124, 097601 (2020).
- Bultinck et al. (2020a) N. Bultinck, E. Khalaf, S. Liu, S. Chatterjee, A. Vishwanath, and M. P. Zaletel, “Ground State and Hidden Symmetry of Magic-Angle Graphene at Even Integer Filling,” Phys. Rev. X 10, 031034 (2020a).
- Bultinck et al. (2020b) N. Bultinck, S. Chatterjee, and M. P. Zaletel, “Mechanism for Anomalous Hall Ferromagnetism in Twisted Bilayer Graphene,” Phys. Rev. Lett. 124, 166601 (2020b).
- Zhang et al. (2020) Y. Zhang, K. Jiang, Z. Wang, and F. Zhang, “Correlated insulating phases of twisted bilayer graphene at commensurate filling fractions: A Hartree-Fock study,” Phys. Rev. B 102, 035136 (2020).
- Kang and Vafek (2020) J. Kang and O. Vafek, “Non-Abelian Dirac node braiding and near-degeneracy of correlated phases at odd integer filling in magic-angle twisted bilayer graphene,” Phys. Rev. B 102, 035161 (2020).
- Wu and Das Sarma (2020) F. Wu and S. Das Sarma, “Collective Excitations of Quantum Anomalous Hall Ferromagnets in Twisted Bilayer Graphene,” Phys. Rev. Lett. 124, 046403 (2020).
- Liu and Dai (2021b) J. Liu and X. Dai, “Theories for the correlated insulating states and quantum anomalous Hall effect phenomena in twisted bilayer graphene,” Phys. Rev. B 103, 035427 (2021b).
- Hejazi et al. (2021) K. Hejazi, X. Chen, and L. Balents, “Hybrid Wannier Chern bands in magic angle twisted bilayer graphene and the quantized anomalous Hall effect,” Phys. Rev. Research 3, 013242 (2021).
- Liu et al. (2021) S. Liu, E. Khalaf, J. Y. Lee, and A. Vishwanath, “Nematic topological semimetal and insulator in magic-angle bilayer graphene at charge neutrality,” Phys. Rev. Research 3, 013033 (2021).
- Da Liao et al. (2021) Y. Da Liao, J. Kang, C. N. Breiø, X. Y. Xu, H.-Q. Wu, B. M. Andersen, R. M. Fernandes, and Z. Y. Meng, “Correlation-Induced Insulating Topological Phases at Charge Neutrality in Twisted Bilayer Graphene,” Phys. Rev. X 11, 011014 (2021).
- Lin and Ni (2020) X. Lin and J. Ni, “Symmetry breaking in the double moiré superlattices of relaxed twisted bilayer graphene on hexagonal boron nitride,” Phys. Rev. B 102, 035441 (2020).
- Bernevig et al. (2021a) B. A. Bernevig, Z.-D. Song, N. Regnault, and B. Lian, “Twisted bilayer graphene. III. Interacting Hamiltonian and exact symmetries,” Phys. Rev. B 103, 205413 (2021a).
- Lian et al. (2021) B. Lian, Z.-D. Song, N. Regnault, D. K. Efetov, A. Yazdani, and B. A. Bernevig, “Twisted bilayer graphene. IV. Exact insulator ground states and phase diagram,” Phys. Rev. B 103, 205414 (2021).
- Bernevig et al. (2021b) B. A. Bernevig, B. Lian, A. Cowsik, F. Xie, N. Regnault, and Z.-D. Song, “Twisted bilayer graphene. V. Exact analytic many-body excitations in Coulomb Hamiltonians: Charge gap, Goldstone modes, and absence of Cooper pairing,” Phys. Rev. B 103, 205415 (2021b).
- Kwan et al. (2021) Y. H. Kwan, G. Wagner, T. Soejima, M. P. Zaletel, S. H. Simon, S. A. Parameswaran, and N. Bultinck, “Kekulé Spiral Order at All Nonzero Integer Fillings in Twisted Bilayer Graphene,” Phys. Rev. X 11, 041063 (2021).
- Cea et al. (2020) T. Cea, P. A. Pantaleón, and F. Guinea, “Band structure of twisted bilayer graphene on hexagonal boron nitride,” Phys. Rev. B 102, 155136 (2020).
- Lin et al. (2021) X. Lin, K. Su, and J. Ni, “Misalignment instability in magic-angle twisted bilayer graphene on hexagonal boron nitride,” 2D Mater. 8, 025025 (2021).
- Shi et al. (2021) J. Shi, J. Zhu, and A. H. MacDonald, “Moiré commensurability and the quantum anomalous Hall effect in twisted bilayer graphene on hexagonal boron nitride,” Phys. Rev. B 103, 075122 (2021).
- Mao and Senthil (2021) D. Mao and T. Senthil, “Quasiperiodicity, band topology, and moiré graphene,” Phys. Rev. B 103, 115110 (2021).
- Shin et al. (2021) J. Shin, Y. Park, B. L. Chittari, J.-H. Sun, and J. Jung, “Electron-hole asymmetry and band gaps of commensurate double moire patterns in twisted bilayer graphene on hexagonal boron nitride,” Phys. Rev. B 103, 075423 (2021).
- Long et al. (2022) M. Long, P. A. Pantaleón, Z. Zhan, F. Guinea, J. Ángel Silva-Guillén, and S. Yuan, “An atomistic approach for the structural and electronic properties of twisted bilayer graphene-boron nitride heterostructures,” npj Computational Materials 8, 73 (2022).
- Serlin et al. (2020) M. Serlin, C. L. Tschirhart, H. Polshyn, Y. Zhang, J. Zhu, K. Watanabe, T. Taniguchi, L. Balents, and A. F. Young, “Intrinsic quantized anomalous Hall effect in a moiré heterostructure,” Science 367, 900 (2020).
- Tschirhart et al. (2021) C. L. Tschirhart, M. Serlin, H. Polshyn, A. Shragai, Z. Xia, J. Zhu, Y. Zhang, K. Watanabe, T. Taniguchi, M. E. Huber, and A. F. Young, “Imaging orbital ferromagnetism in a moiré Chern insulator,” Science 372, 1323 (2021).
- Kumar et al. (2021) A. Kumar, M. Xie, and A. H. MacDonald, “Lattice collective modes from a continuum model of magic-angle twisted bilayer graphene,” Phys. Rev. B 104, 035119 (2021).