Coherent States and Generalized Hermite Polynomials for Fractional statistics - interpolating from fermions to bosons
Abstract
This article develops the geometric structure that results from the -commutator that provides a continuous interpolation between the Clifford and Heisenberg algebras. We first demonstrate the most general geometrical picture, applicable to all values of . After listing the properties of this Hilbert space, we study the calculus of generalized coherent states that result when , for , including a calculation of the free-energy for particles of intermediate statistics. Lastly, we solve the generalized harmonic oscillator problem and derive generalized versions of the Hermite polynomials for general .
Some remarks are made to connect this study to the case of anyons. This study represents the first steps towards developing an anyonic field theory.
I Introduction & Motivation
In an earlier paperSatish1 , we analyzed the Hilbert space derived from the “commutator”
| (1) |
in the case where where are co-prime non-zero natural numbers and where we also define . This algebra was inspired by the properties of anyons and was intended to interpolate between fermionic and bosonic statistics. In particular, we had considered the general case where the vacuum state had a non-zero eigenvalue. When the vacuum state has a zero eigenvalue, however, we are naturally led to the study of variables , such that . Such variables, which may be referred to as generalized Grassmann variables have been the subject of much study in the past Biedenharn ; MacFarlane ; Chaichian , of which the most complete and relevant is Chaichian . The difference is that since our focus is on the full range of fractional statistics between fermions and bosons in 2+1 dimensions, we study a full calculus starting with integration rules to a physically reasonable construction of the path integral for the free energy.
In addition to the generalization of the Grassmann variables mentioned above, there is also a rather simple geometrical picture that emerges from the arithmetic for the operators in the algebra Hallnas . Akin to the fuzzy solid representations used for the angular momentum algebra, we prove that the relevant geometrical picture here is a pancake that goes from a sphere (for ) to a plane (for ).
II Summary of Properties
We are going to, in this paper, analyze several properties of the Hilbert space, in the special and physically interesting case where the vacuum state has zero eigenvalue for the operators , as well as . Hence, in the notation of Satish1 , we set .
For general integer , we deduce the following properties.
-
1.
States are labeled by their eigenvalues under , i.e.,
(2) The eigenvectors can be constructed to be orthogonal, since these are also the eigenvectors of the usual number operator .
We propose to call these states “overons”, since they represent one of the two ways to flip anyons (“over” and “under”). The complex conjugate states would be then called “underons”. In Appendix 1, we study possible dynamical system analogs that might result from such excitations.
-
2.
The actions of the operators are
(3) -
3.
A consistent identification is , i.e., the commutator is ..
-
4.
When we take the complex conjugate of the basic commutator, we get, by an entirely similar procedure to the above, that the eigenstates of are . The chain of reasoning is
(4) Taking the complex conjugate of the third equation above, we get . This leads to the equations
(5) Continuing, we can now write as a linear combination of the . In fact, it is easy to see, from the geometry of the eigenvectors on the complex plane in Fig. 3, that
(6) Using this,
(7) Using this, and defining as the usual hermitian conjugate transpose of ,
(8) The traditional “number” operator is diagonal in the same basis that is. Since is a hermitian operator, it is consistent that the is an orthonormal basis Banks .
-
5.
The eigenvalue spectrum of (magnitude as well as complex vectors) is as below and in reference Satish1 and is plotted in Fig. 1. Note that we have and we have used for the graphs in Fig. 1.
(9) Figure 1: Eigenvalue Spectrum 
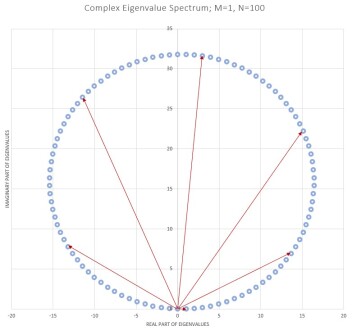
-
6.
The matrices and are displayed explicitly below, for . They are matrices, since the eigenstates are -dimensional vectors. The eigenvectors are as below
(46) while the operators are
(56) (66) while the commutator is
(77) (78) and
(79) and
(80) The top-left component of is not determined by the above commutator since for the state . However, we can determine it by taking the limit of the expressions for as in Satish1 ; it becomes , which is for the fermion limit and for the bosonic limit. Hence is (the identity matrix) for fermions and for bosons.
-
7.
When we compute scattering amplitude matrix elements for different particles, we will have to re-order the annihilation and creation operators, then will be left with a product of terms like , i.e.,
When we compute expectation values in the vacuum state (i.e., ), only the constant terms will be left and they are, for the first few powers
(81) where we have represented the polynomial by just its coefficients (the Mahonian numbers Mahon ) in the last case. As can be checked quickly, these are the polynomials etc.
III Geometrical Interpretation
The most general geometrical construction is
| (82) |
and observe that
| (83) |
we obtain the equation
| (84) |
This equation can be re-phrased as an invariant of the group that underlies the algebra. The algebra can be written most simply with the creation/annihilation operators as
| (85) |
In Equation (17), the two limits and are consistent on both sides of the equation. Additionally, and are the matrices as defined in Equation (23) and is the real, diagonal matrix
| (86) |
which is the finite-difference Laplacian of a diagonal matrix with absolute values of the eigenvalues along the diagonal. In this notation, from Equation (17), , so that the commutator in that equation can be written in the interesting form
| (87) |
Incidentally, for , this is consistent with the previous paper’sSatish1 Equation (25) at the points resolved within the fuzzy ellipsoid (). In this case,
| (94) | |||
| (98) | |||
| (105) |
satisfies both the Equations (25) and following in the previous paper Satish1 , i.e.,
| (106) |
We have already noted the equivalence for .
The surface described by the above equation is pancake-shaped aligned along the z-axes, as in Fig. 2.
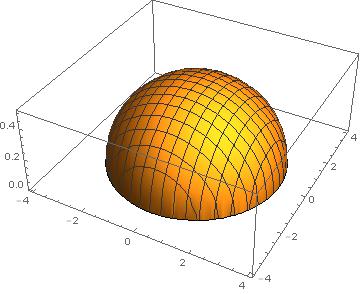
For large , we can write the solutions to the above equation (in terms of the polar radius coordinate ) as
| (107) |
which yields concentric circular strips on the plane , where each state has radius . This is the usual picture for Landau levels; here this is a geometrical representation of the usual bosonic levels.
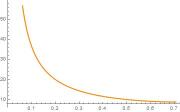
To show how a spherical object for transforms into the flat plane in the limit, we can compute the surface area of the pancake. The area integral is computed (define ) as
| (108) |
Clearly, this diverges as , which corresponds to , since .
We plot the area as a function of in Fig. 3. Indeed, the pancake like closed surface turns into the infinite plane as .
IV Coherent States for general - Generalized Grassmann variables
For a general -type algebra, we can write down an eigenstate for as
| (109) |
The above expansion is identical to the usual formula for boson coherent states in the limit , as well as for fermion coherent states at (the usual Grassmann variables). We also define the “bra” vector as the adjoint vector, where is the adjoint of and is independent of , i.e.,
| (110) |
That they are eigenvectors may be checked by applying to the state and using Equation (3), we postulate that and commute. Additionally, we posit that and the transposition relations (the matrix is as defined in Equation (12))
| (111) |
What sort of object is ? The two relations above make sense only if were itself an matrix, for consistency, we assume is a direct product of a “generalized Grassmann matrix” and a unit matrix in the states’ eigenbasis, hence, commutes with all other complex number matrices in the same eigenbasis. Hence and are all reasonable objects to define. The above statements and equations are also consistent with the statement that a term like is “real”. This is true, since is a real matrix. In addition, since , it is consistent to require the equations below (in line with Equation (4)),
The description of this algebra is similar to the treatment in reference Chaichian , however, the difference here is that these variables are directly coherent state variables, as in the usual definition Murayama1 .
Some auxiliary results are written below. Again, note that all these products are scalars times the unit matrix.
| (113) |
Note that in the limit, when , , which is appropriate for bosonic coherent states. Taking the limit in the opposite direction, the behavior is appropriate for fermions, when the algebra automatically yields .
We can now write down, from the expansion in Equation (28), a series expansion for , which also terminates at the term , since higher powers are .
The following integrals are postulated, in order to match the boundary cases for bosonic variables as well as for fermionic Grassmanns. We set
| (114) |
which is consistent with
| (115) |
While the first (moment) variety of integral can be checked for the limiting fermion and boson cases, the second variety of integrals (without the normalization) cannot be properly defined in the bosonic cases since it isn’t convergent. The first method can be treated as a regularized integral.
The one-variable version of these integrals can be defined, in consistency with the above equations, as
| (116) |
It is possible to define an identity operator, so that (using Equation (29)),
| (117) |
V The Trace and Path Integrals
The trace of an operator that commutes with and can be taken through is
| (118) |
where we have used the regularized integrals from Equation (29).
The action integral is, for a “Hamiltonian” ,
| (119) |
The bracketed term can be “split” into sub-integrals using the identity operator from Equation (40). We define and .
| (120) |
Using the scalar products as defined in Equation (28) and expanding the logarithm to lowest order,
| (121) |
the integral reduces to
| (122) |
with boundary conditions for appropriate to .
V.1 Periodicity of
To define boundary conditions, we use the as the boundary condition. This is consistent with for bosons and for fermions Murayama1 . Hence, defining ,
| (123) |
We generalize
| (124) |
This leads to the integral for finite-, using the rules we postulated before in Equations (29) and (30)
In the above, we use the relations ( is real in the below and the third equation is a general version of the second)
| (126) |
Hence, with , i.e., for fermions, we get . Separately, when , i.e., for bosons, the above formula reduces to the expression for bosons, i.e.,
VI Differentiation of generalized Grassmann variables
We wish to replicate the operator -commutator with coherent state variables. Realizing that ’s have to be treated as matrices and comparing the situation with Equation (1) and (10), we impose,
| (127) |
so that there is a or that accompanies switching the derivative and the variable. This is consistent with the bosonic and fermionic case and permits us to deduce the uncertainty relation for the coherent variable and its conjugate momentum, i.e.,
| (128) |
An immediate consequence is
| (129) |
The above equation is consistent on both sides if we were to set , for , as well as and .
We are going to assume that and are all independent of each other. By demanding consistency as in
| (130) |
we deduce the rules for switching the partial derivative and the transposed variable,
| (131) |
Also,
| (132) |
In addition, by considering switching the order of partial derivatives, we get
| (133) |
which is derived from
| (134) |
VII 2-d and 1-d harmonic oscillator: Generalized Hermite polynomials
Let’s solve for the two-dimensional oscillator first. The operators are the usual annihilation and creation operators. Let’s assume are all complex numbers that commute with the .
| (135) |
If we want this to be consistent with
| (136) |
we derive the simplest solution, that matches the conditions for the case of fermions as well as bosons, i.e.,
| (137) |
i.e.,
| (138) |
The ground state wave-function is found from , which leads to
| (139) |
Note that upon expanding the exponential multiplying by the polynomial in , we’d keep terms up to as higher powers are . We can construct higher wavefunctions using the creation operator, etc.
To obtain the wave-function for the 1-d harmonic oscillator, it is reasonable to assume (in line with the method one uses with the bosonic caseWess ) that are real. In addition, to not allow powers of in the ground-state function, we set . We then deduce
| (140) |
which yields, when one carries out the above construction, terms that reduce to Hermite polynomials (albeit with series and exponentials terminated at ), i.e.,
| (141) |
We note that this construction does not work for , the ’s cannot be real.
VIII Wave-function for two anyons
The excitations described in this paper represent one of the two ways two anyons can be braided amongst each other. While we have yet to construct a description for anyons here, we could consider start by studying “overons” (as opposed to “underons” which have the complex conjugate eigenvalues).
For two dimensions, we had, for the ground state for overons (as well as for underons)
| (142) |
which are the usual holomorphic functions.
For two excitations, the wave-function needs to possess the proper symmetry upon exchange, hence would be
| (143) |
This works as the exchange causes to go to
| (144) |
which produces a wave-function for the excitation with the opposite exchange characteristic, i.e., for “underons”. While this would not be a possible symmetry for “overons”, it could represent an appropriate anyon wave-function.
However, as can be quickly checked, the overlap of this function with the Laughlin-like Laughlin alternative
| (145) |
is non-zero only for odd , as only terms with both raised to powers gives non-zero results.
This is clear, as looking at individual non-zero terms in the overlap integral, i.e.,
| (146) |
which shows that the overlap integral is 0 for even- and proportional to () for odd-. The overlap is of order unity for small odd-, which explains why the function works so well, even for particles with fractional statistics.
IX Remarks on the propagation of Anyons
In the usual field theory of fermions Banks ; QFT , the evolution of a two-particle state is expressed as a perturbative series, starting with the two “bare” propagators followed by successively more complex interactions, involving vertices of the interactions and loops between such vertices.
Let’s say we start with two identical fermions ( and ), treated as a product of fairly well-separated wave-functions, at points or . Starting at these separated spots, they can be end up at two widely-separated spots with in all possible ways - either through direct propagation, or with crossed propagation, i.e.,
| (147) |
Usually, the wave-function with exchanged coordinates (the second term) is extremely small, so we can approximate the propagation neglecting the crossed term.
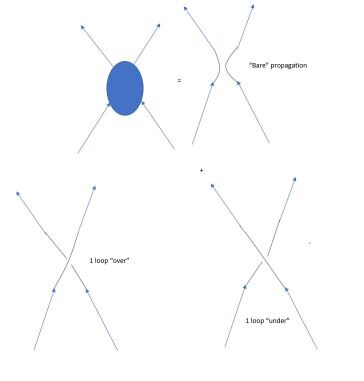
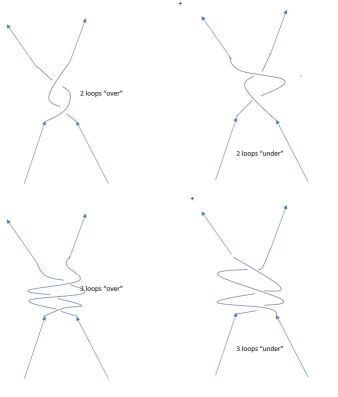
The propagator for two anyons, however, has an interesting twist. The propagation of “bare” anyons is connected to the value of . Two anyons can propagate, as in Fig. 2 while winding around each other 0,2,4,… times (since the final result would then be indistinguishable from no winding) and we need to sum over all these possible alternatives. Suppose where is an integer and the integers are co-prime. Each “winding” produces a multiplicative factor of into the amplitude for the two-anyon propagator. Since we need to sum over all the separate ways this can happen, we have to restrict the number of windings to be less than , when we revert to zero windings. The following factors are useful to define.
so that the amplitude for the propagation of two anyons is proportional to since
| (148) |
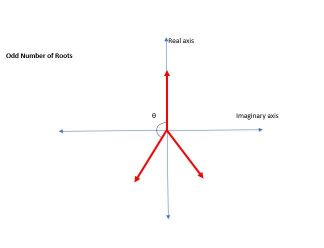
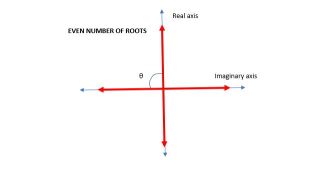
On the other hand, if , with the caveat and co-prime, then the corresponding sums are
so that the amplitude for the propagation is below since
| (149) |
The exclusion of (in the ‘even’ case above) is also easy to see (this explicitly means two fermions can indeed propagate). Note that if , the individual terms are all or . There are no cancellations.
Anyons with even-denominator cannot propagate freely, purely from geometrical considerations, while those with odd-denominator can.
This result might seem surprising, but it is clear from studying the roots of unity on the complex plane. Consider Fig. 3, where the odd and even roots of unity are displayed for the case of 3 and 4, respectively. It is clear, for instance, that the sum is non-zero in the odd-case, while the sum is zero in the even case.
The factors multiply the total amplitudes, assuming there are no energetic consequences within the action to meandering paths that wind around each other multiple number of times. It would, therefore, not be surprising that multiple anyon propagation is suppressed with even-denominator theta. It is, however, possible that higher order interaction terms will allow propagation for even-denominator-theta anyons. This will have physical consequences for transport and localization of states with odd and even denominator .
This behavior (for odd and even-denominator ) is quite robust to the addition of a small cost for extra windings. Suppose the anyons encountered a cost, a factor of , small cost, for each extra winding around the other anyon. Then the corresponding sums would become, for even-denominator ,
| (150) |
while the odd-denominator results are of to the same order. The suppression is, therefore, robust for small additional cost for anyons “winding” around each other.
X Conclusions
We have studied the arithmetic and calculus of overons, excitations under generalized statistics interpolating between fermions and bosons. We have described the fuzzy “pancake” surface that best describes the eigenvalue surface for the algebra. Further, the calculus of coherent state variables is studied, as is the partition function for these states. We then proceed to study generalizations of the Hermite polynomials.
Using the results, we have studied some consequences for the field theory of anyons that immediately result from the calculus of coherent state variables as well as from the geometrical interpretation. These demonstrate the appropriateness of the Laughlin wave-function to describe 2-anyon states. In addition, there are rather simple geometrical reasons why even-denominator anyons cannot propagate freely and can only do so in the presence of anyon-anyon interactions.
XI Acknowledgments
SR acknowledges the hospitality and intellectual stimulation of the Rutgers Department of Physics & Astronomy and the NHETC at Rutgers. Much of this work benefited from very useful advice and suggestions from Professor Scott Thomas. He also acknowledges the collaborative atmosphere provided at the ITP, Santa Barbara.
XII APPENDIX 1: A dynamical system analog for the eigenvalue spectrum
XII.1 Boson starting point
Consider the problem of a boson, represented as a scalar field, defined on a circle around another boson. The circle is discretized into points, labelled . The lattice constant (between the discrete points) is . The potential energy part of the Hamiltonian, after partial integration, leads to
| (151) |
Transform to Fourier coordinates
| (152) |
XII.2 Fermion starting point
Start with a fermion, represented by a complex field defined on the same circle. The Hamiltonian would have a first-order derivative, as below
| (153) |
Again, writing this in Fourier space, using ,
| (154) |
Fermion doubling - this would go away if we set .
XII.3 A composite particle starting point
Composing the above Hamiltonians, choosing to appropriately interpolate between the boson and fermion cases, we write the discretized version of the fractional () derivative as follows (assume wrap-around coordinatization for a circle)
| (155) |
which, in Fourier space becomes
| (156) |
This is a version of fermion doubling for the composite particles.
References
- (1) Ramakrishna, Satish Algebra for Fractional Statistics - interpolating from fermions to bosons arxiv:2005.02172, submitted to Nucl. Phys. B
- (2) Ramakrishna, Satish A generalized q-commutator and other diversions Paper in preparation
- (3) Chaichian, M., Demichev, A. P. Path Integrals with Generalized Grassmann Variables arxiv:9504016
- (4) MacMahon, P.A. Combinatory Analysis, Vol. 1 and 2, Cambridge Univ.Press, Cambridge, 1915, reprinted by Chelsea, New York (1955).
- (5) Fivel, Daniel I. Interpolation between Fermi and Bose Statistics Using Generalized Commutators Phy. Rev. Lett. 65, 3361 (1990)
- (6) Iida, Shinji, Kuratsuji, Hiroshi Quantum Algebra near q=1 and a Deformed Symplectic Structure Phy. Rev. Lett. 69, 1833 (1992)
- (7) Greenberg, Oscar W. Interactions of particles having small violations of statistics Physica A 180, 419-427 (1992)
- (8) Leinaas, J. M., Myrheim, J, Nuovo Cimento B 37 (1977) 1.
- (9) Rao, Sumathi Anyons: a primer, arxiv.org/abs/hep-th/9209066
- (10) Khare, Avinash Fractional Statistics And Quantum Theory, World Scientific, 2005.
- (11) Boschi-Filho, H. , Farina, C. , de Souza Dutra, A. , The Partition Function for an Anyon-Like Oscillator, arxiv.org/abs/hep-th/9410098
- (12) Lorek A., Ruffing A., Wess J., A q-deformation of the Harmonic Oscillator Zeitschrift fur Physik C Particles and Fields, June 1997, Volume 74, Issue 2, pp. 369-377 also arxiv:hep-th/960516v1 22 May 1996
- (13) Sang, Chung Won New q-Deformed Fermionic Oscillator Algebra and Thermodynamics, J. Adv. Physics Vol. 4, pp. 1-4, 2015
- (14) MacFarlane A. J., On q-analogues of the quantum harmonic oscillator and the quantum group J. Phys. A.: Math. Gen 22 4581
- (15) Biedenharn L. C., The quantum group SUq(2) and a q-analogue of the boson operators J. Phys. A.: Math. Gen 22 L873
- (16) Murayama, H. Unpublished Lecture Notes “Statistical Mechanics of Bosons” http://hitoshi.berkeley.edu/221B/bosons.pdf
- (17) Murayama, H. Unpublished Lecture Notes “Statistical Mechanics of Fermions” http://hitoshi.berkeley.edu/221B/fermions.pdf
- (18) Lavagno A., Narayana Swamy P. Generalized thermodynamics of q-deformed bosons and fermions arxiv:cond-mat/0111112v1 7 Nov 2000
- (19) Banks, T. Quantum Mechanics: An Introduction Taylor & Francis (2018)
- (20) Griffiths, David J. Introduction to Quantum Mechanics Prentics Hall (1994)
- (21) Laughlin R. B., Anomalous Quantum Hall Effect: An incompressible Quantum Fluid with Fractionally Charged Excitations Phys. Rev. Lett. 50, 18 (1983)
- (22) Hallnas, Martin The fuzzy sphere, a noncommutative geometry http://courses.theophys.kth.se/SI2350/fuzzy.pdf
- (23) Oliveira, E. C de, Machado, J. A. T. A Review of Definitions for Fractional Derivatives and Integral Vol. 2014 doi.org/10.1155/2014/238459