Coexistence of - and -wave gaps due to pair-hopping and exchange interactions
Abstract
I investigate the superconductivity of the three-band –– model derived from the three-band Hubbard model using the Schrieffer–Wolff transformation. My model is designed considering the hole-doped high- superconducting cuprate. The model does not exclude the double occupancy of Cu sites by electrons, and there is a pair-hopping interaction between the and bands together with the exchange interaction. I analyse the superconducting transition temperature, electronic state, and superconducting gap function based on strong coupling theory and find that the superconductivity emerges due to the pair-hopping and exchange interactions via the Suhl-Kondo mechanism. In the superconducting state, the extended - and -wave superconducting gaps coexist, where both charge fluctuations and – band hybridization are key ingredients.
-
Received 12 April 2021, revised 26 June 2021
1 Introduction
The – model is one of the model Hamiltonians that form the basis of many theoretical studies of strongly correlated electron systems [1, 2]. The – model can also be derived as the low-energy effective Hamiltonian of the two-dimensional (2D) multiband Hubbard model [3, 4, 5], regarded as the fundamental model Hamiltonian for the high- superconducting cuprate (HTSC). Many theoretical studies of HTSC to date use the – model as the model Hamiltonian [6, 7, 8, 10, 9, 11, 12, 13]. These studies often exclude the double occupancy of Cu sites by electrons, considering that the on-site Coulomb repulsion between orbitals is much larger than the transfer energy between the and orbitals. As a result, the – model contains only one electron (or hole) band and a localized spin.
However, the double occupancy of Cu sites need not necessarily be excluded when the on-site Coulomb repulsion is comparable to the transfer energy. Relaxing the single occupancy constraint and explicitly considering instead results in the –– model that includes both the – model and the single-band Hubbard model as one of its limits [14, 15, 16, 17, 18, 19, 20]. Thus, the –– model serves as an interpolation between the – model and the single-band Hubbard model and is able to account for more properties caused by strong correlation. However, the charge transfer gap should be comparable to in the charge transfer regime. In this case, electron scattering by electrons cannot be negligible, and both and electrons must be considered.
In this paper, I derive the three-band –– model from the 2D three-band Hubbard model as its effective Hamiltonian by using the Schrieffer–Wolff (SW) transformation [21] and assume that double occupancy is not excluded. In my model, the pair-hopping interaction between the and bands exists separately from the exchange interaction. Treating these interactions using iterative perturbation theory (IPT) approximation, I investigate the superconductivity of the model in a strong coupling framework. The results show that the multicomponent superconductivity emerges with the hole doping, which introduces the - band hybridization through exchange and pair-hopping interactions. This emergence of the superconductivity is due to the pair-hopping and exchange interactions via the Suhl-Kondo (SK) mechanism [22, 23, 24], which stabilizes the superconducting gaps with different signs in a multiband system. In the superconducting state, the extended - and -wave superconducting gaps coexist, and the - and -wave gaps emerge due to the pair-hopping and exchange interactions, respectively.
2 Formulation
Consider the three-band Hubbard model [25] that expresses the Hamiltonian as , where
| (1) |
and
| (2) |
Here, ; is the annihilation (creation) operator for the electron of spin at Cu site ; is the annihilation (creation) operator for electrons of spin with momentum , based on oxygen sites in real space; and are the and electron site energies, respectively; is the on-site Coulomb repulsion between orbitals; and is the number of k-space points in the first Brillouin zone (FBZ). The lattice constant of the square lattice of Cu sites is the length unit. Thus, and , where is the transfer energy between the orbital and the neighbouring orbital.
In order to derive the effective Hamiltonian for , I adopt the SW transformation as follows:
| (3) | |||||
using and
| (4) |
Here, , , and H.c. indicates the Hermitian conjugate of the terms already written. The observable has or as its eigenvalue for each and . Using Eqs. (2) and (4), the following results:
Hereafter, I consider only the first two terms of the right-hand side of Eq. (3), i.e., up to the second order of . Now, I assume that the distribution of the electron is spatially uniform in the ground state and that the ground state is paramagnetic. Thus, and for any where is a c-number equal to the number of electrons in the ground state, where indicates the average in the ground state. I apply this approximation to Eqs. (3) and (LABEL:eq:06) and treat as a parameter that should be determined self-consistently. When I set to zero, i.e., , and omit the constant terms, I obtain the effective Hamiltonian:
| (6) |
is the Hartree-Fock approximation of :
| (7) |
where ,
| (8) |
and
| (9) |
with , ,
| (10) |
and
| (11) |
is an exchange interaction term:
| (12) |
is a pair-hopping term:
| (13) |
is the Coulomb interaction term excluding the component with :
| (14) |
As a consequence, [Eq. (6)] can be characterized by the three parameters [Eq. (10)], [Eq. (11)], and , and it can be regarded as the three-band –– model.
Here, in Eq. (10) is positive near the half-filling in the charge-transfer regime, i.e., . For instance, in the case , for , and the electron band dispersion in Eq. (8) is the same as that for the single-band Hubbard model on a square lattice. in Eq. (11) is always positive in the charge-transfer regime. Thus, in Eq. (12) describes the transverse component of the antiferromagnetic exchange interaction between the and electrons, while the longitudinal component of this interaction narrows the bandwidth of in Eq. (9) from to . Further, indicates that the electron is affected by the spin fluctuation of the electron. As will be shown later, the -wave superconducting gap composed of and electrons emerges from . in Eq. (13) appears for the first time by considering the double occupancy of Cu sites. The pair-hopping term is not included in the single-band – model if double occupancy is excluded. In the model that includes the pair-hopping interaction, electrons favour pair formation [26]. This is also true in the presence of the on-site interaction [27, 28] and in the zero-bandwidth limit [29]. Thus, the pair-hopping term in my model is expected to provide superconductivity in another way.
I introduce another assumption according to the speculation about the ground state of the three-band Hubbard model [30]. In the normal ground state, the and electrons should be combined to construct coherent quasi-particles through hybridization. The matrix elements of the hybridization between the and electrons can be found in the components with in Eqs. (12) and (13) as follows. Defining
| (15) |
can be rewritten as
| (16) |
where
| (17) |
Here, in Eq. (15) means the expectation value of in the ground state of . and indicate the exchange interaction and pair-hopping terms excluding the component with from Eqs. (12) and (13), respectively. Thus, in the ground state of , the and electrons are combined to construct the coherent quasi-particles when .
Hereafter, I treat as the unperturbed part of on the assumption that . I diagonalize and derive the unperturbed Green functions as follows:
| (18) | |||
| (19) | |||
| (20) |
and
| (23) | |||
| (26) |
Here, I use the fermion Matsubara frequencies, , with integer and temperature . is the chemical potential and
| (28) |
For , Eq. (15) can be rewritten as
| (29) |
where means the Heaviside step function.
In order to investigate the superconductivity in a strong coupling framework, I start with the Dyson-Gor’kov equations:
| (30) | |||
| (31) | |||
| (32) |
The orbital indices , , , and run over , , and , and I adopt the Einstein summation convention. and represent the normal and anomalous Green functions, respectively, and and correspond to the normal and anomalous self-energies, respectively. When in Eq. (16) is treated as a perturbation, the normal self-energies up to the second order of and are evaluated by the IPT approximation as follows:
| (36) | |||||
The IPT approximation was first applied in the study of the half-filled single-impurity Anderson model [31, 32], and it was adopted to solve the effective impurity model in the study of the Hubbard model [33, 34]. In these works, it was shown that the second order perturbation theory in large energy scale could reproduce not only the coherent band but also the lower and upper incoherent bands. In a later section, it will be shown that my approach can reproduce similar band structure to be justified as the theory for the 2D three-band –– model.
The anomalous self-energies up to the second order of and are evaluated as follows:
| (37) | |||
| (38) | |||
| (39) | |||
| (40) |
Here, the orbital indices and run over and , and
| (41) | |||
| (42) | |||
| (43) | |||
| (44) | |||
| (45) | |||
| (46) | |||
| (47) | |||
| (48) | |||
| (49) | |||
| (50) | |||
| (51) | |||
| (52) | |||
| (53) | |||
| (54) |
using the boson Matsubara frequencies, with integer . In Eqs. (44) and (45), , , , and denote or , respectively. Note that , , , and the chemical potential must be determined self-consistently in the ground state of through Eqs. (8)–(10), (28), and (29). To this end, I approximate by the number of electrons in the ground state of :
| (55) |
Specifically, I regard as a given parameter and solve Eqs. (8)–(10), (28), (29), and (55) to determine , , and the number of doped holes for the ground state of , where
Once , , and are determined for the ground state of , I treat , , and as temperature independent parameters, whose values do not change from those at . Then, Eqs. (8)–(54) are solved in a fully self-consistent manner to obtain and . To determine the transition temperature , I perform these calculations in two steps. First, is calculated with , and is self-consistently determined so that obtained from becomes equal to . In the first step, is correctly adjusted to compensate the temperature-dependent shift by with . Here, , where
| (56) | |||||
| (57) |
and and are the number of and holes, respectively. Next, using the determined , fully self-consistent calculations are performed to obtain and . At this time, only the temperature-dependent shift by is reflected in obtained from . That is, if deviates from , . Therefore, the temperature at which deviates from is . Also in the second step, can be self-consistently determined so that obtained from becomes equal to with . In this case, the temperature at which deviates from the value with is , which is consistent with the temperature at which deviates from with fixed .
3 Results and discussion
To perform the numerical calculations, I divide the FBZ into a meshes and prepare or Matsubara frequencies. I commonly use for my calculations, and here, I only consider the case . For this case, we have when . I find fully self-consistent solutions with in . The ones in have and the others in have . The former solutions correspond to metallic phase and the latter to superconducting phase. Although I find other fully self-consistent solutions with in , which correspond to insulating phase, I cannot find any solutions in . The absence of solutions in this doping range indicates that some of my assumptions break down. In particular, it is difficult to achieve the spatially uniform distribution of the electron in this range. For instance, the chemical potential shift suppression is observed in La2-xSrxCuO4 () by photoemission spectroscopy [35, 36]. This suppression suggests the possibility of electronic phase separation between the insulating phase and the superconducting phase [37], where the electrons are inhomogeneously distributed due to the strong electron correlation. Therefore, the theory in should consider the possibility of the spatially non-uniform distribution of the electron.
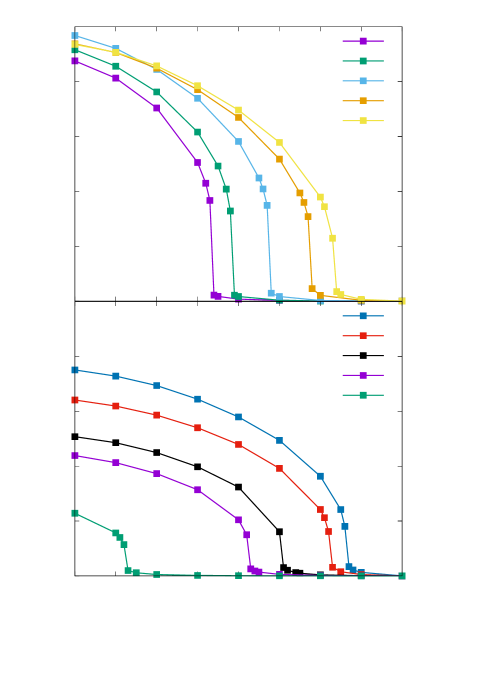
Figure 1 summarizes these results with the doping dependences of and . Comparing with , at which the divergence of the Cooper susceptibility occurs, is higher than by since reflects the fluctuation of . While increases monotonically with , reaches its maximum, , at and then decreases. This doping dependence of reproduces the dome-shaped superconducting phase that is typical for the hole-doped HTSC [38, 39]. This behavior is related to the doping dependence of the density of states, and it will be explained later.
Figure 2 shows the temperature dependences of for every , which are used to determine . Here, I define the temperature at which jumps as . The jumps of at in the underdoped regime, [Fig. 2(a)], are larger than those in the overdoped regime, [Fig. 2(b)]. In other words, while strong coupling superconductivity is established in the underdoped regime, the superconductivity in the overdoped regime remains with weak coupling. This tendency must be reflected in the superconducting gap magnitude, which has been shown to decrease with doping by the low-temperature specific heats of La2-xSrxCuO4 [40, 41].
\makebox(0.0,0.0)[]{{} }
\makebox(0.0,0.0)[]{{} }
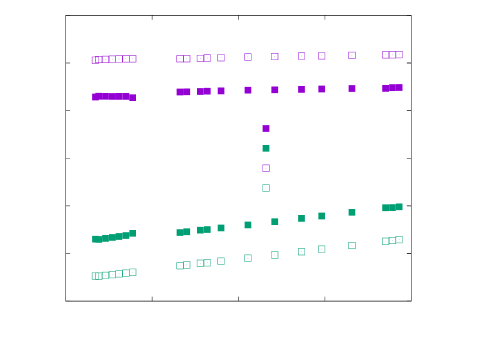
The electronic states of the obtained solutions are reconstructed from the unperturbed ground state. Figure 3 shows the doping dependences of , , , and at . Here, and , and and are the numbers of and holes in the unperturbed ground state, respectively.
\makebox(0.0,0.0)[]{{} }
As shown in Fig. 3, holes are transferred from the band to the band due to the charge fluctuations via the normal self-energies in Eqs. (36)–(36). As a consequence, while mainly increases with , , which means that the band is always electron doped. Since the band deviates from the half-filling due to the charge fluctuations, there is room for the pair-hopping interaction in Eq. (13) to work effectively between the and electrons despite the strong correlations among electrons. Later, I show how the pair-hopping interaction works for the superconductivity in the analysis of the superconducting gap function.
Figures 4 and 5 show the doping dependences of and at , which elucidate how the dome-shaped superconducting phase develops.
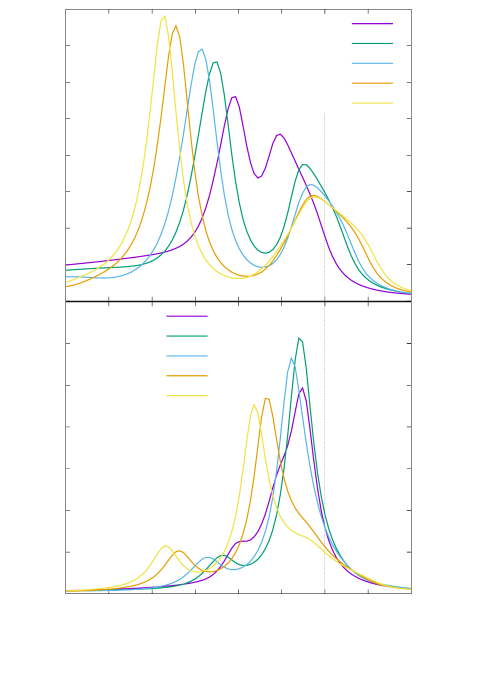
\makebox(0.0,0.0)[]{{} }
\makebox(0.0,0.0)[]{{} }
Here,
| (58) | |||||
| (59) |
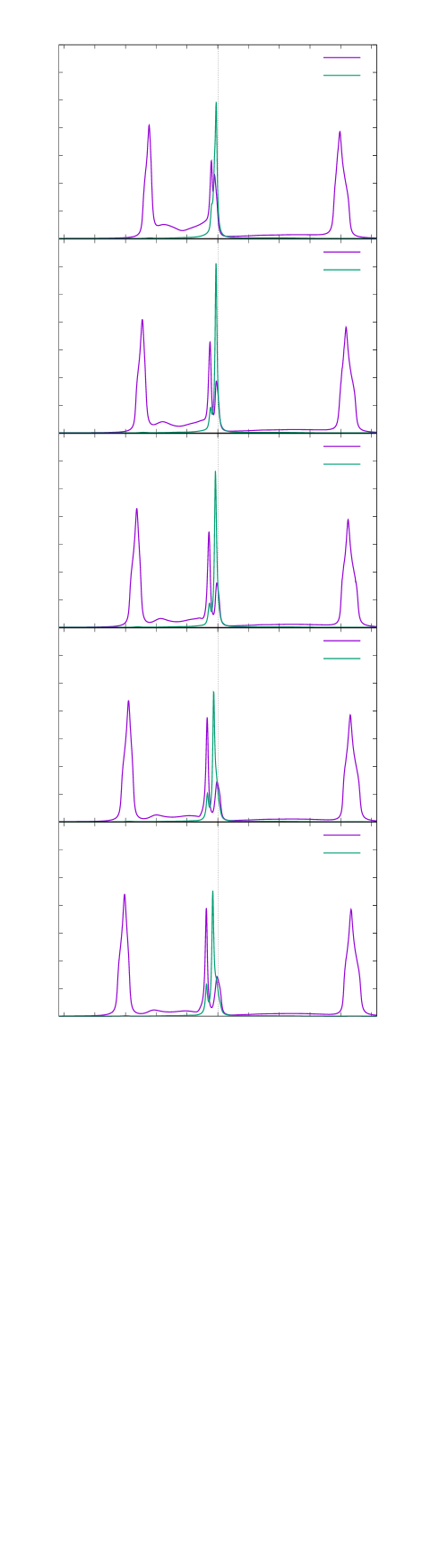
indicates the performance of analytic continuation, for which I use the Pad approximation [42] and . and represent the density of states (DOS) of the and bands, respectively. It has been confirmed that the peak positions of and hardly change even if is changed to . The three blocks appearing in correspond to the lower Hubbard band, coherent band, and upper Hubbard band. The coherent band is split due to the hybridization with the band, and the higher peak energy approaches the Fermi level with the hole doping [Fig. 5(a)]. In contrast, is large in the coherent band only. Reflecting that the holes are mainly doped into the band, as shown in Fig. 3, the peak energy moves away from the Fermi level with the hole doping [Fig. 5(b)]. Due to the competitive effect of these changes in DOS in the coherent band, there is a dome-shaped superconducting phase.
The superconducting gap function, given in matrix form by , is defined as follows:
| (60) |
where and . Here, I use the Pad approximation for analytic continuation and . It has been confirmed that hardly changes even if is changed to . The components of the superconducting gap function are classified into two classes. The first class is composed of and , where runs over and . The real parts of these components with are shown in Fig. 6. The imaginary parts of these components with are all zero. One can see that [Fig. 6(a)] and [Fig. 6(b)] are roughly proportional to . These momentum dependences are derived from the first-order terms of in Eqs. (38) and (39), which originate from the exchange interaction in Eq. (12). Thus, and emerge due to the exchange interaction via the SK mechanism. It can be verified that the SK mechanism can work effectively with the exchange interaction only if . Moreover, the signs of and differ from the signs of and , respectively. Therefore, as shown in Fig. 6(c), the linear combination has line nodes at and and behaves like a nodal -wave superconducting gap.


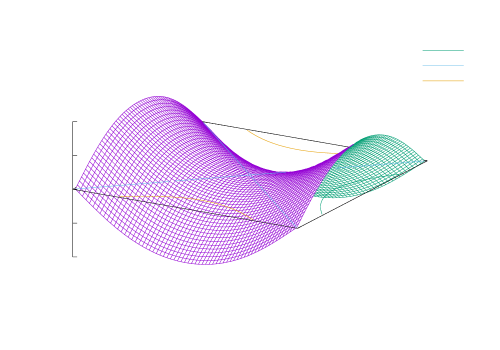
The second class is composed of and , where and run over and . The real part of these components with are shown in Fig. 7. The imaginary part of these components with are all zero. [Fig. 7(b) and (c)] is roughly proportional to . This momentum dependence is derived from the first-order term of in Eq. (40), which originates from the pair-hopping interaction in Eq. (13). [Fig. 7(a)] has the momentum dependence of an extended -wave, and its sign differs from the signs of and . Thus, –as well as –emerges due to the pair-hopping interaction via the SK mechanism, although it is affected by the terms of and in Eq. (2). It can be verified that the SK mechanism can work with the pair-hopping interaction even if . Moreover, the absolute values of are larger than those of for all , , and . Therefore, as shown in Fig. 7(d), the linear combination behaves like an extended -wave superconducting gap.

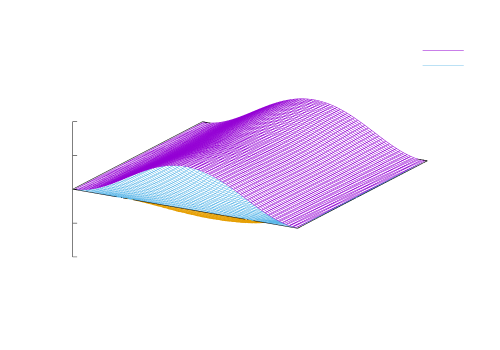


I have shown that the coexistence of extended - and -wave gaps is theoretically possible in the three-band –– model. The coexistence of - and -wave gaps was originally proposed to explain the apparently conflicting results of scanning tunnelling spectroscopy in HTSC [43]. So far, the experiments on Bi2Sr2CaCu2O8+δ (Bi2212) utilizing tunneling effect in the superconducting phase, which include -axis twist Josephson experiments [44, 45, 46, 47, 48, 49, 50], -axis scanning tunnelling microscopy [51, 52, 53], and intrinsic Josephson junction terahertz emission [54, 55], provide clear evidences that the superconducting gap has -wave symmetry. These experiments can directly observe the superconducting gap without breaking the gap into quasiparticles, and this result is also reasonable for the coexistence of - and -wave gaps. In the superconducting phase, where - and -wave gaps coexist, the -wave gap is dominant over the -wave gap in the energy , where indicates the -wave gap magnitude. On the other hand, only when the -wave gap magnitude satisfies , the -wave gap becomes dominant over the -wave gap in the energy .
In contrast, the quasiparticles from the -wave gap can be observed in the energy , where their excitation energies are always smaller than those of the quasiparticles from the -wave gap. Thus, the experimental method breaking the gap into quasiparticles does mainly observe the -wave gap. For example, both temperature and magnetic field dependences of low-temperature specific heat indicate that the -wave superconducting gap exists in near optimally doped Bi2Sr2-xLaxCuO [56].
The above discussion holds even if the -wave gap is not a superconducting gap. The angle-resolved photoemission spectroscopy (ARPES) experiment on Bi2212 shows the marked change of temperature dependence of spectral intensity across critical value with hole doping [57]. This change with hole doping can be interpreted as a result of the coexistence of - and -wave gaps when we replace energy with temperature in the above discussion. For , the -wave gap affects the electronic structure above if . The electronic structure affected by the -wave gap is called pseudogap. However, for , both the - and -wave gaps do not affect the electronic structure above if . Therefore, the pseudogap disappears across with hole doping, which has also been observed by the ARPES experiment [57].
Furthermore, Raman spectroscopy [58] and the magnetic field penetration depth measurement by muon-spin rotation [59, 60, 61] have provided evidence that supports the coexistence of - and -wave gaps in hole-doped HTSC. In theoretical work, the possibility of the coexistence of an extended - and -wave superconducting state has been shown with the analysis of the 2D – model considering fluctuation effects [13], and further experimental and theoretical research that assumes such coexistence is desired in the future.
I conclude by comparing the obtained superconducting state to that found in other theoretical work. The -wave superconducting gap composed of and , which emerges due to the exchange interaction via the SK mechanism, corresponds to the one mediated by antiferromagnetic spin fluctuations (AFSF) [62]. This is clear because the superexchange interaction among electrons, which is responsible for the AFSF, can be derived from the exchange interaction between and electrons. In general, once the superexchange interaction acts between charge carriers, the -wave superconductivity can emerge [63]. Moreover, the -wave superconductivity in my model can emerge only with the - band hybridization. Therefore, it must be important that the electron is implicitly hybridized with the electron in the AFSF-mediated superconductivity. This speculation is supported by the studies of Kondo lattice models proposed for copper oxide [64, 65, 66, 67, 68, 69, 70, 71]. The Kondo interaction between localized spin and electron in Kondo lattice models corresponds to the exchange interaction between and electrons in the large- limit of my model. The studies of Kondo lattice models indicate that superconductivity emerges due to the Kondo effect, the compensation for the localized spin by the electrons via the Kondo interaction. As the Kondo effect corresponds to the formation of a Fermi liquid state through the - band hybridization [30], the superconductivity in Kondo lattice models is consistent with the -wave superconductivity in my model.
The extended -wave superconducting gap composed of and , which emerges due to the pair-hopping interaction via the SK mechanism, corresponds to the kinetic-energy-driven superconductivity of the single-band – model [72, 73, 74, 75, 76, 77, 78, 79, 80]. In the kinetic-energy-driven superconductivity, the charge carriers form the superconducting pairs to gain kinetic energy. This energy gain can be derived from the pair-hopping interaction between and electrons, which works to form the extended -wave superconducting gap in my model.
4 Summary
In summary, the three-band –– model is derived assuming that the double occupancy by electrons is not excluded. When the electron is hybridized with the electron through exchange and pair-hopping interactions, the dome-shaped superconducting phase can be reproduced despite the strong correlations among electrons. In the superconducting phase, the extended - and -wave superconducting gaps coexist. The extended -wave gap emerges due to the pair-hopping interaction via the SK mechanism, which works effectively due to the charge fluctuations. In contrast, the -wave gap emerges due to the exchange interaction via the SK mechanism, which can effectively work only with the - band hybridization. The obtained superconducting state is consistent with those in other theoretical work, which include AFSF-mediated superconductivity and kinetic-energy-driven superconductivity.
Acknowledgements
The author would like to thank Prof. T. Tohyama and Prof. H. Yamase for their invaluable comments. The author is also grateful to anonymous reviewers for providing informations on many important references and insightful comments.
References
References
- [1] Chao K A, Spałek J and Oleś A M 1977 J. Phys. C: Solid State Phys.10 L271
- [2] Chao K A, Spałek J and Oleś A M 1978 Phys. Rev.B 18 3453
- [3] Zhang F C and Rice T M 1988 Phys. Rev.B 37 3759
- [4] Zaanen J and Oleś A M 1988 Phys. Rev.B 37 9423
- [5] Matsukawa H and Fukuyama H 1989 J. Phys. Soc. Japan58 2845
- [6] Mori M, Tohyama T and Maekawa S 2002 Phys. Rev.B 66 064502
- [7] Plakida N M 2002 Cond. Matter Phys. 5 707
- [8] Rösch O and Gunnarsson O 2004 Phys. Rev. Lett.92 146403
- [9] Ishihara S and Nagaosa N 2004 Phys. Rev.B 69 144520
- [10] Tohyama T 2004 Phys. Rev.B 70 174517
- [11] Mishchenko A S and Nagaosa N 2004 Phys. Rev. Lett.93 036402
- [12] Mishchenko A S and Nagaosa N 2006 Phys. Rev.B 73 092502
- [13] Mallik Aabhaas V, Gupta Gaurav K, Shenoy Vijay B and Krishnamurthy H R 2020 Phys. Rev. Lett.124 147002
- [14] Zhang F C 2003 Phys. Rev. Lett.90 207002
- [15] Yuan F, Yuan Q and Ting C S 2005 Phys. Rev.B 71 104505
- [16] Wang Q H, Wang Z D, Chen Y and Zhang F C 2006 Phys. Rev.B 73 092507
- [17] Abram M, Kaczmarczyk J, Jędrak J and Spałek J 2013 Phys. Rev.B 88 094502
- [18] Spałek J, Zegrodnik M and Kaczmarczyk J 2017 Phys. Rev.B 95 024506
- [19] Zegrodnik M and Spałek J 2017 Phys. Rev.B 96 054511
- [20] Fidrysiak M and Spałek J 2020 Phys. Rev.B 102 014505
- [21] Schrieffer J R and Wolff P A 1966 Phys. Rev.149 491
- [22] Suhl H, Matthias B T and Walker L R 1959 Phys. Rev. Lett.3 552
- [23] Kondo J 1963 Prog. Theor. Phys. 29 1
- [24] Kondo J 2002 J. Phys. Soc. Japan71 1353
- [25] Emery V J 1987 Phys. Rev. Lett.58 2794
- [26] Penson K A and Kolb M 1986 Phys. Rev.B 33 1663
- [27] Belkasri A and Buzatu F D 1996 Phys. Rev.B 53 7171
- [28] Robaszkiewicz S and Bułka B D 1999 Phys. Rev.B 59 6430
- [29] Kapcia K J 2014 Acta Phys. Pol. A 126 53
- [30] Yamada K, Yosida K and Hanzawa K 1992 Prog. Theor. Phys. Suppl. No. 108 141
- [31] Yamada K 1975 Prog. Theor. Phys. 53 970
- [32] Yosida K and Yamada K 1975 Prog. Theor. Phys. 53 1286
- [33] Georges A and Kotliar G 1992 Phys. Rev.B 45 6479
- [34] Zhang X Y, Rozenberg M J and Kotliar G 1993 Phys. Rev. Lett.70 1666
- [35] Ino A, Mizokawa T, Fujimori A, Tamasaku K, Uchida S, Kimura T, Sasagawa T and Kishio K 1997 Phys. Rev. Lett.79 2101
- [36] Fujimori A, Ino A, Mizokawa T, Kim C, Shen Z X, Sasagawa T, Kimura T, Kishio K, Takaba M, Tamasaku K, Eisaki H and Uchida S 1998 J. Phys. Chem. Solids 59 1892
- [37] Fujimori A, Ino A, Yoshida T, Mizokawa T, Shen Z X, Kim C, Kakeshita T, Eisaki H and Uchida S 2001, Open Problems in Strongly Correlated Electron Systems ed J. Bonca et al. (Dordrecht: KluIr Academic Pub.) p 119
- [38] Tsukada A, Yamamoto H and Naito M 2006 Phys. Rev.B 74 174515
- [39] Yoshida T, Zhou X J, Tanaka K, Yang W L, Hussain Z, Shen Z X, Fujimori A, Sahrakorpi S, Lindroos M, Markiewicz R S, Bansil A, Komiya Seiki, Ando Yoichi, Eisaki H, Kakeshita T and Uchida S 2006 Phys. Rev.B 74 224510
- [40] Wen H-H, Shan L, Wen X G, Wang Y, Gao H, Liu Z Y, Zhou F, Xiong J W and Ti W X 2005 Phys. Rev.B 72 134507
- [41] Wang Y, Yan J, Shan L, Wen H-H, Tanabe Y, Adachi T and Koike Y 2007 Phys. Rev.B 76 064512
- [42] Vidberg H J and Serene J W 1977 J. Low. Temp. Phys. 29 179
- [43] Müller K A 1995 Nature 377 133
- [44] Li Qiang, Tsay Y N, Suenaga M, Klemm R A, Gu G D and Koshizuka N 1999 Phys. Rev. Lett.83 4160
- [45] Takano Y, Hatano T, Fukuyo A, Ishii A, Ohmori M, Arisawa S, Togano K and Tachiki M 2002 Phys. Rev.B 65 140513(R)
- [46] Takano Y, Hatano T, Ohmori M, Kawakami S, Ishii A, Arisawa S, Kim S-J, Yamashita T, Togano K and Tachiki M 2003 J. Low. Temp. Phys. 131 533
- [47] Takano Y, Hatano T, Kawakami S, Ohmori M, Ikeda S, Nagao M, Inomata K, Yun K S, Ishii A, Tanaka A, Yamashita T and Tachiki M 2004 Physica C 408-410 296
- [48] Latyshev Y I, Orlov A P, Nikitina A M, Monceau P and Klemm R A 2004 Phys. Rev.B 70 094517
- [49] Klemm R A 2005 Phil. Mag. 85 801
- [50] Zhu Y, Liao M, Zhang Q, Xe H-Y, Meng F, Liu Y, Bai Z, Ji S, Zhang J, Jiang K, Zhong R, Schneeloch J, Gu G, Gu L, Ma X, Zhang D and Xue Q-K 2021 arXiv:1903.07965v2
- [51] Misra S, Oh S, Hornbaker D J, DiLuccio T, Eckstein J N and Yazdani A 2002 Phys. Rev. Lett.89 087002
- [52] Hoogenboom B W, Kadowaki K, Revaz B and Fischer Ø 2003 Physica C 391 376
- [53] Zhong Y, Wang Y, Han S, Lv Y-F, Wang W-L, Zhang D, Ding H, Zhang Y-M, Wang L, He K, Zhong R, Schneeloch J, Gu G-D, Song C-L, Ma X-C and Xue Q-K 2016 Sci. Bull. 61 1239
- [54] Kashiwagi T, Sakamoto K, Kubo H, Shibano Y, Enomoto T, Kitamura T, Asanuma K, Yasui T, Watanabe C, Nakade K, Saiwai Y, Katsuragawa T, Tsujimoto M, Yoshizaki R, Yamamoto T, Minami H, Klemm R A and Kadowaki K 2015 Appl. Phys. Lett. 107 082601
- [55] Kashiwagi T, Yamamoto T, Minami H, Tsujimoto M, Yoshizaki R, Delfanazari K, Kitamura T, Watanabe C, Nakade K, Yasui T, Asanuma K, Saiwai Y, Shibano Y, Enomoto T, Kubo H, Sakamoto K, Katsuragawa T, Marković B, Mirković J, Klemm R A and Kadowaki K 2015 Phys. Rev.Appl. 4 054018
- [56] Wang Y, Liu Z-Y, Lin C T and Wen H-H 2011 Phys. Rev.B 83 054509
- [57] Chen S-D, Hashimoto M, He Y, Song D, Xu K-J, He J-F, Devereaux T P, Eisaki H, Lu D-H, Zaanen J, Shen Z-X 2019 Science 366 1099
- [58] Masui T, Limonov M, Uchiyama H, Lee S, Tajima S and Yamanaka A 2003 Phys. Rev.B 68 060506(R)
- [59] Khasanov R, Shengelaya A, Maisuradze A, La Mattina F, Bussmann-Holder A, Keller H and Müller K A 2007 Phys. Rev. Lett.98 057007
- [60] Khasanov R, Strässle S, Di Castro D, Masui T, Miyasaka S, Tajima S, Bussmann-Holder A and Keller H 2007 Phys. Rev. Lett.99 237601
- [61] Khasanov R, Shengelaya A, Bussmann-Holder A, Karpinski J, Keller H and Müller K A 2008 J. Supercond. Nov. Magn. 21 81
- [62] Moriya T and Ueda K 2000 Adv. Phys. 49 555 and references therein
- [63] Que W-M and Kirczenow G 1987 Solid State Commun.64 1052
- [64] Prelovšek P 1988 Phys. Lett.A 126 287
- [65] Ramšak A and Prelovšek P 1989 Phys. Rev.B 40 2239
- [66] Castellani C, Di Castro C and Grilli M 1988 Physica C 153-155 1659
- [67] Castellani C, Di Castro C and Grilli M 1988 Int. J. Mod. Phys. B 2 659
- [68] Cancrini N, Caprara S, Castellani C, Di Castro C, Grilli M and Raimondi R 1991 Europhys. Lett. 14 597
- [69] Kamimura H 1988 Int. J. Mod. Phys. B 2 699
- [70] Andrei N and Coleman P 1989 Phys. Rev. Lett.62 595
- [71] Hatsugai Y, Imada M and Nagaosa N 1989 J. Phys. Soc. Japan58 1347
- [72] Hirsch J E 1992 Physica C 201 347
- [73] Tsunetsugu H and Imada M 1998 J. Phys. Soc. Japan67 1864
- [74] Tsunetsugu H and Imada M 1999 J. Phys. Soc. Japan68 3162
- [75] Imada M and Onoda S 2001, Open Problems in Strongly Correlated Electron Systems ed J. Bonca et al. (Dordrecht: KluIr Academic Pub.) p 69
- [76] Sarker S K and Lovorn T 2010 Phys. Rev.B 82 014504
- [77] Sarker S K and Lovorn T 2012 Phys. Rev.B 85 144502
- [78] Feng S, Zhao H and Huang Z 2012 Phys. Rev.B 85 054509
- [79] Feng S, Kuang L and Zhao H 2015 Physica C 517 5
- [80] Gao D, Mou Y and Feng S 2018 J. Low Temp. Phys. 192 19