Coexistence of Multifold and Multidimensional Topological Phonons in KMgBO₃

Introduction: Topological properties of fermionic states enforced by spatial and non-spatial symmetries have been ubiquitously explored in the literature.Kaustuv ; YXia ; ShuoWang ; HaoZheng ; MasatoshiSato The same for bosons (photons, phonons), however, has started only recentlySebastian ; Roman ; Emil and there are only limited studies along these lines. The concept of chiral phonons is further extended to materials with non-symmorphic crystalline symmetry, which unlocks the applications in THz frequency range.Tiantian ; Jiangxu ; JiangxuLi In addition, topological phonons also find applications in unconventional heat transfer, electron phonon coupling, and phonon diode.Jiangxu ; Emil ; Yizhou The advantage of topological bosons over fermions is the possibility of probing topological states in any frequency range using experimental techniques unlike fermionic states, where this is mostly possible only near the Fermi level (E_F). In line with electronic states, topological phonons also show anomalous transport behaviour, such as anomalous phonon hall effect.Lifa ; KangtaiSun ; TaoQin Over the years, diverse quasiparticle excitations have emerged as a consequence of different band crossings which can host non-zero topological Chern number. For instance, conventional spin-$\frac{1}{2}$ Weyl fermions possess Chern number $\pm$1. Moreover, unconventional chiral particles with Chern number greater than unity have also been realised in crystalline systems. Threefold spin-1 and fourfold charge-2 Dirac fermions are examples of such higher Chern number quasiparticles.Zhicheng ; ShiXinZhang ; chanchal These multifold band crossings yield a zero dimensional (0D) point degeneracy in momentum space.MZahidHasan There exists other types of topological band crossings such as nodal line/loop and nodal surface which induce one dimensional(1D) and two dimensional (2D) degeneracy respectively.XiaotianWang

A proper understanding and hunt for real materials which host multiple topological phonons have emerged as a frontline area of research due to its demand from both fundamental and application point of view. Several 3-dimensional and 2-dimensional materials are investigated for topological phonons.RYWang ; ChengwuXie ; YuanjunJin Coexistence of a few multidimensional topological phonons have been identified in some materials.Jianhua However, to the best of our knowledge, coexistence of multifold and multidimensional (such as nodal points(NP), nodal line(NL) and nodal surfaces(NS)) phononic quasiparticles is never reported in a real material.

Tuning the topological properties of a material via strain/pressure/doping is a well accepted method which helps to modify the symmetry and hence the electronic structure, facilitating the onset of trivial/nontrivial topological excitations.CJEklund ; LeiJin There has been several theoretical/experimental studies which has showcased such symmetry mediated transition from topological insulator to semimetal and vice versa, creation and annihilation of Weyl/Dirac and other kinds of topological nodes.ChunLin ; SteveM ; YanSun A similar band engineering and the associated transition can be expected for phonon quasiparticles as well.

In this letter, we present the co-existence of several topological phonon excitations in a single compound, KMgBO₃, which crystallizes in a cubic phase. KMgBO₃ is an experimentally synthesised chiral compound, which has been explored for nonlinear optical properties.exp_paper ; JianghuiZheng Recently, this compound is also found to show interesting topological electronic properties by us.chanchal One of the main focus of the present study is to investigate the topological phonon excitations and the effect of symmetry breaking on topological properties of this material. Pristine KMgBO₃ has a rich phonon band dispersion, showing several topologically non-trivial multifold/multidimensional band crossings in different frequency range. This includes spin-1 Weyl, charge 2 Dirac, single Weyl, nodal line, nodal loop and nodal surface states. These states are topologically protected by crystalline and time reversal symmetries. Application of strain breaks the C₃ rotational symmetry, which annihilates the spin-1 double Weyl nodes but preserve the charge 2 Dirac node and nodal surface states. We have further disturbed the symmetry by doping with Rb, transforming it to a triclinic structure. Though doping preserves the total chirality, it destroys all the topological phonon features. Additionally, we have explored two other prototype compounds RbMgBO₃RVKurbatov and CsCdBO₃,HongweiYu which show similar topological features.

Computational Details: First-principles calculations are done using the Vienna Ab initio Simulation Package (VASP)Kresse1 ; Kresse2 and Phonopy.Togo Other computational details are provided in the supplementary material(SM).suppl

Crystal Structure : KMgBO₃ crystallizes in cubic structure with space group P2₁3 (#198).exp_paper The theoretically optimised lattice parameter (6.09 $\AA$) matches fairly well with the experiment (6.8345 $\AA$).exp_paper Figure 1(a,b) show the real space crystal structure and bulk and (001) surface Brillouin zone (BZ). The space group 198 holds the tetrahedron (T4) point group symmetry, which provides two twofold screw rotations, S_2z = {C${}_{2z}|\frac{1}{2},0,\frac{1}{2}|$}, S_2y ={C${}_{2z}|0,\frac{1}{2},\frac{1}{2}|$} and one threefold rotation, S₃= {C⁺_3,111$|$0,0,0} as generators at $\Gamma$ point. At R point, the generators are S_2x = {C${}_{2x}|\frac{1}{2},\frac{3}{2},0|$}, S_2y = {C${}_{2y}|0,\frac{3}{2},\frac{1}{2}|$} and S₃= {C^-_3,111$|$0,0,0}, while at X point, they are S_2y = {C${}_{2y}|0,\frac{1}{2},\frac{1}{2}|$} and S_2z = {C${}_{2z}|\frac{1}{2},0,\frac{1}{2}|$}.book In addition, the space group preserves time-reversal symmetry($T$).

Phonon spectra: KMgBO₃ structure involves four formula units per unit cell leading to 24 atoms in the cell, which generate 3 acoustic and 69 optical phonon modes. The absence of imaginary modes confirms the dynamical stability of the compound. Phonon dispersion over a wider frequency range (0-40 THz) is presented in Fig. S1(a).suppl A close inspection of bulk phonon dispersion reveals the prosperity of different nature of band crossings in different frequency range, yielding topological Weyl, nodal line/loop and nodal surface states, as detailed below. We have also studied the surface phonon spectra.

Double Weyl Phonons : A symmetry enforced 3- or 4-fold band crossings can induce unconventional topological excitations.BBradlyn Let us first consider the case at $\Gamma$ point. For phonons, the square of the time-reversal symmetry operator($T$) is identity($I$). The generators S_2z and S_2y commute each other at $\Gamma$ point, which can be understood by considering the transformation of lattice coordinates as a function of the twofold screws C_2z and C_2y. These transformations are shown in Ref. footnote0, .

To understand the degeneracy of bands at $\Gamma$, one need to consider the eigenstates generated by these symmetry operators which commute with the Hamiltonian of the system, S_2z$|\psi>$ = $\lambda$₁$|\psi>$, S_2y$|\psi>$ = $\lambda$₂$|\psi>$, where $\lambda$₁ =$\pm$1, $\lambda$₂ =$\pm$1 according to S²_2z = 1 and S²_2y = 1. S₃ obeys S_2zS₃=S₃S_2y and S₃S_2zS_2y = S_2yS₃, which impose a threefold degeneracy at $\Gamma$ with eigenstates $|\psi>$, $|$S₃$\psi$$>$ and $|$S²₃$\psi$$>$, when screws are nontrivial.chanchal When screws are trivial, the $\Gamma$ point can hold either nondgenerate or twofold degeneracy.chanchal The threefold degenerate bands at $\Gamma$ arises from a combination of two highly linearised bands and one flat band, which can be defined by spin-1 states with chirality +2,0 and -2.BBradlyn ; chanchal Two screws S_2x and S_2y anticommute each other at R point, and S²_2x = -1, S²_2y = -1. This induces a twofold degenerate state (with eigenvalue $\pm$i) at R point. Further, the combination of threefold rotation S₃ and twofold screws create two more distinct states, enabling a fourfold charge 2 Dirac point with chirality $-2$,$-2$, $+2$ and $+2$. Further symmetry related details can be found in our previous study performed for electronic excitation.chanchal

Figure 1(c) displays the phonon dispersion in a smaller frequency range where a threefold spin-1 Weyl point (at $\Gamma$) and a fourfold charge 2 Dirac point (at R) are observed. At $\Gamma$ point, near 18.76 THz, three bands (band number 54, 55 and 56) cross degenerately, with Chern number -2 (for band 54), 0 (for 55) and +2 (for 56). At R point, near 18.73 THz, a fourfold degenerate band crossing arises which involve 53, 54, 55 and 56^th bands (Fig. 1(c)). This fourfold unconventional Dirac like node can be seen as a combination of two identical spin- $\frac{1}{2}$ Weyl phonons, with a net topological charge 2.BBradlyn A similar spin-1 Weyl and charge $2$ Dirac node also occur at other frequency range, one of which is shown in Fig. S1(b) of SM.suppl Simulated Berry curvature at $\Gamma$ point (for -2 chirality) in the k_x-k_y plane is shown in Fig. S1(c),suppl clearly confirming the flow of Berry flux from $\Gamma$ point. Due to the large separation between bulk double Weyl phonons, a clean surface spectra is expected as analysed below.

Surface states of the double Weyl phonons are examined on (001) and (111) surfaces. Figure 1(d) and 1(f) show the (001) surface state corresponding to spin-1 Weyl point and charge $2$ Dirac point projected on $\bar{\Gamma}$ and $\bar{M}$ points respectively. Two linearly dispersed and one parabolic surface state can be seen at $\bar{\Gamma}$ point, which are originated from three bulk bands with chirality $-2$ ,$0$,$2$, while a highly linearised surface state is observed at $\bar{M}$ point, which represent the charge 2 Dirac point. Since these two nodes at $\bar{\Gamma}$ and $\bar{M}$ possess opposite chirality, one can expect a surface arc connecting these two points. A surface arc simulated at 18.76 THz is shown in Fig. 1(e), which indirectly connects $\bar{\Gamma}$ and $\bar{M}$ points. Figure 1(g) shows the surface arc projected at a slightly lower frequency (18.73 THz) which directly connects the two points, with a long diagonal. Such large surface arcs are much easier to probe experimentally, as reported earlier for other topological phonon materials.Tiantian Further, the analysis of (111) surface shows the presence of charge 2 Dirac node, see Fig. S1(d) of SM.suppl The surface state of spin-1 Weyl point located at higher phonon frequency is also presented in SMsuppl (see Fig. S1(e)).

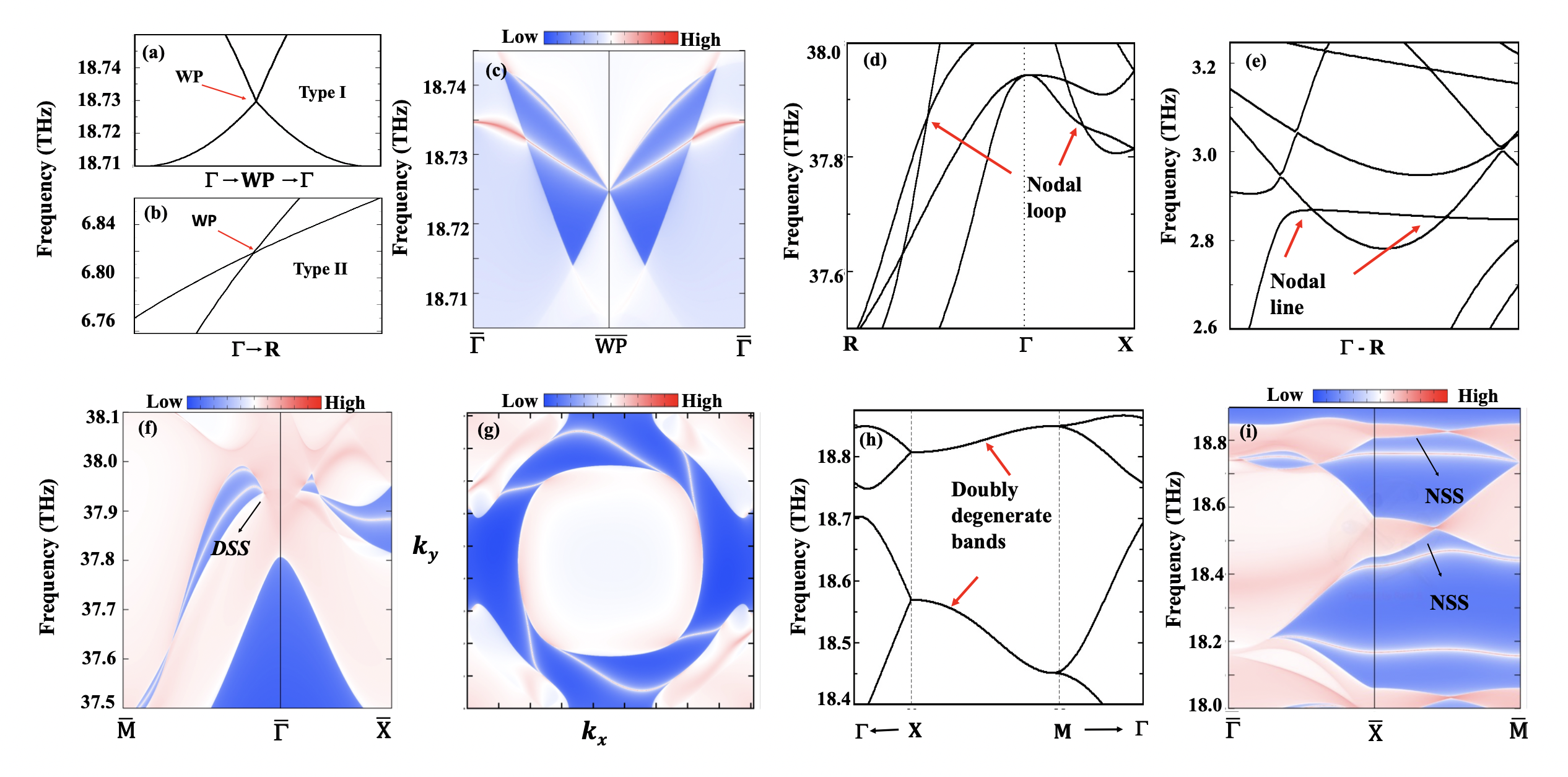
Single Weyl Phonons : Pristine KMgBO₃ also hosts two types of spin $\frac{1}{2}$ topological states, (1) zero dimensional Weyl points and (2) one dimensional Nodal line/Nodal ring. First let us discuss the single Weyl point. Weyl nodes can be formed by breaking either the time-reversal symmetry or the inversion symmetry. In the present case, it arises from the noncentrosymmetric nature of KMgBO₃. Weyl nodes can be further classified into type I and II, according to the nature of band crossings.footnote1 ; Alexey ; BWXia In KMgBO₃ phonon spectra, both types of Weyl nodes are observed, as shown in Fig. 2(a,b). Type I is observed on ’$xy$’ plane in the frequency range 18.71-18.74 THz (formed by the crossing of 54^th and 55^th phonon bands). While, type II is observed along $\Gamma$-R line in the frequency range 6.76-6.84 THz (formed by the crossing of 28^th and 29^th bands). We have chosen one of the Weyl points (type-I) to present its surface state on (001) surface, as shown in Fig. 2(c). Clearly, this is a highly linearised surface state with a pristine surface arc.

Next, we will discuss two other types of spin-$\frac{1}{2}$ topological nodal points. Presence of more than one nodal points at the same frequency but different momentum forms one dimensional nodal line/loop like band crossing. Figure 2(d) shows one such example where two tilted nodal points are observed along two different high symmetry lines ($\Gamma$-X and $\Gamma$-R) at the same frequency. This causes the formation of a nodal loop. Similarly, there exists nodal loops along other directions such as $\Gamma$-Y and $\Gamma$-R, $\Gamma$-Z and $\Gamma$-R. Additionally, the phonon dispersion along $\Gamma$-R show two nodal points at same frequency which provides a nodal line behaviour (see Fig. 2(e)). Since the bulk R point projects as $\bar{M}$ on (001) surface, it gives a drumhead-like surface due to the nodal loop around $\bar{\Gamma}$ point. This is shown in Fig. 2(f) and the corresponding iso-surface arc in Fig. 2(g). A similar nature of iso-surface has been observed in a carbon allotrope.JingYangYou

Nodal Surface : Higher dimensional band degeneracy has been theoretically predictedQingBo and experimentally realised in recent past.Yihao There are few symmetry mediated conditions which impose such high dimensional band degeneracy.footnote2 The bands along X-M and X-R aligned in k_x=$\pi$ plane provide a minimum of double degeneracy due to the above condition.ChengwuXie ; QingBo Figure 2(h) shows the double degenerate band along X-M. Similarly, a doubly degenerate phonon band can be seen in k_y,z=$\pi$ planes. It is evident from the figure that, these doubly degenerate bands are well separated and hence can be easily realised experimentally. Figure 2(i) shows the corresponding surface states, which is mostly flat with a low spread in frequency range enabling KMbBO₃ to be a promising candidate for ideal nodal surface. In a similar way, one can observe a nodal surface on other two surfaces. A combined visual of these nodal surface create and nodal cube around the BZ centre. This is a unique surface feature of KMgBO₃ which stands out in comparison to other reported topological nodal surface materials.Xiaotian

Strain effects : Both uni-axial (along $c$ axis) and bi-axial (along $a$ and $b$ axes) compressive and tensile strains are applied on KMgBO₃ to illustrate the effect of symmetry breaking on topological phonon excitations. Such strain breaks the cubic symmetry and transforms the structure to an orthorhombic space group P2₁2₁2₁ (# 19), which lacks the threefold C₃ rotational symmetrybook along with deltahedron type (D⁴₂) point group (see footnotefootnote3 for more symmetry related details).

Let us now understand the emergence of different topological phonon excitations as a function of uni-axial strain. Here we applied a maximum of 3$\%$ strain (both in compressive and tensile forms) in an interval of 1$\%$ along $c$ axis. At ambient state (cubic phase), KMgBO₃ hosts two kinds of double Weyl phonons i.e. spin-1 type at $\Gamma$ and charge 2 Dirac type at R points. It is clear that, in strained system, the generators at $\Gamma$ will enforce the bands to become non-degenerate (since the two screw operators commute), which should destroy the spin-1 type double Weyl phonon nature. The eigenvalues can be $\pm$1 at $\Gamma$ point.RMatthias This is precisely shown in Fig. 3(a) (under 3$\%$ compressive strain). Coming to R point, the possible combinations of eigenvalues are ($1$,-$1$,-$1$), (-$1$,$1$,-$1$), (-$1$,-$1$,$1$) and ($1$,$1$,$1$)RMatthias which provide a fourfold degeneracy and assure the possibility of preserving the charge 2 Dirac point. The bulk phonon dispersion at R point is shown in Fig. 3(b)(under 3$\%$ compressive strain), confirming the persistence of charge 2 Dirac state at R. To confirm the double Weyl phonon nature, the surface state of charge 2 Dirac point is simulated, which shown in Fig. 3(c). A highly linearised surface state along with a clear surface arc is clearly visible from this figure.

Further, let us analyse the effect of strain on spin-$\frac{1}{2}$ Weyl phonons. The analysis of band topology between 54^th and 55^th bands shows the presence of two Weyl points with +1 chirality around $\Gamma$-point (with locations (0,0,+k_z) and (0,0,-k_z)). This balances the chirality generated due the double Weyl phonons at R point. Figure 3(d) displays the computed Berry curvature on k_x-k_z plane, which shows the outcome as expected. Importantly, the combination of double and single Weyl phonons conserves the Ninomiya theoremHBNielsen in strained state. To further understand this point, we have disturbed the symmetry by substituting one of the K element by Rb. This transforms the system to a low symmetry triclinic space group (P1), which lacks all the screw rotation symmetries. The phonon dispersion of strained (P2₁2₁2₁) and the doped phase (P1) are presented in Fig. 3(e) and 3(f) respectively. The Dirac nature at R point is defaced in the P1 phase, which arises purely due to the breaking of screw symmetry, with the simultaneous defacing of +1 chiral Weyl points along -Z- $\Gamma$-Z direction.

Further, the ‘1D’ nodal ring/loop is destroyed under uni-axial strain, with the opening of a gap along $\Gamma$-R. Regarding the ‘2D’ nodal surface, the presence of screws and time-reversal symmetry induce a Kramers like doubly degeneracy at k_i=$\pi$ which cause the formation of nodal surface. The application of biaxial strain alters the topological phonon excitations in a similar way. The phonon dispersion around the $\Gamma$ and R point under 3$\%$ bi-axial strain are shown in SM.suppl Changes in other topological features remain in line with those of uni-axial strain.

Other materials : We have also analysed the topological phonon excitations of two other experimentally synthesized prototype compounds RbMgBO₃ and CsCdBO₃. Optimised lattice parameter for RbMgBO₃ and CsCdBO₃ are 7.02 $\AA$ and 7.629 $\AA$ respectively, which are in good agreement with experiment.RVKurbatov ; HongweiYu A similar nature of phonon dispersion is observed for these two compounds, see Fig. 4(a,b). They show various topological phonons, including double Weyl, single Weyl, nodal line/loop and nodal surface. Full phonon dispersion in larger frequency interval and bulk/surface states of spin-1 type double Weyl nodes are shown in SM.suppl

Summary : We propose three promising candidate materials (KMgBO₃, RbMgBO₃, and CsCdBO₃) for topological phononic applications in different THz frequency range. At ambient condition, these materials provide a rich platform to simultaneously host several multifold and multidimensional topological Weyl phonons, such as spin-1 Weyl, charge 2 Dirac, single Weyl, nodal line/loop and nodal surface. These topological states are protected by crystalline and time reversal symmetries. Application of strain breaks the C₃ rotational symmetry which mediates the annihilation of spin-1 double Weyl nodes while preserves the other topological features. Substitution at K/Rb/Cs-site also lowers the symmetry to triclinic structure, and destroys most of the topological features. The present work, for the first time, showcase a novel candidate material where multiple topological phonon excitations coexist and hence can be an interesting platform for future theoretical/experimental investigations.

Acknowledgements: AA acknowledges DST SERB, India (Grant No. CRG/2019/002050) for funding to support this research. SPC thank IIT Bombay for institute postdoctoral fellowship and computing facility.C.M. would like to thank Institute for Basic Science in Korea (Grant No. IBS-R009-D1) for funding.