Coexistence of extended and localized states in one-dimensional non-Hermitian Anderson model
Abstract
In one-dimensional Hermitian tight-binding models, mobility edges separating extended and localized states can appear in the presence of properly engineered quasi-periodical potentials and coupling constants. On the other hand, mobility edges don’t exist in a one-dimensional Anderson lattice since localization occurs whenever a diagonal disorder through random numbers is introduced. Here, we consider a nonreciprocal non-Hermitian lattice and show that the coexistence of extended and localized states appears with or without diagonal disorder in the topologically nontrivial region. We discuss that the mobility edges appear basically due to the boundary condition sensitivity of the nonreciprocal non-Hermitian lattice.
I Introduction
Anderson localization (AL), a well-understood fundamental problem in condensed matter, is the absence of diffusion of waves in a disordered medium due to interference of waves AL0 . Specifically in AL, all states are exponentially localized in the presence of any disorder in one and two-dimensional Anderson model at which a random disordered on-site potential is introduced. On the other hand for weak disorder if the localization length is bigger than the system size then the system behaves as it is delocalized. In three dimensions, we would have a mobility edge separating localized and extended states. On contrary to the one dimensional (1D) Anderson model, in the Aubry-André model in which its disorder is modeled as a quasi-periodic on-site potential depending on the strength of incommensurate potential, all states are localized or delocalized AL1 . This means that the system can undergo a metal-insulator transition even in 1D. However, this transition is sharp, i.e. all single-particle eigenstates in the spectrum suddenly become exponentially localized above a threshold level of disorder. In both cases, localized and extended states generally do not coexist since non of these models possess a mobility edge in 1D, i.e., critical energy separates localized and delocalized energy eigenstates. Recent studies show that the transition is not sharp beyond the one-dimensional Aubry-André model with correlated disorder and hopping amplitudes. It was shown that an intermediate regime characterized by the coexistence of localized and extended states at different energies may occur AL3 ; AL4 ; AL4uneki ; AL4uneki2 ; AL4uneki3 ; AL4uneki4 . The theoretical findings were confirmed in an experimental realization of a system with a single-particle mobility edge AL5 . There is a vast literature on mobility edges in Hermitian systems, but it has only been recently that mobility edges have been explored for various 1D tight-binding non-Hermitian models NH0 ; NH1 ; NH2 ; NH3 ; NH4 ; NH5 ; NH6 ; NH6a ; NH7 ; NH8 ; NH9 ; NH10 ; NH11 ; NH13 ; NH14 ; NH15 ; NH16 ; NH16cemy ; NH17 ; NH17jgek . The first such model was considered in the pioneering paper by Hatano and Nelson hatano . In non-Hermitian systems, in comparison to the Hermitian ones, the mobility edges not only separate localized states from the extended states but also indicate the coexistence of complex and real energies. The latter allows us to come out with a topological characterization of mobility edges NH1 . Apart from these models, extended and localized states can coexist in some other Hermitian lattices with inhomogeneous trap NH1a ; NH1b and with partially disordered potential NH1d . In general, such systems require complicated engineering of the hopping parameters and onsite potentials NH1c .
In this work we consider non-Hermitian extensions of the one dimensional Anderson and Aubry-André-Harper models with asymmetric (nonreciprocal) hopping amplitudes at which non-Hermitian skin effect (NHSE) plays important roles on the localization cy0 ; cy1 ; cy2 ; ek1 ; cy3 ; cy4 ; cy5 ; ek4 ; cy6 ; cy7 ; cy8 ; ek2 ; ek3 ; ek5 ; ek6 . We introduce mixed boundary conditions (MBC) as a mixture of periodic (PBC ) and open (OBC) boundary conditions and show that extended and localized states can coexist even for the lattice without the disorder. We show that extended states form a closed loop in the complex energy plane while the localized states have real energies. We further explore the effect of onsite potentials and show that localized and extended states survive in the presence of the onsite potentials until topological phase transition occurs at strong disorder and all states are localized.
II Model
The starting point of our analysis is provided by the one-dimensional nonreciprocal lattice with asymmetric nearest-neighbor couplings and onsite potentials. The field amplitudes at various sites of the lattice can be obtained by solving
| (1) |
where with being the total number of sites, and are positive-valued coupling constants in the left and right directions, respectively, are real-valued onsite potentials. We assume , unless otherwise stated. Two different types of onsite potentials should be distinguished here. The first one is for the non-Hermitian Anderson model at which the onsite potentials are independent random potentials uniformly distributed in the interval with disorder strength . This model exhibits an Anderson transition at a non-zero value of the disorder strength in contrast to the Hermitian system, whose eigenstates are always localized in the presence of a random potential hatano ; PRX . The second one is for the non-Hermitian Aubry-André model at which the onsite potential is the quasi-periodic potential to describe an intermediate case between ordered and disordered systems, i. e., , where is the amplitude of the onsite incommensurate potential and is an irrational number. This model exhibits a metal-insulator transition when the potential strength is above a critical point cy7 .
The spectrum for the non-Hermitian lattice described by Eq. (1) shows strong sensitivity to the boundary conditions in topologically nontrivial region PRX . Consider for example, the case without onsite potentials, which is topologically nontrivial as long as . In this case, the spectrum describes a loop in the complex energy plane when the lattice has no edges (under PBC), whereas the spectrum is real when the lattice has two edges (under OBC). The change in the spectrum is also dramatic if the lattice has only one edge. In fact, there can be two such cases. The first one is the semi-infinite lattice () whose spectrum fills the interior of the PBC loop in the complex plane. However, this case is not physical since any experiment naturally contains a finite number of lattice sites. The second one is the finite lattice with only one edge, i. e., the lattice has an open edge on the left and the other edge is bent to form a circular ring on the right. Suppose that the right end of the lattice is coupled to the lattice at the lattice site . For an illustration, such a lattice with and is depicted in Fig.1 (a). In this case, the system satisfies mixed boundary conditions (MBC). In this case, Eq. (1) is modified at (due to the extra coupling at )
| (2) |
where is a site number in the bulk . Note that in order to obtain the solution of the former equation, we suppose
| (3) |
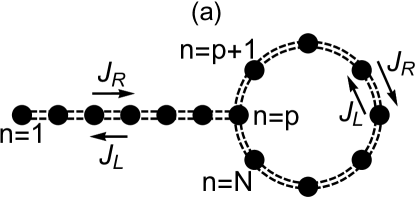
In the Hermitian lattice, , MBC is of no special importance since the extra coupling between the right edge and a bulk point of the lattice has only perturbative effects for a long lattice (the MBC, PBC and OBC energy spectra almost coincide). On the other hand, in the non-Hermitian lattice, MBC leads to the coexistence of extended (delocalized) and localized eigenstates even in the absence of any onsite potentials. We emphasize that the delocalized states are not extended only in the circular ring, but throughout the whole lattice. Note that such a coexistence was shown to appear in the presence of tailored quasi-periodical potentials and coupling constant NH1 ; NH2 ; NH3 ; NH4 ; NH5 ; NH6 ; NH6a ; NH7 ; NH8 ; NH9 ; NH10 ; NH11 ; NH13 ; NH14 . However, we see it in our system as a result of the boundary condition sensitivity of the nonreciprocal non-Hermitian systems.
Let us start with the case without onsite potentials, in a long but finite lattice. The spectrum under MBC describes both a line segment on the real axis and a loop that is slightly deformed from the PBC loop in the complex plane. Nat. Comm. 11, 5491 2020The states distributed on the MBC loop are extended states, whereas the ones on the line segment are skin states that are exponentially localized at the left edge. The parameter has the key role on the total number of extended states. In fact, there are extended eigenstates and the rest are all skin states. As a special case, we have only one skin state that is also topologically robust against the coupling disorder at . Oppositely, at , there exists one pair of extended states with real energies and all other states are localized skin states. To quantify localization and extension of an eigenstate with eigenvalue , we can use the inverse participation ratio (IPR)
| (4) |
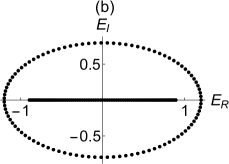
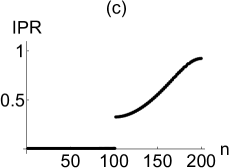
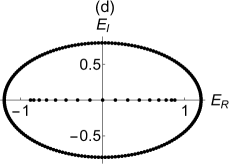
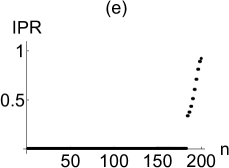
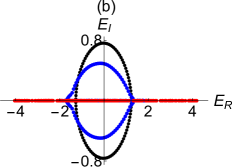
Specifically, IPR is of the order of for an extended eigenstate while it is close to for a localized eigenstate. To illustrate our discussion, we firstly plot the spectra in the complex plane for two different values of at , and in Fig.1 (b,d). The points on the loop are very dense for small values of and become sparse with increasing at fixed . The line segment on the real axis is always in the MBC loop. We then plot the IPR values corresponding to the cases (b,d) in Fig.1 (c,e). One can notice the gap in these plots where the IPR values jump from almost zero values to nearly at . This sharp increase of IPR implies the coexistence of localized and extended states in the absence of the disorder. To this end, let us write the analytical solution available for the unidirectional lattice with under MBC. In this case, the extended state is given by with eigenvalues , where and , respectively. There is just one skin state at zero energy since the system has an exceptional point of order .
Introducing disorder through random onsite potentials deforms the energy loop in the complex plane at fixed (contraction in the imaginary axis and elongation in the real axis as the disorder strength increases). Furthermore, it reduces the total number of extended states described by the points on the energy loop and hence increases the total number of localized states described by the points located on the real axis. At weak disorder strength, localized states are mostly skin states localized at the left edge. Beyond the Anderson transition point at which all eigenstates are localized, localization occurs all over the lattice. We plot the IPR values and complex energy spectra in Fig.2 (a,b) for the system described in Fig.1 but with various disorder strengths. As can be seen, increasing the disorder strength reduces the total number of extended states until the disorder strength is equal to a critical strength ( ) at which Anderson transition occurs. Therefore, there are still some extended eigenstates at (in black) and (in blue), but all eigenstates are localized at (in red). The corresponding spectrum becomes real valued and the OBC and MBC spectra are almost the same when all eigenstates are localized (Fig.2 (b)). The Anderson transition point also corresponds to a topological phase transition point as we will see below. As a result, we say that extended and localized states coexist only in the topologically nontrivial region. The critical disorder strength at which Anderson transition occurs depends on at fixed . Roughly speaking, at fixed increases slightly with unless is close to at which decreases sharply since the system has already a few extended eigenstates even in the absence of the disorder.
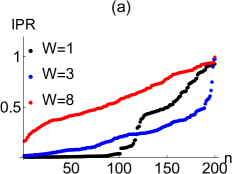
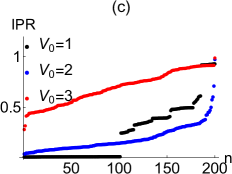
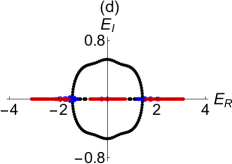
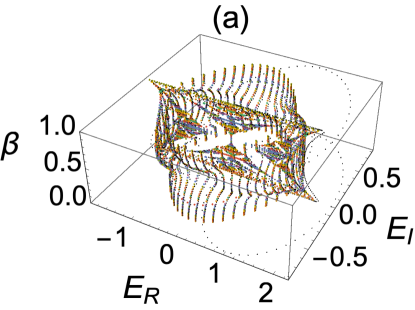
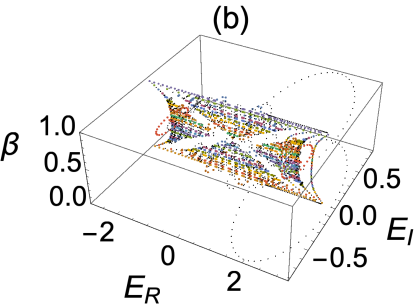
We perform another computations for the quasi-periodical potential and plot the IPR values and energy spectra in Fig.2 (c,d) and for three different values of at and . At , we see a sharp increase in the IPR values from to nearly , indicating that almost half of the states are extended while the rest are localized (in black). It is well known that the critical point at which localization-delocalization transition occurs is at in the Hermitian Aubry-Andre model. This value is almost equal to the critical point for the MBC (a slight perturbation comes from the left edge and coupling between the right edge and the lattice point ). The critical point also coincides with the topological phase transition point as we will see below. One can see a few complex eigenvalues (in blue) at with complex eigenvalues in Fig.2 (d) (in blue). Beyond the critical point the spectrum is real and all eigenstates are localized ( in red). As a result, we say that extended and localized states coexist in the quasi-periodical lattice under the MBC as long as is below than the critical number at which a topological phase transition occurs. To this end, we plot the butterfly spectra for the MBC in 3 dimensions, where is the vertical axis and the other two axes are the real and imaginary parts of the spectrum (Fig.3 ). Note that such a three dimensional butterfly structure is not possible under OBC, which has real spectrum.
Let us discuss topological features in our system. The spectral winding number at the zero base energy for the Hatano-Nelson model in the absence of onsite potentials is equal to when PRX . The system remains to be in the topological phase in the presence of onsite disorder until the disorder strength is strong enough to make all eigenstates to have real eigenvalues at which the Anderson transition occurs. To compute the topological number in the presence of the onsite potentials under MBC, we follow a similar method introduced in Ref. PRX . Suppose that the coupling constant at the lattice closing point (between and sites) are multiplied by , where is a fictitious magnetic flux. Then the winding number at zero base energy for a disordered lattice is given by
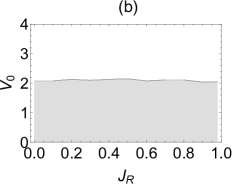
| (5) |
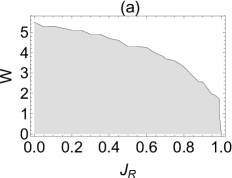
where is the corresponding Hamiltonian for the model (1) under MBC. The spectral winding number counts the number of times the complex spectral trajectory encircles base energy when varies from zero to . Apparently, the winding number becomes zero when the spectrum is real and all eigenstates are localized. Note that the above formula works well when the number is not close to since the spectral loop in the complex plane is less denser when increases. The MBC lattice is required to be a finite lattice, so we approximate the derivative with finite difference in the numerical differentiation. We present our numerical results and plot the winding number as a function of in Fig.4, where the shaded and unshaded area has and , respectively. In (a), the critical strength is around at and reduced to zero at (the spectrum becomes real in the Hermitian limit). On the other hand, it is almost constant for the quasi-periodical lattice (b). Small fluctuations around is the result of the perturbative effect due to the imposition of the MBC on the finite lattice.
We finally make a brief discussion for . Without loss of generality, we suppose that . Consider first that . Due to NHSE, bulk states are localized at the right edge under OBC. If we consider the MBC, the right edge is coupled to a bulk point. In this case, there are extended states and the rest are exponentially localized states centered at the bulk point where the right edge is closed. As opposed to the cases considered above, the extended states are extended only in the circular lattice at any value of and localized states have complex eigenvalues. Therefore, there are multiple energy loops in the complex plane, one for the extended states and another one(s) for the localized states. The localization length of the localized state increases and diffuses more into the straight lattice () as is increased. In the presence of the disorder, the number of extended states decreases and localized states appear centered at various points of the lattice. If the disorder is sufficiently strong, then Anderson transition takes place and all eigenstates have real eigenvalues and get localized.
III Conclusion
It is generally believed that mobility edges separating extended and localized states in one-dimensional tight-binding models appear if correlated disorder and coupling constants are specially tailored. Here we introduce the mixed boundary conditions to study a finite lattice with one open edge as an alternative to the semi-infinite boundary conditions, which also requires one open edge. The finite lattice we consider is the one whose one edge is bent to form a circular ring and coupled to the lattice at the lattice point . We have shown that extended and localized states can coexist even without onsite potentials in such a lattice as a result of the boundary condition sensitivity of the nonreciprocal non-Hermitian systems as long as the system is topologically nontrivial. We have also shown that the total number of extended states is exactly equal to , where is the total number of the lattice sites. In the presence of the disordered onsite potentials, the total number of the extended states reduces with increasing disorder strength and the extended states disappear when the disorder strength is at the critical point at which topological phase transition occurs since the corresponding spectrum become real valued. Experimental observation of mobility edges in non-Hermitian systems often requires complicated designs of couplings or onsite potentials. The mixed boundary conditions can be utilized in non-Hermitian systems to obtain mobility edges more easily.
Acknowledgments– C. Y. wishes to acknowledge the support from the Scientific and Technological Research Council of Turkey through the 2219 program with grant number 1059B191900044. H. R. acknowledge the support by the Army Research Office Grant No. W911NF-20-1-0276 and NSF Grant No. PHY-2012172. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein.
References
- (1) P. W. Anderson, Absence of diffusion in certain random lattices, Phys. Rev. 109, 1492 (1958).
- (2) S. Aubry and G. André, Analyticity breaking and Anderson localization in incommensurate lattices, Ann. Isr. Phys. Soc. 3, 133 (1980).
- (3) J. Biddle and S. Das Sarma, Predicted mobility edges in one-dimensional incommensurate optical lattices: an exactly solvable model of Anderson localization, Phys. Rev. Lett. 104, 070601 (2010).
- (4) Xiao Li, Xiaopeng Li, and S. Das Sarma, Mobility edges in one-dimensional bichromatic incommensurate potentials, Phys. Rev. B 96, 085119 (2017).
- (5) H. Yao, H. Khouldi, L. Bresque, and L. Sanchez-Palencia, Critical behavior and fractality in shallow one-dimensional quasi-periodic potentials, Phys. Rev. Lett. 123, 070405 (2019),
- (6) T. Liu, X. Xia, S. Longhi, and L. Sanchez-Palencia, Anomalous mobility edges in one-dimensional quasiperiodic models, SciPost Phys. 12 , 27 (2022).
- (7) Gergo Roosz, Uma Divakaran, Heiko Rieger, and Ferenc Igloi, Nonequilibrium quantum relaxation across a localization-delocalization transition, Phys. Rev. B 90, 184202 (2014).
- (8) Deylon F, Kunz H, Souillard B, One-dimensional wave equations in disordered media., J. Phys. A: Math. Gen. 16 25 (1983).
- (9) Henrik P. Lüschen, Sebastian Scherg, Thomas Kohlert, Michael Schreiber, Pranjal Bordia, Xiao Li, S. Das Sarma, and Immanuel Bloch, Phys. Rev. Lett. 120 , 160404 (2018).
- (10) Xu Xia, Ke Huang, Shubo Wang, and Xiao Li, Exact mobility edges in the non-Hermitian - model: Theory and possible experimental realizations, Phys. Rev. B 105, 014207 (2022).
- (11) Tong Liu, Hao Guo, Yong Pu, and Stefano Longhi, Generalized Aubry-André self-duality and mobility edges in non-Hermitian quasiperiodic lattices, Phys. Rev. B 102, 024205 (2020).
- (12) Longwen Zhou and Wenqian Han, Non-Hermitian quasicrystal in dimerized lattices, Chinese Phys. B 30, 100308 (2021).
- (13) Yucheng Wang, Xu Xia, Yongjian Wang, Zuohuan Zheng, and Xiong-Jun Liu, Duality between two generalized Aubry-André models with exact mobility edges, Phys. Rev. B 103, 174205 (2021).
- (14) Longwen Zhou, Yongjian Gu, Topological delocalization transitions and mobility edges in the nonreciprocal Maryland model, J. Phys.: Condens. Matter 34, 115402 (2022).
- (15) Liang-Jun Zhai, Guang-Yao Huang, and Shuai Yin, Cascade of the delocalization transition in a non-Hermitian interpolating Aubry-André-Fibonacci chain, Phys. Rev. B 104, 014202 (2021).
- (16) Tong Liu, Xu Xia, Real-complex transition driven by quasiperiodicity: A class of non-PT symmetric models, Phys. Rev. B 105, 054201 (2022).
- (17) Tong Liu, Shujie Cheng, Mobility edges in PT-symmetric cross-stitch flat band lattices, arXiv:2105.14724 (2021).
- (18) Li-Mei Chen, Yao Zhou, Shuai A. Chen, Peng Ye, Quantum Entanglement of Non-Hermitian Quasicrystals, arXiv:2112.13411 (2021).
- (19) Yanxia Liu, Xiang-Ping Jiang, Junpeng Cao, and Shu Chen, Non-Hermitian mobility edges in one-dimensional quasicrystals with parity-time symmetry, Phys. Rev. B 101, 174205 (2020).
- (20) Yanxia Liu, Yucheng Wang, Xiong-Jun Liu, Qi Zhou, and Shu Chen, Exact mobility edges, PT-symmetry breaking, and skin effect in one-dimensional non-Hermitian quasicrystals, Phys. Rev. B 103, 014203 (2021).
- (21) Yanxia Liu, Yongjian Wang, Zuohuan Zheng, Shu Chen, Exact non-Hermitian mobility edges in one-dimensional quasicrystal lattice with exponentially decaying hopping and its dual lattice, Phys. Rev. B 103, 134208 (2021).
- (22) Linhu Li, Ching Hua Lee, Jiangbin Gong, Impurity induced scale-free localization, Communications Physics 4, 42 (2021).
- (23) Souvik Roy, Santanu K. Maiti,Laura, M. Perez, Judith Helena Ojeda Silva, David Laroze, Localization Properties of a Quasiperiodic Ladder under Physical Gain and Loss: Tuning of Critical Points, Mixed-Phase Zone and Mobility Edge, Materials 15, 597 (2022).
- (24) Chaohua Wu, Jingtao Fan, Gang Chen, Suotang Jia, Non-Hermiticity-induced reentrant localization in a quasiperiodic lattice, New J. Phys. 23, 123048 (2021).
- (25) Zhen-Hua Wang, Fuming Xu, Lin Li, Dong-Hui Xu, and Bin Wang, Topological superconductors and exact mobility edges in non-Hermitian quasicrystals, Phys. Rev. B 105, 024514 (2021).
- (26) Xuedong Zhao, Yan Xing, Lu Qi, Shutian Liu, Shou Zhang, Hong-Fu Wang, Real-potential-driven anti-PT-symmetry breaking in non-Hermitian Su-Schrieffer-Heeger model New J. Phys.23, 073043 (2021).
- (27) Sen Mu, Longwen Zhou, Linhu Li, Jiangbin Gong, Non-Hermitian pseudo mobility edge in a coupled chain system, ArXiv:2111.11914 (2021).
- (28) Shujie Cheng and Xianlong Gao, Majorana zero modes, unconventional real-complex transition, and mobility edges in a one-dimensional non-Hermitian quasi-periodic lattice, Chinese Phys. B. 31, 017401 (2022).
- (29) Linhu Li, Ching Hua Lee, Sen Mu, Jiangbin Gong, Critical non-Hermitian Skin Effect, Nat. Comm. 11, 5491 (2020).
- (30) Luca Pezze and Laurent Sanchez-Palencia, Localized and extended states in a disordered trap, Phys. Rev. Lett. 106, 040601 (2011).
- (31) Titas Chanda, Ruixiao Yao, Jakub Zakrzewski, Coexistence of localized and extended phases: Many-body localization in a harmonic trap, Phys. Rev. Research 2, 032039(R) (2020).
- (32) Yi-Xin Xiao, Zhao-Qing Zhang, C. T. Chan, A band of bound states in the continuum induced by disorder, Sci. Rep. 8, 5160 (2018).
- (33) Alberto Rodriguez, Arunava Chakrabarti, and Rudolf A. Römer, Controlled engineering of extended states in disordered systems, Phys. Rev. B 86, 085119 (2012).
- (34) Hui Jiang, Li-Jun Lang, Chao Yang, Shi-Liang Zhu, and Shu Chen, Interplay of non-Hermitian skin effects and Anderson localization in nonreciprocal quasiperiodic lattices, Phys. Rev. B 100, 054301 (2019).
- (35) Stefano Longhi, Spectral deformations in non-Hermitian lattices with disorder and skin effect: A solvable model, Phys. Rev. B 103, 144202 (2021).
- (36) Yanxia Liu, Qi Zhou, and Shu Chen, Localization transition, spectrum structure, and winding numbers for one-dimensional non-Hermitian quasicrystals, Phys. Rev. B 104, 024201 (2021).
- (37) C Yuce, PT Symmetric Aubry-André Model, Phys. Lett. A 378, 2024 (2014).
- (38) Jahan Claes and Taylor L. Hughes, Skin effect and winding number in disordered non-Hermitian systems, Phys. Rev. B 103, L140201 (2021).
- (39) Ling-Zhi Tang, Guo-Qing Zhang, Ling-Feng Zhang, and Dan-Wei Zhang, Localization and topological transitions in non-Hermitian quasiperiodic lattices, Phys. Rev. A 103, 033325 (2021).
- (40) Qi-Bo Zeng and Yong Xu, Winding numbers and generalized mobility edges in non-Hermitian systems, Phys. Rev. Research 2, 033052 (2020).
- (41) C Yuce, Nonlinear non-Hermitian skin effect, Phys. Lett. A 408, 127484 (2021).
- (42) Yifei Yi and Zhesen Yang, Non-Hermitian Skin Modes Induced by On-Site Dissipations and Chiral Tunneling Effect, Phys. Rev. Lett. 125, 186802 (2020).
- (43) S. Longhi, Topological Phase Transition in non-Hermitian Quasicrystals, Phys. Rev. Lett. 122, 237601 (2019).
- (44) Sebastian Schiffer, Xia-Ji Liu, Hui Hu, and Jia Wang, Anderson localization transition in a robust PT-symmetric phase of a generalized Aubry-André model, Phys. Rev. A 103, L011302 (2021).
- (45) Z. O. Turker, C. Yuce, Open and closed boundaries in non-Hermitian topological systems, Phys. Rev. A 99, 022127 (2019).
- (46) C Yuce, Non-Hermitian anomalous skin effect, Phys. Lett. A 384, 126094 (2020).
- (47) Xiaoming Cai, Boundary-dependent self-dualities, winding numbers, and asymmetrical localization in non-Hermitian aperiodic one-dimensional models, Phys. Rev. B 103, 014201 (2021).
- (48) Tianyu Li, Yong-Sheng Zhang, Wei Yi, Engineering Dissipative Quasicrystals, arXiv:2111.14436 (2021).
- (49) Naomichi Hatano and David R. Nelson, Localization Transitions in Non-Hermitian Quantum Mechanics, Phys. Rev. Lett. 77, 570 (1996).
- (50) Zongping Gong, Yuto Ashida, Kohei Kawabata, Kazuaki Takasan, Sho Higashikawa, and Masahito Ueda, Topological Phases of Non-Hermitian Systems, Phys. Rev. X 8, 031079 (2018).