CodePAD: Sequence-based Code Generation with Pushdown Automaton
Abstract
In the process of code generation, it is essential to guarantee the generated code satisfies grammar constraints of programming language (PL). However, neglecting grammar constraints is a fatal drawback of commonly used sequence-based code generation. In this paper, we devise a pushdown automaton (PDA)-based methodology to address this problem, exploiting the principle that PL is a subset of PDA recognizable language and code accepted by PDA is grammatical. Specifically, we construct a PDA module and design an algorithm to constrain the generation of sequence-based models to ensure grammatical correctness. Guided by this methodology, we further propose CodePAD, a sequence-based code generation framework equipped with a PDA module, to integrate the deduction of PDA into deep learning. Additionally, this framework can leverage states of PDA deduction (including state representation, state prediction task, and joint prediction with state) to assist models in learning PDA deduction. To comprehensively evaluate CodePAD, we construct a PDA for Python and conduct extensive experiments on four public benchmark datasets. CodePAD can leverage existing sequence-based models, and we show that it can achieve 100% grammatical correctness percentage on these benchmark datasets. Thus, it relatively improve 17% CodeBLEU on CONALA, 8% EM on DJANGO, and 15% CodeBLEU on JUICE-10K compared to base models. In addition, our method significantly enhances pre-trained models, e.g., CodeBLEU of CodeGen-350M improvement from 3.21 to 21.54 on MBPP in zero-shot setting.
1 Introduction
Code generation is a hot research spot in the field of natural language processing (NLP) and software engineering Ling et al. (2016); Yin and Neubig (2018); Wei et al. (2019); Dong et al. (2022); Shen et al. (2022), which aims to help facilitate software development and revolutionize user programming. A well-designed code generation approach requires consideration of grammar in addition to semantics, as semantics ensures the functionality of code meets developer’s intention, while satisfying grammar is a basic requirement for programming.
Sequence-based approaches are the most commonly used in code generation Raychev et al. (2014); Jia and Liang (2016); Cao et al. (2019); Wang et al. (2021); Fried et al. (2022); Nijkamp et al. (2022), which has the following three advantages: 1) High efficiency. Sequence-based approach directly generates a token sequence of code along the order of human writing in one pass. 2) Convenient operation. It can obtain partially generated code with ease even if the result is incomplete or the generation is not finished, thus can be adopted for various code generation scenarios 111For example, code completion, a popular variant of code generation in practice, which completes code with contexts.. 3) Easy data accessibility. Sequence structured data is the most general form that can be obtained without much effort compared to other structured data. Thus, pre-trained methods with big data-driven usually employ sequence-based approaches Wang et al. (2021); Ahmad et al. (2021); Guo et al. (2022); Fried et al. (2022); Nijkamp et al. (2022). However, most sequence-based approaches generate codes with no guarantee of grammatical correctness (GC), which hinders the usability of generated codes.
According to automata theory, we find that PDA is suitable for PL grammar and has the following properties for dealing with non-grammatical problems. The first property is a valid terminal symbol set for next token prediction, and the second is an accept state set for recognizing completed code. In a practical code generation process, what we really care about are two typical grammatical error: terminal symbol mismatch (TSM) error and end with non-accept state (ENS) error, where ENS error can be tolerable until the end of code generation process. As a result, satisfying grammar constraints during code generation require the above two properties, and constraining code generation based on PDA to guarantee GC is a matter of course.

It is inspired by the operating principle of programming language parsers in practice. Fig. 1 demonstrates some examples of a parser parsing python code, which contains two specific grammatical error codes (a) and (b), and a grammatically correct code (c). Case (a) indicates ENS error, and case (b) indicates TSM error. All cases are recognized by a parser according to grammar. Therefore, a straightforward way is applying a parser to constrain sequence-based code generation, but it has the following two problems. First, sequence-based models need to recognize grammatical errors during code generation process. However, the vast majority of codes generated during this situation are incomplete, i.e., parsing these codes will produce ENS errors like case (a). Second, a parser can only recognize TSM errors like case (b) if terminal symbol is fed to the parser. It implies that sequence-based models need to attempt each generated code token in the candidate set one by one, which is strenuous 222For example, there are only 83 syntax-strings and 10 token-types in Python, and for a 10k-length vocabulary, more than 99% of tokens belong to three token-types NAME, STRING, and NUMBER. If models want to generate these types of tokens based on semantics but are prevented by grammar, the cost of attempts could be overwhelming.. In short, although code can be grammatically bounded by a parser, it is still challenging to work directly with a parser on sequence-based code generation.
In this paper, we propose CodePAD (a Code generation framework based on Pushdown Automaton moDule) to ensure GC for sequence-based models. PDA module facilitates CodePAD to generate bounded next prediction in a valid set and end with an accept state, utilizing the principle that PDA can recognize grammatical codes. CodePAD not only ensures GC but also maintains the advantages of commonly used sequence-based code generation. We conduct a series of experiments on four public benchmark datasets. Extensive experimental results and analyses verify the effectiveness and generality of CodePAD. The main contribution of this paper can be summarized as follows:
-
•
We devise a PDA-based methodology to guarantee grammatical correctness for code generation, which consists of a PDA module and an algorithm to simulate the deduction of PDA.
-
•
We propose CodePAD, a novel sequence-based code generation framework incorporating the PDA module. In addition to using the PDA-based methodology, CodePAD leverages PDA state through state representation, state prediction task, and joint prediction with state, which helps learn PDA deduction.
-
•
CodePAD significantly enhances the performance of base models. Even in zero-shot setting, pre-trained models still show remarkable improvements.
2 Motivation Example

An example of code generation constrained by PDA module is shown in Fig. 2. Given an NL, CodePAD needs to generate code that satisfies its intended functionality with the guarantee of GC. PDA module gives a valid set of terminal symbols (i.e., candidate syntax-strings and token-types) depending on grammar constraints, to which the generated token of CodePAD should belong. Specifically, in the beginning, CodePAD wants to generate first token from the vocabulary of a model according to NL. Based on production rules, PDA module shrinks the candidate set from entire vocabulary to 35 syntax-strings and 6 token-types, where each candidate token is constrained by grammar. As a result, at step 1, CodePAD picks a token (i.e., ‘import’) from the candidate set according to semantics. At each subsequent generation step, CodePAD predicts a token in the same manner, which satisfies grammar constraints. Until the end of generation steps, CodePAD outputs the token of ENDMARKER token-type (e.g., </s>), which ends with an accept state. Thus, CodePAD generates a grammatical code with the help of PDA module.
In the way of the above example, we first introduce PDA into deep learning (DL), which drastically shrinks the candidate set at each step of generation and reduces the difficulty for the model to select tokens from it, thus ensuring GC and improving the quality of code generation.
3 Related Work
3.1 DL-based Code Generation
In recent years, two kinds of prevailing approaches have been used for DL-based code generation.
3.1.1 Sequence-based Approaches
Ling et al. (2016) considered code generation task as a conditional text generation task and adopted a sequence-based model to address it. Some later work Jia and Liang (2016); Cao et al. (2019) followed this generation approach. For example, Wei et al. (2019) proposed a dual training framework to train both code generation and representation tasks simultaneously. CodeT5 Wang et al. (2021), UniXcoder Guo et al. (2022), Codegen Nijkamp et al. (2022), and InCoder Fried et al. (2022) applied pre-trained models to code generation task. In addition, Wang et al. (2022) considered code compilability as a training objective based on pre-trained models, but it still fails to guarantee GC.
Although sequence-based approaches are most commonly used, they usually cannot guarantee GC.
3.1.2 Tree-based Approaches
Dong and Lapata (2016) first considered tree-based models for code generation, which are generally used to ensure GC by deriving the syntactic structure Rabinovich et al. (2017). To exploit the grammatical information of code, Yin and Neubig (2017) adopted the encoder-decoder architecture to output an abstract syntax tree (AST) node sequence. On this basis, TRANX Yin and Neubig (2018) was proposed and became an effective and widely used tree-based model. Many works were based on and improved upon TRANX, such as ASED Jiang et al. (2022), Subtoken-TranX Shen et al. (2022), and APT Dong et al. (2022). Moreover, Sun et al. (2019) and Sun et al. (2020) applied tree-based CNN and Transformer for code generation.
A comparative view of the tree-based and sequence-based approaches is shown in Table 1. Although tree-based approaches can ensure GC, they have three major disadvantages: 1) AST node sequence is much longer (about 1.5-2 times) than token sequence Dong et al. (2022), leading to increased difficulty in generation. 2) The tree-based approach has to generate code with a complete tree structure, which makes the operation of obtaining arbitrary code snippets more difficult. 3) Assembling data for the tree-based approach is laborious because it requires the generation of AST based on syntactically complete code.
Compared to tree-based approaches, our proposed method not only ensures GC but also avoids the disadvantages of tree-based methods.
| Sequence-based | Tree-based | |
|---|---|---|
| Output length | Same as token | Much longer than token sequence |
| sequence of code | of code (about 1.5-2 times) | |
| Operation / NLP | Easy | Medium |
| technologies transfer | ||
| Data collection | Easy | Hard |
| (Especially for large-scale data) | ||
| Grammatical | No | Yes |
| correctness |
3.2 Domain-specific Grammatical Sequence-based Code Generation
Scholak et al. (2021) proposed PICARD that constrains auto-regressive decoders of language models through incremental parsing for a domain-specific language (DSL), i.e., Structured Query Language (SQL). PICARD used a parser for filtering in the beam search phase, meaning its candidate hypotheses might have terminal symbol mismatch errors. Poesia et al. (2022) proposed constrained semantic decoding (CSD) to address this problem for DSLs. However, both of them cannot extend to general-purpose languages (GPLs) like Python. For Scholak et al. (2021), the cost of attempts could be overwhelming for large vocabulary, and GPLs usually have a much larger vocabulary than DSLs. For Poesia et al. (2022), they use a intuitive method to deal with easy grammar of DSLs, but GPLs usually have more complicated grammar than DSLs, so as mentioned at the end of Poesia et al. (2022), CSD cannot handle GPLs like Python.
There is a great need to ensure GC of sequence-based approaches for all PLs (including DSLs and GPLs), thus we introduce PDA to ensure GC for sequence-based code generation, which can be applied to all PLs.
4 Methodology
We first describe the core module of the proposed approach – a PDA-based methodology consisting of a PDA module and the corresponding algorithm to obtain a valid set for ensuring GC during code generation.

PLs belong to context-free languages, such as Python, Java, C++, etc., which can be accepted by a PDA Chomsky (1962); Schützenberger (1963); Evey (1963). A PDA can be defined as:
| (1) |
where is a finite set of states, is a finite set of input symbols, is a finite set of stack symbols, is a start state, is a starting stack symbol, , where is the set of accept states, and is a transition function, mapping into the finite subsets of , where is Kleene star.
To construct a PDA module for a PL grammar, we first define , , , , , and . In this paper, we adopt non-terminal symbols of production rules in PL grammar as , which can be changed with the PDA you build. is set to terminal symbols of production rules and is the union of and . In PL grammar, and are the starting non-terminal symbol, and is the set of ending terminal symbols. As an example, in Python grammar PDA, and can be chosen as ‘file_input’, and is the set of ENDMARKER token-type. Then, the definition of is:
-
•
For each , (s, ,) = {(s, ) | is a production rule in PL grammar}.
-
•
For each , (s, , ) = {(s, )}.
The input symbols in are finite, because grammar of PLs merges the same type of tokens. For instance, each in Python belongs to one of 83 syntax-strings and 10 token-types. As shown in Fig. 3, ‘import’ and ‘as’ are syntax-strings, while ‘numpy’ and ‘np’ belong to NAME token-type. Fig. 3 illustrates a Python grammar PDA parsing ‘import numpy as np’. For a valid ‘import’, PDA jumps to valid states and stacks based on .
As shown in Algorithm 1, given current state and current stack , PDA is able to provide the set of valid according to . If belongs to the set of valid , the state and stack transferred after entering should be taken into account as well. Eventually, we merge all sets of under each state and stack and remove from them.
5 CodePAD
In this section, we introduce CodePAD, which is constrained by the PDA module constructed under methodology. This framework can be applied to any sequence-based model, no matter it is an encoder-decoder or a decoder only. In this paper, we employ Transformer-based encoder-decoder model Vaswani et al. (2017) as the backbone. We mainly modify the decode side, which adds PDA module, state representation, state prediction task, and joint prediction to help models generate grammatical code.
Fig. 4 shows the model architecture of CodePAD. At the encoder side of models, it maps an input sequence of NL utterances to a sequence of continuous NL representations . At the decoder side of models, given the NL representation sequence , it then generates a token sequence of code, one element at a time. At each step, models generate the next token in an auto-regressive manner Graves (2013), which deploys previous generation results as additional input.
5.1 State Representation
The state is a type of valuable information to comprehend the status of the generated valid prefix in PDA module. In order to exploit states provided by PDA module, we set both tokens and corresponding states as the input of decoder. Specifically, given tokens , we can obtain corresponding states from PDA module. Then, and are converted into as follows:
| (2) | |||
| (3) | |||
| (4) |
where and are the embedding of and respectively, indicates the concatenation of and , and indicates the positional encoding Gehring et al. (2017).

5.2 Token Prediction Task
To generate code, and the NL representation sequence are fed into the decoder:
| (5) |
According to , we can compute the following probabilities:
| (6) | |||
| (7) | |||
| (8) | |||
| (9) |
where , , and are three different parameter matrices, indicates one of tokens in the vocabulary, and is calculated by the pointer network Vinyals et al. (2015). Finally, at t step, the probability of generated token can be defined as:
| (10) |
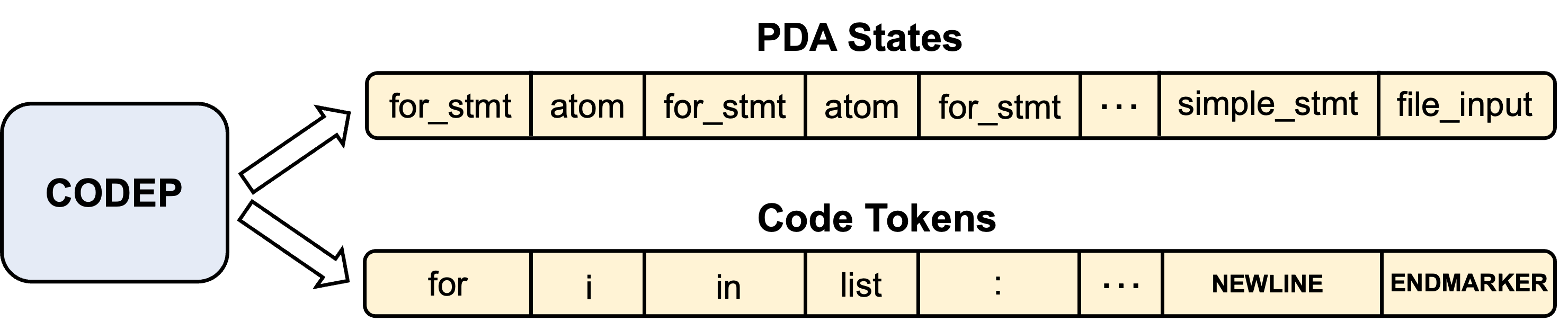
5.3 State Prediction Task
To better understand the deduction process of PDA, we introduce an auxiliary task of PDA state prediction. Similar to token prediction, given , , and , we can calculate the probability of a state at step as follows:
| (11) |
where indicates one of states in the vocabulary, is another parameter matrix, and is calculated via (5). Fig. 5 shows an example of state prediction task. We can see that state prediction task also gives guidance for generating tokens. For example, ‘for’, ‘in’, and ‘:’ are the fixed pairing of ‘for_stmt’ in Python.
5.4 Training and Inference
The purpose of the training stage is to minimize the sum of cross-entropy loss for two tasks, which is defined as:
| (12) | |||
| (13) | |||
| (14) |
where is CodePAD’s parameter, and are losses of token prediction task and state prediction task, respectively, and is used to control the impact of them.
In the inference stage, we are able to calculate via (10) with additional constraints of PDA module , where is obtained according to Algorithm 1. Similarly, we can calculate via (11).
5.4.1 Joint Prediction with State
We can leverage both probabilities to jointly predict the result as follows:
| (15) |
where indicates the actual state of PDA module, which is obtained from . Joint prediction wants to prevent CodePAD from generating tokens of inappropriate PDA states.
6 Experiment Setup
6.1 PL and Datasets
We build a PDA for the most popular PL Python (both Python2 and Python3) and conduct experiments on four public benchmark datasets, i.e., CONALA Yin et al. (2018), DJANGO Oda et al. (2015), JUICE-10K Agashe et al. (2019), and MBPP Austin et al. (2021).
| Model | CONALA | DJANGO | JUICE-10K | |||||
|---|---|---|---|---|---|---|---|---|
| BLEU | CodeBLEU | GCP | EM | GCP | BLEU | CodeBLEU | GCP | |
| CodePAD (LSTM-based) | ||||||||
| -JP | 5.96 | 15.04 | ||||||
| -SPT | 5.38 | 14.26 | ||||||
| -SR | 5.54 | 14.47 | ||||||
| -PDA-JP | 5.09 | 13.87 | ||||||
| -PDA-SR-SPT-JP | ||||||||
| CodePAD (Transformer-based) | ||||||||
| -JP | 78.9 | |||||||
| -SPT | 77.8 | |||||||
| -SR | 78.3 | |||||||
| -PDA-JP | 76.7 | |||||||
| -PDA-SR-SPT-JP | ||||||||
6.2 Baselines
We select two typical sequence-based models, i.e., LSTM Hochreiter and Schmidhuber (1997) and Transformer Vaswani et al. (2017), as our base models. For non-pre-trained tree-based methods, we compare CodePAD with TRANX Yin and Neubig (2019), ML-TRANX (Xie et al., 2021), TRANX-RL (Jiang et al., 2021), APT Dong et al. (2022), and Transformer-AST 333Transformer-AST indicates a tree-based method based on Transformer instead of LSTM adopted in other tree-based methods mentioned above., which ensure GC of generated codes relying on AST. For pre-trained sequence-based methods, we choose encoder-decoder models, including BART Lewis et al. (2020) and CodeT5 Wang et al. (2021), and decoder-only models, including CodeGen Nijkamp et al. (2022) and InCoder Fried et al. (2022).
6.3 Evaluation Metrics
We use three widely-used evaluation metrics in code generation: exact matching accuracy (EM), corpus-level BLEU-4 (BLEU), and CodeBLEU Ren et al. (2020), which consider important grammar and semantic features of codes. We also use GC and GC percentage (GCP). GCP indicates the percentage of grammatically generated codes in all generated codes.
6.4 Implementation Details
7 Experimental Results
We conduct experiments to answer the following research questions (RQs):
7.1 RQ1: CodePAD vs Tree-based Methods
From Tables 2, we can observe that CodePAD substantially outperforms SOTA tree-based methods without pre-training on three public benchmark datasets in terms of BLEU, CodeBLEU, and EM. It indicates that although both tree-based methods and CodePAD generate grammatical codes, CodePAD takes advantage of the shorter generation sequence length of code tokens than AST nodes. We also find that Transformer-based CodePAD achieves competitive performance against LSTM-based CodePAD on CONALA. However, on DJANGO and JUICE-10K, Transformer-based CodePAD exhibits its superiority due to more extensive training data and longer generated token sequence. Therefore, for large dataset and long code generation, we recommend employing Transformer as the base model of CodePAD. Since the decoder of most tree-based methods without pre-training is based on LSTM, we implement Transformer-AST to verify that the effect of CodePAD is derived from our proposed method rather than the base model. The experimental results show that the base model is not the main factor affecting performance.
| Model | Code |
|---|---|
| BART-125M | Write a function to find the similar elements from the given two tuple lists. |
| \hdashlineCodeT5-220M | def f_elements( ) |
| \hdashlineCodeT5-770M | to find the similar elements ." ," ." ," a function to find the similar elements from the given two tuple lists . |
| \hdashlineCodeGen-350M | def find_similar ( t1 , t2 ): n """ n Finds the similar elements from the given two tuples. n n |
| \hdashlineInCoder-1B | def similar_elements ( t1, t2 ): n n n n n n n n n n n n |
| CodeGen-350M +PDA | def find ( a , b ): n for i in range ( len ( a ) ): n if a [ i ] == b [ i ]: n return a[i] |
| \hdashlineGOLD | def similar_elements ( test_tup1, test_tup2 ) : n res = tuple ( set ( test_tup1 ) & set ( test_tup2 ) ) n return ( res ) |
7.2 RQ2: Ablation Study
In Table 3, we demonstrate the performance of LSTM-based and Transformer-based CodePAD with the reduction of some parts of them. The results indicate that each part of CodePAD contributes, and PDA module is the most critical part of CodePAD. When PDA module is removed, GCP drops sharply, which is inversely correlated with the average code length of datasets, and other evaluation metrics also have degradation. JP becomes unavailable due to the dependence of JP on the mapping from the token to the corresponding state provided by PDA module. In addition, it can be seen that only reducing JP or SR leads to a relatively small decrease in performance, because they have some overlap with other parts in helping the model. ‘-PDA-SR-SPT-JP’ means that only the base model is used, which has a significant performance degradation compared to CodePAD (both LSTM-based and Transformer-based). As shown in Tables 2, it relatively improves 17% CodeBLEU on CONALA, 8% EM on DJANGO, and 15% CodeBLEU on JUICE-10K compared to base models.
7.3 RQ3: Improvements of Sequence-based Methods with PDA Module
It is apparent from Table 5 that pre-trained models fail to work on MBPP in zero-shot setting, because they are working in unfamiliar territory. With the help of PDA module, pre-trained sequence-based models achieve significant improvements. The reason may be that pre-training models have the ability to answer questions, but do not know how to organize them into well-formed codes. Under the constraints of PDA module, pre-training models are guided to exert their capabilities by generating grammatical codes. Especially, (BLEU, CodeBLEU) of CodeGen-350M without prompt 444We explore the performance of decoder-only models under conditions that no prompt is given or only ”def” is given as prompt, because traditional prompt ‘def + function signature’ contains much valid information, including function name, argument type and name, and even return value type. improvement from (1.55, 3.21) to (14.44, 21.54) on MBPP in zero-shot setting.
7.4 RQ4: Case Study
In Table 4, we demonstrate examples of code generation for each pre-trained model in zero-shot setting. We can see that they cannot generate grammatical code or even complete code without prompt in zero-shot setting. For example, CodeGen-350M generates the function signature and some comments capturing semantic information, which shows the ability to generate complete code if under proper guidelines. Under the constraints of PDA module, CodeGen-350M generates grammatical code. Although the code generated by CodeGen-350M + PDA still falls short of GOLD, we still think it is an impressive result considering that it is under the zero-shot setting.
| Model | MBPP (Zero-shot) | ||
|---|---|---|---|
| BLEU | CodeBLEU | GC | |
| Encoder-decoder methods w/ pre-training | |||
| BART-125M | 0.02 | 3.74 | False |
| +PDA | 4.83 | 9.17 | True |
| \hdashlineCodeT5-220M | 0.01 | 0.57 | False |
| +PDA | 4.75 | True | |
| \hdashlineCodeT5-770M | 0.02 | 3.98 | False |
| +PDA | 9.31 | True | |
| Decoder-only methods w/ pre-training | |||
| CodeGen-350M | 1.55 | 3.21 | False |
| +prompt | 0.33 | 10.13 | False |
| +PDA | 14.44 | 21.54 | True |
| \hdashlineInCoder-1B | 0.12 | 7.41 | False |
| +prompt | 0.82 | 7.22 | False |
| +PDA | 9.84 | 17.38 | True |
8 Limitation
There are three major limitations of our work:
-
•
First, a specific PDA should be built for each PL, and we only built PDA for Python (including both Python2 and Python3). However, PDA can recognize context-free language to which PL belongs, due to time and memory limitations of running PL Salomaa et al. (2001). In future work, we will build PDAs for more PLs.
-
•
Second, our work ensures GC, but neither our method nor other methods can prevent compilation errors. With our proposed training framework, our method outperforms other methods on compilation rates, e.g., CODEP has 99.2% compilation rates after training on CONALA.
-
•
Third, using PDA will increase CPU operation and memory overhead, but it is still acceptable.
9 Conclusion and Discussion
In this paper, we have proposed a sequence-based framework, namely CodePAD, that first integrates the deduction of PDA into deep learning for code generation. CodePAD adds PDA module, state representation, state prediction task, and joint prediction for the decoder of CodePAD. PDA module guarantees the GC of generated codes, while the others make use of valid information provided by PDA module (i.e., PDA state) to generate codes better. As a result, CodePAD dramatically enhances the performance of base models and outperforms SOTA tree-based methods without pre-training on three benchmark datasets. The ablation study demonstrates each component of CodePAD contributes. With the help of PDA module, pre-trained models also achieve significant improvements.
PDA module shows excellent potential in code generation tasks in zero-shot setting, which can help pre-trained models apply to niche PLs that have little data. Furthermore, PDA can accommodate context-free language to satisfy grammar constraints, not just PL. We hope this work sheds light on future work in this direction.
Appendix A Syntax-strings and Token-types in Python
In Table 6, we show each of 83 syntax-strings and 10 token-types in Python.
| Python | |
|---|---|
| Syntax-string | ‘for’, ‘in’, ‘try’, ‘finally’, ‘with’, ‘except’, ‘lambda’, ‘or’, ‘and’, ‘not’, ‘del’, ‘pass’, |
| ‘break’, ‘continue’, ‘return’, ‘raise’, ‘from’, ‘import’, ‘as’, ‘nonlocal’, ‘global’, | |
| ‘assert’, ‘if’, ‘else’, ‘elif’, ‘while’, ‘async’, ‘def’, ‘@’, ‘(’, ‘)’, ‘->’, ‘:’, ‘**’, ‘*’, ‘,’, | |
| ‘=’, ‘;’, ‘^=’, ‘%=’, ‘//=’, ‘@=’, ‘<<=’, ‘**=’, ‘&=’, ‘*=’, ‘|=’, ‘>>=’, ‘-=’, ‘+=’, ‘/=’, | |
| ‘.’, ‘…’, ‘<=’, ‘>=’, ‘is’, ‘==’, ‘<’, ‘>’, ‘<>’, ‘!=’, ‘|’, ‘^’, ‘&’, ‘<<’, ‘>>’, ‘+’, ‘-’, ‘%’, | |
| ‘/’, ‘//’, ‘~’, ‘!’, ‘await’, ‘False’, ‘[’, ‘{’, ‘True’, ‘None’, ‘]’, ‘}’, ‘class’, ‘yield’ | |
| Token-type | ‘NAME’, ‘STRING’, ‘NUMBER’, ‘INDENT’, ‘DEDENT’, ‘FSTRING_START’, |
| ‘FSTRING_END’, ‘FSTRING_STRING’, ‘NEWLINE’, ‘ENDMARKER’ |
Appendix B Deterministic Pushdown Automaton
Due to computer memory constraints, most of PLs are deterministic context-free languages, which can be accepted by a deterministic pushdown automaton (DPDA) Salomaa et al. (2001). A PDA is deterministic only if both the following two conditions are satisfied:
-
•
, where indicates the element number of the set .
-
•
, if , then .
For the same deterministic context-free grammar, the general PDA is more accessible to construct than the DPDA. In addition, deterministic context-free languages are a proper subset of context-free languages. Therefore, in this paper, our proposed method is based on the general PDA, which is also applicable to the DPDA.
Appendix C Elementary Knowledge of Model Architecture
The positional encoding Gehring et al. (2017) is defined as:
where is the position, is the dimension, and is the number of dimensions (i.e., embedding size).
The output of the multi-headed self-attention in the decoder layer is computed via:
| (16) | |||
| (17) | |||
| (18) |
Where are learnable parameter matrices. After that, a feed-forward layer and layer normalization are followed.
Appendix D Details of Datasets, Hyperparameters, Baselines, and Research Questions
D.1 Datasets
-
•
CONALA Yin et al. (2018) contains 2879 real-world data of manually annotated NL questions and their Python3 solutions on STACK OVERFLOW.
-
•
DJANGO Oda et al. (2015) contains 18805 NL-annotated python2 code extracted from the Django Web framework.
-
•
JUICE-10K contains 10K training samples randomly selected from the training set of JUICE Agashe et al. (2019), and the validation and test sets of JUICE-10K are consistent with those of JUICE. Due to the high demand for training resources, we use a subset instead of the full JUICE.
-
•
MBPP Austin et al. (2021) contains 974 Python programming problems, and each sample consists of an NL, a code, and 3 test cases.
| Dataset | Examples Num | Avg Length | |||
|---|---|---|---|---|---|
| Train | Dev | Test | NL | Code | |
| CONALA | 2175 | 200 | 500 | 10.2 | 15.1 |
| DJANGO | 16000 | 1000 | 1805 | 14.1 | 10.6 |
| JUICE-10K | 10000 | 1831 | 2115 | 40.4 | 43.4 |
| MBPP | - | - | 974 | 16.0 | 33.0 |
D.2 Hyperparameters
We train our model with Adam Kingma and Ba (2015) optimizer on a single GPU of Tesla A100-PCIe-40G. We set sizes of the word embedding, code embedding, state embedding, and hidden state as 256, 256, 256, and 512, respectively. The learning rate is set to for Transformer-based CodePAD and for LSTM-based CodePAD. For additional hyperparameter , we pick on validation sets. The beam size is set to 2 for MBPP and 15 for the other datasets.
D.3 Baselines
D.3.1 Non-pre-trained Tree-based Methods
-
•
TRANX Yin and Neubig (2019) uses a tree-based model to generate the AST as the intermediate representation of code.
-
•
ML-TRANX (Xie et al., 2021) adopts a mutual learning framework to train models for different traversals-based decodings jointly.
-
•
TRANX-RL (Jiang et al., 2021) uses a context-based branch selector to determine optimal branch expansion orders for multi-branch nodes dynamically.
-
•
APT Dong et al. (2022) uses antecedent prioritized loss to help tree-based models attach importance to antecedent predictions by exploiting the position information of the generated AST nodes.
D.3.2 Pre-trained Sequence-based Methods
-
•
BART Lewis et al. (2020) is a pre-training approach for text generation tasks that learns to map corrupted documents to the original.
-
•
CodeT5 Wang et al. (2021) is a unified pre-trained encoder-decoder Transformer model that makes better use of the code semantics conveyed from developer-assigned identifiers.
-
•
CodeGen Nijkamp et al. (2022) is a unified generation model that allows left-to-right code generation and code infilling/editing by the causal mask language modeling training objective.
-
•
InCoder Fried et al. (2022) is a series of large-scale language models trained on NL and programming data for conversation-based program synthesis.
D.4 Research Questions
We conduct experiments to answer the following research questions (RQs):
-
•
RQ1: How well does the proposed CodePAD perform compared to the SOTA tree-based methods, which guarantees the syntactical correctness of generated codes relying on AST, without pre-training?
-
•
RQ2: How does each part of our proposed method contribute to CodePAD?
-
•
RQ3: How does the proposed PDA module improve the effectiveness of the SOTA pre-trained sequence-based methods?
-
•
RQ4: How does CodePAD generate grammatical codes with the help of PDA module?

Appendix E Effect of
The coefficient is an important hyperparameter that controls the relative impacts of the state prediction task in the training stage and that of the joint prediction with the state probability in the inference stage. Therefore, we investigate the effect of on our proposed framework in Fig. 6, which varies from 0 to 1 with an increment of 0.2 on the validation set of CONALA, DJANGO, and JUICE-10K datasets. The experimental results show that as increases, the performance of CodePAD increases when , and its tendency is related to the base model and the dataset when . What stands out in Fig. 6 is that CodePAD performs relatively well on each of the above datasets when is set to 1.0, which indicates the effectiveness of the state prediction task and joint prediction. For experiments in this paper, we set as the optimal in Fig. 6. In particular, the of the LSTM-based CodePAD and the transformer-based CodePAD are set to (0.6, 1.0), (0.8, 1.0), and (1.0, 0.4) on CONALA, DJANGO, and JUICE-10K dataset, respectively.
| Type | Example |
|---|---|
| I | 1 = [ ( i , 2 ) for i in range(1) ] |
| \hdashlineII | plt.plot(x, var1, color=‘str0’, color=‘str1’) |
| \hdashlineIII | html = response.read(str0, ‘str0’) |
| slot_map={str0: http://www.example.com/} |
Appendix F Compilation Error Analysis
Program execution needs to be compiled correctly in addition to being grammatically correct, and GC is the foundation of compilation. The compilation rate of CodePAD on CONALA dataset is , and Table 8 demonstrates examples of three types of compilation error. The first type of compilation error is because the number type cannot be assigned, the second type of compilation error is the error of the duplicate parameter, and the third type of compilation error is the mapping error. We found that the above types of errors also occur in tree-based methods. For the first two types of errors, we are able to modify the transfer function, while the last type of error can be avoided using engineering methods.
References
- Agashe et al. (2019) Rajas Agashe, Srinivasan Iyer, and Luke Zettlemoyer. 2019. Juice: A large scale distantly supervised dataset for open domain context-based code generation. In EMNLP/IJCNLP (1), pages 5435–5445.
- Ahmad et al. (2021) Wasi Uddin Ahmad, Saikat Chakraborty, Baishakhi Ray, and Kai-Wei Chang. 2021. Unified pre-training for program understanding and generation. In NAACL-HLT, pages 2655–2668. Association for Computational Linguistics.
- Austin et al. (2021) Jacob Austin, Augustus Odena, Maxwell I. Nye, Maarten Bosma, Henryk Michalewski, David Dohan, Ellen Jiang, Carrie J. Cai, Michael Terry, Quoc V. Le, and Charles Sutton. 2021. Program synthesis with large language models. CoRR, abs/2108.07732.
- Cao et al. (2019) Ruisheng Cao, Su Zhu, Chen Liu, Jieyu Li, and Kai Yu. 2019. Semantic parsing with dual learning. In ACL (1), pages 51–64.
- Chomsky (1962) Noam Chomsky. 1962. Context-free grammars and pushdown storage. MIT Res. Lab. Electron. Quart. Prog. Report., 65:187–194.
- Dong and Lapata (2016) Li Dong and Mirella Lapata. 2016. Language to logical form with neural attention. In ACL (1).
- Dong et al. (2022) Yihong Dong, Ge Li, and Zhi Jin. 2022. Antecedent predictions are dominant for tree-based code generation. CoRR, abs/2208.09998.
- Evey (1963) R James Evey. 1963. Application of pushdown-store machines. In Proceedings of the November 12-14, 1963, fall joint computer conference, pages 215–227.
- Fried et al. (2022) Daniel Fried, Armen Aghajanyan, Jessy Lin, Sida Wang, Eric Wallace, Freda Shi, Ruiqi Zhong, Wen-tau Yih, Luke Zettlemoyer, and Mike Lewis. 2022. Incoder: A generative model for code infilling and synthesis. CoRR, abs/2204.05999.
- Gehring et al. (2017) Jonas Gehring, Michael Auli, David Grangier, Denis Yarats, and Yann N. Dauphin. 2017. Convolutional sequence to sequence learning. In ICML, volume 70 of Proceedings of Machine Learning Research, pages 1243–1252. PMLR.
- Graves (2013) Alex Graves. 2013. Generating sequences with recurrent neural networks. CoRR, abs/1308.0850.
- Guo et al. (2022) Daya Guo, Shuai Lu, Nan Duan, Yanlin Wang, Ming Zhou, and Jian Yin. 2022. Unixcoder: Unified cross-modal pre-training for code representation. In ACL (1), pages 7212–7225. Association for Computational Linguistics.
- Hochreiter and Schmidhuber (1997) Sepp Hochreiter and Jürgen Schmidhuber. 1997. Long short-term memory. Neural Comput., 9(8):1735–1780.
- Jia and Liang (2016) Robin Jia and Percy Liang. 2016. Data recombination for neural semantic parsing. In ACL (1).
- Jiang et al. (2022) Hui Jiang, Linfeng Song, Yubin Ge, Fandong Meng, Junfeng Yao, and Jinsong Su. 2022. An AST structure enhanced decoder for code generation. IEEE ACM Trans. Audio Speech Lang. Process., 30:468–476.
- Jiang et al. (2021) Hui Jiang, Chulun Zhou, Fandong Meng, Biao Zhang, Jie Zhou, Degen Huang, Qingqiang Wu, and Jinsong Su. 2021. Exploring dynamic selection of branch expansion orders for code generation. In ACL/IJCNLP, pages 5076–5085.
- Kingma and Ba (2015) Diederik P. Kingma and Jimmy Ba. 2015. Adam: A method for stochastic optimization. In ICLR.
- Lewis et al. (2020) Mike Lewis, Yinhan Liu, Naman Goyal, Marjan Ghazvininejad, Abdelrahman Mohamed, Omer Levy, Veselin Stoyanov, and Luke Zettlemoyer. 2020. BART: denoising sequence-to-sequence pre-training for natural language generation, translation, and comprehension. In ACL, pages 7871–7880. Association for Computational Linguistics.
- Ling et al. (2016) Wang Ling, Phil Blunsom, Edward Grefenstette, Karl Moritz Hermann, Tomás Kociský, Fumin Wang, and Andrew W. Senior. 2016. Latent predictor networks for code generation. In ACL (1).
- Nijkamp et al. (2022) Erik Nijkamp, Bo Pang, Hiroaki Hayashi, Lifu Tu, Huan Wang, Yingbo Zhou, Silvio Savarese, and Caiming Xiong. 2022. A conversational paradigm for program synthesis. CoRR, abs/2203.13474.
- Oda et al. (2015) Yusuke Oda, Hiroyuki Fudaba, Graham Neubig, Hideaki Hata, Sakriani Sakti, Tomoki Toda, and Satoshi Nakamura. 2015. Learning to generate pseudo-code from source code using statistical machine translation. In 2015 30th IEEE/ACM International Conference on Automated Software Engineering (ASE), pages 574–584. IEEE.
- Poesia et al. (2022) Gabriel Poesia, Oleksandr Polozov, Vu Le, Ashish Tiwari, Gustavo Soares, Christopher Meek, and Sumit Gulwani. 2022. Synchromesh: Reliable code generation from pre-trained language models. CoRR, abs/2201.11227.
- Rabinovich et al. (2017) Maxim Rabinovich, Mitchell Stern, and Dan Klein. 2017. Abstract syntax networks for code generation and semantic parsing. In ACL (1), pages 1139–1149.
- Raychev et al. (2014) Veselin Raychev, Martin T. Vechev, and Eran Yahav. 2014. Code completion with statistical language models. In PLDI, pages 419–428.
- Ren et al. (2020) Shuo Ren, Daya Guo, Shuai Lu, Long Zhou, Shujie Liu, Duyu Tang, Neel Sundaresan, Ming Zhou, Ambrosio Blanco, and Shuai Ma. 2020. Codebleu: a method for automatic evaluation of code synthesis. CoRR, abs/2009.10297.
- Salomaa et al. (2001) Arto Salomaa, Derick Wood, and Sheng Yu. 2001. A half-century of automata theory: celebration and inspiration. World scientific.
- Scholak et al. (2021) Torsten Scholak, Nathan Schucher, and Dzmitry Bahdanau. 2021. PICARD: parsing incrementally for constrained auto-regressive decoding from language models. In EMNLP (1), pages 9895–9901. Association for Computational Linguistics.
- Schützenberger (1963) Marcel Paul Schützenberger. 1963. On context-free languages and push-down automata. Information and control, 6(3):246–264.
- Shen et al. (2022) Sijie Shen, Xiang Zhu, Yihong Dong, Qizhi Guo, Yankun Zhen, and Ge Li. 2022. Incorporating domain knowledge through task augmentation for front-end javascript code generation. In ESEC/SIGSOFT FSE, pages 1533–1543. ACM.
- Sun et al. (2019) Zeyu Sun, Qihao Zhu, Lili Mou, Yingfei Xiong, Ge Li, and Lu Zhang. 2019. A grammar-based structural CNN decoder for code generation. In AAAI, pages 7055–7062.
- Sun et al. (2020) Zeyu Sun, Qihao Zhu, Yingfei Xiong, Yican Sun, Lili Mou, and Lu Zhang. 2020. Treegen: A tree-based transformer architecture for code generation. In AAAI, pages 8984–8991.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In NIPS, pages 5998–6008.
- Vinyals et al. (2015) Oriol Vinyals, Meire Fortunato, and Navdeep Jaitly. 2015. Pointer networks. In NIPS, pages 2692–2700.
- Wang et al. (2022) Xin Wang, Yasheng Wang, Yao Wan, Fei Mi, Yitong Li, Pingyi Zhou, Jin Liu, Hao Wu, Xin Jiang, and Qun Liu. 2022. Compilable neural code generation with compiler feedback. In ACL (Findings), pages 9–19. Association for Computational Linguistics.
- Wang et al. (2021) Yue Wang, Weishi Wang, Shafiq R. Joty, and teven C. H. Hoi. 2021. Codet5: Identifier-aware unified pre-trained encoder-decoder models for code understanding and generation. In EMNLP (1), pages 8696–8708.
- Wei et al. (2019) Bolin Wei, Ge Li, Xin Xia, Zhiyi Fu, and Zhi Jin. 2019. Code generation as a dual task of code summarization. In NeurIPS, pages 6559–6569.
- Xie et al. (2021) Binbin Xie, Jinsong Su, Yubin Ge, Xiang Li, Jianwei Cui, Junfeng Yao, and Bin Wang. 2021. Improving tree-structured decoder training for code generation via mutual learning. In AAAI, pages 14121–14128.
- Yin et al. (2018) Pengcheng Yin, Bowen Deng, Edgar Chen, Bogdan Vasilescu, and Graham Neubig. 2018. Learning to mine aligned code and natural language pairs from stack overflow. In MSR, pages 476–486.
- Yin and Neubig (2017) Pengcheng Yin and Graham Neubig. 2017. A syntactic neural model for general-purpose code generation. In ACL (1), pages 440–450.
- Yin and Neubig (2018) Pengcheng Yin and Graham Neubig. 2018. TRANX: A transition-based neural abstract syntax parser for semantic parsing and code generation. In EMNLP (Demonstration), pages 7–12.
- Yin and Neubig (2019) Pengcheng Yin and Graham Neubig. 2019. Reranking for neural semantic parsing. In ACL, pages 4553–4559.