Coarse-grained binning in Drell-Yan transverse momentum spectra
Abstract
We report a study of the determination of the intrinsic transverse momentum of partons, the intrinsic , from the dilepton transverse momentum in Drell-Yan (DY) production at hadron colliders. The result shows that a good sensitivity to the intrinsic distribution is achieved by measuring relative ratios between the cross sections of suitably defined low- and high- regions. The study is performed through both a pseudo-data test and an extraction from measurements of the DY process by the CMS collaboration. Since the methodology does not rely on any dedicated partition of bins, this -ratio observable requires less special treatment in very low regions, and propagates lower systematic uncertainties induced from unfolding or momentum migration, in contrast with previous proposals of using a fine-binning measurement of the differential cross section.
1 Introduction
Measurements of transverse momentum spectra of electroweak bosons via Drell-Yan (DY) lepton-pair production [1] are at the core of many aspects of the physics program at the Large Hadron Collider (LHC), ranging from precision determinations of Standard Model parameters in the strong and electroweak sectors, to non-perturbative features of hadron structure and transverse momentum dependent (TMD) parton distribution functions [2].
Recent applications of DY transverse momentum measurements include the determination of the strong coupling from perturbative Quantum Chromodynamics (QCD) predictions matched with resummation [3, 4]; the extraction of TMD parton distributions both in analytic-resummation [5, 6, 7, 8] and parton-branching [9] approaches; the modeling of TMD contributions in soft-collinear effective theory [10]; the determination of intrinsic- parameters in the tuning of Monte Carlo event generators [11].
A common thread in these applications is that high-precision measurements of the low transverse-momentum region (, where and are the dilepton’s transverse momentum and invariant mass) with fine binning in will improve our ability to unravel QCD dynamics, involving multiple soft-gluon emissions as well as the non-perturbative intrinsic transverse motion of partons. See for instance the role of fine-binned measurements in the context of analytic-resummation studies [12] and parton-branching studies [13].
However, recent measurements of the DY process by the ATLAS [14] and CMS [15] collaborations indicate that such fine-binned treatments require an extremely delicate control of systematic uncertainties. Experimentally, the determination of the low- fine-binned structure is challenging. Under these circumstances, it becomes important to assess the capabilities of methodologies which do not require the fine-binned measurement of distributions, and rather rely on coarse-grained binning.
In this paper we explore one such methodology, by studying the intrinsic determination in TMD parton distributions from the measurement of in the region (with small compared to ) based on coarse-grained partitions of this region. We subdivide the region into two bins with separation momentum , and , and investigate the sensitivity to the intrinsic distribution from measuring the ratio between the low cross section (predominantly sensitive to TMD dynamics and resummed soft-parton radiation) and the high cross section (predominantly sensitive to fixed-order hard-parton radiation) as a function of varying . We study the role of bin-to-bin migration effects on the ratio. Although the high cross section is not sensitive to intrinsic , it acts as a reference in the relative ratio between the strength of the intrinsic and fixed-order contribution. We find that the intrinsic can be determined by measuring its overall strength through the -ratio instead of measuring the low differential cross section. This conclusion is relevant, from a practical viewpoint, in order to achieve a good determination of intrinsic from analyses of experimental data with reduced systematic uncertainties. We illustrate this methodology by presenting an extraction of intrinsic from DY measurements by the CMS collaboration [16].
To perform this study, we use the parton branching (PB) approach [17, 18] to TMD evolution. This approach provides the basis for including TMD distributions in parton shower Monte Carlo calculations, and has been shown to give a consistent description of DY spectra [9] as well as of the multiple-jet structure associated with DY production [19]. At inclusive level, it can be related to the evolution of collinear parton distribution functions (PDF), and correctly describes deep-inelastic scattering structure functions [20]. Given the wide applicability of the PB TMD approach, this provides a useful framework to assess the performance of the -ratio methodology.
The paper is organized as follows. In Sect. 2, we briefly review the PB TMD approach. In Sect. 3, we propose the -ratio as a new observable and methodology for studies of TMD dynamics. The sensitivity of the -ratio to the intrinsic distribution is investigated with a pseudo-data sample, and is compared to that from the fine-binning structure of the low- differential cross section. In Sect. 4, we apply the methodology to the distribution measured by the CMS collaboration [16] at 13 TeV across a wide range in DY mass from 50 GeV to 1 TeV. We give conclusions in Sect. 5.
2 PB TMD method
In this section we briefly describe the main features of the PB approach [17, 18, 20] which will be used for the analysis in this work. We first recall the PB evolution equations; then we discuss the intrinsic- distribution, the soft-gluon resolution scale, the treatment of the strong coupling, and the application of the method to the computation of DY distributions.
We consider the TMD parton distribution of parton flavor , , as a function of the longitudinal momentum fraction , the transverse momentum and the evolution scale . According to Refs. [18, 20], the distributions fulfill evolution equations of the form
| (2.1) | |||||
where is the Sudakov form factor and are the evolution kernels, which are specified in Ref. [18] as functionals of the Sudakov form factors , of the real-emission splitting functions , and of phase space constraints collectively denoted by in Eq. (2.1). The functions that appear in the evolution kernels are perturbatively computable as power series expansions in the strong coupling . The explicit expressions of these expansions for all flavor channels are given to two-loop order in Ref. [18].
The evolution in Eq. (2.1) is expressed in terms of two branching variables, and : is the longitudinal momentum transfer at the branching, controlling the rapidity of the parton emitted along the branching chain; is the mass scale at which the branching occurs, and is related to the branching’s kinematic variables according to the ordering condition. It is worth noting that the double evolution in rapidity and mass for TMD distributions can also be formulated in a CSS [21, 22], rather than PB, approach — see e.g. [23, 12, 24]. A study of the relationship of the PB Sudakov evolution kernel with the CSS formalism is performed in [25, 26]. Eq. (2.1) is obtained for the case of angular ordering [27, 28, 29], which gives , where is the emitted parton’s transverse momentum. The angular-ordered branching is motivated by the treatment of the endpoint region in the TMD case [18, 30].
The initial evolution scale in Eq. (2.1) is denoted by (), and is usually taken to be of order 1 GeV. The distribution at scale in the first term on the right hand side of Eq. (2.1) provides the intrinsic distribution. This is a nonperturbative boundary condition to the evolution equation, and may be determined from comparisons of theory predictions to experimental data. In the calculations of this paper, for simplicity we will parameterize , following previous applications of the PB TMD method [20, 9], as
with the width of the Gaussian distribution given by , independent of parton flavor and , where is the intrinsic- parameter.
The evolution kernels and Sudakov form factors in Eq. (2.1) contain kinematic constraints which embody the phase space of the branchings along the parton cascade. These can be described, using the “unitarity” picture of QCD evolution [31], by separating resolvable and non-resolvable branchings in terms of a resolution scale to classify soft-gluon emissions [17]. (See e.g. [32] for a study of the interplay of resolution scale with transverse momentum recoils in parton showers.) Applications of the PB TMD method can be carried out either by taking the soft-gluon resolution scale to be a fixed constant value close to the kinematic limit or by allowing for a running, -dependent resolution (see, e.g., discussions in [29, 33, 9]). In the computations of this paper, we will take fixed resolution scale. This is the same as what is done in the studies of Refs. [20, 13, 9], which we will use as benchmarks.
The scale at which the strong coupling is
to be evaluated in
Eq. (2.1)
is a function of the branching variable.
Two scenarios are commonly studied in PB TMD applications:
i) ;
ii) .
Case i) corresponds to
DGLAP
evolution [34, 35, 36] , while
case ii) corresponds to angular ordering,
e.g. CMW evolution [27, 28].
In Ref. [20], fits to
precision deep inelastic scattering
HERA data [37]
are performed for both scenarios i) and ii),
using the fitting platform
xFitter [38, 39].
It is found that fits with good
values can be achieved
in either case. Correspondingly, PB-NLO-2018 Set1
(with the DGLAP-type
)
and PB-NLO-2018 Set2 (with the angular-ordered CMW-type
) are obtained.
On the other hand, it is found that PB-NLO-2018 Set2 provides a much better description, compared to PB-NLO-2018 Set1, of measured spectra at the LHC [13] and in low-energy experiments [40], and of di-jet azimuthal correlations near the back-to-back region at the LHC [41, 42]. Further, it is shown that a good description is also obtained for DY + jets final-state distributions [43, 44, 19, 45]. We will therefore base the analysis of this work on PB-NLO-2018 Set2. As in [20, 9], the strong coupling is modeled according to a “pre-confinement” picture [46, 47] as , where is a semi-hard scale, taken to be GeV. The PB TMD sets are available from the TMDlib library [48, 49].
The calculation of DY production cross sections in the PB TMD method proceeds as described in Ref. [13]. NLO hard-scattering matrix elements are obtained from the MadGraph5_aMC@NLO [50] (hereafter, MCatNLO) event generator and matched with TMD parton distributions and showers obtained from PB evolution [20, 18, 17] and implemented in the Cascade Monte Carlo event generator [51, 52], using the subtractive matching procedure proposed in [13] and further analyzed in [45]. In particular, the Herwig6 [53, 54] subtraction terms are used in MCatNLO, as they are based on the same angular ordering conditions as the PB TMD distributions [45]. Final state parton showers are generated from Pythia6.428 [55], including photon radiation.
Ref. [9] uses the approach described above to compute theoretical results for DY transverse momentum distributions, and to make a determination of the intrinsic- parameter in Eq. (2) by performing fits of the results to DY experimental measurements of DY [16, 56, 57, 58, 59, 60, 61, 62, 63]. The study [9] includes a detailed treatment of statistical, correlated and uncorrelated uncertainties. The CMS data [16] at center of mass energy 13 TeV cover DY invariant masses from 50 GeV to 1 TeV. The other data cover energies from 13 TeV down to 38 GeV. With the fitted values [9], PB TMD distributions are thus obtained. Further discussions of the PB TMD distributions [9] are given in [64, 65, 66, 67].
In the next section we will use Monte Carlo predictions from the PB TMD method to explore the feasibility of extracting intrinsic- distributions from experimental measurements with coarse-grained binning in the low region.
3 Ratio of low and high bins
In this section we present the -ratio observable and methodology for studies of TMD dynamics. We will focus on the process in the transverse momentum region , where is taken to be small compared to the invariant mass .
We construct PB TMD predictions for the DY distribution, as described in the previous section, from MCatNLO + Cascade Monte Carlo, with initial-scale TMD distributions given in Eq. (2). To explore the intrinsic- parameter space, we generate 7 template samples with different values using the TMD grid files available on the TMDlib [48] website: these are = 0.5 GeV (using the PB TMD set PB-NLO-HERAI+II-2018-set2 [20]), = 0.59, 0.74, 0.89 GeV (using the set PB-NLO-HERAI+II-2023-set2-qs=0.74 [9]), and = 0.96, 1.04, 1.12 GeV (using the set PB-NLO-HERAI+II-2023-set2-qs=1.04 [9]). We study the influence of the intrinsic- width by examining the templates firstly in the full phase space (later on we will consider an experimental fiducial phase space). Results are shown in Fig. 1 over the range GeV.
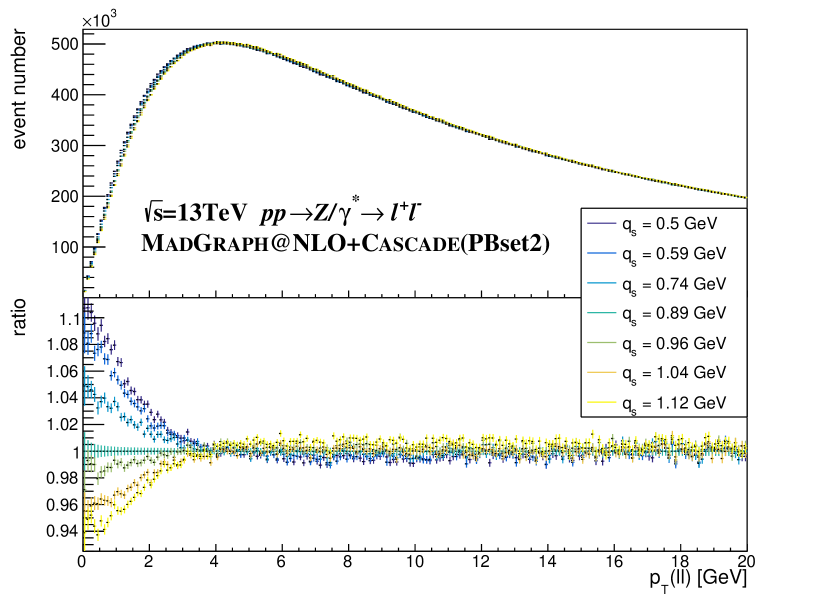
The shape in the rising part of the spectrum is altered by , with the peak position shifting to higher when increases. However, the trend is mild, suggesting that the essential information on the intrinsic width may be extracted from a well-defined ratio between the low and high regions. To this end, we introduce a momentum parameter to separate the regions and , and construct the 2-bin -ratio between the lower and higher regions. The -ratio is defined from the integral of event numbers in the relatively low () and high () region, i.e., from the two-binned ,
| (3.1) |
The uncertainty of the -ratio is obtained from propagating statistical uncertainties in the low and high bins, and is given by
| (3.2) |
The 2-bin distribution and corresponding -ratio are plotted, for the case of a given value GeV, in Fig. 2. The fall-off of the -ratio with increasing indicates that one may be able to extract TMD parameters from this ratio instead of the complete fine-binned shape, which results into a significant advantage from the standpoint of controlling experimental systematic uncertainties.
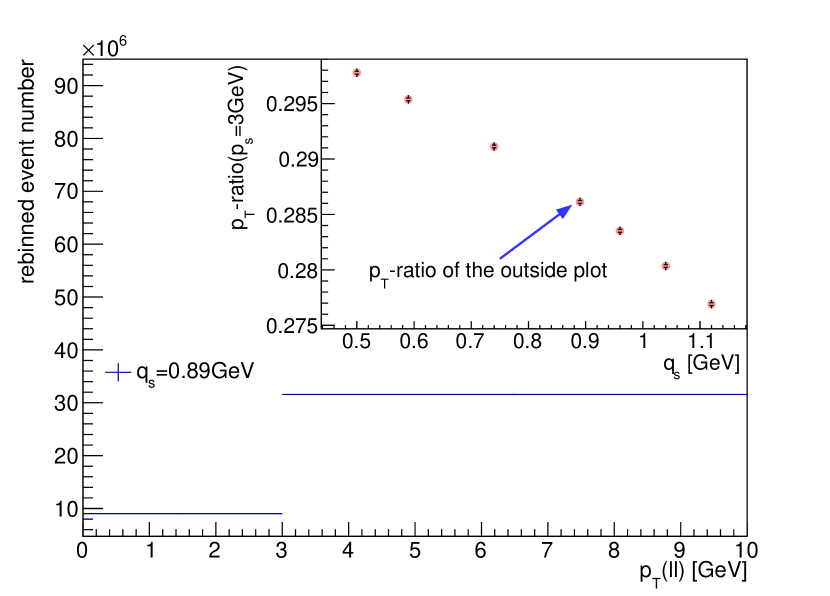
The separation momentum will play a critical role in the extraction from the -ratio. TMD sensitivity arises primarily from the low- region. If is too low inside this region, a proportion of soft-gluon splitting transverse momenta will be integrated into the upper region, causing a loss of sensitivity to TMD parameter determination. If, on the other hand, is higher than the peak, the information on low will tend to become undetectable.
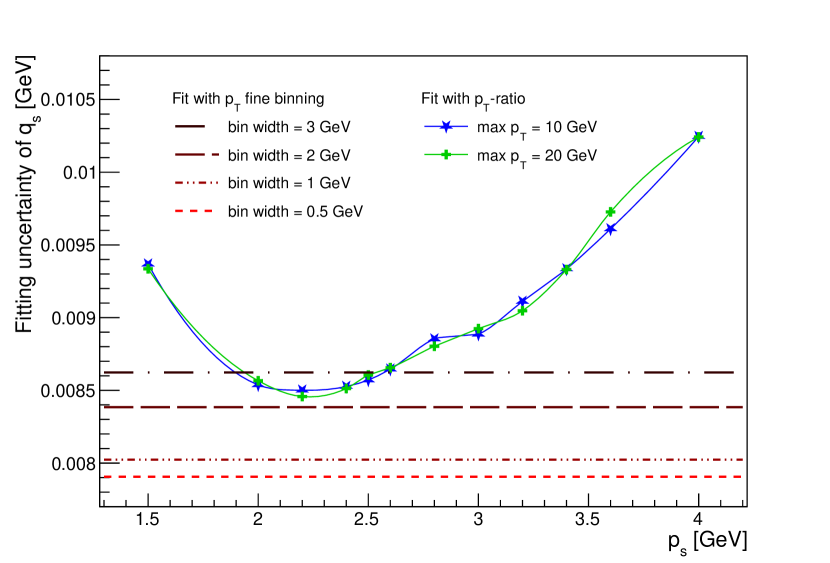
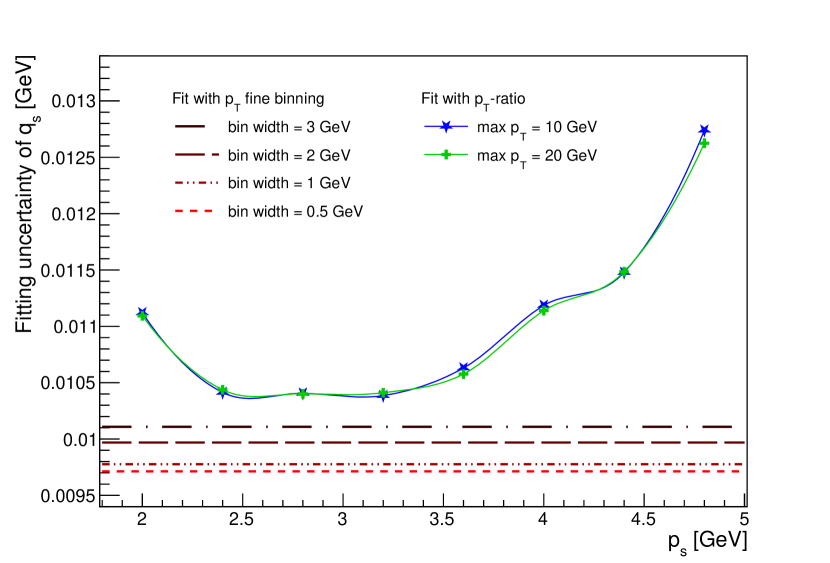
We next perform a sensitivity test on both the fine-binned and the -ratio. We test the former with different bin width from 0.5 GeV to 3 GeV, to examine the potential of the fine-binned shape in extracting . We test the latter, on the other hand, focusing on the sensitivity change due to different choice of . We shift from 1.5 GeV to 4 GeV to find an optimal definition of the -ratio, as well as to verify whether it has statistically the same sensitivity as the fine-binned shape. The greater than 10 GeV is expected to be ancillary in TMD performance studies. In this test, we will consider 10 GeV, 20 GeV, in a similar spirit to previous studies of intrinsic- distributions (see e.g. Refs. [8, 9, 12]).
In this test, we choose the sample with as the pseudo-data, and extract with the PB TMD replicas in the phase space with final-state lepton selections GeV and , in which leptons are dressed with photons reconstructed within . This is close to the fiducial phase space in real experiments at ATLAS and CMS. Sensitivity is represented by the fitting uncertainty of . Each sample in PB TMD template contains 100 million events. The fitting is performed with least square method, in which the estimator is defined as
| (3.3) |
with and being the observed and predicted data point, respectively, and the covariance matrix. We consider uncorrelated statistical uncertainties from the pseudo-data and template as the only sources contributing to , making it a diagonal matrix. The fitting uncertainties in both cases are depicted in Fig. 3. The result indicates that the -ratio is as sensitive as the fine-binned shape.
In real experiments, momentum resolution causes bin-to-bin migration. Since the migration effect is a dominant systematic uncertainty, it is essential to verify that such effect on the -ratio is not destructive. To study this, we apply a 3% resolution on the four-momentum of the dressed leptons as
| (3.4) |
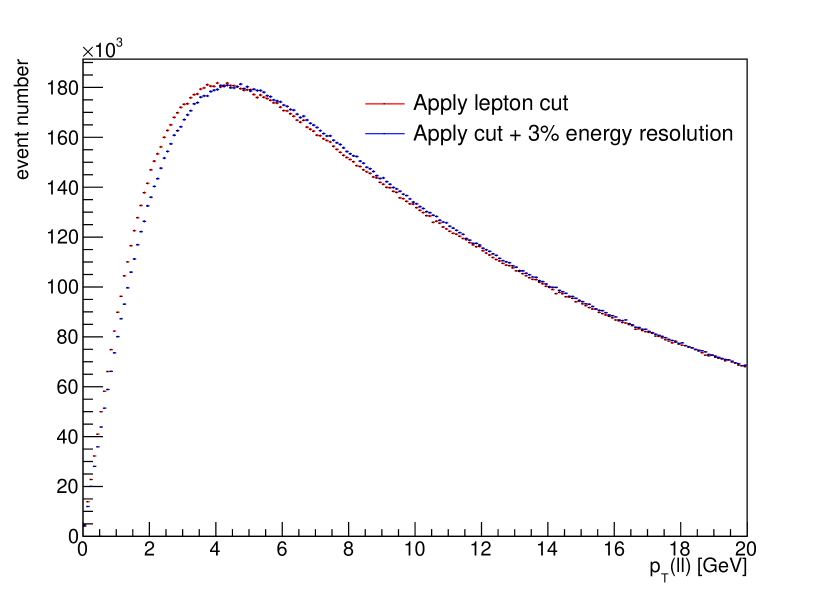
where follows a Gaussian distribution . The migration effect is illustrated in Fig. 4. It moves the peak position to a higher value, which is a similar trend as the effect. Also, owing to this the optimal separation choice is different from the non-migration scenario. If is defined correctly in this case, we expect the behavior to be the same as it is at truth level. We also note that in the bottom plot in Fig. 4 the relative ratio for GeV is smaller at the reco-level. This should result in a mild decrease in sensitivity.
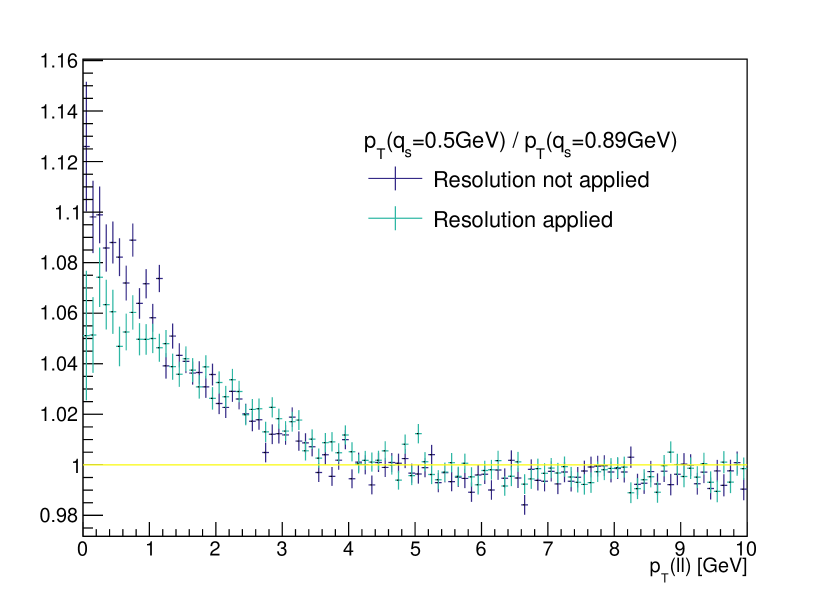
We now repeat the sensitivity test after the 3% energy resolution is applied to the dressed leptons. The results are shown in Fig. 5. The uncertainties are slightly larger than those in Fig. 3. Also, by comparing the fitting uncertainties in the cases of fine-binned and -ratio, we see that the decrease in sensitivity due to the migration effect is similar. We are led to conclude that the -ratio still has a good sensitivity to the intrinsic , so that this methodology can be applied directly in the experiments for TMD performance studies.
4 Extraction of from -ratio
Having performed a test with pseudo-data in the previous section, in this section we move on to consider a real experimental data analysis.
DY spectra are measured at the LHC with bin widths equal to or greater than 1 GeV. Measuring the fine-binned structure, on the other hand, is challenging. Sizeable systematic uncertainties have been reported in recent DY differential cross section measurements [14, 15], with luminosity of approximately 36 data collected in 2016, especially for the GeV bins. This is due to the uncertainties mostly induced from lepton efficiency and momentum resolution. Moreover, since the bin-to-bin correlation of the unfolding method uncertainties and momentum migration uncertainties are negative, increasing the bin numbers in such regions inevitably increases these systematic uncertainties.
Given these difficulties in achieving finer binning in the very low range, we next test the -ratio methodology of the previous section, based on less fine binning in the low- fiducial region, by applying it to real experimental data. We emphasize that the purpose of this study is not to carry out a precision extraction of , but to perform a feasibility study for the 2-bin -ratio in the context of TMD parameters determination.
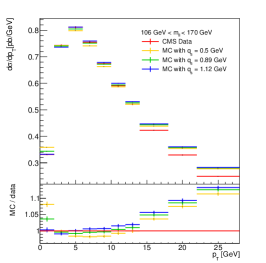
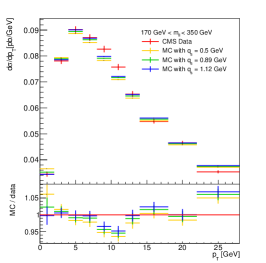
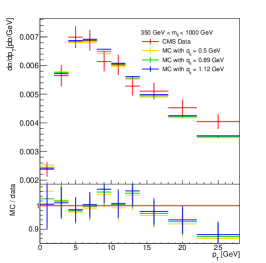
The CMS collaboration has measured the distribution in a wide mass range from 50 GeV to 1 TeV, with a bin width of 1 GeV in the DY invariant mass bin around the -boson mass [16]. This measurement has been used for the determination of the dependence on DY mass in Ref. [9]. We here perform an extraction of from this measurement using the -ratio, and compare the results with those in Ref. [9]. Besides testing the feasibility of the -ratio proposal with real data, we also aim to check that the -ratio is not biased by the high- region, where contributions from higher jet multiplicities are important [43, 19].
The selections of the leptons are
-
•
for both lepton,
-
•
GeV for leading lepton,
-
•
GeV for subleading lepton.
We use dressed-level leptons, defined with 0.1. The scale uncertainties are treated as fully correlated, and computed by varying the renormalization and factorization scales by a factor of 2 separately, excluding the two extreme cases. Since the model-induced statistical uncertainty is negligible comparing to the experimental uncertainty, the final covariance matrix comprises total covariance matrix from experiment and scale uncertainty:
| (4.1) |
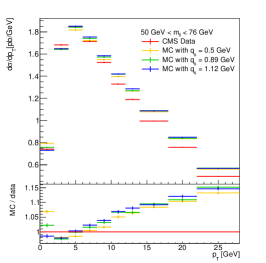
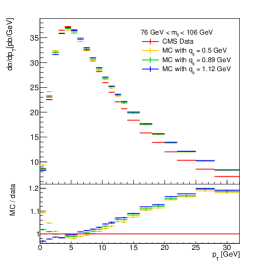
The description of the CMS data by the theoretical predictions is shown in Fig. 6. In our study, the range is the same as in Ref. [9] – 6 GeV for the first bin, 7 GeV for the second bin, and 8 GeV for the rest. This limitation prevents the ratio from being biased by the difference between prediction and data in the higher region. The choice of is largely restricted by the measurement, which affects the final sensitivity, as is suggested in the sensitivity study in Sect. 3. We stress that, if the -ratio is used for TMD parameter extractions, the choice of the value will need careful investigation. For our test in this paper, is set to 2 GeV for all bins.
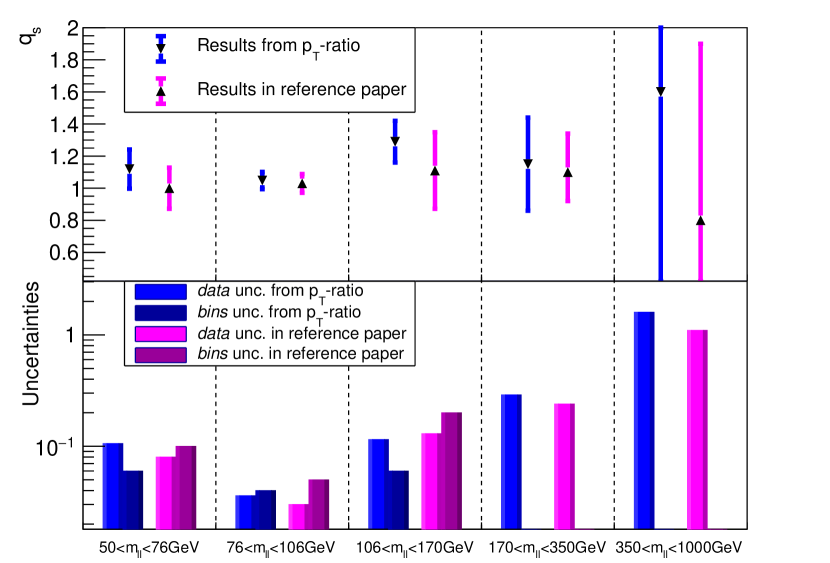
Final results are reported in Fig. 7. For comparison, the statistical uncertainties and scale uncertainties from data are considered, and compared to those in the analysis [9]. The uncertainties labeled with data at 68% confidence level are obtained from the gap defined by , and should be compared with the uncertainties labeled with data in Ref. [9]. Another source of uncertainties comes from the choice of the range. In Ref. [9], this is estimated by varying the numbers of bins in the fit. In this study, we obtain it in the same way. For the last two bins, it is not estimated for the lack of statistics. The result in every region is consistent with the previous result [9].
5 Conclusion
In this paper we propose the -ratio, which is defined as the ratio of low and high transverse momentum region of DY lepton pairs, as a sensitive observable and methodology for the extraction of a TMD parameter, the intrinsic Gaussian width . We firstly review the basic idea of the parton branching method for TMD evolution, and the calculation of in the DY process. We then point out that the sensitivity of the shape to the intrinsic distribution actually lies in the shift of the spectrum from low to high . This observation leads to the proposal of the -ratio. We numerically test the sensitivity of the -ratio to by comparing its statistical uncertainty with the same procedure on fine-binning structure. The result shows that the -ratio has comparable sensitivity to the fine-binned shape.
The precision in the most sensitive regions in real measurements at the LHC is largely restricted by experimental systematic uncertainties. These make the fine-binned structure difficult to access experimentally, and point to the need to explore approaches based on coarse-grained binning. The relative ratio of low and high regions avoids the fine binning. In this paper, we illustrate its effectiveness by extracting from the -ratio in a wide invariant-mass range of DY lepton pairs measured by the CMS collaboration recently. Since the CMS is binned into 2 GeV (or 1 GeV), we can only conduct this test by rebinning the distributions and covariance matrices, which means we cannot arbitrarily choose the separation momentum . Nevertheless, the result is consistent with previous results obtained from the low- distribution of DY lepton pairs as a function of invariant mass, and has the same level of precision.
From this perspective, this methodology can be tested in future studies by using more complex TMD parameterization forms, or investigating extreme conditions of very small or very large values, to make sure the extraction is unbiased. It could be used in forthcoming experiments for TMD performance studies, since it avoids the need to control large systematics in the low region. Unlike the extraction from a distribution that has been already binned, the -ratio requires a dedicated study of the separation momentum , affecting the sensitivity to TMD parameters, for example along the lines of the pseudo-data test carried out in this work.
Acknowledgement
We are grateful to Hannes Jung for discussion and for assistance with the use of PB TMD templates. We thank Laurent Favart, Jibo He, Hengne Li, Louis Moureaux and Hang Yin for useful conversations. This work was supported by the National Natural Science Foundation of China under Grants No.11721505, No.12061141005, and No.12105275, and supported by the “USTC Research Funds of the Double First-Class Initiative”.
References
- [1] S.. Drell and Tung-Mow Yan “Massive Lepton Pair Production in Hadron-Hadron Collisions at High-Energies” [Erratum: Phys.Rev.Lett. 25, 902 (1970)] In Phys. Rev. Lett. 25, 1970, pp. 316–320 DOI: 10.1103/PhysRevLett.25.316
- [2] R. Angeles-Martinez “Transverse Momentum Dependent (TMD) parton distribution functions: status and prospects” In Acta Phys. Polon. B 46.12, 2015, pp. 2501–2534 DOI: 10.5506/APhysPolB.46.2501
- [3] Stefano Camarda, Giancarlo Ferrera and Matthias Schott “Determination of the strong-coupling constant from the Z-boson transverse-momentum distribution” In Eur. Phys. J. C 84.1, 2024, pp. 39 DOI: 10.1140/epjc/s10052-023-12373-2
- [4] Georges Aad “A precise determination of the strong-coupling constant from the recoil of bosons with the ATLAS experiment at TeV”, 2023 arXiv:2309.12986 [hep-ex]
- [5] Alessandro Bacchetta et al. “Unpolarized transverse momentum distributions from a global fit of Drell-Yan and semi-inclusive deep-inelastic scattering data” In JHEP 10, 2022, pp. 127 DOI: 10.1007/JHEP10(2022)127
- [6] Alessandro Bacchetta et al. “Flavor dependence of unpolarized quark transverse momentum distributions from a global fit” In JHEP 08, 2024, pp. 232 DOI: 10.1007/JHEP08(2024)232
- [7] Marcin Bury et al. “PDF bias and flavor dependence in TMD distributions” In JHEP 10, 2022, pp. 118 DOI: 10.1007/JHEP10(2022)118
- [8] Valentin Moos, Ignazio Scimemi, Alexey Vladimirov and Pia Zurita “Extraction of unpolarized transverse momentum distributions from the fit of Drell-Yan data at N4LL” In JHEP 05, 2024, pp. 036 DOI: 10.1007/JHEP05(2024)036
- [9] I. Bubanja “The small region in Drell-Yan production at next-to-leading order with the parton branching method” In Eur. Phys. J. C 84.2, 2024, pp. 154 DOI: 10.1140/epjc/s10052-024-12507-0
- [10] Georgios Billis, Johannes K.. Michel and Frank J. Tackmann “Drell-Yan Transverse-Momentum Spectra at N3LL′ and Approximate N4LL with SCETlib”, 2024 arXiv:2411.16004 [hep-ph]
- [11] A. Hayrapetyan “Energy scaling behavior of intrinsic transverse momentum parameters in Drell-Yan simulation”, 2024 arXiv:2409.17770 [hep-ph]
- [12] Francesco Hautmann, Ignazio Scimemi and Alexey Vladimirov “Non-perturbative contributions to vector-boson transverse momentum spectra in hadronic collisions” In Phys. Lett. B 806, 2020, pp. 135478 DOI: 10.1016/j.physletb.2020.135478
- [13] A. Bermudez Martinez “Production of Z-bosons in the parton branching method” In Phys. Rev. D 100.7, 2019, pp. 074027 DOI: 10.1103/PhysRevD.100.074027
- [14] G. Aad et al. “Measurement of the transverse momentum distribution of Drell-Yan lepton pairs in proton-proton collisions at TeV with the ATLAS detector” In The European Physical Journal C 80.7, 2020 DOI: 10.1140/epjc/s10052-020-8001-z
- [15] A.. Sirunyan et al. “Measurements of differential Z boson production cross sections in proton-proton collisions at = 13 TeV” In Journal of High Energy Physics 2019.12, 2019 DOI: 10.1007/jhep12(2019)061
- [16] Armen Tumasyan “Measurement of the mass dependence of the transverse momentum of lepton pairs in Drell-Yan production in proton-proton collisions at = 13 TeV” In Eur. Phys. J. C 83.7, 2023, pp. 628 DOI: 10.1140/epjc/s10052-023-11631-7
- [17] F. Hautmann et al. “Soft-gluon resolution scale in QCD evolution equations” In Phys. Lett. B772, 2017, pp. 446–451 DOI: 10.1016/j.physletb.2017.07.005
- [18] F. Hautmann et al. “Collinear and TMD Quark and Gluon Densities from Parton Branching Solution of QCD Evolution Equations” In JHEP 01, 2018, pp. 070 DOI: 10.1007/JHEP01(2018)070
- [19] A. Bermudez Martinez, F. Hautmann and M.. Mangano “Multi-jet merging with TMD parton branching” In JHEP 09, 2022, pp. 060 DOI: 10.1007/JHEP09(2022)060
- [20] A. Bermudez Martinez “Collinear and TMD parton densities from fits to precision DIS measurements in the parton branching method” In Phys. Rev. D 99.7, 2019, pp. 074008 DOI: 10.1103/PhysRevD.99.074008
- [21] John C. Collins, Davison E. Soper and George F. Sterman “Transverse Momentum Distribution in Drell-Yan Pair and W and Z Boson Production” In Nucl. Phys. B 250, 1985, pp. 199–224 DOI: 10.1016/0550-3213(85)90479-1
- [22] John Collins “Foundations of Perturbative QCD” 32, Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology Cambridge University Press, 2023 DOI: 10.1017/9781009401845
- [23] Ignazio Scimemi and Alexey Vladimirov “Systematic analysis of double-scale evolution” In JHEP 08, 2018, pp. 003 DOI: 10.1007/JHEP08(2018)003
- [24] Francesco Hautmann, Ignazio Scimemi and Alexey Vladimirov “Determination of the rapidity evolution kernel from Drell-Yan data at low transverse momenta” In SciPost Phys. Proc. 8, 2022, pp. 123 DOI: 10.21468/SciPostPhysProc.8.123
- [25] A. Bermudez Martinez “The Parton Branching Sudakov and its relation to CSS” In PoS EPS-HEP2023, 2024, pp. 270 DOI: 10.22323/1.449.0270
- [26] Aleksandra Lelek “NNLL Transverse Momentum Dependent evolution in the Parton Branching method” In 42nd International Symposium on Physics In Collision, 2024 arXiv:2412.09108 [hep-ph]
- [27] G. Marchesini and B.. Webber “Monte Carlo Simulation of General Hard Processes with Coherent QCD Radiation” In Nucl. Phys. B310, 1988, pp. 461–526 DOI: 10.1016/0550-3213(88)90089-2
- [28] S. Catani, B.. Webber and G. Marchesini “QCD coherent branching and semiinclusive processes at large x” In Nucl. Phys. B349, 1991, pp. 635–654 DOI: 10.1016/0550-3213(91)90390-J
- [29] F. Hautmann, L. Keersmaekers, A. Lelek and A.. Van Kampen “Dynamical resolution scale in transverse momentum distributions at the LHC” In Nucl. Phys. B 949, 2019, pp. 114795 DOI: 10.1016/j.nuclphysb.2019.114795
- [30] F. Hautmann “Endpoint singularities in unintegrated parton distributions” In Phys. Lett. B 655, 2007, pp. 26–31 DOI: 10.1016/j.physletb.2007.08.081
- [31] B.. Webber “Monte Carlo Simulation of Hard Hadronic Processes” In Ann. Rev. Nucl. Part. Sci. 36, 1986, pp. 253–286 DOI: 10.1146/annurev.ns.36.120186.001345
- [32] S. Dooling, P. Gunnellini, F. Hautmann and H. Jung “Longitudinal momentum shifts, showering, and nonperturbative corrections in matched next-to-leading-order shower event generators” In Phys. Rev. D87.9, 2013, pp. 094009 DOI: 10.1103/PhysRevD.87.094009
- [33] S. Sadeghi Barzani “PB TMD fits at NLO with dynamical resolution scale” In 29th International Workshop on Deep-Inelastic Scattering and Related Subjects, 2022 arXiv:2207.13519 [hep-ph]
- [34] V.. Gribov and L.. Lipatov “Deep inelastic e p scattering in perturbation theory” In Sov. J. Nucl. Phys. 15, 1972, pp. 438–450
- [35] Guido Altarelli and G. Parisi “Asymptotic Freedom in Parton Language” In Nucl. Phys. B 126, 1977, pp. 298–318 DOI: 10.1016/0550-3213(77)90384-4
- [36] Yuri L. Dokshitzer “Calculation of the Structure Functions for Deep Inelastic Scattering and e+ e- Annihilation by Perturbation Theory in Quantum Chromodynamics.” In Sov. Phys. JETP 46, 1977, pp. 641–653
- [37] H. Abramowicz “Combination of measurements of inclusive deep inelastic scattering cross sections and QCD analysis of HERA data” In Eur. Phys. J. C 75.12, 2015, pp. 580 DOI: 10.1140/epjc/s10052-015-3710-4
- [38] H. Abdolmaleki “xFitter: An Open Source QCD Analysis Framework. A resource and reference document for the Snowmass study”, 2022 arXiv:2206.12465 [hep-ph]
- [39] S. Alekhin “HERAFitter” In Eur. Phys. J. C 75.7, 2015, pp. 304 DOI: 10.1140/epjc/s10052-015-3480-z
- [40] A. Bermúdez Martínez “The transverse momentum spectrum of low mass Drell–Yan production at next-to-leading order in the parton branching method” In Eur. Phys. J. C 80.7, 2020, pp. 598 DOI: 10.1140/epjc/s10052-020-8136-y
- [41] M.. Abdulhamid “Azimuthal correlations of high transverse momentum jets at next-to-leading order in the parton branching method” In Eur. Phys. J. C 82.1, 2022, pp. 36 DOI: 10.1140/epjc/s10052-022-09997-1
- [42] A. Bermudez Martinez and F. Hautmann “Azimuthal di-jet correlations with parton branching TMD distributions” In 29th International Workshop on Deep-Inelastic Scattering and Related Subjects, 2022 arXiv:2208.08446 [hep-ph]
- [43] A. Bermudez Martinez, F. Hautmann and M.. Mangano “TMD evolution and multi-jet merging” In Phys. Lett. B 822, 2021, pp. 136700 DOI: 10.1016/j.physletb.2021.136700
- [44] A. Bermudez Martinez, F. Hautmann and M.. Mangano “Multi-jet physics at high-energy colliders and TMD parton evolution”, 2021 arXiv:2109.08173 [hep-ph]
- [45] H. Yang “Back-to-back azimuthal correlations in jet events at high transverse momentum in the TMD parton branching method at next-to-leading order” In Eur. Phys. J. C 82.8, 2022, pp. 755 DOI: 10.1140/epjc/s10052-022-10715-0
- [46] D. Amati et al. “A Treatment of Hard Processes Sensitive to the Infrared Structure of QCD” In Nucl. Phys. B173, 1980, pp. 429–455 DOI: 10.1016/0550-3213(80)90012-7
- [47] A. Bassetto, M. Ciafaloni and G. Marchesini “Jet Structure and Infrared Sensitive Quantities in Perturbative QCD” In Phys. Rept. 100, 1983, pp. 201–272 DOI: 10.1016/0370-1573(83)90083-2
- [48] N.. Abdulov “TMDlib2 and TMDplotter: a platform for 3D hadron structure studies” In Eur. Phys. J. C 81.8, 2021, pp. 752 DOI: 10.1140/epjc/s10052-021-09508-8
- [49] F. Hautmann et al. “TMDlib and TMDplotter: library and plotting tools for transverse-momentum-dependent parton distributions” In Eur. Phys. J. C74, 2014, pp. 3220 DOI: 10.1140/epjc/s10052-014-3220-9
- [50] J. Alwall et al. “The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations” In JHEP 07, 2014, pp. 079 DOI: 10.1007/JHEP07(2014)079
- [51] S. Baranov “CASCADE3 A Monte Carlo event generator based on TMDs” In Eur. Phys. J. C 81.5, 2021, pp. 425 DOI: 10.1140/epjc/s10052-021-09203-8
- [52] H. Jung “The CCFM Monte Carlo generator CASCADE version 2.2.03” In Eur. Phys. J. C 70, 2010, pp. 1237–1249 DOI: 10.1140/epjc/s10052-010-1507-z
- [53] G. Corcella et al. “HERWIG 6.5 release note”, 2002 arXiv:hep-ph/0210213
- [54] Gennaro Corcella et al. “HERWIG 6: an event generator for hadron emission reactions with interfering gluons (including supersymmetric processes)” In Journal of High Energy Physics 2001.01, 2001, pp. 010 DOI: 10.1088/1126-6708/2001/01/010
- [55] Torbjorn Sjostrand, Stephen Mrenna and Peter Skands “PYTHIA 6.4 physics and manual” In Journal of High Energy Physics 2006.05, 2006, pp. 026 DOI: 10.1088/1126-6708/2006/05/026
- [56] Georges Aad “Measurement of the transverse momentum and distributions of Drell–Yan lepton pairs in proton–proton collisions at TeV with the ATLAS detector” In Eur. Phys. J. C 76.5, 2016, pp. 291 DOI: 10.1140/epjc/s10052-016-4070-4
- [57] R. Aaij “Precision measurement of forward boson production in proton-proton collisions at TeV” In JHEP 07, 2022, pp. 026 DOI: 10.1007/JHEP07(2022)026
- [58] B. Abbott “Measurement of the inclusive differential cross section for bosons as a function of transverse momentum in collisions at TeV” In Phys. Rev. D 61, 2000, pp. 032004 DOI: 10.1103/PhysRevD.61.032004
- [59] T. Affolder “The transverse momentum and total cross section of pairs in the boson region from collisions at TeV” In Phys. Rev. Lett. 84, 2000, pp. 845–850 DOI: 10.1103/PhysRevLett.84.845
- [60] T. Aaltonen “Transverse momentum cross section of pairs in the -boson region from collisions at TeV” In Phys. Rev. D 86, 2012, pp. 052010 DOI: 10.1103/PhysRevD.86.052010
- [61] C. Aidala “Measurements of pairs from open heavy flavor and Drell-Yan in collisions at GeV” In Phys. Rev. D 99.7, 2019, pp. 072003 DOI: 10.1103/PhysRevD.99.072003
- [62] Albert M Sirunyan “Study of Drell-Yan dimuon production in proton-lead collisions at 8.16 TeV” In JHEP 05, 2021, pp. 182 DOI: 10.1007/JHEP05(2021)182
- [63] G. Moreno “Dimuon Production in Proton - Copper Collisions at = 38.8-GeV” In Phys. Rev. D 43, 1991, pp. 2815–2836 DOI: 10.1103/PhysRevD.43.2815
- [64] H. Jung “The non-perturbative Sudakov Form Factor and the role of soft gluons” In 30th Cracow Epiphany Conference on on Precision Physics at High Energy Colliders: dedicated to the memory of Staszek Jadach, 2024 arXiv:2404.06905 [hep-ph]
- [65] I. Bubanja et al. “Center-of-mass energy dependence of intrinsic- distributions obtained from Drell-Yan production”, 2024 arXiv:2404.04088 [hep-ph]
- [66] S. Monfared “Recent progress in transverse momentum dependent (TMD) Parton Densities and corresponding parton showers” In 31st International Workshop on Deep-Inelastic Scattering and Related Subjects, 2024 arXiv:2410.05853 [hep-ph]
- [67] Natasa Raicevic “Non-Perturbative Contributions to Low Transverse Momentum Drell-Yan Pair Production Using the Parton Branching Method” In 13th International Conference on New Frontiers in Physics, 2024 arXiv:2412.00892 [hep-ph]