CnGAN: Generative Adversarial Networks for Cross-network User Preference Generation for Non-overlapped Users
Abstract.
A major drawback of cross-network recommender solutions is that they can only be applied to users that are overlapped across networks. Thus, the non-overlapped users, which form the majority of users are ignored. As a solution, we propose CnGAN, a novel multi-task learning based, encoder-GAN-recommender architecture. The proposed model synthetically generates source network user preferences for non-overlapped users by learning the mapping from target to source network preference manifolds. The resultant user preferences are used in a Siamese network based neural recommender architecture. Furthermore, we propose a novel user-based pairwise loss function for recommendations using implicit interactions to better guide the generation process in the multi-task learning environment. We illustrate our solution by generating user preferences on the Twitter source network for recommendations on the YouTube target network. Extensive experiments show that the generated preferences can be used to improve recommendations for non-overlapped users. The resultant recommendations achieve superior performance compared to the state-of-the-art cross-network recommender solutions in terms of accuracy, novelty and diversity.
1. Introduction
Cross-network recommender systems utilize auxiliary information from multiple source networks to create comprehensive user profiles for recommendations on a target network. Therefore, unlike traditional recommender solutions which are limited to information within a single network, cross-network solutions are more robust against cold-start and data sparsity issues (Mehta et al., 2005). For example, the additional information from Twitter and Flicker, increased recommender precision on Delicious by 10% (Abel et al., 2011). Similarly, the transfer of information from various source networks to target networks such as Google+ to YouTube (Deng et al., 2013), Twitter to YouTube (Roy et al., 2012; Perera and Zimmermann, 2017) and Wikipedia to Twitter (Osborne et al., 2012) have consistently improved recommender accuracy. Furthermore, cross-network solutions allow user preferences to be captured from diverse perspectives, which increases the overall recommender quality in terms of diversity and novelty (Perera and Zimmermann, 2018, 2017). However, despite the growing success of cross-network recommender solutions, the majority of existing solutions can only be applied to users that exist in multiple networks (overlapped users). The remaining non-overlapped users, which form the majority are unable to enjoy the benefits of cross-network solutions.
Deep learning and generative modeling techniques have been successfully used in the recommender systems domain in the past few years. For example, restricted Boltzmann machines (Salakhutdinov et al., 2007), Autoencoders (Ouyang et al., 2014), Hidden Markov Models (Sahoo et al., 2012) and Recurrent Neural Networks (RNN) (Hidasi et al., 2015) are some of the models used for rating prediction tasks. Recent advancements in Generative Adversarial Networks (GANs) have also drawn recommender systems researchers to apply the new minimax game framework to information retrieval. For example, IRGAN (Wang et al., 2017) and RecGAN (Bharadhwaj et al., 2018) were designed to predict relevant documents to users. Existing solutions use GAN to generate simple rating values (Wang et al., 2017; Bharadhwaj et al., 2018; Yoo et al., 2017) or synthetic items (e.g., images (Kang et al., 2017)). In contrast, we use GAN to generate complex user data (i.e., user preferences on the source network).
We propose a novel GAN model (CnGAN) to generate cross-network user preferences for non-overlapped users. Unlike the standard GAN model, we view the learning process as a mapping from target to source network preference manifolds. The proposed model solves two main tasks. First, a generator task learns the corresponding mapping from target to source network user preferences and generates auxiliary preferences on the source network. Second, a recommender task uses the synthetically generated preferences to provide recommendations for users who only have interactions on the target network. Furthermore, we propose two novel loss functions to better guide the generator and recommender tasks. The proposed solution is used to provide recommendations for YouTube users by incorporating synthesized preferences on Twitter. However, the solution is generic and can be extended to incorporate multiple source networks.
In this paper, we first briefly provide preliminaries to the proposed model and present the proposed CnGAN solution detailing its two main components, the generator and recommender tasks. Then, we compare the proposed model against multiple baselines to demonstrate its effectiveness in terms of accuracy, novelty and diversity. We summarize our main contributions as follows:
-
•
To the best of our knowledge, this is the first attempt to apply a GAN based model to generate missing source network preferences for non-overlapped users.
-
•
We propose CnGAN, a novel GAN based model which includes a novel content loss function and user-based pairwise loss function for the generator and recommender tasks.
-
•
We carry out extensive experiments to demonstrate the effectiveness of CnGAN to conduct recommendations for non-overlapped users and improve the overall quality of recommendations compared to state-of-the-art methods.
2. Model
2.1. Model Preliminaries
2.1.1. Bayesian Personalized Ranking (BPR):
Learning user preferences from implicit feedback is challenging since implicit feedback does not indicate preference levels toward items, it only indicates the presence or absence of interactions with items. BPR (Rendle et al., 2009) was proposed to rank items based on implicit feedback using a generic optimization criterion. BPR is trained using pairwise training instances , where is the set of all items and is the set of items user has interacted with. BPR uses a pairwise loss function to rank interacted items higher than non-interacted items, and maximizes their margin using a pairwise loss as follows:
| (1) |
where , are model parameters, is a sigmoid function and are regularization parameters.
2.1.2. Feature extraction on a continuous space:
CnGAN is trained using target network interactions of each user at each time interval and their corresponding source network interactions. We used topic modeling to capture user interactions on a continuous topical space since CnGAN is a GAN based model and requires inputs in a continuous space. Let denote an overlapped user at time , where and are target and source network interactions spanned over time intervals. A non-overlapped user is denoted only using target network interactions. We used YouTube as the target and Twitter as the source network to conduct video recommendations on YouTube. Therefore, is the set of interacted videos (i.e., liked or added to playlists) and is the set of tweets. We assumed that each interaction (video or tweet) is associated with multiple topics, and extracted the topics from the textual data associated with each interaction (video titles, descriptions and tweet contents). We used the Twitter-Latent Dirichlet Allocation (Twitter-LDA) (Zhao et al., 2011) for topic modeling since it is most effective against short and noisy contents. Based on topic modeling, each user on the target network is represented as a collection of topical distributions over time intervals, where is the number of topics. Each vector is the topical distribution at time , where is the relative frequency of topic k, and is the absolute frequency of the corresponding topic. Similarly, on the source network, interactions are represented as . The resultant topical frequencies indicate user preference levels towards corresponding topics. Therefore, represents user preferences over time intervals on a continuous topical space, and forms the input to the proposed model.
2.2. Generator Task
The generator task learns the function that maps the target network preferences manifold to the source network preferences manifold using Encoders (), Discriminator () and Generator ().
2.2.1. Encoders:
User preferences captured as topical distribution vectors and become sparse when is set to a sufficiently large value to capture finer level user preferences, and/or the number of interactions at a time interval is low. One of the most effective methods to train machine learning models with highly sparse data is to model interactions between input features (Blondel et al., 2016) (e.g., using neural networks (He et al., 2017)). Therefore, we used two neural encoders and for target and source networks to transform the input topical distributions to dense latent encodings. The resultant encodings are represented as and , where is the dimensionality of the latent space. These encodings form the input to the generator task.

2.2.2. Generator task formulation:
For a non-overlapped user , let denote the target network encoding at time interval . The generator task aims to synthetically generate the mapping source network encoding that closely reflects the missing source network encoding . Hence, uses target encoding and attempts to generate the mapping source encoding to fool . Similarly, tries to differentiate between real source encoding and generated encoding . Note that, we refer to the actual and generated target and source network encodings of non-overlapped users as synthetically mapped data and the actual target and source network encodings of overlapped users as real mapping data.
2.2.3. Discriminator:
Analogous to in standard GANs, the real and synthetically mapped pairs could be used to learn . However, may only learn to differentiate between actual and generated source network encodings in a given pair of inputs, without learning to check if the given pair is a mapping pair. Therefore, during training, we input mismatching source and target network encodings to ensure that an effective mapping is learned. We modified the loss function for to minimize output scores for mismatching pairs and maximize output scores for matching pairs. For a given target network encoding, we drew mismatching source encodings only from real data to avoid potential biases. Mismatching pairs were created by pairing real encodings from different users at the same time interval or by pairing encodings from the same user at different time intervals (see Figure 1). Accordingly, the loss function for is formed as follows:
| (2) |
where and are matching and mismatching target and source network topical distributions, are the target network topical distributions and is the generated matching source network encoding for the given target network encoding . Furthermore, , and , where is the probability that and are matching target and source network encodings. Therefore, and work together to maximize the discriminator value function . The encoders ( and ) assist the process by encoding the topical distributions that are optimized for learning (e.g., extract encodings that express the latent mapping between target and source networks).
2.2.4. Generator:
Once and are trained, they adversarially guide by effectively identifying real and synthetically generated data. Specifically, takes in a target network encoding and synthetically generates the mapping source network encoding that resemble drawn from real mapping data.
GAN models are typically used to generate real-like images from random noise vectors. For a given noise vector, different GANs can learn multiple successful mappings from the input space to the output space. In contrast, CnGAN aims to learn a specific mapping from target to source network encodings. Hence, for given pairs of real mapping data , minimizes an additional content loss between the generated and real source encodings to provide additional guidance for . Therefore, we formulated the loss function for as follows:
| (3) |
where is the content loss computed as the -norm loss between real and generated encodings.
2.3. Recommender Task
The recommender task uses the generated preferences to conduct recommendations for non-overlapped users.
2.3.1. Recommender task formulation:
Let denote a non-overlapped user at time based on synthetically mapped data, which reflects current preferences. To capture previous preferences, we used a previous interaction vector , where is the number of items. Each element is set to 1 if the user had an interaction with item before time , and 0 if otherwise. Thus, we formulated the recommender task as a time aware Top-N ranking task where, current and previous user preferences are used to predict a set of items that the user is most likely interact with, in the next time interval .
2.3.2. Recommender loss:
Typically, BPR optimization is performed using Stochastic Gradient Descent (SGD) where, for each training instance , parameter () updates are performed as follows:
| (4) |
where is the learning rate, is the pairwise loss for a given triplet and is the predicted rating for user and item . Since BPR is a generic optimization criterion, can be obtained using any standard collaborative filtering approach (e.g., MF). Considering the rating prediction function in MF (, where and are latent representations of user and item ), for MF based BPR optimization can be defined as .
For each instance, three updates are performed when , and . For each update on the latent user representation (), two updates are performed on the latent item representations and . Hence, the training process is biased towards item representation learning, and we term the standard BPR optimization function as an item-based pairwise loss function. Since our goal is to learn effective user representations to conduct quality recommendations, we introduce a user-based pairwise loss function ( loss), which is biased towards user representation learning.
We used a fixed time-length sliding window approach in the training process where, at each time interval, the model is trained using the interactions within the time interval (see Section 3.2.1). Thus, we denote the training instances for the new user-based BPR at each time interval as where is the set of users who have interactions with item , at time . Compared to in the standard item-based BPR, user-based BPR contains where, for item at time , user has an interaction and user does not. Thus, intuitively, the predictor should assign a higher score for compared to . Accordingly, we defined the user-based loss function to be minimized as follows:
| (5) |
where . During optimization, updates are performed as follows:
| (6) |
For different values, the following partial derivations are obtained:
| (7) |
Since the user-based BPR performs two user representation updates for each training instance, it is able to efficiently guide to learn user representations during training.
2.3.3. Recommender architecture:
We used a Siamese network for the recommender architecture since it naturally supports pairwise learning (see Figure 2). Given a non-overlapped user with current preferences and previous preferences at time , we learned a transfer function , which maps the user to the latent user space for recommendations as follows:
| (8) |
The transfer function is learned using a neural network since neural networks are more expressive and effective than simple linear models. Accordingly, for a non-overlapped user at time , the predicted rating for any given item is obtained using the inner-product between the latent user and item representations as follows:
| (9) |

2.4. Multi-Task Learning (MTL)
Although the generator and recommender tasks are separate, they depend on each other to achieve a higher overall performance. The generator task increases the accuracy of the recommender by synthesizing source network encodings that effectively represent user preferences. The recommender task guides the generator to efficiently learn the target to source mapping by reducing the search space. Therefore, we trained both interrelated tasks in a MTL environment to benefit from the training signals of each other. Hence, we formulated the multi-task training objectives as follows:
| (10) |
| (11) |
where is the value function for , and , is the loss function, and and are model parameters. The loss is back-propagated all the way to since and are compositions of the functions and (see Equation 8) and the generator and recommender tasks are trained as an end-to-end process. Hence, equation 11 can be restated as follows:
| (12) |
3. Experiments
3.1. Dataset
Due to the lack of publicly available timestamped cross-network datasets, we extracted overlapped users on YouTube (target) and Twitter (source) networks from two publicly available datasets (Yan et al., 2014; Lim et al., 2015). We scraped timestamps of interactions and associated textual contents (video titles, descriptions and tweet contents) over a 2-year period from 1st March 2015 to 29th February 2017. In line with common practices, we filtered out users with less than 10 interactions on both networks for effective evaluations. The final dataset contained 2372 users and 12,782 YouTube videos.
3.2. Experimental Setup
The recommender systems literature often uses training and testing datasets with temporal overlaps (Campos et al., 2012), which provides undue advantages as it does not reflect a realistic recommender environment. To avoid such biases, at each time interval, the proposed model is trained using only the interactions during the current and previous time intervals. We randomly selected 50% of users as non-overlapped users and removed their source network interactions. The model was first trained offline using overlapped users (see Section 3.2.1). Then, testing and online training were conducted using both overlapped and non-overlapped users (see Section 3.2.2).
3.2.1. Offline Training:
We used the sliding window approach and data from the first 16 months () of overlapped users to learn the mapping from target to source network preferences for the generator task, the neural transfer function , and item latent representations for the recommender task. At each training epoch, the generator task is learned first. Hence, , and are trained using real mapping data and the trained is used to generate synthetically mapped data. The generated preferences are used as inputs to the recommender task to predict interactions at the next time interval. The ground truth interactions at the same time interval are used to propagate the recommender error from the recommender to the generator task and learn parameters of both processes.
3.2.2. Testing and Online Training:
We used data from the last 8 months ( onward) to test and retrain the model online in a simulated real-world environment. At each testing time interval , first, mapping source network preferences are generated for non-overlapped users based on their target network preferences. Second, the synthetically mapped data for non-overlapped users are used as inputs to conduct Top-N recommendations for (see Equation 9). The entire model is then retrained online before moving to the next time interval, as follows: First, the recommender parameters and are updated based on the recommendations for both overlapped and non-overlapped users. Second, the components of the generator task , and are updated based on the real mapping data from overlapped users. Finally, to guide from the training signals of the recommender, the model synthesizes mapping data for overlapped users, which are used as inputs for recommendations. The error is back-propagated from the recommender task to , and consequently, the parameters , and are updated. This process is repeated at subsequent time intervals as the model continues the online retraining process. In line with common practices in sliding window approaches, the model is retrained multiple times before moving to the next time interval.
3.3. Evaluation
We formulated video recommendation as a Top-N recommender task and predicted a ranked set of videos that the user is most likely to interact with at each time interval. To evaluate model accuracy, we calculated the Hit Ratio (HR) and Normalized Discounted Cumulative Gain (NDCG) (He et al., 2015). Both metrics were calculated for each participating user at each time interval and the results were averaged across all users and testing time intervals.
3.3.1. Baselines
We evaluated CnGAN against single network, cross-network, linear factorization and GAN based baselines.
-
•
TimePop: Recommends the most popular items in the previous time interval to all users in the current time interval.
-
•
TBKNN (Campos et al., 2010): Time-Biased KNN computes a set of neighbors for each user at each time interval based on complete user interaction histories, and recommends their latest interactions to the target user at the next time interval. Similar to the original work, we used several values from 4 to 50, and the results were averaged.
-
•
TDCN (Perera and Zimmermann, 2017): Time Dependent Cross-Network is an offline, MF based cross-network recommender solution, which provides recommendations only for overlapped users. TDCN learns network level transfer matrices to transfer and integrate user preferences across networks and conduct MF based recommendations.
-
•
CRGAN: Due to the absence of GAN based cross-network user preference synthesizing solutions, we created Cross-network Recommender GAN, as a variation of our solution. Essentially, CRGAN uses the standard and loss functions and does not contain the and loss components.
-
•
NUBPR-O and NUBPR-NO: Due to the absence of neural network based cross-network recommender solutions, we created two Neural User-based BPR solutions, as variations of our solution. Essentially, both models do not contain the generator task. NUBPR-O considers both source and target network interactions and NUBPR-NO only considers target network interactions to conduct recommendations.
3.4. Model Parameters
We used Adaptive Moment Estimation (Adam) (Kingma and Ba, 2015) for optimizations since Adam adaptively updates the learning rate during training. We set the initial learning rate to 0.1, a fairly large value for faster initial learning before the rate is updated by Adam. We used only one hidden layer for all neural architectures, and given the size of the output layer , the size of the hidden layer was set to to reduce the number of hyper-parameters. We used the dropout regularization technique and the dropout was set to 0.4 during training to prevent neural networks from overfitting.
4. Discussion
4.0.1. Offline training loss:
We compared the offline training loss of , and (see Figure 4). All three processes converge around 50 epochs, and compared to and , the drop in is low. Therefore, we further examined the proposed loss against the vanilla loss for the same training process (see Figure 4). Inline with standard GANs, the vanilla loss component in the proposed loss increases while the proposed loss slowly decreases. Hence, despite the low decrease in the overall loss, loss has notably decreased.
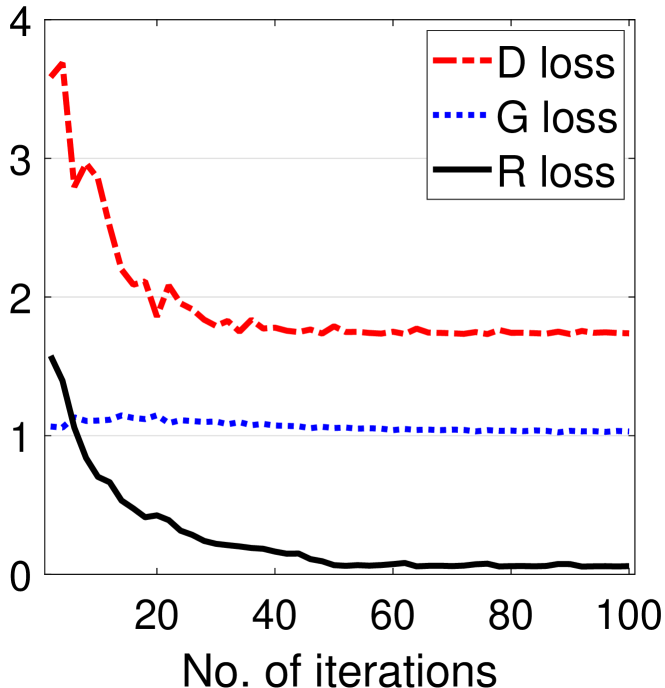

4.0.2. Online training loss:

We observed loss during the online training process (see Figure 5). Updates are most effective within the first 10-15 iterations and after around 20 iterations, the recommender accuracy reaches its peak. Additional iterations tend to overfit the model and degrade performance. Therefore, the proposed solution is feasible in real-world applications since online training requires only a few iterations and retraining is costly.
4.0.3. Prediction accuracy:


We compared recommender accuracy (HR and NDCG) against multiple Top-N values (see Figure 6). The neural network based solutions (Proposed, NUBPR-O, NUBPR-NO and CRGAN) show a higher accuracy since they capture complex relationships in user preferences. Among the non-neural network based solutions, TimePop has the lowest accuracy since it is based on a simple statistic - the popularity of videos. TDCN outperforms TBKNN and TimePop since it effectively utilizes both source and target network interactions to model user preferences.
As expected, NUBPR-O which does not have a data generation process and is only trained and tested with real mapping data from overlapped users has the best accuracy. We used NUBPR-O as the benchmark, since the goal is to synthesize data similar to the data used to train NUBPR-O. The proposed model shows the closest accuracy to NUBPR-O and consistently outperforms NUBPR-NO, which only used target network interactions. Therefore, the proposed model is able to generate user preferences that increases the recommender accuracy, even when the user overlaps are unknown. Furthermore, the improvements gained over CRGAN, which uses vanilla GAN loss functions, show the effectiveness of the proposed and loss functions.
4.0.4. Prediction accuracy for different number of topics ():


We compared recomender accuracy against the dimensionality of the encoded topical space () (see Section 2.1.2 and Figure 7). A grid search algorithm was used to select an effective value, and the highest accuracy is achieved when is around 64 topics for all Top-N values. Smaller number of topics fail to effectively encode diverse user preferences, while a higher number of topics create highly sparse inputs and reduce recommender performance. Further experiments using the standard perplexity measure (Blei et al., 2003) showed that 64 topics lead to a smaller perplexity with faster convergence.
4.0.5. Diversity and novelty:
A higher recommendation accuracy alone is insufficient to capture overall user satisfaction. For example, continuously recommending similar items (in terms of topics, genre, etc.) could lead to a decline in recommendation accuracy as users lose interest over time. Therefore, we compared the diversity (Avazpour et al., 2014) and novelty (Zhang, 2013) of recommended items. The proposed model was able to recommend videos with better novelty and diversity, and was the closest to NUBPR-O model (only a 2.4% and 3.8% novelty and diversity drop). Compared to the single-network based solutions, cross-network solutions showed better results as they utilize rich user profiles with diverse user preferences. Against the closest CRGAN approach, the proposed model showed considerable improvements in novelty (by 8.9%) and diversity (by 12.3%).
4.0.6. Alternative GAN architectures:
Designing and training GAN models can be challenging due to the unbalance between and , diminishing gradients and non-convergence (Arjovsky and Bottou, 2017; Salimans et al., 2016). Various GAN architectures and training techniques were recently introduced to handle such issues. Therefore, despite the effectiveness of CnGAN, we designed two alternative solutions based on two widely popular GAN architectures, Deep convolutional GAN (DCGAN) (Radford et al., 2015) and Wasserstein GAN (WGAN) (Arjovsky et al., 2017) to replace the and learning processes. We found that DCGAN becomes highly unstable in this environment, where D error is constantly increased. This can be because, DCGAN is based on Convolution Neural Networks, known to capture the local features within the input data. However, unlike typical image data, user preferences in the vectors may not provide any interesting local features. Hence, DCGAN was less effective. Further experiments using WGAN also did not improve the performances.
5. Conclusion and Further Work
Typical cross-network recommender solutions are applied to users that are fully overlapped across multiple networks. Thus to the best of our knowledge, we propose the first Cross-network Generative Adversarial Network based model (CnGAN), which generates user preferences for non-overlapped users. The proposed model first uses a generator task to learn the mapping from target to source network user preferences and synthesize source network preferences for non-overlapped users. Second, the model uses a recommender task based on a Siamese network to incorporate synthesized source network preferences and conduct recommendations. The proposed model consistently outperformed multiple baselines in terms of accuracy, diversity and novelty of recommendations. As future work, we plan to investigate the recommender quality improvements when using both generated and real data for overlapped users. Furthermore, the model can be extended to use social information of the users. Overall, CnGAN alleviates a significant limitation in cross-network recommender solutions, and provides a foundation to make quality cross-network recommendations for all users.
Acknowledgments
This research has been supported by Singapore Ministry of Education Academic Research Fund Tier 2 under MOE’s official grant number MOE2018-T2-1-103. We gratefully acknowledge the support of NVIDIA Corporation with the donation of a Titan Xp GPU used for this research.
References
- (1)
- Abel et al. (2011) Fabian Abel, Samur Araújo, Qi Gao, and Geert-Jan Houben. 2011. Analyzing cross-system user modeling on the social web. In International Conference on Web Engineering. Springer, 28–43.
- Arjovsky and Bottou (2017) Martin Arjovsky and Léon Bottou. 2017. Towards principled methods for training generative adversarial networks. arXiv preprint arXiv:1701.04862 (2017).
- Arjovsky et al. (2017) Martin Arjovsky, Soumith Chintala, and Léon Bottou. 2017. Wasserstein gan. arXiv preprint arXiv:1701.07875 (2017).
- Avazpour et al. (2014) Iman Avazpour, Teerat Pitakrat, Lars Grunske, and John Grundy. 2014. Dimensions and metrics for evaluating recommendation systems. In Recommendation systems in software engineering. Springer, 245–273.
- Bharadhwaj et al. (2018) Homanga Bharadhwaj, Homin Park, and Brian Y Lim. 2018. RecGAN: Recurrent generative adversarial networks for recommendation systems. In Proceedings of the 12th ACM Conference on Recommender Systems. ACM, 372–376.
- Blei et al. (2003) David M Blei, Andrew Y Ng, and Michael I Jordan. 2003. Latent dirichlet allocation. Journal of machine Learning research 3, Jan (2003), 993–1022.
- Blondel et al. (2016) Mathieu Blondel, Masakazu Ishihata, Akinori Fujino, and Naonori Ueda. 2016. Polynomial networks and factorization machines: New insights and efficient training algorithms. In Proceedings of International Conference on Machine Learning.
- Campos et al. (2010) Pedro G Campos, Alejandro Bellogín, Fernando Díez, and J Enrique Chavarriaga. 2010. Simple time-biased KNN-based recommendations. In Proceedings of the Workshop on Context-Aware Movie Recommendation. ACM, 20–23.
- Campos et al. (2012) Pedro G Campos, Fernando Dıez, and Iván Cantador. 2012. A performance comparison of time-aware recommendation models.
- Deng et al. (2013) Zhengyu Deng, Jitao Sang, Changsheng Xu, et al. 2013. Personalized video recommendation based on cross-platform user modeling. In 2013 IEEE International Conference on Multimedia and Expo (ICME). IEEE, 1–6.
- He et al. (2015) Xiangnan He, Tao Chen, Min-Yen Kan, and Xiao Chen. 2015. Trirank: Review-aware explainable recommendation by modeling aspects. In Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. ACM, 1661–1670.
- He et al. (2017) Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, and Tat-Seng Chua. 2017. Neural collaborative filtering. In Proceedings of the 26th International Conference on World Wide Web. International World Wide Web Conferences Steering Committee, 173–182.
- Hidasi et al. (2015) Balázs Hidasi, Alexandros Karatzoglou, Linas Baltrunas, and Domonkos Tikk. 2015. Session-based recommendations with recurrent neural networks. International Conference on Learning Representations (2015).
- Kang et al. (2017) Wang-Cheng Kang, Chen Fang, Zhaowen Wang, and Julian McAuley. 2017. Visually-aware fashion recommendation and design with generative image models. In 2017 IEEE International Conference on Data Mining (ICDM). IEEE, 207–216.
- Kingma and Ba (2015) Diederik P Kingma and Jimmy Lei Ba. 2015. Adam: Amethod for stochastic optimization. In International Conference on Learning Representation.
- Lim et al. (2015) Bang Hui Lim, Dongyuan Lu, Tao Chen, and Min-Yen Kan. 2015. # mytweet via instagram: Exploring user behaviour across multiple social networks. In Advances in Social Networks Analysis and Mining (ASONAM), 2015 IEEE/ACM International Conference on. IEEE, 113–120.
- Mehta et al. (2005) Bhaskar Mehta, Claudia Niederee, Avare Stewart, Marco Degemmis, Pasquale Lops, and Giovanni Semeraro. 2005. Ontologically-enriched unified user modeling for cross-system personalization. In International Conference on User Modeling. Springer, 119–123.
- Osborne et al. (2012) Miles Osborne, Saša Petrovic, Richard McCreadie, Craig Macdonald, and Iadh Ounis. 2012. Bieber no more: First story detection using Twitter and Wikipedia. In SIGIR 2012 Workshop on Time-aware Information Access.
- Ouyang et al. (2014) Yuanxin Ouyang, Wenqi Liu, Wenge Rong, and Zhang Xiong. 2014. Autoencoder-based collaborative filtering. In International Conference on Neural Information Processing. Springer, 284–291.
- Perera and Zimmermann (2017) Dilruk Perera and Roger Zimmermann. 2017. Exploring the use of time-dependent cross-network information for personalized recommendations. In Proceedings of the 2017 ACM on Multimedia Conference. ACM, 1780–1788.
- Perera and Zimmermann (2018) Dilruk Perera and Roger Zimmermann. 2018. LSTM Networks for Online Cross-Network Recommendations.. In IJCAI. 3825–3833.
- Radford et al. (2015) Alec Radford, Luke Metz, and Soumith Chintala. 2015. Unsupervised representation learning with deep convolutional generative adversarial networks. International Conference on Learning Representations (ICLR).
- Rendle et al. (2009) Steffen Rendle, Christoph Freudenthaler, Zeno Gantner, and Lars Schmidt-Thieme. 2009. BPR: Bayesian personalized ranking from implicit feedback. In Proceedings of the twenty-fifth conference on uncertainty in artificial intelligence. AUAI Press, 452–461.
- Roy et al. (2012) Suman Deb Roy, Tao Mei, Wenjun Zeng, and Shipeng Li. 2012. Socialtransfer: Cross-domain transfer learning from social streams for media applications. In Proceedings of the 20th ACM International Conference on Multimedia. ACM, 649–658.
- Sahoo et al. (2012) Nachiketa Sahoo, Param Vir Singh, and Tridas Mukhopadhyay. 2012. A hidden Markov model for collaborative filtering. MIS Quarterly (2012), 1329–1356.
- Salakhutdinov et al. (2007) Ruslan Salakhutdinov, Andriy Mnih, and Geoffrey Hinton. 2007. Restricted Boltzmann machines for collaborative filtering. In Proceedings of the 24th International Conference on Machine learning. ACM, 791–798.
- Salimans et al. (2016) Tim Salimans, Ian Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, and Xi Chen. 2016. Improved techniques for training gans. In Advances in Neural Information Processing Systems. 2234–2242.
- Wang et al. (2017) Jun Wang, Lantao Yu, Weinan Zhang, Yu Gong, Yinghui Xu, Benyou Wang, Peng Zhang, and Dell Zhang. 2017. Irgan: A minimax game for unifying generative and discriminative information retrieval models. In Proceedings of the 40th International ACM SIGIR conference on Research and Development in Information Retrieval. ACM, 515–524.
- Yan et al. (2014) Ming Yan, Jitao Sang, and Changsheng Xu. 2014. Mining cross-network association for youtube video promotion. In Proceedings of the 22nd ACM International conference on Multimedia. ACM, 557–566.
- Yoo et al. (2017) Jaeyoon Yoo, Heonseok Ha, Jihun Yi, Jongha Ryu, Chanju Kim, Jung-Woo Ha, Young-Han Kim, and Sungroh Yoon. 2017. Energy-based sequence gans for recommendation and their connection to imitation learning. Proceedings of ACM Conference.
- Zhang (2013) Liang Zhang. 2013. The definition of novelty in recommendation system. Journal of Engineering Science & Technology Review 6, 3.
- Zhao et al. (2011) Wayne Xin Zhao, Jing Jiang, Jianshu Weng, Jing He, Ee-Peng Lim, Hongfei Yan, and Xiaoming Li. 2011. Comparing twitter and traditional media using topic models. In European Conference on Information Retrieval. Springer, 338–349.