Cluster-aware Contrastive Learning for Unsupervised Out-of-distribution Detection
Abstract
Unsupervised out-of-distribution (OOD) Detection aims to separate the samples falling outside the distribution of training data without label information. Among numerous branches, contrastive learning has shown its excellent capability of learning discriminative representation in OOD detection. However, for its limited vision, merely focusing on instance-level relationship between augmented samples, it lacks attention to the relationship between samples with same semantics. Based on the classic contrastive learning, we propose Cluster-aware Contrastive Learning (CCL) framework for unsupervised OOD detection, which considers both instance-level and semantic-level information. Specifically, we study a cooperation strategy of clustering and contrastive learning to effectively extract the latent semantics and design a cluster-aware contrastive loss function to enhance OOD discriminative ability. The loss function can simultaneously pay attention to the global and local relationships by treating both the cluster centers and the samples belonging to the same cluster as positive samples. We conducted sufficient experiments to verify the effectiveness of our framework and the model achieves significant improvement on various image benchmarks.
1 Introduction
Different from the traditional closed world assumption, OOD detection requires the model to distinguish samples with different distributions from in-distribution (ID) samples. It has demonstrated huge potential in diverse fields such as autonomous driving Chan et al. (2021), industrial defect detection Bergmann et al. (2019), medical diagnosis Schlegl et al. (2017), etc.
Recent methods of OOD detection include density-based Ren et al. (2019), reconstruction-based Perera et al. (2019), and classification-based Hsu et al. (2020) approaches, which mostly belong to supervised or semi-supervised OOD detection methods. However, further attention need be paid to the more difficult unsupervised OOD detection when the label information is completely unavailable. In unsupervised OOD detection, self-supervised methods Hendrycks et al. (2019); Golan and El-Yaniv (2018) learn discriminative representation by designing different auxiliary tasks and as one of them, contrastive learning method Reiss and Hoshen (2021) has made great contributions.
The original goal of contrastive learning is to obtain individual, task-agnostic representation for each sample. It is obvious that merely caring about instance-level features does not take advantage of latent semantic information. More intuitively, it’s beneficial to distinguish the OOD samples during online testing by clustering ID samples with the same semantics in a denser area. However, there is a mutual repulsion between feature extraction at the instance-level and class relationship preservation at the semantic-level in contrastive learning. How to reasonably introduce clustering to contrastive learning needs further research. Though some deep clustering methods Li et al. (2021); Zhang et al. (2021); Sharma et al. (2020) have discussed the possibility of combining contrastive learning and clustering, these works increase the inter-class variance of training samples to ensure the classification accuracy, which are not suitable for OOD detection. And some clustering contrastive learning methods Li et al. (2020); Caron et al. (2020) do not fully extract semantic information for ignoring the local relationship between samples. Given above introduction, we further discuss the possibility of combining contrastive learning and clustering in unsupervised OOD detection.
In this paper, we propose cluster-aware contrastive learning (CCL) framework, a novel framework not only retains discriminative representation ability for each individual instance but also has a wider vision that pays attention to the global and local similarity relationship between samples. On the one hand, it is vital to study a proper strategy to introduce clustering operation to contrastive learning. We perform clustering at appropriate location to extract semantic information effectively. And a warm-up stage acquiring enough instance representation ability is required before periodically updating the cluster centers. On the other hand, we design a cluster-aware contrastive loss function containing two parts, Cluster Center Loss and Cluster Instance Loss. The former one makes the augmented samples close to their corresponding cluster center while pushes them away from other cluster centers for the global relationship. And the latter one increases the similarity between samples in the same cluster for the local relationship.
The contributions of this paper can be summarized as follows:
-
•
We propose a novel unsupervised OOD detection framework, cluster-aware contrastive learning, CCL, which makes the contrastive learning model take advantage of instance- and semantic-level information. And we discuss the clustering strategy introducing clustering to contrastive learning.
-
•
We design a cluster-aware contrastive loss function. It pays attention to the global and local sample relationship by making individual samples closer to their corresponding cluster centers and the other samples within the same cluster.
-
•
We conduct plenty of comprehensive experiments and compare CCL with state-of-the-art methods. Both the comparison results and the ablation experimental results prove the effectiveness of our approach.
2 Related Work
2.1 Unsupervised Out-of-distribution Detection
On account of the massive amount of image data and the high cost of labeling data, semi-supervised learning or unsupervised learning in OOD detection have been received great attention. For example, ODIN Liang et al. (2017) uses a basic pre-trained model and separates the softmax score distributions between ID and OOD images by a temperature scaling adding perturbation. Yang et al. (2021) designs a unsupervised dual grouping (UDG) to solve the semantically coherent unsupervised OOD. In particular, as one of unsupervised learning methods, self-supervised method is widely used in OOD detection. For examples, Madan et al. (2022) presents a self-supervised masked convolutional transformer block (SSMCTB). Zhou (2022) designs a hierarchical semantic reconstruction framework, which maximizes the compression of the auto-encode latent space. SSD Sehwag et al. (2020) uses self-supervised representation learning and Mahalanobis distance score to identify OOD samples on the pre-trained softmax neural classifier. Different from some methods based on pre-trained models, we solve the completely unsupervised OOD problem which does not introduce any prior semantic label information.
2.2 Contrastive Learning
In self-supervised learning, contrastive learning methods have been widely used because of excellent representation ability via instance discrimination, such as SimCLR Chen et al. (2020) and MoCo He et al. (2020). Contrastive learning considers two augmented views of the same instance as the positive to be pulled closer, and the rest samples are considered as the negative to be pushed farther apart. In OOD detection, CSI Tack et al. (2020) uses data enhancement in contrastive learning to generate OOD negative samples to improve the sensitivity to OOD samples. Cho et al. (2021) proposes masked contrastive learning for OOD detection, performing a designed auxiliary task class-conditional mask in contrastive learning. To introduce semantic information, some researches try to add clustering as an auxiliary task to contrastive learning, such as PCL Li et al. (2020) and SWAV Caron et al. (2020). However, it is difficult to integrate instance and semantic representation ability at the same time and there are few studies on combining clustering and contrastive learning to solve OOD problems. We design a novel framework to introduce clustering, which has a wider vision to extract semantic information from sample relationship.
2.3 Contrastive Cluster
Contrastive clustering is essentially a deep clustering method based on contrastive learning and has been widely used in images Sharma et al. (2020), contexts Zhang et al. (2021) and graphs Wang et al. (2022). For example, Li et al. (2021) proposes a basic framework of contrastive clustering. The instance- and semantic-level contrastive learning are respectively conducted in the row and column feature space by a similarity loss function. And Graph Contrastive Clustering (GCC) Zhong et al. (2021) proposes a novel graph-based contrastive learning strategy to learn more compact clustering assignments. The core of contrastive clustering is performing the instance- and semantic-level contrastive learning to minimize the intra-cluster variance and maximize the inter-cluster variance, which gives a lot of inspiration for OOD detection. In OOD detection, Albert et al. (2022) applies an outlier sensitive clustering at the semantic level to detect the OOD clusters and ID noisy outliers. Lehmann and Ebner (2021) performs a layer-wise cluster analysis at inference to identify OOD samples. Since contrastive clustering will increase the inter-class variance for classification, it is inappropriate for direct application in OOD task. However, we could refer to its idea of combining clustering and contrast learning in OOD detection.
3 Methodology
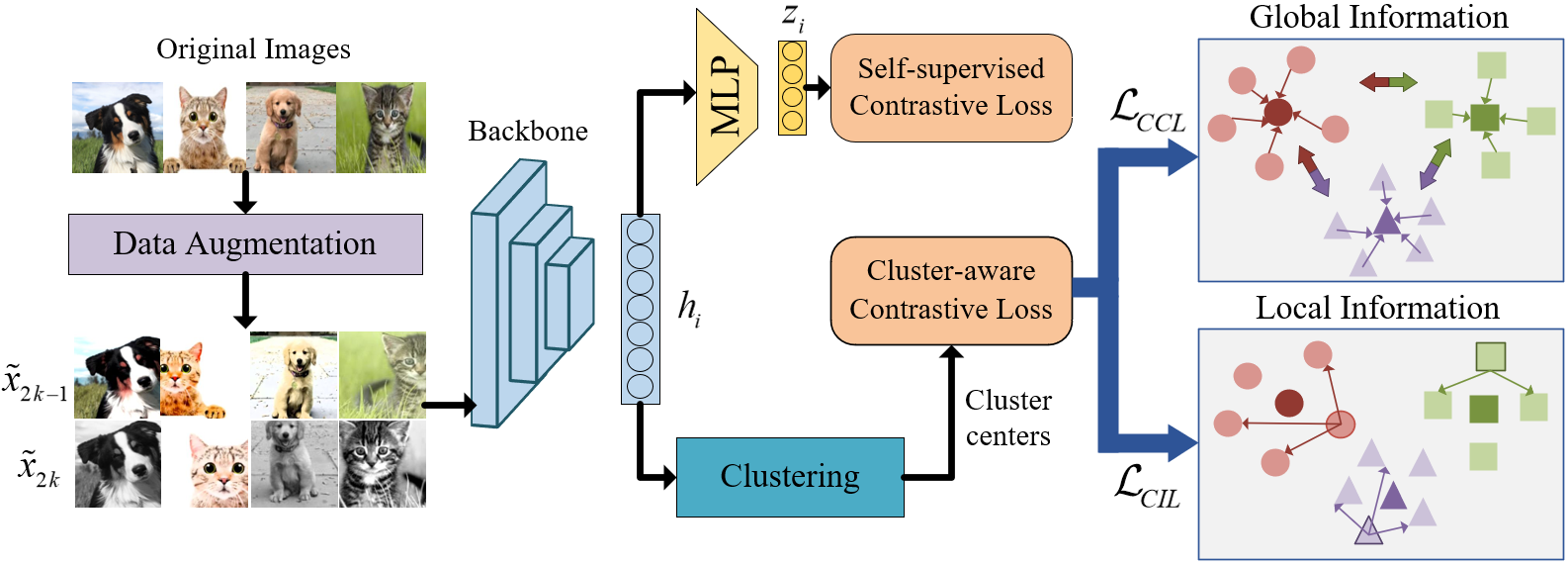
3.1 Framework
As shown in Figure 1, the proposed CCL framework contains two modules, a basic contrastive learning module and a clustering module. Considering a training set batch of unlabeled images , image pairs , are obtained by data augmentation including random cropping, random color distortions, random Gaussian blur same with SimCLR Chen et al. (2020). The augmented image dataset is . For the sake of description, the last layer of backbone encoder is called embedding layer and the last layer of MLP is called projection layer. The augmented image is input into the backbone encoder to obtain high-dimensional feature vector on the embedding layer. And is input into MLP to obtain on the projection layer.
| (1) |
In the basic contrastive learning module, a classic self-supervised contrastive loss is calculated on the projection layer,which focuses on the relationship between samples and their enhancement samples for instance-level representation. In the clustering module, for each on the embedding layer, the corresponding cluster center , , is obtained by K-means to calculate the cluster-aware contrastive loss . It includes two parts: a cluster center loss and a cluster instance loss . The self-supervised contrastive loss updates the MLP and are simultaneously combined with the cluster-aware contrastive loss to update the backbone encoder. Finally, OOD detection needs a score function to identify whether a new input image is OOD sample according to its score.
3.2 Loss Function
The loss function plays a decisive role in contrastive learning. Although traditional contrastive learning has strong individual discrimination capacity, it ignores the relationship among instances with similar semantic. On the contrary, Supervised contrastive learning (SupCon) Khosla et al. (2020), uses label information to extract the relationship between samples. Moreover, it is a natural and common way to introduce semantic information in unsupervised tasks utilizing cluster centers obtained by clustering as pseudo labels. Combining the above two advantages of using semantic information, we design a novel loss function as an auxiliary task in contrastive learning.
3.2.1 Contrastive Loss
The instance-level discrimination capacity of contrastive learning is obtained by self-supervised contrastive loss. We adopt the classic contrastive learning loss function in SimCLR, Chen et al. (2020). For a positive pair of examples , it defined as follows:
| (2) |
where is an indicator function evaluating to 1 if and denotes a temperature parameter. And, is the cosine similarity between the projection layer features . For every sorted image pair , the whole self-supervised contrastive learning loss is:
| (3) |
3.2.2 Cluster-aware Contrastive Loss
To make the backbone encoder pay attention to the latent semantic information, we cluster the output of the encoder to obtain cluster centers as the semantic labels. The cluster-aware contrastive loss includes two parts, Cluster Center Loss for global semantic information and Cluster Instance Loss for local semantic information.
Cluster Center Loss.
Clustering is performed on the embedding layer to obtain the cluster centers. The cluster center loss takes the cluster center that a specific sample belonging to as the positive and the other cluster centers as the negative.
Specifically, for each output of the encoder , there is a corresponding cluster center calculated by K-means using all ID samples. The cluster center is the positive sample and the other cluster centers are the negative samples. Similar to instance-level contrastive loss function, we use the cosine similarity , and the cluster center loss function is defined as follows:
| (4) |
where means removing the cluster center to which the sample encoding belongs. denotes the number of cluster centers and is a temperature parameter. We adopt the same cluster concentration estimation Li et al. (2020) to adaptively adjust the temperature parameter :
| (5) |
where is the number of samples in the same cluster and is a smooth parameter to ensure that small clusters do not have an overlarge .
Cluster Instance Loss.
The cluster centers are the semantic information concentration of all samples and the cluster center loss focuses on the relationship between samples and cluster centers, which ignores the relationship between samples in a cluster to a certain extent. To make the model focus on the local sample relationship, we design the cluster instance loss based on SupCon Khosla et al. (2020). In the batch , cluster instance loss takes the samples in the same cluster as the positive, and the rest samples as the negative, which can be formulated as follows:
| (6) |
where is the rest samples except , is the set belonging to the same cluster center of in batch . is the set number. is a temperature parameter. Overall, the whole cluster-aware contrastive loss takes the mean of cluster center loss and cluster instance loss, formulated as follows:
| (7) |
Finally, the loss function in training phase is the combination of self-supervised contrastive loss and cluster-aware contrastive loss by a weight , which is:
| (8) |
3.3 How clustering works
Though the idea that combining contrastive learning and clustering is not proposed for the first time, how to make it appropriate for OOD detection needs further discussion. Recent research Sinhamahapatra et al. (2022) concludes that the data clustering performance of the self-supervised contrastive learning is not as good as supervised contrastive learning, which means it is potential to improve clustering ability without label information. Given that most works appreciate the output feature of embedding layer rather than projection layer, we first propose an assumption that the performance of clustering on the embedding layer is better than that on the projection layer. Further, to guarantee clustering more stably, we think it is necessary to commit a warm-up operation and update the cluster centers periodically in training phase. Detailed discussions of the above ideas are as follows:
Where to cluster
Given that most existing works Chen et al. (2020); Sinhamahapatra et al. (2022) operate the downstream task fine-tune or linear evaluation on the embedding layer. It is reasonable to believe that the high-dimensional features on the embedding layer contain more semantic information than the low-dimensional features on the projection layer.
Moreover, considering reducing the distance between a sample and its augmented sample will increase the distance between the sample and other samples with same semantics, we think the model optimizations of self-supervised contrastive loss and cluster-aware contrastive loss are mutually exclusive to some extent. Specially, the former one only focuses on pulling different data augmentation versions of a sample closer while the samples with similar semantics may be pushed away and the latter one focuses on bringing the samples within a same cluster closer. Based on the above analysis, when basic contrastive learning module is on the projection layer, clustering module on the embedding layer can effectively agglomerate semantic information and make model optimization possible.
When to cluster
In CCL framework, we treat clustering as an auxiliary task. Therefore, we think only after the model obtains enough instance representation ability through the basic contrastive learning module, then it could focus on the relationship between samples by clustering, which means a warm-up stage is required at beginning.
In addition, according to the cluster centers obtained on the embedding layer, the cluster-aware contrastive loss is calculated to optimize the backbone encoder. We assume that updating cluster centers too frequently is not conducive for the encoder to extract semantics. Therefore, the updating frequency of cluster centers needs to be determined. Overall, CCL needs a warm-up at beginning and cluster centers need to be updated periodically.
Further, we’ll prove our viewpoints though detailed experiments and the result of ablation experiments will be show in Section 4.2.
3.4 Score function
In OOD detection, the score function is finally used to identify whether a sample is an OOD sample. The commonly using Mahalanobis distance as the score function is not suitable when the number of training samples is small. The another common score function proposed in CSI Tack et al. (2020) uses L2-norm and cosine similarity, formulated as follows:
| (9) |
Based on the score function , we design a novel score function by combining cosine similarity and ID sample variance, described as follows:
| (10) |
where the denominator is the standard deviation of ID set . is the first ID samples with highest score . is the sample mean.
| CIFAR-10 | ||||||||
| Method | Score Function | SVHN | LSUN | ImageNet | LSUN(Fix) | ImageNet(Fix) | CIFAR-100 | Interp. |
| Rot | - | 97.6 | 89.2 | 90.5 | 77.7 | 83.2 | 79.0 | 64.0 |
| Rot+Trans | - | 97.8 | 92.8 | 94.2 | 81.6 | 86.7 | 82.3 | 68.1 |
| GOAD | - | 96.3 | 89.3 | 91.8 | 78.8 | 83.3 | 77.2 | 59.4 |
| SSD | - | 99.6 | - | - | - | - | 90.6 | - |
| CSI | 99.8 | 97.5 | 97.6 | 90.3 | 93.3 | 89.2 | 79.3 | |
| CSI | 99.7 | 97.3 | 97.3 | 92.8 | 95.2 | 91.4 | 82.5 | |
| SimCLR | 97.5 | 96.7 | 93.5 | 97.3 | 95.8 | 90.5 | 85.9 | |
| CCL | 98.0 | 98.4 | 96.4 | 97.8 | 96.0 | 91.2 | 87.2 | |
| CCL | 98.4 | 98.5 | 96.6 | 97.8 | 96.0 | 91.2 | 87.2 | |
-
•
denotes results shown in CSI Tack et al. (2020) and denotes results we reproduced.
4 Experiments
We compare CCL with some competitive baselines in Section 4.1 and perform some ablation experiments to validate our framework in Section 4.2. The detailed experimental settings are as follows:
Datasets and Evaluation metrics.
To compare with the SOTA methods, the dataset setting is consistent with CSI Tack et al. (2020). We take the unlabeled CIFAR-10 training sub-dataset as the ID training data. In the test phase, the OOD datasets include SVHN, resized LSUN and ImageNet, the fixed version of LSUN and ImageNet, CIFAR-100, and linearly-interpolated samples of CIFAR-10 (Interp.). Like many OOD researches, we report the area under the receiver operating characteristic curve (AUROC) as the threshold-free evaluation metric.
Implementation details.
We adopt ResNet-18 as the backbone encoder for all experiments. Specifically, the model is trained for 1000 epochs using self-supervised contrastive loss at the warm-up stage, and then for 1000 epochs using both self-supervised and cluster-aware contrastive loss function. The number of cluster centers is set to 10 and the batch size is 128. The learning rate is 0.1 with a CosineAnnealingLR scheduler and has a 50 epoch warm-up, which is same with CSI Tack et al. (2020). The CCL is compared with various methods including, Rot Hendrycks et al. (2019), GOAD Bergman and Hoshen (2020), SSD Sehwag et al. (2020), SimCLR Chen et al. (2020) that is the base framework of CCL, and CSI Tack et al. (2020) that is a competitive contrastive learning method.
4.1 Main Results
The main experiment results are shown in Table 1. We can make the following observations from it:
-
•
Compared with SimCLR that only considers instance-level representation, CCL outperforms on all OOD datasets, which indicates that it is beneficial to take semantic information into account for unsupervised OOD detection and our framework could take advantage of semantic information to improve representation ability of the backbone encoder.
-
•
Among the methods, CCL achieves the best performance on four OOD datasets including LSUN(98.5%), LSUN-Fix(97.8%), ImageNet-Fix(96.0%) and Interp(87.2%). Specially, CCL with surpasses the CSI in Tack et al. (2020) by 7.9% on Interp, by 7.5% on LSUN-Fix, by 2.7% on ImageNet-Fix and by 2% on CIFAR-100. On the other two datasets, SVHN and ImageNet, CCL is slightly inferior to CSI. Although CCL does not perform best on all datasets, it shows greater robustness. Compare to CSI that needs designed specific OOD augmentation approaches, CCL is more general and can perform unsupervised OOD detection on more types of datasets.
-
•
From the comparison of scoring functions, it can be seen that the designed variance scoring function can improve performance to a certain extent, which is helpful for unsupervised OOD detection.
| CIFAR-10 | ||||||
| SVHN | LSUN | ImageNet | CIFAR-100 | |||
| ✔ | 97.7 | 97.0 | 93.8 | 90.3 | ||
| ✔ | ✔ | 98.6 | 98.0 | 96.5 | 91.2 | |
| ✔ | ✔ | 98.3 | 97.7 | 95.9 | 91.5 | |
| ✔ | ✔ | ✔ | 98.4 | 98.5 | 97.8 | 91.2 |
4.2 Ablation Experiments
In this section, we carry out some targeted ablation experiments to verify the effectiveness of our framework and the rationality of our assumptions in Section 3, including four parts as follows:
Loss function.
To verify the effectiveness of cluster-aware contrastive loss function, we compare the performance of the model using different loss functions. The results in Table 2 show the combination of self-supervised and cluster-aware contrastive loss function has the best performance on LSUN and ImageNet. Although the joint loss function is 0.2% lower than the maximum value on SVHN and 0.3% lower on CIFAR-100, it shows greater robustness. Overall, only when self-supervised and cluster-aware contrastive loss function jointly update the backbone encoder, the model has the best performance. It is confirmed that the combination of instance and semantic recognition maximizes unsupervised OOD detection capability in our framework.
| CIFAR-10 | ||||
| Layer | SVHN | LSUN | ImageNet | CIFAR-100 |
| SimCLR | 97.7 | 97.0 | 93.8 | 90.3 |
| Projection | 97.4 | 97.9 | 95.3 | 91.4 |
| Embedding | 98.4 | 98.5 | 97.8 | 91.2 |
| CIFAR-10 | |||||
| Epoch | Warm-up | SVHN | LSUN | ImageNet | CIFAR-100 |
| 10 | ✘ | 98.2 | 98.0 | 95.3 | 89.9 |
| 10 | ✔ | 98.4 | 98.5 | 97.8 | 91.2 |
| 0 | ✔ | 97.9 | 96.8 | 93.9 | 90.7 |
| 1 | ✔ | 97.9 | 97.8 | 96.9 | 91.3 |
| 50 | ✔ | 98.2 | 97.5 | 95.2 | 91.2 |






Clustering on Embedding layer vs. Projection layer.
To verify our assumption about where to cluster, we respectively calculate the cluster-aware contrastive loss using the output of the embedding layer and projection layer. The results are shown in Table 3. Apparently, the performance of clustering on the embedding layer is much better than that on the projection layer.
Moreover, we visualize the features of the two layers through t-SNE to observe the effect of clustering. Figure 2 and 2 show that the feature distributions of SimCLR on two layers are similar. And clustering on the projection layer does not change the feature distribution of the two layers from Figure 2 and 2. Figure 2 and 2 show because of clustering on projection layer, features on projection layer are denser in the feature space than SimCLR, which makes the performance of OOD detection improve as shown in Table 3. Figure 2 and 2 indicate clustering on embedding layer makes feature distribution significantly different on the two layers. From Table 3 and Figure 2, it can be inferred that clustering on embedding layer causes a clearer feature distribution, which improves the unsupervised OOD detection ability. Overall, clustering and calculating cluster-aware contrastive loss on the embedding layer is better than the projection layer, which is consistent with our assumption.
Update method of cluster centers.
In Section 3, we propose CCL needs a warm-up stage and cluster centers need to be updated periodically. The better performance with warm-up in Table 4 indicates only when the backbone encoder is fully capable of instance-level representation can cluster-aware contrastive loss play a stable role, which confirms our viewpoint. Furthermore, we set a series of updating epoch intervals to study the influence of updating frequency. The results show the model has the best performance in unsupervised OOD detection when cluster centers are updated with 10 epoch intervals to calculate the cluster-aware contrastive loss. In practical application, the hyper-parameter needs to be adjusted individually.
| Number | CIFAR-10 | SVHN | LSUN | ImageNet | CIFAR-100 |
| Similarity | AUROC/Similarity | ||||
| 5 | 0.988 | 98.2 / 0.924 | 96.4 / 0.912 | 93.9 / 0.946 | 91.4 / 0.947 |
| 10 | 0.985 | 98.4 / 0.954 | 98.5 / 0.858 | 97.8 / 0.891 | 91.2 / 0.928 |
| 50 | 0.771 | 98.4 / 0.588 | 97.4 / 0.662 | 95.4 / 0.713 | 91.2 / 0.718 |
| 100 | 0.773 | 98.3 / 0.671 | 98.1 / 0.669 | 96.7 / 0.690 | 91.3 / 0.731 |
| 500 | 0.639 | 97.6 / 0.705 | 96.9 / 0.555 | 94.5 / 0.585 | 91.3 / 0.628 |
| 1000 | 0.623 | 97.8 / 0.663 | 98.2 / 0.576 | 96.2 / 0.656 | 91.1 / 0.638 |
| 5000 | 0.556 | 97.6 / 0.423 | 97.6 / 0.467 | 96.0 / 0.497 | 90.1 / 0.486 |
The number of cluster centers.
Since we use K-means as clustering method, the number of cluster centers need be determined in advance. We set different numbers of cluster centers to study its influence on CCL. Table 5 shows that when it is set to 10, the actual number of CIFAR-10 classes, the model has the best performance. As a result, we think our method could achieve the best performance in practice if there is the prior information about the number of ID sample classes.
Moreover, to further study the influence of cluster center number on the semantic representation ability of clustering, we calculate the mean of maximum cosine similarity between test samples and cluster centers on the embedding layer. The results in Table 5 show that the larger number of cluster centers reduces the similarity with ID samples, which indicates the increase in cluster center number leads to the weakening of semantic representation of cluster centers.
5 Conclusion
In this paper, we propose a novel Cluster-aware Contrastive Learning (CCL) framework for unsupervised OOD detection. To take advantage of semantic information in comparative learning, we study where and when to cluster to fully extract the latent semantic information between samples. And we design a cluster-aware contrastive loss function to make the model pay attention to the global and local sample relationship. Extensive experiments conducted on seven benchmark datasets demonstrate the effectiveness of our proposed model.
References
- Albert et al. [2022] Paul Albert, Eric Arazo, Noel E O’Connor, and Kevin McGuinness. Embedding contrastive unsupervised features to cluster in-and out-of-distribution noise in corrupted image datasets. In European Conference on Computer Vision, pages 402–419. Springer, 2022.
- Bergman and Hoshen [2020] Liron Bergman and Yedid Hoshen. Classification-based anomaly detection for general data. arXiv preprint arXiv:2005.02359, 2020.
- Bergmann et al. [2019] Paul Bergmann, Michael Fauser, David Sattlegger, and Carsten Steger. Mvtec ad–a comprehensive real-world dataset for unsupervised anomaly detection. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 9592–9600, 2019.
- Caron et al. [2020] Mathilde Caron, Ishan Misra, Julien Mairal, Priya Goyal, Piotr Bojanowski, and Armand Joulin. Unsupervised learning of visual features by contrasting cluster assignments. Advances in Neural Information Processing Systems, 33:9912–9924, 2020.
- Chan et al. [2021] Robin Chan, Matthias Rottmann, and Hanno Gottschalk. Entropy maximization and meta classification for out-of-distribution detection in semantic segmentation. In Proceedings of the ieee/cvf international conference on computer vision, pages 5128–5137, 2021.
- Chen et al. [2020] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. A simple framework for contrastive learning of visual representations. In International conference on machine learning, pages 1597–1607. PMLR, 2020.
- Cho et al. [2021] Hyunsoo Cho, Jinseok Seol, and Sang-goo Lee. Masked contrastive learning for anomaly detection. arXiv preprint arXiv:2105.08793, 2021.
- Golan and El-Yaniv [2018] Izhak Golan and Ran El-Yaniv. Deep anomaly detection using geometric transformations. Advances in neural information processing systems, 31, 2018.
- He et al. [2020] Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, and Ross Girshick. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 9729–9738, 2020.
- Hendrycks et al. [2019] Dan Hendrycks, Mantas Mazeika, Saurav Kadavath, and Dawn Song. Using self-supervised learning can improve model robustness and uncertainty. Advances in neural information processing systems, 32, 2019.
- Hsu et al. [2020] Yen-Chang Hsu, Yilin Shen, Hongxia Jin, and Zsolt Kira. Generalized odin: Detecting out-of-distribution image without learning from out-of-distribution data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 10951–10960, 2020.
- Khosla et al. [2020] Prannay Khosla, Piotr Teterwak, Chen Wang, Aaron Sarna, Yonglong Tian, Phillip Isola, Aaron Maschinot, Ce Liu, and Dilip Krishnan. Supervised contrastive learning. Advances in Neural Information Processing Systems, 33:18661–18673, 2020.
- Lehmann and Ebner [2021] Daniel Lehmann and Marc Ebner. Layer-wise activation cluster analysis of cnns to detect out-of-distribution samples. In International Conference on Artificial Neural Networks, pages 214–226. Springer, 2021.
- Li et al. [2020] Junnan Li, Pan Zhou, Caiming Xiong, and Steven CH Hoi. Prototypical contrastive learning of unsupervised representations. arXiv preprint arXiv:2005.04966, 2020.
- Li et al. [2021] Yunfan Li, Peng Hu, Zitao Liu, Dezhong Peng, Joey Tianyi Zhou, and Xi Peng. Contrastive clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, pages 8547–8555, 2021.
- Liang et al. [2017] Shiyu Liang, Yixuan Li, and Rayadurgam Srikant. Enhancing the reliability of out-of-distribution image detection in neural networks. arXiv preprint arXiv:1706.02690, 2017.
- Madan et al. [2022] Neelu Madan, Nicolae-Catalin Ristea, Radu Tudor Ionescu, Kamal Nasrollahi, Fahad Shahbaz Khan, Thomas B Moeslund, and Mubarak Shah. Self-supervised masked convolutional transformer block for anomaly detection. arXiv preprint arXiv:2209.12148, 2022.
- Perera et al. [2019] Pramuditha Perera, Ramesh Nallapati, and Bing Xiang. Ocgan: One-class novelty detection using gans with constrained latent representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 2898–2906, 2019.
- Reiss and Hoshen [2021] Tal Reiss and Yedid Hoshen. Mean-shifted contrastive loss for anomaly detection. arXiv preprint arXiv:2106.03844, 2021.
- Ren et al. [2019] Jie Ren, Peter J Liu, Emily Fertig, Jasper Snoek, Ryan Poplin, Mark Depristo, Joshua Dillon, and Balaji Lakshminarayanan. Likelihood ratios for out-of-distribution detection. Advances in neural information processing systems, 32, 2019.
- Schlegl et al. [2017] Thomas Schlegl, Philipp Seeböck, Sebastian M Waldstein, Ursula Schmidt-Erfurth, and Georg Langs. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. In International conference on information processing in medical imaging, pages 146–157. Springer, 2017.
- Sehwag et al. [2020] Vikash Sehwag, Mung Chiang, and Prateek Mittal. Ssd: A unified framework for self-supervised outlier detection. In International Conference on Learning Representations, 2020.
- Sharma et al. [2020] Vivek Sharma, Makarand Tapaswi, M Saquib Sarfraz, and Rainer Stiefelhagen. Clustering based contrastive learning for improving face representations. In 2020 15th IEEE International Conference on Automatic Face and Gesture Recognition (FG 2020), pages 109–116. IEEE, 2020.
- Sinhamahapatra et al. [2022] Poulami Sinhamahapatra, Rajat Koner, Karsten Roscher, and Stephan Günnemann. Is it all a cluster game?–exploring out-of-distribution detection based on clustering in the embedding space. arXiv preprint arXiv:2203.08549, 2022.
- Tack et al. [2020] Jihoon Tack, Sangwoo Mo, Jongheon Jeong, and Jinwoo Shin. Csi: Novelty detection via contrastive learning on distributionally shifted instances. Advances in neural information processing systems, 33:11839–11852, 2020.
- Wang et al. [2022] Yanling Wang, Jing Zhang, Haoyang Li, Yuxiao Dong, Hongzhi Yin, Cuiping Li, and Hong Chen. Clusterscl: Cluster-aware supervised contrastive learning on graphs. In Proceedings of the ACM Web Conference 2022, pages 1611–1621, 2022.
- Yang et al. [2021] Jingkang Yang, Haoqi Wang, Litong Feng, Xiaopeng Yan, Huabin Zheng, Wayne Zhang, and Ziwei Liu. Semantically coherent out-of-distribution detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 8301–8309, 2021.
- Zhang et al. [2021] Dejiao Zhang, Feng Nan, Xiaokai Wei, Shangwen Li, Henghui Zhu, Kathleen McKeown, Ramesh Nallapati, Andrew Arnold, and Bing Xiang. Supporting clustering with contrastive learning. arXiv preprint arXiv:2103.12953, 2021.
- Zhong et al. [2021] Huasong Zhong, Jianlong Wu, Chong Chen, Jianqiang Huang, Minghua Deng, Liqiang Nie, Zhouchen Lin, and Xian-Sheng Hua. Graph contrastive clustering. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 9224–9233, 2021.
- Zhou [2022] Yibo Zhou. Rethinking reconstruction autoencoder-based out-of-distribution detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 7379–7387, 2022.