Classification of real algebraic curves under blow-spherical homeomorphisms at infinity

José Edson Sampaio and Euripedes Carvalho da Silva José Edson Sampaio: Departamento de Matemática, Universidade Federal do Ceará, Rua Campus do Pici, s/n, Bloco 914, Pici, 60440-900, Fortaleza-CE, Brazil.
E-mail: [email protected] Euripedes Carvalho da Silva: Departamento de Matemática, Instituto Federal de Educação, Ciência e Tecnologia do Ceará, Av. Parque Central, 1315, Distrito Industrial I, 61939-140, Maracanaú-CE, Brazil.
E-mail: [email protected]

Abstract.

In this article, we present a complete classification, with normal forms, of the real algebraic curves under blow-spherical homeomorphisms at infinity.

Key words and phrases:

Blow-spherical equivalence; Algebraic curves; Classification of algebraic curves.

2010 Mathematics Subject Classification:

14B05; 32S50

The first named author was partially supported by CNPq-Brazil grant 310438/2021-7. This work was supported by the Serrapilheira Institute (grant number Serra – R-2110-39576).

1. Introduction

In this article, we study real algebraic curves under blow-spherical homeomorphisms from the global point of view. Roughly speaking, two subsets of Euclidean spaces are blow-spherical homeomorphic, if their spherical modifications (see Definition 2.1) are homeomorphic and, in particular, this homeomorphism induces a homeomorphism between their tangent links (see Definition 2.2). This gives an equivalence which lives between topological equivalence and semialgebraic bi-Lipschitz equivalence.

The study of analytic sets under blow-spherical homeomorphisms from the local point of view has been studied in some works, e.g., [1, 2, 6, 7, 8]. In [7], the first author, among other things, presented a complete classification of the germs of complex analytic curves under blow-spherical homeomorphisms. In [8], the first author presented several results of related to blow-spherical homeomorphism between germs of real analytic sets and, in particular, he presented a classification of germs of real analytic curves under blow-spherical homeomorphisms.

Recently, the authors of this article in [9] presented a complete classification of complex algebraic curves under (global) blow-spherical homeomorphisms (see Theorem 4.6 in [9]). They also presented a complete classification of complex algebraic curves under blow-spherical homeomorphisms at infinity with normal forms (see Theorems 4.2 and 4.3 in [9]).

So, it becomes natural to try classifying real algebraic curves under blow-spherical homeomorphisms.

The main aim of this article is to present a complete classification of real algebraic curves under blow-spherical homeomorphisms at infinity (see Proposition 3.1). Moreover, we also present normal forms for this classification (see Proposition 3.2). We also present a result of realization of our (complete) invariant (see Proposition 3.7).

In order to be a bit more precise, for a real algebraic curve $X$ , we define our invariant $k(X,\infty)$ (see Definition 2.12), which is a point of $(\mathbb{Z}_{>0})^{n}$ and $n$ is the cardinality of the link (at 0) of the tangent cone of $X$ at infinity (see Subsection 2.2), and in Proposition 3.1, we prove that two real algebraic curve $X$ and $\widetilde{X}$ are blow-spherical homeomorphic at infinity if and only if $k(X,\infty)=k(\widetilde{X},\infty)$ .

In Subsection 3.1, we present a collection of real algebraic curves and we prove in Proposition 3.2 that a real algebraic curve is blow-spherical homeomorphic at infinity to exactly one curve of that collection.

In Subsection 3.2, we observe that $k(X,\infty)\in\mathcal{N}$ , where $\mathcal{N}=\bigcup\limits_{n=1}^{\infty}\mathcal{N}_{n}$ and $\mathcal{N}_{n}$ is the set of all $(\eta_{1},\eta_{2},\cdots,\eta_{n})\in(\mathbb{Z}_{>0})^{n}$ such that $\eta_{1}\leq\eta_{2}\leq\cdots\leq\eta_{n}$ . Moreover, given $\eta=(\eta_{1},...,\eta_{k})\in\mathcal{N}$ , we prove in Proposition 3.7 that there is a real algebraic curve $X$ such that $k(X,\infty)=\eta$ if and only if $\eta_{1}+...+\eta_{k}$ is an even number.

2. Preliminaries

Here, all the real algebraic sets are supposed to be pure dimensional.

2.1. Definition of the blow-spherical equivalence

Let us consider the spherical blowing-up at infinity (resp. $p$ ) of $\mathbb{R}^{n+1}$ , $\rho_{\infty}\colon\mathbb{S}^{n}\times(0,+\infty)\to\mathbb{R}^{n+1}$ (resp. $\rho_{p}\colon\mathbb{S}^{n}\times[0,+\infty)\to\mathbb{R}^{n+1}$ ), given by $\rho_{\infty}(x,r)=\frac{1}{r}x$ (resp. $\rho_{p}(x,r)=rx+p$ ).

Note that $\rho_{\infty}\colon\mathbb{S}^{n}\times(0,+\infty)\to\mathbb{R}^{n+1}\setminus\{0\}$ (resp. $\rho_{p}\colon\mathbb{S}^{n}\times(0,+\infty)\to\mathbb{R}^{n+1}\setminus\{0\}$ ) is a homeomorphism with inverse mapping $\rho_{\infty}^{-1}\colon\mathbb{R}^{n+1}\setminus\{0\}\to\mathbb{S}^{n}\times(0,+\infty)$ (resp. $\rho_{p}\colon\mathbb{S}^{n}\times(0,+\infty)\to\mathbb{R}^{n+1}\setminus\{0\}$ ) given by $\rho_{\infty}^{-1}(x)=(\frac{x}{\|x\|},\frac{1}{\|x\|})$ (resp. $\rho_{p}^{-1}(x)=(\frac{x-p}{\|x-p\|},\|x-p\|)$ ).

Definition 2.1.

The strict transform of the subset $X$ under the spherical blowing-up $\rho_{\infty}$ is $X^{\prime}_{\infty}:=\overline{\rho_{\infty}^{-1}(X\setminus\{0\})}$ (resp. $X^{\prime}_{p}:=\overline{\rho_{p}^{-1}(X\setminus\{0\})}$ ). The subset $X_{\infty}^{\prime}\cap(\mathbb{S}^{n}\times\{0\})$ (resp. $X_{p}^{\prime}\cap(\mathbb{S}^{n}\times\{0\})$ ) is called the boundary of $X^{\prime}_{\infty}$ (resp. $X^{\prime}_{p}$ ) and it is denoted by $\partial X^{\prime}_{\infty}$ (resp. $\partial X^{\prime}_{p}$ ).

Definition 2.2.

Let $X$ and $Y$ be subsets in $\mathbb{R}^{n}$ and $\mathbb{R}^{m}$ , respectively. Let $p\in\mathbb{R}^{n}\cup\{\infty\}$ , $q\in\mathbb{R}^{m}\cup\{\infty\}$ . A homeomorphism $\varphi:X\rightarrow Y$ such that $q=\lim\limits_{x\rightarrow p}{\varphi(x)}$ is said a blow-spherical homeomorphism at $p$ , if the homeomorphism

\rho^{-1}_{q}\circ\varphi\circ\rho_{p}\colon X^{\prime}_{p}\setminus\partial X^{\prime}_{p}\rightarrow Y^{\prime}_{q}\setminus\partial Y^{\prime}_{q}

extends to a homeomorphism $\varphi^{\prime}\colon X^{\prime}_{p}\rightarrow Y^{\prime}_{q}$ . A homeomorphism $\varphi\colon X\rightarrow Y$ is said a blow-spherical homeomorphism if it is a blow-spherical homeomorphism for all $p\in\overline{X}\cup\{\infty\}$ . In this case, we say that the sets $X$ and $Y$ are blow-spherical homeomorphic or blow-isomorphic (at $(p,q)$ ).

Definition 2.3.

Let $X$ and $Y$ be subsets in $\mathbb{R}^{n}$ and $\mathbb{R}^{m}$ , respectively. We say that a blow-spherical homeomorphism $h\colon X\rightarrow Y$ is a strong blow-spherical homeomorphism if $h({\rm Sing}_{1}(X))={\rm Sing}_{1}(Y)$ and $h|_{X\setminus{\rm Sing}_{1}(X)}\colon X\setminus{\rm Sing}_{1}(X)\rightarrow Y\setminus{\rm Sing}_{1}(Y)$ is a $C^{1}$ diffeomorphism, where, for $A\subset\mathbb{R}^{p}$ , ${\rm Sing}_{k}(A)$ denotes the points $x\in A$ such that, for any open neighbourhood $U$ of $x$ , $A\cap U$ is not a $C^{k}$ submanifold of $\mathbb{R}^{p}$ . A blow-spherical homeomorphism at $\infty$ , $\varphi\colon X\rightarrow Y$ , is said a strong blow-spherical homeomorphism at $\infty$ if there are compact sets $K\subset\mathbb{R}^{n}$ and $\tilde{K}\subset\mathbb{R}^{m}$ such that $\varphi(X\setminus K)=Y\setminus\tilde{K}$ and the restriction $\varphi|_{X\setminus K}\colon X\setminus K\to Y\setminus\tilde{K}$ is a strong blow-spherical homeomorphism.

Remark 2.4.

We have some examples:

(1)

$\mbox{Id}:X\rightarrow X$ is a blow-spherical homeomorphism for any $X\subset\mathbb{R}^{n}$ ;
(2)

Let $X\subset\mathbb{R}^{n}$ , $Y\subset\mathbb{R}^{m}$ and $Z\subset\mathbb{R}^{k}$ be subsets. If $f\colon X\rightarrow Y$ and $g\colon Y\rightarrow Z$ are blow-spherical homeomorphisms, then $g\circ f\colon X\rightarrow Z$ is a blow-spherical homeomorphism.

Thus we have a category called blow-spherical category, which is denoted by BS, where its objects are all the subsets of Euclidean spaces and its morphisms are all blow-spherical homeomorphisms.

By definition, if $X$ and $Y$ are strongly blow-spherical homeomorphic then they are blow-spherical homeomorphic, but the converse does not hold in general, as we can see in the next example.

Example 2.5.

Let $V=\{(x,y)\in\mathbb{R}^{2};y=|x|\}$ . The mapping $\varphi\colon\mathbb{R}\to V$ given by $\varphi(x)=(x,|x|)$ is a blow-spherical homeomorphism. However, since ${\rm Sing}_{1}(\mathbb{R})=\emptyset$ and ${\rm Sing}_{1}(V)=\{(0,0)\}$ , there is no strong blow-spherical homeomorphism $h\colon\mathbb{R}\to V$ and, in particular, $\mathbb{R}$ and $V$ are not strongly blow-spherical homeomorphic.

Proposition 2.6 (Proposition 3.12 in [9]).

Let $X\subset\mathbb{R}^{n}$ and $Y\subset\mathbb{R}^{m}$ be semialgebraic sets. If $h\colon X\rightarrow Y$ is a semialgebraic outer lipeomorphism then $h$ is a blow-spherical homeomorphism.

Example 2.7.

$V=\{(x,y)\in\mathbb{R}^{2};y^{2}=x^{3}\}$ and $W=\{(x,y)\in\mathbb{R}^{2};y^{2}=x^{5}\}$ are blow-spherical homeomorphic, but are not outer bi-Lipschitz homeomorphic.

2.2. Tangent Cones

Let $X\subset\mathbb{R}^{n+1}$ be an unbounded semialgebraic set (resp. subanalytic set with $p\in\overline{X}$ ). We say that $v\in\mathbb{R}^{n+1}$ is a tangent vector of $X$ at infinity (resp. $p$ ) if there are a sequence of points $\{x_{i}\}\subset X$ tending to infinity (resp. $p$ ) and a sequence of positive real numbers $\{t_{i}\}$ such that

\lim\limits_{i\to\infty}\frac{1}{t_{i}}x_{i}=v\quad(\mbox{resp. }\lim\limits_{i\to\infty}\frac{1}{t_{i}}(x_{i}-p)=v).

Let $C(X,\infty)$ (resp. $C(X,p)$ ) denote the set of all tangent vectors of $X$ at infinity (resp. $p$ ). We call $C(X,\infty)$ the tangent cone of $X$ at infinity (resp. $p$ ).

We have the following characterization.

Corollary 2.8 (Corollary 2.16 [3]).

Let $X\subset\mathbb{R}^{n}$ be an unbounded semialgebraic set. Then $C(X,\infty)=\{v\in\mathbb{R}^{n};\,\exists\gamma:(\varepsilon,+\infty)\to Z$ $C^{0}$ semialgebraic such that $\lim\limits_{t\to+\infty}|\gamma(t)|=+\infty$ and $\gamma(t)=tv+o_{\infty}(t)\}$ , where $g(t)=o_{\infty}(t)$ means $\lim\limits_{t\to+\infty}\frac{g(t)}{t}=0$ .

Thus, we have the following

Corollary 2.9 (Corollary 2.18 [3]).

Let $Z\subset\mathbb{R}^{n}$ be an unbounded semialgebraic set. Let $\phi:\mathbb{R}^{n}\setminus\{0\}\to\mathbb{R}^{n}\setminus\{0\}$ be the semialgebraic mapping given by $\phi(x)=\frac{x}{\|x\|^{2}}$ and denote $X=\phi(Z\setminus\{0\})$ . Then $C(Z,\infty)$ is a semialgebraic set satisfying $C(Z,\infty)=C(X,0)$ and $\dim_{\mathbb{R}}C(Z,\infty)\leq\dim_{\mathbb{R}}Z$ .

Remark 2.10.

Another way to present the tangent cone at infinity (resp. $p$ ) of a subset $X\subset\mathbb{R}^{n+1}$ is via the spherical blow-up at infinity (resp. $p$ ) of $\mathbb{R}^{n+1}$ . In fact, if $X\subset\mathbb{R}^{n+1}$ is a semialgebraic set, then $\partial X^{\prime}_{\infty}=(C(X,\infty)\cap\mathbb{S}^{n})\times\{0\}$ (resp. $\partial X^{\prime}_{p}=(C(X,p)\cap\mathbb{S}^{n})\times\{0\}$ ).

2.3. Relative multiplicities

Let $X\subset\mathbb{R}^{m+1}$ be a $d$ -dimensional subanalytic subset and $p\in\mathbb{R}^{m+1}\cup\{\infty\}$ . We say $x\in\partial X^{\prime}_{p}$ is a simple point of $\partial X^{\prime}_{p}$ , if there is an open subset $U\subset\mathbb{R}^{m+2}$ with $x\in U$ such that:

a)

the connected components $X_{1},\cdots,X_{r}$ of $(X^{\prime}_{p}\cap U)\setminus\partial X^{\prime}_{p}$ are topological submanifolds of $\mathbb{R}^{m+2}$ with $\dim X_{i}=\dim X$ , for all $i=1,\cdots,r$ ;
b)

$(X_{i}\cup\partial X^{\prime}_{p})\cap U$ is a topological manifold with boundary, for all $i=1,\cdots,r$ .

Let ${\rm Smp}(\partial X^{\prime}_{p})$ be the set of simple points of $\partial X^{\prime}_{p}$ and we define $C_{\rm Smp}(X,p)=\{t\cdot x;\,t>0\mbox{ and }x\in{\rm Smp}(\partial X^{\prime}_{p})\}$ . Let $k_{X,p}\colon{\rm Smp}(\partial X^{\prime}_{p})\to\mathbb{N}$ be the function such that $k_{X,p}(x)$ is the number of connected components of the germ $(\rho_{p}^{-1}(X\setminus\{p\}),x)$ .

Remark 2.11.

It is known that ${\rm Smp}(\partial X^{\prime}_{p})$ is an open dense subset of the $(d-1)$ -dimensional part of $\partial X^{\prime}_{p}$ whenever $\partial X^{\prime}_{p}$ is a $(d-1)$ -dimensional subset. where $d=\dim X$ (see [5]).

Definition 2.12.

It is clear the function $k_{X,p}$ is locally constant. In fact, $k_{X,p}$ is constant on each connected component $X_{j}$ of ${\rm Smp}(\partial X^{\prime}_{p})$ . Then, we define the relative multiplicity of $X$ at $p$ (along of $X_{j}$ ) to be $k_{X,p}(X_{j}):=k_{X,p}(x)$ with $x\in X_{j}$ . Let $X_{1},...,X_{r}$ be the connected components of ${\rm Smp}(\partial X^{\prime}_{p})$ . By reordering the indices, if necessary, we assume that $k_{X,p}(X_{1})\leq\cdots\leq k_{X,p}(X_{r})$ . Then we define $k(X,p)=(k_{X,p}(X_{1}),...,k_{X,p}(X_{r}))$ .

Remark 2.13.

Let $X\subset\mathbb{R}^{n}$ be an unbounded real algebraic curve such that $C(X,\infty)\cap\mathbb{S}^{n-1}=\{a_{1},...,a_{r}\}$ . By the Conical Structure Theorem at infinity for semialgebraic sets that there exists a constant $R_{0}\gg 1$ such that for all $R\geq R_{0}$ , we have

X\setminus B_{R}(0)=\bigcup_{j=1}^{r}\bigcup_{l=1}^{k_{j}}{\Gamma_{j,l}}

and there is a semialgebraic diffeomorphism $h\colon X\setminus B_{R}(0)\rightarrow{\rm Cone}_{\infty}(X\cap\mathbb{S}^{n-1}_{R}(0))$ such that $\|h(x)\|=\|x\|$ and $h|_{X\cap\mathbb{S}^{n-1}_{R}(0)}=Id$ and, moreover, for each $j\in\{1,...,r\}$ , $C(\Gamma_{j,l},\infty)\cap\mathbb{S}^{n-1}=\{a_{j}\}$ for all $l=1,...,k_{j}$ . These $\Gamma_{j,l}$ ’s are called the branches of $X$ at infinity. In particular, $k_{j}=k_{X,\infty}(a_{j},0)$ , i.e., $k_{X,\infty}(a_{i},0)$ is the number of branches of $X$ at infinity that are tangent to $a_{i}$ at infinity.

Proposition 2.14 (Proposition 3.5 in [9]).

Let $X$ and $Y$ be semialgebraic sets in $\mathbb{R}^{n}$ and $\mathbb{R}^{m}$ respectively. Let $\varphi\colon X\rightarrow Y$ be a blow-spherical homeomorphism at $p\in\mathbb{R}^{n}\cup\{\infty\}$ . Then

k_{X,p}(x)=k_{Y,q}(\varphi^{\prime}(x)),

for all $x\in Smp(\partial X^{\prime}_{p})\subset\partial X^{\prime}_{p}$ , where $q=\lim\limits_{x\to p}\varphi(x)$ . In particular, $k(X,p)=k(Y,q)$ .

Proposition 2.15 (Proposition 3.6 in [9]).

If $h\colon X\rightarrow Y$ is a blow-spherical homeomorphism at $p\in X\cup\{\infty\}$ , then $C(X,p)$ and $C(Y,h(p))$ are blow-spherical homeomorphic at $0$ .

3. On the classification of real algebraic curves

In this section, we present some examples and results about the classification of real algebraic curves under blow-spherical homeomorphisms.

Proposition 3.1.

Let $X,\widetilde{X}\subset\mathbb{R}^{n}$ be two real semialgebraic curves. Then the following statements are equivalent:

(1)

$X$ and $\widetilde{X}$ are blow-spherical homeomorphic at infinity;
(2)

$k(X,\infty)=k(\widetilde{X},\infty)$ ;
(3)

$X$ and $\widetilde{X}$ are strongly blow-spherical homeomorphic at infinity;

Proof.

Assume that $C(X,\infty)\cap\mathbb{S}^{n-1}=\{a_{1},...,a_{r}\}$ and $C(\widetilde{X},\infty)\cap\mathbb{S}^{n-1}=\{\widetilde{a}_{1},...,\widetilde{a}_{s}\}$ . By Remark 2.11, ${\rm Smp}(\partial X^{\prime}_{\infty})$ is an open dense subset of the $0$ -dimensional part of $\partial X^{\prime}_{\infty}$ , hence ${\rm Smp}(\partial X^{\prime}_{\infty})=\partial X^{\prime}_{\infty}$ .

Clearly, (3) $\Rightarrow$ (1).

(1) $\Rightarrow$ (2). Assume that $X$ and $\widetilde{X}$ are blow-spherical homeomorphic at infinity. By Proposition 2.14, $k(X,\infty)=k(\widetilde{X},\infty)$ .

(2) $\Rightarrow$ (3). Assume that $k(X,\infty)=k(\widetilde{X},\infty)$ . Thus, $r=s$ and by reordering the indices, if necessary, we may assume that $k_{i}=k_{X,\infty}(a_{i},0)=k_{\widetilde{X},\infty}(\widetilde{a_{i}},0)$ for all $i=1,...,r$ and $k_{1}\leq k_{2}\leq....\leq k_{r}$ . Thus, it follows from Remark 2.13 and the Conical Structure Theorem at infinity for semialgebraic sets that there exists a constant $R_{0}\gg 1$ such that for all $R\geq R_{0}$ , we have

X\setminus B_{R}(0)=\bigcup_{j=1}^{r}\bigcup_{l=1}^{k_{j}}{\Gamma_{j,l}}

and there is a semialgebraic diffeomorphism $h\colon X\setminus B_{R}(0)\rightarrow{\rm Cone}_{\infty}(X\cap\mathbb{S}^{n-1}_{R}(0))$ such that $\|h(x)\|=\|x\|$ and $h|_{X\cap\mathbb{S}^{n-1}_{R}(0)}=Id$ and, moreover, for each $j\in\{1,...,r\}$ , $C(\Gamma_{j,l},\infty)\cap\mathbb{S}^{n-1}=\{a_{j}\}$ for all $l=1,...,k_{j}$ . In particular, we consider $h|_{\Gamma_{j,l}}\colon\Gamma_{j,l}\rightarrow{\rm Cone}_{\infty}(\Gamma_{j,l}\cap\mathbb{S}^{n-1}_{R}(0))$ .

Now define the curve $\alpha_{j,l}\colon[R,+\infty)\rightarrow{\rm Cone}_{\infty}(\Gamma_{j,l}\cap\mathbb{S}^{n-1}_{R}(0))$ given by $\alpha_{j,l}(t)=t\frac{a_{j,l}}{|a_{j,l}|}$ , where $\{a_{j,l}\}=\Gamma_{j,l}\cap\mathbb{S}^{n-1}_{R}(0)$ . Thus, we define the curve $\beta_{j,l}\colon[R,+\infty)\rightarrow\Gamma_{j,l}$ by $\beta_{j,l}(t):=(h^{-1}\circ\alpha_{j,l})(t)$ .

Analogously, we also have

\widetilde{X}\setminus B_{R}(0)=\bigcup_{j=1}^{r}\bigcup_{l=1}^{k_{j}}{\widetilde{\Gamma}_{j,l}},

and there are semialgebraic diffeomorphisms $\widetilde{h}\colon\widetilde{X}\setminus B_{R}(0)\rightarrow{\rm Cone}_{\infty}(\widetilde{X}\cap\mathbb{S}^{n-1}_{R}(0))$ , $\widetilde{\alpha}_{j,l}\colon[R,+\infty)\rightarrow{\rm Cone}_{\infty}(\widetilde{\Gamma}_{j,l}\cap\mathbb{S}^{n-1}_{R}(0))$ and $\widetilde{\beta}_{j,l}\colon[R,+\infty)\rightarrow\widetilde{\Gamma}_{j,l}$ and, moreover, for each $j$ , $C(\widetilde{\Gamma}_{j,l},\infty)\cap\mathbb{S}^{n-1}=\{\widetilde{a}_{j}\}$ for all $l=1,...,k_{j}$ .

Let $A=X\setminus B_{R}(0)$ and $\widetilde{A}=\widetilde{X}\setminus B_{R}(0)$ and define $\varphi\colon A\rightarrow\widetilde{A}$ by $\varphi(z)=\widetilde{\beta}_{j,l}\circ\beta^{-1}_{j,l}(z)$ if $z\in\Gamma_{j,l}$ . We have that $\varphi$ is a strong blow-spherical homeomorphism at infinity and $\varphi^{\prime}\colon X^{\prime}_{\infty}\rightarrow\widetilde{X}^{\prime}_{\infty}$ is given by

\varphi^{\prime}(x,s)=\left\{\begin{array}[]{ll}\left(\frac{\varphi(\frac{x}{s})}{\|\varphi(\frac{x}{s})\|},\frac{1}{\|\varphi(\frac{x}{s})\|}\right),&\mbox{ if }s\not=0;\\ (\widetilde{a}_{j},0),&\mbox{ if }(x,s)=(a_{j},0).\end{array}\right.

In order to see that, it is enough to prove that $\varphi$ is a blow-spherical homeomorphism at infinity. Let us prove that $\varphi^{\prime}$ is continuous at each $(a_{j},0)\in\partial A^{\prime}_{\infty}$ . Thus take $(a_{j},0)\in\partial A^{\prime}_{\infty}$ and consider a sequence $(x_{k},s_{k})_{k\in\mathbb{N}}\subset A^{\prime}_{\infty}\setminus\partial A^{\prime}_{\infty}$ such that $(x_{k},s_{k})\rightarrow(a_{j},0)$ . Thus, for any subsequence $\{(x_{k_{i}},s_{k_{i}})\}_{i\in\mathbb{N}}$ , there is some $l\in\{1,...,k_{j}\}$ and a subsequence $\{(z_{k},t_{k})\}_{k\in\mathbb{N}}\subset\{(x_{k_{i}},s_{k_{i}})\}_{i\in\mathbb{N}}$ such that $\frac{z_{k}}{t_{k}}\in\Gamma_{j,l}$ for all $k$ . Since

$\displaystyle\\|\beta_{j,l}(t)\\|$	$\displaystyle=$	$\displaystyle\\|h^{-1}\circ\alpha_{j,l}(t)\\|$
	$\displaystyle=$	$\displaystyle\left\\|h^{-1}\left(t\frac{a_{j,l}}{\\|a_{j,l}\\|}\right)\right\\|$
	$\displaystyle=$	$\displaystyle t,$

we have

\frac{z_{k}}{t_{k}}=\beta_{j,l}\left(\frac{1}{t_{k}}\right).

Therefore,

\displaystyle\varphi^{\prime}(z_{k},t_{k})

\displaystyle=

\displaystyle\left(\frac{\widetilde{\beta}_{j,l}(\frac{1}{t_{k}})}{\|\widetilde{\beta}_{j,l}(\frac{1}{t_{k}})\|},\frac{1}{\|\widetilde{\beta}_{j,l}(\frac{1}{t_{k}})\|}\right).

Since $\lim\limits_{t\to 0^{+}}\frac{\widetilde{\beta}_{j,l}(\frac{1}{t})}{\|\widetilde{\beta}_{j,l}(\frac{1}{t})\|}=\widetilde{a}_{j}$ , we have $\lim\limits_{k\rightarrow+\infty}{\varphi^{\prime}(z_{k},t_{k})}=(\widetilde{a}_{j},0).$ This shows that $\lim\limits_{k\rightarrow+\infty}{\varphi^{\prime}(x_{k},s_{k})}=(\widetilde{a}_{j},0).$

Thus, $\varphi^{\prime}$ is continuous at each $(a_{j},0)$ . Analogously, $(\varphi^{-1})^{\prime}$ is continuous at each $(\widetilde{a}_{j},0)\in\partial\widetilde{A}^{\prime}_{\infty}$ . Therefore, $\varphi$ is a strong blow-spherical homeomorphism at infinity. ∎

3.1. Normal forms for the classification at infinity

Let $\mathcal{F}(\{0,1\};\mathbb{Z}_{\geq 0})$ be the set of all non-null functions from $\{0,1\}$ to $\mathbb{Z}_{\geq 0}$ . For each positive integer number $N$ , let $\mathcal{A}_{N}$ be the subset of $(\mathcal{F}(\{0,1\};\mathbb{Z}_{\geq 0}))^{N}$ formed by all $(r_{1},...,r_{N})$ satisfying the following:

(1)

$r_{l}(0)\leq r_{l+1}(0)$ for all $l\in\{1,\cdots,N-1\}$ ;
(2)

If $r_{l}(0)=r_{l+1}(0)$ then $r_{l}(1)\leq r_{l+1}(1)$ .

Let $\mathcal{A}=\bigcup\limits_{N=1}^{\infty}\mathcal{A}_{N}$ . Let $A=(r_{1},...,r_{N})\in\mathcal{A}$ . For $j\in\{0,1\}$ and $r_{l}(j)>0$ , we define the following curves:

X_{A,1}=\left\{(x,y)\in\mathbb{R}^{2};\prod_{l=1}^{N}\prod_{r=1}^{r_{l}(1)}{((y-lx)^{2}-r(y+lx))}=0\right\},

and

X_{A,0}=\left\{(x,y)\in\mathbb{R}^{2};\prod_{l=1}^{N}\prod_{r=1}^{r_{l}(0)}{((y-lx)-r)}=0\right\}.

Moreover, if $r_{l}(j)=0$ we define $X_{A,j}=\{0\}$ . Finally, we define the realization of $A=(r_{1},...,r_{N})$ to be the curve $X_{A}:=X_{A,0}\cup X_{A,1}$ .

Thus, it follows from Proposition 3.1 and the definition of $A$ , the following classification result:

Proposition 3.2.

For each real algebraic curve $X\subset\mathbb{R}^{n}$ , there exists a unique $A\in\mathcal{A}$ such that $X_{A}$ and $X$ are blow-spherical homeomorphic at infinity.

Proof.

We consider $\overline{X}$ the projective closure of $X$ and $\{c_{1},\cdots,c_{N}\}=\overline{X}\cap L_{\infty}$ , where $L_{\infty}$ is the hyperplane at infinity.

By taking local charts, it follows from Lemma 3.3.5 in [4] that there exist an open neighborhood $V_{l}\subset\mathbb{RP}^{n}$ of $c_{l}$ and $\Upsilon_{l,1},\cdots,\Upsilon_{l,r_{l}}$ such that $\Upsilon_{l,i}\cap\Upsilon_{l,i^{\prime}}=\{c_{l}\}$ whenever $i\neq i^{\prime}$ and

Y\cap V_{l}=\bigcup_{i=1}^{r_{l}}{\Upsilon_{l,i}}

and, moreover, for each $i\in\{1,\cdots,r_{l}\}$ , there exists an analytic homeomorphism $\upsilon_{l,i}\colon(-\epsilon,\epsilon)\rightarrow\Upsilon_{l,i}$ with $\upsilon_{i}(0)=c_{l}$ . By shrinking $V_{l}$ , if necessary, we may assume that for each $i\in\{1,\cdots,s_{l}\}$ , $\Upsilon_{l,i}\subset L_{\infty}$ or $\Upsilon_{l,i}\cap L_{\infty}=\{c_{l}\}$ . By reordering the indices, if necessary, there is $r_{l}>0$ such that $\Upsilon_{l,i}\cap L_{\infty}=\{c_{l}\}$ for all $i\in\{1,\cdots,r_{l}\}$ and $\Upsilon_{l,i}\subset L_{\infty}$ for all $i\in\{r_{l}+1,\cdots,s_{l}\}$ . By reordering the indices again, if necessary, we may assume that $r_{l}\leq r_{l+1}$ , for all $j\in\{1,...,N\}$ .

We denote the half-branch by $\Upsilon_{l,i}^{+}=\upsilon_{l,i}(0,\epsilon)$ and $\Upsilon_{l,i}^{-}=\upsilon_{l,i}(-\epsilon,0)$ . So, denoting $\Gamma_{l,i}^{+}=\Upsilon_{l,i}^{+}\cap\mathbb{R}^{n}$ and $\Gamma_{l,i}^{-}=\Upsilon_{l,i}^{-}\cap\mathbb{R}^{n}$ , we obtain that

\{\Gamma_{l,1}^{+},\Gamma_{l,1}^{-},\cdots,\Gamma_{l,r_{l}}^{+},\Gamma_{l,r_{l}}^{-}\}_{l=1}^{N}

are all the branches of $X$ at infinity. For each $l\in\{1,..,N\}$ , there is $a_{l}\in\mathbb{S}^{n-1}$ such that $\pi^{-1}(c_{l})\cap\mathbb{S}^{n-1}=\{-a_{l},a_{l}\}$ , where $\pi\colon\mathbb{R}^{n}\setminus\{0\}\to\mathbb{RP}^{n-1}\cong L_{\infty}$ is the canonical projection. Thus, for each $l\in\{1,..,N\}$ , $C(\Gamma_{l,i},\infty)\cap\mathbb{S}^{n-1}\subset\{-a_{l},a_{l}\}$ .

For each $l\in\{1,..,N\}$ , by reordering the indices, if necessary, there are non-negative integer numbers $n_{l},p_{l}$ and $z_{l}$ such that:

•

$C(\Gamma_{l,i}^{+},\infty)=-C(\Gamma_{l,i}^{-},\infty)$ for all $i\in\{1,...,z_{l}\}$ ;
•

$C(\Gamma_{l,i}^{+},\infty)\cap\mathbb{S}^{n-1}=C(\Gamma_{l,i}^{-},\infty)\cap\mathbb{S}^{n-1}=\{-a_{l}\}$ , for all $i\in\{z_{l}+1,...,z_{l}+n_{l}\}$ ;
•

$C(\Gamma_{l,i}^{+},\infty)\cap\mathbb{S}^{n-1}=C(\Gamma_{l,i}^{-},\infty)\cap\mathbb{S}^{n-1}=\{a_{l}\}$ , for all $i\in\{z_{l}+n_{l}+1,...,r_{l}=z_{l}+n_{l}+p_{l}\}$ .

By changing $a_{l}$ by $-a_{l}$ , if necessary, we may assume that $n_{l}\leq p_{l}$ . Thus, we define $\tilde{\Gamma}_{l,i}^{+}=\Gamma_{l,i}^{+}$ for all $i\in\{1,...,r_{l}\}$ and

\tilde{\Gamma}_{l,i}^{-}=\left\{\begin{array}[]{ll}\Gamma_{l,i}^{-},\mbox{ if }i\in\{1,...,z_{l}\}\cup\{z_{l}+n_{l}+1,...,r_{l}\}\\ \Gamma_{l,i+n_{l}}^{-},\mbox{ if }i\in\{z_{l}+1,...,z_{l}+n_{l}\}.\end{array}\right.

Thus, we have the following:

•

$C(\tilde{\Gamma}_{l,i}^{+},\infty)=-C(\tilde{\Gamma}_{l,i}^{-},\infty)$ for all $i\in\{1,...,z_{l}+n_{l}\}$ ;
•

$C(\tilde{\Gamma}_{l,i}^{+},\infty)=C(\tilde{\Gamma}_{l,i}^{-},\infty)\}$ , for all $i\in\{z_{l}+n_{l}+1,...,r_{l}\}$ .

For each $l\in\{1,..,N\}$ , we define $r_{l}\colon\{0,1\}\to\mathbb{N}$ by $r_{l}(0)=z_{l}+n_{l}$ and $r_{l}(1)=p_{l}$ .

By reordering the indices, if necessary, we may assume that

(1)

$r_{l}(0)\leq r_{l+1}(0)$ for all $l\in\{1,\cdots,N-1\}$ ;
(2)

If $r_{l}(0)=r_{l+1}(0)$ then $r_{l}(1)\leq r_{l+1}(1)$ .

Therefore, $A={(r_{1},...,r_{N})}\in\mathcal{A}$ and by Proposition 3.1, we have that $X_{A}$ is blow-spherical homeomorphic at infinity to $X$ . The uniqueness of $A$ follows from the definition of $\mathcal{A}$ and Proposition 3.1. ∎

Remark 3.3.

Proposition 3.2 says in particular that any spacial real algebraic curve is blow-spherical homeomorphic at infinity to a plane real algebraic curve.

Note that Remark 3.3 is not true in the global case, as it is shown in the next example.

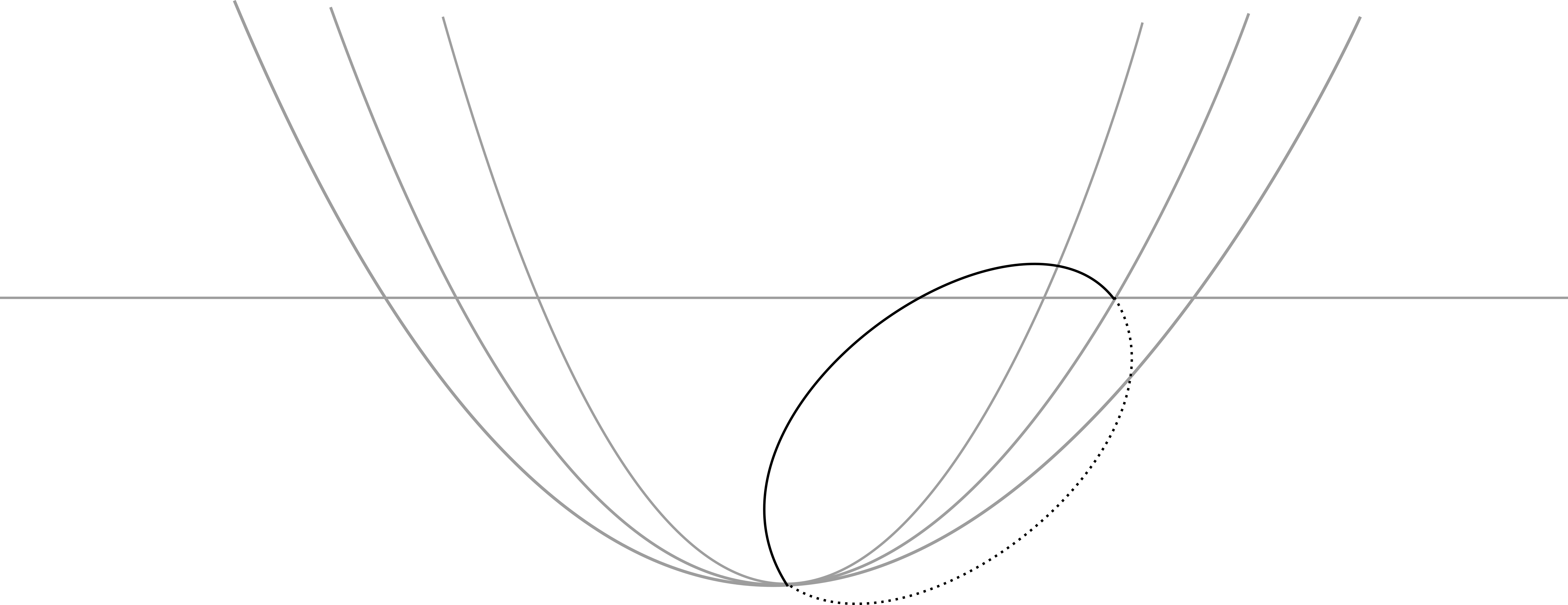
Example 3.4.

Let $Y$ and $Z$ be the algebraic curves in $\mathbb{R}^{3}$ given by

Y=\textstyle{\left\{(x,y,z)\in\mathbb{R}^{3};(y-1)(y-\frac{x^{2}}{2})(y-x^{2})(y-2x^{2})=0\mbox{ and }z=0\right\}}

and

Z=\textstyle{\left\{(x,y,z)\in\mathbb{R}^{3};\left((x-\frac{1}{2})^{2}+(y-\frac{1}{2})^{2}+z^{2}-\frac{1}{2}\right)=0\mbox{ and }x=y\right\}}.

Thus the spatial algebraic curve $X=Y\cup Z$ is not blow-spherical equivalent to a plane curve (see figure 1).

Refer to caption — Figure 1. The spatial algebraic curve $X$

3.2. Realization of the invariant $k(\cdot,\infty)$

Definition 3.5.

For each positive integer $n$ , let $\mathcal{N}_{n}$ be the set of all $(\eta_{1},\eta_{2},\cdots,\eta_{n})\in(\mathbb{Z}_{>0})^{n}$ such that $\eta_{1}\leq\eta_{2}\leq\cdots\leq\eta_{n}$ . Let $\mathcal{N}=\bigcup\limits_{n=1}^{\infty}\mathcal{N}_{n}$ .

By definition, we have that if $X\subset\mathbb{R}^{n}$ is a semialgebraic curve then $k(X,\infty)\in\mathcal{N}$ . Reciprocally, for $\eta=(\eta_{1},\eta_{2},\cdots,\eta_{N})\in\mathcal{N}$ , it is easy to find a semialgebraic curve $X\subset\mathbb{R}^{n}$ such that $k(X,\infty)=\eta$ . For example,

X=\bigcup_{l=1}^{N}\bigcup_{r=1}^{\eta_{l}}\left\{(x,y)\in\mathbb{R}^{2};y-lx-r=0\mbox{ and }y+lx\geq 0\right\}.

Definition 3.6.

We say that $\eta=(\eta_{1},\eta_{2},\cdots,\eta_{r})\in\mathcal{N}$ is algebraically realizable, if there exists a real algebraic curve $X\subset\mathbb{R}^{n}$ such that $k(X,\infty)=\eta$ .

The next result gives a necessary and sufficient condition for a $\eta=(\eta_{1},\eta_{2},\cdots,\eta_{n})\in\mathcal{N}$ to be algebraically realizable. Let $v=(v_{1},\cdots,v_{n})\in\mathbb{R}^{n}$ a vector, we denote by $\|\cdot\|_{1}$ the norm given by $\|v\|_{1}=|v_{1}|+\cdots+|v_{n}|$ .

Proposition 3.7.

$\eta=(\eta_{1},\cdots,\eta_{k})\in\mathcal{N}$ is algebraically realizable if and only if $\|\eta\|_{1}\equiv 0\pmod{2}$ .

Proof.

Assume that $\eta=(\eta_{1},\cdots,\eta_{k})\in\mathcal{N}$ is algebraically realizable, that is, there exists an unbounded real algebraic curve $X\subset\mathbb{R}^{n}$ such that $\eta=k(X,\infty)$ . We consider $\overline{X}$ the projective closure of $X$ and $\{c_{1},\cdots,c_{N}\}=\overline{X}\cap L_{\infty}$ , where $L_{\infty}$ is the hyperplane at infinity.

By the proof of Proposition 3.2, we obtain that there exist an open neighbourhood $V_{l}\subset\mathbb{RP}^{n}$ of $c_{l}$ and $\Upsilon_{l,1},\cdots,\Upsilon_{l,r_{l}}$ such that $\Upsilon_{l,i}\cap\Upsilon_{l,i^{\prime}}=\{c_{l}\}$ whenever $i\neq i^{\prime}$ ,

Y\cap V_{l}=\bigcup_{i=1}^{r_{l}}{\Upsilon_{l,i}}

and, moreover, for each $i\in\{1,\cdots,r_{l}\}$ , there exists an analytic homeomorphism $\upsilon_{l,i}\colon(-\epsilon,\epsilon)\rightarrow\Upsilon_{l,i}$ with $\upsilon_{i}(0)=c_{l}$ . Additionally, there is $r_{l}>0$ such that $\Upsilon_{l,i}\cap L_{\infty}=\{c_{l}\}$ for all $i\in\{1,\cdots,r_{l}\}$ and $\Upsilon_{l,i}\subset L_{\infty}$ for all $i\in\{r_{l}+1,\cdots,s_{l}\}$ . By reordering the indices again, if necessary, we may assume that $r_{l}\leq r_{l+1}$ , for all $j\in\{1,...,N\}$ .

\{\Gamma_{l,1}^{+},\Gamma_{l,1}^{-},\cdots,\Gamma_{l,r_{l}}^{+},\Gamma_{l,r_{l}}^{-}\}_{l=1}^{N}

are all the branches of $X$ at infinity. For each $l\in\{1,..,k\}$ , there is $b_{l}\in\mathbb{S}^{n-1}$ such that $\pi^{-1}(c_{l})\cap\mathbb{S}^{n-1}=\{-b_{l},b_{l}\}$ , where $\pi\colon\mathbb{R}^{n}\setminus\{0\}\to\mathbb{RP}^{n-1}\cong L_{\infty}$ is the canonical projection. Thus, for each $l\in\{1,..,k\}$ , $C(\Gamma_{l,i},\infty)\cap\mathbb{S}^{n-1}\subset\{-b_{l},b_{l}\}$ . By Remark 2.13,

k_{X,\infty}(b_{l},0)+k_{X,\infty}(-b_{l},0)=2r_{l}\equiv 0\pmod{2},

where $k_{X,\infty}(v)$ is defined to be zero if $v\not\in Smp(\partial X^{\prime})$ .

Assume that $C(X,\infty)\cap\mathbb{S}^{n-1}=\{a_{1},...,a_{k}\}$ and $\eta_{l}=k_{X,\infty}(a_{l},0)$ for all $l\in\{1,...,k\}$ .

We consider the following decomposition of $\{1,...,k\}$ :

\{l_{1},...,l_{2s}\}=\{l\in\{1,...,k\};-a_{l},a_{l}\in C(X,\infty)\}

and

\{l_{2s+1},...,l_{k}\}=\{1,...,k\}\setminus\{l_{1},...,l_{2s}\}

and such that $a_{l_{i}}=-a_{l_{i+s}}$ for all $i\in\{1,...,s\}$ . Therefore, by writing $k_{X,\infty}(a)$ instead of $k_{X,\infty}(a,0)$ , we have

$\displaystyle\\|\eta\\|_{1}$	$\displaystyle=$	$\displaystyle k_{X,\infty}(a_{1_{1}})+k_{X,\infty}(a_{l_{1+s}})+\cdots+k_{X,\infty}(a_{1_{s}})+k_{X,\infty}(a_{l_{2s}})$
		$\displaystyle+k_{X,\infty}(a_{1_{2s+1}})+k_{X,\infty}(-a_{1_{2s+1}})+\cdots+k_{X,\infty}(a_{1_{k}}))+k_{X,\infty}(-a_{l_{k}})$
	$\displaystyle=$	$\displaystyle 2r_{l_{1}}+\cdots+2r_{l_{s}}+2r_{l_{2s+1}}+\cdots+2r_{l_{k}}$
	$\displaystyle\equiv$	$\displaystyle 0\pmod{2}.$

For the converse, assume that $\eta=(\eta_{1},\cdots,\eta_{k})\in\mathcal{N}$ satisfies $\|\eta\|_{1}\equiv 0\pmod{2}$ . Thus, $\#\{j;\eta_{j}\equiv 1\pmod{2}\}\equiv 0\pmod{2}$ . Let $J=\{j_{1}\leq...\leq j_{2m}\}\subset I:=\{1,...,k\}$ be the indices such that $\eta_{j}\equiv 1\pmod{2}$ if and only if $j\in J$ . For each $j_{i}\in J$ , let $n_{i}$ be the non-negative integer number such that $\eta_{j_{i}}=2n_{i}+1$ . Let $I\setminus J=\{q_{1},...,q_{N}\}$ . We consider the following three algebraic curves

X^{+}=\left\{(x,y)\in\mathbb{R}^{2};\prod_{l=1}^{m}(y-lx)\prod_{r=1}^{n_{l}}{((y-lx)^{2}-r(y+lx))}=0\right\},

X^{-}=\left\{(x,y)\in\mathbb{R}^{2};\prod_{l=1}^{m}\prod_{r=1}^{n_{m+l}}{((y-lx)^{2}+r(y+lx))}=0\right\}

and

X^{0}=\left\{(x,y)\in\mathbb{R}^{2};\prod_{l=1}^{N}\prod_{r=1}^{\eta_{q_{l}}}{((y-(m+l)x)^{2}-r(y+(m+l)x))}=0\right\}

Then, for $X=X_{0}\cup X^{+}\cup X^{-}$ , we have that $k(X,\infty)=\eta$ .

∎

3.3. Some considerations on the global case

In the global case, the problem of classification is harder. For instance, two homeomorphic algebraic curves having the same relative multiplicities may not be blow-spherical homeomorphic, as we can see in the next example.

Example 3.8.

Let

\textstyle{X=\left\{(x,y)\in\mathbb{R}^{2};p(x,y)\left(x^{2}-y^{2}-y^{3}\right)\left((x+\frac{7\sqrt{12}}{8})^{2}+(y-3)^{2}-\frac{76}{64}\right)=0\right\}}

and

\textstyle{\widetilde{X}=\left\{(x,y)\in\mathbb{R}^{2};q(x,y)\left(x^{2}-y^{2}-y^{3}\right)\left((x+\frac{7\sqrt{12}}{8})^{2}+(y-3)^{2}-\frac{76}{64}\right)=0\right\}},

where $p$ and $q$ are the polynomials given by $p(x,y)=((x-\frac{7\sqrt{12}}{8})^{2}+(y-3)^{2}-\frac{76}{64})$ and $q(x,y)=((x+\frac{27\sqrt{80}}{28})^{2}+(y-5)^{2}-\frac{864}{784})$ . Then $X$ and $\widetilde{X}$ are homeomorphic algebraic curves and there is a bijection $\sigma\colon{\rm Sing}(X)\cup\{\infty\}\to{\rm Sing}(\widetilde{X})\cup\{\infty\}$ such that $\sigma(\infty)=\infty$ and $k(X,p)=k(\widetilde{X},\sigma(p))$ for all $p\in{\rm Sing}(X)\cup\{\infty\}$ . However, $X$ and $\widetilde{X}$ are not blow-spherical homeomorphic (see Figures 3 and 3).

[Uncaptioned image] — Figure 2. Curve $X$

Thus, we need of the following notion:

Definition 3.9.

We say that a homeomorphism $\phi\colon X\to\widetilde{X}$ between two analytic curves is a tangency-preserving homeomorphism if, for each $p\in X\cup\{\infty\}$ , two half-branches $\Gamma_{1}$ and $\Gamma_{2}$ of $(X,p)$ are tangent at $p$ if and only if $\phi(\Gamma_{1})$ and $\phi(\Gamma_{2})$ are tangent at $\phi(p)$ .

Proposition 3.10.

Let $X,\widetilde{X}\subset\mathbb{R}^{n}$ be two connected real algebraic curves. Then the following statements are equivalent:

(1)

$X$ and $\widetilde{X}$ are blow-spherical homeomorphic;
(2)

There is a tangency-preserving homeomorphism $\phi\colon X\to\widetilde{X}$ ;
(3)

$X$ and $\widetilde{X}$ are strongly blow-spherical homeomorphic.

Proof.

It follows from Propositions 2.14 and 2.15 that $(1)\Rightarrow(2)$ .

Since $(3)\Rightarrow(1)$ , we only have to prove $(2)\Rightarrow(3)$ . Assume that there is a tangency-preserving homeomorphism $\phi\colon X\to\widetilde{X}$ .

Let ${\rm Sing}_{1}(X)=\{p_{1},...,p_{r}\}$ and ${\rm Sing}_{1}(\widetilde{X})=\{\widetilde{p}_{1},...,\widetilde{p}_{s}\}$ . Since $\phi$ is a tangency-preserving homeomorphism, it follows from [8, Proposition 6.9] that $\phi({\rm Sing}_{1}(X))={\rm Sing}_{1}(\widetilde{X})$ and, in particular, $r=s$ . Thus, we assume that $\phi(p_{i})=\widetilde{p}_{i}$ for all $i\in\{1,...,r\}$ .

By following the proof of Theorem 6.19 in [8], we can find $\epsilon>0$ and a strong blow-spherical homeomorphism $\varphi\colon\bigcup\limits_{i=1}^{r}(X\cap B_{\epsilon}(p_{i}))\to\bigcup\limits_{i=1}^{r}(\widetilde{X}\cap B_{\epsilon}(\widetilde{p}_{i}))$ such that for each $i\in\{1,...,r\}$ , $\|\varphi(x)-\widetilde{p}_{i}\|=\|x-p_{i}\|$ for all $x\in X\cap B_{\epsilon}(p_{i})$ .

It follows from Proposition 3.1 that there exists a strong blow-spherical homeomorphism $h\colon X\setminus B_{R}(0)\rightarrow\widetilde{X}\setminus B_{R}(0)$ such that $\|h(x)\|=\|x\|$ for all $x\in X\setminus B_{R}(0)$ .

Now, we define the following set

X_{\epsilon,R}=\left(X\cap B_{2R}(0)\right)\setminus\left\{B_{\epsilon/2}(p_{1})\cup\cdots\cup B_{\epsilon/2}(p_{s})\right\},

and

\widetilde{X}_{\epsilon,R}=\left(\widetilde{X}\cap B_{2R}(0)\right)\setminus\left\{B_{\epsilon/2}(p_{1})\cup\cdots\cup B_{\epsilon/2}(p_{s})\right\}.

Note that $X_{\epsilon,R}$ (resp. $\widetilde{X}_{\epsilon,R}$ ) is a finite union of compact one-dimensional with boundary, i.e, $X_{\epsilon,R}=\bigcup_{i=1}^{l_{0}}{X_{\epsilon,R}^{i}}$ (resp. $\widetilde{X}_{\epsilon,R}=\bigcup_{i=1}^{l_{0}}{\widetilde{X}_{\epsilon,R}^{i}}$ ), where each $X_{\epsilon,R}^{i}$ (resp. $\widetilde{X}_{\epsilon,R}^{i}$ ) is diffeomorphic to the compact interval $[0,1]$ . Thus there is a diffeomorphism $\Phi\colon X_{\epsilon,R}\rightarrow\widetilde{X}_{\epsilon,R}$ such that each $\Phi(X_{\epsilon,R}^{i})$ is contained in the connected component of $\widetilde{X}\setminus{\rm Sing}_{1}(\widetilde{X})$ which contains $\phi(X_{\epsilon,R}^{i})$ . By using standard arguments of bump functions, we may define a strong blow-spherical homeomorphism $F\colon X\rightarrow\widetilde{X}$ such that

F(x)=\begin{cases}\varphi(x),&\quad\text{if}\ x\in X;\|x-p_{j}\|\leq\epsilon/2\\ h(x),&\quad\text{if}\ x\in E_{i};\|x\|\geq 2R\\ \Phi(x),&\quad\text{if}\ x\in X_{2\epsilon,R/2},\end{cases}

which finishes the proof. ∎

References

[1] Birbrair, L.; Fernandes, A. and Grandjean, V. Collapsing topology of isolated singularities. arXiv:1208.4328 [Math,MG] (2012).
[2] Birbrair, L.; Fernandes, A. and Grandjean, V. Thin-thick decomposition for real definable isolated singularities. Indiana University Math. J., vol. 66 (2017), 547–557.
[3] Fernandes, A. and Sampaio, J. E. On Lipschitz rigidity of complex analytic sets. The Journal of Geometric Analysis, vol. 30 (2020), 706–718.
[4] Milnor, J. Singular points of complex hypersurfaces. Princeton: Princeton University Press, 1968.
[5] Pawłucki, W. Quasi-regular boundary and Stokes’ formula for a sub-analytic leaf. In: Ławrynowicz J. (eds) Seminar on Deformations. Lecture Notes in Math., vol 1165. Berlin, Heidelberg: Springer. 1985.
[6] Sampaio, J.E. Regularidade lipschitz, invariância da multiplicidade e a geometria dos cones tangentes de conjuntos analíticos. Ph.D. thesis, Universidade Federal Do Ceará (2015).
[7] Sampaio, J. E. Multiplicity, regularity and blow-spherical equivalence of complex analytic set. The Asian Journal of Mathematics, vol. 24 (2020), no. 5, 803-820.
[8] Sampaio, J. E. Multiplicity, regularity and blow-spherical equivalence of real analytic sets. Math. Z., vol. 301, 385–410 (2022).
[9] Sampaio, J. E. and da Silva, E. C. Classification of complex algebraic curves under blow-spherical equivalence. Preprint (2023), arXiv:2302.02026 [math.AG].

Classification of real algebraic curves under blow-spherical homeomorphisms at infinity

Abstract.

Key words and phrases:

2010 Mathematics Subject Classification:

1. Introduction

2. Preliminaries

2.1. Definition of the blow-spherical equivalence

Definition 2.1.

Definition 2.2.

Definition 2.3.

Remark 2.4.

Example 2.5.

Proposition 2.6 (Proposition 3.12 in [9]).

Example 2.7.

2.2. Tangent Cones

Corollary 2.8 (Corollary 2.16 [3]).

Corollary 2.9 (Corollary 2.18 [3]).

Remark 2.10.

2.3. Relative multiplicities

Remark 2.11.

Definition 2.12.

Remark 2.13.

Proposition 2.14 (Proposition 3.5 in [9]).

Proposition 2.15 (Proposition 3.6 in [9]).

3. On the classification of real algebraic curves

Proposition 3.1.

Proof.

3.1. Normal forms for the classification at infinity

Proposition 3.2.

Proof.

Remark 3.3.

Example 3.4.

3.2. Realization of the invariant k​(⋅,∞)k(\cdot,\infty)

Definition 3.5.

Definition 3.6.

Proposition 3.7.

Proof.

3.3. Some considerations on the global case

Example 3.8.

Definition 3.9.

Proposition 3.10.

Proof.

References

3.2. Realization of the invariant $k(\cdot,\infty)$