Classification of non-free Kleinian groups generated by two parabolic transformations

Hirotaka Akiyoshi Department of Mathematics
Graduate School of Science
Osaka City University
3-3-138, Sugimoto, Sumiyoshi-ku Osaka, 558-8585, Japan [email protected] , Ken’ichi Ohshika Department of Mathematics
Faculty of Science
Gakushuin University
Mejiro 1-5-1, Toshima-ku, 171-8588, Japan [email protected] , John Parker Department of Mathematical Sciences
Durham University, Science Laboratories
South Road, Durham, DH1 3LE, United Kingdom [email protected] , Makoto Sakuma Department of Mathematics
Faculty of Science
Hiroshima University
Higashi-Hiroshima, 739-8526, Japan [email protected] and Han Yoshida National Institute of Technology, Nara College
22 Yata-cho, Yamatokoriyama, Nara, 639-1058, Japan [email protected]

Abstract.

We give a full proof to Agol’s announcement on the classification of non-free Kleinian groups generated by two parabolic transformations.

2010 Mathematics Subject Classification:

Primary 57M50, Secondary 57M25

1. Introduction

Motivated by knot theory, Riley studied Kleinian groups generated by two parabolic transformations (see [44, 45, 46, 47, 48]). In particular, the construction of the complete hyperbolic structure on the figure-eight knot complement [45] inspired Thurston to establish the uniformisation theorem of Haken manifolds. The space of marked subgroups of $\mbox{$\mathrm{PSL}$}(2,\mathbb{C})$ generated by two non-commuting parabolic transformations is parametrised by a non-zero complex number. There is an open set, ${\mathcal{R}}$ , called the Riley slice of Schottky space, of Kleinian groups of this type that are free and discrete, and for which the quotient of the domain of discontinuity is a four times punctured sphere. For every group in ${\mathcal{R}}$ , the Klein manifold (the quotient of union of the hyperbolic space and the domain of discontinuity) is homeomorphic to the complement of the 2-strand trivial tangle. Keen and Series [29] studied the Riley slice by applying their theory of pleating rays, and it was supplemented by Komori and Series [31]. Motivated by knot theory, Akiyoshi, Sakuma, Wada and Yamashita [6] studied the combinatorial structures of the Ford domains, by extending Jorgensen’s work [28] on punctured torus groups, which leads to a natural tessellation of ${\mathcal{R}}$ (see Figure 0.2b in [6]). Ohshika and Miyachi [42] proved that the closure of ${\mathcal{R}}$ is equal to the space of marked Kleinian groups with two parabolic generators which are free and discrete. Building on his joint work [24], [26] and [36] with Gehring, Hinkkanen and Marshall, respectively, Martin [35] identified the exterior of ${\mathcal{R}}$ as the Julia set of a certain semigroup of polynomials and proved a “supergroup density theorem” for groups in the exterior of ${\mathcal{R}}$ . The problem to detect freeness and non-freeness of (not necessarily discrete) groups generated by two non-commuting parabolic transformations has attracted attention of various researchers (see [33, 23, 56, 30] and references therein).

In this paper, we are interested in Kleinian groups that are in the complement of the closure of ${\mathcal{R}}$ , namely the groups that are discrete but not free. The essential simple loops on the boundary of the complement of the 2-strand trivial tangle, which are not null homotopic in the ambient space, are parametrised by a slope $r$ in $\mathbb{Q}/2\mathbb{Z}$ . The Heckoid groups, introduced by Riley [47] and formulated by Lee and Sakuma [32] following Agol [2], are Kleinian groups with two parabolic generators in which the element corresponding to the curve $\alpha_{r}$ of slope $r$ has finite order. The most extreme case is the group $G(r)$ where this element is the identity, in which case, the quotient of hyperbolic space by this group is the complement of a 2-bridge knot or link.

In [1, Theorem 4.3], Adams proved that a non-free and torsion-free Kleinian group $\Gamma$ is generated by two parabolic transformations if and only if the quotient hyperbolic manifold $\mathbb{H}^{3}/\Gamma$ is homeomorphic to the complement of a $2$ -bridge link $K(r)$ which is not a torus link. (We regard a knot as a one-component link.) This refines the result of Boileau and Zimmermann [11, Corollary 3.3] that a link in $S^{3}$ is a $2$ -bridge link if and only if its link group is generated by two meridians.

In 2002, Agol [2] announced the following classification theorem of non-free Kleinian groups generated by two parabolic transformations, which generalises Adams’ result. The main purpose of this paper is to give a full proof to this theorem.

Theorem 1.1.

A non-free Kleinian group $\Gamma$ is generated by two non-commuting parabolic elements if and only if one of the following holds.

(1)

$\Gamma$ is conjugate to the hyperbolic $2$ -bridge link group, $G(r)$ , for some rational number $r=q/p$ , where $p$ and $q$ are coprime integers such that $q\not\equiv\pm 1\pmod{p}$ .
(2)

$\Gamma$ is conjugate to the Heckoid group, $G(r;n)$ , for some $r\in\mathbb{Q}$ and some $n\in\frac{1}{2}\mathbb{N}_{\geq 3}$ .

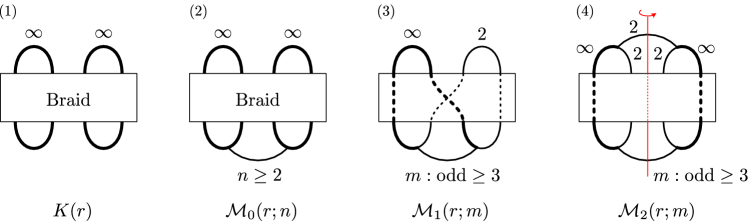
Refer to caption — Figure 1. Weighted graphs representing $2$ -bridge links and Heckoid orbifolds, where the thick edges with weight $\infty$ correspond to parabolic loci and thin edges with integral weights represent the singular set. See Definition 3.4 for the precise description of the weighted graphs.

In the remainder of the introduction, we explain the meaning of the theorem more precisely.

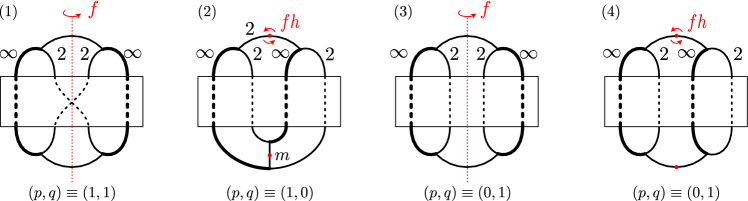
Recall that a $2$ -bridge link is a knot or a two-component link which is represented by a diagram in the $x$ - $y$ plane that has two maximal points and two minimal points with respect to the height function determined by the $y$ -coordinate. We may assume that the two maximal points and the two minimal points, respectively, have the same $y$ -coordinates. Such a diagram gives a plait (or plat) representation of the $2$ -bridge link consisting of two upper bridges, two lower bridges, and a $4$ -strand braid connecting the upper and lower bridges (see Figure 1(1)). The $2$ -bridge links are parametrized by the set $\mathbb{Q}\cup\{\infty\}$ , and the $2$ -bridge link corresponding to $r\in\mathbb{Q}\cup\{\infty\}$ is denoted by $K(r)$ and is called the $2$ -bridge link of slope $r$ (see Section 2 for the precise definition). If $r=\infty$ then $K(r)$ is the $2$ -component trivial link, and if $r\in\mathbb{Z}$ then $K(r)$ is the trivial knot. If $r=q/p\in\mathbb{Q}$ , where $p$ and $q$ are coprime integers, then $K(q/p)$ is hyperbolic, i.e., $S^{3}-K(r)$ admits a complete hyperbolic structure of finite volume, if and only if $q\not\equiv\pm 1\pmod{p}$ . In this case, there is a torsion-free Kleinian group $\Gamma$ , unique up to conjugation, such that $\mathbb{H}^{3}/\Gamma$ is homeomorphic to the link complement $S^{3}-K(r)$ as oriented manifold. We denote the Kleinian group $\Gamma$ , by $G(r)$ , and call it the hyperbolic $2$ -bridge link group of slope $r$ .

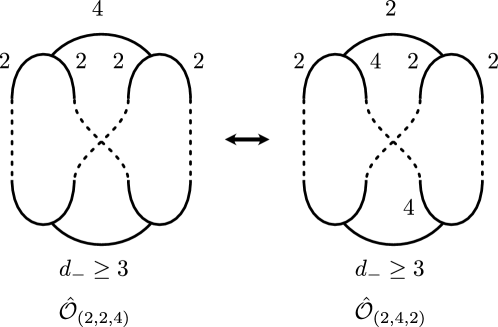
The Heckoid groups were first introduced by Riley [47] as an analogy of the classical Hecke groups considered by Hecke [25]. The topological structure of their quotient orbifolds was worked out by Lee and Sakuma [32], following the description by Agol [2]. Specifically, they showed that the Heckoid groups are the orbifold fundamental groups of the Heckoid orbifolds illustrated in Figure 1(2)-(4). (See [7, 10, 19] for basic terminologies and facts concerning orbifolds.) These figures illustrate weighted graphs $(S^{3},\Sigma,w)$ whose explicit descriptions are given by Definition 3.4. For each weighted graph $(S^{3},\Sigma,w)$ in the figure, let $(M_{0},P)$ be the pair of a compact $3$ -orbifold $M_{0}$ and a compact $2$ -suborbifold $P$ of $\partial M_{0}$ determined by the rules described below. Let $\Sigma_{\infty}$ be the subgraph of $\Sigma$ consisting of the edges with weight $\infty$ , and let $\Sigma_{s}$ be the subgraph of $\Sigma$ consisting of the edges with integral weight.

(1)

The underlying space $|M_{0}|$ of the orbifold $M_{0}$ is the complement of an open regular neighbourhood of the subgraph $\Sigma_{\infty}$ .
(2)

The singular set of $M_{0}$ is $\Sigma_{0}:=\Sigma_{s}\cap|M_{0}|$ , where the index of each edge of the singular set is given by the weight $w(e)$ of the corresponding edge $e$ of $\Sigma_{s}$ .
(3)
For an edge $e$ of $\Sigma_{\infty}$ , let $P$ be the $2$ -suborbifold of $\partial M_{0}$ defined as follows.
1. (a)
  
  In Figure 1(2), $P$ consists of two annuli in $\partial M_{0}$ whose cores, respectively, are meridians of the two edges of $\Sigma_{\infty}$ .
2. (b)
  
  In Figure 1(3), $P$ consists of an annulus in $\partial M_{0}$ whose core is a meridian of the single edge of $\Sigma_{\infty}$ .
3. (c)
  
  In Figure 1(4), $P$ consists of two copies of the annular orbifold $D^{2}(2,2)$ (the $2$ -orbifold with underlying space the disc and with two cone points of index $2$ ) in $\partial M_{0}$ each of which is bounded by a meridian of an edge of $\Sigma_{\infty}$ .

By [32, Lemmas 6.3 and 6.6], the orbifold pair $(M_{0},P)$ is a Haken pared orbifold (see Definition 3.1 or [10, Definition 8.3.7]) and admits a unique complete hyperbolic structure, which is geometrically finite (see Section 3 or [32, Proposition 6.7]). Namely there is a geometrically finite Kleinian group $\Gamma$ , unique up to conjugation, such that $M:=\mathbb{H}^{3}/\Gamma$ is isomorphic to the interior of the compact orbifold $M_{0}$ , such that $P$ represents the parabolic locus. The pair $(M_{0},P)$ is also regarded as a relative compactification of the pair consisting of a non-cuspidal part of $M$ and its boundary (see Section 3).

We denote the pared orbifold $\mathcal{M}:=(M_{0},P)$ by $\mathcal{M}_{0}(r;n)$ , $\mathcal{M}_{1}(r;m)$ , or $\mathcal{M}_{2}(r;m)$ according as it is described by the weighted graph in Figure 1(2), (3), or (4). We also denote the Kleinian group $\Gamma$ by $\pi_{1}(\mathcal{M})$ .

Then the assertion (2) of the main Theorem 1.1 is equivalent to the following assertion (2’)

(2’)

$\Gamma$ is conjugate to the Kleinian group $\pi_{1}(\mathcal{M})$ for some pared orbifold $\mathcal{M}=\mathcal{M}_{0}(r;n)$ , $\mathcal{M}_{1}(r;m)$ , or $\mathcal{M}_{2}(r;m)$ in Definition 3.4.

Agol [2] also announced the following classification of parabolic generating pairs of the groups in Theorem 1.1, which refines and extends Adams’ results that every hyperbolic $2$ -bridge link group has only finitely many parabolic generating pairs [1, Corollary 4.1] and that the figure-eight knot group has precisely two parabolic generating pairs up to equivalence [1, Corollary 4.6].

Theorem 1.2.

(1) If $\Gamma$ is a hyperbolic $2$ -bridge link group, then it has precisely two parabolic generating pairs, up to equivalence.

(2) If $\Gamma$ is a Heckoid group, then it has a unique parabolic generating pair, up to equivalence.

Here, by a parabolic generating pair of a Kleinian group $\Gamma$ , we mean an unordered pair $\{\alpha,\beta\}$ of parabolic transformations $\alpha$ and $\beta$ that generate $\Gamma$ . Two parabolic generating pairs $\{\alpha,\beta\}$ and $\{\alpha^{\prime},\beta^{\prime}\}$ are said to be equivalent if $\{\alpha^{\prime},\beta^{\prime}\}$ is equal to $\{\alpha^{\epsilon_{1}},\beta^{\epsilon_{2}}\}$ for some $\epsilon_{1},\epsilon_{2}\in\{\pm 1\}$ up to simultaneous conjugacy. In the companion [4] of this paper by Shunsuke Aimi, Donghi Lee, Shunsuke Sakai and the fourth author, an alternative proof of the theorem is given.

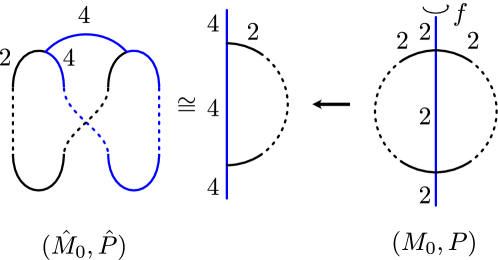
Theorems 1.1 and 1.2 are beautifully illustrated by a figure produced by Yasushi Yamashita upon request of Caroline Series, which is to be included in her article [52] in preparation. The figure is produced by using the results announced in [6, Section 3 of Preface]. (See also Figure 0.2b in [6], which was also produced by Yamashita.) For further properties of Heckoid groups, please see the article [5] in preparation.

This paper is organised as follows. In Section 2, we recall basic facts concerning $2$ -bridge links. In Section 3, we give the precise definitions of the Heckoid orbifolds and Heckoid groups. In Section 4, we give the classification of dihedral orbifolds, i.e., good orbifolds with dihedral orbifold fundamental groups (Theorem 4.1), which holds a key to the proof of the main theorem. In Section 5, we prove the relative tameness theorem for hyperbolic orbifolds (Theorem 5.1), following Bowditch’s proof of the tameness theorem for hyperbolic orbifolds ([15]). This theorem is used in the treatment of geometrically infinite two parabolic generator non-free Kleinian groups. In fact, it turns out there is no such groups. In Section 6, we introduce a convenient method for describing pared orbifolds (Convention 6.1) and the concept of an orbifold surgery (Definition 6.3), and then prove a simple but useful lemma for orbifold surgeries (Lemma 6.4). In Section 7, we follow Adams [1], and recall basic facts concerning two parabolic generator Kleinian groups, in particular an estimate of the length of parabolic generators with respect to the maximal cusp (Lemma 7.1). In Section 8, we give an outline of the proof of the main theorem. Sections 9, 10, and 11 are devoted to the proof of the main theorem. In the appendix, which consists of Sections 12 and 13, we give the classification of geometric dihedral orbifolds that is necessary for the proof Theorem 4.1.

Throughout this paper, we use the following notation.

Notation 1.3.

(1) For an orbifold ${\mathcal{O}}$ , the symbol $\pi_{1}({\mathcal{O}})$ denotes the orbifold fundamental group of ${\mathcal{O}}$ , $H_{1}({\mathcal{O}})$ denotes the abelianisation of $\pi_{1}({\mathcal{O}})$ , and $H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ denotes $H_{1}({\mathcal{O}})\otimes\mathbb{Z}_{2}$ .

(2) For a natural number $n$ , $\mathbb{Z}_{n}$ denotes the cyclic group (or the ring) $\mathbb{Z}/n\mathbb{Z}$ of order $n$ , and $(\mathbb{Z}_{n})^{\times}$ denotes the unit group of the ring $\mathbb{Z}/n\mathbb{Z}$ .

(3) By a dihedral group, we mean a group generated by two elements of order $2$ . Thus it is isomorphic to the group $D_{n}:=\langle a,b\,|\,a^{2},b^{2},(ab)^{n}\rangle$ for some $n\in\mathbb{N}\cup\{\infty\}$ . Note that $D_{n}$ has order $2n$ or $\infty$ according to whether $n\in\mathbb{N}$ or $n=\infty$ . Note also that the order $2$ cyclic group $D_{1}$ is also regarded as a dihedral group.

Acknowledgement. M.S. would like to thank Ian Agol for sending the slide of his talk [2], encouraging him (and any of his collaborators) to write up the proof, and describing key ideas of the proof. He would also like to thank Michel Boileau for enlightening conversation in an early time. His sincere thanks also go to all the other authors for joining the project to give a proof to Agol’s announcement. J.P. would like to thank Sadayoshi Kojima for supporting his trip to Japan. H.A. was supported by JSPS Grants-in-Aid 19K03497. K.O. was supported by JSPS Grants-in-Aid 17H02843 and 18KK0071. M.S. was supported by JSPS Grants-in-Aid 15H03620.

2. Basic facts concerning $2$ -bridge links

In this section, we recall basic facts concerning $2$ -bridge links, which we use in the definitions of the Heckoid orbifolds and the Heckoid groups. The description of $2$ -bridge links given in this section is a mixture of those in [14, 51].

Let ${\mathcal{J}}$ be the group of isometries of the Euclidean plane $\mathbb{R}^{2}$ generated by the $\pi$ -rotations around the points in $\mathbb{Z}^{2}$ . Set $(\mbox{\boldmath$S$}^{2},\mbox{\boldmath$P$}^{0})=(\mathbb{R}^{2},\mathbb{Z}^{2})/{\mathcal{J}}$ and call it the Conway sphere. Then $\mbox{{\boldmath$P$}}^{0}$ consists of four points in the $2$ -sphere $\mbox{\boldmath$S$}^{2}$ . Let $\check{\mbox{\boldmath$S$}}^{2}:=\mbox{\boldmath$S$}^{2}-\mbox{{\boldmath$P$}}^{0}$ be the complementary $4$ -times punctured sphere. For each $s\in\mathbb{Q}\cup\{\infty\}$ , let $\alpha_{s}$ as be the simple loop in $\check{\mbox{\boldmath$S$}}^{2}$ obtained as the projection of a line in $\mathbb{R}^{2}-\mathbb{Z}^{2}$ of slope $s$ . Then $\alpha_{s}$ is essential in $\check{\mbox{\boldmath$S$}}^{2}$ , i.e., it does not bound a disc nor a once-punctured disc in $\check{\mbox{\boldmath$S$}}^{2}$ . Conversely, any essential simple loop in $\check{\mbox{\boldmath$S$}}^{2}$ is isotopic to $\alpha_{s}$ for a unique $s\in\mathbb{Q}\cup\{\infty\}$ : we call $s$ the slope of the essential loop. For each $s\in\mathbb{Q}\cup\{\infty\}$ , let $\delta_{s}$ be the pair of mutually disjoint arcs in $\mbox{\boldmath$S$}^{2}$ with $\partial\delta_{s}=\mbox{{\boldmath$P$}}^{0}$ , obtained as the image of the union of the lines in $\mathbb{R}^{2}$ which intersect $\mathbb{Z}^{2}$ . Note that the union $\delta_{0/1}\cup\delta_{1/0}$ is a circle in $\mbox{\boldmath$S$}^{2}$ containing $\mbox{{\boldmath$P$}}^{0}$ , which divides $\mbox{\boldmath$S$}^{2}$ into two discs $\mbox{\boldmath$S$}^{2}_{+}:=pr([0,1]\times[0,1])$ and $\mbox{\boldmath$S$}^{2}_{-}:=pr([1,2]\times[0,1])$ , where $pr:\mathbb{R}^{2}\to\mbox{\boldmath$S$}^{2}$ is the projection.

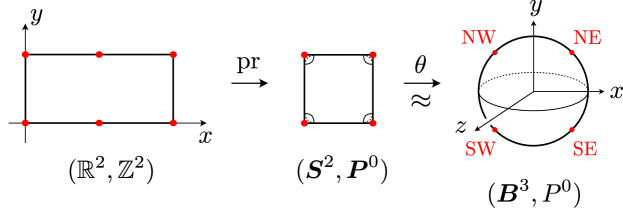
Let $\mbox{\boldmath$B$}^{3}:=\{(x,y,z)\in\mathbb{R}^{3}\,|\,x^{2}+y^{2}+z^{2}\leq 2\}$ be the round $3$ -ball in $\mathbb{R}^{3}\subset\mathbb{R}^{3}\cup\{\infty\}\cong S^{3}$ , whose boundary contains the set $P^{0}$ consisting of the four marked points

\mbox{$\mathrm{SW}$}:=(-1,-1,0),\quad\mbox{$\mathrm{SE}$}:=(1,-1,0),\quad\mbox{$\mathrm{NE}$}:=(1,1,0),\quad\mbox{$\mathrm{NW}$}:=(-1,1,0).

Fix a homeomorphism $\theta:(\mbox{\boldmath$S$}^{2},\mbox{\boldmath$P$}^{0})\to(\partial\mbox{\boldmath$B$}^{3},P^{0})$ satisfying the following conditions (see Figure 2).

(1)

$\theta$ maps the quadruple $(pr(0,0),pr(1,0),pr(1,1),pr(0,1))$ to the quadruple $(\mbox{$\mathrm{SW}$},\mbox{$\mathrm{SE}$},\mbox{$\mathrm{NE}$},\mbox{$\mathrm{NW}$})$ .
(2)

$\theta$ maps the circle $\delta_{0/1}\cup\delta_{1/0}$ to the equatorial circle $\partial\mbox{\boldmath$B$}^{3}\cap(\mathbb{R}^{2}\times\{0\})$ , and maps the hemispheres $\mbox{\boldmath$S$}^{2}_{+}$ and $\mbox{\boldmath$S$}^{2}_{-}$ onto the hemispheres $\partial\mbox{\boldmath$B$}^{3}\cap(\mathbb{R}^{2}\times\mathbb{R}_{\geq 0})$ to $\partial\mbox{\boldmath$B$}^{3}\cap(\mathbb{R}^{2}\times\mathbb{R}_{\leq 0})$ , respectively.
(3)

$\theta$ is equivariant with respect to the natural $(\mathbb{Z}_{2})^{2}$ -actions on $(\mbox{\boldmath$S$}^{2},\mbox{\boldmath$P$}^{0})$ and $(\partial\mbox{\boldmath$B$}^{3},P^{0})$ . Here the natural $(\mathbb{Z}_{2})^{2}$ -action on $(\mbox{\boldmath$S$}^{2},\mbox{\boldmath$P$}^{0})$ is that which lifts to the group of isometries of the Euclidean plane $\mathbb{R}^{2}$ generated by the $\pi$ -rotations around the points in $(\frac{1}{2}\mathbb{Z})^{2}$ , and the natural $(\mathbb{Z}_{2})^{2}$ -action on $(\partial\mbox{\boldmath$B$}^{3},P^{0})$ is that generated by the $\pi$ -rotations about the coordinate axes of $\mathbb{R}^{3}$ .

We identify $(\partial\mbox{\boldmath$B$}^{3},P^{0})$ with $(\mbox{\boldmath$S$}^{2},\mbox{\boldmath$P$}^{0})$ through the homeomorphism $\theta$ . Thus for $s\in\mathbb{Q}\cup\{\infty\}$ , $\alpha_{s}$ is regarded as an essential simple loop in $\partial\mbox{\boldmath$B$}^{3}-P^{0}$ , and $\delta_{s}$ is regarded as a union of two disjoint arcs in $\partial\mbox{\boldmath$B$}^{3}$ such that $\partial\delta_{s}=P^{0}$ . Moreover, we can choose $\alpha_{s}$ and $\delta_{s}$ so that they are $(\mathbb{Z}_{2})^{2}$ -invariant.

For a rational number $r=q/p\in\mathbb{Q}\cup\{\infty\}$ , let $t(r)$ be a pair of arcs properly embedded in $\mbox{\boldmath$B$}^{3}$ such that $t(r)\cap\partial\mbox{\boldmath$B$}^{3}=\partial t(r)=P^{0}$ , which is obtained from $\delta_{r}$ by pushing its interior into $\operatorname{int}\mbox{\boldmath$B$}^{3}$ . The pair $(\mbox{\boldmath$B$}^{3},t(r))$ is called the rational tangle of slope $r$ . We may assume $t(r)$ is invariant by the natural $(\mathbb{Z}_{2})^{2}$ -action on $\mbox{\boldmath$B$}^{3}$ . In particular, the $x$ -axis intersects $t(r)$ transversely in two points: Let $\tau_{r}$ be the subarc of the $x$ -axis they bound, and call it the core tunnel of $(\mbox{\boldmath$B$}^{3},t(r))$ (see Figure 4). Two meridional circles of $t(r)$ near $\partial\tau_{r}$ together with a subarc of $\tau_{r}$ forms a graph in $\mbox{\boldmath$B$}^{3}-t(r)$ homeomorphic to a pair of eyeglasses. This determines a canonical generating meridian pair of the rank $2$ free group $\pi_{1}(\mbox{\boldmath$B$}^{3}-t(r))\cong\pi_{1}(\check{\mbox{\boldmath$S$}}^{2})/\langle\langle\alpha_{r}\rangle\rangle$ .

By gluing the boundaries of the rational tangles $(\mbox{\boldmath$B$}^{3},t(\infty))$ and $(\mbox{\boldmath$B$}^{3},t(r))$ by the identity map, we obtain a link in the $3$ -sphere: we denote it by $(S^{3},K(r))$ , and call it the $2$ -bridge link of slope $r=q/p$ . The number of components, $|K(r)|$ , of $K(r)$ is one or two (i.e., $K(r)$ is a knot or a two-component link) according to whether the denominator $p$ is odd or even. The images of the core tunnels $\tau_{\infty}$ and $\tau_{r}$ in $(S^{3},K(r))$ are called the upper tunnel and the lower tunnel of $K(r)$ , respectively. We denote them by $\tau_{+}$ and $\tau_{-}$ , respectively. The canonical generating meridian pairs of $\pi_{1}(\mbox{\boldmath$B$}^{3}-t(\infty))$ and $\pi_{1}(\mbox{\boldmath$B$}^{3}-t(r))$ descend to generating meridian pairs of the link group $\pi_{1}(S^{3}-K(r))\cong\pi_{1}(\check{\mbox{\boldmath$S$}}^{2})/\langle\langle\alpha_{\infty},\alpha_{r}\rangle\rangle$ : we call them the upper meridian pair and the lower meridian pair, respectively.

When we need to care about the orientation of the ambient $3$ -sphere $S^{3}$ , we regard $(S^{3},K(r))$ as being obtained from $(-\mbox{\boldmath$B$}^{3},t(\infty))$ and $(\mbox{\boldmath$B$}^{3},t(r))$ , where $\mbox{\boldmath$B$}^{3}$ inherits the standard orientation of $\mathbb{R}^{3}$ . In other words, we identify the ambient $3$ -sphere $S^{3}$ with the one-point compactification $\mathbb{R}^{3}\cup\{\infty\}$ of $\mathbb{R}^{3}$ , in such a way that the $\mbox{\boldmath$B$}^{3}$ containing $t(r)$ is identified with the original round ball $\mbox{\boldmath$B$}^{3}$ via the identity map, whereas the $\mbox{\boldmath$B$}^{3}$ containing $t(\infty)$ is identified with $\operatorname{cl}(\mathbb{R}^{3}\cup\{\infty\}-\mbox{\boldmath$B$}^{3})$ via the inversion $\iota$ in $\partial\mbox{\boldmath$B$}^{3}$ . Thus $K(r)=t(r)\cup\iota(t(\infty))\subset\mathbb{R}^{3}\cup\{\infty\}=S^{3}$ . Under this orientation convention, a regular projection is read from the continued fraction expansion

in such a way that $a_{i}$ corresponds to the $a_{i}$ right-hand or left-hand half-twists according to whether $i$ is odd or even (see Figure 3).

The natural $(\mathbb{Z}_{2})^{2}$ -actions on $(\mbox{\boldmath$B$}^{3},t(\infty))$ and $(\mbox{\boldmath$B$}^{3},t(r))$ can be glued to produce a $(\mathbb{Z}_{2})^{2}$ -action on $(S^{3},K(r))$ . Let $f$ and $h$ be the generators of the action whose restrictions to $(\mbox{\boldmath$B$}^{3},t(\infty)))$ are the $\pi$ -rotations about the $y$ -axis and $x$ -axis, respectively (see Figure 4). We call $f$ , $h$ , and $fh$ , respectively, the vertical involution, the horizontal involution, and the planar involution of $K(r)$ . They are characterized by the following properties.

(1)

$\operatorname{Fix}(h)$ contains $\tau_{+}$ , whereas each of $\operatorname{Fix}(f)$ and $\operatorname{Fix}(fh)$ intersects $\tau_{+}$ transversely in a single point.
(2)

The horizontal simple loop $\alpha_{0}$ in $\partial(\mbox{\boldmath$B$}^{3}-t(\infty))$ is mapped by $f$ to itself preserving orientation, and it is mapped by $fh$ to itself reversing orientation.

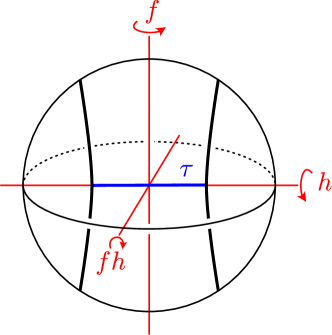
If the rational number $r=q/p$ satisfies the congruence $q^{2}\equiv 1\pmod{p}$ , then $K(r)$ admits an additional orientation-preserving symmetry which interchanges $(\mbox{\boldmath$B$}^{3},t(\infty))$ and $(\mbox{\boldmath$B$}^{3},t(r))$ . For a description of such symmetries, see e.g. [4, Sections 4 and 6], [49, Section 3].

We finally recall the classification theorem for $2$ -bridge links due to Schubert [53] (cf. [17, Chapter 12]).

Proposition 2.1.

For two rational numbers $r=q/p$ and $r^{\prime}=q^{\prime}/p^{\prime}$ , with $p$ and $p^{\prime}$ positive, the following holds.

(1) There is an orientation-preserving auto-homeomorphism $\varphi$ of $S^{3}$ which maps $K(r)$ to $K(r^{\prime})$ if and only if $p=p^{\prime}$ and either $q\equiv q^{\prime}\pmod{p}$ or $qq^{\prime}\equiv 1\pmod{p}$ . Moreover the following hold.

(a)

If $p=p^{\prime}$ and $q\equiv q^{\prime}\pmod{p}$ , then there there is an orientation-preserving auto-homeomorphism $\varphi$ of $S^{3}$ which maps $(K(r),\tau_{+},\tau_{-})$ to $(K(r^{\prime}),\tau_{+},\tau_{-})$ and respects the $(\mathbb{Z}_{2})^{2}$ -action. Moreover, the conjugate of the vertical involution of $K(r)$ by $\varphi$ is either the vertical or planar involution of $K(r^{\prime})$ , according to whether $q^{\prime}\equiv q\pmod{2p}$ or $q^{\prime}\equiv q+p\pmod{2p}$ .
(b)

If $p=p^{\prime}$ and $qq^{\prime}\equiv 1\pmod{p}$ , then there there is an orientation-preserving auto-homeomorphism of $S^{3}$ which maps $(K(r),\tau_{+},\tau_{-})$ to $(K(r^{\prime}),\tau_{-},\tau_{+})$ which respects the $(\mathbb{Z}_{2})^{2}$ -action.

(2) There is an orientation-reversing auto-homeomorphism $\varphi$ of $S^{3}$ which maps $K(r)$ to $K(r^{\prime})$ if and only if $p=p^{\prime}$ and either $q\equiv-q^{\prime}\pmod{p}$ or $qq^{\prime}\equiv-1\pmod{p}$ .

3. Heckoid orbifolds and Heckoid groups

In this section, we recall the definition of Heckoid orbifolds and Heckoid groups given by [32, Section 3].

Consider the quotient orbifold $(\mbox{\boldmath$B$}^{3}-t(\infty))/(\mathbb{Z}_{2})^{2}$ , where $(\mathbb{Z}_{2})^{2}$ is the natural action illustrated in Figure 4. Note that its boundary is identified with $\check{\mbox{\boldmath$S$}}^{2}/(\mathbb{Z}_{2})^{2}\cong S^{2}(2,2,2,\infty)$ , which is the quotient of $\mathbb{R}^{2}-\mathbb{Z}^{2}$ by the group generated by the $\pi$ -rotations around the points in $(\frac{1}{2}\mathbb{Z})^{2}$ . Note that $\pi_{1}(\check{\mbox{\boldmath$S$}}^{2})$ is identified with a normal subgroup of $\pi_{1}(\check{\mbox{\boldmath$S$}}^{2}/(\mathbb{Z}_{2})^{2})$ of index $4$ . For each $s\in\mathbb{Q}\cup\{\infty\}$ , let $\beta_{s}$ be the simple loop in $\check{\mbox{\boldmath$S$}}^{2}/(\mathbb{Z}_{2})^{2}$ obtained as the projection of a line in $\mathbb{R}^{2}-(\frac{1}{2}\mathbb{Z})^{2}$ of slope $s$ . The simple loop $\alpha_{s}$ in $\check{\mbox{\boldmath$S$}}^{2}$ doubly covers $\beta_{s}$ , and so we have $\alpha_{s}=\beta_{s}^{2}$ as conjugacy classes in $\pi_{1}(\check{\mbox{\boldmath$S$}}^{2}/(\mathbb{Z}_{2})^{2})$ .

For $r\in\mathbb{Q}$ and $m\in\mathbb{N}_{\geq 3}$ , consider the $3$ -orbifold $\mbox{\boldmath$B$}(\infty;2):=\operatorname{cl}(\mbox{\boldmath$B$}^{3}-N(t_{\infty}))/(\mathbb{Z}_{2})^{2}$ , attach a 2-handle orbifold $D^{2}(m)\times I$ to it along the simple loop $\beta_{r}$ . Since $\beta_{r}$ divides $\check{\mbox{\boldmath$S$}}^{2}/(\mathbb{Z}_{2})^{2}\cong S^{2}(2,2,2,\infty)$ into $D^{2}(2,2)$ and $D^{2}(2,\infty)$ , the resulting $3$ -orbifold has a spherical boundary $S^{2}(2,2,m)\cong S^{2}/D_{m}$ , where $D_{m}$ is the dihedral group of order $2m$ (cf. Notation 1.3(3)). Cap this spherical boundary with the $3$ -handle orbifold $B^{3}(2,2,m)\cong B^{3}/D_{m}$ , and denote the resulting $3$ -orbifold by $\mathcal{H}(r;m)$ . (Though this orbifold was denoted by ${\mathcal{O}}(r;m)$ in [32], we employ this symbol, because we use the symbol ${\mathcal{O}}$ to mainly denote spherical dihedral orbifolds.) Then we have

\pi_{1}(\mathcal{H}(r;m))\cong\pi_{1}(S^{2}(2,2,2,\infty))/\langle\langle\beta_{\infty}^{2},\beta_{r}^{m}\rangle\rangle.

Let $P$ be the annular orbifold $\operatorname{fr}N(t_{\infty})/(\mathbb{Z}_{2})^{2}\cong D^{2}(2,2)$ on $\partial\mathcal{H}(r;m)$ , and continue to denote the orbifold pair $(\mathcal{H}(r;m),P)$ by the symbol $\mathcal{H}(r;m)$ .

In [32, Section 6], it is proved that the orbifold pair $\mathcal{H}(r;m)$ is a pared $3$ -orbifold (see [10, Definition 8.3.7]).

Definition 3.1.

An orbifold pair $(M_{0},P)$ is a pared $3$ -orbifold if it satisfies the following conditions

(1)

$M_{0}$ is a compact, orientable, irreducible $3$ -orbifold which is very good (i.e., $M_{0}$ has a finite manifold cover).
(2)

$P\subset\partial M_{0}$ is a disjoint union of incompressible toric and annular $2$ -suborbifolds.
(3)

Every rank $2$ free abelian subgroup of $\pi_{1}(M_{0})$ is conjugate to a subgroup of some $\pi_{1}(P_{i})$ , where $P_{i}\subset P$ is a connected component.
(4)

Any properly embedded annular $2$ -suborbifold $(A,\partial A)$ of $(M_{0},P)$ whose boundary rests on essential loops in $P$ is parallel to $P$ .

It is also observed in [32, Section 6] that $\mathcal{H}(r;m)=(\mathcal{H}(r;m),P)$ is a Haken pared orbifold (see [10, Definitions 8.0.1 and 8.3.7]). Hence, by the hyperbolization theorem of Haken pared orbifolds [10, Theorem 8.3.9], the pared orbifold $\mathcal{H}(r;m)$ admits a geometrically finite complete hyperbolic structure, namely, the interior of the orbifold $\mathcal{H}(r;m)$ admits a geometrically finite complete hyperbolic structure such that $P$ represents the parabolic locus (see Section 5 for definitions).

Moreover, such a hyperbolic structure is unique, because the ends of the non-cuspidal part of $\mathcal{H}(r;m)$ are isomorphic to $(\mathrm{a\ turnover})\times[0,\infty)$ , which are quasi-isometrically rigid, and every orbifold homeomorphism between two geometrically finite structures preserving the parabolicity in both directions is isotopic to a quasi-isometry, as can be seen by the same argument as Marden’s theorem [34]. We denote the unique (up to conjugation) Kleinian group that uniformises the pared orbifold $\mathcal{H}(r;m)$ by the symbol $\pi_{1}(\mathcal{H}(r;m))$ .

Now the Heckoid groups and the Heckoid orbifolds are defined as follows [32, p.242 and Definition 3.2].

Definition 3.2.

For $r\in\mathbb{Q}$ and $n=\frac{m}{2}\in\frac{1}{2}\mathbb{N}_{\geq 3}$ , the Heckoid group $G(r;n)$ of slope $r$ and index $n$ is the Kleinian group that is obtained as the image of the natural homomorphism

\psi:\pi_{1}(\operatorname{cl}(\mbox{\boldmath$B$}^{3}-N(t_{\infty})))\to\pi_{1}(\operatorname{cl}(\mbox{\boldmath$B$}^{3}-N(t_{\infty}))/(\mathbb{Z}_{2})^{2})\to\pi_{1}(\mathcal{H}(r;m))<\mbox{$\mathrm{PSL}$}(2,\mathbb{C}).

The Heckoid orbifold $\mathcal{S}(r;n)$ of slope $r$ and index $n$ is the pared orbifold, that is obtained as the covering of the pared orbifold $\mathcal{H}(r;m)$ associated with the subgroup $G(r;n)<\pi_{1}(\mathcal{H}(r;m))$ . We also denote the Kleinian group $G(r;n)$ by $\pi_{1}(\mathcal{S}(r;n))$ .

Then we have the following proposition. (The main Theorem 1.1 implies that the converse to the first assertion of the proposition holds.)

Proposition 3.3.

For any $r\in\mathbb{Q}$ and $n=\frac{m}{2}\in\frac{1}{2}\mathbb{N}_{\geq 3}$ , the Heckoid group is a (non-free) Kleinian group with nontrivial torsion which is generated by two non-commuting parabolic transformations. Moreover, the image of the conjugacy class of the simple loop $\alpha_{r}$ in $G(r;n)$ is an elliptic transformation of rotation angle $\frac{2\pi}{n}=\frac{4\pi}{m}$ .

Proof.

Let $\{x,y\}$ be the canonical generating meridian pair of the rank $2$ free group $\pi_{1}(\operatorname{cl}(\mbox{\boldmath$B$}^{3}-N(t_{\infty})))$ (see Section 2). Then $G(r;n)$ is generated by the image $\{\psi(x),\psi(y)\}\subset\pi_{1}(\mathcal{H}(r;m))$ . Since $\pi_{1}(\mathcal{H}(r;m))$ is the Kleinian group which uniformises the pared orbifold $\mathcal{H}(r;m)$ , the generating pair of $G(r;n)$ consists of non-commuting parabolic transformations. Since $\alpha_{r}=\beta_{r}^{2}$ and since $\beta_{r}$ is a meridian of the singular set of $\mathcal{H}(r;n)$ of index $2n=m$ , it follows that $\psi(\alpha_{r})$ is an elliptic transformation of rotation angle $\frac{2\pi}{n}=\frac{4\pi}{m}$ . ∎

Next, we recall the topological description of the Heckoid orbifolds. In Definition 3.2, the Heckoid orbifold $\mathcal{S}(r;n)$ is defined as a covering of the pared orbifold $\mathcal{H}(r;m)$ . Their explicit topological description is given by [32, Propositions 5.2 and 5.3], which says that the Heckoid orbifold $\mathcal{S}(r;n)$ is isomorphic to one of the orbifold pairs depicted in Figure 1, that is specified by the following formula.

\displaystyle\mathcal{S}(r;n)\cong\begin{cases}\mathcal{M}_{0}(r;n)&\text{if $n\in\mathbb{N}_{\geq 2}$,}\\ \mathcal{M}_{1}(\hat{r};m)&\text{if $n=m/2$ for some odd $m>2$ and if $p$ is odd,}\\ \mathcal{M}_{2}(\hat{r};m)&\text{if $n=m/2$ for some odd $m>2$ and if $p$ is even,}\\ \end{cases}

where $\hat{r}$ is defined from $r=q/p$ by the following rule.

\hat{r}=\begin{cases}\frac{q/2}{p}&\text{if $p$ is odd and $q$ is even,}\\ \frac{(p+q)/2}{p}&\text{if $p$ is odd and $q$ is odd,}\\ \frac{q}{p/2}&\text{if $p$ is even.}\end{cases}

Thus the following precise definition of the orbifold pairs in Figure 1 gives an explicit topological picture of the Heckoid orbifold $\mathcal{S}(r;n)$ .

Definition 3.4.

(1) For $r\in\mathbb{Q}$ and for a positive integer $n\geq 2$ , $\mathcal{M}_{0}(r;n)$ denotes the orbifold pair determined by the weighted graph $(S^{3},K(r)\cup\tau_{-},w_{0})$ , where $w_{0}$ is given by

w_{0}(K(r))=\infty,\quad w_{0}(\tau_{-})=n.

(2) For $r=q/p\in\mathbb{Q}$ with $p$ odd and an odd integer $m\geq 3$ , $\mathcal{M}_{1}(r;m)$ denotes the orbifold pair determined by the weighted graph $(S^{3},K(r)\cup\tau_{-},w_{1})$ , where $w_{1}$ is given by the following rule. Let $J_{1}$ and $J_{2}$ be the edges of the graph $K(r)\cup\tau_{-}$ distinct from $\tau_{-}$ . Then

w_{1}(J_{1})=\infty,\quad w_{1}(J_{2})=2,\quad w_{1}(\tau_{-})=m.

(3) For $r=q/p\in\mathbb{Q}$ and an odd integer $m\geq 3$ , $\mathcal{M}_{2}(r;m)$ denotes the orbifold pair determined by the weighted graph $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-},w_{2})$ , where $w_{2}$ is given by the following rule. Let $J_{1}$ and $J_{2}$ be unions of two mutually disjoint edges of the graph $K(r)\cup\tau_{+}\cup\tau_{-}$ distinct from $\tau_{\pm}$ . Moreover, if $p$ is even, then both $J_{1}$ and $J_{2}$ are preserved by the vertical involution $f$ of $K(r)$ . (Thus $f$ interchanges the two components of each of $J_{1}$ and $J_{2}$ .) Then

w_{2}(J_{1})=\infty,\quad w_{2}(J_{2})=2,\quad w_{2}(\tau_{+})=2,\quad w_{2}(\tau_{-})=m.

In Defunition 3.4(3), the ‘identity’ $w_{2}(J_{1})=\infty$ means that $w_{2}(e)=\infty$ for each edge $e$ contained in $J_{1}$ . Similarly, $w_{2}(J_{2})=2$ means that $w_{2}(e)=2$ for each edge $e$ contained in $J_{2}$ . We employ this kind of convention throughout the paper.

Remark 3.5.

(1) Because of the $(\mathbb{Z}_{2})^{2}$ -symmetry of $2$ -bridge links, the choice of the edges $J_{1}$ and $J_{2}$ in (2) and (3) does not affect the isomorphism class of the resulting orbifolds (see [32, Remark 5.4]).

(2) Suppose $p$ is odd. Then, in the definition of $\mathcal{M}_{2}(r;m)$ , the disjointness condition of $J_{1}$ and $J_{2}$ determines the pair $(J_{1},J_{2})$ up to the horizontal involution $h$ of $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-})$ . Moreover, according to whether $q$ is odd or even, both $J_{1}$ and $J_{2}$ are preserved by $f$ or $fh$ , respectively (see Figure 5(1),(2)).

(3) Suppose $p$ is even. Then, in the definition of $\mathcal{M}_{2}(r;m)$ , the condition that both $J_{1}$ and $J_{2}$ are preserved by $f$ is not essential in the following sense. Let $J_{i,1}$ and $J_{i,2}$ be the components of $J_{i}$ for $i=1,2$ , such that $J_{1,1}\cap J_{2,1}=\emptyset$ and $J_{1,2}\cap J_{2,2}=\emptyset$ . Set $J_{1}^{\prime}=J_{1,1}\cup J_{2,1}$ and $J_{2}^{\prime}=J_{1,2}\cup J_{2,2}$ . Then $J_{1}^{\prime}$ and $J_{2}^{\prime}$ are unions of two mutually disjoint edges of the graph $K(r)\cup\tau_{+}\cup\tau_{-}$ distinct from $\tau_{\pm}$ , such that both $J_{1}^{\prime}$ and $J_{2}^{\prime}$ are preserved by the planar involution $fh$ , instead of the vertical involution $f$ (see Figure 5(3),(4)). Let $w_{2}^{\prime}$ be the weight function on the graph $K(r)\cup\tau_{+}\cup\tau_{-}$ defined by

w_{2}^{\prime}(J_{1}^{\prime})=\infty,\quad w_{2}^{\prime}(J_{2}^{\prime})=2,\quad w_{2}^{\prime}(\tau_{+})=2,\quad w_{2}^{\prime}(\tau_{-})=m.

Then $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-},w_{2}^{\prime})$ represents the orbifold $\mathcal{M}_{2}(r^{\prime};m)$ , where $r^{\prime}=(p+q)/p$ for $r=q/p$ . This follows from the fact that there is a homeomorphism from $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-})$ to $(S^{3},K(r^{\prime})\cup\tau_{+}\cup\tau_{-})$ sending $(\tau_{\pm},J_{1},J_{2})$ to $(\tau_{\pm},J_{1}^{\prime},J_{2}^{\prime})$ (see Proposition 2.1(1a)).

4. Classification of dihedral orbifolds

In this section, we give a classification of the dihedral orbifolds, which plays a key role in the proof of the main theorem. We refer to [8, 9, 19] for standard terminologies for orbifolds.

By using the the orbifold theorem, the geometrisation theorem of compact orientable $3$ -manifolds, and the classification of geometric dihedral orbifolds (see Appendix), we obtain the following classification of good orbifolds with dihedral orbifold fundamental groups.

Theorem 4.1.

Let ${\mathcal{O}}$ be a compact orientable $3$ -orbifold with nonempty singular set satisfying the following conditions.

(i)

${\mathcal{O}}$ does not contain a bad $2$ -suborbifold.
(ii)

Any component of $\partial{\mathcal{O}}$ is not spherical.
(iii)

$\pi_{1}({\mathcal{O}})$ is a dihedral group.

Then ${\mathcal{O}}$ is isomorphic to one of the following orbifolds.

(1)

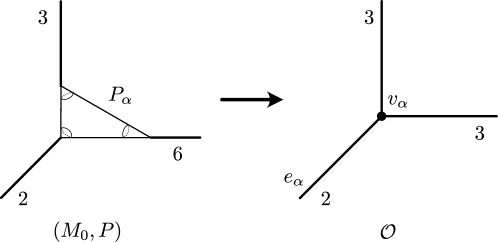
The spherical dihedral orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ represented by the weighted graph $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-},w)$ for some $r\in\mathbb{Q}$ and coprime positive integers $d_{+}$ and $d_{-}$ , where $w$ is given by the following rule (see Figure 6).

$w(K(r))=2,\quad w(\tau_{+})=d_{+},\quad w(\tau_{-})=d_{-}.$
(2)

The $S^{2}\times\mathbb{R}$ orbifold ${\mathcal{O}}(\infty)$ represented by the weighted graph $(S^{3},K(\infty),w)$ , where $w$ takes the value $2$ at each component of the $2$ -bridge link $K(\infty)$ of slope $\infty$ , i.e. the $2$ -component trivial link.
(3)

The $S^{2}\times\mathbb{R}$ orbifold ${\mathcal{O}}(\mathbb{RP}^{3},O)$ represented by the weighted graph $(\mathbb{RP}^{3},O,w)$ , where $O$ is the trivial knot in the projective $3$ -space $\mathbb{RP}^{3}$ with $w(O)=2$ .
(4)

The orbifold $D^{2}(2,2)\times I$ .

Remark 4.2.

For the orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ , if $d_{+}=1$ (resp. $d_{-}=1$ ), then $\tau_{+}$ (resp. $\tau_{-}$ ) does not belong to the singular set (cf. Convention 6.2(1)). In particular, ${\mathcal{O}}(r):={\mathcal{O}}(r;1,1)$ is the $\pi$ -orbifold associated with the $2$ -bridge link $K(r)$ in the sense of [11], i.e. the orbifold with underlying space $S^{3}$ and with singular set $K(r)$ , whose index is $2$ . In Adam’s classification of torsion-free Kleinian groups generated by two parabolic transformations [1, Theorem 4.3], the $\pi$ -orbifolds ${\mathcal{O}}(r)$ played a key role, whereas the orbifolds ${\mathcal{O}}(r;d_{+},d_{-})$ play the corresponding key role in this paper.

Proof.

Let ${\mathcal{O}}$ be a $3$ -orbifold satisfying the three conditions. We first treat the case where ${\mathcal{O}}$ is irreducible, i.e., any spherical $2$ -suborbifold of ${\mathcal{O}}$ bounds a discal $3$ -suborbifold (a quotient of a $3$ -ball by a finite orthogonal group). We can observe that ${\mathcal{O}}$ is topologically atoroidal as follows. Suppose on the contrary that ${\mathcal{O}}$ contains an essential toric suborbifold $F$ . Then the inclusion map induces an injective homomorphism from $\pi_{1}(F)$ into $\pi_{1}({\mathcal{O}})$ , as explained below. Since ${\mathcal{O}}$ does not contain a bad $2$ -suborbifold by the condition (i), ${\mathcal{O}}$ is very good, by [8, Corollary 1.3]. Thus by applying the equivariant loop theorem to the group action, $\pi_{1}(F)$ embeds into $\pi_{1}({\mathcal{O}})$ (see [9, Corollary 3.20]). This contradicts the fact that the dihedral group $\pi_{1}({\mathcal{O}})$ does not contain $\mathbb{Z}^{2}$ .

Hence, by the orbifold theorem [8, Corollary 1.2], ${\mathcal{O}}$ is geometric, i.e., either $\operatorname{int}{\mathcal{O}}$ admits one of Thurston’s geometry or ${\mathcal{O}}$ is a discal $3$ -orbifold. The latter possibility does not happen by the assumption (ii), and so $\operatorname{int}{\mathcal{O}}$ admits one of Thurston’s geometry. If the geometry is $S^{3}$ , then by Proposition 12.2, ${\mathcal{O}}$ is isomorphic to the orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ in (1). If the geometry is $S^{2}\times\mathbb{R}$ , then by Proposition 13.1, ${\mathcal{O}}$ is isomorphic to the orbifold ${\mathcal{O}}(\infty)$ in (2) or the orbifold ${\mathcal{O}}(\mathbb{RP}^{3},O)$ in (3). (But this does not happen, because these orbifolds are reducible whereas we currently assume that ${\mathcal{O}}$ is irreducible.) If the geometry is one of the remaining 6 geometries, then by Proposition 13.2, ${\mathcal{O}}$ is isomorphic to the orbifold $D^{2}(2,2)\times I$ in (4).

Next, we treat the case when ${\mathcal{O}}$ is reducible. Note that ${\mathcal{O}}$ does not contain a non-separating spherical $2$ -suborbifold, because $H_{1}({\mathcal{O}})$ is finite. Thus we do not need to worry about the paradoxical problems concerning spherical splitting of $3$ -orbifolds pointed out by Petronio [43]. By [43, Theorems 0.1], there is a finite system of spherical $2$ -suborbifolds $\mathcal{S}$ such that (a) no component of ${\mathcal{O}}-\mathcal{S}$ is punctured discal (a discal $3$ -orbifold minus regular neighbourhoods of a finite set) and (b) all prime factors of ${\mathcal{O}}$ (the orbifolds obtained from the components of ${\mathcal{O}}-\mathcal{S}$ by capping the boundary components with discal orbifolds) are irreducible. It should be noted that some prime component may be a manifold, i.e., its branching locus is empty. By the geometrisation theorem of compact orientable $3$ -manifolds (see e.g. [7]) and the the geometrisation theorem of compact orientable $3$ -orbifolds (see e.g. [9, Theorem 3.27]), each prime component of ${\mathcal{O}}$ admits a canonical decomposition into geometric pieces by a family of essential toric $2$ -orbifolds. In particular, each prime factor has a nontrivial orbifold fundamental group. Since the only nontrivial free product decomposition of a dihedral group is the decomposition of the infinite dihedral group $D_{\infty}$ into the free product $\mathbb{Z}_{2}*\mathbb{Z}_{2}$ , ${\mathcal{O}}$ is the connected sum (along a $2$ -sphere with empty branching set) of two irreducible $3$ -orbifolds ${\mathcal{O}}_{1}$ and ${\mathcal{O}}_{2}$ , such that $\pi_{1}({\mathcal{O}}_{i})\cong\mathbb{Z}_{2}$ . Since ${\mathcal{O}}_{i}$ is geometric, ${\mathcal{O}}_{i}$ is isomorphic to (a) the discal $3$ -orbifold $B^{3}/\mathbb{Z}_{2}$ , (b) the orbifold $(S^{3},O,w)$ , where $O$ is a trivial knot and $w(O)=2$ , or (c) $\mathbb{RP}^{3}$ . By condition (ii), ${\mathcal{O}}_{i}$ cannot be a discal orbifold. Since ${\mathcal{O}}={\mathcal{O}}_{1}\#{\mathcal{O}}_{2}$ has nonempty ramification locus, at least one of ${\mathcal{O}}_{i}$ is not isomorphic to $\mathbb{RP}^{3}$ . Hence, ${\mathcal{O}}$ is isomorphic to the orbifold $(S^{3},O,w)\#(S^{3},O,w)\cong{\mathcal{O}}(\infty)$ in (2) or the orbifold $(S^{3},O,w)\#\mathbb{RP}^{3}\cong{\mathcal{O}}(\mathbb{RP}^{3},O)$ in (3). ∎

Remark 4.3.

By considering the image of ${\mathcal{O}}(r;d_{+},d_{-})$ by a $\pi$ -rotation about a horizontal axis in Figure 6, we can interchange the role of $d_{+}$ and $d_{-}$ . To be precise, we can see from Proposition 2.1(1b) that ${\mathcal{O}}(q/p;d_{+},d_{-})\cong{\mathcal{O}}(q^{\prime}/p;d_{-},d_{+})$ if $qq^{\prime}\equiv 1\pmod{p}$ .

5. Relative tameness theorem for hyperbolic orbifolds

We first recall basic terminology for hyperbolic orbifolds, following [9, Chapter 6]. Let $\Gamma$ be a finitely generated Kleinian group and $M=\mathbb{H}^{3}/\Gamma$ the quotient hyperbolic orbifold. For a real number $\epsilon>0$ , the $\epsilon$ -thin part $M_{(0,\epsilon]}$ of $M$ is the set of all points $x\in M$ such that $d(\tilde{x},\gamma\tilde{x})\leq\epsilon$ for some lift $\tilde{x}$ of $x$ to $\mathbb{H}^{3}$ and some $\gamma\in\Gamma$ of order $>1/\epsilon$ (including $\infty$ ). By the Margulis Lemma, there is a constant $\mu>0$ , such that for any real number $\epsilon\in(0,\mu]$ , each component $X$ of $M_{(0,\epsilon]}$ is either a Margulis tube or a cuspidal end. Here a Margulis tube is a compact quotient of the $r$ -neighbourhood of a geodesic in $\mathbb{H}^{3}$ by an elementary subgroup of $\Gamma$ which preserves the geodesic, and a cuspidal end is the quotient of a horoball in $\mathbb{H}^{3}$ by an elementary parabolic subgroup of $\Gamma$ which preserves the horoball.

Topologically, a cuspidal end is a product $F\times[0,+\infty)$ , where $F$ is a Euclidean $2$ -orbifold. Thus we have the following possibilities for $F$ .

(1)

$F$ is the open annulus $S^{1}\times\mathbb{R}$ or $S^{2}(2,2,\infty)$ , the quotient of $S^{1}\times\mathbb{R}$ by an involution.
(2)

$F$ is the torus $T^{2}$ or $S^{2}(2,2,2,2)$ , the quotient of $T^{2}$ by an involution.
(3)

$F$ is $S^{2}(2,3,6)$ , $S^{2}(2,4,4)$ or $S^{2}(3,3,3)$ , the quotient of $T^{2}$ by a finite cyclic group action of order $6$ , $4$ or $3$ , respectively.

A cusp $F\times[0,+\infty)$ is said to be rigid if $F\cong S^{2}(2,3,6)$ , $S^{2}(2,4,4)$ or $S^{2}(3,3,3)$ . Otherwise it is said to be flexible. It is well-known that a cusp $F\times[0,+\infty)$ is rigid if and only if the holonomy representation of the orbifold fundamental group $\pi_{1}(F\times[0,+\infty)$ admits no nontrivial deformation (see [37, Proposition 1]).

Let $M^{\mathrm{cusp}}_{(0,\epsilon]}$ be the union of the cuspidal ends of $M_{(0,\epsilon]}$ , and let $M_{0}:=M-\operatorname{int}M^{\mathrm{cusp}}_{(0,\epsilon]}$ be the non-cuspidal part of $M$ . Then $P:=\partial M_{0}$ is a disjoint union of euclidean $2$ -orbifolds, and is called the parabolic locus of $M_{0}$ . Note that $M\cong\operatorname{int}M_{0}$ and that $P$ consists of (closed) toric orbifolds (closed $2$ -orbifolds obtained as quotients of the $2$ -dimensional torus) and open annular orbifolds (open $2$ -orbifolds obtained as quotients of the open annulus $S^{1}\times\mathbb{R}$ ).

The following theorem is an orbifold version of (the relative version of) the tameness theorem established by Agol [2] and Calegari-Gabai [18] (see also Soma [55] and Bowditch [15]).

Theorem 5.1.

Let $M=\mathbb{H}^{3}/\Gamma$ be a hyperbolic $3$ -orbifold with finitely generated orbifold fundamental group $\Gamma$ . Then there is a compact $3$ -orbifold $\bar{M}_{0}$ and a compact suborbifold $\bar{P}$ of $\partial\bar{M}_{0}$ , such that (i) $\operatorname{int}\bar{M}_{0}=\operatorname{int}M_{0}\cong M$ and (ii) the interior of $\bar{P}$ in $\partial\bar{M}_{0}$ is equal to $P=\partial M_{0}$ .

Proof.

We give a proof following the arguments of Bowditch [15, Section 6.6] (cf. [2, Lemma 14.3]). By Selberg’s lemma, $M$ admits a finite regular manifold cover, namely there is a complete hyperbolic manifold $N$ and a finite group $G$ of orientation-preserving isometries of $N$ such that $N/G\cong M$ . The inverse image, $N_{0}$ , of $M_{0}$ in $N$ forms a $G$ -invariant non-cuspidal part of $N$ , and we have $N_{0}/G\cong M_{0}$ . By the relative version of the tameness theorem [18, Theorem 7.3] (cf. [15, Section 6]), there is a compact $3$ -manifold $\bar{N}_{0}$ and a compact submanifold $\bar{Q}$ of $\partial\bar{N}_{0}$ , such that (i) $\operatorname{int}\bar{N}_{0}=\operatorname{int}N_{0}$ and (ii) the interior of $\bar{Q}$ in $\partial\bar{N}_{0}$ is equal to $\partial N_{0}$ . Let $D(N_{0})$ and be the double of $N_{0}$ along $\partial N_{0}$ . Then the action of $G$ on $N_{0}$ extends to an action on $D(N_{0})$ , and $D(N_{0})/G$ is isomorphic to the double, $D(M_{0})$ , of $M_{0}$ along $\partial M_{0}$ . Consider the double, $D(\bar{N}_{0})$ , of $\bar{N}_{0}$ along $\bar{Q}$ . Then $D(\bar{N}_{0})$ is a compact manifold with interior $D(N_{0})$ . By [40, Theorem 8.5], the action of $G$ on $D(N_{0})$ extends to an action on $D(\bar{N}_{0})$ , and $\operatorname{int}(D(\bar{N}_{0})/G)=D(N_{0})/G$ is identified with $D(M_{0})$ . Let $\bar{M}_{0}$ be the closure in $D(\bar{N}_{0})/G$ of one of the two copies of $M_{0}$ in $D(M_{0})\subset D(\bar{N}_{0})/G$ , and let $\bar{P}$ be the image of $\bar{Q}\subset D(\bar{N}_{0})$ in $D(\bar{N}_{0})/G$ . Then the pair $(\bar{M}_{0},\bar{P})$ satisfies the desired conditions. ∎

The above theorem together with the following theorem enables us to reduce the treatment of geometrically infinite case to that of geometrically finite case.

Theorem 5.2.

Under the setting of Theorem 5.1, $(\bar{M}_{0},\bar{P})$ is a pared orbifold. Moreover, the pared orbifold $(\bar{M}_{0},\bar{P})$ admits a geometrically finite complete hyperbolic structure. Namely, there is a geometrically finite Kleinian group $\Gamma^{\prime}$ such that (i) the orbifold $\mathbb{H}^{3}/\Gamma^{\prime}$ is isomorphic to the orbifold $\operatorname{int}\bar{M}_{0}\cong M$ and (ii) $P$ is the parabolic locus of $\Gamma^{\prime}$ .

Proof.

The first assertion that $(\bar{M}_{0},\bar{P})$ is a pared orbifold can be proved as in the proof of [41, Corollary 6.10 in Chapter V]. So we prove the second assertion that the pared orbifold $(\bar{M}_{0},\bar{P})$ admits a geometrically finite hyperbolic structure. If the orbifold $\bar{M}_{0}$ is Haken in the sense of [10, Definition 8.0.1] then it follows from [10, Theorem 8.3.9] that the pared orbifold $(\bar{M}_{0},\bar{P})$ admits a geometrically finite hyperbolic structure, as desired. So we may assume the orbifold $\bar{M}_{0}$ is non-Haken, i.e., either it contains no essential $2$ -suborbifold or it contains an essential turnover. In the first case, $\partial M_{0}$ consists only of turnovers by [9, Proposition 9.4]. This implies that every end of $M\cong\operatorname{int}\bar{M}_{0}$ has a neighbourhood isomorphic to the product of $(\mbox{a turnover})\times[0,\infty)$ . Since a hyperbolic turnover is always realised by a totally geodesic surface, each end has a neighbourhood containing no closed geodesics. Thus every end of the hyperbolic orbifold $M$ is geometrically finite and rigid. Thus $M$ admits a unique complete hyperbolic structure, and it is geometrically finite. In the latter case, by the turnover splitting theorem [9, Theorem 4.8], $\bar{M}_{0}$ admits a decomposition by a finite disjoint family of essential hyperbolic turnovers into Haken orbifolds and small orbifolds. By the orbifold theorem, each piece admits a geometrically finite hyperbolic structure, respecting the parabolic locus. By gluing these hyperbolic structures along the totally geodesic hyperbolic turnovers, we obtain a geometrically finite hyperbolic structure on $(\bar{M}_{0},\bar{P})$ . ∎

Remark 5.3.

In [2], Agol suggested to prove the last assertion of Theorem 5.2 by using a relative version of the work of Feighn and Mess [22, Theorem 2] which proves the existence of a compact core of an orbifold $M=\mathbb{H}^{3}/\Gamma$ with a finitely generated orbifold fundamental group $\Gamma$ . Such a relative version is proved by Matsuzaki [37, Lemma 2] under the assumption that $\Gamma$ is indecomposable (over finite cyclic groups and with respect to the parabolic subgroups) in the sense of [37, Definition in p.26]. But we are not sure if non-free two-parabolic generator Kleinian groups satisfy this property. Though Theorem 5.1, which is proved by using the deep tameness theorem, of course, guarantees the existence of a relative core of complete hyperbolic orbifolds with finitely generated fundamental groups, we are not sure if more ‘elementary’ proof is possible.

6. Orbifold surgery

In this section, we introduce a convenient method for representing pared orbifolds by weighted graphs, generalising the convention in the introduction (Convention 6.1). Then we introduce the concept of an orbifold surgery (Definition 6.3), which is a key ingredient of the proof of the main theorem, and prove a basic Lemma 6.4 for the orbifold surgery. At the end of this section, we also state another basic Lemma 6.5 concerning the $\mathbb{Z}_{2}$ -homology of an orbifold, which is repeatedly used in the proof of the main theorem.

Convention 6.1.

Consider a triple $(W,\Sigma,w)$ , where $W$ is a compact oriented $3$ -manifold, $\Sigma$ is a finite trivalent graph properly embedded in $W$ , and $w$ is a function on the edge set of $\Sigma$ which takes value in $\mathbb{N}_{\geq 2}\cup\{\infty\}$ . Here, a loop component of $\Sigma$ is regarded as a single edge, $\Sigma\cap\partial M$ is the set of degree $1$ vertices of $\Sigma$ , and all other vertices have degree $3$ . For each edge $e$ of $\Sigma$ , its value $w(e)$ by $w$ is called the weight of the edge. We call the triple $(W,\Sigma,w)$ a weighted graph and call $w$ the weight function of the weighted graph. Let $\Sigma_{\infty}$ be the subgraph of $\Sigma$ consisting of the edges with weight $\infty$ , and let $\Sigma_{s}$ be the subgraph of $\Sigma$ consisting of the edges with integral weight.

We regard each component, $F$ , of $\partial W$ as a $2$ -orbifold as follows: the underling space is the complement of an open regular neighbourhood of $F\cap\Sigma_{\infty}$ in $F$ , and the singular set is $F\cap\Sigma_{s}$ , where the index of a singular point is given by the weight of the corresponding edge of $\Sigma_{s}$ . We assume that the following condition (SC) is satisfied.

(SC)

For any sphere component $S$ of $\partial W$ , the corresponding $2$ -orbifold is not a bad orbifold, a spherical orbifold, a discal orbifold, nor an annulus. Namely, (i) $|S\cap W|\geq 3$ and (ii) if $|S\cap W|=3$ then $\sum_{i=1}^{3}\frac{1}{w(e_{i})}\leq 1$ , where $e_{i}$ ( $i=1,2,3$ ) are the (germs of) edges of $\Sigma$ which have an endpoint in $F$ .

A trivalent vertex $v$ of $\Sigma$ is said to be spherical, euclidean or hyperbolic according to whether $\sum_{i=1}^{3}\frac{1}{w(e_{i})}$ is bigger than, equal to, or smaller than $1$ , where $e_{i}$ ( $i=1,2,3$ ) are the (germs of) edges incident on $v$ . Let $V_{E}$ (resp. $V_{H}$ ) be the set of the euclidean (resp. hyperbolic) vertices.

Let $M_{0}$ be the complement of an open regular neighbourhood of $\Sigma_{\infty}\cup V_{E}\cup V_{H}$ in $M$ . Then $M_{0}$ has the structure of an orbifold, with singular set $\Sigma_{0}:=M_{0}\cap\Sigma_{s}$ , where the indices of the edge of $\Sigma_{0}$ are given by $w$ .

For each edge $e$ of $\Sigma_{\infty}$ , let $m_{e}\subset\partial M_{0}$ be a meridian loop of $e$ , let $P_{\infty}$ be the disjoint union of the regular neighbourhoods in $\partial M_{0}$ of $m_{e}$ , where $e$ runs over the edges of $\Sigma_{\infty}$ . The condition (SC) implies that each component of $\operatorname{cl}(\partial M_{0}-P_{\infty})$ is either a euclidean or hyperbolic $2$ -orbifold. Let $P$ be the union of $P_{\infty}$ and the euclidean components of $\operatorname{cl}(\partial M_{0}-P_{\infty})$ . Then $P$ is a disjoint union of euclidean $2$ -orbifolds.

We call $(M_{0},P)$ the orbifold pair determined by the weighted graph $(M,\Sigma,w)$ .

Convention 6.2.

It is sometimes convenient to employ the following slight extension of Convention 6.1.

(1) We allow $w$ to have an edge $e$ with $w(e)=1$ . In this case, we consider the weighted graph $(W,\Sigma^{\prime},w^{\prime})$ , where $\Sigma^{\prime}$ is the subgraph of $\Sigma$ consisting of those edges with $w(e)\neq 1$ and $w^{\prime}$ is the restriction of $w$ to $\Sigma^{\prime}$ . If $\Sigma^{\prime}$ is also trivalent graph properly embedded in $W$ and the condition (SC) is satisfied, then we define the orbifold pair determined by $(W,\Sigma,w)$ to be that determined by $(W,\Sigma^{\prime},w^{\prime})$ .

(2) We allow a quadrivalent vertex, $v$ , such that the four edge germs incident on it have index $2$ . In this case, $v$ represents a parabolic locus, $P(v)$ , isomorphic to $S^{2}(2,2,2,2)$ .

A key ingredient of the proof of the main theorem is an orbifold surgery.

Definition 6.3.

Let $(M_{0},P)$ be a pared orbifold, represented by a weighted graph $(W,\Sigma,w)$ satisfying the condition (SC). By replacing the weight function $w$ with another weight function $w^{\prime}$ (which also takes value in $\mathbb{N}_{\geq 2}\cup\{\infty\}$ ), we obtain another weighted graph $(W,\Sigma,w^{\prime})$ . This fails to satisfy the condition (SC) only when some sphere component $S$ of the topological boundary $\partial W$ determines a spherical $2$ -orbifold with three singular points. In this case, we cap all such sphere boundaries of $W$ with a cone over $(S,S\cap\Sigma)$ to obtain a new weighted graph, which we call the augmentation of $(W,\Sigma,w^{\prime})$ . It satisfies the condition (SC), and determines an orbifold pair $(N_{0},Q)$ . We call the $3$ -orbifold ${\mathcal{O}}:=N_{0}$ the orbifold obtained from $(M_{0},P)$ by the orbifold surgery determined by the replacement of the weight function $w$ with the new weight function $w^{\prime}$ .

The following simple lemma is used repeatedly in the proof of the main theorem.

Lemma 6.4.

Let $(M_{0},P)$ be a pared orbifold, and let ${\mathcal{O}}$ be the orbifold obtained from $(M_{0},P)$ by an orbifold surgery. Then ${\mathcal{O}}$ does not contain a bad $2$ -suborbifold and $\partial{\mathcal{O}}$ does not contain a spherical component. In particular, ${\mathcal{O}}$ is very good.

Proof.

Let $(W,\Sigma,w)$ be a weighted graph representing the pared orbifold $(M_{0},P)$ , and let $w^{\prime}$ be the weight function on $\Sigma$ that gives the orbifold ${\mathcal{O}}=N_{0}$ , where $(N_{0},Q)$ is the orbifold pair that is represented by the augmentation of $(W,\Sigma,w^{\prime})$ . Assume to the contrary that $N_{0}$ contains a bad $2$ -suborbifold, $S$ , which is either a teardrop $S^{2}(n)$ or a spindle $S^{2}(m,n)$ for some integers $m>n\geq 2$ . Since the underlying space $|S|$ is disjoint from the vertex set of the singular set, $\Sigma(N_{0})$ , of $N_{0}$ , we may assume $|S|$ is a submanifold of $W$ transversal to $\Sigma$ . Then it determines a suborbifold, $S^{*}$ , of $M_{0}$ , such that $|S^{*}|=|S|\cap|M_{0}|$ . The singular set of $S^{*}$ is equal to $|S^{*}|\cap\Sigma_{s}$ , where $\Sigma_{s}$ is the subgraph of $\Sigma$ consisting of the edges of integral $w$ -weight, and the index of each singular point is given by the $w$ -weight of the corresponding edge of $\Sigma_{s}$ .

First, suppose that $S\cong S^{2}(n)$ for $n\geq 2$ . Let $e$ be the edge of $\Sigma$ such that $|S|\cap e$ is the singular point of $S$ . If $e$ is an edge of $\Sigma_{s}$ , then $S^{*}$ is isomorphic to the teardrop $S^{2}(w(e))$ , which contradicts the fact that $M_{0}$ is good. If $e$ is an edge of $\Sigma_{\infty}$ , then $S^{*}$ is a disc whose boundary is an essential simple loop on $P$ . This contradicts the fact that $P$ is incompressible in $M_{0}$ .

Next, suppose that $S\cong S^{2}(m,n)$ for $m>n\geq 2$ . Let $e_{1}$ and $e_{2}$ be the edges of $\Sigma$ corresponding to the singular point of $S$ of index $m$ and $n$ , respectively. Then $w^{\prime}(e_{1})=m\neq n=w^{\prime}(e_{2})$ , and so $e_{1}$ and $e_{2}$ are distinct. If both $e_{1}$ and $e_{2}$ are contained in $\Sigma_{s}$ , then $S^{*}\cong S^{2}(m^{*},n^{*})$ for some $m^{*},n^{*}\geq 2$ . Since $M_{0}$ does not contain a bad $2$ -suborbifold, $m^{*}$ and $n^{*}$ must be equal, and hence $S^{*}$ is an spherical suborbifold of $M_{0}$ . Since $M_{0}$ is irreducible, $S^{*}$ bounds a discal $3$ -orbifold. This implies $e_{1}$ and $e_{2}$ determine the same edge of $\Sigma(N_{0})$ . By the condition (SC), this in turn implies $e_{1}=e_{2}$ , a contradiction. If exactly one of $e_{1}$ and $e_{2}$ is contained in $\Sigma_{s}$ , then $S^{*}$ is a discal orbifold whose boundary is an essential simple loop on $P$ . This contradicts the assumption that $P$ is incompressible in $M_{0}$ . If none of $e_{1}$ and $e_{2}$ is contained in $\Sigma_{s}$ , then $S^{*}$ is an annulus whose boundary consists of a pair of essential simple loops on $P$ . Thus $S^{*}$ is parallel to $P$ by Definition 3.1(4), and so $e_{1}=e_{2}$ , a contradiction.

Thus we have proved that ${\mathcal{O}}=N_{0}$ does not contain a bad $2$ -suborbifold. The assertion that $\partial{\mathcal{O}}$ does not contain a spherical orbifold follows from the fact that ${\mathcal{O}}=N_{0}$ is represented by the augmentation of $(W,\Sigma,w^{\prime})$ . The assertion that ${\mathcal{O}}$ is very good follows from [8, Corollary 1.3], which is a consequence of the orbifold theorem. ∎

Another key tool for the proof of the main theorem is the homology with $\mathbb{Z}_{2}$ coefficient. Under Notation 1.3, we have the following lemma, which can be easily deduced from the definition of $H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ and the Alexander duality.

Lemma 6.5.

Suppose an orbifold ${\mathcal{O}}$ is represented by a weighted graph $(S^{3},\Sigma,w)$ in $S^{3}$ . Let $\Sigma_{\mathrm{even}}$ be the subgraph of $\Sigma$ spanned by the edges of even weight. Then $H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ is determined by $H_{1}(\Sigma_{\mathrm{even}};\mathbb{Z}_{2})$ . To be precise, we have the following natural isomorphisms.

H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong H_{1}(S^{3}-\Sigma_{\mathrm{even}};\mathbb{Z}_{2})\cong H^{1}(\Sigma_{\mathrm{even}};\mathbb{Z}_{2})\cong\mathrm{Hom}(H_{1}(\Sigma_{\mathrm{even}};\mathbb{Z}_{2}),\mathbb{Z}_{2})

In particular, the following hold.

(1)

$H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ is generated by the meridians of edges of $\Sigma_{\mathrm{even}}$ .
(2)

The meridian of an edge of $\Sigma$ of odd degree represents the trivial element of $H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ .
(3)

Let $e_{i}$ ( $i=1,2,3$ ) be edges of $\Sigma$ incident on a vertex of $\Sigma$ , and suppose that $w(e_{1})$ is odd and $w(e_{2})$ and $w(e_{3})$ are even. Then the meridians of $e_{2}$ and $e_{3}$ represent the same element of $H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ .

7. Canonical horoball pairs for Kleinian groups generated by two parabolic transformations

Throughout Sections 7 $\sim$ 11, $\Gamma=\langle\alpha,\beta\rangle$ denotes a non-elementary Kleinian group generated by two parabolic transformations $\alpha$ and $\beta$ , and $M=\mathbb{H}^{3}/\Gamma$ denotes the quotient hyperbolic $3$ -orbifold. Let $\eta$ be the geodesic joining the parabolic fixed points of $\alpha$ and $\beta$ , and let $h$ be the $\pi$ -rotation around $\eta$ . Then we have

(h\alpha h^{-1},h\beta h^{-1})=(\alpha^{-1},\beta^{-1}).

We call $h$ the inverting elliptic element for the parabolic generating pair $\{\alpha,\beta\}$ of the Kleinian group $\Gamma$ . As shown in [57, Section 5.4], we can find a geodesic intersecting $\eta$ orthogonally, such that the $\pi$ -rotation, $f$ , around it satisfies the following identity.

(f\alpha f^{-1},f\beta f^{-1})=(\beta,\alpha).

We call $f$ the exchanging elliptic element for the parabolic generating pair $\{\alpha,\beta\}$ of the Kleinian group $\Gamma$ . It should be noted that $fh$ is the exchanging elliptic element for the parabolic generating pair $\{\alpha,\beta^{-1}\}$ of $\Gamma$ .

By abuse of notation, we denote the isometries of $M$ induced by $f$ and $h$ by the same symbols $f$ and $h$ , respectively. Each of them is either the identity map or a (nontrivial) involution of $M$ , i.e., its order is $1$ or $2$ . We call the isometries $f$ and $h$ , the exchanging involution and the inverting involution of $M$ associated with the parabolic generating pair $\{\alpha,\beta\}$ . It should be noted that if $\Gamma$ is isomorphic to a hyperbolic $2$ -bridge link group $G(K(r))$ and $\{\alpha,\beta\}$ is the upper-meridian pair, then the involutions $f$ and $h$ on $M\cong S^{3}-K(r)$ are the restrictions of the vertical and horizontal involutions of $K(r)$ (see Figure 4). This is the reason why we use the symbols $f$ and $h$ with two different meanings.

Let $\hat{\Gamma}:=\langle\Gamma,f\rangle$ be the group generated by $\Gamma$ and the exchanging elliptic element $f$ associated with the parabolic generating pair $\{\alpha,\beta\}$ of $\Gamma$ . Then $\hat{\Gamma}$ is a Kleinian group which is either equal to $\Gamma$ or a $\mathbb{Z}_{2}$ -extension of $\Gamma$ according to whether $f$ belongs to $\Gamma$ or not. Let $\hat{M}:=\mathbb{H}^{3}/\hat{\Gamma}$ be the quotient hyperbolic orbifold, and let $\hat{C}_{\alpha,\beta}$ be the maximal cusp of $\hat{M}$ corresponding to the conjugacy class of $\hat{\Gamma}$ containing both $\alpha$ and $\beta=f\alpha f^{-1}$ . Then the inverse image $p^{-1}(\hat{C}_{\alpha,\beta})$ of $\hat{C}_{\alpha,\beta}$ by the projection $p:\mathbb{H}^{3}\to\hat{M}$ is a union of horoballs with disjoint interiors but whose boundaries have nonempty tangential intersections. We call it the canonical horoball system associated with the parabolic generating pair $\{\alpha,\beta\}$ of $\Gamma$ . If a parabolic element $\gamma$ of $\Gamma$ stabilises a member of the canonical horoball system, we denote the horoball by $H_{\gamma}$ . We denote the translation length of $\gamma$ on the horosphere $\partial H_{\gamma}$ by the symbol $|\gamma|=|\gamma|_{\partial H_{\gamma}}$ , and call it the length of $\gamma$ in the canonical horosphere. We call the pair $(H_{\alpha},H_{\beta})$ the canonical horoball pair for the parabolic generating pair $\{\alpha,\beta\}$ of the Kleinian group $\Gamma$ .

Note that the definition of $|\gamma|$ depends on the parabolic generating pair $\{\alpha,\beta\}$ , because the exchanging elliptic element $f$ is involved in the definition. However, it actually depends only on the pair $\{\operatorname{Fix}(\alpha),\operatorname{Fix}(\beta)\}$ , because any orientation-preserving isometry, which exchanges $\operatorname{Fix}(\alpha)$ and $\operatorname{Fix}(\beta)$ , also exchanges the members $H_{\alpha}$ and $H_{\beta}$ of the canonical horoball pair associated with $\{\alpha,\beta\}$ . (Otherwise, the product of $f$ and an unexpected involution, which exchanges $\operatorname{Fix}(\alpha)$ and $\operatorname{Fix}(\beta)$ but does not exchange $H_{\alpha}$ and $H_{\beta}$ , gives a loxodromic transformation which fixes the parabolic fixed points $\operatorname{Fix}(\alpha)$ and $\operatorname{Fix}(\beta)$ . This contradicts the assumption that $\Gamma$ is discrete.)

The following lemmas are proved by Adams [1, Lemma 3.1, Theorem 3.2, and p.197] (see also Brenner [16]). Since they holds a key to the proof of the main theorem and since we described the setting in a slightly different way, we include the proof.

Lemma 7.1.

Under the above setting, the following hold.

(1)

For any parabolic element $\gamma\in\Gamma$ which stabilises a member of the canonical horoball system, we have $|\gamma|\geq 1$ .
(2)

$1\leq|\alpha|=|\beta|$ .
(3)

If $\Gamma$ is non-free then $|\alpha|=|\beta|<2$ .

Proof.

(1) We may assume $\partial H_{\gamma}$ is the horosphere $\mathbb{C}\times\{1\}$ in the upper half space model $\mathbb{H}^{3}=\mathbb{C}\times\mathbb{R}_{+}$ . Then some other member, $H_{g}$ , of the canonical horoball system touches $\partial H_{\gamma}$ and hence has Euclidean diameter $1$ . Since $\gamma(H_{g})=H_{\gamma g\gamma^{-1}}$ is also a member of the canonical horoball system, $H_{g}$ and $\gamma(H_{g})$ have disjoint interiors. Hence we have $|\gamma|\geq 1$ .

(2) Since $\alpha$ and $\beta$ are conjugate in $\hat{\Gamma}$ , $|\alpha|$ and $|\beta|$ are equal. Moreover, $|\alpha|=|\beta|$ is $\geq 1$ by (1).

(3) We refer the proof to [1, Theorem 3.2] and Brenner [16]. ∎

Lemma 7.2.

Both $\alpha$ and $\beta$ are primitive in $\Gamma$ .

Proof.

If $\Gamma$ is a free, then the assertion follows from the fact that any member of a free-generating system of a free group is primitive. So, we may assume $\Gamma$ is non-free. Suppose on the contrary that one of the two elements, say $\alpha$ , is imprimitive, namely there is an element $\alpha_{0}\in\Gamma$ and an integer $n\geq 2$ such that $\alpha=\alpha_{0}^{n}$ . Then $|\alpha|=n|\alpha_{0}|\geq n\geq 2$ by Lemma 7.1(1). But, this contradicts Lemma 7.1(3). ∎

8. Outline of the proof of Theorem 1.1

We now state an outline of the proof of Theorem 1.1. Since the if part is clear (cf. Proposition 3.3), we prove the only if part. To this end, we summarise the setting of Theorem 1.1.

Assumption 8.1.

Let $\Gamma=\langle\alpha,\beta\rangle$ be a non-free Kleinian group generated by two non-commuting parabolic transformations $\alpha$ and $\beta$ , and let $M=\mathbb{H}^{3}/\Gamma$ be the quotient hyperbolic orbifold. Let $M_{0}$ be the non-cuspidal part of $M$ , and $P=\partial M_{0}$ the parabolic locus. By Theorem 5.1, $(M_{0},P)$ admits a relative compactification $(\bar{M}_{0},\bar{P})$ , which is a pared orbifold by Theorem 5.2. The pared orbifold $(\bar{M}_{0},\bar{P})$ can be represented by a weighted graph $(W,\Sigma,w)$ , where $W$ is a compact $3$ -manifold, $\Sigma$ is a trivalent graph properly embedded in $W$ , and $w$ is a weight function on the edge set of $\Sigma$ (see Convention 6.1). We abuse notation to denote the (compact) pared orbifold $(\bar{M}_{0},\bar{P})$ by $(M_{0},P)$ . We denote the components of $\bar{P}$ , which is now denoted by $P$ , corresponding to the cusps $C_{\alpha}$ and $C_{\beta}$ by $P_{\alpha}$ and $P_{\beta}$ , respectively.

Outline of the proof of Theorem 1.1.

Under Assumption 8.1, the proof is divided into the following two cases.

Case 1.

$P_{\alpha}\cong P_{\beta}$ is a flexible cusp (Section 9 for generic case and Section 11 for exceptional case).
Case 2.

$P_{\alpha}\cong P_{\beta}$ is a rigid cusp (Section 10).

In both cases, the first task is to find an orbifold surgery that yields an orbifold ${\mathcal{O}}$ with dihedral orbifold fundamental group.

In Case 1, this can be generically done by using Lemma 7.2. In fact, if $P_{\alpha}\cong P_{\beta}$ is a flexible cusp, then Lemma 7.2 implies that each of the parabolic elements $\alpha$ and $\beta$ can be represented by simple loops of $P_{\alpha}$ and $P_{\beta}$ , respectively. Generically, these simple loops are disjoint, and such an surgery obviously exists. This generic case is treated in Section 9.

However, there is an exceptional case where $P_{\alpha}=P_{\beta}\cong S^{2}(2,2,2,2)$ and the simple loops representing $\alpha$ and $\beta$ intersect nontrivially (Lemma 9.1). In this case, the exchanging elliptic element $f$ does not belong to $\Gamma$ , and we need to consider the $\mathbb{Z}_{2}$ -extension $\hat{\Gamma}:=\langle\Gamma,f\rangle$ of $\Gamma$ and consider the corresponding pared orbifold $(\hat{M}_{0},\hat{P}):=(M_{0},P)/f$ , where $\hat{P}_{\alpha\beta}$ is isomorphic to the rigid cusp $S^{2}(2,4,4)$ . The treatment of this case is deferred to Section 11, after the treatment of the rigid cusp Case 2 in Section 10, described below.

In Case 2, if $P_{\alpha}\cong P_{\beta}$ is isomorphic to either $S^{2}(2,4,4)$ or $S^{2}(2,3,6)$ , the dihedral surgery can be found by using an estimate of the shortest, second shortest, and third shortest lengths of parabolic elements on the maximal rigid cusp, which in turn is based on Lemma 7.1. If $P_{\alpha}\cong P_{\beta}$ is isomorphic to $S^{2}(3,3,3)$ , the inverting parabolic element $h$ does not belong to $\Gamma$ , and we consider the $\mathbb{Z}_{2}$ -extension $\Gamma_{h}:=\langle\Gamma,h\rangle$ and the corresponding pared orbifold $(M_{h,0},P_{h}):=(M_{0},P)/h$ . The images of $P_{\alpha}$ and $P_{\beta}$ in this quotient is isomorphic to $S^{2}(2,3,6)$ , and this case can be treated by using arguments in the case where $P_{\alpha}\cong P_{\beta}\cong S^{2}(2,3,6)$ .

After finding an orbifold surgery that yields an orbifold ${\mathcal{O}}$ with dihedral orbifold fundamental group, we can appeal to the classification Theorem 4.1 of the dihedral orbifolds, because Lemma 6.4 guarantees that the orbifold ${\mathcal{O}}$ satisfies the three conditions in Theorem 4.1. So, ${\mathcal{O}}$ belongs to the list in the theorem. The original pared orbifold $(M_{0},P)$ is obtained from the dihedral orbifold ${\mathcal{O}}$ by inverse surgery operations. Through case-by-case arguments, by using the homology with $\mathbb{Z}_{2}$ -coefficients, a result concerning the symmetries of the spherical dihedral orbifold (Corollary 12.7), and a ‘surgery trick’ (the last paragraph in Case 1 in Section 10 and Case 1 in Section 11), we prove the following.

(1)

If $P_{\alpha}\cong P_{\beta}$ is a flexible cusp, then, in the generic case, the pared orbifold $(M_{0},P)$ is isomorphic to either a hyperbolic $2$ -bridge link exterior or a Heckoid orbifold (Section 9): in the exceptional case, we encounter a contradiction (Section 11).
(2)

If $P_{\alpha}\cong P_{\beta}$ is a rigid cusp, then we encounter a contradiction (Section 10).

This ends an outline of the proof of the main Theorem 1.1. ∎

9. Proof of Theorem 1.1 - flexible cusp: generic case -

Under Assumption 8.1, suppose that $P_{\alpha}\cong P_{\beta}$ is a flexible cusp. Then the $2$ -orbifold $P_{\alpha}\cong P_{\beta}$ is isomorphic to the torus $T^{2}$ , the pillowcase $S^{2}(2,2,2,2)$ , the annulus $A^{2}$ , or $D^{2}(2,2)$ . The following fact is the starting point of this section.

Lemma 9.1.

Under the above setting, $\alpha$ and $\beta$ are represented by simple loops on $P_{\alpha}$ and $P_{\beta}$ , respectively. Moreover, if $P_{\alpha}=P_{\beta}$ , then one of the following holds.

(1)

The parabolic elements $\alpha$ and $\beta$ are represented by the same (possibly oppositely oriented) simple loop.
(2)

$P_{\alpha}=P_{\beta}\cong S^{2}(2,2,2,2)$ , $f\notin\Gamma$ , and $P_{\alpha}/f=P_{\beta}/f\cong S^{2}(2,4,4)$ , where the first $f$ is the exchanging elliptic element associated with $\{\alpha,\beta\}$ and the last two $f$ ’s denote the involution on $(M_{0},P)$ induced by the exchanging elliptic element $f$ (see Figure 11).

Proof.

The first assertion directly follows from Lemma 7.2, because any primitive parabolic element in the orbifold fundamental group of the $2$ -dimensional orbifold $T^{2}$ , $S^{2}(2,2,2,2)$ , $A^{2}$ , or $D^{2}(2,2)$ is represented by a simple loop on the $2$ -orbifold. For the proof of the second assertion, suppose that $P_{\alpha}=P_{\beta}$ . If the exchanging elliptic element $f$ belongs to $\Gamma$ , then $\beta$ is conjugate to $\alpha$ in $\Gamma$ , and so they are represented by the same simple loop. Thus we may suppose $f\notin\Gamma$ . Then $f$ descends to a nontrivial orientation-preserving involution on $M$ , which we continue to denote by $f$ , on the flexible cusp $P_{\alpha}$ . By the classification of orientation-preserving involutions on flexible cusps, we can observe that either (a) the involution $f$ on $M_{0}$ preserves or reverses the homotopy class of each essential simple loop on $P_{\alpha}$ , or (b) $P_{\alpha}\cong S^{2}(2,2,2,2)$ and $P_{\alpha}/f\cong S^{2}(2,4,4)$ . In the first case, $\alpha$ and $\beta^{\pm 1}$ are represented by the same simple loop, and so we obtain the desired conclusion. ∎

In this section, we treat the case where either $P_{\alpha}\neq P_{\beta}$ or $P_{\alpha}=P_{\beta}$ and the conclusion (1) in Lemma 9.1 holds. Thus we assume the following condition in the remainder of this section. The other case is treated in Section 11.

Assumption 9.2.

Under Assumption 8.1, we further assume that (a) $P_{\alpha}\cong P_{\beta}$ is a flexible cusp and that (b) either $P_{\alpha}\neq P_{\beta}$ or $P_{\alpha}=P_{\beta}$ and the conclusion (1) in Lemma 9.1 holds. It should be noted that either $\alpha$ and $\beta$ are represented by disjoint simple loops or they are represented by the same (possibly oppositely oriented) simple loop.

Under this assumption, we can apply an orbifold surgery on $(M_{0},P)$ to the pared orbifold $(M_{0},P)$ to obtain a dihedral orbifold, ${\mathcal{O}}$ , as follows. Note that Assumption 9.2 implies that the pared orbifold $(M_{0},P)$ is represented by a weighted graph $(W,\Sigma,\tilde{w})$ , such that there are (possibly identical) edges $e_{\alpha}$ and $e_{\beta}$ of $\Sigma$ whose meridians represent $\alpha$ and $\beta$ , respectively. Let $w$ be a weight function on $\Sigma$ which is identical with $\tilde{w}$ , except that $w(e_{\alpha})=w(e_{\beta})=2$ . Then the orbifold ${\mathcal{O}}$ represented by the augmentation of the weighted graph $(W,\Sigma,w)$ is a result of an “order $2$ ” orbifold surgery on $(M_{0},P)$ , and $\pi_{1}({\mathcal{O}})$ is dihedral, as shown below.

Note that there is a natural epimorphism from $\Gamma=\pi_{1}(M_{0})$ to $\pi_{1}({\mathcal{O}})$ , and the images of $\alpha$ and $\beta$ in $\pi_{1}({\mathcal{O}})$ have order $\leq 2$ . Moreover, the images of $\alpha$ and $\beta$ have the same order, because (a) if $f\in\Gamma$ then $\alpha$ and $\beta$ are conjugate in $\Gamma$ and so in $\pi_{1}({\mathcal{O}})$ , and (b) if $f\notin\Gamma$ then $f$ descends to an involution on ${\mathcal{O}}$ which interchanges the images of $\alpha$ and $\beta$ . So $\pi_{1}({\mathcal{O}})$ is either the trivial group or a dihedral group. Since ${\mathcal{O}}$ is very good by Lemma 6.4 and since ${\mathcal{O}}$ has nonempty singular set, $\pi_{1}({\mathcal{O}})$ is nontrivial and so isomorphic to a dihedral group.

Thus ${\mathcal{O}}$ satisfies the three conditions in Theorem 4.1 and so ${\mathcal{O}}$ belongs to the list in the theorem. We have the following lemma.

Lemma 9.3.

The orbifold ${\mathcal{O}}$ is isomorphic to the spherical dihedral orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ for some $r\in\mathbb{Q}$ and coprime positive integers $d_{+}$ and $d_{-}$ .

Proof.

We show that the possibilities (2), (3) and (4) in Theorem 4.1 cannot happen. Suppose (2) happens. Then we can see that one of the following holds, by recalling the fact that ${\mathcal{O}}$ is obtained from the pared orbifold $(M_{0},P)$ an order $2$ orbifold surgery.

(i)

$M_{0}$ is the exterior of the two-component trivial link, $P=\partial M_{0}$ , and the singular set of $M_{0}$ is empty.
(ii)

The underlying space of $M_{0}$ is the solid torus (the exterior of a trivial knot), $P=\partial M_{0}$ , and the singular set is a trivial knot in the solid torus with index $2$ .

In each case, $(M_{0},P)$ is reducible, a contradiction.

By the same reasoning, we can see that (3) cannot happen.

If (4) happens, then as in the above, we can see that one of the following holds, where $(B^{3},t_{1}\cup t_{2})$ is a two-strand trivial tangle.

(i)

$(M_{0},P)\cong(\operatorname{cl}(B^{3}-N(t_{1}\cup t_{2})),\operatorname{fr}N(t_{1}\cup t_{2}))$ and the singular set of $M_{0}$ is empty.
(ii)

$(M_{0},P)\cong(\operatorname{cl}(B^{3}-N(t_{1})),\operatorname{fr}N(t_{1}))$ and the singular set of $M_{0}$ is $t_{2}$ with index $2$ .

In the first case, $\Gamma=\pi_{1}(M_{0})$ is a rank $2$ free group, which contradicts the assumption that $\Gamma$ is non-free. In the second case, note that $H_{1}(M_{0})$ , the abelianization of the orbifold fundamental group $\pi_{1}(M_{0})$ , is $\mathbb{Z}\oplus\mathbb{Z}_{2}$ . On the other hand, both $\alpha$ and $\beta$ are represented by the core loop of the annulus $P=\operatorname{fr}N(t_{1})$ , and the pair $\{\alpha,\beta\}$ cannot generate $H_{1}(M_{0})$ , a contradiction. ∎

By Lemma 9.3, the original orbifold $(M_{0},P)$ is recovered from ${\mathcal{O}}={\mathcal{O}}(r;d_{+},d_{-})$ by applying the inverse orbifold surgery operation. This leads us to the following proposition.

Proposition 9.4.

Under the notation in Lemma 9.3, the following hold, if necessary by replacing $r=q/p$ with $q^{\prime}/p$ where $q^{\prime}=q+p$ or $qq^{\prime}\equiv 1\pmod{p}$ .

(1)
If $|K(r)|=1$ , then one of the following holds.
1. (i)
  
  $d_{+}=d_{-}=1$ and $(M_{0},P)\cong(E(K(r)),\partial E(K(r)))$ , where $q\not\equiv\pm 1\pmod{p}$ .
2. (ii)
  
  $d_{+}=1$ , $d_{-}\geq 2$ , and $(M_{0},P)\cong\mathcal{M}_{0}(r;d_{-})$ .
3. (iii)
  
  $d_{+}=1$ , $d_{-}$ is an odd integer $\geq 3$ , and $(M_{0},P)\cong\mathcal{M}_{1}(r;d_{-})$ .
4. (iv)
  
  $d_{+}=2$ , $d_{-}$ is an odd integer $\geq 3$ , and $(M_{0},P)\cong\mathcal{M}_{2}(r;d_{-})$ .
(2)
If $|K(r)|=2$ , then one of the following holds.
1. (i)
  
  $d_{+}=d_{-}=1$ and $(M_{0},P)\cong(E(K(r)),\partial E(K(r)))$ , where $q\not\equiv\pm 1\pmod{p}$ .
2. (ii)
  
  $d_{+}=1$ , $d_{-}\geq 2$ , and $(M_{0},P)\cong\mathcal{M}_{0}(r;d_{-})$ .
3. (iii)
  
  $d_{+}=2$ , $d_{-}$ is an odd integer $\geq 3$ , and $(M_{0},P)\cong\mathcal{M}_{2}(r;d_{-})$ .

Proof.

Recall that ${\mathcal{O}}={\mathcal{O}}(r;d_{+},d_{-})$ is represented by the weighted graph $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-},w)$ for some $r\in\mathbb{Q}$ and for some coprime positive integers $d_{+}$ and $d_{-}$ , and $w$ is given by the following rule (see Figure 6):

w(K(r))=2,\quad w(\tau_{+})=d_{+},\quad w(\tau_{-})=d_{-}

Then $(M_{0},P)$ is represented by the weighted graph $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-},\tilde{w})$ , where $\tilde{w}$ is obtained from $w$ by replacing the label $2$ of the edges $e_{\alpha}$ and $e_{\beta}$ , which correspond to $P_{\alpha}$ and $P_{\beta}$ respectively, with the label $\infty$ . By Remark 4.3, we may assume $1\leq d_{+}\leq d_{-}$ , if necessary by replacing $r=q/p$ with $q^{\prime}/p$ where $qq^{\prime}\equiv 1\pmod{p}$ .

Case 1. $d_{+}=d_{-}=1$ . Then $\Sigma({\mathcal{O}})$ is the $2$ -bridge link $K(r)$ . Thus $(M_{0},P)\cong(S^{3},K(r),\tilde{w})$ , where either (a) $\tilde{w}(K(r))=\infty$ or (b) $K(r)$ is a $2$ -component link $K_{1}\cup K_{2}$ and $(\tilde{w}(K_{1}),\tilde{w}(K_{2}))=(\infty,2)$ . In the first case, $(M_{0},P)\cong(E(K(r)),\partial E(K(r)))$ , and so $\mathbb{H}^{3}/\Gamma$ is the hyperbolic $2$ -bridge link complement, $S^{3}-K(r)$ : in particular, $q\not\equiv\pm 1\pmod{p}$ . In the second case, both $\alpha$ and $\beta$ are meridians of the component $K_{1}$ , which contradicts the fact that $H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ .

Case 2. $d_{+}=1<d_{-}$ .

Subcase 2.1. $|K(r)|=2$ (see Figure 7(1)). Then the edge set of $\Sigma({\mathcal{O}})$ consists of $\tau_{-}$ and the two components $K_{1}$ , $K_{2}$ of $K(r)$ . Let $x_{-}$ , $x_{1}$ and $x_{2}$ be the meridians of $\tau_{-}$ , $K_{1}$ and $K_{2}$ , respectively. By Lemma 6.5, $H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ is freely generated by $\{x_{1},x_{2}\}$ , and moreover we have $x_{-}=0$ . Since $H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ is generated by (the images of) $\alpha$ and $\beta$ , we may assume $e_{\alpha}=K_{1}$ and $e_{\beta}=K_{2}$ . Thus $(M_{0},P)$ is represented by $(S^{3},K(r)\cup\tau_{-},\tilde{w})$ , where $\tilde{w}(K_{1})=\tilde{w}(K_{2})=\infty$ and $\tilde{w}(\tau_{-})=d_{-}$ . Hence $(M_{0},P)\cong\mathcal{M}_{0}(r;d_{-})$ .

Subcase 2.2. $|K(r)|=1$ (see Figure 7(2)). Then the edge set of $\Sigma({\mathcal{O}})$ consists of $\tau_{-}$ and the two subarcs $J_{1}$ and $J_{2}$ of $K(r)$ bounded by $K(r)\cap\tau_{-}$ . Let $x_{-}$ , $x_{1}$ and $x_{2}$ be the meridians of $\tau_{-}$ , $J_{1}$ and $J_{2}$ , respectively.

Suppose first that $d_{-}$ is odd. Then we see by Lemma 6.5 that $x_{-}=0$ in $H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong\mathbb{Z}_{2}$ and that $H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong\mathbb{Z}_{2}$ is generated by $x_{1}=x_{2}$ . Hence one of the following holds.

(1)

$\{e_{\alpha},e_{\beta}\}=\{J_{1},J_{2}\}$ and so $(M_{0},P)$ is represented by $(S^{3},K(r)\cup\tau_{-},\tilde{w})$ , where $\tilde{w}(J_{1})=\tilde{w}(J_{2})=\infty$ and $\tilde{w}(\tau_{-})=d_{-}$ . Hence $(M_{0},P)\cong\mathcal{M}_{0}(r;d_{-})$ .
(2)

$e_{\alpha}=e_{\beta}=J_{i}$ for $i=1$ or $2$ . By the symmetry of ${\mathcal{O}}$ , we may assume $i=1$ and so $(M_{0},P)$ is represented by $(S^{3},K(r)\cup\tau_{-},\tilde{w})$ , where $\tilde{w}(J_{1})=\infty$ , $\tilde{w}(J_{2})=2$ and $\tilde{w}(\tau_{-})=d_{-}$ . Hence $(M_{0},P)\cong\mathcal{M}_{1}(r;d_{-})$ .

Suppose next that $d_{-}$ is even. Then $x_{1}+x_{2}+x_{-}=0$ in $H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ . Since $H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ is generated by $\alpha$ and $\beta$ , we have $e_{\alpha}\neq e_{\beta}$ . This implies that the exchanging elliptic element $f$ for $\{\alpha,\beta\}$ does not belong to $\Gamma$ , and $f$ descends to an involution on ${\mathcal{O}}$ interchanging $e_{\alpha}$ with $e_{\beta}$ . We now use Corollary 12.7 on the symmetry of the orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ . We first consider the generic case where $p\neq 1$ (i.e., $K(r)$ is a nontrivial knot) or $d_{-}>2$ . (Recall the current assumption $d_{+}=1$ .) Then, by Corollary 12.7(1), any orientation-preserving involution of ${\mathcal{O}}$ preserves $\tau_{-}$ . So, $e_{\alpha}$ and $e_{\beta}$ are different from $\tau_{\pm}$ , and therefore $\{e_{\alpha},e_{\beta}\}=\{J_{1},J_{2}\}$ . Hence, as in the previous case, we can conclude $(M_{0},P)\cong\mathcal{M}_{0}(r;d_{-})$ . In the exceptional case where $p=1$ and $d_{-}=2$ , The orbifold ${\mathcal{O}}\cong{\mathcal{O}}(0/1;1,2)$ has the $3$ -fold cyclic symmetry as illustrated in Figure 15. Thus, if necessary after applying this symmetry, we may assume $\{e_{\alpha},e_{\beta}\}=\{J_{1},J_{2}\}$ . Hence we have $(M_{0},P)\cong\mathcal{M}_{0}(r;d_{-})\cong\mathcal{M}_{0}(0/1;2)$ .

Since we repeatedly use the above argument in the remainder of the proof of Proposition 9.4, we state an expanded version of the argument as a lemma.

Lemma 9.5.

Under the setting of Proposition 9.4, suppose $(d_{+},d_{-})\neq(1,1)$ and $H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ . Then $e_{\alpha}\neq e_{\beta}$ , and the exchanging elliptic element $f$ does not belong to $\Gamma$ and it descends to an orientation-preserving involution of ${\mathcal{O}}={\mathcal{O}}(r;d_{+},d_{-})$ interchanging $e_{\alpha}$ and $e_{\beta}$ . Moreover, the following hold.

(1)

Except when $p=1$ and $\{d_{+},d_{-}\}=\{1,2\}$ , $e_{\alpha}$ and $e_{\beta}$ are different from $\tau_{\pm}$ .
(2)

If $d_{+},d_{-}\geq 2$ , then the inverting elliptic element $h$ belongs to $\Gamma$ .

Proof.

We have only to prove (2). If $h$ does not belong to $\Gamma$ , then it descends to an orientation-preserving involution of ${\mathcal{O}}(r;d_{+},d_{-})$ which preserves both $e_{\alpha}$ and $e_{\beta}$ . However, if $d_{+},d_{-}\geq 2$ , then by Corollary 12.7(2), no orientation-preserving involution of ${\mathcal{O}}(r;d_{+},d_{-})$ preserves an edge of the singular set different from $\tau_{\pm}$ . This contradicts the assertion (1). ∎

Case 3. $2\leq d_{+}\leq d_{-}$ . Since $d_{+}$ and $d_{-}$ are coprime, we see $2\leq d_{+}<d_{-}$ and one of $d_{+}$ and $d_{-}$ is odd.

Subcase 3.1. $|K(r)|=2$ (see Figure 7(3)). Let $K_{1}$ and $K_{2}$ be the components of $K(r)$ , and let $J_{i,j}$ ( $1\leq i,j\leq 2$ ) be the edges of $\Sigma({\mathcal{O}})$ such that $K_{j}=J_{1,j}\cup J_{2,j}$ for $j=1,2$ and that the vertical involution of $K(r)$ interchanges $J_{i,1}$ and $J_{i,2}$ for $i=1,2$ . Let $x_{\pm}$ and $x_{i,j}$ be the meridians of $\tau_{\pm}$ and $J_{i,j}$ , respectively. Then by using Lemma 6.5 and the fact that one of $d_{+}$ and $d_{-}$ is odd, we see that $H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ is freely generated by $x_{1}:=x_{1,1}=x_{2,1}$ and $x_{2}:=x_{1,2}=x_{2,2}$ : moreover we have $x_{\pm}=0$ . Hence, we may assume $e_{\alpha}\subset K_{1}$ and $e_{\beta}\subset K_{2}$ . Since the horizontal involution of $K(r)$ interchanges $J_{1,j}$ and $J_{2,j}$ ( $j=1,2$ ), we may assume $e_{\alpha}=J_{1,1}\subset K_{1}$ and $e_{\beta}=J_{i,2}\subset K_{2}$ for some $i=1$ or $2$ . By Lemma 9.5(2), we have $h\in\Gamma$ , and so $P_{\alpha}\cong P_{\beta}$ is homeomorphic to $D^{2}(2,2)$ or $S^{2}(2,2,2,2)$ . Since $2\leq d_{+}<d_{-}$ , we must have $d_{+}=2$ . If $i=1$ , i.e. $e_{\beta}=J_{1,2}$ , then $\tilde{w}$ is given by

\tilde{w}(J_{1,1})=\tilde{w}(J_{1,2})=\infty,\quad\tilde{w}(J_{1,2})=\tilde{w}(J_{2,2})=2,\quad\tilde{w}(\tau_{+})=2,\quad\tilde{w}(\tau_{-})=d_{-}.

Since the vertical involution of $K(r)$ preserves $J_{1}:=J_{1,1}\cup J_{1,2}$ , we see that $(M_{0},P)$ is isomorphic to $\mathcal{M}_{2}(r;d_{-})$ . If $i=2$ , i.e. $e_{\beta}=J_{2,2}$ , then the planar involution of $K(r)$ preserves $J_{1}:=J_{1,1}\cup J_{2,2}$ . Hence, we see by Remark 3.5 that $(M_{0},P)$ is isomorphic to $\mathcal{M}_{2}(r^{\prime};d_{-})$ , where $r^{\prime}=(p+q)/p$ .

Subcase 3.2. $|K(r)|=1$ (see Figure 7(4)). Suppose first that one of $d_{+}$ and $d_{-}$ is even. Then $H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ by Lemma 6.5. Hence, by Lemma 9.5(2), both $e_{\alpha}$ and $e_{\beta}$ are contained in $K(r)$ , and $h\in\Gamma$ . In particular, $P_{\alpha}\cong P_{\beta}\cong D^{2}(2,2)$ or $S^{2}(2,2,2,2)$ . Let $e_{i}$ ( $1\leq i\leq 4$ ) be the edges of the singular set of ${\mathcal{O}}$ contained in the knot $K(r)$ in this cyclic order. We also assume that $\partial\tau_{+}=(e_{1}\cap e_{2})\cup(e_{3}\cap e_{4})$ and $\partial\tau_{-}=(e_{2}\cap e_{3})\cup(e_{4}\cap e_{1})$ . Since the $(\mathbb{Z}_{2})^{2}$ -symmetry of ${\mathcal{O}}(r;d_{+},d_{-})$ acts transitively on the edge set $\{e_{i}\}_{1\leq i\leq 4}$ (see Figure 14), we may assume $e_{1}=e_{\alpha}$ and so $\tilde{w}(e_{1})=\infty$ . Since $e_{\alpha}$ joins $\tau_{+}$ with $\tau_{-}$ and since $d_{\pm}$ are coprime integers such that $2\leq d_{+}\leq d_{-}$ , the condition that $P_{\alpha}\cong D^{2}(2,2)$ or $S^{2}(2,2,2,2)$ implies that $d_{+}=2$ and $d_{-}\geq 3$ . This in turn implies that $P_{\alpha}\cong P_{\beta}\cong D^{2}(2,2)$ . Since $\partial D^{2}(2,2)$ is isotopic to the simple loop $\alpha$ in $\partial M_{0}$ , we must have $\tilde{w}(e_{2})=2$ . Thus $e_{\beta}$ is equal to $e_{3}$ or $e_{4}$ . However, if $e_{\beta}=e_{4}$ then $e_{\alpha}$ , $e_{\beta}$ , and the odd index edge $\tau_{-}$ share a vertex, it follows from Lemma 6.5(3) that the meridian $\alpha$ of $e_{1}$ and the meridian $\beta$ of $e_{4}$ represent the same element of $H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ , a contradiction. Hence $e_{\beta}=e_{3}$ . Set $J_{1}=e_{1}\cup e_{3}$ and $J_{2}=e_{2}\cup e_{4}$ . Then $J_{1}$ and $J_{2}$ are disjoint, $K(r)=J_{1}\cup J_{2}$ and the following hold.

\tilde{w}(J_{1})=\infty,\ \tilde{w}(J_{2})=2,\ \tilde{w}(\tau_{+})=2,\ \tilde{w}(\tau_{-})=d_{-}

Hence we have $(M_{0},P)\cong\mathcal{M}_{2}(r;d_{-})$ (cf. Remark 3.5(2)).

Suppose finally that both $d_{+}$ and $d_{-}$ are odd. Then, by Lemma 6.5, the meridians $x_{\pm}$ of $\tau_{\pm}$ represent the trivial element of $H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong\mathbb{Z}_{2}$ , and hence both $e_{\alpha}$ and $e_{\beta}=f(e_{\alpha})$ are contained in $K(r)$ . On the other hand, since $d_{\pm}>2$ , we have $P_{\alpha}\cong P_{\beta}$ is homeomorphic to an annulus, and hence the inverting elliptic element $h$ descends to an involution of ${\mathcal{O}}$ which preserves each of the two mutually different edges $e_{\alpha}$ and $e_{\beta}$ and restricts to an orientation-reversing involution on each of the edges. But, such an involution does not exist by Corollary 12.7(2), a contradiction.

This completes the proof of Proposition 9.4. ∎

10. Proof of Theorem 1.1 - rigid cusp case -

Under Assumption 8.1, suppose that $P_{\alpha}\cong P_{\beta}$ is a rigid cusp. Thus the $2$ -orbifold $P_{\alpha}\cong P_{\beta}$ is isomorphic to $S^{2}(p,q,r)$ where $(p,q,r)=(2,4,4)$ , $(2,3,6)$ , or $(3,3,3)$ .

Let $G<\Gamma$ be the orbifold fundamental group $\pi_{1}(P_{\alpha})$ , and let $\Lambda$ be the subgroup of $G$ consisting of parabolic transformations. We may assume that (a) $G$ stabilises the ideal point $\infty$ of the upper-half space model of $\mathbb{H}^{3}$ , and (b) the boundary $\partial H_{\alpha}$ of the canonical horoball $H_{\alpha}$ is identified with the horosphere $\mathbb{C}\times\{1\}\subset\mathbb{H}^{3}$ . For each element $g\in\Lambda$ , let $|g|$ be the length of $g$ in the canonical horosphere (see Section 7), namely $|g|=|g|_{\partial H_{\alpha}}$ , the translation length of $g$ in $\partial H_{\alpha}$ , and simply call it the length of $g$ . Let $L_{1}(\Lambda)>0$ be the minimum of the lengths of nontrivial elements of $\Lambda$ . More generally, for each $n\in\mathbb{N}$ , let $L_{n}(\Lambda)$ be the $n$ -th shortest length of nontrivial elements of $\Lambda$ .

Case 1. $P_{\alpha}\cong S^{2}(2,4,4)$ . Then $G\cong\langle a,b,c\ |\ a^{2},\ b^{4},\ c^{4},abc\rangle$ , and $\Lambda$ is the rank $2$ free abelian group with free basis $\{b^{2}a,c^{2}a\}$ . We may assume the action of $G$ on the horosphere $\partial H_{\alpha}=\mathbb{C}\times 1\cong\mathbb{C}$ is given by the following rule. There is a positive real $\ell$ such that $a$ is the $\pi$ rotation about $0$ , and $b$ and $c$ are the $\pi/2$ rotations about $\ell$ and $\ell i$ , respectively. We can easily observe the following.

(i)

The shortest length $L_{1}(\Lambda)$ is equal to $2\ell$ , and it is attained precisely by the conjugates of $b^{2}a$ in $G$ . (Note that $c^{2}a=(b^{-1}a^{-1})^{2}a=b^{-1}a^{-1}b^{-1}=b^{3}ab^{-1}=b(b^{2}a)b^{-1}$ is conjugate to $b^{2}a$ .)
(ii)

The second shortest length $L_{2}(\Lambda)$ is equal to $2\sqrt{2}\ell$ , and it is attained precisely by the conjugates of $b^{2}ac^{2}a$ in $G$ .
(iii)

The third shortest length $L_{3}(\Lambda)$ is equal to $4\ell$ , and it is attained precisely by the conjugates of $(b^{2}a)^{2}$ in $G$ .

By Lemma 7.1(1), $2\ell=L_{1}(\Lambda)\geq 1$ , and so $\ell\geq\frac{1}{2}$ . Since $\Gamma$ is non-free, Lemma 7.1(3) implies that the length $|\alpha|$ of the parabolic element $\alpha\in\Lambda$ is less than $2$ . Since $L_{3}(\Lambda)=4\ell\geq 2$ , $|\alpha|$ is equal to either $L_{1}(\Lambda)$ or $L_{2}(\Lambda)$ . By using this fact, we obtain the following lemma.

Lemma 10.1.

The parabolic element $\alpha\in\Lambda$ is conjugate to $b^{2}a$ or $b^{2}ac^{2}a$ in $G$ . Moreover the following hold.

(1)

If $\alpha$ is conjugate to $b^{2}a$ , then the images of $\alpha$ by the natural epimorphisms from $G\cong\pi_{1}(S^{2}(2,4,4))$ to $\pi_{1}(S^{2}(2,2,2))$ , $\pi_{1}(S^{2}(2,2,4))$ , and $\pi_{1}(S^{2}(2,4,2))$ have order $2$ .
(2)

If $\alpha$ is conjugate to $b^{2}ac^{2}a$ , then the images of $\alpha$ by the natural epimorphisms from $G\cong\pi_{1}(S^{2}(2,4,4))$ to $\pi_{1}(S^{2}(2,2,2))$ , $\pi_{1}(S^{2}(2,2,4))$ , and $\pi_{1}(S^{2}(2,4,2))$ have order $1$ , $2$ and $2$ , respectively. Moreover, the $\mathbb{Z}_{2}$ -homology class of $\alpha$ vanishes.

Proof.

The assertion in the first line follows from the observations preceding the lemma. The assertions (1) and (2) can be checked easily, by using the fact that $b^{2}a$ is conjugate to $c^{2}a$ in $G$ . ∎

Now let ${\mathcal{O}}$ be the orbifold obtained from the pared orbifold $(M_{0},P)$ by the orbifold surgery as illustrated in Figure 8. Namely, for each index $4$ edge of the singular set which has an endpoint in $P_{\alpha}$ or $P_{\beta}$ , we replace the index $4$ with the index $2$ , and then cap all resulting spherical boundary components with discal $3$ -orbifolds. Then each of $P_{\alpha}$ and $P_{\beta}$ shrinks into a vertex of ${\mathcal{O}}$ with link $S^{2}(2,2,2)$ , which we denote by $v_{\alpha}$ and $v_{\beta}$ , respectively. We denote by $e_{\alpha}$ (resp. $e_{\beta}$ ) the edge of the singular set $\Sigma({\mathcal{O}})$ incident on $v_{\alpha}$ (resp. $v_{\beta}$ ) whose index in the original orbifold $M_{0}$ is $2$ .

Lemma 10.2.

The orbifold ${\mathcal{O}}$ is isomorphic to a spherical dihedral orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ for some $r\in\mathbb{Q}$ and coprime positive integers $d_{+}$ and $d_{-}$ . Moreover, $\alpha\in\Lambda$ is conjugate to $b^{2}a$ in $G$ , and the homology class $[\alpha]\in H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ determined by $\alpha$ is equal to the meridian of the edge $e_{\alpha}$ . Similarly, the homology class $[\beta]\in H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ is equal to the meridian of the edge $e_{\beta}$ .

Proof.

By Lemma 10.1, $\alpha$ is conjugate to $b^{2}a$ or $b^{2}ac^{2}a$ in $G=\pi_{1}(S^{2}(2,4,4))$ , its image in $\pi_{1}(S^{2}(2,2,2))$ has order $2$ or $1$ accordingly. Hence the image of $\alpha$ in $\pi_{1}({\mathcal{O}})$ has order $\leq 2$ . Moreover, the images of $\alpha$ and $\beta$ have the same order, because (a) if the exchanging involution $f$ belongs to $\Gamma$ then $\alpha$ and $\beta$ are conjugate in $\Gamma$ and so in $\pi_{1}({\mathcal{O}})$ , and (b) if $f\notin\Gamma$ then $f$ descends to an involution on ${\mathcal{O}}$ which interchanges the images of $\alpha$ and $\beta$ . Hence $\pi_{1}({\mathcal{O}})$ is either the trivial group or a dihedral group. Since ${\mathcal{O}}$ is very good by Lemma 6.4 and since it has a singular point with link $S^{2}(2,2,2)$ , $\pi_{1}({\mathcal{O}})$ is a noncyclic dihedral group. Hence, by Theorem 4.1, ${\mathcal{O}}$ is isomorphic to a spherical dihedral orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ .

We prove the remaining assertions. If $\alpha\in\Gamma$ is conjugate to $b^{2}ac^{2}a$ , then it descends to the trivial element of $\pi_{1}(S^{2}(2,2,2))$ , and so it represents the trivial element of $\pi_{1}({\mathcal{O}})$ . This contradicts the fact that $\pi_{1}({\mathcal{O}})$ is a dihedral group generated by the images of $\alpha$ and $\beta$ . Hence $\alpha$ is conjugate to $b^{2}a$ . This implies that the $\mathbb{Z}_{2}$ -homology class $[\alpha]\in H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ is equal to that represented by the element $a$ , and so it is the meridian of the edge $e_{\alpha}$ . The existence of the exchanging elliptic element $f$ implies the corresponding assertion for $[\beta]$ . ∎

Lemma 10.3.

The pared orbifold $(M_{0},P)$ is represented by the weighted graph $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-},\tilde{w})$ for some $r\in\mathbb{Q}$ , where $\tilde{w}$ is determined by the following rule (see Figure 9):

\tilde{w}(J_{1})=2,\quad\tilde{w}(J_{2})=4,\quad\tilde{w}(\tau_{+})=4,\quad\tilde{w}(\tau_{-})=m,

for some odd integer $m\geq 3$ , where $J_{1}$ and $J_{2}$ are unions of two mutually disjoint edges of the graph $K(r)\cup\tau_{+}\cup\tau_{-}$ distinct from $\tau_{\pm}$ , such that $K(r)=J_{1}\cup J_{2}$ . Moreover, $P_{\alpha}$ and $P_{\beta}$ correspond to distinct endpoints of $\partial\tau_{+}$ (in the sense of Convention 6.1(3)).

Proof.

By Lemma 10.2, ${\mathcal{O}}$ is represented by the weighted graph $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-},w)$ for some $r\in\mathbb{Q}$ , where $w$ is given by the rule

w(K(r))=2,\quad w(\tau_{+})=d_{+},\quad w(\tau_{-})=d_{-}

for some coprime positive integers $d_{+}$ and $d_{-}$ . Since ${\mathcal{O}}$ is obtained from $(M_{0},P)$ by an orbifold surgery, there is a weight function $\tilde{w}$ on the graph $K(r)\cup\tau_{+}\cup\tau_{-}$ such that the pared orbifold $(M_{0},P)$ is represented by the weighted graph $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-},\tilde{w})$ . By Remark 4.3, we may assume $d_{-}$ is odd, if necessary by replacing $r=q/p$ with $q^{\prime}/p$ where $qq^{\prime}\equiv 1\pmod{p}$ . Hence, we see $H_{1}({\mathcal{O}};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ by Lemma 6.5. Since $H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ is generated by $[\alpha]$ and $[\beta]$ , which are the meridians of the edges $e_{\alpha}$ and $e_{\beta}$ , respectively (see Lemma 10.2), we have $e_{\alpha}\neq e_{\beta}$ .

Since the links of $v_{\alpha}$ and $v_{\beta}$ are isomorphic to $S^{2}(2,2,2)$ , we see $w(\tau_{+})=2$ and $\{v_{\alpha},v_{\beta}\}\subset\partial\tau_{+}$ . Since $e_{\alpha}$ (resp. $e_{\beta}$ ) is the unique edge of the trivalent graph $K(r)\cup\tau_{+}\cup\tau_{-}$ incident on the vertex $v_{\alpha}$ (resp. $v_{\beta}$ ) with $\tilde{w}$ -weight $2$ , and since $e_{\alpha}\neq e_{\beta}$ , we see that $v_{\alpha}$ and $v_{\beta}$ are distinct endpoints of $\tau_{+}$ . (If $v_{\alpha}=v_{\beta}$ , then its ‘link’ in $M_{0}$ is of the form $S^{2}(2,2,*)\not\cong S^{2}(2,4,4)$ .) Hence $P_{\alpha}$ and $P_{\beta}$ correspond to distinct endpoints of $\partial\tau_{+}$ .

We observe that $e_{\alpha}$ and $e_{\beta}$ are not equal to $\tau_{+}$ . If, say $e_{\alpha}$ was equal to $\tau_{+}$ , then it is incident on $v_{\beta}\in\partial\tau_{+}$ . Since $\tilde{w}(e_{\alpha})=2$ , this implies we have $e_{\alpha}=e_{\beta}$ , a contradiction. This observation implies that both $e_{\alpha}$ and $e_{\beta}$ are contained in $K(r)$ .

We next observe that $d_{-}\geq 3$ . If $d_{-}=1$ , then the endpoints of $e_{\alpha}$ and $e_{\beta}$ are all contained in $\partial\tau_{+}=\{v_{\alpha},v_{\beta}\}$ . This together with the previous observation implies that the ‘links’ of $v_{\alpha}$ and $v_{\beta}$ in $M_{0}$ are isomorphic to $S^{2}(2,2,4)$ , a contradiction.

We now show that $e_{\alpha}$ and $e_{\beta}$ are disjoint. If they are not disjoint, then they share an endpoint of $\tau_{-}$ , which has odd weight $d_{-}$ . This implies that the meridians of $e_{\alpha}$ and $e_{\beta}$ represent an identical element of $H_{1}({\mathcal{O}};\mathbb{Z}_{2})$ (see Lemma 6.5(3)), and so $[\alpha]=[\beta]$ , a contradiction.

Set $J_{1}:=e_{\alpha}\cup e_{\beta}$ and let $J_{2}:=\operatorname{cl}(K(r)-J_{1})$ . Then $J_{1}$ and $J_{2}$ satisfy the desired conclusion with $m=d_{-}$ . ∎

We show that the situation described in Lemma 10.3 cannot happen. To this end, we perform another orbifold surgery on $(M_{0},P)$ which replaces the weight $4$ of $\tau_{+}$ with $2$ . To be precise, we consider the orbifold ${\mathcal{O}}^{\prime}$ represented by the weighted graph $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-},\tilde{w}^{\prime})$ for some $r\in\mathbb{Q}$ , where $\tilde{w}^{\prime}$ is given by the following rule.

\tilde{w}^{\prime}(J_{1})=2,\quad\tilde{w}^{\prime}(J_{2})=4,\quad\tilde{w}^{\prime}(\tau_{+})=2,\quad\tilde{w}^{\prime}(\tau_{-})=m

Note that $P_{\alpha}\cong S^{2}(2,4,4)$ shrinks into a singular point of ${\mathcal{O}}^{\prime}$ with link $S^{2}(2,2,4)$ or $S^{2}(2,4,2)$ . Since $\alpha$ is conjugate to $b^{2}a$ in $\pi_{1}(S^{2}(2,4,4))<\pi_{1}(M_{0})=\Gamma$ , we see by Lemma 10.1(1) that the image of $\alpha$ in $\pi_{1}({\mathcal{O}}^{\prime})$ has order $\leq 2$ . The same argument can be applied to $\beta$ and we see that the image of $\beta$ in $\pi_{1}({\mathcal{O}}^{\prime})$ also has order $\leq 2$ . Since ${\mathcal{O}}^{\prime}$ is very good by Lemma 6.4 and since the singular set of ${\mathcal{O}}^{\prime}$ contains a trivalent vertex, $\pi_{1}({\mathcal{O}}^{\prime})$ is a noncyclic dihedral group. Since the singular set of ${\mathcal{O}}^{\prime}$ contains four trivalent vertices, Theorem 4.1 implies that ${\mathcal{O}}^{\prime}$ must be isomorphic to a spherical dihedral orbifold ${\mathcal{O}}(r^{\prime};d_{+}^{\prime},d_{-}^{\prime})$ with $d_{+}^{\prime},d_{-}^{\prime}\geq 2$ . In particular, the singular set $\Sigma({\mathcal{O}}^{\prime})$ of ${\mathcal{O}}^{\prime}$ must contain precisely four or five edges with index $2$ . This contradicts the fact that $\Sigma({\mathcal{O}}^{\prime})$ contains precisely three edges of index $2$ (see Figure 9).

Case 2. $P_{\alpha}\cong S^{2}(2,3,6)$ . Then $G\cong\langle a,b,c\ |\ a^{2},\ b^{3},\ c^{6},\ abc\rangle$ , and $\Lambda$ is the rank $2$ free abelian group with free basis $\{ac^{3},c(ac^{3})c^{-1}=cac^{2}\}$ . We may assume the action of $G$ on the horosphere $\partial H_{\alpha}=\mathbb{C}\times 1\cong\mathbb{C}$ is given by the following rule. There is a positive real $\ell$ such that $a$ is the $\pi$ rotation about $\sqrt{3}\ell$ , $b$ is the $2\pi/3$ rotation about $2\ell e^{\pi i/6}=\sqrt{3}\ell+\ell i$ , and $c$ is the $\pi/3$ rotations about $0$ . The action of the generators of $\Lambda$ is given by

ac^{3}(z)=z+2\sqrt{3}\ell,\quad cac^{2}(z)=z+2\sqrt{3}\ell e^{\pi i/3}.

We can easily observe the following.

(i)

$L_{1}(\Lambda)=2\sqrt{3}\ell$ , and it is attained precisely by the conjugates of $ac^{3}$ in $G$ .
(ii)

$L_{2}(\Lambda)=6\ell$ , and it is attained precisely by the conjugates of $(ac^{3})(cac^{2})=ac^{4}ac^{2}$ in $G$ .
(iii)

$L_{3}(\Lambda)=4\sqrt{3}\ell$ , and it is attained precisely by the conjugates of $(ac^{3})^{2}$ in $G$ .

By Lemma 7.1(1), $2\sqrt{3}\ell=L_{1}(\Lambda)\geq 1$ , and so $\ell\geq\frac{1}{2\sqrt{3}}$ . Since $\Gamma$ is non-free, Lemma 7.1(3) implies that the length $|\alpha|$ of the parabolic element $\alpha\in\Lambda$ is less than $2$ . Hence we obtain the following.

Lemma 10.4.

The parabolic element $\alpha\in\Lambda$ is conjugate to $ac^{3}$ or $ac^{4}ac^{2}$ in $G$ .

Now let ${\mathcal{O}}$ be the orbifold obtained from the pared orbifold $(M_{0},P)$ by the orbifold surgery as illustrated in Figure 10. Namely, for each edge of the singular set which has the index $6$ cone point of $P_{\alpha}$ or $P_{\beta}$ as an endpoint, we replace the weight $6$ with the new weight $3$ , and then cap all resulting spherical boundary components with discal $3$ -orbifolds. Then $P_{\alpha}$ and $P_{\beta}$ shrink into singular points, $v_{\alpha}$ and $v_{\beta}$ , of ${\mathcal{O}}$ with link $S^{2}(2,3,3)$ .

Lemma 10.5.

The image of $\alpha$ by the natural epimorphism from $\pi_{1}(S^{2}(2,3,6))$ to $\pi_{1}(S^{2}(2,3,3))$ has order $2$ .

Proof.

By Lemma 10.4, $\alpha$ is conjugate to either $ac^{3}$ or $ac^{4}ac^{2}$ in $G=\pi_{1}(S^{2}(2,3,6))$ . Moreover, the images of $ac^{3}$ and $ac^{4}ac^{2}$ in $\pi_{1}(S^{2}(2,3,3))\cong\langle a,b,c\ |\ a^{2},\ b^{3},\ c^{3},\ abc\rangle$ have order $2$ . This is obvious for $ac^{3}$ , and the assertion for $ac^{4}ac^{2}$ is verified as follows. In $\pi_{1}(S^{2}(2,3,3))$ , we have $1=b^{3}=(ac^{-1})^{3}$ and so $ac^{-1}=(ac^{-1})^{-2}=(ca)^{2}$ . Hence the image of $ac^{4}ac^{2}$ in $\pi_{1}(S^{2}(2,3,3))$ is equal to $acac^{-1}=ac(ca)^{2}=ac^{2}aca=(ca)^{-1}a(ca)$ . Thus it is conjugate to $a$ , and so has order $2$ , as desired. ∎

By the above lemma, the image of $\alpha$ in $\pi_{1}({\mathcal{O}})$ has order $\leq 2$ . The existence of the exchanging elliptic element $f$ implies that the images of $\alpha$ and $\beta$ in $\pi_{1}({\mathcal{O}})$ have the same order. Thus $\pi_{1}({\mathcal{O}})$ is either a dihedral group or the trivial group. Since ${\mathcal{O}}$ is very good by Lemma 6.4 and since the singular set of ${\mathcal{O}}$ contains a trivalent vertex, $\pi_{1}({\mathcal{O}})$ is a noncyclic dihedral group. Hence, Theorem 4.1 implies that ${\mathcal{O}}$ must be isomorphic to a spherical dihedral orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ with $(d_{+},d_{-})\neq(1,1)$ . However, the orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ does not contain a singular point with link $S^{2}(2,3,3)$ , a contradiction.

Case 3. $P_{\alpha}\cong S^{2}(3,3,3)$ . Then the inverting elliptic element $h$ does not belong to $\Gamma$ , and the group, $\Gamma_{h}$ , obtained from $\Gamma$ by adding $h$ is a $\mathbb{Z}_{2}$ -extension of $\Gamma$ . Consider the hyperbolic orbifold $M_{h}:=\mathbb{H}^{3}/\Gamma_{h}$ . Then $M_{h}$ is the quotient of $M=\mathbb{H}^{3}/\Gamma$ by the isometric involution induced by $h$ , which we continue to denote by $h$ . Set $(M_{h,0},P_{h}):=(M_{0}/h,P/h)$ , $P_{h,\alpha}:=P_{\alpha}/h$ and $P_{h,\beta}:=P_{\beta}/h$ . Then $P_{h,\alpha}\cong P_{h,\beta}$ is isomorphic to $S^{2}(2,3,6)$ . Thus $G_{h}:=\pi_{1}(P_{h,\alpha})\cong\langle a,b,c\ |\ a^{2},\ b^{3},\ c^{6},\ abc\rangle$ . Since the subgroup $\Gamma$ of $\Gamma_{h}$ generated by $\alpha$ and $\beta$ is non-free, we see by the arguments in Case 2 that $\alpha$ is conjugate to $ac^{3}$ or $ac^{4}ac^{2}$ in $G_{h}$ .

Let ${\mathcal{O}}_{h}$ be the orbifold obtained from the pared orbifold $(M_{h,0},P_{h})$ by the orbifold surgery as illustrated in Figure 10 at both $P_{h,\alpha}$ and $P_{h,\beta}$ . Then $P_{h,\alpha}$ and $P_{h,\beta}$ shrink into singular points, $v_{h,\alpha}$ and $v_{h,\beta}$ , of ${\mathcal{O}}_{h}$ with link $S^{2}(2,3,3)$ . The images of $\alpha$ and $\beta$ in $\pi_{1}({\mathcal{O}}_{h})$ have the same order $\leq 2$ , and so the subgroup of $\pi_{1}({\mathcal{O}}_{h})$ they generate is either a dihedral group or the trivial group. This subgroup has index $\leq 2$ in $\pi_{1}({\mathcal{O}}_{h})$ , because $\Gamma=\langle\alpha,\beta\rangle$ has index $2$ in $\Gamma_{h}$ . Hence the group $\pi_{1}({\mathcal{O}}_{h})$ is a trivial group, a dihedral group, $\mathbb{Z}_{2}$ (the $\mathbb{Z}_{2}$ -extension of the trivial group) or a $\mathbb{Z}_{2}$ -extension of a dihedral group.

Since ${\mathcal{O}}_{h}$ is very good by Lemma 6.4 and ${\mathcal{O}}_{h}$ contains a singular point with link $S^{2}(2,3,3)$ , $\pi_{1}({\mathcal{O}})$ is either a noncyclic dihedral group or a $\mathbb{Z}_{2}$ -extension of a noncyclic dihedral group. Hence Theorem 4.1 implies that ${\mathcal{O}}_{h}$ is isomorphic to (a) a spherical dihedral orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ or (b) the quotient of ${\mathcal{O}}(r;d_{+},d_{-})$ by an isometric involution, where $(d_{+},d_{-})\neq(1,1)$ . Since ${\mathcal{O}}(r;d_{+},d_{-})$ does not have a singular point with link $S^{2}(2,3,3)$ , (a) cannot happen, and so we may assume (b) holds. Since $\pi_{1}(S^{2}(2,3,3))$ does not have an index $2$ subgroup, the link of an inverse image of the singular point $v_{h,\alpha}$ in the double cover ${\mathcal{O}}(r;d_{+},d_{-})$ of ${\mathcal{O}}_{h}$ is also isomorphic to $S^{2}(2,3,3)$ . But, this is impossible. Hence $P_{\alpha}$ cannot be isomorphic to $S^{2}(3,3,3)$ .

Thus we have proved that $P_{\alpha}\cong P_{\beta}$ cannot be a rigid cusp.

11. Proof of Theorem 1.1 - flexible cusp: exceptional case -

In this section, we treat the case where the following assumption is satisfied, and prove that this assumption is never satisfied.

Assumption 11.1.

Under Assumption 8.1, we further assume that $P_{\alpha}=P_{\beta}$ and it is a flexible cusp $S^{2}(2,2,2,2)$ and that the conclusion (2) in Lemma 9.1 holds. Namely, $f\notin\Gamma$ , and $P_{\alpha}/f=P_{\beta}/f\cong S^{2}(2,4,4)$ (see Figure 11).

Let $\hat{\Gamma}:=\langle\Gamma,f\rangle$ be the group generated by $\Gamma$ and $f$ . Let $\hat{M}:=\mathbb{H}^{3}/\hat{\Gamma}$ be the quotient hyperbolic orbifold. Let $\hat{M}_{0}$ be the non-cuspidal part of $\hat{M}$ , and $\hat{P}=\partial\hat{M}_{0}$ the parabolic locus. By abuse of notation, we denote the pared orbifold obtained as the relative compactification of $(\hat{M}_{0},\hat{P})$ by the same symbol $(\hat{M}_{0},\hat{P})$ . We denote the component of the compact euclidean $2$ -orbifold $\hat{P}$ corresponding to the conjugacy class containing $\alpha$ and $\beta=f\alpha f^{-1}$ by $\hat{P}_{\alpha\beta}$ . Thus $\hat{P}_{\alpha\beta}\cong P_{\alpha}/f=P_{\beta}/f\cong S^{2}(2,4,4)$ and $(M_{0},P)/f\cong(\hat{M}_{0},\hat{P})$ , where $f$ denotes the involution on the pared orbifold $(M_{0},P)$ induced by the exchanging involution $f$ . In particular, $M_{0}$ is the double orbifold covering of $\hat{M}_{0}$ , associated with the homomorphism $\xi:\pi_{1}(\hat{M}_{0})=\Gamma\to\mathbb{Z}_{2}$ such that $\xi(\alpha)=\xi(\beta)=0$ and $\xi(f)=1$ . We denote the homomorphism $H_{1}(\hat{M}_{0};\mathbb{Z}_{2})\to\mathbb{Z}_{2}$ induced by $\xi$ by the same symbol.

Note that $\pi_{1}(\hat{P}_{\alpha\beta})\cong\pi_{1}(S^{2}(2,4,4))\cong\langle a,b,c\ |\ a^{2},\ b^{4},\ c^{4},abc\rangle$ . As in Case 1 in Section 10, we identify $\pi_{1}(\hat{P}_{\alpha\beta})$ with the stabiliser $\operatorname{Stab}_{\hat{\Gamma}}(\operatorname{Fix}(\alpha))$ . Then the proof of Lemma 10.1 also works in this setting, because $\{\alpha,\beta\}$ generates the non-free subgroup $\Gamma$ of the Kleinian group $\hat{\Gamma}$ , and we have the following lemma.

Lemma 11.2.

The parabolic element $\alpha$ is conjugate to $b^{2}a$ or $b^{2}ac^{2}a$ in $\operatorname{Stab}_{\hat{\Gamma}}(\operatorname{Fix}(\alpha))$ $\cong$ $\pi_{1}(S^{2}(2,4,4))$ , and of course, the assertions (1) and (2) in Lemma 10.1 also hold.

Let $e_{i}$ and $\hat{e}_{i}$ ( $i=1,2,3$ ) be the edges of the singular sets $\Sigma(M_{0})$ and $\Sigma(\hat{M}_{0})$ as illustrated in Figure 11. Thus $e_{2}$ and $e_{3}$ are contained in the fixed point set of the involution $f$ on $M_{0}$ , and $\hat{e}_{i}$ is the image of $e_{i}$ by the covering projection $M_{0}\to\hat{M}_{0}$ . (Note that it can happen that some of them are identical, though their germs near the parabolic locus are different.) Then the following holds.

Lemma 11.3.

The homomorphism $\xi:H_{1}(\hat{M}_{0};\mathbb{Z}_{2})\to\mathbb{Z}_{2}$ , that determines the double orbifold covering $M_{0}\to\hat{M}_{0}$ , satisfies

\xi(m_{1})=0,\quad\xi(m_{2})=\xi(m_{3})=1,

where $m_{i}$ denotes the meridian of the edge $\hat{e}_{i}$ . Moreover, the homology class $[f]\in H_{1}(\hat{M}_{0};\mathbb{Z}_{2})$ determined by $f\in\hat{\Gamma}$ is equal to either $m_{2}$ or $m_{3}$ .

Proof.

The formula for $\xi$ follows from the fact that the fixed point set of the involution $f$ on $M_{0}$ contains $e_{2}$ and $e_{3}$ , which project to $\hat{e}_{2}$ and $\hat{e}_{3}$ , respectively. It is also obvious that $\xi([f])=1$ . So, if $H_{1}(\hat{M}_{0};\mathbb{Z}_{2})\cong\mathbb{Z}_{2}$ , we have $[f]=m_{2}=m_{3}$ . Suppose that $H_{1}(\hat{M}_{0};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ . Then, since $H_{1}(\hat{M}_{0};\mathbb{Z}_{2})$ is generated by $[f]$ and $[\alpha]$ , we see $[\alpha]\neq 0$ . So, $\alpha$ is conjugate to $b^{2}a$ by Lemma 11.2. (Otherwise $\alpha$ is conjugate to $b^{2}ac^{2}a$ and so $[\alpha]=0$ .) Therefore $[\alpha]=[a]=m_{1}$ is contained in $\operatorname{Ker}(\xi)\cong\mathbb{Z}_{2}$ . Thus $\operatorname{Ker}(\xi)$ is generated by $m_{1}$ . Since $\xi([f])=\xi(m_{2})$ , it follows that $[f]$ is equal to either $m_{2}$ or $m_{1}+m_{2}=m_{3}$ . ∎

Let $\hat{\mathcal{O}}$ be the orbifold obtained from the pared orbifold $(\hat{M}_{0},\hat{P}_{\alpha\beta})$ by the orbifold surgery that replaces the index $4$ of the edges $\hat{e}_{2}$ and $\hat{e}_{3}$ with the index $2$ . Then $\hat{P}_{\alpha\beta}$ shrinks into a singular point, $v_{\alpha\beta}$ , with link $S^{2}(2,2,2)$ , and the image of $\alpha$ in $\pi_{1}(\hat{\mathcal{O}})$ has order $\leq 2$ by Lemma 11.2. Since $\hat{\Gamma}$ is generated by $f$ and $\alpha$ , $\pi_{1}(\hat{\mathcal{O}})$ is either trivial, $\mathbb{Z}_{2}=D_{1}$ or a noncyclic dihedral group. By using Lemma 6.4, Theorem 4.1 and the fact that $\hat{\mathcal{O}}$ has a singular point with link $S^{2}(2,2,2)$ , we see that $\hat{\mathcal{O}}$ is isomorphic to a spherical dihedral orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ with noncyclic dihedral orbifold fundamental group. Moreover, we may assume that $d_{+}=2$ and that $v_{\alpha\beta}$ is an endpoint of $\tau_{+}$ . By Lemma 6.5, we have $H_{1}(\hat{\mathcal{O}};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ .

Lemma 11.4.

Under the above setting, $|K(r)|=1$ and so the edges $\hat{e}_{i}$ ( $i=1,2,3$ ) are all distinct.

Proof.

We first observe that $\alpha$ cannot be conjugate to $b^{2}ac^{2}a$ . In fact, if $\alpha$ was conjugate to $b^{2}ac^{2}a$ , then its image in $\pi_{1}(\hat{\mathcal{O}})$ is trivial by Lemma 11.2 (cf. Lemma 10.1(2)), and so $\pi_{1}(\hat{\mathcal{O}})$ is generated by the image of $f$ . This contradicts the fact that $\pi_{1}(\hat{\mathcal{O}})$ is a noncyclic dihedral group. This observation together with Lemma 11.2 implies that $\alpha$ is conjugate to $b^{2}a$ and so $[\alpha]=[a]=m_{1}\in\operatorname{Ker}(\xi)$ . Moreover, $[f]=m_{2}$ or $m_{3}$ by Lemma 11.3. Hence $H_{1}(\hat{\mathcal{O}};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ is generated by the meridians of the three edges $\hat{e}_{i}$ ( $i=1,2,3$ ) incident on the vertex $v_{\alpha\beta}\in\partial\tau_{+}$ .

Now suppose on the contrary that $|K(r)|=2$ . Then we see, by using Lemma 6.5, that the meridian of $\tau_{+}$ represents the trivial element of $H_{1}(\hat{\mathcal{O}};\mathbb{Z}_{2})$ and the meridians of the remaining two edges incident on $v_{\alpha\beta}\in\partial\tau_{+}$ represent the identical element of $H_{1}(\hat{\mathcal{O}};\mathbb{Z}_{2})$ . This contradicts the fact that $H_{1}(\hat{\mathcal{O}};\mathbb{Z}_{2})\cong(\mathbb{Z}_{2})^{2}$ . Hence $|K(r)|=1$ . This implies that the the edges $\hat{e}_{i}$ ( $i=1,2,3$ ) incident on $v_{\alpha\beta}\in\partial\tau_{+}$ are all distinct, as desired. ∎

Recall that the weights of the edges $\hat{e}_{1}$ , $\hat{e}_{2}$ , $\hat{e}_{3}$ of $\Sigma(\hat{M}_{0})$ are $2,4,4$ . Since $\hat{e}_{2}\neq\hat{e}_{3}$ by Lemma 11.4, we can apply the orbifold surgery on $(\hat{M}_{0},\hat{P})$ of “type $(2,4,4)\to(2,2,4)$ ”, namely we can replace the index $4$ of the edge $\hat{e}_{2}$ of the singular set $\Sigma(\hat{M}_{0})$ with the index $2$ , and leave the other indices, including the index $4$ of $\hat{e}_{3}$ , unchanged. We denote the resulting orbifold by $\hat{\mathcal{O}}_{(2,2,4)}$ . By Lemma 11.2, $\alpha$ has order at most $2$ in $\pi_{1}(\hat{\mathcal{O}}_{(2,2,4)})$ . Hence, by using Lemma 6.4, Theorem 4.1, and the fact that $\hat{\mathcal{O}}_{(2,2,4)}$ has a singular point with link $S^{2}(2,2,4)$ , we see that $\hat{\mathcal{O}}_{(2,2,4)}$ is isomorphic to a spherical dihedral orbifold ${\mathcal{O}}(r;d_{+},d_{-})$ with noncyclic dihedral orbifold fundamental group. Moreover, we may assume $d_{+}=4$ and that the parabolic locus $P_{\alpha\beta}$ degenerates into a singular point, $v_{\alpha\beta}$ , which is an endpoint of $\tau_{+}$ . It should be noted that the edge $\hat{e}_{3}$ of $\Sigma(\hat{M}_{0})$ corresponds to $\tau_{+}$ . (Here, we reset the notation, and the symbols ${\mathcal{O}}(r;d_{+},d_{-})$ and $v_{\alpha\beta}$ now represent objects different from those they had represented in the paragraph preceding Lemma 11.4.)

Case 1. $d_{-}\geq 3$ . We apply the orbifold surgery on $(\hat{M}_{0},\hat{P})$ of “type $(2,4,4)\to(2,4,2)$ ”, namely we replace the index $4$ of the edge $\hat{e}_{3}=\tau_{+}$ of the singular set $\Sigma(\hat{M}_{0})$ with the index $2$ , and leave the other indices, including the index $4$ of $\hat{e}_{2}$ , unchanged. (This is possible by Lemma 11.4.) We denote the resulting orbifold by $\hat{\mathcal{O}}_{(2,4,2)}$ . By Lemma 11.2, $\alpha$ has order at most $2$ in $\pi_{1}(\hat{\mathcal{O}}_{(2,4,2)})$ . Hence, again by using Lemma 6.4, Theorem 4.1, and the fact that $\hat{\mathcal{O}}_{(2,4,2)}$ has a singular point with link $S^{2}(2,4,2)$ , we see that $\hat{\mathcal{O}}_{(2,4,2)}$ is isomorphic to a spherical dihedral orbifold with noncyclic dihedral orbifold fundamental group. Note that the edges $\hat{e}_{2}$ and $\tau_{-}$ of $\Sigma(\hat{\mathcal{O}}_{(2,4,2)})$ , which have indices $4$ and $d_{-}\geq 3$ , respectively, share a common endpoint (see Figure 12). But this cannot happen in any spherical dihedral orbifold, a contradiction.

Case 2. $d_{-}=1$ . Then $(\hat{M}_{0},\hat{P})$ is represented by a weighted graph $(S^{3},K(r)\cup\tau_{+},\hat{w})$ , such that $K(r)=\hat{e}_{1}\cup\hat{e}_{2}$ is a knot, $\hat{e}_{3}=\tau_{+}$ , and

\hat{w}(\tau_{+})=4,\quad\hat{w}(\hat{e}_{1})=2,\quad\hat{w}(\hat{e}_{2})=4.

Recall that the subset $\hat{e}_{2}\cup\hat{e}_{3}=\hat{e}_{2}\cup\hat{\tau}_{+}$ of $\Sigma(\hat{M}_{0})$ are the images of the fixed point set of the involution $f$ on $M_{0}$ . This implies that the map $|M_{0}|\to|\hat{M}_{0}|$ induced by the orbifold covering $M_{0}\to\hat{M}_{0}$ is the double branched covering branched over $\hat{e}_{2}\cup\hat{e}_{3}$ . Hence $(M_{0},P)$ is represented by the weighted graph illustrated in Figure 13. Here, we assume the extended Convention 6.2, and the two $4$ -valent vertices represent parabolic loci isomorphic to $S^{2}(2,2,2,2)$ . Hence we see by Lemma 6.4 that $H_{1}(M_{0};\mathbb{Z})\cong(\mathbb{Z}_{2})^{3}$ , a contradiction.

Thus we have proved that the situation in Assumption 11.1 cannot occur. This completes the proof of the main Theorem 1.1.

12. Appendix 1: Spherical orbifolds with dihedral orbifold fundamental groups

In this appendix, we classify the orientable spherical $3$ -orbifolds with dihedral orbifold fundamental groups (Proposition 12.2), and determine the (orientation-preserving) isometry groups of these orbifolds (Propositions 12.5 and 12.6). Proposition 12.2 is used in the proof of Theorem 4.1, and Corollary 12.7 is used in Section 9. Propositions 12.5 and 12.6 are used in the companion [4] of this paper. The classification of the spherical dihedral orbifolds is implicitly contained in Dunber’s work [21], which classifies the Seifert fibered orbifolds. The isometry groups of the dihedral spherical orbifolds obtained as the $\pi$ -orbifolds associated with $2$ -bridge links are calculated by [50, 27]. Moreover, in the recent papers [38, 39], Mecchia and Seppi classified the Seifert fibered spherical $3$ -orbifolds and calculated the isometry groups of such orbifolds. Since every spherical dihedral orbifold is Seifert fibered, the results in this section are implicitly contained in [38, 39]. However, we give a self-contained proof, because it is not a simple task to translate their results into the form we need.

We first recall basic facts concerning the $3$ -dimensional spherical geometry following [54, 50]. Let $\mathcal{H}$ be the quaternion skew field. We use the symbol $q$ to denote a generic quaternion

q=a+bi+cj+dk\in\mathcal{H}\quad(a,b,c,d\in\mathbb{R}).

(We believe this does not cause any confusion, even though $q$ is also used to denote the numerator of a rational number $r=q/p$ .) For each $q\in\mathcal{H}$ , $\bar{q}=a-bi-cj-dk$ denotes its conjugate, $\Re(q)=a$ denotes its real part, and $|q|$ denotes its norm $\sqrt{q\bar{q}}=\sqrt{a^{2}+b^{2}+c^{2}+d^{2}}$ . We identify $S^{n}$ ( $n=1,2,3$ ) with the following subspaces of $\mathcal{H}$ .

	$\displaystyle S^{3}$	$\displaystyle:=\{q\in\mathcal{H}\,\|\,\|q\|=1\}$
	$\displaystyle S^{2}$	$\displaystyle:=\{q\in\mathcal{H}\,\|\,\|q\|=1,\quad\Re(q)=0\}$
	$\displaystyle S^{1}$	$\displaystyle:=\{z\in\mathbb{C}\subset\mathcal{H}\,\|\,\|z\|=1\}$

The norm $|\cdot|$ induces a Euclidean metric on $\mathcal{H}$ , and $S^{n}$ ( $n=1,2,3$ ) are endowed with the induced metrics. The subspaces $S^{3}$ and $S^{1}$ form a Lie group with respect to the restriction of the product in $\mathcal{H}$ . The group $S^{3}$ acts on itself by conjugation leaving $S^{2}$ invariant. This gives an epimorphism $\psi:S^{3}\to\operatorname{Isom}^{+}(S^{2})$ , with $\ker\psi=\langle-1\rangle$ , defined by

\psi(q)(x)=qx\bar{q}\quad(q\in S^{3},\ x\in S^{2}).

If $q=\cos\theta+q_{0}\sin\theta$ with $q_{0}\in S^{2}$ , then $\psi(q)$ is the rotation of $S^{2}$ , by angle $2\theta$ , with fixed points $\pm q_{0}$ .

For a positive integer $n$ , any cyclic subgroup of order $n$ (resp. any dihedral subgroup of order $2n$ ) of $\operatorname{Isom}^{+}(S^{2})$ is conjugate to the subgroup $\mathbb{Z}_{n}:=\psi(\mathbb{Z}_{n}^{*})$ (resp. $\mathbb{D}_{n}:=\psi(\mathbb{D}_{n}^{*})$ ), where $\mathbb{Z}_{n}^{*}:=\langle\omega\rangle$ and $\mathbb{D}_{n}^{*}:=\langle\omega,\ j\rangle$ with $\omega=\exp(\pi i/n)$ . Note that these groups are contained in the subgroup $\mathbb{D}_{S}:=\langle S^{1},j\rangle=S^{1}\sqcup S^{1}j$ of $S^{3}$ . Then the following hold (see, e.g. [50, Proposition 2.6]).

Lemma 12.1.

(1) If $n\geq 2$ , then the normaliser $N(\mathbb{Z}_{n}^{*})$ of $\mathbb{Z}_{n}^{*}$ in $S^{3}$ is equal to $\mathbb{D}_{S}$ .

(2) If $n\geq 3$ , then the normaliser $N(\mathbb{D}_{n}^{*})$ of $\mathbb{D}_{n}^{*}$ in $S^{3}$ is equal to $\mathbb{D}_{2n}^{*}$ . If $n=2$ , then $N(\mathbb{D}_{n}^{*})$ is equal to the binary octahedral group $O^{*}=\psi^{-1}(O)$ , where $O<\operatorname{Isom}^{+}(S^{2})$ is the octahedral group obtained as the subgroup of $\operatorname{Isom}^{+}(S^{2})$ preserving the regular octahedron in the $3$ -dimensional Euclidean subspace $\langle i,j,k\rangle$ of $\mathcal{H}$ spanned by the $6$ vertices $\{\pm i,\pm j,\pm k\}$ .

Let $\phi:S^{3}\times S^{3}\to\operatorname{Isom}^{+}(S^{3})$ be the homomorphism defined by

\phi(q_{1},q_{2})(q)=q_{1}qq_{2}^{-1}.

Then $\phi$ is an ephimorphism with $\operatorname{Ker}\phi=\langle(-1,-1)\rangle\cong\mathbb{Z}_{2}$ .

We occasionally identify $S^{3}\subset\mathcal{H}$ with the unit sphere

S^{3}=\{(z_{1},z_{2})\in\mathbb{C}^{2}\,|\,|z_{1}|^{2}+|z_{2}|^{2}=1\}

in $\mathbb{C}^{2}$ by the correspondence $q=z_{1}+z_{2}j\leftrightarrow(z_{1},z_{2})$ . Let ${\mathrm{L}}:S^{1}\times S^{1}\to\operatorname{Isom}^{+}(S^{3})$ be the injective homomorphism defined by

{\mathrm{L}}(\omega_{1},\omega_{2})(z_{1},z_{2})=(\omega_{1}z_{1},\omega_{2}z_{2}).

When $\omega_{\ell}=\exp(2\pi i\frac{k_{\ell}}{n_{\ell}})$ ( ${\ell}=1,2$ ), where $\frac{k_{\ell}}{n_{\ell}}$ is a rational number, we write

(1)

\displaystyle{\mathrm{L}}(\omega_{1},\omega_{2})={\mathrm{L}}(\frac{k_{1}}{n_{1}},\frac{k_{2}}{n_{2}}),

because its restriction to the circles $S^{3}\cap(\mathbb{C}\times\{0\})$ and $S^{3}\cap(\{0\}\times\mathbb{C})$ are the ‘ $\frac{k_{1}}{n_{1}}$ -rotation’ and ‘ $\frac{k_{2}}{n_{2}}$ -rotation’, respectively. Though the symbol ${\mathrm{L}}(\cdot,\cdot)$ is used in two different ways, we believe this does not cause any confusion, because its meaning is clearly understood from the context according to whether $\cdot$ is a unit complex or a rational number.

Observe that

\phi(\eta_{1},\eta_{2})={\mathrm{L}}(\eta_{1}\bar{\eta}_{2},\eta_{1}\eta_{2})\quad((\eta_{1},\eta_{2})\in S^{1}\times S^{1}).

In particular, we have

(2)

\displaystyle\phi(S^{1}\times S^{1})={\mathrm{L}}(S^{1}\times S^{1})<\operatorname{Isom}^{+}(S^{3}).

Consider the isometries $J:=\phi(j,j)$ , $J_{1}:=\phi(1,j)$ and $J_{2}:=\phi(j,1)$ , which acts on $S^{3}\subset\mathbb{C}^{2}$ as follows.

J(z_{1},z_{2})=(\bar{z}_{1},\bar{z}_{2}),\ J_{1}(z_{1},z_{2})=(z_{2},-z_{1}),\ J_{2}(z_{1},z_{2})=(-\bar{z}_{2},\bar{z}_{1})

Observe $J=J_{1}J_{2}$ and that

(3)

\displaystyle\phi(\mathbb{D}_{S}\times\mathbb{D}_{S})=\langle{\mathrm{L}}(S^{1}\times S^{1}),J,J_{1}\rangle,\quad\langle J,J_{1}\rangle\cong\mathbb{Z}_{2}\times\mathbb{Z}_{2}.

In fact, $\phi(\mathbb{D}_{S}\times\mathbb{D}_{S})$ is the split extension of ${\mathrm{L}}(S^{1}\times S^{1})$ by $\langle J,J_{1}\rangle\cong\mathbb{Z}_{2}\times\mathbb{Z}_{2}$ , where the action of $\langle J,J_{1}\rangle$ on ${\mathrm{L}}(S^{1}\times S^{1})$ by conjugation is given by the following formula.

(4)

\displaystyle J{\mathrm{L}}(\omega_{1},\omega_{2})J^{-1}={\mathrm{L}}(\bar{\omega}_{1},\bar{\omega}_{2}),\quad J_{1}{\mathrm{L}}(\omega_{1},\omega_{2})J_{1}^{-1}={\mathrm{L}}(\omega_{2},\omega_{1})

The following proposition gives a classification of the orientable spherical $3$ -orbifolds with dihedral orbifold fundamental groups.

Proposition 12.2.

Let ${\mathcal{O}}$ be an oriented spherical $3$ -orbifold. Then $\pi_{1}({\mathcal{O}})$ is isomorphic to a dihedral group, if and only if ${\mathcal{O}}$ is isomorphic to the orbifold, ${\mathcal{O}}(r;d_{1},d_{2})$ , represented by the weighted graph $(S^{3},K(r)\cup\tau_{+}\cup\tau_{-},w)$ in Figure 6 for some $r\in\mathbb{Q}$ and coprime positive integers $d_{1}$ and $d_{2}$ , where $w$ is given by the following rule.

w(K(r))=2,\quad w(\tau_{+})=d_{1},\quad w(\tau_{-})=d_{2}.

In fact, ${\mathcal{O}}(r;d_{1},d_{2})$ with $r=q/p$ is isomorphic to $S^{3}/\Gamma$ , where $\Gamma$ is the subgroup of $\operatorname{Isom}^{+}(S^{3})$ given by

(5)

\displaystyle\Gamma=\left\langle{\mathrm{L}}(\frac{k_{1}}{pd_{2}},\frac{k_{2}}{pd_{1}}),\ J\right\rangle\cong D_{n}\quad\mbox{with $n=pd_{1}d_{2}$}

for some integers $k_{1}$ and $k_{2}$ such that

(6)

\displaystyle\gcd(pd_{2},k_{1})=1,\quad\gcd(pd_{1},k_{2})=1,\quad k_{2}\equiv qk_{1}\pmod{p}.

Moreover, the spherical structure of ${\mathcal{O}}(r;d_{1},d_{2})$ is unique, i.e., if $\Gamma^{\prime}$ is a subgroup of $\operatorname{Isom}^{+}(S^{3})$ such that $S^{3}/\Gamma^{\prime}$ is isomorphic to ${\mathcal{O}}(r;d_{1},d_{2})$ as oriented orbifolds, then $\Gamma^{\prime}$ is conjugate to the subgroup $\Gamma$ defined by (5).

Proof.

We first prove the only if part of the first assertion. Let $\Gamma$ be a subgroup of $\operatorname{Isom}^{+}(S^{3})$ isomorphic to the dihedral group $D_{n}$ , and let $f$ and $h$ be the elements of $\Gamma$ such that

\Gamma\cong\langle f,h\,|\,f^{n}=1,h^{2}=1,hfh^{-1}=f^{-1}\rangle.

(Though the symbols $\Gamma$ , $f$ and $h$ are used in different meanings in the previous sections, we believe this does not cause any confusion.) We show that $S^{3}/\Gamma$ is isomorphic to some ${\mathcal{O}}(q/p;d_{1},d_{2})$ , such that $n=pd_{1}d_{2}$ .

Claim 12.3.

After taking conjugation in $\operatorname{Isom}^{+}(S^{3})$ , we may assume $f={\mathrm{L}}(\frac{k_{1}}{pd_{2}},\frac{k_{2}}{pd_{1}})$ , where $p$ , $d_{1}$ , $d_{2}$ , $k_{1}$ , and $k_{2}$ are positive integers such that $\gcd(d_{1},d_{2})=1$ , $\gcd(pd_{2},k_{1})=1$ , $\gcd(pd_{1},k_{2})=1$ , and $n=pd_{1}d_{2}$ .

Proof of Claim 12.3.

Since any element of $S^{3}$ is conjugate to an element in $S^{1}$ , we may assume, by taking conjugation, that $f\in\phi(S^{1}\times S^{1})={\mathrm{L}}(S^{1}\times S^{1})$ (see (2)). Since $f$ has order $n$ , we may assume $f={\mathrm{L}}(\frac{k_{1}^{\prime}}{n},\frac{k_{2}^{\prime}}{n})$ for some integers $k_{1}^{\prime}$ and $k_{2}^{\prime}$ such that $\gcd(n,k_{1}^{\prime},k_{2}^{\prime})=1$ . For $\ell=1,2$ , set $d_{\ell}=\gcd(n,k_{\ell}^{\prime})$ , $n_{\ell}=\frac{n}{d_{\ell}}$ and $k_{\ell}=\frac{k_{\ell}^{\prime}}{d_{\ell}}$ , so that $f={\mathrm{L}}(\frac{k_{1}^{\prime}}{n},\frac{k_{2}^{\prime}}{n})={\mathrm{L}}(\frac{k_{1}}{n_{1}},\frac{k_{2}}{n_{2}})$ , where $\gcd(k_{1},n_{1})=\gcd(k_{2},n_{2})=1$ . Note also that $\gcd(d_{1},d_{2})=\gcd(n,k_{1}^{\prime},k_{2}^{\prime})=1$ . Set $p=\gcd(n_{1},n_{2})$ and $n_{\ell}^{\prime}=\frac{n_{\ell}}{p}$ ( ${\ell}=1,2$ ). Then $n=\operatorname{lcm}(n_{1},n_{2})=pn_{1}^{\prime}n_{2}^{\prime}$ . Thus $n_{1}d_{1}=n=pn_{1}^{\prime}n_{2}^{\prime}=n_{1}n_{2}^{\prime}$ and so $d_{1}=n_{2}^{\prime}$ . Similarly we have $d_{2}=n_{1}^{\prime}$ . Hence we have $n=pd_{1}d_{2}$ and $f={\mathrm{L}}(\frac{k_{1}}{n_{1}},\frac{k_{2}}{n_{2}})={\mathrm{L}}(\frac{k_{1}}{pd_{2}},\frac{k_{2}}{pd_{1}})$ . ∎

Now consider the subgroup $\langle f^{p}\rangle\cong\mathbb{Z}_{d_{1}d_{2}}$ generated by $f^{p}={\mathrm{L}}(\frac{k_{1}}{d_{2}},\frac{k_{2}}{d_{1}})$ . Since $\gcd(d_{1},d_{2})=1$ , we have

\langle f^{p}\rangle\cong\langle f^{pd_{2}}\rangle\times\langle f^{pd_{1}}\rangle\cong\mathbb{Z}_{d_{1}}\times\mathbb{Z}_{d_{2}}.

Note that

\langle f^{pd_{2}}\rangle=\langle{\mathrm{L}}(0,\frac{k_{2}d_{2}}{d_{1}})\rangle=\langle{\mathrm{L}}(0,\frac{1}{d_{1}})\rangle,\quad\langle f^{pd_{1}}\rangle=\langle{\mathrm{L}}(\frac{k_{1}d_{1}}{d_{2}},0)\rangle=\langle{\mathrm{L}}(\frac{1}{d_{2}},0)\rangle.

Hence we have

\langle f^{p}\rangle=\langle{\mathrm{L}}(0,\frac{1}{d_{1}})\rangle\times\langle{\mathrm{L}}(\frac{1}{d_{2}},0)\rangle.

Thus $S^{3}/\langle f^{p}\rangle$ is the orbifold with underlying space $S^{3}$ and with singular set the Hopf link, where one component has index $d_{1}$ and the other component has index $d_{2}$ . To give a precise description of this orbifold, identify $S^{3}$ with the join $S^{1}*S^{1}$ , by the correspondence $(tz_{1},\sqrt{1-t^{2}}z_{2})\leftrightarrow tz_{1}+(1-t)z_{2}$ . Thus the first and second factor circles of $S^{1}*S^{1}$ correspond to the circles $S^{1}\times\{0\}$ and $\{0\}\times S^{1}$ in $S^{3}\subset\mathbb{C}^{2}$ , respectively. For $\omega\in S^{1}$ , let ${\mathrm{L}}(\omega)$ be the isometry of $S^{1}$ defined by ${\mathrm{L}}(\omega)(z)=\omega z$ ( $z\in S^{1}$ ). Then the isometry ${\mathrm{L}}(\omega_{1},\omega_{2})$ is identified with the self-homeomorphism ${\mathrm{L}}(\omega_{1})*{\mathrm{L}}(\omega_{2})$ of $S^{1}*S^{1}$ , defined by

({\mathrm{L}}(\omega_{1})*{\mathrm{L}}(\omega_{2}))(tz_{1}+(1-t)z_{2})=t\omega_{1}z_{1}+(1-t)\omega_{2}z_{2}.

Under the above convention, the orbifold $S^{3}/\langle f^{p}\rangle$ is described as follows. The underlying space of the orbifold is given by

|S^{3}/\langle f^{p}\rangle|\cong\left(S^{1}/{\mathrm{L}}(\frac{1}{d_{2}})\right)*\left(S^{1}/{\mathrm{L}}(\frac{1}{d_{1}})\right)\cong S^{1}*S^{1}\cong S^{3},

and the singular set is the union of the two circles which gives the join structure of $S^{3}$ , where the first factor circle (which corresponds to $S^{1}/{\mathrm{L}}(\frac{1}{d_{2}})$ ) has index $d_{1}$ and the second factor circle (which corresponds to $S^{1}/{\mathrm{L}}(\frac{1}{d_{1}})$ ) has index $d_{2}$ . Here, ${\mathrm{L}}(\frac{1}{d_{\ell}})$ denotes ${\mathrm{L}}(e^{\frac{2\pi i}{d_{\ell}}})$ as in (1).

The isometry $f$ descends to the periodic isomorphism of the orbifold $S^{3}/\langle f^{p}\rangle\cong S^{1}*S^{1}$ given by ${\mathrm{L}}(\frac{k_{1}}{p})*{\mathrm{L}}(\frac{k_{2}}{p})$ , because the periodic map ${\mathrm{L}}(\frac{k_{1}}{pd_{2}})$ (resp. ${\mathrm{L}}(\frac{k_{2}}{pd_{1}})$ ) on $S^{1}$ descends to the periodic map ${\mathrm{L}}(\frac{k_{1}}{p})$ (resp. ${\mathrm{L}}(\frac{k_{2}}{p})$ ) on the circle $S^{1}/{\mathrm{L}}(\frac{1}{d_{2}})$ (resp. $S^{1}/{\mathrm{L}}(\frac{1}{d_{1}})$ ). Note that $\langle{\mathrm{L}}(\frac{k_{1}}{p})*{\mathrm{L}}(\frac{k_{2}}{p})\rangle=\langle{\mathrm{L}}(\frac{1}{p})*{\mathrm{L}}(\frac{q}{p})\rangle$ , with $q\equiv k_{1}^{-1}k_{2}\pmod{p}$ , where $k_{1}^{-1}$ is the inverse of $k_{1}$ in the multiplicative group $(\mathbb{Z}_{p})^{\times}$ (cf. Notation 1.3(2)). Hence we see that the orbifold $S^{3}/\langle f\rangle$ is isomorphic to the orbifold, ${\mathcal{O}}(L(p,q),d_{1},d_{2})$ , with underlying space the lens space, $L(p,q)$ , and with singular set the union of the core circles of the standard genus $1$ Heegaard splitting of $L(p,q)$ with indices $d_{1}$ and $d_{2}$ , respectively. (Though the notation $L(p,q)$ looks similar to the notation ${\mathrm{L}}(\cdot,\cdot)$ in (1), we believe there is no fear of confusion.)

Since $h^{2}=1$ and $hfh^{-1}=f^{-1}$ , we see by using Lemma 12.1(1) that $h=\phi(q_{1},q_{2})$ for some $(q_{1},q_{2})\in S^{1}j\times S^{1}j$ . Since any element of $S^{1}j$ is conjugate to $j$ by an element of $S^{1}$ , we may assume $h=\phi(j,j)=J$ , and so $h(z_{1},z_{2})=(\bar{z}_{1},\bar{z}_{2})$ . This implies that the involution $h$ of $S^{3}$ descends to the hyper-elliptic involution of $|S^{3}/\langle f\rangle|\cong L(p,q)$ . Recall that (i) the quotient map determined by the hyper-elliptic involution gives the double branched covering of $S^{3}$ branched over the $2$ -bridge link $K(q/p)$ and that (ii) the core circles of the genus $1$ Heegaard splitting project to the upper and lower tunnels, respectively. Hence, the quotient $S^{3}/\Gamma$ , with $\Gamma=\langle f,h\rangle\cong D_{n}$ , is isomorphic to the orbifold ${\mathcal{O}}(q/p;d_{1},d_{2})$ . This completes the proof of the only if part of the first assertion. The proof also shows that the group $\Gamma$ is given by the formula (5) for some integers $k_{1}$ and $k_{2}$ satisfying the condition (6).

The if part of the first assertion follows from the above argument and the following claim.

Claim 12.4.

For any rational number $r=q/p$ and a pair of coprime integers $(d_{1},d_{2})$ , there is a pair $(k_{1},k_{2})$ of integers which satisfies the condition (6).

Proof of Claim 12.4.

Consider the homomorphism

\Psi:(\mathbb{Z}_{pd_{2}})^{\times}\times(\mathbb{Z}_{pd_{1}})^{\times}\to(\mathbb{Z}_{p})^{\times}\times(\mathbb{Z}_{p})^{\times}\to(\mathbb{Z}_{p})^{\times},

where the first homomorphism is the product of the natural projections and the second homomorphism maps $(k_{1},k_{2})\in(\mathbb{Z}_{p})^{\times}\times(\mathbb{Z}_{p})^{\times}$ to $k_{1}^{-1}k_{2}\in(\mathbb{Z}_{p})^{\times}$ . Then both of the two homomorphisms are surjective and so is their composition $\Psi$ . Regard the numerator $q$ of the rational number $r=q/p$ as an element of $(\mathbb{Z}_{p})^{\times}$ , and let $(k_{1},k_{2})$ be a pair of integers which projects to an element in the inverse image $\Psi^{-1}(q)$ . Then $(k_{1},k_{2})$ satisfies the condition (6). ∎

Finally we prove the uniqueness of the spherical structure on the orbifold ${\mathcal{O}}(q/p;d_{1},d_{2})$ . The preceding arguments show that the triple $(q/p,d_{1},d_{2})\in\mathbb{Q}\times\mathbb{N}\times\mathbb{N}$ uniquely determines a dihedral subgroup $\Gamma<\operatorname{Isom}^{+}(S^{3})$ , up to conjugation, such that $S^{3}/\Gamma$ is isomorphic to ${\mathcal{O}}(q/p;d_{1},d_{2})$ as oriented orbifolds. Thus we have only to show that there are no unexpected orientation-preserving topological isomorphism between two orbifolds, ${\mathcal{O}}(q/p;d_{1},d_{2})=S^{3}/\Gamma$ and ${\mathcal{O}}(q^{\prime}/p^{\prime};d_{1}^{\prime},d_{2}^{\prime})=S^{3}/\Gamma^{\prime}$ .

Assume that ${\mathcal{O}}(q/p;d_{1},d_{2})$ and ${\mathcal{O}}(q^{\prime}/p^{\prime};d_{1}^{\prime},d_{2}^{\prime})$ are isomorphic as oriented orbifolds. Then $pd_{1}d_{2}=p^{\prime}d_{1}^{\prime}d_{2}^{\prime}$ and $\{d_{1},d_{2}\}=\{d_{1}^{\prime},d_{2}^{\prime}\}$ , because they have isomorphic orbifold fundamental groups and the same index sets of the singular sets. In particular we have $p=p^{\prime}$ .

Suppose first that $n:=pd_{1}d_{2}\geq 3$ . Then $D_{n}$ has the unique cyclic subgroup of index $2$ , and so each of ${\mathcal{O}}(q/p;d_{1},d_{2})$ and ${\mathcal{O}}(q^{\prime}/p^{\prime};d_{1}^{\prime},d_{2}^{\prime})$ has the unique double orbifold covering with cyclic orbifold fundamental group. The underlying spaces of the covering orbifolds are the lens spaces $L(p,q)$ and $L(p^{\prime},q^{\prime})$ , respectively. Hence, by the classification of lens spaces, we have $p=p^{\prime}$ and either $q\equiv q^{\prime}\pmod{p}$ or $qq^{\prime}\equiv 1\pmod{p}$ . Moreover, by using the uniqueness of the genus one Heegaard splittings (see [12, 13]), we see that ${\mathcal{O}}(q/p;d_{1},d_{2})$ and ${\mathcal{O}}(q^{\prime}/p^{\prime};d_{1}^{\prime},d_{2}^{\prime})$ are isomorphic as oriented orbifolds if and only if one of the following conditions hold.

(1)

$p=p^{\prime}$ , $q\equiv q^{\prime}\pmod{p}$ , and $(d_{1},d_{2})=(d_{1}^{\prime},d_{2}^{\prime})$ .
(2)

$p=p^{\prime}$ , $qq^{\prime}\equiv 1\pmod{p}$ , and $(d_{1},d_{2})=(d_{2}^{\prime},d_{1}^{\prime})$ .

In both cases, we can see that the subgroups $\Gamma$ and $\Gamma^{\prime}$ are conjugate in $\operatorname{Isom}^{+}(S^{3})$ .

In the exceptional case when $n:=pd_{1}d_{2}=2$ , we have either (i) $p=p^{\prime}=1$ and $\{d_{1},d_{2}\}=\{d_{1}^{\prime},d_{2}^{\prime}\}=\{1,2\}$ or (ii) $p=p^{\prime}=2$ and $d_{1}=d_{2}=d_{1}^{\prime}=d_{2}^{\prime}=1$ . We can easily see that the subgroups $\Gamma$ and $\Gamma^{\prime}$ are conjugate in $\operatorname{Isom}^{+}(S^{3})$ .

This completes the uniqueness of the spherical structure. ∎

Next, we calculate the (orientation-preserving) isometry group of the dihedral spherical $3$ -orbifold ${\mathcal{O}}(q/p;d_{1},d_{2})$ . If $(d_{1},d_{2})=(1,1)$ , then ${\mathcal{O}}(q/p;d_{1},d_{2})$ is the $\pi$ -orbifold, ${\mathcal{O}}(q/p)$ , associated with the $2$ -bridge link $K(q/p)$ (cf. [11]) and its isometry group is calculated by [50, Theorem 4.1] and [27, Corollary 3.2.11]. (There are errors in [50, Theorem 4.1] for the special case when $p=1$ , $2$ . There are also misprints for the generic case in the statement of Theorem 4.1, though the correct result can be found in the tables in [50, p.184].)

Proposition 12.5.

The orientation-preserving isometry group of the spherical orbifold ${\mathcal{O}}(q/p):={\mathcal{O}}(q/p;1,1)$ is described as follows.

(1)

If $q\not\equiv\pm 1\pmod{p}$ , then the following holds.

\operatorname{Isom}^{+}({\mathcal{O}}(q/p))\cong\begin{cases}(\mathbb{Z}_{2})^{2}&\text{if $q^{2}\not\equiv 1\pmod{p}$}\\ D_{4}&\text{if $p$ is odd and $q^{2}\equiv 1\pmod{p}$}\\ &\text{or if $p$ is even and $q^{2}\equiv p+1\pmod{2p}$}\\ (\mathbb{Z}_{2})^{3}&\text{if $p$ is even and $q^{2}\equiv 1\pmod{2p}$}\end{cases}

(2)

If $q\equiv\pm 1\pmod{p}$ , then then the following holds.

\operatorname{Isom}^{+}({\mathcal{O}}(q/p))\cong\begin{cases}S^{1}\rtimes\mathbb{Z}_{2}&\text{if $p$ is odd and $\geq 3$}\\ S^{1}\rtimes(\mathbb{Z}_{2})^{2}&\text{if $p$ is even and $\geq 4$}\\ (S^{1}\times S^{1})\rtimes(\mathbb{Z}_{2})^{2}&\text{if $p=2$}\\ (S^{1}\times S^{1})\rtimes\mathbb{Z}_{2}&\text{if $p=1$}\end{cases}

In the remainder of this section, we treat the remaining case $(d_{1},d_{2})\neq(1,1)$ . In the very special case, when $p=1$ and $\{d_{1},d_{2}\}=\{1,2\}$ , we call ${\mathcal{O}}(0/1;1,2)$ the trivial $\theta$ -orbifold, because its singular set is the trivial $\theta$ -curve in $S^{3}$ . Then we have the following proposition.

Proposition 12.6.

The orientation-preserving isometry group of the spherical dihedral orbifold ${\mathcal{O}}(q/p;d_{1},d_{2})$ with $(d_{1},d_{2})\neq(1,1)$ is described as follows.

(1)

$\operatorname{Isom}^{+}({\mathcal{O}}(q/p;d_{1},d_{2}))\cong(\mathbb{Z}_{2})^{2}$ , except when ${\mathcal{O}}(q/p;d_{1},d_{2})$ is isomorphic to the trivial $\theta$ -orbifold ${\mathcal{O}}(0/1;1,2)$ , i.e. except when $p=1$ and $\{d_{1},d_{2}\}=\{1,2\}$ .
(2)

For the the trivial $\theta$ -orbifold ${\mathcal{O}}(0/1;1,2)$ , we have $\operatorname{Isom}^{+}({\mathcal{O}}(0/1;1,2))\cong D_{3}\times\mathbb{Z}_{2}$ .

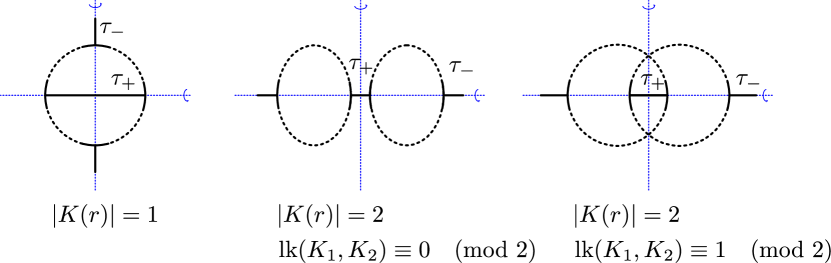
Before proving the proposition, we give the following consequence of the proposition (and the orbifold theorem), which is used in the proof of the main theorem.

Corollary 12.7.

Consider a spherical orbifold ${\mathcal{O}}(q/p;d_{1},d_{2})$ with $(d_{1},d_{2})\neq(1,1)$ , and let $g$ be an orientation-preserving involution of the orbifold. Then the following hold.

(1)

Except when $p=1$ and $\{d_{1},d_{2}\}=\{1,2\}$ , (i.e. except when ${\mathcal{O}}(q/p;d_{1},d_{2})$ is isomorphic to the trivial $\theta$ -orbifold ${\mathcal{O}}(0/1;1,2)$ ), $g$ stabilises the edges $\tau_{+}$ and $\tau_{-}$ of the singular set (when it is contained in the singular set).
(2)

If $d_{1},d_{2}\geq 2$ , then $g$ does not stabilise any edge of the singular set different from $\tau_{\pm}$ .

Proof of Corollary 12.7.

By the orbifold theorem, we may assume $g$ is an isometry of the spherical orbifold. (This is proved by applying the orbifold theorem to the finite group action on the universal cover $S^{3}$ of ${\mathcal{O}}(q/p;d_{1},d_{2})$ generated by a lift of $g$ and the covering transformation group.) On the other hand, the action of $\operatorname{Isom}^{+}({\mathcal{O}}(q/p;d_{1},d_{2}))$ in the generic case is as illustrated in Figure 14. (See also [4, Figure 6-8], and replace the weights $\infty$ with $2$ , then we obtain the desired visualisation, besides the exceptional case.) The exceptional case where the orbifold is the trivial $\theta$ -orbifold is illustrated in Figure 15. The assertion (1) is now obvious from Figure 14. The assertion (2) also follows from the figure by noting that $K(r)$ consists of four edges if $d_{1},d_{2}\geq 2$ (otherwise, $K(r)$ consists of two edges). ∎

The proof of Proposition 12.6 presented below is parallel to that of [50, Theorem 4.1]. Consider the dihedral spherical $3$ -orbifold ${\mathcal{O}}(q/p;d_{1},d_{2})$ with $(d_{1},d_{2})\neq(1,1)$ . By Proposition 12.2, the orbifold fundamental group $\pi_{1}({\mathcal{O}}(q/p;d_{1},d_{2}))$ is identified with the subgroup

\Gamma=\left\langle{\mathrm{L}}(\frac{k_{1}}{pd_{2}},\frac{k_{2}}{pd_{1}}),\ J\right\rangle=\langle{\mathrm{L}}(\omega_{1},\omega_{2}),\ J\rangle<\operatorname{Isom}^{+}(S^{3})

where $\omega_{1}=\exp(2\pi i\frac{k_{1}}{pd_{2}})$ , $\omega_{2}=\exp(2\pi i\frac{k_{2}}{pd_{1}})$ for some integers $k_{1}$ and $k_{2}$ satisfying the condition (6). Pick $(\eta_{1},\eta_{2})\in S^{1}\times S^{1}$ such that $(\omega_{1},\omega_{2})=(\eta_{1}\bar{\eta}_{2},\eta_{1}\eta_{2})$ . Then $\Gamma=\langle\phi(\eta_{1},\eta_{2}),\phi(j,j)\rangle$ . Set

\tilde{\Gamma}:=\phi^{-1}(\Gamma)=\langle(\eta_{1},\eta_{2}),(j,j)\rangle<S^{3}\times S^{3}.

Then $\operatorname{Isom}^{+}{\mathcal{O}}(q/p;d_{1},d_{2})\cong N(\tilde{\Gamma})/\tilde{\Gamma}$ , where $N(\tilde{\Gamma})$ is the normaliser of $\tilde{\Gamma}$ in $S^{3}\times S^{3}$ .

For $\ell=1,2$ , set $\tilde{\Gamma}_{\ell}=\mathrm{pr}_{\ell}(\tilde{\Gamma})$ , where $\mathrm{pr}_{\ell}:S^{3}\times S^{3}\to S^{3}$ is the projection to the $\ell$ -th factor. Then $\tilde{\Gamma}_{\ell}=\langle\eta_{\ell},j\rangle=\mathbb{D}_{m_{\ell}}^{*}$ for some positive integer $m_{\ell}$ . Then the following lemma is obvious from the definition of $\mathbb{D}_{m_{\ell}}^{*}$ , where $o(\cdot)$ denotes the order of a group element.

Lemma 12.8.

(1) $o(\eta_{\ell}^{2})=m_{\ell}$ .

(2) If $m_{\ell}$ is even, then $o(\eta_{\ell})=2m_{\ell}$ . If $m_{\ell}$ is odd, then $o(\eta_{\ell})$ is either $m_{\ell}$ or $2m_{\ell}$ .

Note that the orientation-reversing isometry $c:S^{3}\to S^{3}$ , defined by $c(q)=\bar{q}$ , acts on $\operatorname{Isom}^{+}(S^{3})$ by conjugation, as follows:

c\phi(q_{1},q_{2})c^{-1}=\phi(q_{2},q_{1})

Hence, we assume $m_{1}\leq m_{2}$ without loss of generality.

Lemma 12.9.

(1) $2\leq m_{1}\leq m_{2}$ .

(2) If $m_{1}=2$ , then $m_{2}=2m_{2}^{\prime}$ for some odd integer $m_{2}^{\prime}$ , and $\{d_{1},d_{2}\}=\{1,2\}$ . Moreover, $m_{1}=m_{2}=2$ if and only if $p=1$ .

Proof.

(1) Suppose on the contrary that $m_{1}=1$ . Then $\eta_{1}=\pm 1$ , and so $(\omega_{1},\omega_{2})=\pm(\bar{\eta}_{2},\eta_{2})$ . This implies $pd_{2}=o(\omega_{1})=o(\omega_{2})=pd_{1}$ and therefore $d_{1}=d_{2}$ . Since $\gcd(d_{1},d_{2})=1$ , we have $d_{1}=d_{2}=1$ , a contradiction.

(2) Suppose $m_{1}=2$ . Then $\eta_{1}=\pm i$ , and so $(\omega_{1},\omega_{2})=\pm(i\bar{\eta}_{2},i\eta_{2})$ . By using Lemma 12.8, we can verify the following, from which the assertion (2) follows.

(i)

If $m_{2}$ is odd, then $(o(\omega_{1}),o(\omega_{2}))=(4m_{2},4m_{2})$ and so $d_{1}=d_{2}=1$ as in (1), a contradiction.
(ii)

If $m_{2}=2m_{2}^{\prime}$ for some odd integer $m_{2}^{\prime}$ , then $\omega_{1}^{m_{2}^{\prime}}=-\omega_{2}^{m_{2}^{\prime}}=\pm 1$ and so $\{pd_{2},pd_{1}\}=\{o(\omega_{1}),o(\omega_{2})\}=\{m_{2}^{\prime},2m_{2}^{\prime}\}$ . Hence we have $p=m_{2}^{\prime}$ and $\{d_{1},d_{2}\}=\{1,2\}$ .
(iii)

If $m_{2}=4m_{2}^{\prime}$ for some integer $m_{2}^{\prime}$ , then $\omega_{1}^{2m_{2}^{\prime}}=-\omega_{2}^{2m_{2}^{\prime}}=\pm i$ and so $o(\omega_{1})=o(\omega_{2})=8m_{2}^{\prime}$ . Hence $d_{1}=d_{2}=1$ , a contradiction.

∎

Lemma 12.10.

Except for the special case where $p=1$ and $\{d_{1},d_{2}\}=\{1,2\}$ , namely except when ${\mathcal{O}}(q/p;d_{1},d_{2})$ is the trivial $\theta$ -orbifold, we have

N(\tilde{\Gamma})<\mathbb{D}_{2m_{1}}^{*}\times\mathbb{D}_{2m_{2}}^{*}<\mathbb{D}_{S}\times\mathbb{D}_{S}.

Proof.

If $m_{1}\geq 3$ , then Lemma 12.1 implies $N(\tilde{\Gamma}_{\ell})=\mathbb{D}_{2m_{\ell}}^{*}$ for each $\ell=1,2$ (because $m_{2}\geq m_{1}$ by assumption), and hence we have $N(\tilde{\Gamma})<N(\tilde{\Gamma}_{1})\times N(\tilde{\Gamma}_{2})<\mathbb{D}_{2m_{1}}^{*}\times\mathbb{D}_{2m_{2}}^{*}$ .

Since $m_{2}\geq m_{1}\geq 2$ by Lemma 12.9(1), we have only to treat the case where $m_{1}=2$ . Since we exclude the case where $p=1$ and $\{d_{1},d_{2}\}=\{1,2\}$ , Lemma 12.9(2) implies $m_{2}\geq 3$ , and so $N(\tilde{\Gamma}_{2})=\mathbb{D}_{2m_{2}}^{*}$ . On the other hand, since $m_{1}=2$ , we see by Lemma 12.1 that $N(\tilde{\Gamma}_{1})=O^{*}$ . Hence $N(\tilde{\Gamma})<O^{*}\times\mathbb{D}_{2m_{2}}^{*}$ .

Now observe that the decomposition $\mathbb{D}_{S}=S^{1}\sqcup S^{1}j$ induces the decomposition of $\tilde{\Gamma}<\mathbb{D}_{S}\times\mathbb{D}_{S}$ into the following two non-empty subsets.

\tilde{\Gamma}^{(1)}:=\tilde{\Gamma}\cap(S^{1}\times S^{1})\quad\mbox{and}\quad\tilde{\Gamma}^{(j)}:=\tilde{\Gamma}\cap(S^{1}j\times S^{1}j).

Note that $\mathrm{pr}_{1}(\tilde{\Gamma}^{(1)})=\langle i\rangle=\{\pm 1,\pm i\}$ and $\mathrm{pr}_{1}(\tilde{\Gamma}^{(j)})=\langle i\rangle j=\{\pm j,\pm k\}$ . Pick an arbitrary element $(q_{1},q_{2})\in N(\tilde{\Gamma})$ . Then $q_{2}\in\mathbb{D}_{2m_{2}}^{*}<\mathbb{D}_{S}$ , and so the inner-automorphism of $S^{3}$ determined by $q_{2}$ preserves the subgroup $S^{1}<\mathbb{D}_{S}$ . Thus the inner-automorphism of $S^{3}\times S^{3}$ determined by $(q_{1},q_{2})$ preserves the subset $\tilde{\Gamma}^{(1)}$ of $\tilde{\Gamma}=\tilde{\Gamma}^{(1)}\sqcup\tilde{\Gamma}^{(j)}$ . Hence the inner-automorphism of $S^{3}$ determined by $q_{1}$ preserves the subgroup $\mathrm{pr}_{1}(\tilde{\Gamma}^{(1)})=\langle i\rangle$ , and so it preserves the subset $\{\pm i\}$ , i.e., $q_{1}i\bar{q}_{1}=\pm i$ . By the description of $O^{*}$ in Lemma 12.1, this implies that $q_{1}\in\mathbb{D}_{2}^{*}<\mathbb{D}_{2m_{1}}^{*}$ . Hence $(q_{1},q_{2})\in\mathbb{D}_{2m_{1}}^{*}\times\mathbb{D}_{2m_{2}}^{*}$ , as desired. ∎

Lemma 12.11.

The normaliser $N(\Gamma)$ of $\Gamma$ in $\operatorname{Isom}^{+}S^{3}$ is contained in $\langle{\mathrm{L}}(S^{1}\times S^{1}),J\rangle$ .

Proof.

By the formula (3) and Lemma 12.10, we have

N(\Gamma)=\phi(N(\tilde{\Gamma}))<\phi(\mathbb{D}_{S}\times\mathbb{D}_{S})=\langle{\mathrm{L}}(S^{1}\times S^{1}),J,J_{1}\rangle.

Since $J\in\Gamma$ , we have only to show that $J_{1}\notin N(\Gamma)$ . To this end, recall that $\Gamma=\langle{\mathrm{L}}(\frac{k_{1}}{pd_{2}},\frac{k_{2}}{pd_{1}}),J\rangle$ . Now suppose on the contrary that $J_{1}\in N(\Gamma)$ . Then the conjugation by $J_{1}$ preserves the subgroup $\langle{\mathrm{L}}(\frac{k_{1}}{pd_{2}},\frac{k_{2}}{pd_{1}})\rangle$ and we have $J_{1}{\mathrm{L}}(\frac{k_{1}}{pd_{2}},\frac{k_{2}}{pd_{1}})J_{1}^{-1}={\mathrm{L}}(\frac{k_{2}}{pd_{1}},\frac{k_{1}}{pd_{2}})$ by (4). Thus we have $d_{1}=d_{2}$ and so $d_{1}=d_{2}=1$ , a contradiction. Hence $J_{1}\notin N(\Gamma)$ as desired. ∎

Lemma 12.12.

Except when ${\mathcal{O}}(q/p;d_{1},d_{2})$ is the trivial $\theta$ -orbifold, we have the following.

	$\displaystyle N(\Gamma)$	$\displaystyle=\left\langle{\mathrm{L}}(\frac{k_{1}}{2pd_{2}},\frac{k_{2}}{2pd_{1}}),\ {\mathrm{L}}(\frac{1}{2},0),\ {\mathrm{L}}(0,\frac{1}{2}),\ J\right\rangle$
		$\displaystyle\cong\left\langle{\mathrm{L}}(\frac{k_{1}}{2pd_{2}},\frac{k_{2}}{2pd_{1}}),\ {\mathrm{L}}(\frac{1}{2},0),\ {\mathrm{L}}(0,\frac{1}{2})\right\rangle\rtimes\langle J\rangle$

Proof.

Recall that $\Gamma=\langle{\mathrm{L}}(\omega_{1},\omega_{2}),J\rangle$ where $\omega_{1}=\exp(2\pi i\frac{k_{1}}{pd_{2}})$ and $\omega_{2}=\exp(2\pi i\frac{k_{2}}{pd_{1}})$ . Set $\sqrt{\omega_{1}}=\exp(\pi i\frac{k_{1}}{pd_{2}})$ and $\sqrt{\omega_{2}}=\exp(\pi i\frac{k_{2}}{pd_{1}})$ . Suppose an element ${\mathrm{L}}(\zeta_{1},\zeta_{2})\in{\mathrm{L}}(S^{1}\times S^{1})$ belongs to $N(\Gamma)$ . Then ${\mathrm{L}}(\zeta_{1}^{2},\zeta_{2}^{2})J={\mathrm{L}}(\zeta_{1},\zeta_{2})J{\mathrm{L}}(\zeta_{1},\zeta_{2})^{-1}\in\Gamma$ , and hence $(\zeta_{1},\zeta_{2})$ belongs to the subgroup $\langle(\sqrt{\omega_{1}},\sqrt{\omega_{2}}),\ (-1,1),\ (1,-1)\rangle$ .

Conversely, the image by ${\mathrm{L}}$ of any element in the above subgroup belongs to $N(\Gamma)$ . Hence

	$\displaystyle N(\Gamma)\cap{\mathrm{L}}(S^{1}\times S^{1})$	$\displaystyle=\langle{\mathrm{L}}(\sqrt{\omega_{1}},\sqrt{\omega_{2}}),\ {\mathrm{L}}(-1,1),\ {\mathrm{L}}(1,-1)\rangle$
		$\displaystyle=\left\langle{\mathrm{L}}(\frac{k_{1}}{2pd_{2}},\frac{k_{2}}{2pd_{1}}),\ {\mathrm{L}}(\frac{1}{2},0),\ {\mathrm{L}}(0,\frac{1}{2})\right\rangle.$

(Recall the abuse of notation given by (1).) This together with Lemma 12.11 implies the desired result. ∎

Proof of Proposition 12.6.

Consider the spherical dihedral orbifold ${\mathcal{O}}(q/p;d_{1},d_{2})$ with $(d_{1},d_{2})\neq(1,1)$ . We first treat the generic case where ${\mathcal{O}}(q/p;d_{1},d_{2})$ is not the trivial $\theta$ -orbifold ${\mathcal{O}}(0/1;1,2)$ . Then, by using Lemma 12.12 and the fact that $J\in\Gamma$ , $\operatorname{Isom}^{+}{\mathcal{O}}(q/p;d_{1},d_{2})\cong N(\Gamma)/\Gamma$ is isomorphic to the quotient of the group $N:=\langle{\mathrm{L}}(\frac{k_{1}}{2pd_{2}},\frac{k_{2}}{2pd_{1}}),{\mathrm{L}}(\frac{1}{2},0),{\mathrm{L}}(0,\frac{1}{2})\rangle$ by its subgroup $G:=\langle{\mathrm{L}}(\frac{k_{1}}{pd_{2}},\frac{k_{2}}{pd_{1}})\rangle$ . Set $a={\mathrm{L}}(\frac{k_{1}}{2pd_{2}},\frac{k_{2}}{2pd_{1}})$ , $b_{1}={\mathrm{L}}(\frac{1}{2},0)$ and $b_{2}={\mathrm{L}}(0,\frac{1}{2})$ . It should be noted that $\langle b_{1},b_{2}\rangle\cong(\mathbb{Z}_{2})^{2}$ and that the subset $\{b_{1},b_{2},b_{1}b_{2}\}$ is equal to the set of all order $2$ elements of ${\mathrm{L}}(S^{1}\times S^{1})$ .

Note that the order of $L(\frac{k_{1}}{2pd_{2}})$ is equal to $2pd_{2}$ or $pd_{2}$ according to whether $k_{1}$ is odd or even. Similarly, the order of $L(\frac{k_{2}}{2pd_{1}})$ is equal to $2pd_{1}$ or $pd_{1}$ according to whether $k_{2}$ is odd or even. Thus the order of $a={\mathrm{L}}(\frac{k_{1}}{2pd_{2}},\frac{k_{2}}{2pd_{1}})$ is $2pd_{1}d_{2}$ or $pd_{1}d_{2}$ , where the latter happens if and only if both $k_{1}$ and $k_{2}$ are even.

Case 1. $o(a)=2pd_{1}d_{2}$ . Then the element $a^{pd_{1}d_{2}}\in L(S^{1}\times S^{1})$ has order $2$ . Hence it is equal to one of the elements of $\{b_{1},b_{2},b_{1}b_{2}\}$ . Thus $\langle a\rangle\cap\langle b_{1},b_{2}\rangle\cong\mathbb{Z}_{2}$ . This implies that $N\cong\langle a\,|\,a^{2pd_{1}d_{2}}\rangle\oplus\langle b_{\ell}\,|\,b_{\ell}^{2}\rangle$ for some ${\ell}\in\{1,2\}$ . Since $G$ corresponds to the subgroup $\langle a^{2}\rangle$ , we have

\operatorname{Isom}^{+}{\mathcal{O}}(q/p;d_{1},d_{2})\cong N/\langle a^{2}\rangle\cong\langle a\,|\,a^{2}\rangle\oplus\langle b_{\ell}\,|\,b_{\ell}^{2}\rangle\cong(\mathbb{Z}_{2})^{2}.

Case 2. $o(a)=pd_{1}d_{2}$ . Since $o(a^{2})=o({\mathrm{L}}(\frac{k_{1}}{pd_{2}},\frac{k_{2}}{pd_{1}}))=pd_{1}d_{2}$ , we have $o(a)=o(a^{2})$ , and so $o(a)=pd_{1}d_{2}$ is odd. Thus $\langle a\rangle\cap\langle b_{1},b_{2}\rangle=\{1\}$ , and therefore $N\cong\langle a\,|\,a^{pd_{1}d_{2}}\rangle\oplus\langle b_{1}\,|\,b_{1}^{2}\rangle\oplus\langle b_{2}\,|\,b_{2}^{2}\rangle$ . Hence, we have

\operatorname{Isom}^{+}{\mathcal{O}}(q/p;d_{1},d_{2})\cong N/\langle a^{2}\rangle\cong N/\langle a\rangle\cong\langle b_{1}\,|\,b_{1}^{2}\rangle\oplus\langle b_{2}\,|\,b_{2}^{2}\rangle\cong(\mathbb{Z}_{2})^{2}.

This completes the proof of Proposition 12.6 in the generic case.

In the exceptional case, where ${\mathcal{O}}(q/p;d_{1},d_{2})$ is the trivial $\theta$ -orbifold ${\mathcal{O}}(0/1;1,2)$ , we may assume

\tilde{\Gamma}=\langle(i,i),(j,j)\rangle=\{\pm(1,1),\pm(i,i),\pm(j,j),\pm(k,k)\}.

Then, by using Lemma 12.1, we can see that $N(\tilde{\Gamma})=\{(q,q)\,|\,q\in O^{*}\}\rtimes\langle J_{1}\rangle$ . Hence we have

\operatorname{Isom}^{+}{\mathcal{O}}(0/1;1,2)\cong\left(O^{*}/(\mathbb{Z}_{2})\right)\rtimes\mathbb{Z}_{2}\cong D_{3}\times\mathbb{Z}_{2}.

∎

13. Appendix 2: Non-spherical geometric orbifolds with dihedral orbifold fundamental groups

In this section, we classify the non-spherical geometric orbifolds with dihedral orbifold fundamental groups (Propositions 13.1 and 13.2). These results are used in the proof of Theorem 4.1.

We first deal with the dihedral orbifolds with $S^{2}\times\mathbb{R}$ geometry.

Proposition 13.1.

Let ${\mathcal{O}}$ be a compact orientable $S^{2}\times\mathbb{R}$ orbifold with nonempty singular set which satisfies the following conditions.

(i)

No component of $\partial{\mathcal{O}}$ is spherical.
(ii)

$\pi_{1}({\mathcal{O}})$ is a dihedral group.

Then ${\mathcal{O}}$ is isomorphic to one of the following orbifolds.

(1)

${\mathcal{O}}(\infty)$ , the orbifold represented by the weighted graph $(S^{3},K(\infty),w)$ , where $w$ takes the value $2$ at each component of the $2$ -bridge link $K(\infty)$ of slope $\infty$ , i.e. the $2$ -component trivial link.
(2)

${\mathcal{O}}(\mathbb{RP}^{3},O)$ , the orbifold with underlying space $\mathbb{RP}^{3}$ whose singular set is the trivial knot (i.e., the boundary of an embedded disc in $\mathbb{RP}^{3}$ ) with index $2$ .

Proof.

By the assumption that ${\mathcal{O}}$ has the geometry $S^{2}\times\mathbb{R}$ , we have $\pi_{1}({\mathcal{O}})<\operatorname{Isom}(S^{2}\times\mathbb{R})\cong\operatorname{Isom}(S^{2})\times\operatorname{Isom}(\mathbb{R})$ and $\operatorname{int}{\mathcal{O}}\cong(S^{2}\times\mathbb{R})/\pi_{1}({\mathcal{O}})$ . By the condition (ii), $\pi_{1}({\mathcal{O}})\cong D_{n}$ for some $n\in\mathbb{N}\cup\{\infty\}$ .

If $n\in\mathbb{N}$ , then the action of the finite dihedral group $\pi_{1}({\mathcal{O}})$ on $S^{2}\times\mathbb{R}$ extends to an action on the compact $3$ -manifold $S^{2}\times[-\infty,\infty]$ , where $[-\infty,\infty]\cong I$ is a compactification of $\mathbb{R}$ , and ${\mathcal{O}}$ is identified with $S^{2}\times[-\infty,\infty]/\pi_{1}({\mathcal{O}})$ . Thus ${\mathcal{O}}$ has a spherical boundary component, which contradicts the condition (i). So $n=\infty$ and $\pi_{1}({\mathcal{O}})\cong\langle f,h\ |\ h^{2},\ hfh=f^{-1}\rangle$ . Since the action of $\pi_{1}({\mathcal{O}})$ on $S^{2}\times\mathbb{R}$ is properly discontinuous, $f\in\operatorname{Isom}(S^{2}\times\mathbb{R})$ is the product of a (possibly trivial) rotation of $S^{2}$ and a nontrivial translation of $\mathbb{R}$ . Thus the orbifold ${\mathcal{O}}(f):=(S^{2}\times\mathbb{R})/\langle f\rangle$ is homeomorphic to the manifold $S^{2}\times S^{1}$ . The isometry $h$ descends to a fiber-preserving involution of ${\mathcal{O}}(f)\cong S^{2}\times S^{1}$ which acts on the second factor as a reflection. Thus ${\mathcal{O}}={\mathcal{O}}(f)/h$ is the quotient of $S^{2}\times[0,1]$ by an equivalence relation $(x,0)\sim(\gamma_{0}(x),0)$ and $(x,1)\sim(\gamma_{1}(x),1)$ where $\gamma_{0}$ and $\gamma_{1}$ are orientation-reversing involutions of $S^{2}$ . Thus $\gamma_{i}$ is conjugate to either the reflection in a great circle or the antipodal map. According to the combination (reflection, reflection), (reflection, antipodal map), or (antipodal map, antipodal map), ${\mathcal{O}}$ is isomorphic to ${\mathcal{O}}(\infty)$ , ${\mathcal{O}}(\mathbb{RP}^{3},O)$ , or $\mathbb{RP}^{3}\#\mathbb{RP}^{3}$ . The last case cannot happen because ${\mathcal{O}}$ has the empty singular set. ∎

The following proposition deals with the dihedral orbifolds with the remaining $6$ geometries.

Proposition 13.2.

Let ${\mathcal{O}}$ be a compact orientable $3$ -orbifold with nonempty singular set which has one of the $6$ geometries different from $S^{3}$ and $S^{2}\times\mathbb{R}$ and satisfies the following conditions.

(i)

$\pi_{1}({\mathcal{O}})$ is a dihedral group.
(ii)

No component of $\partial{\mathcal{O}}$ is spherical.

Then ${\mathcal{O}}$ is isomorphic to $D^{2}(2,2)\times I$ .

Proof.

Let $X$ be the geometry which ${\mathcal{O}}$ possesses. Then $X$ is $\mathbb{H}^{3}$ , $\mathbb{E}^{3}$ , $\widetilde{SL_{2}(\mathbb{R})}$ , $Nil$ or $Sol$ , and $\operatorname{int}{\mathcal{O}}$ is isomorphic to $X/\Gamma$ for some discrete subgroup $\Gamma\cong\pi_{1}({\mathcal{O}})$ of $\operatorname{Isom}(X)$ . Note that the underlying topological space of $X$ is homeomorphic to $\mathbb{R}^{3}$ . The proof is divided into two cases according to whether $\pi_{1}({\mathcal{O}})$ is finite or infinite.

Case 1. Suppose that $\pi_{1}({\mathcal{O}})$ is a finite dihedral group $D_{n}$ . Then, as will be shown below, the action of $D_{n}$ on $X$ has a global fixed point $x$ . Then the exponential map from $T_{x}X$ , the tangent space to $X$ at $x$ , to $X$ is a $D_{n}$ -equivariant homeomorphism. This implies that $\partial{\mathcal{O}}\cong S^{2}(2,2,n)$ , contradicting the condition (ii).

The existence of a global fixed point can be proved as follows. For the constant curvature case $X=\mathbb{H}^{3}$ or $\mathbb{E}^{3}$ , this is well-known. We shall first deal with the case where $X$ is $Nil$ , $\mathbb{H}^{2}\times\mathbb{R}$ , or $\widetilde{\mbox{$\mathrm{SL}$}_{2}\mathbb{R}}$ . Recall that there is an exact sequence

1\to\operatorname{Isom}(\mathbb{R})\to\operatorname{Isom}(X)\to\operatorname{Isom}(E)\to 1,

where $E$ is the Euclidean plane $\mathbb{E}^{2}$ when $X$ is $Nil$ and the hyperbolic plane $\mathbb{H}^{2}$ when $X$ is $\mathbb{H}^{2}\times\mathbb{R}$ or $\widetilde{\mbox{$\mathrm{SL}$}_{2}\mathbb{R}}$ . We also note that the projection $\operatorname{Isom}(X)\to\operatorname{Isom}(E)$ above is induced by a fibration $p:X\to E$ . Let $\bar{D}_{n}$ be the image of $D_{n}$ in $\operatorname{Isom}(E)$ and $K$ the kernel in $D_{\infty}$ of the projection to $\bar{D}_{n}$ . Then the action of $\bar{D}_{n}$ on $E$ has a global fixed point $y$ , and the action of $K$ on the fibre $p^{-1}(y)$ has a global fixed point since both of them are finite. Thus $D_{n}$ has a global fixed point on $X$ when $X$ is $Nil$ , $\mathbb{H}^{2}\times\mathbb{R}$ , or $\widetilde{\mbox{$\mathrm{SL}$}_{2}\mathbb{R}}$ .

We shall now show the same property when $X=Sol$ . In this case, there is an exact sequence

1\to\operatorname{Isom}(\mathbb{E}^{2})\to\operatorname{Isom}(Sol)\to\operatorname{Isom}(\mathbb{R})\to 1,

and the projection $\operatorname{Isom}(Sol)\to\operatorname{Isom}(\mathbb{R})$ is induced by a fibration $q:Sol\to\mathbb{R}$ . Let $\bar{D}_{n}$ be the projection of $D_{n}$ in $\operatorname{Isom}(\mathbb{R})$ . Then $\bar{D}_{n}$ is either trivial or $\mathbb{Z}_{2}$ generated by a reflection on $\mathbb{R}$ . In either case, it fixes a point $y$ on $\mathbb{R}$ . In the former case, $D_{n}\cong\langle g,h\ |\ g^{2},h^{2},\ (gh)^{n}\rangle$ acts on the fibre $q^{-1}(y)$ by Euclidean isometries in such a way that $g$ and $h$ correspond to reflections, and hence $D_{n}$ fixes a point on the fibre. In the latter case, the kernel $K$ of the projection $D_{n}\to\bar{D}_{n}$ is isomorphic to $\mathbb{Z}_{n}$ , and fixes a point on the fibre in the same way. Thus we have shown that $D_{n}$ has a fixed point also in the case when $X=Sol$ .

Case 2. Suppose $\pi_{1}({\mathcal{O}})$ is the infinite dihedral group $D_{\infty}\cong\langle g,h\ |\ g^{2},h^{2}\rangle$ . First we shall consider the case when $X$ has constant curvature. Then $g$ and $h$ are order $2$ elliptic transformations, and hence fix pointwise axes $a_{g}$ and $a_{h}$ respectively. They do not meet each other since otherwise the action fixes their intersection and cannot be faithful and discrete. Let $\ell$ be the common perpendicular to $a_{g}$ and $a_{h}$ if it exists. (This does not exist when $X=\mathbb{H}^{3}$ and $a_{g}$ touches $a_{h}$ at infinity. This exceptional case will be considered later.) Let $\Pi_{g}$ be the totally geodesic plane containing $a_{h}$ and perpendicular to $\ell$ . We define $\Pi_{h}$ in the same way. Then the region cobounded by $\Pi_{g}$ and $\Pi_{h}$ constitutes a fundamental domain of the action of $D_{\infty}$ . Suppose now that $X=\mathbb{H}^{3}$ and $a_{g}$ touches $a_{h}$ at infinity. Then there is a totally geodesic plane $H$ containing both $a_{g}$ and $a_{h}$ and it is preserved by $D_{\infty}$ . We then let $\Pi_{g}$ and $\Pi_{h}$ be totally geodesic planes containing $a_{g}$ and $a_{h}$ respectively, which are perpendicular to $H$ . Then a fundamental domain is cobounded by $\Pi_{g}$ and $\Pi_{h}$ again. Therefore, in either case, we can see $\operatorname{int}{\mathcal{O}}\cong\operatorname{int}D^{2}(2,2)\times\mathbb{R}$ and so ${\mathcal{O}}\cong D^{2}(2,2)\times I$ .

Next, we shall consider the case when $X$ is $Nil$ or $\mathbb{H}^{2}\times\mathbb{R}$ or $\widetilde{\mbox{$\mathrm{SL}$}_{2}\mathbb{R}}$ . As before, let $\bar{D}_{\infty}$ be the projection of $D_{\infty}$ to $\operatorname{Isom}(E)$ , and $K$ the kernel of the projection. We first observe that the images $\bar{g}$ and $\bar{h}$ of $g$ and $h$ in $\bar{D}_{\infty}$ are nontrivial. In fact, if say $\bar{g}$ is trivial, then $g$ acts on $\mathbb{R}$ as a nontrivial order $2$ isometry. Thus $g$ acts on $\mathbb{R}$ by a reflection, and so the image $\bar{g}$ must be an orientation-reversing isometry on $E$ , which contradicts our assumption that $\bar{g}$ is trivial.

Since $g$ and $h$ have order $2$ , their images $\bar{g}$ and $\bar{h}$ in $\bar{D}_{\infty}$ also have order $2$ . We first deal with the case where both of them are orientation-preserving, i.e. $\pi$ -rotations. Let $y_{g}$ and $y_{h}$ be the centres of the $\pi$ -rotations $\bar{g}$ and $\bar{h}$ , respectively. Then $g$ and $h$ are $\pi$ -rotations about the geodesics $p^{-1}(y_{g})$ and $p^{-1}(y_{h})$ , respectively. Since the action of $D_{\infty}$ is faithful, we have $y_{g}\neq y_{h}$ . Now consider the geodesic line $\ell$ in $E$ containing $y_{g}$ and $y_{h}$ , and let $\ell_{g}$ and $\ell_{h}$ be the lines which intersects $\ell$ perpendicularly at $y_{g}$ and $y_{h}$ , respectively. Then $\ell_{g}$ and $\ell_{h}$ are disjoint, and they cobound a region $R$ in $E$ . We see that $p^{-1}(R)$ is a fundamental region of the action of $D_{\infty}$ , and we have $\operatorname{int}{\mathcal{O}}\cong\operatorname{int}D^{2}(2,2)\times\mathbb{R}$ .

We next treat the case where both of $\bar{g}$ and $\bar{h}$ are orientation-reversing, i.e. reflections. Let $a_{g}$ and $a_{h}$ be the axes of the reflections $\bar{g}$ and $\bar{h}$ , respectively. Then $g$ and $h$ are the ‘symmetries’ with respect to the geodesics $\tilde{a}_{g}$ and $\tilde{a}_{h}$ , respectively, where $\tilde{a}_{g}$ and $\tilde{a}_{h}$ are lifts of $a_{g}$ and $a_{h}$ , respectively. If $a_{g}$ and $a_{h}$ are disjoint, they cobound a region $R$ in $E$ , and $p^{-1}(R)$ is a fundamental region of the action of $D_{\infty}$ , and we have $\operatorname{int}{\mathcal{O}}\cong\operatorname{int}D^{2}(2,2)\times\mathbb{R}$ . If $a_{g}$ and $a_{h}$ meet each other at a point $y\in E$ . Then $D_{\infty}$ acts effectively and discretely on the fiber $p^{-1}(y)$ , and so the axes $\tilde{a}_{g}$ and $\tilde{a}_{h}$ intersect $p^{-1}(y)$ perpendicularly at distinct points, $z_{g}$ and $z_{h}$ , respectively. Let $P_{g}$ and $P_{h}$ be the ruled surfaces in $X$ obtained as the unions of the geodesics which intersect $p^{-1}(y)$ perpendicularly at $z_{g}$ and $z_{h}$ , respectively. Then $P_{g}$ and $P_{h}$ are disjoint planes in $X$ , and the domain they cobound is a fundamental domain of $D_{\infty}$ , and we can see $\operatorname{int}{\mathcal{O}}\cong\operatorname{int}D^{2}(2,2)\times\mathbb{R}$ .

We now treat the case where one of $\bar{g}$ and $\bar{h}$ is orientation-preserving and the other is orientation-reversing. We may assume $\bar{g}$ is orientation-preserving and $\bar{h}$ is orientation-reversing. Let $y_{g}$ be the center of the $\pi$ -rotation $\bar{g}$ , and let $a_{h}$ be the axis of the reflection $\bar{h}$ . If $y_{g}$ belongs to $a_{h}$ , then the axes of the $\pi$ -rotations of $g$ and $h$ intersect, and the action of $D_{\infty}$ cannot be discrete and faithful. So $y_{g}$ is not contained in $a_{g}$ . Let $\ell$ be a geodesic line in $E$ which passes through $y$ and is disjoint from $a_{h}$ . Let $R$ be the region in $E$ bounded by $a_{h}$ and $\ell$ . Then $p^{-1}(R)$ is a fundamental region of the action of $D_{\infty}$ , and we have $\operatorname{int}{\mathcal{O}}\cong\operatorname{int}D^{2}(2,2)\times\mathbb{R}$ .

Finally, suppose that $X=Sol$ . Then the projection $\bar{D}_{\infty}$ of $D_{\infty}$ to $\operatorname{Isom}(\mathbb{R})$ is either trivial or $\mathbb{Z}_{2}$ or $D_{\infty}$ itself. In the case when $\bar{D}_{\infty}$ is trivial, the generators $g$ and $h$ act on each fibre by $\pi$ -rotations, and their fixed points must differ. Thus $\operatorname{int}{\mathcal{O}}\cong X/D_{\infty}$ is a bundle over $\mathbb{R}$ with fiber $\mathbb{E}^{2}/D_{\infty}\cong\operatorname{int}D^{2}(2,2)$ . So we have $\operatorname{int}{\mathcal{O}}\cong\operatorname{int}D^{2}(2,2)\times\mathbb{R}$ . In the case when $\bar{D}_{\infty}$ is $\mathbb{Z}_{2}$ , the action of $\bar{D}_{\infty}$ is a reflection with respect to a point $x$ . We set $P=q^{-1}(x)$ . Then the $g$ and $h$ act on $P$ by reflections, and by the same argument as in the previous paragraph, we have a homeomorphism $\operatorname{int}{\mathcal{O}}\cong D^{2}(2,2)\times\mathbb{R}$ . Finally, suppose that $\bar{D}_{\infty}=D_{\infty}$ . Then $g$ and $h$ fix points $x_{g}$ and $x_{h}$ on $\mathbb{R}$ respectively, and they differ. We consider fibres $\Pi_{g}=q^{-1}(x_{g})$ and $\Pi_{h}=q^{-1}(x_{h})$ . The elements act on $\Pi_{g}$ and $\Pi_{h}$ as reflections with axes $a_{g}\subset\Pi_{g}$ and $a_{h}\subset\Pi_{h}$ . Then the region cobounded by $\Pi_{g}$ and $\Pi_{h}$ constitutes a fundamental region for the action of $D_{\infty}$ , and we see that $\operatorname{int}{\mathcal{O}}\cong\operatorname{int}D^{2}(2,2)\times\mathbb{R}$ . ∎

References

[1] C. Adams, Hyperbolic $3$ -manifolds with two generators, Comm. Anal. Geom. 4 (1996), 181–206.
[2] I. Agol, The classification of non-free $2$ -parabolic generator Kleinian groups, Slides of talks given at Austin AMS Meeting and Budapest Bolyai conference, July 2002, Budapest, Hungary.
[3] I. Agol, Tameness of hyperbolic 3-manifolds, arXiv:math/0405568.
[4] S. Aimi, D. Lee, S. Sakai, and M. Sakuma, Classification of parabolic generating pairs of Kleinian groups with two parabolic generators, preprint.
[5] H. Akiyoshi, J. Parker, and M. Sakuma, On Hecke groups and Heckoid groups, in preparation.
[6] H. Akiyoshi, M. Sakuma, M. Wada, and Y. Yamashita, Punctured torus groups and $2$ -bridge knot groups (I), Lecture Notes in Mathematics 1909, Springer, Berlin, 2007.
[7] L. Bessiéres, G. Besson, S. Maillot, M. Boileau, J. Porti, Geometrisation of 3-manifolds, EMS Tracts in Mathematics, 13. European Mathematical Society (EMS), Zürich, 2010. x+237 pp.
[8] M. Boileau, B. Leeb, and J. Porti, Geometrization of 3-dimensional orbifolds, Ann. of Math. 162 (2005), 195–290.
[9] M. Boileau, S, Maillot, and J. Porti, Three-dimensional orbifolds and their geometric structures, Panoramas et Synthèses [Panoramas and Syntheses], 15, Société Mathématique de France, Paris, 2003. viii+167 pp.
[10] M. Boileau and J. Porti, Geometrization of $3$ -orbifolds of cyclic type, Appendix A by Michael Heusener and Porti, Astérisque No. 272 (2001).
[11] M. Boileau and B. Zimmermann, The $\pi$ -orbifold group of a link, Math. Z. 200 (1989), 187–208.
[12] F. Bonahon, Difféotopies des espaces lenticulaires, Topology 22 (1983), 305–314.
[13] F. Bonahon and J. P. Otal, Scindements de Heegaard des espaces lenticulaires, C. R. Acad. Sci. Paris Sér. I Math. 294 (1982), 585–587.
[14] F. Bonahon and L. Siebenmann, New geometric splittings of classical knots, and the classification and symmetries of arborescent knots, http://www-bcf.usc.edu/~fbonahon/Research/Publications.html
[15] B. H. Bowditch, Notes on tameness, Enseign. Math. 56 (2010), 229–285.
[16] J. L. Brenner, Quelques groupes libres de matrices, C. R. Acad. Sci. Paris 241 (1955), 1689–1691.
[17] G. Burde, H. Zieschang and M. Heusener, Knots. Third, fully revised and extended edition, De Gruyter Studies in Mathematics, 5. De Gruyter, Berlin, 2014. xiv+417
[18] D. Calegari and D. Gabai, Shrinkwrapping and the taming of hyperbolic 3-manifolds, J. Amer. Math. Soc. 19 (2006), 385–446.
[19] D. Cooper, C. Hodgson and S. Kerckhoff, Three-dimensional orbifolds and cone-manifolds MSJ Memoirs 5, Mathematical Society of Japan, Tokyo, 2000. x+170 pp.
[20] W. D. Dunbar, Hierarchies for 3-orbifolds, Topology Appl. 29 (1988), 267–283.
[21] W. D. Dunbar, Geometric orbifolds, Rev. Mat. Univ. Complut. Madrid 1 (1988), 67–99.
[22] M. Feighn and G. Mess, Conjugacy classes of finite subgroups of Kleinian groups, Amer. J. Math. 113 (1991), 179–188.
[23] J. Gilman, The structure of two-parabolic space: parabolic dust and iteration, Geom. Dedicata 131 (2008), 27–48.
[24] F. W. Gehring and G. J. Martin, Commutators, collars and the geometry of Möbius groups, J. Anal. Math. 63 (1994), 175–219.
[25] E. Hecke, Über die Bestimmung Dirichletscher Reihen durch ihre Funktionalgleichung, Math. Ann. 112 (1936), 664–699.
[26] A. Hinkkanen and G. J. Martin, The dynamics of semigroups of rational functions. I, Proc. London Math. Soc. 73 (1996), 358–384.
[27] T. L. Jeevanjee, Isometries of orbifolds double-covered by lens spaces, J. Knot Theory Ramifications 12 (2003), 819–832.
[28] T. Jorgensen, On pairs of once-punctured tori, Kleinian groups and hyperbolic 3-manifolds (Warwick, 2001), 183–207, London Math. Soc. Lecture Note Ser., 299, Cambridge Univ. Press, Cambridge, 2003.
[29] L. Keen and C. Series, The Riley slice of Schottky space, Proc. London Math. Soc. 69 (1994), 72–90.
[30] S. Kim and T. Koberda, Non-freeness of groups generated by two parabolic elements, arXiv:1901.06375.
[31] Y. Komori and C. Series, The Riley slice revisited, The Epstein birthday schrift, 303–316, Geom. Topol. Monogr., 1, Geom. Topol. Publ., Coventry, 1998.
[32] D. Lee and M. Sakuma, Epimorphisms from $2$ -bridge link groups onto Heckoid groups (I), Hiroshima Math. J. 43 (2013), 239–264.
[33] R. C. Lyndon and J. L. Ullman, Groups generated by two parabolic linear fractional transformations, Canadian J. Math. 21 (1969), 1388–1403.
[34] A. Marden, The Geometry of Finitely Generated Kleinian Groups, Ann. Math. 99 (1974), 383–462.
[35] G. J. Martin, Nondiscrete parabolic characters of the free group $F_{2}$ : supergroup density and Nielsen classes in the complement of the Riley slice, preprint.
[36] G. J. Martin and T. H. Marshall, Polynomial Trace Identities in $SL(2,\mathbb{C})$ , Quaternion Algebras, and Two-generator Kleinian Groups, arXiv 1911.11643.
[37] K. Matsuzaki, Structural stability of Kleinian groups, Michigan Math. J. 44 (1997), 21–36.
[38] M. Mecchia and A. Seppi, Fibered spherical $3$ -orbifolds, Rev. Mat. Iberoam. 31 (2015), 811–840.
[39] M. Mecchia and A. Seppi, Isometry groups and mapping class groups of spherical 3-orbifolds, arXiv:1607.06281.
[40] W.H. Meeks and P. Scott, Finite group actions on 3-manifolds, Invent. Math. 86 (1986), 287–346.
[41] J.W. Morgan and H. Bass, The Smith conjecture, Pure Appl. Math., 112, Academic Press, Orlando, FL, 1984.
[42] K. Ohshika and H. Miyachi, Uniform models for the closure of the Riley slice, In the tradition of Ahlfors-Bers. V, 249–306, Contemp. Math., 510, Amer. Math. Soc., Providence, RI, 2010.
[43] C. Petronio, Spherical splitting of 3-orbifolds, Math. Proc. Cambridge Philos. Soc. 142 (2007), 269–287.
[44] R. Riley, Parabolic representations of knot groups. I, Proc. London Math. Soc. 24 (1972), 217–242.
[45] R. Riley, A quadratic parabolic group, Math. Proc. Cambridge Philos. Soc. 77 (1975), 281–288.
[46] R. Riley, Parabolic representations of knot groups. II, Proc. London Math. Soc. 31 (1975), 495–512.
[47] R. Riley, Algebra for Heckoid groups, Trans. Amer. Math. Soc. 334 (1992), 389–409.
[48] R. Riley, Groups generated by two parabolics $A$ and $B(w)$ for $w$ in the first quadrant, Output of an computer experiment.
[49] M. Sakuma, On strongly invertible knots, Algebraic and topological theories (Kinosaki, 1984), 176–196, Kinokuniya, Tokyo, 1986.
[50] M. Sakuma, The geometries of spherical Montesinos links, Kobe J. Math. 7 (1990), 167–190.
[51] M. Sakuma and J. Weeks, Examples of canonical decompositions of hyperbolic link complements, Japan. J. Math. (N.S.) 21 (1995), 393–439.
[52] C. Series, All about the Riley slice, in preparation.
[53] H. Schubert, Knoten mit zwei Brücken, Math. Z. 65 (1956), 133–170.
[54] P. Scott, The geometries of $3$ -manifolds, Bull. London Math. Soc. 15 (1983), 401–487.
[55] T. Soma, Existence of ruled wrappings in hyperbolic 3-manifolds, Geom. Topol. 10 (2006), 1173–1184.
[56] E. C. Tan and S. P. Tan, Quadratic Diophantine equations and two generator Möbius groups, J. Austral. Math. Soc. Ser. A 61 (1996), 360–368.
[57] W. Thurston, The geometry and topology of three-manifolds, available from http://library.msri.org/books/gt3m/

Classification of non-free Kleinian groups generated by two parabolic transformations

Abstract.

2010 Mathematics Subject Classification:

1. Introduction

Theorem 1.1.

Theorem 1.2.

Notation 1.3.

2. Basic facts concerning 22-bridge links

Proposition 2.1.

3. Heckoid orbifolds and Heckoid groups

Definition 3.1.

Definition 3.2.

Proposition 3.3.

Proof.

Definition 3.4.

Remark 3.5.

4. Classification of dihedral orbifolds

Theorem 4.1.

Remark 4.2.

Proof.

Remark 4.3.

5. Relative tameness theorem for hyperbolic orbifolds

Theorem 5.1.

Proof.

Theorem 5.2.

Proof.

Remark 5.3.

6. Orbifold surgery

Convention 6.1.

Convention 6.2.

Definition 6.3.

Lemma 6.4.

Proof.

Lemma 6.5.

7. Canonical horoball pairs for Kleinian groups generated by two parabolic transformations

Lemma 7.1.

Proof.

Lemma 7.2.

Proof.

8. Outline of the proof of Theorem 1.1

Assumption 8.1.

Outline of the proof of Theorem 1.1.

9. Proof of Theorem 1.1 - flexible cusp: generic case -

Lemma 9.1.

Proof.

Assumption 9.2.

Lemma 9.3.

Proof.

Proposition 9.4.

Proof.

Lemma 9.5.

Proof.

10. Proof of Theorem 1.1 - rigid cusp case -

Lemma 10.1.

Proof.

Lemma 10.2.

Proof.

Lemma 10.3.

Proof.

Lemma 10.4.

Lemma 10.5.

Proof.

11. Proof of Theorem 1.1 - flexible cusp: exceptional case -

Assumption 11.1.

Lemma 11.2.

Lemma 11.3.

Proof.

Lemma 11.4.

Proof.

12. Appendix 1: Spherical orbifolds with dihedral orbifold fundamental groups

Lemma 12.1.

Proposition 12.2.

Proof.

Claim 12.3.

Proof of Claim 12.3.

Claim 12.4.

Proof of Claim 12.4.

Proposition 12.5.

Proposition 12.6.

Corollary 12.7.

2. Basic facts concerning $2$ -bridge links