Circuit Design based on Feature Similarity for Quantum Generative Modeling
Abstract
Quantum generative models may achieve an advantage on quantum devices by their inherent probabilistic nature and efficient sampling strategies. However, current approaches mostly rely on general-purpose circuits, such as the hardware efficient ansatz paired with a random initialization strategy, which are known to suffer from trainability issues such as barren plateaus. To address these issues, a tensor network pretraining framework that initializes a quantum circuit ansatz with a classically computed high-quality solution for a linear entanglement structure has been proposed in literature. In order to improve the classical solution, the quantum circuit needs to be extended, while it is still an open question how the extension affects trainability. In this work, we propose the metric-based extension heuristic to design an extended circuit based on a similarity metric measured between the dataset features. We validate this method on the bars and stripes dataset and carry out experiments on financial data. Our results underline the importance of problem-informed circuit design and show that the metric-based extension heuristic offers the means to introduce inductive bias while designing a circuit under limited resources.
I Introduction
The rise of quantum computing is opening up new possibilities for solving classically intractable problems [1, 2, 3, 4]. Despite significant advancements in the theoretical exploration of quantum advantages in terms of speed-up [5, 6, 7, 2], memory efficiency [8], or model expressiveness [9, 10, 11, 12], the widespread adoption of quantum systems will ultimately depend on its ability to solve problems of high practical interest on hardware with limited resources [13, 14, 15, 16]. In search for an application to explore potential quantum advantages on such limited near- and mid-term quantum devices, quantum machine learning (QML) has emerged as a promising domain [17, 18, 19].
The inherently probabilistic nature of quantum systems potentially allows for an efficient sampling from probability distributions of high complexity [20, 21, 4, 22, 23], making them well suited for the task of generative modeling within the field of QML [24]. Generative models are aiming to learn the underlying distribution of a dataset in order to generate realistic samples [25]. Recent advances in quantum generative modeling [26] led to the adoption of several architectures, including quantum circuit Born machines (QCBMs) [27, 28, 9], quantum generative adversarial networks (QGANs) [29, 30], and quantum Boltzmann machines (QBMs) [31, 32].
While these models provide high expressiveness, rooted in their general-purpose circuit architecture, they suffer from prominent trainability issues, such as cost function concentration and barren plateaus [33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43]. When this occurs, the loss function values exponentially concentrate around a fixed value and the loss gradients become exponentially small with growing problem size, therefore requiring exponential resources to navigate through the loss landscape. This phenomenon originates from several sources [44], including insufficient inductive bias [45], global observables [46, 47], and too much entanglement [48, 49, 50]. Moreover, the quantum no-free-lunch theorem implies that problem-agnostic approaches, such as the QCBM with a hardware-efficient ansatz and random initialization, one of the most popular QML models, tend to exhibit poor average performance [51, 52, 53]. To mitigate these trainability issues, various techniques have been proposed, such as sophisticated parameter initialization strategies [54, 55, 56] and problem-informed circuit design [57, 58, 59, 60].
In this work, we focus on providing experimental results for techniques that are shown to improve trainability on near-term quantum devices. We combine both strategies of initializing the parameters of a general-purpose ansatz by tensor network pretraining, and further extending it to a problem-informed circuit based on classical feature similarity. More specifically, we employ the synergistic pretraining framework [56] that utilizes matrix product states (MPS) [61] to obtain a high-quality solution for a given problem, which can be transferred to a quantum circuit ansatz with linear connectivity [62]. This approach offers a hybrid solution for parameter initialization that is classically scalable to larger qubit numbers, due to its restriction to a linear entanglement structure. However, to gain a potential quantum advantage, the pretrained quantum circuit needs to be extended, in order to introduce the possibility to learn non-linear correlations, that are difficult to capture effectively by an MPS with modest bond dimensions. It is practically shown, that in contrast to a random initialization strategy, pretrained circuits either without any extension or in the case of extending to the trivial all-to-all connectivity, the loss gradients do not vanish when scaling to larger qubit circuits [56]. Although the problem-agnostic all-to-all circuit extension showed promising gradient behavior, as the problem size grows, it becomes infeasible to train on hardware with limited resources due to the constraints in the number of gates and compute time. Further given the proven disadvantages of problem-agnostic approaches, we aim for a practical problem-informed approach to extend the pretrained circuit.
In recent QML literature, probabilistic graphical models (PGMs) [63], especially Bayesian networks (BNs) [64, 65, 11] and Markov networks (MNs) [66] being exploited to construct problem-informed QML models, with the aim of creating new classes of quantum algorithms that may have the potential to demonstrate quantum advantage. In contrast to the works that focus on creating new classes of algorithms, our approach is more practically motivated, similar to Liu and Wang [28], who made the first explicit connection between QCBMs and PGMs. In order to construct a circuit that exploits the close relation of controlled unitary gates and classical PGMs [64], they employed the Chow-Liu dependency tree [67]. By maximizing mutual information, the Chow-Liu tree approximates a high-dimensional joint distribution through a product of second-order distributions, whose corresponding graph represents a BN. However, being a second-order product approximation, this method not only fails to capture higher-order correlations but also does not include cyclical dependencies.
The main contribution of this work is the introduction of the metric-based extension heuristic to design a problem-informed circuit topology that can be used to extend the classically pretrained ansatz in a greedy fashion. Being a practically motivated heuristic, this method might not offer an optimal solution. However, it does not suffer from the drawbacks of the Chow-Liu tree and provides the means for finding a suitable tradeoff between the number of parameters and sufficient inductive bias. As we aim for a flexible method that should also be adapted to real-world datasets, we apply the metric-based extension heuristic not only to a toy problem, the bars and stripes (BAS) dataset, but also to a relevant financial dataset composed of Japanese government bond (JGB) interest rates. From numerical simulations we show that the extended circuit, designed by the metric-based extension heuristic, successfully improves the model performance compared to randomly extended circuits with the same amount of parameters. These results indicate the potential of the metric-based extension heuristic to introduce inductive bias, while also keeping the circuit shallow enough.
The remainder of this paper is structured as follows: In Sec. II we review relevant methods and introduce our extension heuristic. Sec. III and Sec. IV present the results of the BAS and JGB experiments. Finally, we conclude this work with a discussion of the results and future directions in Sec. V.
II Methods
II.1 Quantum Circuit Born Machine
QCBMs are a subclass of parameterized quantum circuits (PQCs) used for generative modeling and they contain a set of parameters, which are adjusted during a training process according to a loss function . The QCBM aims to encode the target joint distribution of a discrete dataset into an -qubit parameterized quantum state , which is, without loss of generality, evolved from the all zero input state , i.e., using a PQC . Measuring the output state yields with sampled from the variational model distribution which is called the Born rule. Unlike in classical models, one does not have access to the explicit model distribution. Therefore the loss function has to be estimated using quantum circuit measurements. Since the widely used Kullback-Leibler (KL) divergence, as an explicit loss function, requires a high number of samples, and is shown to be not trainable for large-scale QCBMs in Ref. [68], we use the implicit loss function, maximum mean discrepancy (MMD) [69]
| (1) |
where is a freely chosen kernel function [70]. As a standard choice in recent literature [28, 9, 68], we employ the Gaussian mixture kernel defined as
| (2) |
The parameters are the bandwidths to adjust the width of the Gaussian kernel and refers to the -norm. For optimizing schemes, both gradient-free and gradient-based procedures have been proposed, although gradient-free schemes failed when scaling to larger number of parameters [27]. Therefore we use the stochastic gradient descent algorithm [71] and ADAM as meta-optimizer [72]. For the MMD loss, it is possible to obtain the gradient with respect to the -th model parameters as
| (3) |
by shifting and performing a projective measurement to obtain samples. The distributions are generated by sampling from the parameter-shifted circuit with parameters [73].
II.2 Tensor Network Pretraining
In the field of quantum mechanics, the development of efficient classical representations of quantum wave functions has been a subject of extensive research, whereby tensor networks (TN) have demonstrated notable effectiveness. Matrix product states (MPS) are a particular type of TNs, whose tensors are arranged in a one-dimensional geometry, facilitating the representation of one-dimensionally entangled quantum states. The MPS provides means to efficient computation of quantum circuits with limited entanglement [74] via the density matrix renormalization group (DMRG) algorithm [75]. Although the original application of DMRG is ground state computation, it has also been successfully applied to unsupervised learning tasks [61], which enables the use of MPS as a pretraining method for quantum generative modeling. In this work, we implemented the synergistic pretraining framework [56], as schematically shown in Fig. 1, to mitigate the problem of barren plateaus in random initialization.

First of all, the MPS is classically trained to find a high-quality solution by a DMRG-like algorithm that minimizes negative log-likelihood [61, 76]. Theoretically, any probability distribution of an -bit system can be represented through an MPS using exponentially large bond dimensions. By removing the components with small singular values in the MPS, we can obtain an approximate MPS, which is known to be locally optimal at each neighboring matrices in the MPS [77]. This truncation corresponds to dropping off minor components of the entanglement spectrum. In the present study, we did not explicitly set the upper bound of the bond dimensions, but instead we used a truncation cutoff of to truncate the bond dimensions. We set the training iterations to 10 and the learning rate to . In both of our experiments in Sec. III and Sec. IV the training concluded after 10 iterations with a realized maximum bond dimension of 5 for the bars and stripes dataset and 25 for the financial dataset. After classical pretraining, the obtained MPS solution is then transferred to a quantum circuit ansatz by analytical decomposition [62, 78]. In order to introduce inductive bias to the model, the next step consists of extending the decomposed quantum circuit by additional gates that change its connectivity, therefore changing its entanglement capabilities. Consequently, the extended circuit should be subsequently retrained on quantum hardware. In this work, we explore the effect of different circuit extensions on this subsequent training process. However, we use numerical simulations instead of real quantum hardware and leave it as a task for future research.
II.3 Metric-based Extension Heuristic
Since the MPS solution exhibits a high-quality solution only for a linear entanglement structure, we do not expect it to significantly improve the solution with limited entanglement even when retraining on a quantum device. However, the MPS solution can be used as a baseline. To learn long-range correlations, it is necessary to introduce more entanglement capacity, which raises the question of how to extend the baseline circuit in a way that uses a minimal amount of gates. For small datasets, connecting the qubits in an all-to-all fashion provided good results [56]. However, the number of parameters gets high with increasing qubits, which leads to deep circuits that are infeasible to train. Instead of all-to-all connections, we introduce an idea called the metric-based extension heuristic to reduce the gate count and introduce inductive bias by utilizing characteristics of the dataset.
II.3.1 Extension Procedure
The metric-based extension heuristic is carried out in the following steps:
-
1.
Construct an undirected graph , where vertices represent binary features and edges represent their pair-wise similarity. From the perspective of the circuit, vertices represent the qubit registers, and edges represent a connection by a two-qubit gate. The initial graph resembles the linear connectivity of the decomposed MPS circuit.
-
2.
Compute the similarity metric as per Sec. II.3.2 between each pair of binary feature vectors.
-
3.
Apply a threshold to the similarity metric to decide whether to add an edge to the graph or not. If the binary features share a high similarity, their representative qubits should be therefore connected.
-
4.
To extend the linear MPS circuit, construct a new quantum circuit by adding extension gates, as in Sec. II.3.3, between qubits that are connected in the graph.
-
5.
Initialize the extension gates as near-identity matrices by choosing random parameters from a normal distribution with mean and small variance, which we set to .
-
6.
Retrain the whole circuit including the parameters of the previously derived MPS solution that formed the linear baseline circuit.
Following this procedure, we can design a problem-informed circuit in a greedy way, since setting a higher threshold increases the number of extension gates in a way that adds inductive bias up to a certain point. However, as the threshold is chosen too high, the graph comes close to an all-to-all connectivity and the inductive bias will be lost. For identifying a suitable number of extension gates, we use the elbow rule. That is, we increase the threshold as long as the number of connections gradually increase and stop before they increase too much. Nevertheless, a practitioner could also experiment with different thresholds and similarity metrics to find a configuration for a given dataset, that results in a sufficient amount of extension gates, but also keeps the circuit shallow enough to be trainable.
II.3.2 Similarity Metrics
The similarity metrics are computed between each of the feature vectors from the training dataset each including the same number of samples. We define two metrics for the experiments.
Particularly well-suited for binary data, is the hamming distance [79], measuring the dissimilarity between two binary vectors of length as
| (4) |
where is the number of occurences of and for . Without imposing any assumptions on the data distribution, the hamming distance directly counts the number of differing bits between two binary vectors. Therefore, low values of represent higher similarity between two binary vectors.
In scenarios where nonlinearity is prevalent, the variation of information [80] turns out to be a more appropriate distance metric than the correlation measure. This metric allows us to address questions about the unique information provided by a random variable, all without imposing specific functional assumptions. The variation of information and its standardized value is defined as
| (5) |
where , denote conditional entropies and denotes the joint entropy for discrete random variables and . and are metrics because they satisfy nonnegativity, symmetry , and the triangle inequality. Further, is bounded as . The variation of information measure can be interpreted as the uncertainty we expect in one variable when we know the value of the other. Therefore, a lower value indicates that more information is shared between both variables.
II.3.3 Extension Gates
For extending the MPS circuit, we use SU(4) gates between qubit pairs with 15 parameters per gate as in Ref. [56], which represent a fully parameterized two-qubit interaction. The SU(4) can be decomposed into four single-qubit U(2) rotations, and the RXX, RYY, RZZ entanglement gates by KAK-decomposition [81];
| (6) |
where is a parameter vector of length 15, and each U(2) gate consists of three parameters, with one parameter assigned to each entangling gate respectively.
III Training on Bars and Stripes
In following sections III and IV, we demonstrate our proposal with two practical datasets. In this section, we use the Bars and Stripes (BAS) dataset, which is composed of binary images, each containing either vertical bars or horizontal stripes, but never both. Since each of these images is unique, the valid BAS-images resemble a uniform target distribution. Here we use a dimension of 3 x 3, therefore in total different configurations exist, but only 14 distinct images are included in the BAS dataset, as shown in Fig. 2, which all appear with equal probability.

The BAS dataset requires the generative model to capture strong non-trivial correlations and is applicable on different scales, making it suitable for evaluating the capabilities of quantum generative models with a low number of qubits. Therefore it is widely used for benchmarking generative modeling tasks in quantum computing literature [27, 82, 83].
III.1 Circuit Design
The BAS dataset exhibits strong correlations between bits in the same row or column. In order to capture these correlations it is necessary to extend the circuit connectivity from the one-dimensional MPS model to a more connected ansatz. Since the BAS dataset only consists of a low number of observations for each binary feature, we use the hamming distance in Eq. (4) as a metric to determine the connections between the qubits. Computing this distance between each possible qubit combination gives us a distance matrix, which is visualized in Fig. 3 (a). By setting a threshold of 0.5, we decide the maximum distance between two qubits that are allowed to be connected, which results in the connections shown in Fig. 3 (b).


In our experiment, we compare the circuit extensions, shown in Fig. 4. The initial linear connections that result from decomposing the MPS can be chosen by a good guess. For the BAS dataset, we therefore switched the features {3,5} to prevent diagonal connections on the two-dimensional grid resembling the BAS-image. The nearest-neighbor extension can then be constructed by connecting each qubit to its neighboring qubits on that grid. This results in two connections for corner qubits, three connections for edge qubits, and four connections for inner qubits. Therefore, we need a total of 4 additional gates to extend the initial circuit. The nearest-neighbor extension can be seen as a problem-informed ansatz, as it aims to resemble the two-dimensional BAS grid. The metric-based extension, however, requires 10 additional connections. We further compare it to random connections with the same amount of extension gates. The problem-agnostic all-to-all extension connects each qubit to each other, requiring 28 extension gates.
III.2 Results
The experiment was conducted using the statevector simulator from the IBM Qiskit Aer simulator and consists of 5 independent training runs with the same initial conditions for each circuit connectivity. The configuration included 9 qubits, with 1000 shots per iteration, and a total of 1000 iterations. The data was split into a training set and a test set with a ratio of 80/20, thus the train set consists of 11 images while the test set includes 3 images. To compute the loss function and its gradient the full training set was used in each iteration, and the kernel bandwidth was set to . In Fig. 5, we compare the performance of different circuit designs with respect to the MMD loss on the train and test set. The MMD values for both train and test set were computed after each training iteration to validate the model performance during the training process.

The circuit connectivity significantly influences the training process. Through evaluation of the MMD loss on the train data in each iteration, we observe a clear separation between each extension method according to the number of their extension gates. With zero extension gates, the linear baseline circuit performs the worst, closely followed by the nearest-neighbor extension with 4 additional gates. Compared to nearest-neighbor the metric-based extension with 10 extension gates shows a large improvement on the train set. However, random connections perform worse than metric-based, despite having the same number of parameters. The train set performance of the all-to-all is the best with 28 extension gates. Despite its good performance on the train set, the all-to-all extension shows an increasing MMD curve on the test set, which is a clear sign of overfitting. We attribute this to the fact that the all-to-all extension includes more parameters without any relation to the underlying dataset characteristics, which makes it more likely to overfit. The metric-based extension on the other hand shows the best performance on the test set, closely followed by the nearest-neighbor extension and random connections. While these observations hint at better generalization capabilities of the metric-based extension, an increasing slope can be observed. Therefore, the question whether these results hold with increasing training iterations or increasing circuit depth, remains open. However, despite having the same amount of parameters as the random connections, the metric-based circuit seems to resemble a lower bound on the MMD loss. These results further motivate our use of the metric-based extension heuristic on a real-world financial dataset.
IV Training on Interest Rates
We apply the metric-based extension heuristic to a financial dataset consisting of daily quotes of interest rates from Japanese government bonds (JGB) to examine its practicality in real-world applications. Despite the fact that the recent literature in generative modeling for finance mainly conducted experiments on the foreign exchange rates dataset [84, 85, 86], we consider the interest rates dataset a more suitable choice, because in contrast to foreign exchange rates, interest rates exhibit particularly stronger correlations driven by the inherent structure of the interest rate curve [87].
IV.1 Dataset
We consider three types of JGBs, which differ by their maturity periods of 5, 10, and 20 years. The dataset can be freely downloaded from the official website of the Ministry of Finance Japan and consists of observations in daily frequency for the interest rates of each JGB, whereas we use a period from 2000-01-04 to 2025-02-28, as visualized in Fig. 6.

The first step in preprocessing the dataset is differencing the interest rates time series by , to represent the day-by-day changes and ensure stationarity. Since the quantum circuit-born machine can only represent data in binary format, as each qubit represents a value of either 0 or 1 upon measurement, it is necessary to quantize the data distributions to a desired bit resolution. As commonly used in recent literature, we adapt the uniform quantization [86]. We convert a decimal value into its -bit binary equivalent by
| (7) |
where and are the minimum and maximum values in the decimal dataset, respectively. The floor operation ensures that the result remains an integer. The conversion from the integer representation of the binary number to the actual bitstring is straightforward. Conversely, to transform the binary value back to its decimal representation, we apply
| (8) |
In our experiments, we restrict the algorithm to utilize 12 qubits, therefore each of the 3 features has to be quantized to a 4-bit resolution.
IV.2 Circuit Design
In order to apply the metric-based extension heuristic, we rely on the variation of information metric in Eq. (II.3.2), since financial datasets are known to exhibit a low signal-to-noise ratio, as well as non-linear correlations that are not captured by linear metrics [88]. The distance matrix between the features is shown in Fig. 7 (a), and the connections between the qubits for a threshold of 0.95 are shown in Fig. 7 (b).
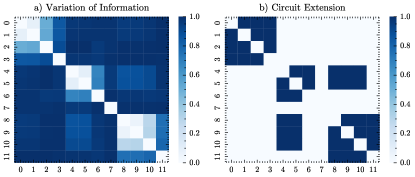
The particular threshold was set by the elbow rule to allow for sufficient connectivity, while maintaining a low number of parameters, as seen in Fig. 8.

As a good guess for the initial connections, we suggest to establish a linear connection between the bits that belong to one time-series feature, e.g. {0,1}, {1,2}, and {2,3}. By applying the metric-based extension heuristic we extend the circuit by 13 additional gates, as shown in Fig. 9. From visual inspection we see that bits within the same feature tend to be connected: {0,1,2,3} for the 5-year rate, {4,6} for the 10-year rate, {8,9,10,11} for the 20-year rate. These connections are expected since the bits represent the same feature in decimal format. The connections between different features are less frequent, although we observe that the bits {4,5} for the 10-year rate and {8,9,10} for the 20-year rate, are all-connected to each other. This could be attributed to the fact that the short end of the interest rate curve is more volatile and shares therefore less correlation with the long end, which is known to be more stable and less affected by short-term market movements [87].

IV.3 Results
The experiment was conducted using the statevector simulator of the Aer Simulator from IBM Qiskit and consists of 5 independent training runs with the same initial conditions for each extension method. The configuration included 12 qubits and 3 time series features, using 1000 shots per iteration over a total of 1000 iterations. The data was split into a training set and a test set with a ratio of 80/20, thus the train set consists of 4932 samples while the test set includes 1233 samples. The loss function was computed on the full training set but for evaluating its gradient we used a mini-batch size of 1000 samples which were randomly drawn from the train set in each iteration. The MMD kernel bandwidth was set to as recommended in [68]. We compare the MMD loss during training, evaluated after each iteration on the train and the test set, for the linear, random, and metric-based extension, as shown in Fig. 10.

While being close to each other, the metric-based extension shows a better performance than random, which confirms the similar results of the BAS dataset. However, the separation between both loss curves is not as clear on the test set, which is why we did not include the graph. Nevertheless, we suggest these results indicate the metric-based extension is a useful approach to improve the training process also on real-world data that exhibit more noisy observations. Especially, with regards to restricting the number of parameters for trainability, the metric-based extension heuristic provided valuable guidelines for circuit design.
V Discussion
In this work, we provided experimental results highlighting the importance of inductive bias in circuit design for generative QML. We introduced a heuristic for designing a circuit under restricted resources and applied it to extend a circuit from a pretrained linear ansatz to a more connected problem-informed ansatz. Carrying out numerical simulations on both a toy problem, the BAS dataset, and a real-world financial dataset composed of JGB interest rates, we explored the effect of different circuit extensions on the subsequent retraining of the extended circuit.
The numerical simulations show that our heuristic was able to perform better than randomly extended circuits. While the test set evaluation of the BAS dataset indicated out-of-sample generalization capabilities, we could not confirm it on the real-world dataset. However, by applying our heuristic we could significantly reduce the number of parameters compared to an all-to-all connection.
Although we provided numerical results for both a toy problem and a real-world dataset, these findings are not enough to fully characterize the extend of which the metric-based method can be used to introduce inductive bias to the circuit. Furthermore, being a heuristic, our method suffers from the limitation of not providing an optimal solution. This is also due to the fact that in the context of this work, we did not establish a mathematical connection between classical feature similarity, entanglement capacity, and the inductive bias of the circuit. While this is the more fundamental open question for future research, we also suggest a path on the experimental side. As we only compared several circuits by connectivity, we did not focus on the effect of circuit depth, more specifically repeating the extension layer for each method.
While challenges remain, the findings of this work provide an experimental basis for future research in circuit design for quantum generative modeling and its applications in finance and beyond.
Acknowledgements.
M.M. acknowledges support from the PROMOS scholarship issued by DAAD and funded by the German Ministry of Education and Research, as well as the MIRAI scholarship issued and funded by RWTH Aachen University. J.K. acknowledges support by SIP Grant Number JPJ012367. This work was supported by MEXT Quantum Leap Flagship Program Grants No. JPMXS0118067285 and No. JPMXS0120319794.References
- Harrow and Montanaro [2017] A. W. Harrow and A. Montanaro, Quantum computational supremacy, Nature 549, 203 (2017).
- Huang et al. [2022] H.-Y. Huang, M. Broughton, J. Cotler, S. Chen, J. Li, M. Mohseni, H. Neven, R. Babbush, R. Kueng, J. Preskill, and J. R. McClean, Quantum advantage in learning from experiments, Science 376, 1182 (2022), https://www.science.org/doi/pdf/10.1126/science.abn7293 .
- Daley et al. [2022] A. J. Daley, I. Bloch, C. Kokail, S. Flannigan, N. Pearson, M. Troyer, and P. Zoller, Practical quantum advantage in quantum simulation, Nature 607, 667 (2022).
- Farhi and Harrow [2019] E. Farhi and A. W. Harrow, Quantum supremacy through the quantum approximate optimization algorithm (2019), arXiv:1602.07674 [quant-ph] .
- Harrow et al. [2009] A. W. Harrow, A. Hassidim, and S. Lloyd, Quantum algorithm for linear systems of equations, Phys. Rev. Lett. 103, 150502 (2009).
- Lloyd et al. [2014] S. Lloyd, M. Mohseni, and P. Rebentrost, Quantum principal component analysis, Nature Physics 10, 631 (2014).
- Huang et al. [2021] H.-Y. Huang, M. Broughton, M. Mohseni, R. Babbush, S. Boixo, H. Neven, and J. R. McClean, Power of data in quantum machine learning, Nature Communications 12, 2631 (2021).
- Anschuetz et al. [2023] E. R. Anschuetz, H.-Y. Hu, J.-L. Huang, and X. Gao, Interpretable quantum advantage in neural sequence learning, PRX Quantum 4, 020338 (2023).
- Coyle et al. [2020] B. Coyle, D. Mills, V. Danos, and E. Kashefi, The Born supremacy: Quantum advantage and training of an Ising Born machine, npj Quantum Inf 6, https://doi.org/10.1038/s41534-020-00288-9 (2020).
- Sweke et al. [2021] R. Sweke, J.-P. Seifert, D. Hangleiter, and J. Eisert, On the quantum versus classical learnability of discrete distributions, Quantum 5, 417 (2021).
- Gao et al. [2022] X. Gao, E. R. Anschuetz, S.-T. Wang, J. I. Cirac, and M. D. Lukin, Enhancing generative models via quantum correlations, Phys. Rev. X 12, 021037 (2022).
- Gili et al. [2023] K. Gili, M. Hibat-Allah, M. Mauri, C. Ballance, and A. Perdomo-Ortiz, Do quantum circuit Born machines generalize?, Quantum Science and Technology 8, 035021 (2023).
- Aaronson [2015] S. Aaronson, Read the fine print, Nature Physics 11, 291 (2015).
- Preskill [2018] J. Preskill, Quantum computing in the NISQ era and beyond, Quantum 2, 79 (2018).
- Horowitz and Grumbling [2019] M. Horowitz and E. Grumbling, Quantum computing: progress and prospects (National Academies Press, 2019).
- Bharti et al. [2022] K. Bharti, A. Cervera-Lierta, T. H. Kyaw, T. Haug, S. Alperin-Lea, A. Anand, M. Degroote, H. Heimonen, J. S. Kottmann, T. Menke, W.-K. Mok, S. Sim, L.-C. Kwek, and A. Aspuru-Guzik, Noisy intermediate-scale quantum algorithms, Rev. Mod. Phys. 94, 015004 (2022).
- Schuld et al. [2014] M. Schuld, I. Sinayskiy, and F. Petruccione, The quest for a Quantum Neural Network, Quantum Information Processing 13, 2567 (2014).
- Maria Schuld and Petruccione [2015] I. S. Maria Schuld and F. Petruccione, An introduction to quantum machine learning, Contemporary Physics 56, 172 (2015), https://doi.org/10.1080/00107514.2014.964942 .
- Biamonte et al. [2017] J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe, and S. Lloyd, Quantum machine learning, Nature 549, 195 (2017).
- Terhal and DiVincenzo [2004] B. M. Terhal and D. P. DiVincenzo, Adaptive quantum computation, constant depth quantum circuits and arthur-merlin games (2004), arXiv:quant-ph/0205133 [quant-ph] .
- Aaronson and Arkhipov [2011] S. Aaronson and A. Arkhipov, The computational complexity of linear optics, in Proceedings of the forty-third annual ACM symposium on Theory of computing (2011) pp. 333–342.
- Arute et al. [2019] F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. S. L. Brandao, D. A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M. P. Harrigan, M. J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà, J. R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Y. Niu, E. Ostby, A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffel, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, K. J. Sung, M. D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z. J. Yao, P. Yeh, A. Zalcman, H. Neven, and J. M. Martinis, Quantum supremacy using a programmable superconducting processor, Nature 574, 505 (2019).
- Madsen et al. [2022] L. S. Madsen, F. Laudenbach, M. F. Askarani, F. Rortais, T. Vincent, J. F. F. Bulmer, F. M. Miatto, L. Neuhaus, L. G. Helt, M. J. Collins, A. E. Lita, T. Gerrits, S. W. Nam, V. D. Vaidya, M. Menotti, I. Dhand, Z. Vernon, N. Quesada, and J. Lavoie, Quantum computational advantage with a programmable photonic processor, Nature 606, 75 (2022).
- Perdomo-Ortiz et al. [2018] A. Perdomo-Ortiz, M. Benedetti, J. Realpe-Gómez, and R. Biswas, Opportunities and challenges for quantum-assisted machine learning in near-term quantum computers, Quantum Science and Technology 3, 030502 (2018).
- Bond-Taylor et al. [2022] S. Bond-Taylor, A. Leach, Y. Long, and C. G. Willcocks, Deep generative modelling: A comparative review of VAEs, GANs, normalizing flows, energy-based and autoregressive models, IEEE Transactions on Pattern Analysis and Machine Intelligence 44, 7327 (2022).
- Tian et al. [2023] J. Tian, X. Sun, Y. Du, S. Zhao, Q. Liu, K. Zhang, W. Yi, W. Huang, C. Wang, X. Wu, et al., Recent advances for quantum neural networks in generative learning, IEEE Transactions on Pattern Analysis and Machine Intelligence 45, 12321 (2023).
- Benedetti et al. [2019] M. Benedetti, D. Garcia-Pintos, O. Perdomo, V. Leyton-Ortega, Y. Nam, and A. Perdomo-Ortiz, A generative modeling approach benchmarking and training shallow quantum circuits, npj Quantum Inf 5, https://doi.org/10.1038/s41534-019-0157-8 (2019).
- Liu and Wang [2018] J.-G. Liu and L. Wang, Differentiable learning of quantum circuit Born machines, Phys. Rev. A 98, 062324 (2018).
- Lloyd and Weedbrook [2018] S. Lloyd and C. Weedbrook, Quantum generative adversarial learning, Phys. Rev. Lett. 121, 040502 (2018).
- Dallaire-Demers and Killoran [2018] P.-L. Dallaire-Demers and N. Killoran, Quantum generative adversarial networks, Phys. Rev. A 98, 012324 (2018).
- Amin et al. [2018] M. H. Amin, E. Andriyash, J. Rolfe, B. Kulchytskyy, and R. Melko, Quantum Boltzmann machine, Phys. Rev. X 8, 021050 (2018).
- Zoufal et al. [2021] C. Zoufal, A. Lucchi, and S. Woerner, Variational quantum Boltzmann machines, Quantum Machine Intelligence 3, 7 (2021).
- McClean et al. [2018] J. R. McClean, S. Boixo, V. N. Smelyanskiy, R. Babbush, and H. Neven, Barren plateaus in quantum neural network training landscapes, Nat Commun 9, https://doi.org/10.1038/s41467-018-07090-4 (2018).
- Arrasmith et al. [2022] A. Arrasmith, Z. Holmes, M. Cerezo, and P. J. Coles, Equivalence of quantum barren plateaus to cost concentration and narrow gorges, Quantum Science and Technology 7, 045015 (2022).
- Larocca et al. [2022a] M. Larocca, P. Czarnik, K. Sharma, G. Muraleedharan, P. J. Coles, and M. Cerezo, Diagnosing barren plateaus with tools from quantum optimal control, Quantum 6, 824 (2022a).
- Cerezo and Coles [2021] M. Cerezo and P. J. Coles, Higher order derivatives of quantum neural networks with barren plateaus, Quantum Science and Technology 6, 035006 (2021), publisher: IOP Publishing.
- Arrasmith et al. [2021] A. Arrasmith, M. Cerezo, P. Czarnik, L. Cincio, and P. J. Coles, Effect of barren plateaus on gradient-free optimization, Quantum 5, 558 (2021).
- Holmes et al. [2021] Z. Holmes, A. Arrasmith, B. Yan, P. J. Coles, A. Albrecht, and A. T. Sornborger, Barren plateaus preclude learning scramblers, Phys. Rev. Lett. 126, 190501 (2021).
- Zhao and Gao [2021] C. Zhao and X.-S. Gao, Analyzing the barren plateau phenomenon in training quantum neural networks with the ZX-calculus, Quantum 5, 466 (2021).
- Thanasilp et al. [2024] S. Thanasilp, S. Wang, M. Cerezo, and Z. Holmes, Exponential concentration in quantum kernel methods, Nature communications 15, 5200 (2024).
- Ragone et al. [2024] M. Ragone, B. N. Bakalov, F. Sauvage, A. F. Kemper, C. Ortiz Marrero, M. Larocca, and M. Cerezo, A Lie algebraic theory of barren plateaus for deep parameterized quantum circuits, Nature Communications 15, 7172 (2024).
- Fontana et al. [2024] E. Fontana, D. Herman, S. Chakrabarti, N. Kumar, R. Yalovetzky, J. Heredge, S. H. Sureshbabu, and M. Pistoia, Characterizing barren plateaus in quantum ansätze with the adjoint representation, Nature Communications 15, 7171 (2024).
- Anschuetz and Kiani [2022] E. R. Anschuetz and B. T. Kiani, Quantum variational algorithms are swamped with traps, Nature Communications 13, 7760 (2022).
- Cerezo et al. [2022] M. Cerezo, G. Verdon, H.-Y. Huang, L. Cincio, and P. J. Coles, Challenges and opportunities in quantum machine learning, Nature Computational Science 2, 567 (2022).
- Holmes et al. [2022] Z. Holmes, K. Sharma, M. Cerezo, and P. J. Coles, Connecting ansatz expressibility to gradient magnitudes and barren plateaus, PRX Quantum 3, 010313 (2022).
- Cerezo et al. [2021] M. Cerezo, A. Sone, T. Volkoff, L. Cincio, and P. J. Coles, Cost function dependent barren plateaus in shallow parametrized quantum circuits, Nature Communications 12, 1791 (2021).
- Uvarov and Biamonte [2021] A. V. Uvarov and J. D. Biamonte, On barren plateaus and cost function locality in variational quantum algorithms, Journal of Physics A: Mathematical and Theoretical 54, 245301 (2021), publisher: IOP Publishing.
- Sharma et al. [2022a] K. Sharma, M. Cerezo, L. Cincio, and P. J. Coles, Trainability of dissipative perceptron-based quantum neural networks, Phys. Rev. Lett. 128, 180505 (2022a).
- Ortiz Marrero et al. [2021] C. Ortiz Marrero, M. Kieferová, and N. Wiebe, Entanglement-induced barren plateaus, PRX Quantum 2, 040316 (2021).
- Patti et al. [2021] T. L. Patti, K. Najafi, X. Gao, and S. F. Yelin, Entanglement devised barren plateau mitigation, Phys. Rev. Res. 3, 033090 (2021).
- Ho and Pepyne [2002] Y.-C. Ho and D. L. Pepyne, Simple explanation of the no-free-lunch theorem and its implications, Journal of optimization theory and applications 115, 549 (2002).
- Poland et al. [2020] K. Poland, K. Beer, and T. J. Osborne, No free lunch for quantum machine learning (2020), arXiv:2003.14103 [quant-ph] .
- Sharma et al. [2022b] K. Sharma, M. Cerezo, Z. Holmes, L. Cincio, A. Sornborger, and P. J. Coles, Reformulation of the no-free-lunch theorem for entangled datasets, Phys. Rev. Lett. 128, 070501 (2022b).
- Verdon et al. [2019] G. Verdon, M. Broughton, J. R. McClean, K. J. Sung, R. Babbush, Z. Jiang, H. Neven, and M. Mohseni, Learning to learn with quantum neural networks via classical neural networks (2019), arXiv:1907.05415 [quant-ph] .
- Grant et al. [2019] E. Grant, L. Wossnig, M. Ostaszewski, and M. Benedetti, An initialization strategy for addressing barren plateaus in parametrized quantum circuits, Quantum 3, 214 (2019).
- Rudolph et al. [2023a] M. S. Rudolph, J. Miller, D. Motlagh, J. Chen, A. Acharya, and A. Perdomo-Ortiz, Synergistic pretraining of parametrized quantum circuits via tensor networks., Nat Commun 14, https://doi.org/10.1038/s41467-023-43908-6 (2023a).
- Larocca et al. [2022b] M. Larocca, F. Sauvage, F. M. Sbahi, G. Verdon, P. J. Coles, and M. Cerezo, Group-invariant quantum machine learning, PRX Quantum 3, 030341 (2022b).
- Meyer et al. [2023] J. J. Meyer, M. Mularski, E. Gil-Fuster, A. A. Mele, F. Arzani, A. Wilms, and J. Eisert, Exploiting symmetry in variational quantum machine learning, PRX Quantum 4, 010328 (2023).
- Zheng et al. [2023] H. Zheng, Z. Li, J. Liu, S. Strelchuk, and R. Kondor, Speeding up learning quantum states through group equivariant convolutional quantum ansätze, PRX Quantum 4, 020327 (2023).
- Bowles et al. [2023] J. Bowles, V. J. Wright, M. Farkas, N. Killoran, and M. Schuld, Contextuality and inductive bias in quantum machine learning, arXiv preprint arXiv:2302.01365 (2023).
- Han et al. [2018a] Z.-Y. Han, J. Wang, H. Fan, L. Wang, and P. Zhang, Unsupervised generative modeling using matrix product states, Phys. Rev. X 8, 031012 (2018a).
- Rudolph et al. [2023b] M. S. Rudolph, J. Chen, J. Miller, A. Acharya, and A. Perdomo-Ortiz, Decomposition of matrix product states into shallow quantum circuits, Quantum Science and Technology 9, 015012 (2023b).
- Koller and Friedman [2009] D. Koller and N. Friedman, Probabilistic Graphical Models: Principles and Techniques (The MIT Press, 2009).
- Low et al. [2014] G. H. Low, T. J. Yoder, and I. L. Chuang, Quantum inference on bayesian networks, Phys. Rev. A 89, 062315 (2014).
- Borujeni et al. [2021] S. E. Borujeni, S. Nannapaneni, N. H. Nguyen, E. C. Behrman, and J. E. Steck, Quantum circuit representation of Bayesian networks, Expert Systems with Applications 176, 114768 (2021).
- Bakó et al. [2024] B. Bakó, D. T. Nagy, P. Hága, Z. Kallus, and Z. Zimborás, Problem-informed graphical quantum generative learning, arXiv preprint arXiv:2405.14072 (2024).
- Chow and Liu [1968] C. Chow and C. Liu, Approximating discrete probability distributions with dependence trees, IEEE Transactions on Information Theory 14, 462 (1968).
- Rudolph et al. [2024] M. S. Rudolph, S. Lerch, S. Thanasilp, O. Kiss, S. Vallecorsa, M. Grossi, and Z. Holmes, Trainability barriers and opportunities in quantum generative modeling, npj Quantum Inf 10, https://doi.org/10.1038/s41534-024-00902-0 (2024).
- Anderson et al. [1994] N. Anderson, P. Hall, and D. Titterington, Two-sample test statistics for measuring discrepancies between two multivariate probability density functions using kernel-based density estimates, Journal of Multivariate Analysis 50, 41 (1994).
- Hofmann et al. [2008] T. Hofmann, B. Schölkopf, and A. J. Smola, Kernel methods in machine learning, The Annals of Statistics 36, 1171 (2008).
- Sweke et al. [2020] R. Sweke, F. Wilde, J. Meyer, M. Schuld, P. K. Faehrmann, B. Meynard-Piganeau, and J. Eisert, Stochastic gradient descent for hybrid quantum-classical optimization, Quantum 4, 314 (2020).
- Kingma and Ba [2014] D. P. Kingma and J. L. Ba, eds., Adam: A Method for Stochastic Optimization, Vol. 3 (International Conference for Learning Representations, 2014).
- Schuld et al. [2019] M. Schuld, V. Bergholm, C. Gogolin, J. Izaac, and N. Killoran, Evaluating analytic gradients on quantum hardware, Phys. Rev. A 99, 032331 (2019).
- Vidal [2003] G. Vidal, Efficient classical simulation of slightly entangled quantum computations, Phys. Rev. Lett. 91, 147902 (2003).
- Schollwöck [2005] U. Schollwöck, The density-matrix renormalization group, Rev. Mod. Phys. 77, 259 (2005).
- Han et al. [2018b] Z.-Y. Han, J. Wang, H. Fan, L. Wang, and P. Zhang, Unsupervised generative modeling using matrix product states (2018b).
- Paeckel et al. [2019] S. Paeckel, T. Köhler, A. Swoboda, S. R. Manmana, U. Schollwöck, and C. Hubig, Time-evolution methods for matrix-product states, Annals of Physics 411, 167998 (2019).
- Ran [2020] S.-J. Ran, Encoding of matrix product states into quantum circuits of one- and two-qubit gates, Phys. Rev. A 101, 032310 (2020).
- Hamming [1950] R. W. Hamming, Error detecting and error correcting codes, The Bell System Technical Journal 29, 147 (1950).
- Arabie and Boorman [1973] P. Arabie and S. A. Boorman, Multidimensional scaling of measures of distance between partitions, Journal of Mathematical Psychology 10, 148 (1973).
- Tucci [2005] R. R. Tucci, An introduction to cartan’s kak decomposition for qc programmers, arXiv preprint (2005).
- Hamilton et al. [2019] K. E. Hamilton, E. F. Dumitrescu, and R. C. Pooser, Generative model benchmarks for superconducting qubits, Phys. Rev. A 99, 062323 (2019).
- Du et al. [2020] Y. Du, M.-H. Hsieh, T. Liu, and D. Tao, Expressive power of parametrized quantum circuits, Phys. Rev. Res. 2, 033125 (2020).
- Coyle et al. [2021] B. Coyle, M. Henderson, J. Chan Jin Le, N. Kumar, M. Paini, and E. Kashefi, Quantum versus classical generative modelling in finance, Quantum Science and Technology 6, 024013 (2021), publisher: IOP Publishing.
- Kondratyev [2021] A. Kondratyev, Non-differentiable learning of quantum circuit Born machine with genetic algorithm, Wilmott 2021, 50 (2021).
- Kondratyev and Schwarz [2019] O. Kondratyev and C. Schwarz, The market generator, SSRN https://dx.doi.org/10.2139/ssrn.3384948 (2019).
- Sadr [2009] A. Sadr, Interest Rate Swaps and Their Derivatives: A Practitioner’s Guide (John Wiley & Sons, Ltd, 2009).
- de Prado [2020] M. L. de Prado, Machine Learning for Asset Managers (Cambridge University Press, 2020).