Chromatic Learning for Sparse Datasets

The hashing trick (HT) initially appeared in [8] as a method for dimensionality reduction. HT is a linear transformation $\phi:\mathbb{R}^{D}\rightarrow\mathbb{R}^{d}$ which reduces sparse vectors in a high $D$-dimensional space to a small $d$-dimensional one using two hashes $\eta:[D]\rightarrow[d],\xi:[D]\rightarrow\{\pm 1\}$ [12], $\phi_{i}(\mathbf{x})=\sum_{j:\eta(j)=i}\xi(j)x_{j}$, which approximately preserves linear inner products (i.e., $\operatorname{\mathbb{E}}\left[{\left\langle\phi(\mathbf{x}),\phi(\mathbf{y})\right\rangle}\right]=\left\langle\mathbf{x},\mathbf{y}\right\rangle$ with low variance) and thus reconstructs a linear kernel on the original space $\mathbb{R}^{D}$.

Recently, HT structural requirements were characterized by the upper bound on the ratio $\nicefrac{{\left\lVert\mathbf{x}\right\rVert_{\infty}}}{{\left\lVert\mathbf{x}\right\rVert_{2}}}\leq\nu$ for all inputs $\mathbf{x}$ [13]: with probability $1-\delta$, if $d=\Omega\left({\epsilon^{-2}\log\frac{1}{\delta}}\right)$ and $\nu=\tilde{O}\left({\sqrt{\epsilon}}\right)$, then the relative error between $\left\lVert\phi(\mathbf{x})\right\rVert_{2}$ and $\left\lVert\mathbf{x}\right\rVert_{2}$ is at most $\epsilon$ (a condition related to preserving inner products through the parallelogram law). A $\nu=\tilde{O}\left({\sqrt{\epsilon}}\right)$ condition points to the generality of HT. For $k$-sparse binary vectors in $\mathbb{R}^{n}$, $\nu\leq k^{-1/2}$; however, this relies on at least $k$ non-zero values for every sparse input. For a bag of words representation, a $\nicefrac{{1}}{{k}}$ relative norm error would require sentences of at least $k$ words. An intuitive question that we seek to answer in this work is whether there are dimensionality reduction mechanisms that can take advantage of stronger structure than $\nu$, and even benefit from having few non-zero entries.

Gradient-boosted decision trees (GBDTs) are a supervised learning algorithm for learning over a base decision tree (DT) [14]. For a weak hypothesis class of DTs $\mathcal{F}$, GBDTs provide a mechanism to learn in the larger class of the additive closure $\mathcal{G}$ of $\mathcal{F}$, where, given a running weighted sum $F_{t}=\sum_{i=1}^{t}w_{i}f_{i}$ for $f_{i}\in\mathcal{F}$, a new $f_{t+1}$ is fit to the gradient of the loss at at each data point $\partial_{F_{t}}(\mathbf{x})\ell(F_{t}(\mathbf{x}),y)$ and then added $F_{t+1}=F_{t}+w_{t+1}f_{t+1}$ with an appropriately-chosen weight.

While this approach allows search over the larger class $\mathcal{G}$, DT training at each iteration is expensive, unless alleviated through specialized techniques like exclusive feature bundling (EFB) in [1]. In that work, the authors notice that DT training can be accelerated by reducing dataset width. EFB builds a co-occurrence graph on the set of categorical features $V$ with an edge between two vertices if they ever co-occur (i.e., attain nonzero values in at least one training example). Coloring this graph $G=(V,E)$ provides a map from vertices to colors, where vertices sharing a color must be mutually exclusive among all observed training examples. [1] uses an incremental but serial binary adjacency matrix construction for an $O(V^{2})$ greedy coloring run time.

Unifying each of these color sets into a single categorical variable reduces DT training cost, improving GBDT training speed overall. Similar dimensionality reduction techniques have been observed in other domains, such as register allocation [15]. However, many estimators require numerical inputs, such as linear models, Gaussian Process classifiers, Factorization Machines, and neural networks. Broader application of EFB is thus limited because one-hot encoding, typically used for pre-processing categorical features, inverts bundling: the one-hot encoding of a bundled feature is equivalent to the concatenation of one-hot encodings for its constituents. In this work, we present a method that adapts the general idea of compression via coloring co-occurrence but is suitable for use in models that require numerical inputs.

Recent work [2] shows that the problem of quantizing a fine categorical variable with $D$ values to one with $d$ values while preserving as much mutual information with the binary label as possible is monotone submodular.

A set-valued function $f:2^{V}\rightarrow\mathbb{R}$ is monotone if $f(A)\leq f(B)$ for $A\subset B\subset V$ and submodular if the gain $\Delta(x|Y)=f\left({\left\{{x}\right\}\cup Y}\right)-f(Y)$ satisfies $\Delta(x|A)\geq\Delta(x|B)$ for $A\subset B\subset V$ and $x\in V\setminus B$. Such functions admit deterministic $\left({1-e^{-1}}\right)$-approximate maximization procedures in psuedo-polynomial time [16] and polynomial randomized algorithms [17] for finding $\operatorname*{argmax}_{T}f(T)$.

In a classification setting with a single $[D]$-valued categorical feature $X$ and a binary label $Y$, [18] show that the mapping $Z:[D]\rightarrow[d]$ which maximizes $I(Z(X);Y)$ is defined by $d+1$ splitters $S=\left\{{s_{0}\cdots s_{d}}\right\}$ with $Z_{S}(x)=i$ when $s_{i-1}<x\leq s_{i}$. [2] prove that selecting the set $S\subset[D]$ is monotone submodular maximization problem $I(Z_{S}(X);Y)$.

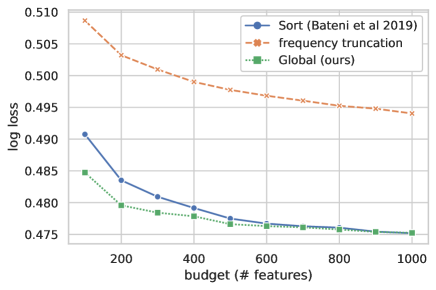
We found direct application of the method unsuccessful. Using label information to featurize results in target leakage [19]. [2] groups features together with similar conditional positive label probability. This artificially reduces label variance within each quanitzed feature cluster and results in overfitting. We verify this on the original dataset used in [2], the Criteo Ad-Click Prediction dataset. To reduce variance from the fitting procedure for evaluation, we train a logistic regression, but note that for such a cheap learner, dimensionality reduction is not necessary for the end classification goal. Figure. 1 shows the training and testing log loss of categorical feature compression applied to estimates of conditional probability made from the training set itself compared to a simple fix, data splitting. With an even split, we estimate conditional probabilities with half of the data, and train on the other half.¹¹1On a practical note, this can be done deterministically without requiring another copy of the data by hashing each example and using the first bit of the resulting hash to split training data. We find that splitting is crucial for low test loss and, as expected, training loss is conspicuously low when double-dipping.

A few challenges with the application of [2] remain:

1. 1.

   Many datasets (Sec. 4) have millions of binary features, rather than few categorical ones with many values.

2. 2.

   [2] extend their method to multiple categorical variables with a heuristic, but it does not perform well when significantly reducing dimension (Sec. 3.3).

Suppose our training set consists of iid examples, $\mathbf{x}_{i}\in 2^{D}$. Associate with each $\mathbf{x}_{i}$ its set of active indices $T_{i}\subset[D]$, and consider the co-occurrence graph $G$ defined by vertices $V=\bigcup_{i}T_{i}$ and edges $E=\bigcup_{i}K(T_{i})$, with $K(\cdot)$ generating the edges from the complete graph on its argument, a set of vertices. Given a proper coloring of $G$, $c:V\rightarrow\mathbb{N}$, we show that the representation of the data defined by categorical vectors $\mathbf{v}$ with $\left\lvert{cV}\right\rvert$ categorical variables (where $v_{i}$ has cardinality $\left\lvert{c^{-1}\{i\}}\right\rvert$) permits learning with low generalization error.

In particular, any Lipschitz-smooth decision function on the original space $2^{D}$ can be approximated by one that operates on the chromatic representation $\mathbf{v}$. By construction this holds for all training examples, but for a test example $T\subset[D]$, two features may have identical colors. In this case, the example must be approximated by an input with one of the colliding features missing.²²2Given two features mapping to the same color outside the training set, the more popular feature is dropped for our evaluation.

For a given $T\subset[D]$, let $\mathrm{CC}(G,T)$ be the count of color collisions, i.e., $\left\lvert{T}\right\rvert-\left\lvert{cT}\right\rvert$. By smoothness, bounding $\operatorname{\mathbb{E}}\mathrm{CC}(G,T)$ implies low average discrepancy between the decision function on the two representations (Appendix A). We find that a greedy coloring has an average color collision count less than one on all our sparse benchmark datasets (Tab. 1).

The previous section motivates constructing the graph $G$ explicitly to obtain a proper coloring. However, construction of $G$ can potentially be expensive. We describe how to efficiently construct $G$.

First, we require the union $E$ of the edge sets $K(T_{i})$. We process the dataset in $P$ parallel chunks on mapper threads. We maintain $W=\alpha P$ global sets of edges, where $\alpha$ is the average ratio of time it takes to generate edges from each point to the time it takes to add such edges to a hashset. We split the hash space of edges into $W$ parts. Each mapper allocates $W$ local buffers and, upon processing $T_{i}$ adds edges from $K(T_{i})$ to the local buffer corresponding to each edge’s shard. Once a buffer is filled, the mapper locks the corresponding global set of edges and adds the global set with its local edges.

The expected contention time on each global set’s mutex is constant by the choice of $\alpha$.³³3In practice, we can choose $\alpha=1$ as the hashing the edge, which is done locally on each mapper, is the most expensive operation. As a result, every edge only requires a constant amount of time to process. Each mapper only requires $O(P)$ local working memory, independent of the data, in contrast to tree-merge paradigms such as map-reduce. This hash-join approach can be applied to vertices as well and can be extended by storing aggregate statistics for each vertex, as is necessary for Sec. 3.3.

Once $E$ is collected and converted in parallel to an adjacency list representation, $G$ is ready for approximate graph coloring, which requires $O\left({\nicefrac{{V\Delta}}{{P}}}\right))$ time, where $\Delta$ is the maximum degree [21]. Converting to an adjacency list in parallel can be done by mapping over the edge set: first computing the degree of each vertex across threads with atomic increments, and next using a cumulative sum across the degree array to define atomic integral offsets in an adjacency array, which can then be filled in another parallel sweep across $E$.

With each feature assigned a color, we view the dataset as a categorical input, with colors as categorical variables and the original input features as categorical values. This permits the use of several categorical encodings.

With target encoding (TE), the average label value replaces categories, yielding just $m$ numeric features, one for each color. With CL combined with frequency truncation (CL+FT) and a budget $b$, we embed the $b$ most frequent categories in $d$ dimensions, yielding an embedding layer that creates $(dm)$-sized embeddings with $bd$ parameters. For neural networks with a first hidden layer of size $h$, using frequency truncation (FT) alone requires the first layer to use $hbd$ parameters, which is prohibitive for all but small $b$.

In addition, we present an extension to submodular-based feature compression (SM). We depart from [2], which recommends compressing to a fixed budget of features $b$ by running categorical feature compression on each categorical variable $X_{i}$ to maximize $I(Z_{i}(X_{i});Y)$, sorting results by marginal gain across all features, and using the top $b$ selections for the final encoding. This results in suboptimal compression relative to our alternative, as the final sorting stage is based on marginal gains made with respect to each individual solution, so the top-$b$ features do not necessarily maintain any optimality properties.

Instead, we maximize the global submodular problem $\sum_{i}I(Z_{i}(X_{i});Y)$ across all colors $i$ simultaneously—adding submodular functions over disjoint inputs retains submodularity. This outperforms the sorting heuristic on the original Criteo task proposed by [2] (Fig. 2). Excerpting logarithmic factors, solving one submodular problem of size $V$ is faster than multiple of mixed sizes summing to $V$, requiring $O(\log^{2}V+V/P)$ time [22].

With this final encoding, an example $\mathbf{x}\in\mathbb{R}^{D}$ is transformed into one in $\mathbb{R}^{b}$ by taking every nonzero feature $j$ in $\mathbf{x}$ and setting the corresponding feature $Z_{c(j)}(j)$, which is then one-hot encoded.

A comparison of chromatic learning with submodular feature compression (CL+SM) to frequency-based truncation (FT) and hashing trick (HT) shows favorable performance in for linear estimators across a variety of budgets. We performed a single pass over the training data via Vowpal Wabbit with default parameters using, which performs online adaptive gradient descent [9]. Our results illustrate that, to achieve equivalent log loss on the test set, FT requires a magnitude more features and HT requires two orders of magnitude (Fig. 3).

For very large budgets that approach the original dimensionality on the two smaller datasets, FT outperforms CL+SM. In this regime, where nearly the full input dimensionality is preserved, we suspect that the quantization may interfere with model confidence.

With a small budget, CL enables learning more sophisticated classifiers that are otherwise not trainable in limited-memory settings. We assess the performance of several deep learning models given different dimensionality reduction approaches in the highly compressed setting of 1024 features.

We used default parameters specified by the deep learning library [24], but reduced batch size to 256 (from 2048) because of an out-of-memory error on the Nvidia V100 GPUs we were using. The library was originally configured for dense datasets, such as Criteo. We reduced the epoch count to 5 (from 15) to account for the increased number of gradient steps and did not change any other settings.

We find that CL compares favorably in terms of test accuracy with several categorical encoding strategies compared to the FT baseline (Tab. 3). Across all 5 evaluated architectures and all 4 datasets, CL+SM outperforms both HT and FT on every dataset, except for DeepFM with url, where it achieves a test log loss of 0.058, compared to FT’s 0.053. Furthermore, CL+FT presents a simpler alternative to CL+SM which enables using the full dataset and many more features directly, on 2 of the 4 datasets, this improves upon the CL+SM representation with 1024 one-hot features.