Chiral spin-phonon bound states and spin-spin interactions with phononic lattices
Abstract
Designing unconventional interactions between single phonons and spins is fascinating for its applications in quantum phononics. Here, we propose a reliable scheme for coupling spins and phonons in phononic dimer and trimer lattices, with the combination of solid-state defects and diamond phononic (optomechanical) crystals. The dimer and trimer lattices used are an array of coupled phononic cavities with spatially modulated hopping rates. We predict a series of unconventional sound-matter interaction phenomena in this hybrid quantum system. In the dimer lattice, we show the formation of chiral spin-phonon bound states and topology-dependent phononic collective radiation. While in the trimer lattice, chiral bound states still exist and the spin relaxation is sublattice-dependent. The chiral bound states existed in both types of lattices are robust to large amount of disorder, which can mediate chiral and robust spin-spin interactions. This work provides a promising platform for phonon-based quantum information processing and quantum simulation.
I introduction
Engineering and controlling dipole-dipole interactions is at the heart of analog quantum simulation, which can be realized through manipulating the field environment between emitters [1]. A fascinating platform is the nanophotonic structure, wherein the dispersion relation can be designed on-demand, and the atom-photon bound states can form within the band and band-gap when atoms are placed nearby [2, 3, 4, 5, 6, 7]. The photonic component in the bound state is virtually excited, thereby can mediate long-range tunable dipole-dipole interactions without dissipations into the guided modes. Usually, the photon bound state is exponentially localized and isotropic around the emitter, which limits the form of dipole-dipole interactions [3, 4]. However, through properly modifying the photonic bath, photon bound states can be anisotropic [8, 9, 10, 11], power-law scaling [6, 7, 12], and even phase tunable [13, 14, 15, 16]. These special bound states can be used to study more exotic many-body phases. In addition, there are other new quantum phenomena when emitters interact with structured photonic baths, which have potential applications in quantum information processing [17, 18, 19, 20, 21, 22].
A new paradigm to capture novel bound states is taking advantage of topological photonic lattices [6, 8, 9, 7, 12, 14, 23]. In particular, in the dimer photonic lattice (a photonic analog of the Su-Schrieffer-Heeger (SSH) model), there exist chiral photonic bound states with only one side envelope with respect to the emitter [8, 9]. These directional bound states can mediate directional dipole-dipole interactions. As a natural extension, the trimer lattice allows for chiral edge states that appear at one side of the lattice [24]. These edge states have a direct connection with that of two-dimensional Aubry-André-Harper (AAH) models [25], thus is robust against disorders. Using such chiral edge modes, the adiabatic topological pumping has been predicted and experimentally observed in 1D phononic lattices [26, 27]. However, so far the interaction with emitters and emitter-emitter interactions in this type of photonic or phononic lattice have been unexplored.
On the other hand, phonon, the quanta of mechanical vibration, is regarded as an alternative quantum information carrier [28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39]. The spin-mechanical hybrid systems may overcome the shortcoming of vacuum radiations in nanophotonic structures, because phonons do not decay into free-space. One of the most promising platforms is diamond crystal [40, 41, 42, 43], since in terms of nanofabrication, it is capable of fabricating high-quality mechanical modes at the GHz frequency, while integrating color centers as long-lived spin qubits [44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54]. So far, the strain coupling mechanism between diamond electric spins and mechanical modes has been widely explored, providing new opportunities for realizing phonon networks in the strong-coupling regime [55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68]. In particular, diamond phononic crystal waveguides can host phononic band gaps and the spin-phonon bound states can form when the spin’s frequency lies within this special frequency range [69, 70, 71]. Such spin-phonon bound states can mediate long-range tunable spin-spin interactions for simulating spin models in hybrid quantum systems. Moreover, the phononic topological states as well as their interactions with one or more emitters at the quantum level are widely investigated in phononic crystals [72, 73, 74, 75]. Combining topological phononic structures with solid-state spins may give rise to exotic spin-phonon bound states and other interesting sound-matter interaction phenomena.
In this work, we consider sound-matter interactions in dimer and trimer phononic lattices, where an array of solid-state defects are integrated into a diamond phononic crystal. The dimer and trimer lattices used are an array of coupled phononic crystal cavities with spatially modulated hopping rates. In contrast to previous works where the phononic edge modes are obtained from the breakdown of the time-reversal symmetry with the assistance of optical modes [76, 73, 77], here we obtain the edge states through the periodic modification of the hopping rates in the 1D phononic crystal.
In the dimer lattice, we show the formation of chiral spin-phonon bound states, where the spin mimics the behaviour of a boundary to localize phonons on its one side. Furthermore, when two spins are considered, the collective decay depends on the phononic waveguide structure between them, and more interestingly, the phonon collective decay can be topology-dependent. While in the trimer lattice, the chiral bound states still exist with a number of six that corresponds to six chiral edge states, occurring at certain energy and sublattices. When the spin’s frequency is resonant with the band, we show the spin relaxation becomes sublattice-dependent as a result of mirror symmetry breaking. Furthermore, due to the topology or topological origin, the chiral spin-phonon bound states in both lattice structures are robust to large amounts of disorder, which can mediate chiral and robust spin-spin interactions. These interactions enable the exploration of exotic many-body phases such as double Néel ordered states [8, 78]. The quantum control over phononic edge states is also considered in a finite system in terms of population inversion between spins and edge states. We also illustrate how to design the required lattice structure in a 1D diamond nanobeam and show that our scheme is feasible under current experimental conditions. This work provides a novel platform for manipulating phonons and is useful for phonon-based quantum applications.
II The setup
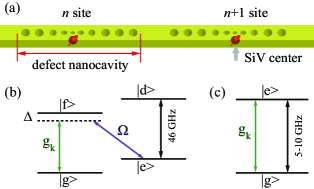
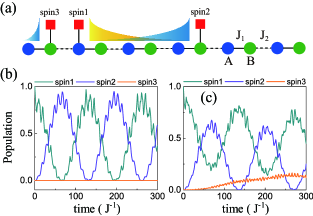
We consider a full lattice of phononic cavities in diamond crystals, where a single solid-state spin is integrated into each lattice site, as depicted in Fig. 1(a). The acoustic resonators have identical resonance frequency and each pair of adjacent ones are coupled via either direct near-field coupling or a phonon waveguide, wherein the hopping rates are tunable via structure designs. The Hamiltonian of this coupled phononic cavity waveguide is written as (setting )
| (1) |
where is the annihilation operator of the phononic mode, and is the tunnelling strength between the th cavity and the th cavity.
The solid-state spins considered in this setup are SiV centers, whose electric ground states have a splitting of GHz and possess a large strain susceptibility due to the spin-orbit coupling. In the presence of a static magnetic field, the two orbit states are split into four energy levels, as shown in Fig. 1(b). The sublevels and can be viewed as a long-lived spin, which can be indirectly coupled to the acoustic modes with frequencies of GHz via a Raman process (see Fig. 1(b)) or directly coupled to the acoustic modes with frequencies of several GHz (see Fig. 1(c)) [33, 64]. In both cases, the single phonon coupling strength can reach MHz such that the strong coupling condition can be satisfied. Under the rotating wave approximation, the total Hamiltonian of the system is
| (2) |
with the (effective) resonance frequency of the th spin, , and the (effective) spin-phonon coupling strength.
III Spin-phonon interactions in a dimer lattice
III.1 The Hamiltonian
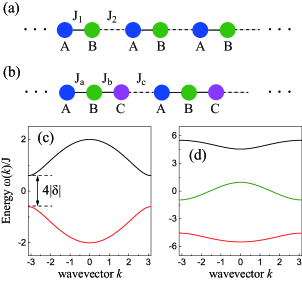
When the hopping rates are spatially designed with a periodicity of , the phononic crystal behaves as a dimer lattice, which is the phononic analog of the Su-Schrieffer-Heeger (SSH) model and allows for topological phonons at the quantum level. The Hamiltonian in Eq. (1) can be rewritten as
| (3) | |||||
where and are respectively the annihilation operator of phonon at sublattice and sublattice of the th unit cell. The hopping rates can be replaced by , and , with the dimerization strength. To transform the Hamiltonian into momentum space, we impose periodic boundary conditions and introduce the Fourier transformation
| (4) |
For simplicity, we take the lattice constant below. Then the Hamiltonian of the phononic bath is transformed into , with and the kernel
| (7) |
Diagonalizing the Hamiltonian and taking as the energy reference, we can get the eigenenergies, that is, the dispersion relation
| (8) | |||||
The two dispersions are symmetric with respect to the zero energy due to chiral symmetry and we set below. The band structure is shown in Fig. 2(c), where a middle bandgap with size is opened. In particular, for , it corresponds to a topological phase of sound and there exists a pair of phononic edge states exponentially localized at the two ends when the system is finite [79].
We now consider the spins are coupled to the topological phonons in dimer lattices. The interaction Hamiltonian of the spins and bath in -space is given by
| (9) | |||||
with and the eigenoperators in the diagonalization basis, the unit cell position and . The first (second) term represents the interactions between the phonons and spins located at the () sublattice. The single spins can acquire extra energy due to their interaction with the quantized phononic field, which is the self-energy expressed as
| (10) |
with . In particular, within the Markovian approximation, describes the decay rate and represents the energy shift. The interaction with the phononic bath can also lead to collective self-energy of the spins, which can be obtained by simply replacing in the summation of . Since the phononic dimer lattice has sublattice (chiral) symmetry, the pairwise collective self-energy can be classified into two categories: one from the spins in the same sublattice and the other from the spins in the different sublattice
| (11) | |||||
| (12) |
where is the cell distance between two spins, with respect to their absolute values and,
| (13) |
The sign in these two self-energy expressions is positive when and negative when . The self-energy of single spins is also given here.
III.2 Chiral spin-phonon bound states
When the quantum emitters are coupled to this bath, the related topological features will be imprinted into the emitter-bath interaction. Specially, if the emitters’ frequency is chosen to be strictly equal to the zero-energy modes, the emitters can act as an effective edge of the lattice and localize the excitation on only one side [8, 9]. In this section, we show the formation of chiral spin-phonon bound states in this SiV-phononic crystal model.
We consider single spins coupled to the phononic dimer lattice, whose frequency lies within the bandgap. The spin no longer decays into the propagating modes, but is dressed by the acoustic modes close to the bandedges. The stationary state wavefunction in the single-excitation subspace can be expanded by
| (14) |
with the probability amplitude of the spin being in the upper state and the probability amplitude for finding a phononic excitation in sublattice at the wavevector . The coefficients can be obtained by solving the secular equation , yielding
| (15) | |||||
| (16) |
where the superscript in the wavefunction labels the sublattice (at the unit cell) to which the spin is coupled. Doing the Fourier transformation, we can obtain the corresponding spatial distribution in sublattice .
In this work, we mainly focus on the bound states at zero energy. A direct observation of the expressions shows that, when setting , , with the unit cell index. The other two spatial distributions can be given analytically, similar to the calculation of the self-energy. For the case of and the spin at the unit cell,
| (17) |
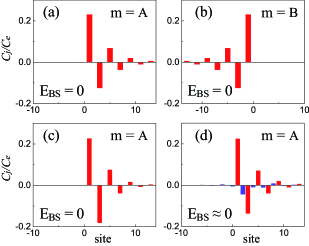
and , which indicates that the left (right) bound state vanishes when the spin is coupled to () sublattice. The chirality of the bound states arises from the inversion symmetry breaking of the phononic bath with respect to the coupling point, and reaches its maximum at . These two perfect chiral bound states are shown in Fig. 3(a) and 3(b), with numerical integrations of Eq. (15) and Eq. (16). Note that the number of chiral bound states is equal to that of the edge states.
We next consider the robustness of this chiral spin-phonon bound states in the dimer lattice. A finite chain with phononic cavities is used to simulate the SSH bath. The chiral bound states in the presence of disorder in the phonon hopping strength are depicted in Fig. 3(c), with adding the random terms to the total Hamiltonian. The disorder strength is chosen within the range for the th lattice site. We show that the chiral behavior of the bound states is protected, where the chiral symmetry persists. As a contrast, the diagonal disorder is also taken into account, which is shown in Fig. 3(d). We find that the middle bound state now has distributions in the A/B sublattices and both sides of the spin. Besides, the energy of the bound state is no longer strictly fixed at zero.
III.3 Topology-dependent collective radiation
Though the main topological feature is most pronounced in the zero-energy modes, the dynamics of spins in the phononic dimer lattice is different from that in the standard waveguide. In the weak coupling limit, the spin dynamics is subject to Eq. (11) and Eq. (12), therein the imaginary part represents the decay rate. From Eq. (11) (in the case ), we show that the decay rate of the spins is sublattice-independent, which can be roughly understood from the viewpoint that the spins couple to the two topology-different semi-infinite waveguides. Without loss of generality, we consider two spins resonant with the phononic band. There are three cases: i) the spins are coupled to sublattice; ii) the spins are coupled to sublattice (from left to right); iii) the spins are coupled to sublattice. In these three situations, the waveguide structures between the spins are standard-like, trivial and topological, respectively. As a result, the phonon-induced collective decay rate is different for the three cases. More interestingly, case II and case III are interchangeable by only varying the sign of the parameter . Therefore, the collective radiation is topology-dependent.
The collective decay rate can also be calculated by using the identical relation , which can provide a more intuitive insight to the features above. In the standard waveguide, the collective decay rate oscillates versus the emitter’s relative position, i.e., . In contrast, the collective decay rate in the SSH bath is given by
| (18) | |||||
| (19) |
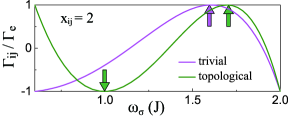
Here, is the cell-distance. Obviously, the topology-dependent parameter (phase) enters into Eq. (19). In Fig. 4, we plot as a function of spin frequency inside the upper band, with setting and . The case is opposite for inside the lower band, i.e., . Perfect super or subradiance occurs when . In particular, we find that the number of phononic super or subradiant points depends on the sign of : In the trivial phase (), there are perfect superradiant points inside the two passbands, while in the topological phase (), there are frequency points.
III.4 Chiral spin-spin interactions
The chiral spin-phonon bound states discussed above can mediate spin-spin interactions through the exchange of virtual phonons. As a result, the spin-spin interactions will inherit the features appearing in the bound states: i) decay exponentially with the spins’ distance; ii) the spin located in sublattice () only interacts with spin located in sublattice () on the one side; iii) robust against the off-diagonal disorder. For , the interaction in the Markovion limit is given as
| (20) |
with the coupling strength and
| (21) |
To numerically show these chiral spin-spin interactions, we use a finite lattice chain with phononic cavities and consider three spins coupled to the second, third and th cavity (see Fig. 5(a)). The off-diagonal disorder is also taken into account. The quantum dynamics of the three spins is plot in Fig. 5(b), with the initial state . We find that the population of spin 3 is always zero and the population is oscillating between spin 1 and spin 2 with an amplitude approaching one, which reflects the directionality and robustness of the spin-spin interactions. Similarly, the quantum dynamics of spins in the presence of diagonal disorder is plot in Fig. 5(c) for comparison. Apart from extra population in spin 3, we find that the population of spin 1 can not reach zero, since the energy value of the bound state is no longer pinned at zero in this case.
III.5 Quantum control over phononic edge states
In the finite system, edge effects inevitably occur especially in the topological phase, where a pair of edge states exponentially localize at the two ends of the lattice chain. The phononic edge states in a phononic crystal can be controlled with the addition of solid-state spins. In that case, the excitation can be transferred between spins and phononic edge states, with eigenenergies and eigenstates . The dynamics is govern by the effective Hamiltonian
| (22) | |||||
with and () when (). When setting and applying the Schrödinger equation, we can obtain the coupled equations of the coefficients
| (23) | |||||
| (24) | |||||
| (25) |
with and the wavefuncions in the states and , respectively. Solving these equations, the spin’s time evolution obeys
| (26) |
with . In the case of a large size cavity chain, and the spin exchanges energies between the left or right phononic edge state, which are symmetry and antisymmetry superpositions of the states , respectively.
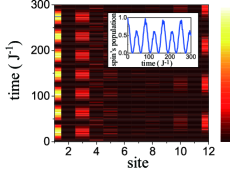
Concretely, we consider a single spin coupled to the th phononic cavity of a cavity chain designed with staggered hopping strengths and being in the topological phase. The system’s dynamics is shown in Fig. 6. We show that the excitation is mainly transferred between the spin and the left phononic edge state, in line with the prediction based on Eq. (26).
IV Spin-phonon interactions in trimer lattices
Previous work on trimer lattices have predicted the emergence of chiral edge states localized at one end of the system, without a counterpart on the opposite edge at the same energy in the phase without inversion symmetry protection [24, 26, 27]. Though there is no topology (no symmetry), these chiral edge states are still robust against large amounts of disorder due to the topological origin. Therefore, it’s still possible to obtain chiral spin-phonon bound states where the spin acts as the effective edges, and realize directional and robust quantum state transfer as well as quantum control over phononic edge states in a trimer lattice. In addition, the emission dynamics of the spins in this lattice is worth investigating since it is different from the one in a symmetry protected system.
IV.1 Hamiltonian
Similar to the dimer lattice, a trimer lattice is modeled with alternating hopping rates and having a periodicity of 3. The Hamiltonian of the phononic waveguide is rewritten as
| (27) | |||||
with , and the annihilation operators for the , and phononic modes at the th unit cell. In a common trimer lattice, the phonon tunneling strengths , and are unequal and there is no symmetry. The inversion symmetry only recovers in the special case of . Performing the same operation as in Sec. III.A, the Hamiltonian can be transformed into momentum space, with the kernel of Hamiltonian
| (31) |
Unlike the dimer lattice where the analytical solution to the dispersion relation is given, here we introduce a unitary matrix to diagonalize the kernel of Hamiltonian as , with () the eigenvectors and () the eigenvalues. The eigenoperators are given by . Then the Hamiltonian of the phononic trimer lattice in -space reads
| (32) |
The band structure is numerically plotted in Fig. 2(d), with , and .
Working in -space, the interaction Hamiltonian for the spins and phonon modes in the trimer lattice becomes
| (33) |
where the interaction is projected to the new basis. The self-energy of the spins is expressed as
| (34) |
The collective self-energy of the spins can be obtained by simply replacing in the summation of and adding a propagation factor to the integral.
IV.2 Chiral spin-phonon bound states
When the spin’s frequency lies within the phononic bandgap, there exist spin-phonon bound states in the single-excitation subspace. The spatial distribution of the phononic part of the bound state can be calculated by solving the stationary Schrödinger equation, yielding
| (35) |
Here, is the wavefunction at sublattice of the unit cell when the spin is coupled to the sublattice at the unit cell.
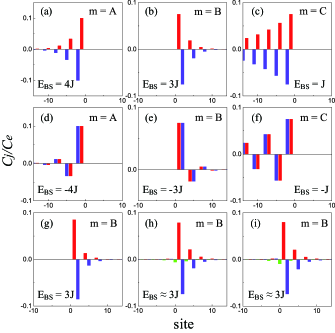
Inspired by the fact that chiral spin-phonon bound states appear at the zero-energy modes in a dimer lattice, we start to find the chiral bound states in a trimer lattice by setting the energy of the bound states equal to that of the chiral phononic edge states. For a finite system with hopping rates , there exist two edge states localized at the right end with energies . Thus, we plot the phononic part of the bound states in Fig. 7(a,d) with setting in Eq. (35). We find the spin-phonon bound state is chiral only when the spin is coupled to the sublattice, i.e., for and for . Also, these bound states have no components in the sublattice , while the amplitudes in the and sublattices are equal . Furthermore, the bound states are fractionally chiral when the spin is coupled to the and sublattices, which is reflected in the components on the sublattice, for and for .
However, the edge modes change when varying the boundary of the trimer lattice. When the finite system is constructed by , there are two pairs of edge states localized at the boundary, with energies and . While for the finite system constructed by , there is no edge mode. The bulk properties of the two cases are the same as that of . Thus, we turn to study the spin-phonon bound states at these frequencies. In Fig. 7(b,e) and 7(c,f), we show two pairs of chiral bound states located on the right/left side of the spin with , when the spin is coupled to the sublattice. Note that the six chiral bound states are one-to-one corresponding to the six edge states.
We now consider the robustness of the chiral bound states in the trimer lattice. As an example, we add disorder to the finite system with unit cells, by setting , where a spin is coupled to the sublattice with energy . In Fig. 7(g), we allow disorder in the intracell hopping and independently. While in Fig. 7(h), disorder in the intercell hopping is plotted. On the other hand, bound states with on-site disorder acting in are shown in Fig. 7(i). We observe several features from the numerical results. First, the directionality is robust to disorder in the intracell hopping. Second, the bound state has weight in each sublattices and both sides while the eigenenergies have a small deviation, in the presence of disorder in the intercell hopping or on-site disorder. Generally, the directional bound state is still robust when the disorder strength is on the order of the coupling/hopping strength. All these results indicate that the directional spin-phonon bound states can inherit the robustness of chiral edge states in the trimer lattice.
IV.3 Sublattice-dependent spin relaxation
From the discussion of chiral spin-phonon bound states in both lattices, we can conclude that the spin indeed acts as an effective boundary of the two semi-infinite waveguide structures. In this case, the system can be divided into three parts: the spin and two semi-infinite phononic waveguides. Contrary to what happens in the dimer lattice where the two semi-infinite structures are the same for spin at the sublattice, there are six different semi-infinite structures in the trimer lattice when the spin is respectively coupled to the sublattice. Thus, we predict that in the inversion-symmetry breaking phase of the trimer lattice, while in the inversion-symmetric phase of the trimer model. We note that the real part of the self-energy is the energy shift, which is small compared to the resonance frequency. Furthermore, the shift is zero when the spin’s frequency lies within the band. Therefore, we mainly focus on the spin relaxation when the frequency is resonant with the phononic waveguide.
Without loss of generality, we consider a single spin with frequency within the upper band, which is coupled to the sublattice, respectively. In the Markovian regime, the spin’s decay rate can be written as
| (36) |
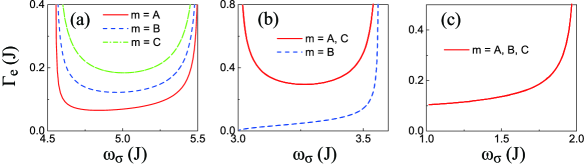
with the group velocity. In Fig. 8, we numerically plot the decay rate of the spin coupled to different sublattices when the spin’s frequency lies within the upper band. The hopping rates are , and in Fig. 8(a), 8(b) and 8(c), respectively. We find for . In the special case where inversion symmetry recovers, . Moreover, the standard 1D band-edge divergence of is canceled in the inversion-symmetric phase of the trimer model, when approaches the lower band-edge of . For comparison, the situation that the spin interacts with a normal coupled cavity waveguide is shown in Fig. 8(c), which predicts a decay rate . In general, the spin relaxation in a trimer lattice is sublattice-dependent, which is consistent with the discussion above.
IV.4 Bound state-mediated spin-spin interactions
We now discuss the spin-spin interactions mediated by the chiral spin-phonon bound states appearing in the trimer lattice. In the weak coupling limit, the interaction strength between two spins is
| (37) |
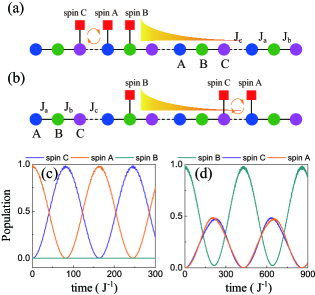
with the cell index, and the sublattice index. As an example, we take advantage of the bound state shown in Fig. 7(b) involving three spins with one at the sublattice and two neighbouring spins at the sublattices. When the spins at the sublattices are placed on the left side of the spin , as shown in Fig. 9(a), the two neighbouring spins are decoupled to the spin due to the directionality of the bound state and the population can be transferred between the two neighbouring spins. For the case of the spins at the sublattices on the right side of the spin , as shown in Fig. 9(b), the excitation is exchanged between the spin at the sublattice and the antisymmetry superposition of the two neighbouring spins. The dynamics of the three spins can be modeled with an effective Hamiltonian in the interaction picture as
| (38) | |||||
with and . In the first situation for , while in the second situation for . This reflects the directionality of the spin-spin interaction when the spin is coupled to the sublattice. When focusing on the case , we find that the transition is not resonant due to the interaction between the neighbouring spins. Note that the detuning (the last term in the second line of Eq. (38)) can be removed by external driving fields; thus the antisymmetric combinations of spin and spin acting as a single spin can be resonantly coupled to spin . Finally, we emphasize that the spin-spin interaction is directional only when one of the spins is at the sublattice.
We consider a resonator chain composed of lattice sites to numerically examine the two cases, as shown in Fig. 9. The disorder in the intracell hopping rate and is also taken into account and the spin’s frequency is in both cases. In the first case, the three spins are placed at the third, th and th lattice sites and the Rabi oscillation between spin and spin is observed in Fig. 9(c), with the initial state . We show the population in spin keeps zero. In the second case, the three spins are placed at the th, th and th lattice sites and the population is transferred between spin and spin with the initial state , as shown in Fig. 9(d). Though the energy of the bound state formed by spin is strictly pinned under disorders (), the energy of the bound states formed by spin and spin are not strictly pinned (). Therefore, the population of the spin can not reach zero with the time evolution.
IV.5 Quantum control over chiral phononic edge states
Because the edge modes in the trimer lattice remain in the bandgap, the quantum control on these modes becomes possible with the addition of spins. Furthermore, since the edge states in the inversion-symmetry breaking phase of the trimer lattice have no degeneracy, we can directly manipulate one of the phononic edge states on the boundary of the phononic crystal with the addition of a single spin. The resonance transfer can occur via tuning the frequency of the spin, with the interaction Hamiltonian
| (39) |
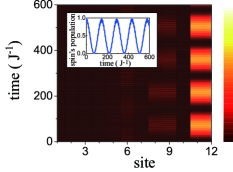
where is the coupling rate. As an example, we consider the situation that a single spin is placed at the th cavity of a cavity chain, with alternating hopping strengths . There exist two edge states localized on the right side of the system with energy . In Fig. 10, we plot the time evolution of the system and show a transition with the amplitude approaching one between the spin and one of the chiral phononic edge states.
V experimental feasibility
In this section, we discuss the experimental feasibility of our system. As illustrated in Fig. 1(a), an array of defect cavities can be fabricated in a diamond nanobeam. As an example, we consider the phononic cavities with resonance frequency GHz and two adjacent phononic cavities are coupled via a phononic waveguide. In the rotating frame, the cavity-waveguide-cavity Hamiltonian takes the form of
| (40) | |||||
where is the detuning between the cavity and the th waveguide mode, () is the creation (annihilation) operator of the th waveguide mode, is the cavity-waveguide coupling and the term accounts for the symmetry of the waveguide modes. Consider that the waveguide is short and a single mode is nearly resonant with the cavity, the Hamiltonian can be simplified to
| (41) | |||||
When taking the large detuning limit and applying the perturbation theory, we can arrive at the effective Hamiltonian describing hopping interactions between the two adjacent cavities
| (42) |
with the effective hopping rate between the phononic cavities. The cavity-waveguide coupling is tunable via designing the mirror section of the nanocavity, which connects the cavity and the waveguide. Meanwhile, the detuning can be tuned via changing the structure of the connecting waveguide. So far, the hopping strengths between adjacent mechanical resonators have been designed and realized with a few megahertz [80, 65].
We now show how to design the lattice structure in this work. As an example, we consider the case of the dimer lattice. The phononic cavities are designed with different mirror sections on the left and right sides: one with a large number of phononic crystal periods and the other with a smaller number of periods, forming a strong mirror and a weak mirror respectively. The strong/weak mirror can give rise to small/large cavity-waveguide coupling [65, 81, 80, 82]. Thus, if we always align the strong mirror section with the strong mirror section and use identical waveguide to connect the nanocavities, the hopping strengths are alternating with the strengths and . Note that the trimer lattice can be engineered with the same method.
For a typical nanobeam cavity shown in Refs. [81, 80, 82], it has an intrinsic decay rate on the order of MHz. However, the phonons are virtually excited in the process of spin-spin interactions, where the excited number of the phonons is at a low level. Furthermore, we can use phononic shielding to surround the nanobeam (the whole network), which can provide a phononic bandgap to mitigate the leakage to the bulk [65]. This protection of phonon modes can result in high quality factor exceeding , and even ultra-high of nanocavities in the 1D/2D optomechanical crystal has been demonstrated in recent experiments [83, 77]. Correspondingly, the intrinsic damping can be reduced to below kilohertz ( kHz).
SiV centers are point defects in diamond with a silicon atom occupying two adjacent vacancies, which can be embedded into diamond crystal via ion implantation technology. As depicted in Fig. 1(c), the phononic modes can be directly coupled to the spin in a single SiV through matching the spin’s frequency to the phonon frequency, where an external magnetic field tilted from the symmetry axis of the defect should be applied. The spin-phonon coupling strength can be estimated by [33, 64]
| (43) |
Here, THz/strain is the strain sensitivity, m/s is the group velocity of acoustic waves in diamond, GHz, kg/, is the volume of the optomechanical nanocavity and is the strain distribution at the position of the SiV centers. Thus, for a typical nanocavity, the single spin-phonon coupling strength can reach MHz.
The main limit of the coherence of SiV centers is the dephasing time , which arises from the coupling to the thermal environment and the nuclear spins in diamond. The thermal occupation can be frozen out in the low temperature and the interactions with the nuclear spins can be suppressed using the dynamical decoupling technology [84, 85, 86]. For the dilution refrigeration temperature mk, the spin dephasing Hz has been realized in the experiment [51]. In general, we choose MHz and MHz in the main text, which leads to the spin-spin coupling strength kHz. The dissipations of the spins and the phononic crystal can be neglected, since .
VI conclusion
We have proposed a feasible scheme in the solid-state platform to explore novel interactions between spins and phonons in dimer and trimer lattices, with an array of SiV centers integrating into a 1D optomechanical crystal. We have predicted a series of unconventional phenomena in this spin-phononic hybrid system.
In the dimer lattice, we show the formation of chiral and robust spin-phonon bound states, which can mediate directional and robust spin-spin interactions. We also show topology-dependent phononic collective radiation effects. The coupling between a single spin and the phononic edge modes is discussed as well. While in the trimer lattice, we show that the chiral and robust spin-phonon bound states still exist and the spin relaxation is sublattice-dependent. The bound state-mediated spin-spin interactions exhibit chiral features and are relatively robust. Quantum control over the chiral edge states, which are unique in the inversion-symmetry breaking phase of the trimer lattice, is also demonstrated with the addition of spins.
Finally, we discuss the feasibility of this scheme under realistic parameters. This work takes the advantage of phononic crystals and SiV centers, thus providing a promising platform for manipulating phonons with spins, and is useful for phonon-mediated quantum information applications.
Acknowledgments
References
- Georgescu et al. [2014] I. M. Georgescu, S. Ashhab, and F. Nori, Quantum simulation, Rev. Mod. Phys. 86, 153 (2014).
- John and Wang [1990] S. John and J. Wang, Quantum electrodynamics near a photonic band gap: Photon bound states and dressed atoms, Phys. Rev. Lett. 64, 2418 (1990).
- González-Tudela et al. [2015] A. González-Tudela, C.-L. Hung, D. E. Chang, J. I. Cirac, and H. J. Kimble, Subwavelength vacuum lattices and atom-atom interactions in two-dimensional photonic crystals, Nat. Photonics 9, 320 (2015).
- Douglas et al. [2015] J. S. Douglas, H. Habibian, C.-L. Hung, A. V. Gorshkov, H. J. Kimble, and D. E. Chang, Quantum many-body models with cold atoms coupled to photonic crystals, Nat. Photonics 9, 326 (2015).
- Hood et al. [2016] J. D. Hood, A. Goban, A. Asenjo-Garcia, M. Lu, S.-P. Yu, D. E. Chang, and H. J. Kimble, Atom–atom interactions around the band edge of a photonic crystal waveguide, Proc. Natl. Acad. Sci. U.S.A. 113, 10507 (2016).
- González-Tudela and Cirac [2018] A. González-Tudela and J. I. Cirac, Exotic quantum dynamics and purely long-range coherent interactions in dirac conelike baths, Phys. Rev. A 97, 043831 (2018).
- García-Elcano et al. [2020] I. n. García-Elcano, A. González-Tudela, and J. Bravo-Abad, Tunable and robust long-range coherent interactions between quantum emitters mediated by weyl bound states, Phys. Rev. Lett. 125, 163602 (2020).
- Bello et al. [2019] M. Bello, G. Platero, J. I. Cirac, and A. González-Tudela, Unconventional quantum optics in topological waveguide QED, Sci. Adv. 5, eaaw0297 (2019).
- Kim et al. [2021] E. Kim, X. Zhang, V. S. Ferreira, J. Banker, J. K. Iverson, A. Sipahigil, M. Bello, A. González-Tudela, M. Mirhosseini, and O. Painter, Quantum electrodynamics in a topological waveguide, Phys. Rev. X 11, 011015 (2021).
- González-Tudela and Galve [2019] A. González-Tudela and F. Galve, Anisotropic quantum emitter interactions in two-dimensional photonic-crystal baths, ACS Photonics 6, 221 (2019).
- Wang et al. [2021] X. Wang, T. Liu, A. F. Kockum, H.-R. Li, and F. Nori, Tunable chiral bound states with giant atoms, Phys. Rev. Lett. 126, 043602 (2021).
- García-Elcano et al. [2021] I. n. García-Elcano, J. Bravo-Abad, and A. González-Tudela, Light-matter interactions near photonic weyl points, Phys. Rev. A 103, 033511 (2021).
- Sánchez-Burillo et al. [2020] E. Sánchez-Burillo, C. Wan, D. Zueco, and A. González-Tudela, Chiral quantum optics in photonic sawtooth lattices, Phys. Rev. Research 2, 023003 (2020).
- Leonforte et al. [2021] L. Leonforte, A. Carollo, and F. Ciccarello, Vacancy-like dressed states in topological waveguide qed, Phys. Rev. Lett. 126, 063601 (2021).
- De Bernardis et al. [2021] D. De Bernardis, Z.-P. Cian, I. Carusotto, M. Hafezi, and P. Rabl, Light-matter interactions in synthetic magnetic fields: Landau-photon polaritons, Phys. Rev. Lett. 126, 103603 (2021).
- Dong et al. [2021] X.-L. Dong, P.-B. Li, T. Liu, and F. Nori, Unconventional quantum sound-matter interactions in spin-optomechanical-crystal hybrid systems, Phys. Rev. Lett. 126, 203601 (2021).
- Goban et al. [2015] A. Goban, C.-L. Hung, J. D. Hood, S.-P. Yu, J. A. Muniz, O. Painter, and H. J. Kimble, Superradiance for atoms trapped along a photonic crystal waveguide, Phys. Rev. Lett. 115, 063601 (2015).
- González-Tudela and Cirac [2017a] A. González-Tudela and J. I. Cirac, Quantum emitters in two-dimensional structured reservoirs in the nonperturbative regime, Phys. Rev. Lett. 119, 143602 (2017a).
- González-Tudela and Cirac [2017b] A. González-Tudela and J. I. Cirac, Markovian and non-markovian dynamics of quantum emitters coupled to two-dimensional structured reservoirs, Phys. Rev. A 96, 043811 (2017b).
- Barik et al. [2018] S. Barik, A. Karasahin, C. Flower, T. Cai, H. Miyake, W. DeGottardi, M. Hafezi, and E. Waks, A topological quantum optics interface, Science 359, 666 (2018).
- González-Tudela et al. [2019] A. González-Tudela, C. S. Muñoz, and J. I. Cirac, Engineering and harnessing giant atoms in high-dimensional baths: A proposal for implementation with cold atoms, Phys. Rev. Lett. 122, 203603 (2019).
- Calajó et al. [2019] G. Calajó, M. J. A. Schuetz, H. Pichler, M. D. Lukin, P. Schneeweiss, J. Volz, and P. Rabl, Quantum acousto-optic control of light-matter interactions in nanophotonic networks, Phys. Rev. A 99, 053852 (2019).
- [23] C. Vega, M. Bello, D. Porras, and A. González-Tudela, Qubit-photon bound states in topological waveguides with long-range hoppings, arXiv:2105.12470 .
- Martinez Alvarez and Coutinho-Filho [2019] V. M. Martinez Alvarez and M. D. Coutinho-Filho, Edge states in trimer lattices, Phys. Rev. A 99, 013833 (2019).
- Jin [2017] L. Jin, Topological phases and edge states in a non-hermitian trimerized optical lattice, Phys. Rev. A 96, 032103 (2017).
- Rosa et al. [2019] M. I. N. Rosa, R. K. Pal, J. R. F. Arruda, and M. Ruzzene, Edge states and topological pumping in spatially modulated elastic lattices, Phys. Rev. Lett. 123, 034301 (2019).
- Xia et al. [2021] Y. Xia, E. Riva, M. I. N. Rosa, G. Cazzulani, A. Erturk, F. Braghin, and M. Ruzzene, Experimental observation of temporal pumping in electromechanical waveguides, Phys. Rev. Lett. 126, 095501 (2021).
- Habraken et al. [2012] S. J. M. Habraken, K. Stannigel, M. D. Lukin, P. Zoller, and P. Rabl, Continuous mode cooling and phonon routers for phononic quantum networks, New J. Phys. 14, 115004 (2012).
- Gustafsson et al. [2014] M. V. Gustafsson, T. Aref, A. F. Kockum, M. K. Ekström, G. Johansson, and P. Delsing, Propagating phonons coupled to an artificial atom, Science 346, 207 (2014).
- Schuetz et al. [2015] M. J. A. Schuetz, E. M. Kessler, G. Giedke, L. M. K. Vandersypen, M. D. Lukin, and J. I. Cirac, Universal quantum transducers based on surface acoustic waves, Phys. Rev. X 5, 031031 (2015).
- Li et al. [2016] P.-B. Li, Z.-L. Xiang, P. Rabl, and F. Nori, Hybrid quantum device with nitrogen-vacancy centers in diamond coupled to carbon nanotubes, Phys. Rev. Lett. 117, 015502 (2016).
- Chu et al. [2017] Y. Chu, P. Kharel, W. H. Renninger, L. D. Burkhart, L. Frunzio, P. T. Rakich, and R. J. Schoelkopf, Quantum acoustics with superconducting qubits, Science 358, 199 (2017).
- Lemonde et al. [2018] M.-A. Lemonde, S. Meesala, A. Sipahigil, M. J. A. Schuetz, M. D. Lukin, M. Loncar, and P. Rabl, Phonon networks with silicon-vacancy centers in diamond waveguides, Phys. Rev. Lett. 120, 213603 (2018).
- Satzinger et al. [2018] K. J. Satzinger, Y. P. Zhong, H.-S. Chang, G. A. Peairs, A. Bienfait, M.-H. Chou, A. Y. Cleland, C. R. Conner, É. Dumur, J. Grebel, I. Gutierrez, B. H. November, R. G. Povey, S. J. Whiteley, D. D. Awschalom, D. I. Schuster, and A. N. Cleland, Quantum control of surface acoustic-wave phonons, Nature 563, 661 (2018).
- Bienfait et al. [2019] A. Bienfait, K. J. Satzinger, Y. P. Zhong, H.-S. Chang, M.-H. Chou, C. R. Conner, É. Dumur, J. Grebel, G. A. Peairs, R. G. Povey, and A. N. Cleland, Phonon-mediated quantum state transfer and remote qubit entanglement, Science 364, 368 (2019).
- Bin et al. [2020] Q. Bin, X.-Y. Lü, F. P. Laussy, F. Nori, and Y. Wu, N-phonon bundle emission via the stokes process, Phys. Rev. Lett. 124, 053601 (2020).
- Li et al. [2020a] P.-B. Li, Y. Zhou, W.-B. Gao, and F. Nori, Enhancing spin-phonon and spin-spin interactions using linear resources in a hybrid quantum system, Phys. Rev. Lett. 125, 153602 (2020a).
- Wang and Lekavicius [2020] H. Wang and I. Lekavicius, Coupling spins to nanomechanical resonators: Toward quantum spin-mechanics, Appl. Phys. Lett. 117, 230501 (2020).
- Neuman et al. [2021] T. Neuman, M. Eichenfield, M. E. Trusheim, L. Hackett, P. Narang, and D. Englund, A phononic interface between a superconducting quantum processor and quantum networked spin memories, npj Quantum Inf. 7, 121 (2021).
- Burek et al. [2016] M. J. Burek, J. D. Cohen, S. M. Meenehan, N. El-Sawah, C. Chia, T. Ruelle, S. Meesala, J. Rochman, H. A. Atikian, M. Markham, D. J. Twitchen, M. D. Lukin, O. Painter, and M. Lončar, Diamond optomechanical crystals, Optica 3, 1404 (2016).
- Sipahigil et al. [2016] A. Sipahigil, R. E. Evans, D. D. Sukachev, M. J. Burek, J. Borregaard, M. K. Bhaskar, C. T. Nguyen, J. L. Pacheco, H. A. Atikian, C. Meuwly, R. M. Camacho, F. Jelezko, E. Bielejec, H. Park, M. Lončar, and M. D. Lukin, An integrated diamond nanophotonics platform for quantum-optical networks, Science 354, 847 (2016).
- Evans et al. [2018] R. E. Evans, M. K. Bhaskar, D. D. Sukachev, C. T. Nguyen, A. Sipahigil, M. J. Burek, B. Machielse, G. H. Zhang, A. S. Zibrov, E. Bielejec, H. Park, M. Lončar, and M. D. Lukin, Photon-mediated interactions between quantum emitters in a diamond nanocavity, Science 362, 662 (2018).
- Chia et al. [2021] C. Chia, B. Machielse, B. Pingault, M. Chalupnik, G. Joe, E. Cornell, S. W. Ding, S. Bogdanović, K. Kuruma, A. H. Piracha, S. Maity, T. M. Babinec, S. Meesala, and M. Lončar, Chapter six - diamond quantum nanophotonics and optomechanics, in Diamond for Quantum Applications Part 2, Vol. 104 (Elsevier, 2021) pp. 219–251.
- Balasubramanian et al. [2009] G. Balasubramanian, P. Neumann, D. Twitchen, M. Markham, R. Kolesov, N. Mizuochi, J. Isoya, J. Achard, J. Beck, J. Tissler, V. Jacques, P. R. Hemmer, F. Jelezko, and J. Wrachtrup, Ultralong spin coherence time in isotopically engineered diamond, Nat. Mater. 8, 383 (2009).
- Maurer et al. [2012] P. C. Maurer, G. Kucsko, C. Latta, L. Jiang, N. Y. Yao, S. D. Bennett, F. Pastawski, D. Hunger, N. Chisholm, M. Markham, D. J. Twitchen, J. I. Cirac, and M. D. Lukin, Room-temperature quantum bit memory exceeding one second, Science 336, 1283 (2012).
- Bar-Gill et al. [2013] N. Bar-Gill, L. Pham, A. Jarmola, D. Budker, and R. Walsworth, Solid-state electronic spin coherence time approaching one second, Nat. Commun. 4, 1743 (2013).
- Hepp et al. [2014] C. Hepp, T. Müller, V. Waselowski, J. N. Becker, B. Pingault, H. Sternschulte, D. Steinmüller-Nethl, A. Gali, J. R. Maze, M. Atatüre, and C. Becher, Electronic structure of the silicon vacancy color center in diamond, Phys. Rev. Lett. 112, 036405 (2014).
- Tao et al. [2014] Y. Tao, J. M. Boss, B. A. Moores, and C. L. Degen, Single-crystal diamond nanomechanical resonators with quality factors exceeding one million, Nat. Commun. 5, 3638 (2014).
- Lee et al. [2017] D. Lee, K. W. Lee, J. V. Cady, P. Ovartchaiyapong, and A. C. B. Jayich, Topical review: Spins and mechanics in diamond, J. Opt. 19, 033001 (2017).
- Bhaskar et al. [2017] M. K. Bhaskar, D. D. Sukachev, A. Sipahigil, R. E. Evans, M. J. Burek, C. T. Nguyen, L. J. Rogers, P. Siyushev, M. H. Metsch, H. Park, F. Jelezko, M. Lončar, and M. D. Lukin, Quantum nonlinear optics with a germanium-vacancy color center in a nanoscale diamond waveguide, Phys. Rev. Lett. 118, 223603 (2017).
- Sukachev et al. [2017] D. D. Sukachev, A. Sipahigil, C. T. Nguyen, M. K. Bhaskar, R. E. Evans, F. Jelezko, and M. D. Lukin, Silicon-vacancy spin qubit in diamond: A quantum memory exceeding 10 ms with single-shot state readout, Phys. Rev. Lett. 119, 223602 (2017).
- Bradac et al. [2020] C. Bradac, W. Gao, J. Forneris, M. E. Trusheim, and I. Aharonovich, Quantum nanophotonics with group iv defects in diamond, Nat. Commun. 10, 5625 (2020).
- Kuruma et al. [2021] K. Kuruma, B. Pingault, C. Chia, D. Renaud, P. Hoffmann, S. Iwamoto, C. Ronning, and M. Lončar, Coupling of a single tin-vacancy center to a photonic crystal cavity in diamond, Applied Physics Letters 118, 230601 (2021).
- [54] R. Debroux, C. P. Michaels, C. M. Purser, N. Wan, M. E. Trusheim, J. A. Martínez, R. A. Parker, A. M. Stramma, K. C. Chen, L. de Santis, et al., Quantum control of the tin-vacancy spin qubit in diamond, arXiv:2106.00723 .
- Bennett et al. [2013] S. D. Bennett, N. Y. Yao, J. Otterbach, P. Zoller, P. Rabl, and M. D. Lukin, Phonon-induced spin-spin interactions in diamond nanostructures: Application to spin squeezing, Phys. Rev. Lett. 110, 156402 (2013).
- Kepesidis et al. [2013] K. V. Kepesidis, S. D. Bennett, S. Portolan, M. D. Lukin, and P. Rabl, Phonon cooling and lasing with nitrogen-vacancy centers in diamond, Phys. Rev. B 88, 064105 (2013).
- MacQuarrie et al. [2013] E. R. MacQuarrie, T. A. Gosavi, N. R. Jungwirth, S. A. Bhave, and G. D. Fuchs, Mechanical spin control of nitrogen-vacancy centers in diamond, Phys. Rev. Lett. 111, 227602 (2013).
- Teissier et al. [2014] J. Teissier, A. Barfuss, P. Appel, E. Neu, and P. Maletinsky, Strain coupling of a nitrogen-vacancy center spin to a diamond mechanical oscillator, Phys. Rev. Lett. 113, 020503 (2014).
- Ovartchaiyapong et al. [2014] P. Ovartchaiyapong, K. W. Lee, B. A. Myers, and A. C. B. Jayich, Dynamic strain-mediated coupling of a single diamond spin to a mechanical resonator, Nat. Commun. 5, 4429 (2014).
- Barfuss et al. [2015] A. Barfuss, J. Teissier, E. Neu, A. Nunnenkamp, and P. Maletinsky, Strong mechanical driving of a single electron spin, Nat. Phys. 11, 820 (2015).
- Golter et al. [2016a] D. A. Golter, T. Oo, M. Amezcua, K. A. Stewart, and H. Wang, Optomechanical quantum control of a nitrogen-vacancy center in diamond, Phys. Rev. Lett. 116, 143602 (2016a).
- Golter et al. [2016b] D. A. Golter, T. Oo, M. Amezcua, I. Lekavicius, K. A. Stewart, and H. Wang, Coupling a surface acoustic wave to an electron spin in diamond via a dark state, Phys. Rev. X 6, 041060 (2016b).
- Sohn et al. [2018] Y.-I. Sohn, S. Meesala, B. Pingault, H. A. Atikian, J. Holzgrafe, M. Gündoğan, C. Stavrakas, M. J. Stanley, A. Sipahigil, J. Choi, et al., Controlling the coherence of a diamond spin qubit through its strain environment, Nature communications 9, 1 (2018).
- Meesala et al. [2018] S. Meesala, Y.-I. Sohn, B. Pingault, L. Shao, H. A. Atikian, J. Holzgrafe, M. Gündoğan, C. Stavrakas, A. Sipahigil, C. Chia, R. Evans, M. J. Burek, M. Zhang, L. Wu, J. L. Pacheco, J. Abraham, E. Bielejec, M. D. Lukin, M. Atatüre, and M. Lončar, Strain engineering of the silicon-vacancy center in diamond, Phys. Rev. B 97, 205444 (2018).
- Kuzyk and Wang [2018] M. C. Kuzyk and H. Wang, Scaling phononic quantum networks of solid-state spins with closed mechanical subsystems, Phys. Rev. X 8, 041027 (2018).
- Maity et al. [2020] S. Maity, L. Shao, S. Bogdanović, S. Meesala, Y.-I. Sohn, N. Sinclair, B. Pingault, M. Chalupnik, C. Chia, L. Zheng, et al., Coherent acoustic control of a single silicon vacancy spin in diamond, Nat. Commun. 11, 193 (2020).
- Qiao et al. [2020] Y.-F. Qiao, H.-Z. Li, X.-L. Dong, J.-Q. Chen, Y. Zhou, and P.-B. Li, Phononic-waveguide-assisted steady-state entanglement of silicon-vacancy centers, Phys. Rev. A 101, 042313 (2020).
- Chen et al. [2021] J.-Q. Chen, Y.-F. Qiao, X.-L. Dong, X.-L. Hei, and P.-B. Li, Dissipation-assisted preparation of steady spin-squeezed states of siv centers, Phys. Rev. A 103, 013709 (2021).
- [69] P.-B. Li, X.-X. Li, and F. Nori, Band-gap-engineered spin-phonon, and spin-spin interactions with defect centers in diamond coupled to phononic crystals, arXiv:1901.04650 .
- Li et al. [2020b] X.-X. Li, B. Li, and P.-B. Li, Simulation of topological phases with color center arrays in phononic crystals, Phys. Rev. Research 2, 013121 (2020b).
- Li et al. [2021] X.-X. Li, P.-B. Li, H.-R. Li, H. Gao, and F.-L. Li, Simulation of topological zak phase in spin-phononic crystal networks, Phys. Rev. Research 3, 013025 (2021).
- Peano et al. [2015] V. Peano, C. Brendel, M. Schmidt, and F. Marquardt, Topological phases of sound and light, Phys. Rev. X 5, 031011 (2015).
- Lemonde et al. [2019] M.-A. Lemonde, V. Peano, P. Rabl, and D. G. Angelakis, Quantum state transfer via acoustic edge states in a 2D optomechanical array, New J. Phys. 21, 113030 (2019).
- Sanavio et al. [2020] C. Sanavio, V. Peano, and A. Xuereb, Nonreciprocal topological phononics in optomechanical arrays, Phys. Rev. B 101, 085108 (2020).
- Liu et al. [2020] Y. Liu, X. Chen, and Y. Xu, Topological phononics: From fundamental models to real materials, Advanced Functional Materials 30, 1904784 (2020).
- Meenehan et al. [2015] S. M. Meenehan, J. D. Cohen, G. S. MacCabe, F. Marsili, M. D. Shaw, and O. Painter, Pulsed excitation dynamics of an optomechanical crystal resonator near its quantum ground state of motion, Phys. Rev. X 5, 041002 (2015).
- Ren et al. [2020] H. Ren, M. H. Matheny, G. S. MacCabe, J. Luo, H. Pfeifer, M. Mirhosseini, and O. Painter, Two-dimensional optomechanical crystal cavity with high quantum cooperativity, Nat. Commun. 11, 3373 (2020).
- [78] M. Bello, G. Platero, and A. González-Tudela, Spin many-body phases in standard and topological waveguide qed simulators, arXiv:2106.11637 .
- Asbóth et al. [2016] J. K. Asbóth, L. Oroszlány, and A. Pályi, A short course on topological insulators, Springer (2016).
- Fang et al. [2017] K. Fang, J. Luo, A. Metelmann, M. H. Matheny, F. Marquardt, A. A. Clerk, and O. Painter, Generalized non-reciprocity in an optomechanical circuit via synthetic magnetism and reservoir engineering, Nat. Photonics 13, 465 (2017).
- Fang et al. [2016] K. Fang, M. H. Matheny, X. Luan, and O. Painter, Optical transduction and routing of microwave phonons in cavity-optomechanical circuits, Nat. Photonics 10, 489 (2016).
- Mirhosseini et al. [2020] M. Mirhosseini, A. Sipahigil, M. Kalaee, and O. Painter, Superconducting qubit to optical photon transduction, Nature 588, 599 (2020).
- MacCabe et al. [2020] G. S. MacCabe, H. Ren, J. Luo, J. D. Cohen, H. Zhou, A. Sipahigil, M. Mirhosseini, and O. Painter, Nano-acoustic resonator with ultralong phonon lifetime, Science 370, 840 (2020).
- Hanson et al. [2008] R. Hanson, V. V. Dobrovitski, A. E. Feiguin, O. Gywat, and D. D. Awschalom, Coherent dynamics of a single spin interacting with an adjustable spin bath, Science 320, 352 (2008).
- Du et al. [2009] J. Du, X. Rong, N. Zhao, Y. Wang, J. Yang, and R. B. Liu, Preserving electron spin coherence in solids by optimal dynamical decoupling, Nature 461, 1265 (2009).
- MacQuarrie et al. [2015] E. R. MacQuarrie, T. A. Gosavi, S. A. Bhave, and G. D. Fuchs, Continuous dynamical decoupling of a single diamond nitrogen-vacancy center spin with a mechanical resonator, Phys. Rev. B 92, 224419 (2015).
- Johansson et al. [2012] J. Johansson, P. Nation, and F. Nori, Qutip: An open-source python framework for the dynamics of open quantum systems, Comput. Phys. Commun. 183, 1760 (2012).
- Johansson et al. [2013] J. Johansson, P. Nation, and F. Nori, Qutip 2: A python framework for the dynamics of open quantum systems, Comput. Phys. Commun. 184, 1234 (2013).