Chebyshev admissible meshes and Lebesgue constants
of complex polynomial projections

Starting from the seminal paper by Calvi and Levenberg [9], the notion of polynomial (admissible) mesh has been emerging in the last years as a fundamental theoretical and computational tool in polynomial approximation. In the present paper we focus on the univariate complex case. We recall that an admissible polynomial mesh of a polynomially determining compact set $K\subset\mathbb{C}$ (i.e., a polynomial vanishing on $K$ vanishes everywhere on $\mathbb{C}$), is a sequence of finite norming subsets $Z_{n}\subset K$ such that

where $\|\cdot\|_{Y}$ denotes the sup-norm on a continuous or discrete compact set $Y$, $card(Z_{n})=O(n^{\alpha})$, $\alpha\geq 1$, and $c$ is a constant independent of $n$. The fact that $card(Z_{n})\geq dim(\mathbb{P}_{n}(\mathbb{C}))=n+1$ necessarily holds, since each $Z_{n}$ is $\mathbb{P}_{n}(\mathbb{C})$-determining. Such a mesh is termed optimal when $\alpha=1$.

To give only a flavour of the topic, we recall that polynomial meshes are invariant by affine transformations, are stable under small perturbations, and can be assembled by finite union, finite product and algebraic transformations, starting from known instances. Moreover, admissible meshes can be conveniently used for least-square approximation, and contain extremal sets for interpolation of Fekete and Leja type, that can be computed by greedy algorithms; cf., e.g., [1, 4, 9, 18].

Existence of admissible meshes with $\mathcal{O}(n^{2})$ cardinality has been proved on any connected compact set of $\mathbb{C}$ whose boundary is a $C^{1}$ parametric curve with bounded tangent vectors, while optimal admissible meshes are known in special instances; cf. [1]. The following Proposition and Remark show how to construct optimal admissible meshes of Chebyshev type on a wide class of complex curves and domains. To this purpose, we need a basic Lemma.

We now show how to extend such inequality to algebraic and trigonometric polynomials of a real variable with complex coefficients. Take $t^{\ast}\in[a,b]$ such that $|\phi(t^{\ast})|=\|\phi\|_{[a,b]}$. We can assume that $\phi(t^{\ast})\neq 0$, since (5) trivially holds for $\phi\equiv 0$. Define the complex number $u=\overline{\phi(t^{\ast})}/|\phi(t^{\ast})|$ (which lies on the unit circle), and observe that $u\phi(t^{\ast})=|\phi(t^{\ast})|^{2}/|\phi(t^{\ast})|=|\phi(t^{\ast})|$.

Now, consider $\psi(t)=u\phi(t)$; clearly, $|\psi(t)|=|\phi(t)|$, and $Im(\psi(t^{\ast}))=0$, since $\psi(t^{\ast})=|\phi(t^{\ast})|$ is real. Since $Re(\psi(t))$ is a real algebraic or trigonometric polynomial, we can write the chain of inequalities

The following Proposition shows that suitable admissible meshes of the form (6) can be conveniently used to evaluate Lebesgue constants, with rigorous error bounds. Again, we begin with a basic Lemma. The result is well-known for interpolation operators (cf. e.g. [19]), nevertheless we prefer to prove it here for more general projection operators (which include for example also least-square approximations). Below by $C(K)$ we denote as usual the space of continuous functions on the compact set $K\subset\mathbb{C}$.

In this section we present several numerical tests (implemented in Matlab), concerning the use of complex Chebyshev-like polynomial meshes for interpolation and least-squares approximation, as well as for the evaluation of the corresponding Lebesgue constants. In all these applications we can work on compact sets whose (outer) boundary has the structure described in Remark 1. A preliminary version of the corresponding software along with the demos can be found at [14].

Concerning interpolation, an appealing set is given by the so-called Fekete points, that are points which maximize the modulus of the Vandermonde determinant. As it is well-known, considering their Lebesgue constant it is immediate to get the (over)estimates $\|L_{n}\|\leq n+1$ for the continuum Fekete points (since $\|\ell_{j}\|_{K}\leq 1$ for each $j$), and

when they are obtained by extraction from a Chebyshev-like polynomial mesh $Z_{n}^{m}=\{z_{1},\dots,z_{M}\}\subset\Gamma$. However, the continuum Fekete points are explicitly known only in two special instances, the interval (where they are the Gauss-Lobatto points) and the circle (where they are equally spaced in the arclength), in both cases with $\|L_{n}\|=\mathcal{O}(\log(n))$.

On the other hand, the computation of Fekete points extracted from a polynomial mesh is known to be a NP-hard problem; cf. [10]. Then, we can resort to points that approximately maximize the modulus of the Vandermonde determinant, extracting them from the polynomial mesh by a greedy algorithm. Starting from [7, 18], such approximate Fekete points have been computed by solving the underdetermined system

in a fixed polynomial basis $\{p_{j}\}$, where $\mathbf{b}$ is any nonzero vector, by $QR$ factorization with column pivoting. Indeed, the $n+1$ nonzero components of the solution vector $\mathbf{u}$ select the interpolation nodes $\Xi\subset Z_{n}^{m}$. This procedure corresponds to a greedy determinantal maximization, and the resulting interpolation points asymptotically behave as the continuum Fekete points, in the sense the corresponding uniform discrete probability measure converge weak-$\ast$ to the potential-theoretic equilibrium measure of the compact set; cf. [4, 7] for a full discussion of these aspects, in both the univariate and the multivariate setting.

An interesting alternative is given by Leja points. For a fixed $\xi_{1}\in K$, the points are defined iteratively as $\xi_{j}=argmax_{z\in K}{\prod_{k=1}^{j-1}{|z-\xi_{k}|}}$, $j=2,\dots,n+1$, which means that differently from Fekete points they form a sequence, i.e. the first $\ell+1$ are Leja points for degree $\ell$. A relevant result has been recently proved by Totik [19], who showed that the Lebesgue constant of Leja points has subexponential growth (a fact empirically well-known but missing before a theoretical base). On the other hand, it was previously proved in [2] that Leja points behave asymptotically as Fekete points, in the sense the corresponding uniform discrete probability measure converge weak-$\ast$ to the potential-theoretic equilibrium measure of $K$.

The same asymptotic property is shared by the two families of Leja-like sequences that we consider in this paper, namely discrete Leja points and pseudo-Leja points, both corresponding to a greedy discrete maximization on polynomial meshes. Indeed, discrete Leja points can be computed by $LU$ factorization with row pivoting of the whole matrix $\mathcal{V}_{n}$ in (16), where the pivots select the interpolation points within $Z_{n}^{m}$, a procedure substantially equivalent to compute $\xi_{j}=argmax_{z\in Z_{n}^{m}}{\prod_{k=1}^{j-1}{|z-\xi_{k}|}}$, $j=2,\dots,n+1$; cf. e.g. [5] for an analysis of this method, also in the multivariate setting. On the other hand, in our implementation we considered the pseudo-Leja points corresponding to the iteration $\xi_{j}=argmax_{z\in Z_{j-1}^{m}}{\prod_{k=1}^{j-1}{|z-\xi_{k}|}}$, $j=2,\dots,n+1$, after choosing the first point $\xi_{1}$ arbitrarily, e.g. $\xi_{1}$ is one of the points in $Z_{1}^{m}$ with larger imaginary component; cf. [1] (and [13] for a multivariate extension).

In Figures 2 and 4, we plot the Lebesgue constants of interpolation at approximate Fekete, discrete Leja and pseudo-Leja points, extracted from Chebyshev-like polynomial meshes $Z_{n}^{m}$ with $m=4$ on six different compact sets (see Figures 1 and 3), for degrees $n=1,\dots,50$. We also plot the Lebesgue constant of standard least-squares approximation of degree $n$ on the whole mesh. All these Lebesgue constants have been computed on the extraction meshes, recalling that with $m=4$ we get a relative error of less than $10\%$ and thus we substantially recover their actual size, cf. (13).

We make some observations on the main computational issues. In order to control the conditioning of the Vandermonde-like matrices, that becomes unacceptable already at moderate degrees with the standard monomial basis, we have chosen to work with a discrete orthonormalization of the shifted and scaled basis $q_{j}(z)=((z-z_{b})/\delta)^{j-1}$, $1\leq j\leq n+1$, where $z_{b}=\frac{1}{M}\,\sum_{i=1}^{M}z_{i}$ is the barycenter of the mesh and $\delta=max_{1\leq i\leq M}|z_{b}-z_{i}|$. This approach allows to keep well-conditioning up to moderately high polynomial degrees (cf. e.g. [4]). Notice that, in view of (10) with $w_{j}\equiv 1$, the Lebesgue constant on the mesh can then be simply computed via the relevant matrices as

where $\{\xi_{j}\}$ are either the interpolation or the least-squares sampling points, and $V_{n}(\{\xi_{j}\})=QR$ the factorization of the corresponding Vandermonde-like matrix with $Q$ (rectangular) hermitian and $R$ square upper-triangular, that is $[\pi_{1}(z),\dots,\pi_{n+1}(z)]=[p_{1}(z),\dots,p_{n+1}(z)]R^{-1}$.

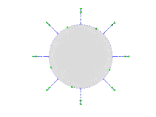
In the numerical experiments we have considered six complex regions whose (outer) boundaries can be tracked parametrically via one or more algebraic or trigonometric polynomials, in particular:

1. 1.

   a M-shaped polygon with $12$ sides;

2. 2.

   a curvilinear polygon, with boundary defined parametrically by linear and cubic splines;

3. 3.

   a sun-shaped domain that consists of a unit disk and 8 rays that are segments of length $0.5$;

4. 4.

   a lune defined as disk difference $B(-1,1.5)\setminus B(1,1.5)$;

5. 5.

   a cardioid, $\partial K$ being the closed curve

   $$z(t)=\cos(t)(1-\cos(t))+i(\sin(t)(1-\cos(t))),{\hskip 5.69046pt}t\in[0,2\pi];$$

6. 6.

   a domain where $\partial K$ is the self-intersecting torpedo curve

   $$z(t)=\cos(t)\cos(2t)\exp(it),{\hskip 5.69046pt}t\in[0,2\pi].$$

First we observe that the interpolation points tend to privilege outward angles/tips/cusps as well as convex portions of the boundary and to avoid inward/concave portions, an electrostatic-like behavior that can be interpreted in connection with their potential theoretic background, cf. [17]. We see that the Lebesgue constants of all discrete extremal sets show a slow increase, but those of Leja-like points have a more erratic behavior with larger oscillations and tendentially higher values with respect to approximate Fekete points (a phenomenon already observed in the real multivariate setting, cf. e.g. [6]). On the other hand, Lebesgue constants of least-squares approximation on the whole polynomial mesh have the lowest values with an essentially logarithmic increase, staying below 5 up to degree 50 in all the six examples.