Charmed weak decays into in the light-front quark model
Abstract
More than ten weak decay modes have been measured with the branching fractions relative to that of . In order to extract the absolute branching fractions, the study of is needed. In this work, we predict with the transition form factors calculated in the light-front quark model. We also predict and . The previous values for have been found to deviate from the most recent observation. Nonetheless, our is able to alleviate the deviation. Moreover, we obtain , which is consistent with the current data.
I Introduction
The lowest-lying singly charmed baryons include the anti-triplet and sextet states and , respectively. The and baryons predominantly decay weakly CroninHennessy:2000bz ; Ammar:2002pf ; Aubert:2007bt ; Yelton:2017uzv ; pdg , whereas the () decays are strong (electromagnetic) processes. There have been more accurate observations for the weak decays in the recent years, which have helped to improve the theoretical understanding of the decay processes Lu:2016ogy ; Geng:2017esc ; Geng:2018plk ; Geng:2018upx ; Hsiao:2019yur ; Zhao:2018mov ; Zou:2019kzq ; Hsiao:2020iwc ; Niu:2020gjw . With the lower production cross section of Yelton:2017uzv , it is an uneasy task to measure decays. Consequently, most of the decays have not been reanalysized since 1990s AvilaAoki:1989yi ; PerezMarcial:1989yh ; Singleton:1990ye ; Hussain:1990ai ; Korner:1992wi ; Xu:1992sw ; Cheng:1993gf ; Cheng:1996cs ; Ivanov:1997ra , except for those in Pervin:2006ie ; Dhir:2015tja ; Zhao:2018zcb ; Gutsche:2018utw ; Hu:2020nkg ; Geng:2017mxn .
One still manages to measure more than ten decays, such as , and , but with the branching fractions relative to pdg . To extract the absolute branching fractions, the study of is crucial. Fortunately, the decay involves a simple topology, which benefits its theoretical exploration. In Fig. 1a, is depicted to proceed through the transition, while is produced from the external -boson emission. Since it is a Cabibbo-allowed process with , a larger branching fraction is promising for measurements. Furthermore, it can be seen that has a similar configuration to those of and , as drawn in Fig. 1, indicating that the three decays are all associated with the transition. While is a decuplet baryon that consists of the totally symmetric identical quarks , behaving as a spin-3/2 particle, the form factors of the transition can be more complicated, which hinders the calculation for the decays. As a result, a careful investigation that relates and has not been given yet, despite the fact that the topology associates them together.
Based on the quark models, it is possible to study the decays into with the transition form factors. However, the validity of theoretical approach needs to be tested, which depends on if the observations, given by
| (1) |
can be interpreted. Since the light-front quark model has been successfully applied to the heavy hadron decays Zhao:2018zcb ; Bakker:2003up ; Ji:2000rd ; Bakker:2002aw ; Choi:2013ira ; Cheng:2003sm ; Schlumpf:1992vq ; Hsiao:2019wyd ; Jaus:1991cy ; Melosh:1974cu ; Dosch:1988hu ; Zhao:2018mrg ; Geng:2013yfa ; Geng:2000if ; Ke:2012wa ; Ke:2017eqo ; Ke:2019smy ; Hu:2020mxk , in this report we will use it to study the transition form factors. Accordingly, we will be enabled to calculate the absolute branching fractions of and , and check if the two ratios in Eq. (I) can be well explained.
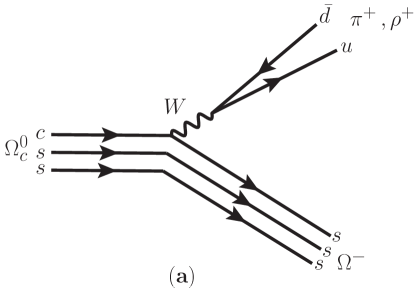
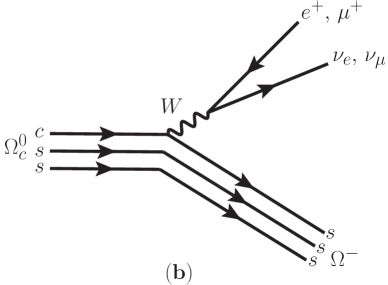
II Theoretical Framework
II.1 General Formalism
To start with, we present the effective weak Hamiltonians for the hadronic and semileptonic charmed baryon decays, respectively Buchalla:1995vs :
| (2) |
where is the Fermi constant, the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements, the effective Wilson coefficients, and . In terms of , we derive the amplitudes of and as Hsiao:2017umx ; Hsiao:2018zqd
| (3) |
where , , and results from the factorization Hsiao:2019ann , with the color number.
With denoting the charmed sextet (decuplet) baryon, the matrix elements of the transition can be parameterized as Zhao:2018mrg ; Gutsche:2018utw
| (4) |
where and represent the masses and spins of , respectively, and () the form factors to be extracted in the light-front quark model. The matrix elements of the meson productions are defined as pdg
| (5) |
where is the decay constant, and is the polarization four-vector with denoting the helicity state.
II.2 The light-front quark model
The baryon bound state contains three quarks , and , with the subscript for . Moreover, and are combined as a diquark state , behaving as a scalar or axial-vector. Subsequently, the baryon bound state in the light-front quark model can be written as Dosch:1988hu
| (6) | |||||
where is the momentum-space wave function, and stand for momentum and helicity of the constituent (di)quark, with for and , respectively. The tilde notations represent that the quantities are in the light-front frame, and one defines and , with and . Besides, are given by
| (7) |
with
| (8) |
where and are the light-front relative momentum variables with from , ensuring that and . According to and in the Melosh transformation Melosh:1974cu , we obtain
| (9) |
Consequently, can be given in the following representation Ke:2012wa ; Ke:2017eqo ; Zhao:2018mrg ; Hu:2020mxk :
| (10) |
with
and
| (11) |
where the vertex function is for the scalar (axial-vector) diquark in , and for the axial-vector diquark in . We have used the variable to describe the internal motions of the constituent quarks in the baryon Jaus:1991cy , which leads to , different from . For the momentum distribution, is presented as the Gaussian-type wave function, given by
| (12) |
where shapes the distribution.
Using and from Eq. (6) and their components in Eqs. (10), (11) and (12), we derive the matrix elements of the transition in Eq. (4) as
| (13) |
with , and . We define and with , where
| (14) |
Then, we multiply () by () as and with and in Eqs. (4) and (13), respectively, resulting in Zhao:2018mrg
| (15) |
In the connection of , we construct four equations. By solving the four equations, the four form factors , , and can be extracted. The form factors can be obtained in the same way.
II.3 Branching fractions in the helicity basis
One can present the amplitude of in the helicity basis of Gutsche:2018utw ; Zhao:2018mrg , where represent the helicity states of the baryon, and those of and . Substituting the matrix elements in Eqs. (II.1) with those in Eqs. (4) and (II.1), the amplitudes in the helicity basis now read and , where with . Explicitly, is written as Gutsche:2018utw
| (16) |
with for . For the semi-leptonic decay, since the system behaves as a scalar or vector, or . The meson only has a zero helicity state, denoted by . On the other hand, the three helicity states of are denoted by . For the lepton pair, we assign or . Subsequently, we expand as
| (17) |
for , where , , and . We also obtain
| (18) |
for , with . Note that the expansions in Eqs. (17) and (II.3) have satisfied for the helicity conservation, with . The branching fractions then read
| (19) |
where
| (20) |
with the lifetime.
III Numerical analysis
In the Wolfenstein parameterization, the CKM matrix elements are adopted as with pdg . We take the lifetime and mass of the baryon and the decay constants MeV from the PDG pdg . With at the scale Buchalla:1995vs , we determine . In the generalized factorization, is taken as an effective color number with Hu:2020nkg ; Gutsche:2018utw ; Hsiao:2019wyd ; Hsiao:2019ann , in order to estimate the non-factorizable effects. For the transition form factors, the theoretical inputs of the quark masses and parameter in Eq. (II.2) are given by Geng:2013yfa ; Geng:2000if
| (21) |
where is to determine for . We hence extract and in Table 1. For the momentum dependence, we have used the double-pole parameterization:
| (22) |
with GeV.
Using the theoretical inputs, we calculate the branching fractions, whose results are given in Table 2.
IV Discussions and Conclusions
| our work | Ref. Xu:1992sw | Ref. Cheng:1996cs | Ref. Gutsche:2018utw | Ref. Pervin:2006ie | data pdg ; Yelton:2017uzv | |
|---|---|---|---|---|---|---|
| 127 | ||||||
| 5.4 | 3.5 | 9.5 | () | |||
In Table 2, we present and with . The errors come from the form factors in Table 1, of which the uncertainties are correlated with the charm quark mass. By comparison, and are compatible with the values in Ref. Gutsche:2018utw ; however, an order of magnitude smaller than those in Refs. Xu:1992sw ; Cheng:1996cs , whose values are obtained with the total decay widths s-1 and s-1, respectively. We also predict as well as , which is much smaller than the value of in Pervin:2006ie . Only the ratios and have been actually observed so far. In our work, is able to alleviate the inconsistency between the previous value and the most recent observation. We obtain with to be consistent with the data, which indicates that with are more favorable.
The helicity amplitudes can be used to better understand how the form factors contribute to the branching fractions. With the identity for the to transition Gutsche:2018utw , in Eq. (II.3) can be rewritten as . From the pre-factors in Eq. (17), we estimate the ratio of , which shows that dominates , instead of . More specifically, it is the term in that gives the main contribution to the branching fraction. By contrast, the terms in largely cancel each other, which is caused by and a minus sign between and (see Table 1); besides, the term with a small is ignorable.
Likewise, we obtain for , where . We find that is ten times larger than . Moreover, is similar to , where the terms largely cancel each other, is ignorable, and gives the main contribution. While and in have a positive interference, giving 20% of , in singly contributes 35%. In Eq. (II.3), the factor of with should be much suppressed, such that . Therefore, receives the main contributions from the terms in , and , which is similar to the analysis for .
In summary, we have studied the and decays, which proceed through the transition and the formation of the meson or lepton pair from the external -boson emission. With the form factors of the transition, calculated in the light-front quark model, we have predicted and . While the previous studies have given the values deviating from the most recent observation, we have presented to alleviate the deviation. Moreover, we have obtained , consistent with the current data.
ACKNOWLEDGMENTS
YKH was supported in part by National Science Foundation of China (No. 11675030). CCL was supported in part by CTUST (No. CTU109-P-108).
References
- (1) D. Cronin-Hennessy et al. (CLEO Collaboration), Phys. Rev. Lett. 86, 3730 (2001).
- (2) R. Ammar et al. (CLEO Collaboration), Phys. Rev. Lett. 89, 171803 (2002).
- (3) B. Aubert et al. (BaBar Collaboration), Phys. Rev. Lett. 99, 062001 (2007).
- (4) J. Yelton et al. (Belle Collaboration), Phys. Rev. D 97, 032001 (2018).
- (5) M. Tanabashi et al. [Particle Data Group], Phys. Rev. D 98, 030001 (2018).
- (6) C.D. Lu, W. Wang and F.S. Yu, Phys. Rev. D 93, 056008 (2016).
- (7) C.Q. Geng, Y.K. Hsiao, Y.H. Lin and L.L. Liu, Phys. Lett. B 776, 265 (2017).
- (8) C.Q. Geng, Y.K. Hsiao, C.W. Liu and T.H. Tsai, Phys. Rev. D 97, 073006 (2018).
- (9) C.Q. Geng, Y.K. Hsiao, C.W. Liu and T.H. Tsai, Phys. Rev. D 99, 073003 (2019).
- (10) Y.K. Hsiao, Y. Yu and H.J. Zhao, Phys. Lett. B 792, 35 (2019).
- (11) H.J. Zhao, Y.L. Wang, Y.K. Hsiao and Y. Yu, JHEP 2002, 165 (2020).
- (12) J. Zou, F. Xu, G. Meng and H.Y. Cheng, Phys. Rev. D 101, 014011 (2020).
- (13) Y.K. Hsiao, Q. Yi, S.T. Cai and H.J. Zhao, arXiv:2006.15291 [hep-ph].
- (14) P.Y. Niu, J.M. Richard, Q. Wang and Q. Zhao, arXiv:2003.09323 [hep-ph].
- (15) M. Avila-Aoki, A. Garcia, R. Huerta and R. Perez-Marcial, Phys. Rev. D 40, 2944 (1989).
- (16) R. Perez-Marcial, R. Huerta, A. Garcia and M. Avila-Aoki, Phys. Rev. D 40, 2955 (1989).
- (17) R.L. Singleton, Phys. Rev. D 43, 2939 (1991).
- (18) F. Hussain and J. Korner, Z. Phys. C 51, 607 (1991).
- (19) J. Korner and M. Kramer, Z. Phys. C 55, 659 (1992).
- (20) Q. Xu and A. Kamal, Phys. Rev. D 46, 3836 (1992).
- (21) H.Y. Cheng and B. Tseng, Phys. Rev. D 48, 4188 (1993).
- (22) H.Y. Cheng, Phys. Rev. D 56, 2799 (1997).
- (23) M.A. Ivanov, J. Korner, V.E. Lyubovitskij and A. Rusetsky, Phys. Rev. D 57, 5632 (1998).
- (24) M. Pervin, W. Roberts and S. Capstick, Phys. Rev. C 74, 025205 (2006).
- (25) R. Dhir and C. Kim, Phys. Rev. D 91, 114008 (2015).
- (26) C.Q. Geng, Y.K. Hsiao, C.W. Liu and T.H. Tsai, JHEP 1711, 147 (2017).
- (27) Z.X. Zhao, Chin. Phys. C 42, 093101 (2018).
- (28) T. Gutsche, M.A. Ivanov, J.G. Korner and V.E. Lyubovitskij, Phys. Rev. D 98, 074011 (2018).
- (29) S. Hu, G. Meng and F. Xu, Phys. Rev. D 101, 094033 (2020).
- (30) H.J. Melosh, Phys. Rev. D 9, 1095 (1974).
- (31) H.G. Dosch, M. Jamin and B. Stech, Z. Phys. C 42, 167 (1989).
- (32) W. Jaus, Phys. Rev. D 44, 2851 (1991).
- (33) F. Schlumpf, Phys. Rev. D 47, 4114 (1993); Erratum: [Phys. Rev. D 49, 6246 (1994)].
- (34) C.Q. Geng, C.C. Lih and W.M. Zhang, Mod. Phys. Lett. A 15, 2087 (2000).
- (35) C.R. Ji and C. Mitchell, Phys. Rev. D 62, 085020 (2000).
- (36) B.L.G. Bakker and C.R. Ji, Phys. Rev. D 65, 073002 (2002).
- (37) B.L.G. Bakker, H.M. Choi and C.R. Ji, Phys. Rev. D 67, 113007 (2003).
- (38) H.Y. Cheng, C.K. Chua and C.W. Hwang, Phys. Rev. D 69, 074025 (2004).
- (39) H.M. Choi and C.R. Ji, Few Body Syst. 55, 435 (2014).
- (40) C.Q. Geng and C.C. Lih, Eur. Phys. J. C 73, 2505 (2013).
- (41) H.W. Ke, X.H. Yuan, X.Q. Li, Z.T. Wei and Y.X. Zhang, Phys. Rev. D 86, 114005 (2012).
- (42) H.W. Ke, N. Hao and X.Q. Li, J. Phys. G 46, 115003 (2019).
- (43) Z.X. Zhao, Eur. Phys. J. C 78, 756 (2018).
- (44) X.H. Hu, R.H. Li and Z.P. Xing, Eur. Phys. J. C 80, 320 (2020).
- (45) H.W. Ke, N. Hao and X.Q. Li, Eur. Phys. J. C 79, 540 (2019).
- (46) Y.K. Hsiao, S.Y. Tsai, C.C. Lih and E. Rodrigues, JHEP 2004, 035 (2020).
- (47) G. Buchalla, A. J. Buras and M. E. Lautenbacher, Rev. Mod. Phys. 68, 1125 (1996).
- (48) Y.K. Hsiao and C.Q. Geng, Eur. Phys. J. C 77, 714 (2017).
- (49) Y.K. Hsiao and C.Q. Geng, Phys. Lett. B 782, 728 (2018).
- (50) Y.K. Hsiao, S.Y. Tsai and E. Rodrigues, Eur. Phys. J. C 80, 565 (2020).