Charging Dynamics of Electrical Double Layers Inside a Cylindrical Pore: Predicting the Effects of Arbitrary Pore Size

The SDL is characterized by electroneutrality, i.e., $\rho=0$. Furthermore, for $|\Psi_{D}|\ll 1$, $s=2$ [2, 36]. Therefore, as per Eq. (2c) and the boundary conditions in Eqs. (4c), (6), and (8), it is straightforward to show that $\Psi$ is linear in $Z$ and is independent of $R$. Mathematically, we write

where $\Psi_{\mathrm{left}}=\Psi(R,0^{-},\tau)$, i.e., the centerline potential to the left of the SDL-pore interface, and is to be determined.

The leading-order terms, i.e., $\rho_{0}$, $s_{0}$ and $\Psi_{0}$ are obtained from the response in the absence of an applied potential, i.e., $\Psi_{D}=0$. Thus, it can be seen that the leading-order coefficients $\rho_{0}=0$, $s_{0}=2$ and $\Psi_{0}=0$ satisfy the set of Eqs. (2) with the initial conditions (3) and boundary conditions (5)–(7).

Inserting the expansions provided in Eq. (10) (with $\rho_{0}=0$, $s=2$ and $\Psi_{0}=0$) in Eq. (2a) and (2d) and collecting the first-order terms in $\Psi_{D}$ yields

Similarly, Poisson’s equation – Eq. (1b) – after substitution of the perturbation expansions takes the form

Only the known leading-order term in the salt concentration enters Eq. (11), such that Eqs. (11) and (12) suffice to determine first-order corrections to charge density and potential in the low potential regime. Therefore, we do not need to further solve Eq. (2b).

We now focus on the transition region between the SDL and the mouth of the pore. First, we emphasize that the transition region is only relevant for overlapping double layer limits. In the thin double layer limit, $\rho=0$ inside the majority of the pore as well as the SDL region, and thus the transition region becomes irrelevant. This is consistent with the derivations in Biesheuvel et al. [2, 30], who assume a continuous variation in $\Psi$ across the SDL-pore interface in the thin double layer limit, thereby implicitly neglecting the transition region.

In contrast, in the overlapping double layer limit, $\rho$ inside the pore is non-zero whereas $\rho$ in the SDL region is zero, and a transition region is required to connect the two regions. Accordingly, inside the transition region, $\rho$ varies from zero to the value inside the pore. To estimate the thickness of the transition region $\delta$ (scaled by $\ell_{p}$), we emphasize that charge density is related to the length scale of the charge gradients by the Poisson equation; see Eq. (2c). Because the radial variation inside the SDL can be ignored, the dimensionless length scale over which charge gradients could be present inside the SDL is $\frac{\ell_{s}}{\ell_{p}}=O(1)$. Therefore, using Eq. (2c) and assuming $\frac{\lambda}{a_{p}}=O(1)$, it is straightforward to show that $\frac{\rho}{\Psi_{D}}=O(\frac{a_{p}}{\ell_{p}})^{2}\ll 1$, enabling us to assume electroneutrality inside the SDL. In contrast, the smallest length scale over which the charge gradients are present inside the pore is $\frac{a_{p}}{\ell_{p}}$, which implies $\frac{\rho}{\Psi_{D}}=O(1)$ [36, 49, 44, 50, 51]; see also Eq. (29). Next, in the transition region, $\rho$ varies from zero to the value inside the pore. Therefore, $\rho$ inside the transition region is on the same order of magnitude as that inside the pore. Accordingly, the relevant length scale is the same as that of the pore, or $\delta=O\left(\frac{a_{p}}{\ell_{p}}\right)\ll 1$. In summary, the transition region is thin due to geometrical features of the pore.

In the limit of $\frac{a_{p}}{\lambda}=O(1)$, the transition region may present finite electric potential and charge density changes [36]. Therefore, in our perturbation expansion model, we approximate this region as a jump discontinuity. Defining $J_{\mathrm{left}}=\left.J_{Z}\right|_{Z=0^{-}}$ and $J_{\mathrm{right}}=\left.J_{Z}\right|_{Z=0^{+}}$, the charge flux in the SDL is given by $J_{\mathrm{left}}=-2\frac{D_{s}}{D_{p}}\frac{\Psi_{\mathrm{left}}\ell_{p}}{\ell_{s}}$ where $\Psi_{\mathrm{left}}=\Psi_{m}(0^{-},\tau)$; see Eqs. (2e) and (9). In contrast, the charge flux inside the pore is given by $J_{\mathrm{right}}=-\left.\frac{2I_{0}\left(\frac{a_{p}}{\lambda}\right)}{I_{0}\left(\frac{a_{p}}{\lambda}\right)-1}\frac{\partial\Psi_{m}}{\partial Z}\right|_{Z=0^{+}}$; see Eqs. (2d), (18) and (19). Therefore, since the transition region is thin and thus has negligible charge storage, we ensure current conservation across it by requiring $J_{\mathrm{left}}A_{s}=J_{\mathrm{right}}A_{p}$, i.e.,

Eq. (23) consists of two variables, i.e., $\Psi_{\mathrm{left}}$ and $\Psi_{\mathrm{right}}$, and we need an additional equation to solve $\Psi_{m}$.

To relate $\Psi_{\mathrm{left}}$ and $\Psi_{\mathrm{right}}$, we require current conservation also on the left surface of the transition region (see Fig. 1b), relating its charge flux to that of the SDL. To do so, we define $\rho_{\mathrm{left}}=\rho_{m}(0^{-},\tau)=0$ and $\rho_{\mathrm{right}}=\rho_{m}(0^{+},\tau)$. The charge flux inside the transition region can be approximated by $J_{Z,\textrm{int}}=-(\frac{\rho_{\mathrm{right}}}{\delta}+2\frac{\Psi_{\mathrm{right}}-\Psi_{\mathrm{left}}}{\delta})$ with a $O(\delta)$ error, where $\delta$ is the dimensionless thickness of the region, scaled by $\ell_{p}$. The current conservation relation, $J_{Z,\mathrm{int}}=J_{\mathrm{left}}$, reads

For $\delta\ll 1$, the right-hand side can be neglected, so $\rho_{\mathrm{right}}+2\Psi_{\mathrm{right}}=2\Psi_{\mathrm{left}}$. Eq. (17) can then be used to derive

Eq. (25) shows that when $\frac{a_{p}}{\lambda}\gg 1$, $\Psi_{\mathrm{left}}=\Psi_{\mathrm{right}}$, which is expected for thin double layers. In contrast, when $\frac{a_{p}}{\lambda}\ll 1$, $\Psi_{\mathrm{right}}=\Psi_{D}$, which is also expected, since the potential will be close to the surface potential everywhere inside the pore. Substituting Eq. (25) in Eq. (23) yields

where $\mathrm{Bi}=\frac{D_{s}}{D_{p}}\frac{\ell_{p}}{\ell_{s}}\frac{a_{s}^{2}}{a_{p}^{2}}$ is the Biot number.

We can now combine Eqs. (22) and (26) to rewrite the governing equation for centerline potential as

We emphasize that Eqs. (18), (19) and (27c) are the key result of this paper. To the best of our knowledge, this is the first solution of the charge density and potential profiles within a cylindrical pore for arbitrary pore size in the limit of low potentials, formally justified by a regular perturbation expansion. This paper highlights that the mathematical structure of $\Psi$ remains identical irrespective of $\frac{a_{p}}{\lambda}$. However, the effect of $\frac{a_{p}}{\lambda}$ modifies the charging timescale

In the thin-double-layer limit, i.e., $\frac{\lambda}{a_{p}}\ll 1$, $t_{c}\approx\frac{2\lambda}{a_{p}}\frac{\ell_{p}^{2}}{D_{p}}$, consistent with the results reported previously [2]. In the overlapping-double-layer limit, i.e., $\frac{\lambda}{a_{p}}\gg 1$, $t_{c}\approx\frac{\ell_{p}^{2}}{D_{p}}$, consistent with the results reported in Gupta et. al. [36]. We illustrate this timescale dependence on pore size with contour plots of the time evolution of the electric potential in Fig. 2, and rationalize its mechanism in the following discussion.

In the thin-double-layer limit, the pore remains uncharged except in the vicinity of its surface. As shown in Fig. 2 and the Supplementary Video, for $a_{p}/\lambda=10$, $\tau=0.2$ displays a charge density profile very close to that of $\tau=1$, indicating an earlier saturation of the profile and therefore a lower timescale. This is also backed up by the calculations, which predict $\tau_{c}\approx 0.19$ for $\frac{a_{p}}{\lambda}=10$; see Eq. (27c). In contrast, when double layers are not thin, i.e., $\frac{a_{p}}{\lambda}=2$, a radial distribution charge forms throughout the pore, producing a transient axial gradient of charge. The charge profiles continue to develop in both radial and axial directions and appear to saturate around $\tau=1$. This is also consistent with our prediction since $\tau_{c}\approx 0.7$; see Eq. (27c). The charging of $\frac{a_{p}}{\lambda}=5$ lies between the two other scenarios described. Finally, we also note that while the overlapping double layers take longer to charge, they also store more charge throughout the pore, resulting in a trade-off of charge density and charging timescale.

The characteristic feature that sets the charging timescale of arbitrary pore sizes is the interplay of electromigrative and diffusive fluxes. Therefore, we construct a vector plot of diffusive and electromigrative fluxes by employing our analytical derivation; see Fig. 3. First, we note that for both $\frac{a_{p}}{\lambda}=2$ and $\frac{a_{p}}{\lambda}=10$, the radial diffusive flux is always balanced by the radial electromigrative flux, even though the radial diffusive and electromigrative fluxes increase with time; see Fig. 3. This is a classical feature of double-layer charging; see Ref. [11] for more details. Overall, the balance in the radial direction implies that the timescale of pore charging is controlled by the fluxes in the axial direction. For $\frac{a_{p}}{\lambda}=10$, the axial gradient of charge vanishes and electromigration is the only mechanism promoting axial transport of charge, in consonance with the literature [27, 28, 2, 30]. In contrast, for $\frac{a_{p}}{\lambda}=2$, both electromigration and diffusion cooperate in driving charge transport; see Fig. 3. However, this increase in charge flux of in the overlapping double layer limit is smaller than the boost in charge density, leading to a longer charging timescale.

The centerline potential, given by Eq. (27b) with $\Psi_{m}=\phi+\frac{\Psi_{D}}{I_{0}(\frac{a_{p}}{\lambda})}$, and the charge density distribution, given by Eq. (17), are shown in Fig. 4. We note that we obtain excellent agreement between the analytical results and DNS for both $\Psi_{m}$ and $\rho_{m}$.

Figs. 4b and 4d show that the centerline charge density increases monotonically as $\frac{a_{p}}{\lambda}$ is reduced, vanishing in the thin-double-layer regime, and approaching twice the applied potential for overlapping double layers. At steady state, $\phi\to 0$, $\Psi_{m}\to\frac{\Psi_{D}}{I_{0}(\frac{a_{p}}{\lambda})}$, and $\rho_{m}\to-\frac{2\Psi_{D}}{I_{0}(\frac{a_{p}}{\lambda})}$; see Eq. (17). The increase in centerline charge induces a larger potential change at the SDL-pore transition in order to balance diffusion and electromigration in this region.

The radial dependence of the pore potential and charge distribution, given by Eqs. (18) and (19), are shown in Fig. 5 for $\frac{a_{p}}{\lambda}=2$. The charge distribution propagates gradually along the $Z$-direction, being larger near the mouth of the pore. The potential and charge distributions are related in the radial direction in such a way that the net radial flux vanishes for all times. Figs. 5a and 5b show opposite dependences of charge density and electric potential on the axial coordinate – $\rho$ decreases and $\Psi$ increases with $Z$. Essentially, the effect of the charge flux in the SDL is to transport charge into the pore, which subsequently diffuses from the mouth to the end of pore. On the other hand, potential is screened, i.e., reduced, by the charge transported from the SDL. Thus, it is lower closer to the mouth of the pore and increases with $Z$. At steady state, the charge and potential distributions become independent of $Z$. Using Eqs. (18) and (19), the distributions for potential and charge throughout the pore at steady state are found to be

and

We note that smaller $\frac{a_{p}}{\lambda}$ implies higher charge density throughout the pore. However, we reiterate that this comes at the cost of a higher charging timescale, since $t_{c}=\frac{2\frac{\lambda}{a_{p}}I_{1}(\frac{a_{p}}{\lambda})\ell_{p}^{2}}{I_{0}(\frac{a_{p}}{\lambda})D_{p}}$.

The centerline potential gives an important physical descriptor of the charging process in the dimensionless charge flux.

Eqs. (2e), (25), and (27b) can be utilized to show that

The charge flux comes out to be initially independent of the relative pore size since double layers have not yet formed in the initial state, and the SDL is subjected to the potential gradient imposed by the applied potential; see Eq. (3). The effect of $\frac{a_{p}}{\lambda}$ is thus to control the charging timescale. In fact, recall that $T=\frac{I_{0}\left(\frac{a_{p}}{\lambda}\right)}{\frac{2\lambda}{a_{p}}I_{1}\left(\frac{a_{p}}{\lambda}\right)}\tau$ and note that $J_{\mathrm{right}}=J_{\mathrm{right}}(T)$, alternatively demonstrating that narrower pores take longer to charge. This is illustrated in Fig. 6, which shows exponential-like behavior at large times, with steeper descents for larger $\frac{a_{p}}{\lambda}$.

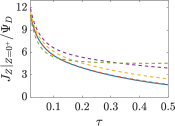
The ratio of diffusion coefficients in the static diffusion layer and in the pore, $\frac{D_{s}}{D_{p}}$, may not be unity. This might be due to different diffusion mechanisms in the SDL and the pore, i.e., bulk diffusion in the former vs. Knudsen diffusion in the latter due to its narrow size [52]. The influence of this ratio is encompassed in the Biot number, $\mathrm{Bi}=\frac{A_{s}D_{s}\ell_{p}}{A_{p}D_{p}\ell_{s}}$, which in this case is a ratio of charge transport resistance in the pore vs. in the SDL. Fig. 7 illustrates the dependence of pore charging on the Biot number. It shows that the higher the Biot number, the lower the resistance to charge transfer in the SDL, producing an intuitive effect: enhancement of charge flux for short-times (e.g., owing to higher SDL diffusivity), but also quicker saturation of the pore charge storage. Thus, the order of the curves for different Biot numbers swap over time. We also find that the long-time charging is given by the dominant timescale $\tau_{c}/\kappa_{1}^{2}$, where $\kappa_{1}$ is the first eigenvalue satisfying the characteristic equation $\kappa_{n}\tan\kappa_{n}=\mathrm{Bi}$. This is illustrated by the good agreement between the charge fluxes and their approximation by the first mode in the Fourier series of Eq. (30), represented by dash-dotted lines. It should be noted that net charge storage is not influenced by $\mathrm{Bi}$, as will be shown in Sec. 5.2.

For higher applied potentials, the full PNP equations assuming radial equilibrium and relaxing the constraint of constant salt follow from Eqs. (2) as

The main simplification that comes from the linear regime $\Psi_{D}\ll 1$ is the neglect of the term $\rho\frac{\partial\Psi}{\partial Z}$, whence the salt transport equation resumes to a transient diffusion equation. Given the initial and boundary conditions for salt, the trivial solution $s(R,Z,\tau)=2$ holds, i.e., we can assume salt to be constant. For higher potentials, though, that approximation ceases to be valid and the variation of salt density in the domain influences the strength of electromigration of charge.

In order to assess the validity of our analysis, beyond which the neglect of higher-order corrections in $\Psi_{D}$ becomes unwarranted, we compare our results to the DNS for different applied potentials in Fig. 8. We obtain good agreement between potentials and charge profiles until the applied potential reaches approximately twice the thermal potential, or approximately 50 mV at room temperature. Above that threshold, a non-linear potential response in the SDL is observed in the DNS, and thus the first-order corrections underpredict the potential in the pore and overpredict the charge stored. Indeed, Fig. 8e shows that the charge flux predictions agree with DNS results for early times ($\tau<0.1$), even for moderately high applied voltages, with an error of 8% for 200 mV (but of 15% for 100 mV). However, for late times, non-linear terms become important, introducing electromigration of salt which can affect the transport of charge.

First, we derive the value of conductivity for arbitrary $\frac{a_{p}}{\lambda}$. Briefly restoring dimensions and utilizing Eqs. (2e), (18) and (19), we find that axial charge flux $J_{z}$ inside the pore is given as

such that dimensional pore conductivity is given by ${\tilde{\sigma}_{p}=\frac{2D_{p}e^{2}c_{0}}{k_{B}T}\frac{I_{0}\left(\frac{a_{p}}{\lambda}\right)}{I_{0}\left(\frac{a_{p}}{\lambda}\right)-1}}$. Note that the conductivity for $\frac{a_{p}}{\lambda}\gg 1$ is only based on electromigrative charge flux. In contrast, the conductivity for $\frac{a_{p}}{\lambda}\ll 1$ is enhanced because both diffusive and electromigrative fluxes contribute to current; see Fig. (3).

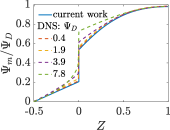
Next, we derive the dimensional capacitance per unit surface area, $\tilde{C}_{p}$. We note that $2\pi a_{p}\tilde{C}_{p}(\psi_{m}-\psi_{D})$ should yield the total charge stored per unit axial length. By utilizing Eq. (19) and integrating along the radial direction, it is straightforward to show that $\tilde{C}_{p}=\frac{\varepsilon}{\lambda}\frac{I_{1}\left(\frac{a_{p}}{\lambda}\right)}{I_{0}\left(\frac{a_{p}}{\lambda}\right)-1}$. In the thin-double-layer limit $\frac{a_{p}}{\lambda}\gg 1$, we recover the usual expression that $\tilde{C}_{p}\rightarrow\frac{\varepsilon}{\lambda}$. In contrast, in the thick-double-layer limit $\frac{a_{p}}{\lambda}\gg 1$, we obtain $\tilde{C}_{p}\rightarrow\frac{2\varepsilon}{a_{p}}$. This result is intuitive since it demonstrates that the length scale of capacitance in the overlapping-double-layer limit is controlled by the pore size. Based on these expressions, we can also recover $t_{c}=\frac{2\pi a_{p}\tilde{C}_{p}}{\pi a_{p}^{2}\tilde{\sigma}_{p}}\ell_{p}^{2}=\frac{\frac{2\lambda}{a_{p}}I_{1}\left(\frac{a_{p}}{\lambda}\right)}{I_{0}\left(\frac{a_{p}}{\lambda}\right)}\frac{\ell_{p}^{2}}{D_{p}}$, consistent with Eq. (27c).

The linear relation between average diffusive and electromigrative axial fluxes allowed us to determine expressions for pore capacitance and resistance that satisfy Ohm’s law and the definition of a capacitive element. However, the key distinguishing feature from the classical thin double layer analysis [27, 28] is the inclusion of potential change across the transition region as derived in Eq. (25), which comes from the charge flux matching. In order to account for this change in potential, we add a resistor representing the interface, as shown in Fig. V.1a. Its dimensional resistance is determined from Ohm’s law,

We derive an expression for dimensionless transition-region resistance $R_{\mathrm{t}}(\tau)$ in Appendix A along with the traditional expression for SDL resistance, since their final expressions are not utilized for further analysis.

Figs. V.1b and V.1c show the pore capacitance and charging time as per the transmission line model. The sharp increase in pore capacitance per unit surface area for smaller $\frac{a_{p}}{\lambda}$ may suggest a blowup of charge flux for overlapping double layers, which is not observed in Fig. 6. In fact, though pore capacitance increases, pore resistance decreases commensurately, in a way that yields $\tau_{c}\sim 1$ for overlapping double layers. Even more importantly, pore capacitance of arbitrary $\frac{a_{p}}{\lambda}$ reported in our manuscript is useful for the transmission circuit analysis that predicts centerline potential, but since it’s based on the potential difference $\Psi_{m}-\Psi_{D}$, it is not representative of experimental measures of capacitance, which are based on $\Psi_{D}$ [3, 43]. This is the motivation for the definition of an effective capacitance that we develop in the next section.