Charged spherically symmetric black holes in scalar-tensor Gauss-Bonnet gravity

Salvatore Capozziello [email protected], corresponding author. Dipartimento di Fisica “E. Pancini“, Università di Napoli “Federico II”, Complesso Universitario di Monte Sant’ Angelo, Edificio G, Via Cinthia, I-80126, Napoli, Italy, Istituto Nazionale di Fisica Nucleare (INFN), Sezione di Napoli, Complesso Universitario di Monte Sant’Angelo, Edificio G, Via Cinthia, I-80126, Napoli, Italy, Scuola Superiore Meridionale, Largo S. Marcellino 10, I-80138, Napoli, Italy. Gamal G. L. Nashed [email protected] Centre for Theoretical Physics, The British University in Egypt, P.O. Box 43, El Sherouk City, Cairo 11837, Egypt,

(December 31, 2024)

Abstract

We derive a novel class of four-dimensional black hole solutions in Gauss-Bonnet gravity coupled with a scalar field in presence of Maxwell electrodynamics. In order to derive such solutions, we assume the ansatz $g_{tt}\neq g_{rr}{}^{-1}$ for metric potentials. Due to the ansatz for the metric, the Reissner Nordström gauge potential cannot be recovered because of the presence of higher-order terms Â ${\mathcal{O}}\left(\frac{1}{r}\right)$ Â which are not allowed to be vanishing. Â Moreover, the scalar field is not allowed to vanish. If it vanishes, a function of the solution results undefined. Â Furthermore, it is possible to show that the electric field is of higher-order in the monopole expansion: this fact explicitly comes from the contribution of the scalar field. Therefore, we can conclude that the Gauss-Bonnet scalar field acts as non-linear electrodynamics creating monopoles, quadrupoles, etc. in the metric potentials. We compute the invariants associated with the black holes and show that, when compared to Schwarzschild or Reissner-Nordström space-times, they have a soft singularity. Also, it is possible to demonstrate that these black holes give rise to three horizons in AdS space-time and two horizons in dS space-time. Finally, thermodynamic quantities can be derived and we show that the solution can be stable or unstable depending on a critical value of the temperature.

Gauss-Bonnet gravity; scalar field; Maxwell field; exact solution; thermodynamics.

pacs:

04.50.Kd, 04.25.Nx, 04.40.Nr

I Introduction

A large amount of observational data indicates that our universe is experiencing an accelerated expansion. There are two basic approaches to explain this cosmic acceleration: Â The first considers the issue of acceleration in the framework of Einstein’s general relativity (GR) and then needs the existence of an odd type of energy called ”dark energy,” which has a repulsive gravity and constitutes an unclustered ingredient of universe components. The second approach proposes extensions of GR by including functions of the curvature invariants like the Ricci scalar $R$ , the Riemann and Ricci tensors or their derivatives in the Lagrangian formulation or modifications of the Einstein paradigm involving torsion tensor or non-metricity. Among these proposals to modify Einstein’s theory there are $f(R)$ gravity, Â braneworld cosmology, Lovelock gravity, Brans-Dicke-like scalar-tensor theories, etc. Brans:1961sx ; Wagoner:1970vr ; Barrabes:1997kk ; Cai:1996pj ; Capozziello:2005bu ; Moffat:2005si ; Dehghani:2006xt ; Faraoni:2007yn ; Maeda:2009js ; Hendi:2012as ; Sharif:2013lea ; Eiroa:2014mca ; Karami:2014tsa ; Darabi:2013caa ; Akbar:2006mq ; deSouza:2007zpn ; Corda:2009bv ; Cognola:2007zu ; Nojiri:2010wj ; Said:2011dg ; Myung:2011ih ; Hwang:2011kg ; Hendi:2011eg ; Mazharimousavi:2011bf ; Man:2013sf ; Miao:2014wpa ; Hendi:2012zg ; Hendi:2014wsa ; Hendi:2013zba ; Ida:1999ui ; Cline:2000xn ; Brax:2003fv ; Mizuno:2004xj ; Nihei:2004xv ; Gergely:2006ei ; Demetrian:2005sr ; Lovelock:1971yv ; Lovelock:1972vz ; Deruelle:1989fj ; Hendi:2015oda ; Hendi:2015pda . Among these extensions a particular role can be that recently assumed by the so called Gauss-Bonnet (GB) gravity where the topological invariant

\mathcal{G}\equiv R^{2}-4R^{\alpha\beta}R_{\alpha\beta}+R^{\alpha\beta\mu\nu}R_{\alpha\beta\mu\nu}\,,

(1)

is considered into dynamics Bajardi ; Paolella ; Dialektopoulos ; Sergey ; Oikonomou:2015qha ; Hendi:2016tiy ; Hod:2019pmb ; Ma:2019ybz ; Ghosh:2019pwy ; Odintsov:2020zkl ; Odintsov:2020sqy ; Blazquez-Salcedo:2020caw ; Pozdeeva:2020shl ; Kleihaus:2020qwo ; Samart:2020mnn ; Haroon:2020vpr ; Parai:2020jrg ; EslamPanah:2020hoj . Specifically, the Lovelock theory is a well-known higher derivative theory of gravity that is a natural extension of GR where GB contributions are taken into account Â Stelle:1977ry ; Maluf:1985fj ; Farhoudi:2005qd . Â Interestingly, there are no ghost terms if GB curvature-squared terms are present, and the associated field equations include only metric’s second derivatives Boulware:1985wk ; Zumino:1985dp ; Cho:2001su ; Cai:2001dz ; Myers:1987qx ; Callan:1988hs . Another interesting feature of GB gravity is the fact that it can arise from the low-energy limit ofÂ string heterotic theory Zwiebach:1985uq ; Gross:1986iv ; Gross:1986mw ; Metsaev:1987bc ; Metsaev:1987zx ; Metsaev:1986yb . It is found that the low-energy expansion of a closed heterotic string effective action possesses a GB term and a scalar field Metsaev:1986yb , however the functional form of the scalar field is still a debated topic in view of some possible observational signature.

In the context of GB gravity,Â several black hole (BH) solutions have been discussed Â in the literature Kim:1999dq ; Cho:2002hq ; Charmousis:2002rc ; Kofinas:2003rz ; Cai:2003gr ; Barrau:2003tk ; Maeda:2003vq ; deRham:2006pe ; Dotti:2007az ; Brown:2006mh ; Maeda:2007cb ; Charmousis:2008kc ; Hendi:2010zza ; Bouhmadi-Lopez:2013gqa ; Hendi:2014bba ; Yamashita:2014cra ; Maselli:2015tta . In Ref. Li:2013cja ; Zeng:2013fsa ; Zhang:2014cga holographic thermalization in GB gravity via the Wilson loops and holographic entanglement entropy has been studied.

If we are dealing with GR corrected by a GB term, we are considering the so-called Einstein-Gauss-Bonnet (EGB) gravity. It has been demonstrated that conserved charges of EGB- AdS gravity emerges in the electric section of the Weyl tensor: this feature broadens the notion of conformal mass Jatkar:2015ffa . A four-dimensional Â EGB gravity possesses many interesting properties. It could, for example, solve some singularity issues. Â In particular, by taking into account four-dimensional EGB gravity and deriving a spherically symmetric BHs, the field of gravity becomes repulsive as $r\to 0$ , and therefore infalling object cannot approach singularity. Â Additionally, spherically symmetric solutions in EGB is distinguish from solutions of GR like the Schwarzschild one. Additionally, investigations into compact objects and their physical characteristics have been conducted within the context of four-dimensional Einstein-Gauss-Bonnet (EGB) gravity. These studies encompass aspects such as black hole stability, quasi-normal modes, shadow phenomena, and the concept of strong cosmic censorship Konoplya:2020bxa ; Mishra:2020gce ; Roy:2020dyy . A wide range of investigations has been carried out in the realm of gravitational physics. These studies encompass various aspects, including: The analysis of the shadow of a rotating black hole Wei:2020ght . Examination of the innermost stable circular orbit and shadow Guo:2020zmf . Investigations into the thermodynamics, phase transitions, and Joule-Thomson expansion of (un)charged Anti-de Sitter black holes Hegde:2020xlv ; Wei:2020poh ; Wang:2020pmb . Exploration of Bardeen solutions Singh:2020xju . Research on rotating black holes Kumar:2020owy ; Ghosh:2020vpc . Development of solutions for relativistic stars Doneva:2020ped . Investigation into Born-Infeld black holes Yang:2020jno . Examination of spinning test particles orbiting around static spherically symmetric black holes Zhang:2020qew . Studies on the thermodynamics and critical behavior of Anti-de Sitter black holes Ghosh:2020ijh . Exploration of gravitational lensing phenomena Islam:2020xmy . Analysis of the thermodynamic geometry of Anti-de Sitter black holes HosseiniMansoori:2020yfj . Investigations into Hayward black holes Kumar:2020xvu . Research on thin accretion disks around black holes Liu:2020vkh . Examination of superradiance and stability in charged Einstein-Gauss-Bonnet black holes Zhang:2020sjh . These studies collectively contribute to our understanding of various aspects of gravitational physics.

This paper delves into the realm of Einstein-Scalar-Gauss-Bonnet (ESGB) gravity involving a scalar field. The emergence of the scalar field can occur through various means, including gravitational processes that arise from induced or spontaneous scalarization, or it can manifest as a gauge field through charged solutions. The presence of a scalar field has a notable impact on the gravitational backdrop and the structure of geodesics, which encompasses the trajectories of photons and the dimensions of a BH’s shadow. Specifically, we will employ the field equations of ESGB theory that incorporate charge, alongside the cosmological constant. It’s widely recognized that when the Gauss-Bonnet (GB) term is coupled in a non-minimal manner with a scalar field denoted as $\zeta$ , the ensuing dynamics exhibit intricate and non-trivial characteristics See Â Nojiri:2005jg ; Nojiri:2005am ; Cognola:2006eg ; Nojiri:2010oco ; Cognola:2009jx ; Capozziello:2008gu ; Sadeghi:2009pu ; Guo:2010jr ; Satoh:2010ep ; Nozari:2013wua ; Lahiri:2016qih ; Mathew:2016anx ; Nozari:2015jca ; Motaharfar:2016dqt ; Carter:2005fu ; Paolella ; vandeBruck:2016xvt ; Granda:2014zea ; Granda:2011kx ; Nojiri:2005vv ; Hikmawan:2015rze ; Kanti:1998jd ; Easther:1996yd ; Rizos:1993rt ; Starobinsky:1980te ; Mukhanov:1991zn ; Brandenberger:1993ef ; Barrow:1993hp ; Damour:1994zq ; Angelantonj:1994dv ; Kaloper:1995tu ; Gasperini:1996in ; Rey:1996ad ; Rey:1996ka ; Easther:1995ba ; Santillan:2017nik ; Bose:1997qv ; KalyanaRama:1996ar ; KalyanaRama:1996im ; KalyanaRama:1997xt ; Brustein:1997ny ; Brustein:1997cv and references therein.Nevertheless, there has been no prior exploration of charged spherically symmetric BH solutions within the ESGB when adopting the assumption that the metric potentials do not follow the ansatz $g_{tt}\neq g_{rr}{}^{-1}$ . This paper endeavors to rectify this gap by obtaining precise spherically symmetric charged black hole solutions in the ESGB theory and subsequently delving into their physical attributes. The structure of the paper is the following. In Section II, we discuss the ghost-free EGB theory to investigate the formation of BH. Furthermore, we study charged field equations to derive exact spherically symmetric space-times with ${\color[rgb]{0,0,1}g_{tt}\neq g_{rr}{}^{-1}}$ . In Sec. III, we discuss the physics related to the charged BH solutions, in particular, the thermodynamical properties. In Sec. IV, we discuss results and draw conclusions¹¹1The full length solutions are reported in a supplementary notebook.

II Charged solutions in Einstein-Scalar-Gauss-Bonnet gravity

Within this section, we will provide a succinct overview of the development of ghost-free $f\left(\mathcal{G}\right)$ gravity employing Lagrange multipliers. Subsequently, we will proceed to get a solution characterized by spherically symmetric charge.

The Lagrangian for a ghost-free formulation can be expressed as follows, as detailed in Nashed:2021pah :

\displaystyle\mathcal{L}=\int d^{4}x\sqrt{-g}\left[\frac{1}{2\kappa^{2}}R+\lambda\left(\frac{1}{2}\omega(\zeta)\partial_{\mu}\zeta\partial^{\mu}\zeta+\frac{\mu^{4}}{2}\right)+h\left(\zeta\right)\mathcal{G}-\tilde{V}\left(\zeta\right)+\mathcal{L}_{\mathrm{matter}}-\Lambda+\mathcal{L}_{\mathrm{em}}\right]\,.

(2)

In this equation, $\mathcal{G}$ represents the Gauss-Bonnet (GB) topological invariant, $V(\zeta)$ stands for the field potential, and $h(\zeta)$ is a function associated with the auxiliary field. Additionally, the constant $\mu$ carries a mass dimension.

The Lagrangian for the electromagnetic field, denoted as $\mathcal{L}_{\mathrm{em}}$ , is defined as follows:

\displaystyle\mathcal{L}_{\mathrm{em}}=-\frac{1}{2}\mathcal{F}\;\left(\mathcal{F}\equiv\mathcal{F}_{\mu\nu}\mathcal{F}^{\mu\nu}\right)\,.

(3)

Here $\mathcal{F}=d\xi$ and $\xi=\xi_{\beta}dx^{\beta}$ is the electromagnetic potential Awad:2017tyz ; Nashed:2021pah . See, in particular, Ref.Vasquez . Variations of the action (2) concerning $\zeta$ , $\lambda$ , and $g_{\mu\nu}$ result in the following equations:

$\displaystyle 0=$	$\displaystyle-\frac{1}{\sqrt{-g}}\partial_{\mu}\left(\lambda\omega(\zeta)g^{\mu\nu}\sqrt{-g}\partial_{\nu}\zeta\right)+h^{\prime}\left(\zeta\right)\mathcal{G}-{\tilde{V}}^{\prime}\left(\zeta\right)+\frac{1}{2}\lambda\omega^{\prime}(\zeta)g^{\mu\nu}\partial_{\mu}\zeta\partial_{\nu}\zeta\,,$	(4)
$\displaystyle 0=$	$\displaystyle\frac{1}{2}\omega(\zeta)\partial_{\mu}\zeta\partial^{\mu}\zeta+\frac{\mu^{4}}{2}\,,$	(5)
$\displaystyle 0=$	$\displaystyle\frac{1}{2\kappa^{2}}\left(-R_{\mu\nu}+\frac{1}{2}g_{\mu\nu}[R-4\Lambda]\right)+\frac{1}{2}T^{\mathrm{matter}}_{\mu\nu}-\frac{1}{2}\lambda\omega(\zeta)\partial_{\mu}\zeta\partial_{\nu}\zeta-\frac{1}{2}g_{\mu\nu}\tilde{V}\left(\zeta\right)+D_{\mu\nu}^{\ \ \tau\eta}\nabla_{\tau}\nabla_{\eta}h\left(\zeta\right)+T^{\mathrm{em}}_{\mu\nu}\,.$	(6)

The energy-momentum tensor of the electromagnetic field $T^{\mathit{em}}_{\mu\nu}$ , is built from the Maxwell field as:

T^{\mathrm{em}\,\nu}_{\mu}=\mathcal{F}_{\mu\alpha}\mathcal{F}^{\nu\alpha}-\frac{1}{4}\delta_{\mu}{}^{\nu}\mathcal{F}\,.

(7)

Additionally, the variation of Lagrangian (2) w.r.t. the gauge potential 1-form $\xi_{\mu}$ gives:

L^{\nu}\equiv\partial_{\mu}\left(\sqrt{-g}\mathcal{F}\mathcal{F}^{\mu\nu}\right)=0\,.

(8)

In this paper, we will not take into account any more the energy-momentum tensor of perfect fluid matter $\mathcal{L}_{\mathrm{matter}}$ because we are interested only in vacuum solutions.

Now, let’s examine the field equations (4), (5), (6), and (8) within a spherically symmetric spacetime characterized by non-equal metric potentials, where $g_{tt}\neq g_{rr}{}^{-1}$ . Our goal is to solve these resulting equations and obtain an analytical solution for the model. The metric can be supposed of the form:

ds^{2}=f(r)dt^{2}-\frac{dr^{2}}{f_{1}(r)}-r^{2}\left[d\theta^{2}+\sin^{2}\theta\,d\phi^{2}\right]\,.

(9)

Here, we have two unspecified functions of the radial coordinate denoted as $f(r)$ and $f_{1}(r)$ . In our investigation, we make an assumption regarding the vector potential of the Maxwell field, as follows Nashed:2019zmy :

\displaystyle\xi=q(r)dt\,,

(10)

where $q(r)$ is the electric field which is a function of the radial coordinate.

From Eqs. (4), (5), (6), and (8) we obtain:

•

the $(0,0)$ of Eq. (4) is:

\displaystyle 0=-\frac{1}{f{r}^{2}}\bigg{[}f+12\,h^{\prime}f^{\prime}_{1}f_{1}f-f\tilde{V}{r}^{2}+q^{\prime 2}f_{1}{r}^{2}-8h^{\prime\prime}ff_{1}+8h^{\prime\prime}ff_{1}{}^{2}-4h^{\prime}ff^{\prime}_{1}-ff^{\prime}_{1}r-ff_{1}\bigg{]}\,,

(11)

•

the $(r,r)$ of Eq. (4) is:

		$\displaystyle 0=\frac{1}{f{r}^{2}\sin^{2}\theta}\bigg{[}\lambda\omega\zeta^{\prime 2}ff_{1}{r}^{2}\sin^{2}\theta+f\tilde{V}{r}^{2}\sin^{2}\theta+4\,h^{\prime}f^{\prime}f_{1}\sin^{2}\theta-12\,h^{\prime}f^{\prime}f_{1}{}^{2}\sin^{2}\theta+f_{1}f^{\prime}r\sin^{2}\theta-q^{\prime 2}f_{1}{r}^{2}\sin^{2}\theta$
		$\displaystyle+ff_{1}\sin^{2}\theta-f\sin^{2}\theta\bigg{]}\,,$		(12)

•

the $(\theta,\theta)=(\phi,\phi)$ of Eq. (4) is:

		$\displaystyle 0=-\frac{1}{4{r}^{2}f^{2}\sin^{2}\theta}\bigg{[}16\,h^{\prime}f_{1}{}^{2}ff^{\prime\prime}r-2\,f_{1}f^{\prime\prime}f{r}^{2}-8\,h^{\prime}f_{1}{}^{2}f^{\prime 2}r-f^{\prime}_{1}f^{\prime}f{r}^{2}+16\,h^{\prime\prime}f_{1}{}^{2}f^{\prime}fr-2\,f_{1}f^{\prime}fr+24\,h^{\prime}f^{\prime}_{1}f_{1}f^{\prime}fr$
		$\displaystyle-16\,h^{\prime}f_{1}{}^{2}ff^{\prime\prime}r\cos^{2}\theta-16\,h^{\prime\prime}f_{1}{}^{2}f^{\prime}fr\cos^{2}\theta-24\,h^{\prime}f^{\prime}_{1}f_{1}f^{\prime}fr\cos^{2}\theta+2\,f_{1}f^{\prime\prime}f{r}^{2}\cos^{2}\theta+8\,h^{\prime}f_{1}{}^{2}f^{\prime 2}r\cos^{2}\theta$
		$\displaystyle+2\,f_{1}f^{\prime}fr\cos^{2}\theta+4\,ff_{1}{r}^{2}q^{\prime 2}\cos^{2}\theta+f^{\prime}_{1}f^{\prime}f{r}^{2}\cos^{2}\theta-f_{1}f^{\prime 2}{r}^{2}\cos^{2}\theta+4\,\tilde{V}f^{\prime 2}{r}^{2}\cos^{2}\theta+2\,f^{\prime}_{1}f^{2}r\cos^{2}\theta$
		$\displaystyle-4\,ff_{1}{r}^{2}q^{\prime 2}-4\,\tilde{V}f^{2}{r}^{2}-2\,f^{\prime}_{1}f^{2}r+f_{1}f^{\prime 2}{r}^{2}\bigg{]}\,,$		(13)

where $q^{\prime}=\frac{\partial q(r)}{\partial r}$ .

The field equations of the scalar field (4) and (5) take the following forms:

		$\displaystyle 0=\frac{1}{2{r}^{2}f^{2}\zeta^{\prime}}\bigg{[}12\,h^{\prime}f^{\prime}_{1}ff^{\prime}f_{1}-4\,h^{\prime}f_{1}{}^{2}f^{\prime 2}-2\,f^{2}{r}^{2}\zeta^{\prime 2}\lambda^{\prime}\omega f_{1}-f^{2}{r}^{2}\zeta^{\prime 2}\lambda\omega f^{\prime}_{1}-4\,f^{2}r\zeta^{\prime 2}\lambda\omega f_{1}-2\,\tilde{V}^{\prime}f^{2}{r}^{2}-4\,h^{\prime}f^{\prime}_{1}ff^{\prime}$
		$\displaystyle-8\,h^{\prime}f_{1}f^{\prime\prime}f+8\,h^{\prime}f_{1}{}^{2}ff^{\prime\prime}+4\,h^{\prime}f_{1}f^{\prime 2}-\lambda\omega^{\prime}f_{1}\zeta^{\prime 2}f^{2}{r}^{2}-f{r}^{2}\zeta^{\prime 2}\lambda\omega f_{1}f^{\prime}-2\,f^{2}{r}^{2}\zeta^{\prime}\lambda\omega f_{1}\zeta^{\prime\prime}\bigg{]}\,,$		(14)

\displaystyle 0=\frac{2\,\lambda\omega f_{1}fr\zeta^{\prime\prime}+2\zeta^{\prime}\left\{\lambda^{\prime}\omega f_{1}fr+\left[\lambda\omega^{\prime}ff_{1}r+1/2\,\left(rff^{\prime}_{1}+f_{1}\left(4\,b+rf^{\prime}\right)\right)\omega\right]\right\}}{2br}\,.

(15)

Ultimately, the component of the field equations (8) that does not equate to zero yields the following result:

\displaystyle L^{t}\equiv{\frac{rf_{1}q^{\prime}f^{\prime}-rf^{\prime}_{1}q^{\prime}f-2\,rf_{1}q^{\prime\prime}f-4\,f_{1}q^{\prime}f}{2f^{2}r}}=0\,,

(16)

where ${}^{\prime}=\frac{d}{dr}$ , and ${}^{\prime\prime}=\frac{d^{2}}{dr^{2}}$ .

Eqs. (11)-(16) are six non-linear differential equations for eight unknown functions $f$ , $f_{1}$ , $h$ , $\tilde{V}^{\prime}$ , $\lambda$ , $\omega$ , $\chi$ , and $q$ , therefore, we are going to fix some of these unknown functions to derive the other ones. First, we solve Eq. (5) and obtain²²2The special form of the solution of the scalar field given by Eq. (17) does not allow us to put the constant $c_{1}$ equal zero, because in this case the function $\omega$ will be undefined. Moreover, if we assume the scalar field equal zero this yields the function $\omega$ will also vanishes and in that case the expression multiplied by the Lagrangian multiplier will be vanishing and the theory in that case will lost one of its main merits which is the ghost free.

\displaystyle\zeta=c_{1}\,r\,,\qquad\qquad\omega(r)=-\frac{\mu^{2}}{c_{1}{}^{2}{f_{1}(r)}}\,.

(17)

Using the above assumptions in Eqs. (11), (• ‣ II), (• ‣ II), (II) and (15), we get:

\displaystyle f(r)=\Lambda r^{2}+1+\frac{c_{2}r}{c_{1}+r^{2}}\,,\qquad\qquad f_{1}(r)=\Lambda r^{2}+\frac{c_{2}}{r}+\frac{c_{1}{}^{5/2}}{r^{5}}\,,

(18)

while the forms of $h$ , $\tilde{V}$ and $\lambda$ are reported in the Supplementary Material. Let us analyze the above solution in which one can show that, from the metric ansatzs, $f$ and $f_{1}$ , cannot be equal to each other in any way. Moreover, the dimensional constant $c_{1}$ , which has a dimension ${\textit{L}}^{2}$ , is not allowed to be vanishing as Eq. (17) shows.

Due to the complicated forms of the electric field $q(r)$ , the Lagrangian multiplier $\lambda$ , the potential $V$ , and the arbitrary function $h$ , we are going to write here their asymptotic forms in view to understand analytically their behavior. The electric field $q(r)$ , for $r\to\infty$ , is:

\displaystyle q(r)\approx c_{3}-\frac{c_{4}}{r}+\frac{c_{4}c_{1}c_{2}}{12\Lambda r^{6}}+\frac{c_{2}c_{4}(c_{1}+c_{1}c_{2}\Lambda-\Lambda)}{16\Lambda^{2}r^{8}}-\frac{c_{4}c_{1}c_{2}{}^{2}}{18\Lambda^{2}r^{9}}\,.

(19)

Eq. (19) shows that if the constant $c_{4}$ is vanishing, we get a constant value of the electric field. Moreover Eq. (19) shows that the electric field has more order than the monopole. These extra terms comes from the contributions due to the scalar field. The behavior of the potential $\tilde{V}(r)$ as $r$ approaches infinity can be expressed as follows:

\displaystyle\tilde{V}(r)\approx-3\Lambda-\frac{4\Lambda c_{4}{}^{2}}{3rc_{2}}+\frac{10c_{1}\Lambda}{3r^{2}}-\frac{20\Lambda c_{1}c_{4}{}^{2}}{9r^{3}c_{2}}-\frac{34\,{c_{1}}^{2}{\Lambda}}{9{{r}^{4}}}\,.

(20)

Moreover, if the constant $c_{4}$ , linked to the electric, is vanishing, we see that the value of the potential is $O\left(\frac{1}{r^{2n}}\right)$ . This implies that when there is no electric field present, the potential order follows a behavior of $O(\frac{1}{r^{2n}})$ , where $n$ is a positive numerical value. Eq. (20) indicates that we have a constant potential as $r\to\infty$ . Eq. (20) shows that the dimensional parameter $c_{2}$ , which has the unit of L, is not allowed to vanish to avoid undefined value of the potential $\tilde{V}$ . Moreover, from Eq. (19), we can not reproduce, in any case, the Reissner Nordström gauge potential.

Now, let’s examine the trend exhibited by the function $h$ as it approaches zero. In this limit, it assumes the following form:

\displaystyle h(r)\approx c_{5}+\frac{r^{7}}{56c_{1}{}^{7/2}}-\frac{c_{3}{r}^{10}}{60{c_{1}}^{5}}-\frac{r^{11}c_{2}(c_{3}{}^{2}+105)}{9240c_{1}{}^{6}}\,.

(21)

Eq. (21) indicates that $h$ is as $r\to 0$ . Ultimately, $\lambda(r)$ , as $r\to\infty$ , yields:

\displaystyle\lambda(r)\approx-\frac{4}{3}{\frac{{c_{4}}^{2}\Lambda}{c_{2}\,{\mu}^{4}r}}+\frac{10}{3}{\frac{c_{1}\,\Lambda}{{\mu}^{4}{r}^{2}}}-{\frac{20}{9}}\,{\frac{{c_{4}}^{2}\Lambda\,c_{1}}{c_{2}\,{\mu}^{4}{r}^{3}}}-{\frac{1}{486}}\,{\frac{648\,{\Lambda}^{3}{c_{4}}^{2}+486\,{\Lambda}^{3}c_{1}+1836\,{c_{1}}^{2}{\Lambda}^{4}}{{\mu}^{4}{\Lambda}^{3}{r}^{4}}}\,.

(22)

Eq. (22) means that, for $r\to\infty$ , we get a vanishing value of the Lagrangian multiplier. Also Eq. (22) shows that if the constant $c_{4}$ , related to the electric field, is vanishing, we get the behavior of the Lagrangian multiplier as $O(\frac{1}{r^{2n}})$ with $n$ being positive number. In Figure 1 we indicate behavior of ${\tilde{V}}$ , $h$ and $\lambda$ for some numerical values characterizing the solution. From these figures, we can see that all these quantities have positive values and approach to zero as $r\to\infty$ .

III Physical behavior of the charged black holes

Now, we will delve into the physical characteristics of the black hole derived in the preceding section. To facilitate this, we express the line element of this black hole in the following manner:

		$\displaystyle ds^{2}=\bigg{[}\Lambda r^{2}+1+\frac{c_{2}r}{c_{1}+r^{2}}\bigg{]}dt^{2}-\frac{dr^{2}}{\Lambda r^{2}+1+\frac{c_{2}}{r}+\frac{c_{1}{}^{5/2}}{r^{5}}}-r^{2}(d\theta^{2}+\sin^{2}\theta d\phi^{2})$
		$\displaystyle\approx\bigg{[}\Lambda r^{2}+1-\frac{2M}{r}+\frac{2Mc_{1}}{r^{3}}-\frac{2Mc_{1}{}^{2}}{r^{5}}\bigg{]}dt^{2}-\frac{dr^{2}}{\Lambda r^{2}+1-\frac{2M}{r}+\frac{c_{1}{}^{5/2}}{r^{5}}}-r^{2}(d\theta^{2}+\sin^{2}\theta d\phi^{2})\,.$		(23)

Here we put $c_{2}=-2M$ . The above metric indicates that in no limit can we obtain a Reissner-Nordström BH.

The curvature scalars, associated to the solution (III), as $r\to\infty$ take the form:

		$\displaystyle R^{\alpha\beta\gamma\rho}R_{\alpha\beta\gamma\rho}\approx 24\Lambda^{2}-\frac{40Mc_{1}\Lambda}{r^{5}}+\frac{48M^{2}}{r^{6}}\,,$
		$\displaystyle R^{\alpha\beta}R_{\alpha\beta}\approx 36\Lambda^{2}+\frac{60Mc_{1}}{r^{5}}+\frac{24Mc_{1}-\Lambda c_{1}[252Mc_{1}-108]}{2r^{7}}\,,$
		$\displaystyle R\approx-12\Lambda-\frac{10Mc_{1}}{r^{5}}-\frac{2Mc_{1}+3\Lambda c_{1}[3c_{1}+14Mc_{1}]}{\Lambda r^{7}}$
		$\displaystyle\mathcal{G}\approx 24\Lambda^{2}+\frac{40M\Lambda c_{1}}{r^{5}}+\frac{12c_{1}}{r^{6}}\,.$		(24)

For $r\to 0$ , they are:

		$\displaystyle R^{\alpha\beta\gamma\rho}R_{\alpha\beta\gamma\rho}\approx C\,r^{2}+C_{1}\,r+C_{2}+\frac{C_{3}}{r}\,,$
		$\displaystyle R^{\alpha\beta}R_{\alpha\beta}\approx\frac{C_{4}}{r^{12}}+\frac{C_{5}}{r^{13}}+\frac{C_{6}}{r^{14}}\,,$
		$\displaystyle R\approx C_{7}\,r^{2}+C_{8}r+C_{9}+\frac{C_{10}}{r}+\frac{C_{11}}{r^{2}}\,,$
		$\displaystyle\mathcal{G}\approx\frac{C_{12}}{c_{1}r^{11}}-\frac{C_{13}}{c_{1}r^{11}}-\frac{60Mc_{1}}{r^{13}}\,,$		(25)

where $C_{i}$ , $i=0\cdots 13$ are constants constructed from $c_{1}$ and $c_{2}$ . Eqs. (III) and (III) show that the above invariants become infinite as $r\to 0$ and have constant values as $r\to\infty$ . Moreover the invariants in Eq. (III) have a mild singularity compared with the Schwarzschild and Reissner-Nordström space-times Nashed:2018oaf , i.e., the leading term for $r\to 0$ is ${\mathcal{O}}\left(\frac{1}{r^{5}}\right)$ while, in Schwarzschild or in Reissner-Nordström space-time, it is ${\mathcal{O}}\left(\frac{1}{r^{6}}\right)$ . The main source of this mild singularity is the dimensional constant $c_{1}$ which is related to the Gauss-Bonnet scalar field.

To derive the horizon radii of solution (III), we have to solve the equation $f_{1}(r)=0$ which gives seven roots. It is hard to derive the analytic expressions of such solutions but we can deduce the asymptotic expressions and plot them using some numerical values characterizing the model. We discuss these solutions which depend on the sign of $\Lambda$ .

III.1 The case $\Lambda<0$

Let us discuss now numerically the horizons of $g_{rr}{}^{-1}=f_{1}(r)=0$ since analytic considerations are very difficult being the algebraic equation for $g_{rr}{}^{-1}=0$ of seventh order. The solution (III) has three real roots which represent the horizons for $g_{rr}{}^{-1}=f_{1}(r)=0$ . As shown in Figure 2 2(a), this might constitute three, two, or one solutions depending on the relative values of $M$ , $c_{1}$ and $\Lambda$ . It is well-known that, for charged (A)dS solutions, one can derive two horizons. This model has three horizons thanks to the dimensional parameter $c_{1}$ which depends on the Gauss-Bonnet scalar field. Now we are going to discuss the formation of these three horizons separately:
i-When $\Lambda=-0.01$ , $c_{1}=3$ , and $M=0.65$ then the metric has one horizon in the $(t,r,\theta,\phi$ ) coordinates. In this case, the horizon emerges because of the cosmological constant $r_{c}$ and, if the cosmological constant is equal zero, then we have a naked singularity where the coordinate $t$ is always timelike and $r$ is always spacelike. But still there is the singularity at $r=0$ , which is now timelike.
ii–When $\Lambda=-0.01$ , $c_{1}=3$ , and $M=1.01$ , the metric has two horizons in the $(t,r,\theta,\phi$ ) coordinates. In this case, $r_{-}$ and $r_{+}$ coincide to form $r_{d}$ which is the degenerate horizon and the other horizon is the one produced by the cosmological constant $r_{c}$ . When the cosmological constant is vanishing, we get one horizon which occurs at $r=2M$ . This represents an event horizon, but the $r$ coordinate is never timelike: it becomes null at $r=2M$ , but it is spacelike on the other side. The singularity at $r=0$ is timelike.
iii-When $\Lambda=-0.01$ , $c_{1}=3$ , and $M=1.15$ , the metric has three horizons in the $(t,r,\theta,\phi$ ) coordinates. In this case, the metric is positive for large $r$ and small $r$ and negative inside the two vanishing points $r_{\pm}$ as Figure 2 2(a) shows. When the cosmological constant is equal zero, the metric has a coordinate singularity at both $r_{-}$ and $r_{+}$ that could be removed by coordinate singularity. The surfaces defined by $r=r_{\pm}$ are both null, and they are both event horizons. The singularity at $r=0$ is timelike, not a spacelike surface as in Schwarzschild. If one is an observer falling into the black hole from far away, $r_{+}$ is just like $2M$ in the Schwarzschild metric; at this radius $r$ switches from being a spacelike coordinate to a timelike coordinate, and one necessarily moves in the direction of decreasing $r$ .

We can discuss now the thermodynamical properties of the BH solution (III). To this purpose, let us define some useful expressions of thermodynamics. Figure 2 2(b), shows that $r_{-}$ and $r_{+}$ are related to the outer horizon as $r=r_{+}$ and the inner horizon of Cauchy as $r=r_{-}$ , and when $c_{1}=3$ , $\Lambda=-0.01$ , and $c_{2}=2.3$ (trapped region). Furthermore, these horizons are related and we can get a degenerate horizon $r_{*}$ (extreme BH) when $c_{2}=-2.1$ . If $c_{2}>-2$ , there appears a naked singularity (untrapped region).

The temperature $T$ of $r_{+}$ is figured as Sheykhi:2012zz ; Sheykhi:2010zz ; Hendi:2010gq ; Sheykhi:2009pf ; Wang:2018xhw ; Zakria:2018gsf :

\displaystyle T(r_{+})=\frac{{\color[rgb]{0,0,1}f^{\prime}}\left(r_{+}\right)}{4\pi}\,,

(26)

and the entropy $S$ is figured as:

\displaystyle S\left(r_{+}\right)=\frac{1}{4}A\left(r_{+}\right)\,,

(27)

The stability, $H$ , of the BH relies on the heat capacity sign. To investigate this we figure $H_{+}$ as Nouicer:2007pu ; Chamblin:1999tk ,

H_{+}=\frac{\partial M}{\partial r_{+}}\left(\frac{\partial T}{\partial r_{+}}\right)^{-1}\,.

(28)

When $H_{+}>0\,(H_{+}<0)$ , the BH is stable (unstable). Additionally, we figure $\mathbb{G}\left(r_{+}\right)$ as Zheng:2018fyn ; Kim:2012cma :

\displaystyle\mathbb{G}\left(r_{+}\right)=M\left(r_{+}\right)-T\left(r_{+}\right)S\left(r_{+}\right)\,,

(29)

with $M\left(r_{+}\right)$ defined as:

\displaystyle M\left(r_{+}\right)=\frac{\Lambda{r_{+}}^{7}+{r_{+}}^{5}+c_{1}}{2{r_{+}}^{4}}\,.

(30)

From Eq. (26), we evaluate the Hawking temperature as:

\displaystyle T\left(r_{+}\right)=\frac{2\Lambda c_{1}{}^{2}{r_{2}}^{5}+3c_{1}\Lambda{r_{2}}^{7}+3\Lambda r_{+}{}^{9}-c_{1}r_{+}{}^{5}+r_{+}{}^{7}-c_{1}{}^{2}+c_{1}r_{+}{}^{2}}{4\pi r_{+}{}^{4}(c_{1}+r_{2}{}^{2})^{2}}\,.

(31)

The behavior of $H_{+}$ is represented in Figure 2 2(c), indicates that $T\left(r_{+}\right)>0$ when $r_{+}>r_{*}$ . Figure 2 2(c) indicates that $T_{+}$ vanishes as $r_{2}=r_{*}$ and, if $r_{+}<r_{*}$ , we have a negative temperature. The vanishing of temperature is a critical temperature and thus we have a positive temperature above the critical temperature and a negative temperature below the critical temperature. We can calculate the heat capacity of BH (III) obtaining:

\displaystyle H\left(r_{+}\right)=-\frac{2\pi(3\Lambda r_{+}{}^{7}+r_{+}{}^{5}-4c_{1})(c_{1}+r_{+}{}^{2})^{3}}{2c_{1}{}^{3}\Lambda r_{+}{}^{5}+3c_{1}{}^{2}\Lambda r_{+}{}^{7}+12c_{1}\Lambda r_{+}{}^{9}+3\Lambda r_{+}{}^{11}-c_{1}{}^{2}r_{+}{}^{5}+6c_{1}r_{+}{}^{7}-r_{+}{}^{9}+6c_{1}{}^{2}r_{+}{}^{2}-6c_{1}{}^{2}r_{+}{}^{4}+4c_{1}{}^{3}}\,.

(32)

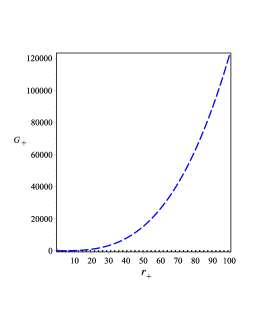
Using the above thermodynamical quantities, we can finally calculate the Gibbs function as:

\displaystyle\mathbb{G}\left(r_{+}\right)=\frac{-\Lambda c_{1}{}^{2}{r_{2}}^{7}-11c_{1}\Lambda r_{+}{}^{9}-7\Lambda r_{+}{}^{11}-4c_{1}{}^{2}r_{+}{}^{5}-7c_{1}r_{+}{}^{7}-5r_{+}{}^{9}-4c_{1}{}^{3}-7c_{1}{}^{2}r_{+}{}^{2}-5c_{1}r_{+}{}^{4}}{4r_{2}{}^{4}(c_{1}+r_{+}{}^{2})^{2}}\,.

(33)

The behavior of $\mathbb{G}\left(r_{+}\right)$ is shown in Figure 2 2(e) which indicates its positivity.

III.2 The case $\Lambda>0$

Following the same procedure of the case $\Lambda<0$ , we obtain the behavior of the solutions of Eq. (III) for $\Lambda>0$ . Also the behavior of the thermodynamical quantities like $T_{+}$ , $H_{+}$ and $\mathbb{G}\left(r_{+}\right)$ are shown in Figure 3. From the figure, it is clear that also for $\Lambda>0$ , a physically relevant model can be achieved.

IV Discussion and Conclusions

In four-dimension AdS space-time, we investigated a class of GB gravitational equations coupled to a scalar field Nojiri:2018ouv ; Nojiri:2021mxf in presence of the electromagnetic field. We obtained a charged BH solution. It is derived choosing the condition $g_{tt}\neq g_{rr}{}^{-1}$ for the metric potentials. It is worth noticing that such a solution cannot yield the standard Reissner-Nordström space-time. The BH presents extra terms coming from the presence of the GB field. Such a contribution is not allowed to have a zero value because one of the unknown functions characterizing the GB coupled scalar field, would be undefined if it vanishes. Therefore, this solution cannot, in general, yield solutions of Einstein’s GR. Moreover, we have shown that the electric field of this solution is different from the Maxwell field, and this difference depends on the contribution of the GB scalar field. This electric field cannot coincide with the electric field of Maxwell theory. Therefore, we can conclude that the GB scalar field, considered in this study, acts as a non-linear electrodynamics field reproducing higher multipole contributions in the metric potential. In contrast to EGB theory in which one can not reproduce any solutions different from the solutions of GR since the GB term act sin this theory as a topological invariant, which is constructed from the Riemann curvature tensor. Thus in the framework of Einstein theory, where the scalar field is coupled with the GB term, we succeeded in deriving a new solution.

We have to stress again the fact that the solution derived in this study can not be reduced, in any case, to the Reissner-Nordström solution. The reasons are the following:
$i)$ If the dimensional parameter $c_{2}$ is vanishing then we can reproduce the Reissner-Nordström gauge potential but this give rise to many issues in the solution as the potential field ${\tilde{V}}$ which is not defined (see Eq. (20)). Additionally, being $c_{2}$ the total mass of the system, it can not go to zero otherwise the gravitational field has no source.

Furthermore, we investigated the relevant physics of the solution and showed that, as $r\to\infty$ , it approaches to the AdS space-time. Furthermore, it is possible to compute the associated curvature invariants and demonstrate that the solution has a soft singularity when compared to the Schwarzschild and Reissner-Nordström space-times. This is because the invariants of Schwarzschild Â space-time behave as $\{K,R^{\mu\nu}R_{\mu\nu},R\}\approx\{{\mathcal{O}}\left(\frac{1}{r^{6}}\right),0,0\}$ while the invariants of this BH behave as $\{K,R^{\mu\nu}R_{\mu\nu},R\}\approx\{{\mathcal{O}}\left(\frac{1}{r^{5}}\right),{\mathcal{O}}\left(\frac{1}{r^{5}}\right),{\mathcal{O}}\left(\frac{1}{r^{5}}\right)\}$ . The main source of this soft singularity comes from the Gauss-Bonnet scalar field. Also, it is possible to show that this BH has a multi-horizon structure. Specifically, we have three-horizons for the AdS space-time and two horizons for the dS space-time.

Finally, the thermodynamic behavior of this solution can be studied by Â calculating some Hawking temperature, heat capacity, and Gibbs free energy. Thermodynamics can be divided into two classes depending on cosmological constant sign, i.e., if $\Lambda>0$ or $\Lambda<0$ . For both classes, we show that, below a critical temperature, Â the BH solution is unstable and undergoes a phase transition whose endpoint is the charged BH dressed with a scalar field. The solution shows a second-order phase transition in which the scalar field condenses below a critical temperature. The Gibbs function can be also evaluated and we showed that, for both classes, it always possesses a positive value.

To summarize, we found a charged solution in the framework of GB gravity coupled to a scalar and demonstrated that it evolves asymptotically to the AdS space-time as $r\to\infty$ . Its singularity is soft compared to the Schwarzschild space-time, it has a multi-horizons structure, and that it is unstable at the critical temperature.

A discussion similar to that reported here can be developed for GB gravity coupled to a scalar but in the framework of non-linear electrodynamics. We expect different BH solutions. This topic will be developed in a forthcoming paper.

Acknowledgements.

S.C. acknowledges the support of Istituto Nazionale di Fisica Nucleare, Sezione di Napoli, iniziative specifiche QGSKY and MOONLIGHT2. This paper is based upon work from COST Action CA21136 - Addressing observational tensions in cosmology with systematics and fundamental physics (CosmoVerse), supported by COST (European Cooperation in Science and Technology).

References

(1) C. Brans and R. H. Dicke, Phys. Rev. 124, 925-935 (1961) doi:10.1103/PhysRev.124.925
(2) R. V. Wagoner, Phys. Rev. D 1, 3209-3216 (1970) doi:10.1103/PhysRevD.1.3209
(3) C. Barrabes and G. F. Bressange, Class. Quant. Grav. 14, 805-824 (1997) doi:10.1088/0264-9381/14/3/021 [arXiv:gr-qc/9701026 [gr-qc]].
(4) R. G. Cai and Y. S. Myung, Phys. Rev. D 56, 3466-3470 (1997) doi:10.1103/PhysRevD.56.3466 [arXiv:gr-qc/9702037 [gr-qc]].
(5) S. Capozziello and A. Troisi, Phys. Rev. D 72, 044022 (2005) doi:10.1103/PhysRevD.72.044022 [arXiv:astro-ph/0507545 [astro-ph]].
(6) J. W. Moffat, JCAP 03, 004 (2006) doi:10.1088/1475-7516/2006/03/004 [arXiv:gr-qc/0506021 [gr-qc]].
(7) M. H. Dehghani, J. Pakravan and S. H. Hendi, Phys. Rev. D 74, 104014 (2006) doi:10.1103/PhysRevD.74.104014 [arXiv:hep-th/0608197 [hep-th]].
(8) V. Faraoni, Phys. Rev. D 75, 067302 (2007) doi:10.1103/PhysRevD.75.067302 [arXiv:gr-qc/0703044 [gr-qc]].
(9) K. i. Maeda and Y. Fujii, Phys. Rev. D 79, 084026 (2009) doi:10.1103/PhysRevD.79.084026 [arXiv:0902.1221 [hep-th]].
(10) S. H. Hendi and R. Katebi, Eur. Phys. J. C 72, 2235 (2012) doi:10.1140/epjc/s10052-012-2235-3
(11) M. Sharif and S. Waheed, JCAP 02, 043 (2013) doi:10.1088/1475-7516/2013/02/043 [arXiv:1403.0556 [gr-qc]].
(12) E. F. Eiroa and C. M. Sendra, Eur. Phys. J. C 74, no.11, 3171 (2014) doi:10.1140/epjc/s10052-014-3171-1 [arXiv:1408.3390 [gr-qc]].
(13) K. Karami, T. Najafi and A. Abdolmaleki, Phys. Rev. D 89, 104041 (2014) doi:10.1103/PhysRevD.89.104041 [arXiv:1401.7549 [gr-qc]].
(14) F. Darabi and A. Parsiya, Class. Quant. Grav. 32, no.15, 155005 (2015) doi:10.1088/0264-9381/32/15/155005 [arXiv:1312.1322 [gr-qc]].
(15) M. Akbar and R. G. Cai, Phys. Lett. B 648, 243-248 (2007) doi:10.1016/j.physletb.2007.03.005 [arXiv:gr-qc/0612089 [gr-qc]].
(16) J. C. C. de Souza and V. Faraoni, Class. Quant. Grav. 24, 3637-3648 (2007) doi:10.1088/0264-9381/24/14/006 [arXiv:0706.1223 [gr-qc]].
(17) C. Corda and H. J. Mosquera Cuesta, EPL 86, no.2, 20004 (2009) doi:10.1209/0295-5075/86/20004 [arXiv:0903.3645 [gr-qc]].
(18) G. Cognola, E. Elizalde, S. Nojiri, S. D. Odintsov, L. Sebastiani and S. Zerbini, Phys. Rev. D 77, 046009 (2008) doi:10.1103/PhysRevD.77.046009 [arXiv:0712.4017 [hep-th]].
(19) S. Nojiri and S. D. Odintsov, Phys. Rept. 505, 59-144 (2011) doi:10.1016/j.physrep.2011.04.001 [arXiv:1011.0544 [gr-qc]].
(20) J. L. Said and K. Z. Adami, Phys. Rev. D 83, 043008 (2011) doi:10.1103/PhysRevD.83.043008 [arXiv:1102.3553 [gr-qc]].
(21) Y. S. Myung, T. Moon and E. J. Son, Phys. Rev. D 83, 124009 (2011) doi:10.1103/PhysRevD.83.124009 [arXiv:1103.0343 [gr-qc]].
(22) D. i. Hwang, B. H. Lee and D. h. Yeom, JCAP 12, 006 (2011) doi:10.1088/1475-7516/2011/12/006 [arXiv:1110.0928 [gr-qc]].
(23) S. H. Hendi, B. Eslam Panah and S. M. Mousavi, Gen. Rel. Grav. 44, 835-853 (2012) doi:10.1007/s10714-011-1307-2 [arXiv:1102.0089 [hep-th]].
(24) S. H. Mazharimousavi, M. Halilsoy and T. Tahamtan, Eur. Phys. J. C 72, 1958 (2012) doi:10.1140/epjc/s10052-012-1958-5 [arXiv:1109.3655 [gr-qc]].
(25) J. Man and H. Cheng, Phys. Rev. D 87, no.4, 044002 (2013) doi:10.1103/PhysRevD.87.044002 [arXiv:1301.2739 [hep-th]].
(26) Y. G. Miao, F. F. Yuan and Z. Z. Zhang, Int. J. Mod. Phys. D 23, no.11, 1450093 (2014) doi:10.1142/S021827181450093X [arXiv:1407.1698 [gr-qc]].
(27) S. H. Hendi, R. B. Mann, N. Riazi and B. Eslam Panah, Phys. Rev. D 86, 104034 (2012) doi:10.1103/PhysRevD.86.104034 [arXiv:1210.3629 [gr-qc]].
(28) S. H. Hendi, Int. J. Theor. Phys. 53, no.12, 4170-4181 (2014) doi:10.1007/s10773-014-2168-8 [arXiv:1410.7527 [gr-qc]].
(29) S. H. Hendi, B. Eslam Panah and C. Corda, Can. J. Phys. 92, no.1, 76-81 (2014) doi:10.1139/cjp-2013-0357 [arXiv:1309.2135 [gr-qc]].
(30) D. Ida, JHEP 09, 014 (2000) doi:10.1088/1126-6708/2000/09/014 [arXiv:gr-qc/9912002 [gr-qc]].
(31) J. M. Cline and H. Firouzjahi, Phys. Rev. D 64, 023505 (2001) doi:10.1103/PhysRevD.64.023505 [arXiv:hep-ph/0005235 [hep-ph]].
(32) P. Brax and C. van de Bruck, Class. Quant. Grav. 20, R201-R232 (2003) doi:10.1088/0264-9381/20/9/202 [arXiv:hep-th/0303095 [hep-th]].
(33) S. Mizuno, S. J. Lee and E. J. Copeland, Phys. Rev. D 70, 043525 (2004) doi:10.1103/PhysRevD.70.043525 [arXiv:astro-ph/0405490 [astro-ph]].
(34) T. Nihei, N. Okada and O. Seto, Phys. Rev. D 71, 063535 (2005) doi:10.1103/PhysRevD.71.063535 [arXiv:hep-ph/0409219 [hep-ph]].
(35) L. A. Gergely, Phys. Rev. D 74, 024002 (2006) doi:10.1103/PhysRevD.74.024002 [arXiv:hep-th/0603244 [hep-th]].
(36) M. Demetrian, Gen. Rel. Grav. 38, 953-962 (2006) doi:10.1007/s10714-006-0275-4 [arXiv:gr-qc/0506028 [gr-qc]].
(37) D. Lovelock, J. Math. Phys. 12, 498-501 (1971) doi:10.1063/1.1665613
(38) D. Lovelock, J. Math. Phys. 13, 874-876 (1972) doi:10.1063/1.1666069
(39) N. Deruelle and L. Farina-Busto, Phys. Rev. D 41, 3696 (1990) doi:10.1103/PhysRevD.41.3696
(40) S. H. Hendi, B. Eslam Panah and S. Panahiyan, Phys. Rev. D 91, no.8, 084031 (2015) doi:10.1103/PhysRevD.91.084031 [arXiv:1510.08557 [hep-th]].
(41) S. H. Hendi, S. Panahiyan and B. Eslam Panah, JHEP 01, 129 (2016) doi:10.1007/JHEP01(2016)129 [arXiv:1507.06563 [hep-th]].
(42) F. Bajardi and S. Capozziello, Eur. Phys. J. C 80 (2020) no.8, 704 doi:10.1140/epjc/s10052-020-8258-2 [arXiv:2005.08313 [gr-qc]].
(43) M. De Laurentis, M. Paolella and S. Capozziello, Phys. Rev. D 91 (2015) no.8, 083531 doi:10.1103/PhysRevD.91.083531 [arXiv:1503.04659 [gr-qc]].
(44) F. Bajardi, K. F. Dialektopoulos and S. Capozziello, Symmetry 12 (2020) no.3, 372 doi:10.3390/sym12030372 [arXiv:1911.03554 [gr-qc]].
(45) S. Capozziello, M. De Laurentis and S. D. Odintsov, Mod. Phys. Lett. A 29 (2014) no.30, 1450164 doi:10.1142/S0217732314501648 [arXiv:1406.5652 [gr-qc]].
(46) V. K. Oikonomou, Phys. Rev. D 92, no.12, 124027 (2015) doi:10.1103/PhysRevD.92.124027 [arXiv:1509.05827 [gr-qc]].
(47) S. H. Hendi, M. Momennia, B. Eslam Panah and M. Faizal, Astrophys. J. 827, no.2, 153 (2016) doi:10.3847/0004-637X/827/2/153 [arXiv:1703.00480 [gr-qc]].
(48) S. Hod, Phys. Rev. D 100, no.6, 064039 (2019) doi:10.1103/PhysRevD.100.064039 [arXiv:1912.07630 [gr-qc]].
(49) L. Ma and H. Lu, Phys. Lett. B 807, 135535 (2020) doi:10.1016/j.physletb.2020.135535 [arXiv:1912.05569 [gr-qc]].
(50) A. Ghosh and C. Bhamidipati, Phys. Rev. D 101, no.4, 046005 (2020) doi:10.1103/PhysRevD.101.046005 [arXiv:1911.06280 [gr-qc]].
(51) S. D. Odintsov and V. K. Oikonomou, Phys. Lett. B 805, 135437 (2020) doi:10.1016/j.physletb.2020.135437 [arXiv:2004.00479 [gr-qc]].
(52) S. D. Odintsov, V. K. Oikonomou and F. P. Fronimos, Nucl. Phys. B 958, 115135 (2020) doi:10.1016/j.nuclphysb.2020.115135 [arXiv:2003.13724 [gr-qc]].
(53) J. L. Blázquez-Salcedo, D. D. Doneva, S. Kahlen, J. Kunz, P. Nedkova and S. S. Yazadjiev, Phys. Rev. D 102, no.2, 024086 (2020) doi:10.1103/PhysRevD.102.024086 [arXiv:2006.06006 [gr-qc]].
(54) E. O. Pozdeeva, Eur. Phys. J. C 80, no.7, 612 (2020) doi:10.1140/epjc/s10052-020-8176-3 [arXiv:2005.10133 [gr-qc]].
(55) B. Kleihaus, J. Kunz and P. Kanti, Phys. Rev. D 102, no.2, 024070 (2020) doi:10.1103/PhysRevD.102.024070 [arXiv:2005.07650 [gr-qc]].
(56) D. Samart and P. Channuie, JHEP 08, 100 (2020) doi:10.1007/JHEP08(2020)100 [arXiv:2004.13787 [gr-qc]].
(57) S. Haroon, R. A. Hennigar, R. B. Mann and F. Simovic, Phys. Rev. D 101, 084051 (2020) doi:10.1103/PhysRevD.101.084051 [arXiv:2002.01567 [gr-qc]].
(58) D. Parai, D. Ghorai and S. Gangopadhyay, Eur. Phys. J. C 80, no.3, 232 (2020) doi:10.1140/epjc/s10052-020-7797-x [arXiv:2001.06525 [hep-th]].
(59) B. Eslam Panah, K. Jafarzade and S. H. Hendi, Nucl. Phys. B 961, 115269 (2020) doi:10.1016/j.nuclphysb.2020.115269 [arXiv:2004.04058 [hep-th]].
(60) K. S. Stelle, Gen. Rel. Grav. 9, 353-371 (1978) doi:10.1007/BF00760427
(61) J. W. Maluf, Gen. Rel. Grav. 19, 57 (1987) doi:10.1007/BF01119811
(62) M. Farhoudi, Gen. Rel. Grav. 38, 1261-1284 (2006) doi:10.1007/s10714-006-0304-3 [arXiv:physics/0509210 [physics]].
(63) D. G. Boulware and S. Deser, Phys. Rev. Lett. 55, 2656 (1985) doi:10.1103/PhysRevLett.55.2656
(64) B. Zumino, Phys. Rept. 137, 109 (1986) doi:10.1016/0370-1573(86)90076-1
(65) Y. M. Cho, I. P. Neupane and P. S. Wesson, Nucl. Phys. B 621, 388-412 (2002) doi:10.1016/S0550-3213(01)00579-X [arXiv:hep-th/0104227 [hep-th]].
(66) R. G. Cai, Phys. Rev. D 65, 084014 (2002) doi:10.1103/PhysRevD.65.084014 [arXiv:hep-th/0109133 [hep-th]].
(67) R. C. Myers, Nucl. Phys. B 289, 701-716 (1987) doi:10.1016/0550-3213(87)90402-0
(68) C. G. Callan, Jr., R. C. Myers and M. J. Perry, Nucl. Phys. B 311, 673-698 (1989) doi:10.1016/0550-3213(89)90172-7
(69) B. Zwiebach, Phys. Lett. B 156, 315-317 (1985) doi:10.1016/0370-2693(85)91616-8
(70) D. J. Gross and E. Witten, Nucl. Phys. B 277, 1 (1986) doi:10.1016/0550-3213(86)90429-3
(71) D. J. Gross and J. H. Sloan, Nucl. Phys. B 291, 41-89 (1987) doi:10.1016/0550-3213(87)90465-2
(72) R. R. Metsaev and A. A. Tseytlin, Phys. Lett. B 191, 354-362 (1987) doi:10.1016/0370-2693(87)90622-8
(73) R. R. Metsaev and A. A. Tseytlin, Nucl. Phys. B 293, 385-419 (1987) doi:10.1016/0550-3213(87)90077-0
(74) R. R. Metsaev and A. A. Tseytlin, Phys. Lett. B 185, 52-58 (1987) doi:10.1016/0370-2693(87)91527-9
(75) J. E. Kim, B. Kyae and H. M. Lee, Phys. Rev. D 62, 045013 (2000) doi:10.1103/PhysRevD.62.045013 [arXiv:hep-ph/9912344 [hep-ph]].
(76) Y. M. Cho and I. P. Neupane, Phys. Rev. D 66, 024044 (2002) doi:10.1103/PhysRevD.66.024044 [arXiv:hep-th/0202140 [hep-th]].
(77) C. Charmousis and J. F. Dufaux, Class. Quant. Grav. 19, 4671-4682 (2002) doi:10.1088/0264-9381/19/18/304 [arXiv:hep-th/0202107 [hep-th]].
(78) G. Kofinas, R. Maartens and E. Papantonopoulos, JHEP 10, 066 (2003) doi:10.1088/1126-6708/2003/10/066 [arXiv:hep-th/0307138 [hep-th]].
(79) R. G. Cai and Q. Guo, Phys. Rev. D 69, 104025 (2004) doi:10.1103/PhysRevD.69.104025 [arXiv:hep-th/0311020 [hep-th]].
(80) A. Barrau, J. Grain and S. O. Alexeyev, Phys. Lett. B 584, 114 (2004) doi:10.1016/j.physletb.2004.01.019 [arXiv:hep-ph/0311238 [hep-ph]].
(81) K. i. Maeda and T. Torii, Phys. Rev. D 69, 024002 (2004) doi:10.1103/PhysRevD.69.024002 [arXiv:hep-th/0309152 [hep-th]].
(82) C. de Rham and A. J. Tolley, JCAP 07, 004 (2006) doi:10.1088/1475-7516/2006/07/004 [arXiv:hep-th/0605122 [hep-th]].
(83) G. Dotti, J. Oliva and R. Troncoso, Phys. Rev. D 76, 064038 (2007) doi:10.1103/PhysRevD.76.064038 [arXiv:0706.1830 [hep-th]].
(84) R. A. Brown, Gen. Rel. Grav. 39, 477-500 (2007) doi:10.1007/s10714-007-0398-2 [arXiv:gr-qc/0602050 [gr-qc]].
(85) H. Maeda, V. Sahni and Y. Shtanov, Phys. Rev. D 76, 104028 (2007) [erratum: Phys. Rev. D 80, 089902 (2009)] doi:10.1103/PhysRevD.76.104028 [arXiv:0708.3237 [gr-qc]].
(86) C. Charmousis, Lect. Notes Phys. 769, 299-346 (2009) doi:10.1007/978-3-540-88460-6_8 [arXiv:0805.0568 [gr-qc]].
(87) S. H. Hendi and B. E. Panah, Phys. Lett. B 684, 77-84 (2010) doi:10.1016/j.physletb.2010.01.026 [arXiv:1008.0102 [hep-th]].
(88) M. Bouhmadi-López, Y. W. Liu, K. Izumi and P. Chen, Phys. Rev. D 89, no.6, 063501 (2014) doi:10.1103/PhysRevD.89.063501 [arXiv:1308.5765 [hep-th]].
(89) S. H. Hendi, S. Panahiyan and E. Mahmoudi, Eur. Phys. J. C 74, no.10, 3079 (2014) doi:10.1140/epjc/s10052-014-3079-9 [arXiv:1406.2357 [gr-qc]].
(90) Y. Yamashita and T. Tanaka, JCAP 06, 004 (2014) doi:10.1088/1475-7516/2014/06/004 [arXiv:1401.4336 [hep-th]].
(91) A. Maselli, P. Pani, L. Gualtieri and V. Ferrari, Phys. Rev. D 92, no.8, 083014 (2015) doi:10.1103/PhysRevD.92.083014 [arXiv:1507.00680 [gr-qc]].
(92) Y. Z. Li, S. F. Wu and G. H. Yang, Phys. Rev. D 88, 086006 (2013) doi:10.1103/PhysRevD.88.086006 [arXiv:1309.3764 [hep-th]].
(93) X. X. Zeng, X. M. Liu and W. B. Liu, JHEP 03, 031 (2014) doi:10.1007/JHEP03(2014)031 [arXiv:1311.0718 [hep-th]].
(94) S. J. Zhang, B. Wang, E. Abdalla and E. Papantonopoulos, Phys. Rev. D 91, no.10, 106010 (2015) doi:10.1103/PhysRevD.91.106010 [arXiv:1412.7073 [hep-th]].
(95) D. P. Jatkar, G. Kofinas, O. Miskovic and R. Olea, Phys. Rev. D 91, no.10, 105030 (2015) doi:10.1103/PhysRevD.91.105030 [arXiv:1501.06861 [hep-th]].
(96) R. A. Konoplya and A. F. Zinhailo, Eur. Phys. J. C 80, no.11, 1049 (2020) doi:10.1140/epjc/s10052-020-08639-8 [arXiv:2003.01188 [gr-qc]].
(97) A. K. Mishra, Gen. Rel. Grav. 52, no.11, 106 (2020) doi:10.1007/s10714-020-02763-2 [arXiv:2004.01243 [gr-qc]].
(98) R. Roy and S. Chakrabarti, Phys. Rev. D 102, no.2, 024059 (2020) doi:10.1103/PhysRevD.102.024059 [arXiv:2003.14107 [gr-qc]].
(99) S. W. Wei and Y. X. Liu, Eur. Phys. J. Plus 136, no.4, 436 (2021) doi:10.1140/epjp/s13360-021-01398-9 [arXiv:2003.07769 [gr-qc]].
(100) M. Guo and P. C. Li, Eur. Phys. J. C 80, no.6, 588 (2020) doi:10.1140/epjc/s10052-020-8164-7 [arXiv:2003.02523 [gr-qc]].
(101) K. Hegde, A. Naveena Kumara, C. L. A. Rizwan, A. K. M. and M. S. Ali, [arXiv:2003.08778 [gr-qc]].
(102) S. W. Wei and Y. X. Liu, Phys. Rev. D 101, no.10, 104018 (2020) doi:10.1103/PhysRevD.101.104018 [arXiv:2003.14275 [gr-qc]].
(103) Y. Y. Wang, B. Y. Su and N. Li, Phys. Dark Univ. 31, 100769 (2021) doi:10.1016/j.dark.2020.100769 [arXiv:2008.01985 [gr-qc]].
(104) D. V. Singh and S. Siwach, Phys. Lett. B 808, 135658 (2020) doi:10.1016/j.physletb.2020.135658 [arXiv:2003.11754 [gr-qc]].
(105) R. Kumar and S. G. Ghosh, JCAP 07, 053 (2020) doi:10.1088/1475-7516/2020/07/053 [arXiv:2003.08927 [gr-qc]].
(106) S. G. Ghosh and S. D. Maharaj, Phys. Dark Univ. 30, 100687 (2020) doi:10.1016/j.dark.2020.100687 [arXiv:2003.09841 [gr-qc]].
(107) D. D. Doneva and S. S. Yazadjiev, JCAP 05, 024 (2021) doi:10.1088/1475-7516/2021/05/024 [arXiv:2003.10284 [gr-qc]].
(108) K. Yang, B. M. Gu, S. W. Wei and Y. X. Liu, Eur. Phys. J. C 80, no.7, 662 (2020) doi:10.1140/epjc/s10052-020-8246-6 [arXiv:2004.14468 [gr-qc]].
(109) Y. P. Zhang, S. W. Wei and Y. X. Liu, Universe 6, no.8, 103 (2020) doi:10.3390/universe6080103 [arXiv:2003.10960 [gr-qc]].
(110) S. G. Ghosh, D. V. Singh, R. Kumar and S. D. Maharaj, Annals Phys. 424, 168347 (2021) doi:10.1016/j.aop.2020.168347 [arXiv:2006.00594 [gr-qc]].
(111) M. Heydari-Fard, M. Heydari-Fard and H. Reza Sepangi, EPL 133, no.5, 50006 (2021) doi:10.1209/0295-5075/133/50006 [arXiv:2004.02140 [gr-qc]].
(112) C. Y. Zhang, P. C. Li and M. Guo, Eur. Phys. J. C 80, no.9, 874 (2020) doi:10.1140/epjc/s10052-020-08448-z [arXiv:2003.13068 [hep-th]].
(113) R. A. Konoplya and A. Zhidenko, Phys. Dark Univ. 30, 100697 (2020) doi:10.1016/j.dark.2020.100697 [arXiv:2003.12492 [gr-qc]].
(114) S. L. Li, P. Wu and H. Yu, [arXiv:2004.02080 [gr-qc]].
(115) S. Shaymatov, J. Vrba, D. Malafarina, B. Ahmedov and Z. Stuchlík, Phys. Dark Univ. 30, 100648 (2020) doi:10.1016/j.dark.2020.100648 [arXiv:2005.12410 [gr-qc]].
(116) S. U. Islam, R. Kumar and S. G. Ghosh, JCAP 09, 030 (2020) doi:10.1088/1475-7516/2020/09/030 [arXiv:2004.01038 [gr-qc]].
(117) S. A. Hosseini Mansoori, Phys. Dark Univ. 31, 100776 (2021) doi:10.1016/j.dark.2021.100776 [arXiv:2003.13382 [gr-qc]].
(118) A. Kumar, D. Baboolal and S. G. Ghosh, Universe 8, no.4, 244 (2022) doi:10.3390/universe8040244 [arXiv:2004.01131 [gr-qc]].
(119) C. Liu, T. Zhu and Q. Wu, Chin. Phys. C 45, no.1, 015105 (2021) doi:10.1088/1674-1137/abc16c [arXiv:2004.01662 [gr-qc]].
(120) C. Y. Zhang, S. J. Zhang, P. C. Li and M. Guo, JHEP 08, 105 (2020) doi:10.1007/JHEP08(2020)105 [arXiv:2004.03141 [gr-qc]].
(121) S. Nojiri and S. D. Odintsov, Phys. Lett. B 631, 1-6 (2005) doi:10.1016/j.physletb.2005.10.010 [arXiv:hep-th/0508049 [hep-th]].
(122) S. Nojiri, S. D. Odintsov and O. G. Gorbunova, J. Phys. A 39, 6627-6634 (2006) doi:10.1088/0305-4470/39/21/S62 [arXiv:hep-th/0510183 [hep-th]].
(123) G. Cognola, E. Elizalde, S. Nojiri, S. D. Odintsov and S. Zerbini, Phys. Rev. D 73, 084007 (2006) doi:10.1103/PhysRevD.73.084007 [arXiv:hep-th/0601008 [hep-th]].
(124) S. Nojiri, S. D. Odintsov, A. Toporensky and P. Tretyakov, Gen. Rel. Grav. 42, 1997-2008 (2010) doi:10.1007/s10714-010-0977-5 [arXiv:0912.2488 [hep-th]].
(125) G. Cognola, E. Elizalde, S. Nojiri, S. D. Odintsov and S. Zerbini, Eur. Phys. J. C 64, 483-494 (2009) doi:10.1140/epjc/s10052-009-1154-4 [arXiv:0905.0543 [gr-qc]].
(126) S. Capozziello, E. Elizalde, S. Nojiri and S. D. Odintsov, Phys. Lett. B 671, 193-198 (2009) doi:10.1016/j.physletb.2008.11.060 [arXiv:0809.1535 [hep-th]].
(127) J. Sadeghi, M. R. Setare and A. Banijamali, Eur. Phys. J. C 64, 433-438 (2009) doi:10.1140/epjc/s10052-009-1152-6 [arXiv:0906.0713 [hep-th]].
(128) Z. K. Guo and D. J. Schwarz, Phys. Rev. D 81, 123520 (2010) doi:10.1103/PhysRevD.81.123520 [arXiv:1001.1897 [hep-th]].
(129) M. Satoh, JCAP 11, 024 (2010) doi:10.1088/1475-7516/2010/11/024 [arXiv:1008.2724 [astro-ph.CO]].
(130) K. Nozari and N. Rashidi, Phys. Rev. D 88, no.8, 084040 (2013) doi:10.1103/PhysRevD.88.084040 [arXiv:1310.3989 [astro-ph.CO]].
(131) S. Lahiri, JCAP 01, 022 (2017) doi:10.1088/1475-7516/2017/01/022 [arXiv:1611.03037 [hep-th]].
(132) J. Mathew and S. Shankaranarayanan, Astropart. Phys. 84, 1-7 (2016) doi:10.1016/j.astropartphys.2016.07.004 [arXiv:1602.00411 [astro-ph.CO]].
(133) K. Nozari, R. Aghabararian and N. Rashidi, Astrophys. Space Sci. 358, no.2, 24 (2015) doi:10.1007/s10509-015-2423-3
(134) M. Motaharfar and H. R. Sepangi, Eur. Phys. J. C 76, no.11, 646 (2016) doi:10.1140/epjc/s10052-016-4474-1 [arXiv:1604.00453 [gr-qc]].
(135) B. M. N. Carter and I. P. Neupane, JCAP 06, 004 (2006) doi:10.1088/1475-7516/2006/06/004 [arXiv:hep-th/0512262 [hep-th]].
(136) C. van de Bruck, K. Dimopoulos and C. Longden, Phys. Rev. D 94, no.2, 023506 (2016) doi:10.1103/PhysRevD.94.023506 [arXiv:1605.06350 [astro-ph.CO]].
(137) L. N. Granda and D. F. Jimenez, Phys. Rev. D 90, no.12, 123512 (2014) doi:10.1103/PhysRevD.90.123512 [arXiv:1411.4203 [gr-qc]].
(138) L. N. Granda and E. Loaiza, Int. J. Mod. Phys. D 2, 1250002 (2012) doi:10.1142/S0218271812500022 [arXiv:1111.2454 [hep-th]].
(139) S. Nojiri, S. D. Odintsov and M. Sasaki, Phys. Rev. D 71, 123509 (2005) doi:10.1103/PhysRevD.71.123509 [arXiv:hep-th/0504052 [hep-th]].
(140) G. Hikmawan, J. Soda, A. Suroso and F. P. Zen, Phys. Rev. D 93, no.6, 068301 (2016) doi:10.1103/PhysRevD.93.068301 [arXiv:1512.00222 [hep-th]].
(141) P. Kanti, J. Rizos and K. Tamvakis, Phys. Rev. D 59, 083512 (1999) doi:10.1103/PhysRevD.59.083512 [arXiv:gr-qc/9806085 [gr-qc]].
(142) R. Easther and K. i. Maeda, Phys. Rev. D 54, 7252-7260 (1996) doi:10.1103/PhysRevD.54.7252 [arXiv:hep-th/9605173 [hep-th]].
(143) J. Rizos and K. Tamvakis, Phys. Lett. B 326, 57-61 (1994) doi:10.1016/0370-2693(94)91192-4 [arXiv:gr-qc/9401023 [gr-qc]].
(144) A. A. Starobinsky, Phys. Lett. B 91, 99-102 (1980) doi:10.1016/0370-2693(80)90670-X
(145) V. F. Mukhanov and R. H. Brandenberger, Phys. Rev. Lett. 68, 1969-1972 (1992) doi:10.1103/PhysRevLett.68.1969
(146) R. H. Brandenberger, V. F. Mukhanov and A. Sornborger, Phys. Rev. D 48, 1629-1642 (1993) doi:10.1103/PhysRevD.48.1629 [arXiv:gr-qc/9303001 [gr-qc]].
(147) J. D. Barrow, Phys. Rev. D 48, 3592-3595 (1993) doi:10.1103/PhysRevD.48.3592
(148) T. Damour and A. M. Polyakov, Nucl. Phys. B 423, 532-558 (1994) doi:10.1016/0550-3213(94)90143-0 [arXiv:hep-th/9401069 [hep-th]].
(149) C. Angelantonj, L. Amendola, M. Litterio and F. Occhionero, Phys. Rev. D 51, 1607-1616 (1995) doi:10.1103/PhysRevD.51.1607 [arXiv:astro-ph/9501008 [astro-ph]].
(150) N. Kaloper, R. Madden and K. A. Olive, Nucl. Phys. B 452, 677-704 (1995) doi:10.1016/0550-3213(95)00398-C [arXiv:hep-th/9506027 [hep-th]].
(151) M. Gasperini and G. Veneziano, Phys. Lett. B 387, 715-720 (1996) doi:10.1016/0370-2693(96)01122-7 [arXiv:hep-th/9607126 [hep-th]].
(152) S. J. Rey, Phys. Rev. Lett. 77, 1929-1932 (1996) doi:10.1103/PhysRevLett.77.1929 [arXiv:hep-th/9605176 [hep-th]].
(153) S. J. Rey, Nucl. Phys. B Proc. Suppl. 52, 344-346 (1997) doi:10.1016/S0920-5632(96)00588-9 [arXiv:hep-th/9607148 [hep-th]].
(154) R. Easther, K. i. Maeda and D. Wands, Phys. Rev. D 53, 4247-4256 (1996) doi:10.1103/PhysRevD.53.4247 [arXiv:hep-th/9509074 [hep-th]].
(155) O. P. Santillan, JCAP 07, 008 (2017) doi:10.1088/1475-7516/2017/07/008 [arXiv:1703.01713 [gr-qc]].
(156) S. Bose and S. Kar, Phys. Rev. D 56, R4444-R4448 (1997) doi:10.1103/PhysRevD.56.R4444 [arXiv:hep-th/9705061 [hep-th]].
(157) S. Kalyana Rama, Phys. Rev. Lett. 78, 1620-1623 (1997) doi:10.1103/PhysRevLett.78.1620 [arXiv:hep-th/9608026 [hep-th]].
(158) S. Kalyana Rama, Phys. Rev. D 56, 6230-6246 (1997) doi:10.1103/PhysRevD.56.6230 [arXiv:hep-th/9611223 [hep-th]].
(159) S. Kalyana Rama, Phys. Lett. B 408, 91-97 (1997) doi:10.1016/S0370-2693(97)00795-8 [arXiv:hep-th/9701154 [hep-th]].
(160) R. Brustein and R. Madden, Phys. Lett. B 410, 110-118 (1997) doi:10.1016/S0370-2693(97)00945-3 [arXiv:hep-th/9702043 [hep-th]].
(161) R. Brustein and R. Madden, Phys. Rev. D 57, 712-724 (1998) doi:10.1103/PhysRevD.57.712 [arXiv:hep-th/9708046 [hep-th]].
(162) S. Nojiri, S. D. Odintsov and V. K. Oikonomou, Phys. Rev. D 99, no.4, 044050 (2019) doi:10.1103/PhysRevD.99.044050 [arXiv:1811.07790 [gr-qc]].
(163) S. Nojiri, S. D. Odintsov, V. K. Oikonomou and A. A. Popov, Nucl. Phys. B 973, 115617 (2021) doi:10.1016/j.nuclphysb.2021.115617 [arXiv:2111.09457 [gr-qc]].
(164) A. H. Chamseddine and V. Mukhanov, JHEP 11 (2013), 135 doi:10.1007/JHEP11(2013)135 [arXiv:1308.5410 [astro-ph.CO]].
(165) S. Nojiri and S. D. Odintsov, [erratum: Mod. Phys. Lett. A 29, no.40, 1450211 (2014)] doi:10.1142/S0217732314502113 [arXiv:1408.3561 [hep-th]].
(166) J. Dutta, W. Khyllep, E. N. Saridakis, N. Tamanini and S. Vagnozzi, JCAP 02 (2018), 041 doi:10.1088/1475-7516/2018/02/041 [arXiv:1711.07290 [gr-qc]].
(167) S. Nojiri and G. G. L. Nashed, Phys. Lett. B 830 (2022), 137140 doi:10.1016/j.physletb.2022.137140 [arXiv:2202.03693 [gr-qc]].
(168) G. G. L. Nashed and E. N. Saridakis, JCAP 05, no.05, 017 (2022) doi:10.1088/1475-7516/2022/05/017 [arXiv:2111.06359 [gr-qc]].
(169) A. M. Awad, S. Capozziello and G. G. L. Nashed, JHEP 07, 136 (2017) doi:10.1007/JHEP07(2017)136 [arXiv:1706.01773 [gr-qc]].
(170) S. Capozziello, P. A. Gonzalez, E. N. Saridakis and Y. Vasquez, JHEP 02 (2013), 039 doi:10.1007/JHEP02(2013)039 [arXiv:1210.1098 [hep-th]].
(171) G. Nashed, Int. J. Mod. Phys. D 28, no.12, 1950158 (2019) doi:10.1142/S021827181950158X
(172) G. G. L. Nashed, Eur. Phys. J. Plus 133, no.1, 18 (2018) doi:10.1140/epjp/i2018-11849-7
(173) A. Sheykhi, Phys. Rev. D 86, 024013 (2012) doi:10.1103/PhysRevD.86.024013 [arXiv:1209.2960 [hep-th]].
(174) A. Sheykhi, Eur. Phys. J. C 69, 265-269 (2010) doi:10.1140/epjc/s10052-010-1372-9 [arXiv:1012.0383 [hep-th]].
(175) S. H. Hendi, A. Sheykhi and M. H. Dehghani, Eur. Phys. J. C 70, 703-712 (2010) doi:10.1140/epjc/s10052-010-1483-3 [arXiv:1002.0202 [hep-th]].
(176) A. Sheykhi, M. H. Dehghani and S. H. Hendi, Phys. Rev. D 81, 084040 (2010) doi:10.1103/PhysRevD.81.084040 [arXiv:0912.4199 [hep-th]].
(177) Y. Q. Wang, Y. X. Liu and S. W. Wei, Phys. Rev. D 99, no.6, 064036 (2019) doi:10.1103/PhysRevD.99.064036 [arXiv:1811.08795 [gr-qc]].
(178) A. Zakria and A. Afzal, [arXiv:1808.04361 [hep-th]].
(179) K. Nouicer, Class. Quant. Grav. 24, 5917-5934 (2007) [erratum: Class. Quant. Grav. 24, 6435 (2007)] doi:10.1088/0264-9381/24/24/C02 [arXiv:0706.2749 [gr-qc]].
(180) A. Chamblin, R. Emparan, C. V. Johnson and R. C. Myers, Phys. Rev. D 60, 064018 (1999) doi:10.1103/PhysRevD.60.064018 [arXiv:hep-th/9902170 [hep-th]].
(181) Y. Zheng and R. J. Yang, Eur. Phys. J. C 78, no.8, 682 (2018) doi:10.1140/epjc/s10052-018-6167-4 [arXiv:1806.09858 [gr-qc]].
(182) W. Kim and Y. Kim, Phys. Lett. B 718, 687-691 (2012) doi:10.1016/j.physletb.2012.11.017 [arXiv:1207.5318 [gr-qc]].