Charge imbalance in $\lambda$ -(BETS)₂GaCl₄ and their interplay with superconductivity

Olga Iakutkina 1. Physikalisches Institut, Universität Stuttgart, 70569 Stuttgart, Germany Ece Uykur 1. Physikalisches Institut, Universität Stuttgart, 70569 Stuttgart, Germany Takuya Kobayashi Graduate School of Science and Engineering, Saitama University, Saitama, 338-8570, Japan Atsushi Kawamoto Department of Physics, Graduate School of Science, Hokkaido University, Sapporo 060-0810, Japan Martin Dressel 1. Physikalisches Institut, Universität Stuttgart, 70569 Stuttgart, Germany Yohei Saito [email protected] 1. Physikalisches Institut, Universität Stuttgart, 70569 Stuttgart, Germany

Abstract

The two-dimensional organic superconductor $\lambda$ -(BETS)₂GaCl₄ exhibits pronounced charge fluctuations below $T\approx 150$ K, in contrast to the sibling compound $\kappa$ -(BETS)₂GaCl₄ that remains metallic down to milli-Kelvin. Infrared spectroscopy reveals only minor splitting in the vibrational features of the latter compound, common to other strongly dimerized $\kappa$ -salts. When the organic molecules are arranged in the $\lambda$ -pattern, however, a strong vibrational $\nu_{27}(b_{1u})$ mode is present, that forms a narrow doublet. Most important, when cooling $\lambda$ -(BETS)₂GaCl₄ below 150 K, two weak side modes appear due to charge disproportionation that amounts to $2\delta=0.14e$ . In analogy to the $\beta^{\prime\prime}$ -type organic conductors, we propose that charge fluctuations play an important role in emerging of unconventional superconductivity in $\lambda$ -(BETS)₂GaCl₄ at $T_{c}=4.7$ K. We discuss the possibility of a charge-density-wave that coexists with the proposed spin-density-wave state.

I Introduction

Unconventional superconductivity in strongly correlated systems such as heavy fermionic systems [1], transition metal oxides [2, 3], organic charge-transfer salts [4, 5] is a major topic in condensed matter physics. Great interest is particularly drawn by the interplay between superconductivity and some ordered state, let it be magnetic or charge order. Concerning the pairing mechanism in cuprates, for instance, the discussion goes about the importance of spin fluctuations, originating from the antiferromagnetic Mott insulating state, and charge fluctuations, associated with dynamical stripes [6, 7, 8, 9].

There is a far-reaching similarity between two-dimensional organic conductors and cuprates [10], including the fact that the superconducting state is found at the border of metal and Mott insulator [11]. The molecular systems actually constitute textbook examples of Mott insulators because the charge-transfer band is located well below the Hubbard bands split by $U\approx 0.5$ -1 eV. Commonly these salts crystallize in $D_{2}X$ stoichiometry, with $D$ the charge donor and $X$ the monovalent acceptor. This implies three-quarter-filled conduction bands as long as the stacks are homogeneous; the formation of dimers, however, results in half-filled bands. In the first case, inter-site Coulomb repulsion $V$ governs the relevant physics, giving rise to a charge-ordered insulating ground state; the latter case the genuine Mott system, completely characterized by the strength of $U$ with respect to the bandwidth $W$ .

For half-filled Mott insulators, spin fluctuations are rather common, possibly related to superconductivity. The $\kappa$ -(BEDT-TTF)₂X compounds are prime examples of antiferromagnetic Mott insulators located next to superconductivity, often with some coexistence regions [12, 13, 14, 15]. Charge-ordered materials, on the other hand, remain non-magnetic at all temperatures; hence any effect of spin fluctuations on the superconducting ground state next to the charge-ordered phase can be rules out. Merino and McKenzie suggested [16] that instead superconductivity is mediated by charge fluctuations here. Subsequently, the importance of charge degrees of freedom for these superconducting compounds was proven experimentally [17, *Kaiser12, 19, *PhysRevB.99.155144].

Refer to caption — Figure 1: (a) Looking along $ac$ -planes, the two-dimensional charge-transfer salts form different dimer patterns. In the $\kappa$ -phase the dimers are rotated with respect to each other, while the $\lambda$ -pattern is organized in stacks with two dimers, i.e. four molecules per unit cell. (b) The BETS donor layers are separated by layers of GaCl ${}_{4}^{-}$ anions. The organic molecules are slightly tilted in alternating directions in case of $\kappa$ -BETS, while uniform in case of $\lambda$ -BETS. (c) Most common are the donor molecules ET = BEDT-TTF, i.e. bis(ethylenedithio)tetrathiafulvalene), but sulfur can be substituted by selenium, leading to STF = BEDT-STF, and BETS = BEDT-TSF, i.e. bis(ethylenedithio)tetraselenafulvalene). The more extended selenium orbitals cause a larger bandwidth favoring metallic conductivity.

Fig. 1(a) illustrates that in the $\kappa$ -type salts the organic molecules are arranged in distinct pairs, while dimerization is less obvious for the $\lambda$ -pattern. The interesting question now arises whether here antiferromagnetic order is present in those compounds, how important spin fluctuations are, and whether charge fluctuations or even charge order can be observed. In this context, the series $\lambda$ - $D_{2}$ GaCl₄ is of particular interest, as the electronic bandwidth $W$ is varied by modifying the organic molecule $D$ = BEDT-TTF, BEDT-STF or BETS [Fig. 1(c)]. The strongest effect of correlations, characterized by $U/W$ , occurs in $\lambda$ -(BEDT-TTF)₂GaCl₄: it resembles a Mott insulator with antiferromagnetic order at $T_{N}=13$ K [21, 22, 23]. The intermediate compound $\lambda$ -(BEDT-STF)₂GaCl₄ does not exhibit magnetic order down to lowest temperatures but rather unconventional behavior assigned to a disordered quantum spin state [24]. $\lambda$ -(BETS)₂GaCl₄, on the other side, remains metallic all the way down to the superconducting transition at $T_{c}=4.7$ K. The picture is confirmed by pressure-dependent studies [21, 22].

The fact that superconductivity does not occur next to the antiferromagnetically ordered phase calls for further investigations. ¹³C-NMR measurements of the superconductor $\lambda$ -(BETS)₂GaCl₄ revealed, that the behavior of $1/T_{1}T$ at high temperature above 55 K is dominated by antiferromagnetic fluctuations similar to what is observed in the $\kappa$ -type salts such as $\kappa$ -(BEDT-TTF)₂Cu[N(CN)₂]Br. Below 30 K, $1/T_{1}T$ becomes temperature independent and $\rho(T)\propto T^{2}$ ; evidencing a Fermi-liquid response. In addition, another increase in spin-lattice relaxation rate of $\lambda$ -(BETS)₂GaCl₄ was observed below 10 K and interpreted as sign of Fermi surface nesting probably related to spin-density wave formation [25]. More light is shed on this issue by considering the series $\lambda$ -(BETS)₂GaBr_xCl_4-x, where the Br substitution acts as negative pressure, driving the system insulating with rising $x$ [26, 27]. ¹³C-NMR spectroscopy infers that spin degree of freedom plays an important role in the pairing mechanism of $\lambda$ -type organic superconductors.

On the other hand, ⁷⁷Se-NMR measurement of $\lambda$ -(BETS)₂FeCl₄ and $\lambda$ -(BETS)₂GaCl₄ showed linewidth broadening at low temperature that is assigned to charge disproportionation [28, 29], which can also contribute to the mechanism of superconductivity. In order to elucidate this point, comprehensive NMR investigations have been performed on $\lambda$ -(BETS)₂GaCl₄ probing different isotopes ⁶⁹Ga and ⁷¹Ga in order to separate contributions of spin and charge dynamics [30]. While there is no enhancement of charge fluctuations below $T=150$ K, spin fluctuations become dominant at low temperature. Obviously NMR spectroscopy is more sensitive to spin than to charge, calling for a detailed investigation of charge distribution in $\lambda$ -(BETS)₂GaCl₄, for instance by probing the electronic charge directly.

For that reason we elucidate the issue of charge disproportionation by infrared spectroscopy with the focus on the range of charge sensitive molecular vibrations of $\lambda$ -(BETS)₂GaCl₄. We compare the findings in this paper with those on $\kappa$ -(BETS)₂GaCl₄, which is a strongly dimerized compound that behaves metallic down to liquid-helium temperatures with no indications of strong correlations and magnetic contributions [26, 31, 32].

II Materials and Methods

Single crystals of the quasi-two-dimensional organic superconductor $\lambda$ -(BETS)₂GaCl₄ (abbreviated as $\lambda$ -BETS) and a metal $\kappa$ -(BETS)₂GaCl₄ ( $\kappa$ -BETS hereafter) were grown by standard electrochemical methods [33, 34]. In these salts, BETS donor molecules are dimerized, forming a triangular lattice in the $\kappa$ -type, and for the $\lambda$ -type they are arranged on a square lattice, as illustrated in Fig. 1(a). $\kappa$ -BETS crystalizes in orthorhombic Pnma space group. Layers of donor molecules tilted in opposite directions with respect to each other, leading to a doubling of the unit cell along the $b$ -axis. The unit cell contains four dimmers, and two BETS molecules in a dimer are connected by a center of symmetry [Fig. 1(b)]. $\lambda$ -BETS has lower symmetry and belong to the triclinic P $\bar{1}$ space group. In contrast to $\kappa$ -BETS, here the donor layers of BETS molecules are identical. As a result, it has two dimmers per unit cell as shown in Fig. 1(b). An interesting difference between both BETS-salts is that in $\lambda$ -BETS two molecules forming a dimer are not identical, but have a slightly different length of C=C double bonds.

For both compounds the temperature dependence of the dc resistivity was measured along the most conducting axis using the conventional four-contacts method. The applied current was limited in the range of 100-200 $\mu$ A; the resistivity data were recorded while warming up from 3 to 295 K.

Optical reflectivity measurements were performed with the light polarized perpendicular to the highly-conducting BETS planes, cf. Fig. 1(b). In this direction we can detect the molecular vibration $\nu_{27}(b_{1u})$ which is the most sensitive local probe for the charge per molecule [35, 36, 37]. For this purpose, a Hyperion infrared microscope was attached to a Bruker Vertex 80v Fourier-transform infrared spectrometer. The data were collected in the spectral range 500-8000 ${\rm cm}^{-1}$ between $T=295$ and 9 K. To perform the Kramers-Kronig transformation, a constant extrapolation was used for frequencies below 500 ${\rm cm}^{-1}$ and the standard $\omega^{-4}$ decay was utilized as high-frequency extrapolation [38].

III Results

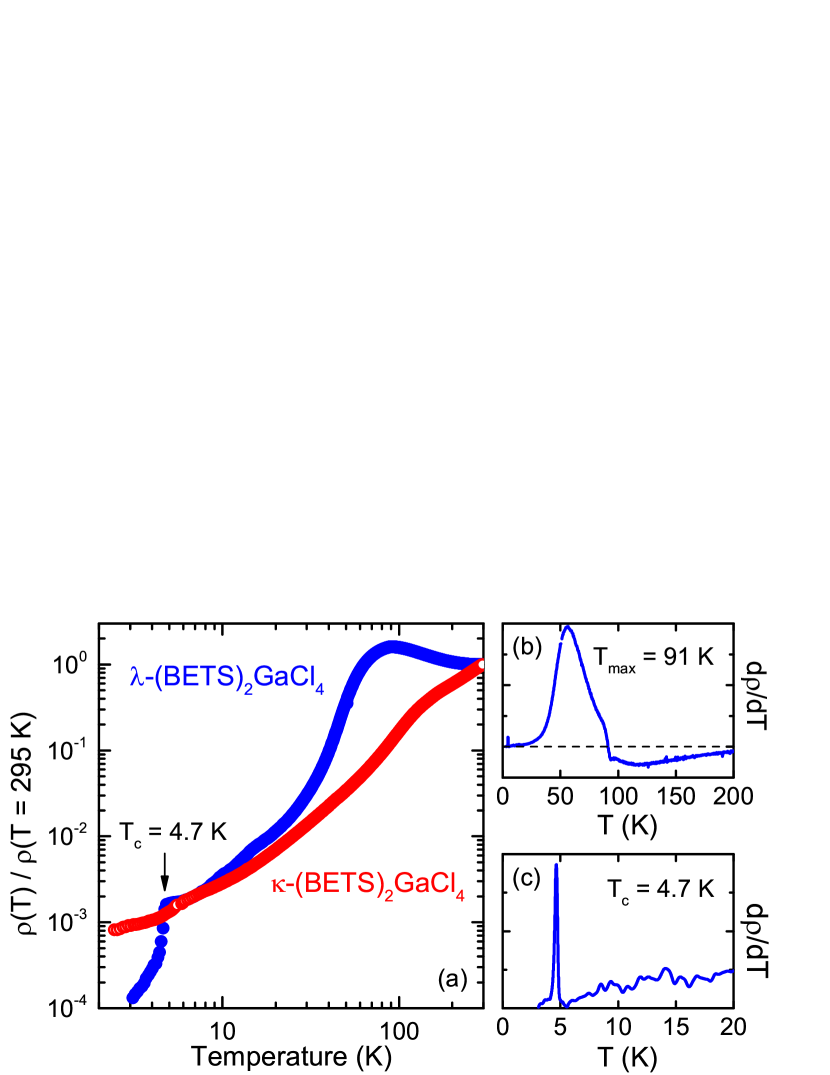
In Fig. 2(a) the temperature dependence of the electrical resistivity $\rho(T)$ of $\kappa$ -(BETS)₂GaCl₄ and $\lambda$ -(BETS)₂GaCl₄ is plotted, normalized to the room temperature value $\rho(T=295{\rm K})$ . The behavior of the two salts is rather different. $\kappa$ -(BETS)₂GaCl₄ remains metallic in the entire temperature range: $\rho(T)$ drops monotonously with minor changes in slope at elevated temperatures. For the $\lambda$ -salt a pronounced maximum is observed at $T_{\rm max}=91$ K [Fig. 2(b)]; while below approximately 40 K, the $\rho(T)\propto T^{2}$ dependence indicates a Fermi-liquid behavior. The compound becomes superconducting at $T_{c}=4.7$ K (onset at 4.8 K) as shown in Fig. 2(c). These results are consistent with previous publications [34].

In order to explore possible charge distribution in organic charge-transfer salts, vibrational spectroscopy is the most sensitive and convenient method. The three modes, $\nu_{2}(a_{g})$ , $\nu_{3}(a_{g})$ and $\nu_{27}(b_{1u})$ , mainly involving C=C stretching, can be utilized to determine the electronic charge per molecule. The two totally symmetric $a_{g}$ modes should usually not be infrared active, but due to electron molecular-vibration (emv) coupling, they can be observed by infrared spectroscopy in the conducting plane. As a result of the coupling to the electronic background, the position of the $\nu_{2}(a_{g})$ and $\nu_{3}(a_{g})$ infrared feature is shifted – compared to the Raman mode – and depends on the midinfrared charge-transfer band. Hence, this way a precise determination of the charge distribution can become pretty tricky. The antisymmetric molecular vibration $\nu_{27}(b_{1u})$ , on the other hand, is infrared active and – in first approximation – its frequency depends linearly on the molecular charge [36]; this makes it perfectly suited for evaluating the charge per molecule. Due to the stacking of the donor molecules in these salts, it can be best observed perpendicular to conducting BETS layers.

Fig. 3 displays the optical conductivity of $\kappa$ - and $\lambda$ -(BETS)₂GaCl₄ in the spectral range of the $\nu_{27}(b_{1u})$ mode, recorded at different temperatures, as indicated. Compared to the BEDT-TTF salts, this molecular vibration shows up slightly lower in frequency because four of the eight sulfur atoms are substituted by heavier selenium atoms in BETS [cf. Fig. 1(c)] [39]. At room temperature, a broad peak is observed around 1453 ${\rm cm}^{-1}$ in $\kappa$ -(BETS)₂GaCl₄, which is assigned to $\nu_{27}(b_{1u})$ . When the temperature is lowered, the feature becomes narrower and below 200 K two peaks can be clearly distinguished. The behavior found in the $\lambda$ -compound is rather different: here the $\nu_{27}(b_{1u})$ mode appears as a doublet with frequencies 1454 and 1458 ${\rm cm}^{-1}$ already at room temperature. Upon cooling a typical narrowing and blue shift occurs, but the separation of the two peaks does not change in the entire temperature range. We explain the presence of these two distinct peaks by the lower crystal symmetry. Most important, however, are the two side peaks at 1451 and 1471 ${\rm cm}^{-1}$ that appear next to this doublet when the temperature is reduced below $T=150$ K, i.e. when the resistivity $\rho(T)$ starts to develop its maximum reached at $T_{\max}=91$ K (Fig. 2).

The $\nu_{28}(b_{1u})$ mode, which is related to ethylene-end groups, is present in both compounds. It shows up as a small peak around 1400 ${\rm cm}^{-1}$ in $\kappa$ -(BETS)₂GaCl₄, and as a doublet around 1405-1410 ${\rm cm}^{-1}$ in the $\lambda$ -analogue due to the lower P $\bar{1}$ symmetry of the latter salt. It is interesting to note that the peak seen around 1423-1425 ${\rm cm}^{-1}$ is very similar to one observed in the quantum spin liquid $\kappa$ -(BEDT-TTF)₂Cu₂(CN)₃ [40]. The tiny features near 1480 ${\rm cm}^{-1}$ in both compounds might correspond to $\nu_{2}(a_{g})$ . No temperature dependence was observed for these modes nor for the shoulder at 1442 ${\rm cm}^{-1}$ .

IV Discussion

IV.1 Charge sensitive $\nu_{27}(b_{1u})$ mode

Fig. 4(a) illustrates the significantly different shape of the vibrational modes in the $\kappa$ - and $\lambda$ -salts by comparing the $T=9$ K spectra in the same graph. While for $\lambda$ -(BETS)₂GaCl₄ the modes can be fitted by simple Lorentz functions, the excitation in $\kappa$ -(BETS)₂GaCl₄ are surprisingly asymmetric indicating some influence of the electronic background. Typically no sizeable conductivity occurs in the out-of-plane direction, however, for $\kappa$ -type salts the donor molecules are tilted within the plane, leading to some appreciable coupling to the in-plane conductivity. In order to account for the interaction of the vibrational modes with the electronic background, the Fano model should be applied in the case of in $\kappa$ -(BETS)₂GaCl₄ [40].

In general, a doubling of charge sensitive modes is taken as evidence for inequivalent bonds due to donor molecules containing different amount of charge $2\delta=\rho_{\rm rich}-\rho_{\rm poor}$ ; the observed peak separation $\Delta\nu_{27}$ allows us to evaluate the charge imbalance $2\delta=\Delta\nu_{27}/(140~{}{\rm cm}^{-1}/e)$ , assuming the same relation as reported for the $\nu_{27}(b_{1u})$ mode of BEDT-TTF salts [36]. Despite the fact that the spectrum is shifted to lower frequencies by almost 10 ${\rm cm}^{-1}$ due to the heavier selenium atoms, our finding can be compared with the observations Sedlmeier et al. made on several $\kappa$ -phase BEDT-TTF compounds [40]. Such minor satellite peaks occur in $\kappa$ -(BEDT-TTF)₂Cu[N(CN)₂]Br and $\kappa$ -(BEDT-TTF)₂Cu[N(CN)₂]Cl and were ascribed to Davydov-like splitting; Maksimuk et.al. gave a detailed description of this phenomenon including symmetry considerations and selection rules [41]. The situation is similar for $\kappa$ -BETS, where the unit cell is doubled due to alternating tilting of the BETS molecules within the planes, as depinced in Fig. 1(b). We conclude therefore that the two maxima separated by $\Delta\nu=9$ ${\rm cm}^{-1}$ are due to structural reasons. This splitting is well resolved at low temperatures but can be followed all the way up to room temperature where it is smaller by about 30%. We exclude the presence of static or dynamic charge disproportionation at any temperature.

The case of $\lambda$ -(BETS)₂GaCl₄ is more complex because there are two rather sharp central peaks, which are distinct by only 3.6 ${\rm cm}^{-1}$ . We assign the doublet to the $\nu_{27}(b_{1u})$ mode of the BETS molecules bearing $+0.5~{}e$ charge. Due to the low symmetry of the $\lambda$ -compound, there are two inequivalent molecules in the unit cell, resulting in a doubling of this vibrational feature; the unequal bonds correspond to a static charge imbalance of only $0.02e$ . No variation with temperature is observed, except of the common thermal smearing above 100 K, demonstrated in Fig. 4(d). The surprising observation is that in addition to this central doublet, two side bands appear below $T\approx 150$ K, right when the resistivity behavior changes from metallic to semiconducting upon cooling (Fig. 2). The emergence of these features is attributed to the noticeable reorganization of charge and will be discussed in all detail in the following.

From Figs. 3(b) and 4(d) we see that the width of central and side peaks in $\lambda$ -(BETS)₂GaCl₄ differs significantly. While the central modes are very narrow, with more than 5 ${\rm cm}^{-1}$ linewidth, the side bands are quite broad, even at low temperatures. We suggest that the satellite peaks are due to a dynamic charge imbalance of $2\delta_{\rm fluct}=0.14e$ emerging only for $T<150$ K. As a matter of fact, each satellite peak should contain a doublet, as well ¹¹1There are some indications of a doublet at the high-frequency satellite, but these features are too weak to make a strong point.; however our data do not allow such an assignment reliably due to the broad features. The splitting of the sidebands was calculated using the average frequency of the central doublet. In addition, we should note that from ⁷⁷Se-NMR measurements on $\lambda$ -(BETS)₂GaCl₄ a charge distribution $2\delta=0.15e$ was concluded considering the low-temperature Knight shift [29], rather similar to the charge disproportionation we found. It is interesting to compare our observations with those reported for the superconductor $\beta^{\prime\prime}$ -(BEDT-TTF)₂SF₅CH₂CF₂SO₃ where at low temperature broad fluctuation modes coexist with localized charges, seen in well separated sharp peaks [43, *girlando2012spectroscopic].

Finally, we want to point out that the $\nu_{27}(b_{1u})$ molecular vibrations involve the inner C=C double bonds. These should not be significantly affected by the freezing-out of the ethylene end-groups motion, that was suggested as a source of charge imbalance by Kobayashi et al. [30]. Varying the cooling rate is a common approach for investigating freezing effects. Yakushi et al. report that the width of the $\nu_{2}(a_{g})$ Raman mode is affected by the cooling rate in $\kappa$ -(BEDT-TTF)₂Cu₂(CN)₃ and relate that to disorder of ethylene end-groups at low temperature [45]. However, we could not identify any dependence of the charge sensitive $\nu_{27}$ ( $b_{1u}$ ) infrared mode on the cooling rate [46]. In addition, the $\nu_{28}$ mode, which involves the terminal CH₂-groups, is also seen up to room temperature (Fig. 3) with no strong variation around 100 K. Since in the present compound the ethylene end-groups are closely linked to the GaCl ${}_{4}^{-}$ anions, investigation of infrared active $\nu_{3}$ vibrational mode of the tetrahedral GaCl ${}_{4}^{-}$ anions (located in the far-infrared range) is highly appreciable to shed light on the influence of ethylene motion on physical properties of $\lambda$ -(BETS)₂GaCl₄. More specific studies in this regard are in progress.

As far as the mode strength is concerned, the intensity of vibrational modes generally increases with electronic charge, corresponding to a shift to lower frequencies, as shown by quantum mechanical calculations [36, *girlando2012spectroscopic]. Indeed, the peak observed in $\lambda$ -(BETS)₂GaCl₄ at $1453$ ${\rm cm}^{-1}$ has a much higher intensity compared to one at $1573$ ${\rm cm}^{-1}$ .

We have seen in Fig. 2 that the $\kappa$ -phase salt is a metal at all temperatures; therefore it is not surprising to find only broad vibrational modes even in the perpendicular direction. The non-monotonous resistivity $\rho(T)$ for $\lambda$ -(BETS)₂GaCl₄ that goes through a maximum around $T_{\rm max}=91$ K upon cooling, indicates that electronic charges are prone to localization, because electronic correlation are more important [31]. The presence of superconductivity right at the metal-insulator transition in the phase diagram raises the question about possible mechanisms.

Now we want to draw the attention to the series of $\beta^{\prime\prime}$ -(BEDT-TTF)₂ $X$ salts, that was subject to extended investigations for many years [47, *Schlueter01, 43, 15], including comprehensive optical studies that focussed on the interplay of charge order and superconductivity. By variation of the all-organic anions $X$ , completely insulating, charge-ordered, superconducting and metallic systems can be achieved. In the latter compound, $\beta^{\prime\prime}$ -(BEDT-TTF)₂SF₅CHFCF₂SO₃, only a very low degree of charge fluctuations is seen, resulting a very broad feature in the optical conductivity. The superconductor $\beta^{\prime\prime}$ -(BEDT-TTF)₂SF₅CH₂CF₂SO₃, on the other hand, exhibits well distinct peaks corresponding to fluctuating charges [17, 19, *PhysRevB.99.155144]; very much fostering the idea of charge fluctuations as glue for superconductivity.

For a more quantitative analysis, the vibrational features were fitted by one Fano function each in case of $\kappa$ -type; for the $\lambda$ -type salt one Lorentzian each suffices . The temperature evolution of the peak positions and the calculated charge imbalance $2\delta$ is plotted in Fig.4(b) and (c), respectively. It is surprising that $2\delta$ does not change significantly upon cooling for any of the features. This behavior is completely different to quasi-one-dimensional (TMTTF)₂ $X$ compounds where the charge imbalance increases below $T_{\rm CO}$ in a mean-field manner [49, 50, 51, 52]. The present behavior instead resembles the finding in the superconducting $\beta^{\prime\prime}$ -(BEDT-TTF)₂SF₅CH₂CF₂SO₃ and metallic $\beta^{\prime\prime}$ -(BEDT-TTF)₂SF₅CHFSO₃ [20].

The temperature dependence of the linewidth is displayed in Fig.4(d) for all modes considered. The peaks of the $\kappa$ -salt are mainly affected by the electronic background and thermal broadening. A similar behavior is observed for the narrow static modes in $\lambda$ -(BETS)₂GaCl₄. The temperature evolution of the sidebands is much smaller, they remain rather broad even at low temperatures. In the following we elaborate on the possible origin of charge fluctuations below $T=150$ K.

IV.2 Interplay of broken symmetry ground states in spin and charge sectors

In $\lambda$ -type salts the Fermi surface comprises cylindrical portions with one-dimensional flat sections [53, 54], thus nesting effects and possible instabilities are expected. Indeed, the spin-density-wave (SDW) state accompanied by the metal-insulator transition was recently observed in $\lambda$ -(BETS)₂GaBr_xCl_4-x series with $x=0.75$ [27]. No doubt that this state of itinerant antiferromagnetism certainly affects electronic properties of adjacent $\lambda$ -(BETS)₂GaCl₄, where the increase of $1/T_{1}T$ just above the superconducting transition was ascribed to the SDW fluctuations [25], and as a result, magnetic fluctuations were considered as a pairing mechanism of superconductivity.

Our current infrared measurements reveal that in $\lambda$ -(BETS)₂GaCl₄ not only magnetic fluctuations but also charge fluctuations are present at low temperature. In this case, the simple Hubbard model is insufficient to describe the underlying physics, instead both on-site Coulomb repulsion $U$ and inter-site interaction $V$ has to be takes into account. The properties of a square lattice at half-filling by using the extended Hubbard model, infer coexistence of spin and charge density waves (SDW and CDW) near the superconducting state when $V=U/4$ [55]. Along this lines, we may now explain how superconductivity arises when both charge- and spin-fluctuations are present.

For the one-dimensional Bechgaard salt (TMTSF)₂PF₆, for instance, several groups have established the low-temperature SDW phase next superconductivity [56, 57, 58, 59]. X-ray scattering experiments revealed features associated with a CDW state even for temperatures below $T_{\rm SDW}$ [60, 61]; thus Clay, Mazumdar and collaborators concluded that charge and spin density waves coexist [62, 63]. Since for (TMTSF)₂PF₆ and $\lambda$ -(BETS)₂GaBr_0.75Cl_3.25 a qualitatively similar situation is observed, we expect that in the latter compound a CDW state can coexist with a SDW ground state. This implies that charge fluctuations and spin fluctuations may occur next to and even cause the superconducting state. Interestingly, several of the strongly dimerized $\kappa$ -type salts with dominant magnetic fluctuations exhibit superconducting transition temperatures of 10 K and more, while those systems with no or weak dimerization $T_{c}$ barely exceeds 5 K. We might speculate that in the present case of $\lambda$ -BETS the charge imbalance prevents a larger $T_{c}$ . Further investigations of the neighboring insulating state are required to eventually prove this suggestion. Pressure-dependent studies could be an option to tune the systems continuously albeit rather challenging. Beside a few examples in the field of quantum spin liquids [64, 65, *Rosslhuber21], here we want to mention the dimer Mott insulator $\beta^{\prime}$ -(BEDT-TTF)₂ICl₂ where superconductivity under pressure is discussed near spin- and charge-density-wave phases [67].

Finally, let us recall the series $\alpha$ -(BEDT-TTF)₂ $M$ Hg(SCN)₄, with $M$ = K, Tl, Rb, NH₄, which is a typical quarter-filled system with clear indications of charge order. Interestingly, $M$ = NH₄ is superconducting while for the other compounds various density-wave scenarios have been suggested because the electronic structure contains quasi-one-dimensional bands at $E_{F}$ [68, 35, 69, *Dressel05, *Drichko06, *Merino06, 73, *Christ00, *Andres05, 76]. As the system is at the verge of a charge-ordered phase, the effect of charge fluctuations on superconductivity is evident and should become subject of further investigations, including the recently synthesized modified compounds which also show density wave states [77, *Ohnuma19].

At this point, we see that both charge and spin fluctuations may be present at low temperature in $\lambda$ -(BETS)₂GaCl₄, but their influence on superconductivity is not completely clear. In the case of the half-filled $\kappa$ -(BEDT-TTF)₂X salts, where $V=0$ and only $U$ is present, charge fluctuations were found to be insignificant. For the quarter-filled $\beta^{\prime\prime}$ -type systems, where $V$ is strong, a link between charge fluctuations and superconductivity were suggested theoretically and proven experimentally [16, 17, 19]. This is consistent with the phase diagram proposed by Onari et al. [55]. When both $U$ and $V$ are present, it is difficult to say whether spin- and charge- fluctuations compete, whether they enhance each other, and in which way their interplay leads to superconductivity. Further investigations are needed to draw firm conclusions. Nevertheless, the present study clearly shows that when going from the bare metal $\kappa$ -(BETS)₂GaCl₄ to the superconductor $\lambda$ -(BETS)₂GaCl₄, the influence of the charge degrees of freedom increases. The $\lambda$ -type salts are another example for the idea that charge fluctuations affect superconductivity.

V Conclusions

In summary, infrared optical spectroscopy was carried out in the range of the charge-sensitive $\nu_{27}(b_{1u})$ mode in order to learn about the interplay of charge order and superconductivity in the two-dimensional organic conductor $\lambda$ -(BETS)₂GaCl₄, using $\kappa$ -(BETS)₂GaCl₄ as a reference. In the latter compound, alternating layers and metallic conductivity results in Fano-shaped slightly distinct modes. When we go to the superconducting $\lambda$ -(BETS)₂GaCl₄, we observe slight splitting of the $\nu_{27}$ mode due to the lower symmetry structure. Most important, two side modes appear upon cooling which are assigned to a dynamical charge imbalance of $2\delta\approx 0.14e$ . We suggest a situation similar to $\alpha$ - and $\beta^{\prime\prime}$ -type salts, where charge fluctuations are closely linked to superconductivity and contribute to their pairing mechanism. In accord with theoretical proposals, we suggest that these charge fluctuations originate in a dynamic charge-density-wave state, which coexists with the dynamic spin-density-wave state evidenced by NMR measurements. A complete picture should eventually explain the properties of charge-ordered $\alpha$ - $\beta^{\prime}$ - and $\beta^{\prime\prime}$ -compounds together with the observations of $\lambda$ -(BETS)₂GaCl₄.

VI Acknowledgements

We would like to thank K. Tsuji and also G. Untereiner for her crucial technical support. The work was supported by the Deutsche Forschungsgemeinschaft via DR228/39-3.

References

White et al. [2015] B. White, J. Thompson, and M. Maple, Unconventional superconductivity in heavy-fermion compounds, Physica C 514, 246 (2015).
Plakida [2010] N. Plakida, High-temperature cuprate superconductors, Springer Series of Solid-State Science, Vol. 166 (Springer-Verlag, Berlin, 2010).
Yamauchi et al. [2005] T. Yamauchi, M. Isobe, and Y. Ueda, Charge order and superconductivity in vanadium oxides, Solid State Sci. 7, 874 (2005).
Lebed [2008] A. G. Lebed, The physics of organic superconductors and conductors (Springer, Berlin, 2008).
Wosnitza [2019] J. Wosnitza, Superconductivity of organic charge-transfer salts, J. Low Temp. Phys. 197, 250 (2019).
Moriya and Ueda [2000] T. Moriya and K. Ueda, Spin fluctuations and high temperature superconductivity, Adv. Phys. 49, 555 (2000).
Misawa and Imada [2014] T. Misawa and M. Imada, Origin of high- ${T}_{c}$ superconductivity in doped Hubbard models and their extensions: Roles of uniform charge fluctuations, Phys. Rev. B 90, 115137 (2014).
Vojta et al. [2006] M. Vojta, T. Vojta, and R. K. Kaul, Spin excitations in fluctuating stripe phases of doped cuprate superconductors, Phys. Rev. Lett. 97, 097001 (2006).
Torchinsky et al. [2013] D. H. Torchinsky, F. Mahmood, A. T. Bollinger, I. Božović, and N. Gedik, Fluctuating charge-density waves in a cuprate superconductor, Nature Mat. 12, 387 (2013).
McKenzie [1997] R. H. McKenzie, Similarities between organic and cuprate superconductors, Science 278, 820 (1997).
Imada et al. [1998] M. Imada, A. Fujimori, and Y. Tokura, Metal-insulator transitions, Rev. Mod. Phys. 70, 1039 (1998).
Kuroki and Aoki [1999] K. Kuroki and H. Aoki, Superconductivity and spin correlation in organic conductors: A quantum Monte Carlo study, Phys. Rev. B 60, 3060 (1999).
Kondo and Moriya [1998] H. Kondo and T. Moriya, Spin fluctuation-induced superconductivity in organic compounds, J. Phys. Soc. Jpn. 67, 3695 (1998).
Lefebvre et al. [2000] S. Lefebvre, P. Wzietek, S. Brown, C. Bourbonnais, D. Jérome, C. Mézière, M. Fourmigué, and P. Batail, Mott transition, antiferromagnetism, and unconventional superconductivity in layered organic superconductors, Phys. Rev. Lett. 85, 5420 (2000).
Dressel and Tomić [2020] M. Dressel and S. Tomić, Molecular quantum materials: electronic phases and charge dynamics in two-dimensional organic solids, Adv. Phys. 69, 1 (2020).
Merino and McKenzie [2001] J. Merino and R. H. McKenzie, Superconductivity mediated by charge fluctuations in layered molecular crystals, Phys. Rev. Lett. 87, 237002 (2001).
Kaiser et al. [2010] S. Kaiser, M. Dressel, Y. Sun, A. Greco, J. J.A.Schlueter, G. Gard, and N. Drichko, Bandwidth tuning triggers interplay of charge order and superconductivity in two-dimensional organic materials, Phys. Rev. Lett. 105, 206402 (2010).
Kaiser et al. [2012] S. Kaiser, S. Yasin, N. Drichko, M. Dressel, T. Rõõm, D. Hüvonen, U. Nagel, G. L. Gard, and J. A. Schlueter, Optical investigations of the superconducting energy gap in $\beta^{\prime\prime}$ -(BEDT-TTF)₂SF₅CH₂CF₂SO₃, phys. stat. sol. (b) 249, 985 (2012).
Pustogow et al. [2019a] A. Pustogow, Y. Saito, A. Rohwer, J. A. Schlueter, and M. Dressel, Coexistence of charge order and superconductivity in $\beta^{\prime\prime}$ -(BEDT-TTF)₂SF₅CH₂CF₂SO₃, Phys. Rev. B 99, 140509 (2019a).
Pustogow et al. [2019b] A. Pustogow, K. Treptow, A. Rohwer, Y. Saito, M. Sanz Alonso, A. Löhle, J. A. Schlueter, and M. Dressel, Charge order in $\beta^{\prime\prime}$ -phase BEDT-TTF salts, Phys. Rev. B 99, 155144 (2019b).
Mori et al. [2001] H. Mori, T. Okano, M. Kamiya, M. Haemori, H. Suzuki, S. Tanaka, Y. Nishio, K. Kajita, and H. Moriyama, Bandwidth and band filling control in organic conductors, Physica C 357-360, 103 (2001).
Minamidate et al. [2015] T. Minamidate, Y. Oka, H. Shindo, T. Yamazaki, N. Matsunaga, K. Nomura, and A. Kawamoto, Superconducting phase in $\lambda$ -(BEDT-STF)₂GaCl₄ at high pressures, J. Phys. Soc. Jpn. 84, 063704 (2015).
Saito et al. [2018] Y. Saito, S. Fukuoka, T. Kobayashi, A. Kawamoto, and H. Mori, Antiferromagnetic ordering in organic conductor $\lambda$ -(BEDT-TTF)₂GaCl₄ probed by ¹³C NMR, J. Phys. Soc. Jpn. 87, 013707 (2018).
Saito et al. [2019] Y. Saito, H. Nakamura, M. Sawada, T. Yamazaki, S. Fukuoka, N. Matsunaga, K. Nomura, M. Dressel, and A. Kawamoto, Disordered quantum spin state in the stripe lattice system consisting of triangular and square tilings (2019), arXiv:1910.09963 .
Kobayashi and Kawamoto [2017] T. Kobayashi and A. Kawamoto, Evidence of antiferromagnetic fluctuation in the unconventional superconductor $\lambda$ -(BETS)₂GaCl₄ by ¹³C NMR, Phys. Rev. B 96, 125115 (2017).
Tanaka et al. [1999] H. Tanaka, A. Kobayashi, A. Sato, H. Akutsu, and H. Kobayashi, Chemical control of electrical properties and phase diagram of a series of $\lambda$ -type BETS superconductors, $\lambda$ -(BETS)₂GaBr_xCl_4-x, J. Am. Chem. Soc. 121, 760 (1999).
Kobayashi et al. [2020a] T. Kobayashi, T. Ishikawa, A. Ohnuma, M. Sawada, N. Matsunaga, H. Uehara, and A. Kawamoto, Spin-density wave in the vicinity of superconducting state in $\lambda$ -(BETS)₂GaBr_xCl_4-x probed by ¹³C NMR spectroscopy, Phys. Rev. Research 2, 023075 (2020a).
Hiraki et al. [2007] K.-I. Hiraki, H. Mayaffre, M. Horvatić, C. Berthier, S. Uji, T. Yamaguchi, H. Tanaka, A. Kobayashi, H. Kobayashi, and T. Takahashi, ⁷⁷Se NMR evidence for the Jaccarino–Peter mechanism in the field induced superconductor, $\lambda$ -(BETS)₂FeCl₄, J. Phys. Soc. Jpn. 76, 124708 (2007).
Hiraki et al. [2010] K.-I. Hiraki, M. Kitahara, T. Takahashi, H. Mayaffre, M. Horvatić, C. Berthier, S. Uji, H. Tanaka, B. Zhou, A. Kobayashi, and H. Kobayashi, Evidence of charge disproportionation in $\lambda$ -type BETS based organic superconductors, J. Phys. Soc. Jpn. 79, 074711 (2010).
Kobayashi et al. [2020b] T. Kobayashi, K. Tsuji, A. Ohnuma, and A. Kawamoto, Selective observation of spin and charge dynamics in an organic superconductor $\lambda$ -(BETS)₂GaCl₄ using ^69,71Ga NMR measurements, Phys. Rev. B 102, 235131 (2020b).
Pesotskii et al. [1999] S. Pesotskii, R. Lyubovskii, N. Kushch, M. V. Kartsovnik, W. Biberacher, K. Andres, H. Kobayashi, and A. Kobayashi, de Haas-van Alphen oscillations and angular magnetoresistance oscillations in the organic metal $\kappa$ -(BETS)₂GaCl₄, JETP 88, 114–117 (1999).
Pratt et al. [2003] F. Pratt, S. Blundell, I. Marshall, T. Lancaster, S. Lee, A. Drew, U. Divakar, H. Matsui, and N. Toyota, Polyhedron 22, 2307 (2003).
Montgomery et al. [1994] L. Montgomery, T. Burgin, J. Huffman, J. Ren, and M.-H. Whangbo, Synthesis, superconductivity, x-ray structure and electronic band structure of $\lambda$ -(BETS)₂GaCl₄, Physica C 219, 490 (1994).
Kobayashi et al. [1993] A. Kobayashi, T. Udagawa, H. Tomita, T. Naito, and H. Kobayashi, New organic metals based on BETS compounds with $MX$ ${}_{4}^{-}$ anions (BETS = bis(ethylenedithio)tetraselenafulvalene $M$ = Ga, Fe, In; $X$ = Cl, Br), Chem. Lett. 22, 2179 (1993).
Dressel and Drichko [2004] M. Dressel and N. Drichko, Optical properties of two-dimensional organic conductors: Signatures of charge ordering and correlation effects, Chem. Rev. 104, 5689 (2004).
Girlando [2011] A. Girlando, Charge sensitive vibrations and electron-molecular vibration coupling in bis(ethylenedithio)-tetrathiafulvalene (BEDT-TTF), J. Phys. Chem. C 115, 19371 (2011).
Painelli and Girlando [1986] A. Painelli and A. Girlando, Electron–molecular vibration (e–mv) coupling in charge‐transfer compounds and its consequences on the optical spectra: A theoretical framework, J. of Chem. Phys. 84, 5655 (1986).
Dressel and Grüner [2002] M. Dressel and G. Grüner, Electrodynamics of Solids (Cambridge University Press, Cambridge, 2002).
Olejniczak et al. [1996] I. Olejniczak, A. Graja, N. Kushch, P. Cassoux, and H. Kobayashi, Polarized ir reflectance studies of the organic conductor $\kappa$ -(BETS)₂FeCl₄, J. Phys. I France 6, 1631 (1996).
Sedlmeier et al. [2012] K. Sedlmeier, S. Elsässer, D. Neubauer, R. Beyer, D. Wu, T. Ivek, S. Tomić, J. A. Schlueter, and M. Dressel, Absence of charge order in the dimerized $\kappa$ -phase BEDT-TTF salts, Phys. Rev. B 86, 245103 (2012).
Maksimuk et al. [2001] M. Maksimuk, K. Yakushi, H. Taniguchi, K. Kanoda, and A. Kawamoto, The C=C stretching vibrations of $\kappa$ -(BEDT–TTF)₂Cu[N(CN)₂]Br and its isotope analogues, Journal of the Physical Society of Japan 70, 3728 (2001).
Note [1] There are some indications of a doublet at the high-frequency satellite, but these features are too weak to make a strong point.
Girlando et al. [2014] A. Girlando, M. Masino, J. A. Schlueter, N. Drichko, S. Kaiser, and M. Dressel, Charge-order fluctuations and superconductivity in two-dimensional organic metals, Phys. Rev. B 89, 174503 (2014).
Girlando et al. [2012] A. Girlando, M. Masino, S. Kaiser, Y. Sun, N. Drichko, M. Dressel, and H. Mori, Spectroscopic characterization of charge order fluctuations in BEDT-TTF metals and superconductors, phys. stat. sol. (b) 249, 953 (2012).
Foury-Leylekian et al. [2018] P. Foury-Leylekian, V. Ilakovac, V. Balédent, P. Fertey, A. Arakcheeva, O. Milat, D. Petermann, G. Guillier, K. Miyagawa, K. Kanoda, P. Alemany, E. Canadell, S. Tomic, and J.-P. Pouget, (BEDT-TTF)₂Cu₂(CN)₃ spin liquid: Beyond the average structure, Crystals 8, 528 (2018).
Sanz Alonso [2016] M. Sanz Alonso, Effect of disorder on the optical propertiesof organic quantum spin-liquid compounds (2016).
Ward et al. [2000] B. H. Ward, J. A. Schlueter, U. Geiser, H. H. Wang, E. Morales, J. P. Parakka, S. Y. Thomas, J. M. Williams, P. G. Nixon, R. W. Winter, G. L. Gard, H.-J. Koo, and M.-H. Whangbo, Comparison of the crystal and electronic structures of three 2:1 salts of the organic donor molecule BEDT-TTF with pentafluorothiomethylsulfonate anions SF₅CH₂SO ${}_{3}^{-}$ , SF₅CHFSO ${}_{3}^{-}$ , and SF₅CF₂SO ${}_{3}^{-}$ , Chem. Mater. 12, 343 (2000).
Schlueter et al. [2001] J. A. Schlueter, B. H. Ward, U. Geiser, H. H. Wang, A. M. Kini, J. Parakka, E. Morales, H.-J. Koo, M.-H. Whangbo, R. W. Winter, J. Mohtasham, and G. L. Gard, Crystal structure, physical properties and electronic structure of a new organic conductor $\beta^{\prime\prime}$ -(BEDT-TTF)₂SF₅CHFCF₂SO₃, J. Mater. Chem. 11, 2008 (2001).
Dressel et al. [2012] M. Dressel, M. Dumm, T. Knoblauch, and M. Masino, Comprehensive optical investigations of charge order in organic chain compounds (TMTTF)₂ $X$ , Crystals 2, 528 (2012).
Knoblauch and Dressel [2012] T. Knoblauch and M. Dressel, Charge disproportionation in (TMTTF)₂ $X$ ( $X$ = PF₆, AsF₆ and SbF₆) investigated by infrared spectroscopy, phys. stat. sol. (c) 9, 1158 (2012).
Rösslhuber et al. [2018] R. Rösslhuber, E. Rose, T. Ivek, A. Pustogow, T. Breier, M. Geiger, K. Schrem, G. Untereiner, and M. Dressel, Structural and electronic properties of (TMTTF)₂ $X$ salts with tetrahedral anions, Crystals 8, 121 (2018).
Pustogow et al. [2016] A. Pustogow, T. Peterseim, S. Kolatschek, L. Engel, and M. Dressel, Electronic correlations versus lattice interactions: Interplay of charge and anion orders in (TMTTF)₂ $X$ , Phys. Rev. B 94, 195125 (2016).
Kobayashi et al. [1996] H. Kobayashi, H. Tomita, T. Naito, A. Kobayashi, F. Sakai, T. Watanabe, and P. Cassoux, New BETS conductors with magnetic anions (BETS = bis(ethylenedithio)tetraselenafulvalene), J. Am. Chem. Soc. 118, 368 (1996).
Mielke et al. [2001] C. Mielke, J. Singleton, M.-S. Nam, N. Harrison, C. C. Agosta, B. Fravel, and L. K. Montgomery, Superconducting properties and fermi-surface topology of the quasi-two-dimensional organic superconductor $\lambda$ -(BETS)₂GaCl₄ (BETS = bis(ethylene-dithio)tetraselenafulvalene), J. Phys.: Condens. Mat. 13, 8325 (2001).
Onari et al. [2004] S. Onari, R. Arita, K. Kuroki, and H. Aoki, Phase diagram of the two-dimensional extended hubbard model: Phase transitions between different pairing symmetries when charge and spin fluctuations coexist, Phys. Rev. B 70, 094523 (2004).
Vuletić et al. [2002] T. Vuletić, P. Auban-Senzier, C. Pasquier, D. Jćrome, M. Héritier, S. Tomić, and K. Bechgaard, Coexistence of superconductivity and spin density wave orderings in the organic superconductor (TMTSF)₂PF₆, Eur. Phys. J. B 25, 319 (2002).
Nagata et al. [2013] S. Nagata, M. Misawa, Y. Ihara, and A. Kawamoto, Commensurability of the spin-density-wave state of $(\mathrm{TMTSF})_{2}\mathrm{PF}_{6}$ observed by ¹³C-NMR, Phys. Rev. Lett. 110, 167001 (2013).
Gerasimenko et al. [2014] Y. A. Gerasimenko, S. V. Sanduleanu, V. A. Prudkoglyad, A. V. Kornilov, J. Yamada, J. S. Qualls, and V. M. Pudalov, Coexistence of superconductivity and spin-density wave in (TMTSF)₂ClO₄: Spatial structure of the two-phase state, Phys. Rev. B 89, 054518 (2014).
Narayanan et al. [2014] A. Narayanan, A. Kiswandhi, D. Graf, J. Brooks, and P. Chaikin, Coexistence of spin density waves and superconductivity in (TMTSF)₂PF₆, Phys. Rev. Lett. 112, 146402 (2014).
Pouget, J. P. and Ravy, S. [1996] Pouget, J. P. and Ravy, S., Structural aspects of the bechgaard salts and related compounds, J. Phys. I France 6, 1501 (1996).
Pouget and Ravy [1997] J. Pouget and S. Ravy, X-ray evidence of charge density wave modulations in the magnetic phases of (TMTSF)₂PF₆ and (TMTTF)₂Br, Synt. Met. 85, 1523 (1997).
Mazumdar et al. [1999] S. Mazumdar, S. Ramasesha, R. Torsten Clay, and D. K. Campbell, Theory of coexisting charge- and spin-density waves in (TMTTF)₂Br, (TMTSF)₂PF₆, and $\alpha$ -(BEDT-TTF)₂ $M$ Hg(SCN)₄, Phys. Rev. Lett. 82, 1522 (1999).
Clay and Mazumdar [2019] R. Clay and S. Mazumdar, From charge- and spin-ordering to superconductivity in the organic charge-transfer solids, Phys. Rep. 788, 1 (2019).
Li et al. [2019] W. Li, A. Pustogow, R. Kato, and M. Dressel, Transition of a pristine mott insulator to a correlated fermi liquid: Pressure-dependent optical investigations of a quantum spin liquid, Phys. Rev. B 99, 115137 (2019).
Pustogow et al. [2021] A. Pustogow, R. Rösslhuber, Y. Tan, E. Uykur, A. Böhme, M. Wenzel, Y. Saito, A. Löhle, R. Hübner, A. Kawamoto, J. A. Schlueter, V. Dobrosavljević, and M. Dressel, Low-temperature dielectric anomaly arising from electronic phase separation at the mott insulator-metal transition, npj Quantum Materials 6, 9 (2021).
Rösslhuber et al. [2021] R. Rösslhuber, A. Pustogow, E. Uykur, A. Böhme, A. Löhle, R. Hübner, J. A. Schlueter, Y. Tan, V. Dobrosavljević, and M. Dressel, Phase coexistence at the first-order mott transition revealed by pressure-dependent dielectric spectroscopy of $\kappa$ -(BEDT-TTF)₂Cu₂(CN)₃, Phys. Rev. B 103, 125111 (2021).
Hashimoto et al. [2015] K. Hashimoto, R. Kobayashi, H. Okamura, H. Taniguchi, Y. Ikemoto, T. Moriwaki, S. Iguchi, M. Naka, S. Ishihara, and T. Sasaki, Emergence of charge degrees of freedom under high pressure in the organic dimer-mott insulator $\beta^{\prime}$ -(BEDT-TTF)₂ICl₂, Phys. Rev. B 92, 085149 (2015).
Mori et al. [1990] H. Mori, S. Tanaka, M. Oshima, G. Saito, T. Mori, Y. Maruyama, and H. Inokuchi, Crystal and electronic structures of (BEDT–TTF)₂[ $M$ Hg(SCN)₄]( $M$ =K and NH₄), Bull. Chem. Soc. Jpn. 63, 2183 (1990).
Dressel et al. [2003] M. Dressel, N. Drichko, J. Schlueter, and J. Merino, Proximity of the layered organic conductors $\alpha$ -(BEDT-TTF)₂ $M$ Hg(SCN)₄ ( $M$ =K, NH₄) to a charge-ordering transition, Phys. Rev. Lett. 90, 167002 (2003).
Dressel et al. [2005] M. Dressel, N. Drichko, and J. Merino, Evidence of charge ordering in the electronic spectra of two-dimensional organic conductors, Physica B 359-361, 454 (2005).
Drichko et al. [2006] N. Drichko, M. Dressel, C. A. Kuntscher, A. Pashkin, A. Greco, J. Merino, and J. Schlueter, Electronic properties of correlated metals in the vicinity of a charge-order transition: Optical spectroscopy of $\alpha$ -(BEDT-TTF)₂ $M$ Hg(SCN)₄ ( $M$ =NH₄, Rb, Tl), Phys. Rev. B 74, 235121 (2006).
Merino et al. [2006] J. Merino, A. Greco, N. Drichko, and M. Dressel, Non-fermi liquid behavior in nearly charge ordered layered metals, Phys. Rev. Lett. 96, 216402 (2006).
Kartsovnik et al. [1993] M. V. Kartsovnik, A. E. Kovalev, and N. D. Kushch, Magnetotransport investigation of the low-temperature state of transition (BEDT-TTF)₂TIHg(SCN)₄: Evidence for a Peierls-type transition, J. Phys. I France 3, 1187 (1993).
Christ et al. [2000] P. Christ, W. Biberacher, M. V. Kartsovnik, E. Steep, E. Balthes, H. Weiss, and H. Müller, Magnetic field-temperature phase diagram of the organic conductor $\alpha$ -(BEDT-TTF)₂KHg(SCN)₄, JETP Lett. 71, 303–306 (2000).
Andres et al. [2005] D. Andres, M. V. Kartsovnik, W. Biberacher, K. Neumaier, E. Schuberth, and H. Müller, Superconductivity in the charge-density-wave state of the organic metal $\alpha$ -(BEDT-TTF)₂KHg(SCN)₄, Phys. Rev. B 72, 174513 (2005).
Kawai and Kawamoto [2008] T. Kawai and A. Kawamoto, Charge disproportionation and inversion symmetry breaking in organic conductor $\alpha\text{$-$}{(\text{BEDT-TTF})}_{2}\text{RbHg}{(\text{SCN})}_{4}$ , Phys. Rev. B 78, 165119 (2008).
Ohnuma et al. [2018] A. Ohnuma, H. Taniguchi, Y. Takahashi, and A. Kawamoto, Density wave state in new $\alpha$ -type organic conductor, $\alpha$ -(BEDT-TTF)₂ $M$ Hg( $X$ CN)₄ ( $M$ = NH₄, $X$ = Se): A key material for universal phase diagram of $X$ = S and $X$ = Se systems, J. Phys. Chem. C 122, 24321 (2018).
Ohnuma and Kawamoto [2019] A. Ohnuma and A. Kawamoto, ¹³NMR study of charge fluctuations in $\alpha$ -(BEDT-TTF)MX salts (X=alkali metal; X=S, Se), Phys. Rev. B 100, 245107 (2019).

Charge imbalance in λ\lambda-(BETS)2GaCl4 and their interplay with superconductivity