Charge density wave and superconducting phase in monolayer InSe

In this work, both the electron- and hole-doped cases are studied within the jellium model for monolayer InSe. A compensate positive or negative background charge is included to guarantee the charge neutrality.
There are different experimental techniques like electrolytic gate Efetov and Kim (2010) to precisely control the rate of the electron and hole densities. Here, we consider electron doping levels $-0.1$ and $-0.2$ electron per formula unit (e/f.u.) precisely corresponding to the electron densities, $7.44\times 10^{13}$ and $1.46\times 10^{14}\,$ cm^-2 respectively. Similarly, $+0.01,+0.04$ (low doping regime), $+0.1,+0.2,+0.3$ and $+0.4$ e/f.u. (high doping regime) for hole-doped cases corresponding to $7.58\times 10^{12}$, $3.0\times 10^{13}$, $7.58\times 10^{13}$, $1.51\times 10^{14}$, $2.26\times 10^{14}$ and $3.0\times 10^{14}$ cm^-2 charge densities are considered. For the sake of simplicity, we promptly drop e/f.u. units corresponding to various doping levels, $+/-$ refers to the hole/electron doping, respectively.

The Fermi surfaces of the system are described in Fig. 1 for different doping levels. Figure 1(a) displays the topology of the Fermi surface for $-0.1$ doping consisting precisely of two types of electronic pockets located at the $\Gamma$ and $M$ points. In the case of the deeper electronic doping level $-0.2$, the specific form of the Fermi surface is similar to the previous doping level. The Fermi surface of the $+0.04$ doping system consists of six separated pockets located around a point between the $\Gamma$ and K as shown in Fig. 1 marked by the red color.

In the hole-doped case [see Fig. 1(b)] and upon more significantly decreasing the Fermi energy $E_{\rm F}$, a Lifshitz transition Zólyomi et al. (2014) occurs. Therefore, the topology of the Fermi surface with six pockets, located between $\Gamma$ and K, changes to two coaxial pockets around the $\Gamma$ point. This fundamental change of the principal character of the Fermi surface results in a tangible variation of the superconductive properties of the hole-doped system which we adequately address in the following. Moreover, this specific concentration is obtained to be equal to 5.8$\times 10^{13}\text{ cm}^{-2}$ or +0.076 e/f.u. which is in good agreement with that reported in Ref.Zólyomi et al. (2014). To begin with, we carefully look at the Eliashberg function in terms of various doping levels. Figures 2(a) and (b) depict the projected $\alpha^{2}\textbf{F}(\omega)$ and phonon DOS for doping level $-0.1$. The projected Eliashberg function along the in-plane and out-of-plane deformations show a mighty peak at around 27 meV related to a scattering process which originates primarily from $\alpha^{2}{\textbf{F}}_{\overline{z},\overline{xy}}+\alpha^{2}{\textbf{F}}_{\overline{z},\overline{z}}$ resulting from the out-of-plane vibration of In atoms and in-plane vibration of Se atoms. This is equally consistent with the projected $\textbf{F}(\omega)$ in Fig. 2(b), where there is a significant density of phonons with In_z and Se_xy deformations. Looking at more reduced energies there is a two-peak structure between $21-24$ meV, which comes from ${\alpha^{2}\textbf{F}}_{\overline{z},\overline{xy}}+{\alpha^{2}\textbf{F}}_{\overline{xy},\overline{xy}}$. On the other hand, peaks at more reduced energies originate from ${\alpha^{2}\textbf{F}}_{\overline{xy},\overline{xy}}$.

The $\alpha^{2}\textbf{F}(\omega)$ and $\textbf{F}(\omega)$ are shown in Figs. 2(c) and (d) for the low hole doping level $+0.01$. A peak around 28 meV comes principally from single optical phonon mode with out-of-plane In and in-plane Se vibrations. In this case, the deformation of ${\alpha^{2}\textbf{F}}_{\overline{z},\overline{z}}$ is considerably larger than ${\alpha^{2}\textbf{F}}_{\overline{z},\overline{xy}}$. Moreover, the lesser peak at around 26 meV has a major ${\alpha^{2}\textbf{F}}_{\overline{xy},\overline{xy}}$ and a minor ${\alpha^{2}\textbf{F}}_{\overline{z},\overline{z}}$ character with a negative contribution from ${\alpha^{2}\textbf{F}}_{\overline{z},\overline{xy}}$, while the strong peak at around 8 meV has a major ${\alpha^{2}\textbf{F}}_{\overline{z},\overline{xy}}$ character with relatively similar contributions from the other two deformations.

As a notable example of high a hole-doped regime, the $\alpha^{2}{\textbf{F}}(\omega)$ and projected ${\textbf{F}(\omega)}$ for $+0.1$ are shown in Figs. 2(e) and (f), respectively. Despite the low hole-doped and electron-doped cases, the prominent peak around 28 meV is absent. In general, the spectrum of $+0.1$ hole-doped is slightly shrunk in comparison with the $+0.01$ one. Moreover, the gapped two-peak structure in the high-energy part of the $\alpha^{2}\textbf{F}(\omega)$ for $+0.01$ is replaced with a gapless one at an energy of about 25-27 meV. The outstanding contribution of this high-energy part arises mainly from the ${\alpha^{2}\textbf{F}}_{\overline{z},\overline{z}}$ and ${\alpha^{2}\textbf{F}}_{\overline{xy},\overline{xy}}$ deformations, however, the ${\alpha^{2}\textbf{F}}_{\overline{z},\overline{xy}}$ has a completely negative contribution. The low-energy peak between 5-7 meV has almost an identical character to the low-energy peak of the $+0.01$ doping level, albeit with a lesser height. Therefore, the peak of $\alpha^{2}{\bf F}$ is shifted to lower energies by passing through the Lifshitz transition point (increasing hole doping levels). In addition, there is a tangible suppression of the proportion of the spectral weight of high-energy phonons to low-energy phonons. Such a modulation of optical phonons affects their superconductive properties, which mainly manifests itself in the suppression of $\omega_{log}$ (see Table. 1).

Looking at the cumulative $\lambda(\omega)$ in Figs. 2(a), (c) and (e), we can fairly state that in hole doping the acoustic branches carry out a more pronounced role in the formation of the $\lambda_{\text{tot}}$. Unlike the hole-doped cases, for electron doping, there is a more uniform distribution of each branch contributing in the formation of the $\lambda_{\text{tot}}$ for the electron doping, as inferred from $\lambda(\omega)$.
The tabulated amounts of $\lambda_{\text{tot}}$ with respect to various doped levels in Table. 1 reveal that increasing the hole/electron doping levels leads to a descending/constant behavior of $\lambda_{\text{tot}}$, respectively.

To perceive the correlation between the DOS at the Fermi energy $N(\varepsilon_{\rm F})$ and $\lambda$, we collect the results of Table. 1 into Fig. 3, where $\lambda$ and $N(\varepsilon_{\rm F})$ are shown for different doping levels. Upon progressively increasing the hole density, while $\lambda$ decreases monotonously, the $N(\varepsilon_{\rm F})$ increases up to doping level $+0.1$ then decreases for a larger doping level.

One can seemly remark that $\lambda$ can take an effect from $N(\varepsilon_{\rm F})$ and the average of the electron-phonon matrix elements on the Fermi surface, and effectively could be represented as $\lambda=2N(\varepsilon_{F})\langle|g|^{2}\rangle/\omega_{0}$, where $\langle|g|^{2}\rangle$ is an average electron-phonon interaction. Therefore, if one considers the $\lambda/N(\varepsilon_{\rm F})$, it will be possible to recognize that the proportion is about unity for all doping levels but, +0.01 and 0.1, for doping level 0.01 an enhancement of the average electron-phonon interaction is expected. To estimate the average electron-phonon interaction we use, $\displaystyle\langle|g|^{2}\rangle=\frac{1}{N(\varepsilon_{\rm F})}\int\alpha^{2}\textbf{F}(\omega)d\omega$, and the results of the $\langle|g|^{2}\rangle$ are presented in the inset of Fig. 3. As seen, the average electron-phonon interaction is enhanced for +0.01, compared to the other hole and electron doping levels. Thus, in general, a larger DOS results in a larger $\lambda$ with a linear dependency, with the only exception being the 0.01 doping level, where $\langle|g|^{2}\rangle$ is enhanced in comparison with the other doping levels where it is almost constant.

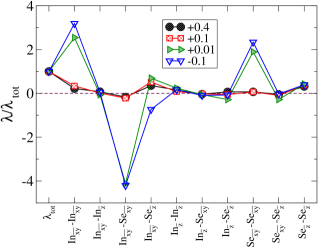
Furthermore, Eq. (10) is used to carefully consider the contribution of the projected $\lambda$ for different atom types and the out-of/in-plane directions in the $\lambda_{\text{tot}}$. Figure 4 shows the projected $\lambda$ while those are rescaled to the $\lambda_{\text{tot}}$ for four doping levels $-0.1,+0.01,+0.1$ and $+0.4$. The desired results show, for the electron-doped case, the highest contribution to the $\lambda_{\text{tot}}$ is attributed to the in-plane displacements. For $-0.1$ the corresponding in-plane/out-of-plane contributions are ${\lambda_{\overline{xy},\overline{xy}}}=0.73>\lambda_{\overline{z},\overline{z}}=0.27>\lambda_{\overline{z},\overline{xy}}=-0.45$.

For the hole-doped levels beyond +0.1, on the other hand, the largest contribution arises from the out-of-plane deformations and mixed in-plane In and out-of-plane Se deformations. For doping level +0.1 the projected $\lambda$s read, ${\lambda_{\overline{z},\overline{z}}}=2.73>\lambda_{\overline{z},\overline{xy}}=2.7>\lambda_{\overline{xy},\overline{xy}}=1.55$.

In the case of +0.01 doping, the system is somewhere between a greater hole doping and the electron-doped cases. While its in-plane contributions share the same behavior as of the electron-doped one; its out-of-plane and mixed in-plane/out-of-plane contributions behave properly similar to the high doping levels, ${\lambda_{\overline{z},\overline{z}}}=2.88>\lambda_{\overline{xy},\overline{xy}}=2.48>\lambda_{\overline{z},\overline{xy}}=2.26$. To be specific, the valuable contribution which comes from (In${}_{\overline{xy}}\,$-Se${}_{\overline{z}}$) deformation has a negative impact for the electron-doped system, while it has a positive contribution for low and high hole-doped cases. This key difference originates from the distinction between the generic forms of the topology of the Fermi surface such that this type of polarization is beneficial for hole-doped cases and it is a disadvantage for the electron-doped ones.

In addition, Table 1 shows the critical transition temperature to the superconducting phase with the aforementioned doped conditions calculated through Eq. (3) by considering three values for $\mu^{*}_{c}=0.1,\,\,0.15\text{ and }0.2$. In the case of hole doping, the highest value of $T_{c}=65$ K is obtained for $\mu^{*}_{c}=0.1$. Our results reveal that $T_{c}$ can be shrunk about 20 percent when $\mu^{*}_{c}=0.2$ was applied. Obviously, while the amount of $\lambda$ is almost the same for the first three hole-doped cases, the $T_{c}$ for $+0.01$ is larger than that of $+0.1$ (by considering $\mu^{*}_{c}=0.1$); stemming from a larger value of $\omega_{\text{log}}$. The larger value of the $\omega_{\text{log}}$ corresponding to the former originates from the fact that the phonon dispersion for $+0.01$ doped is typically harder than $+0.1$. Moreover, the proportion of the high energy peak to the low-energy peak of $\alpha^{2}\textbf{F}$ for the case of +0.01 is appreciably larger than that of $+0.1$ (see Figs. 2(c) and (e)). Thus, $\omega_{\text{log}}$ is enhanced for $+0.01$ in comparison with $+0.1$.

Notice that the highest tabulated temperature is comparable with $T_{c}=88$ K for blue phosphorene studied in Ref. Esfahani and Asgari (2017). Moreover, it is much larger than the reported $T_{c}$ for Li-decorated monolayer graphene and antimonene with $T_{c}\approx 6$ Ludbrook et al. (2015) and $4\,$ K Lugovskoi et al. (2019b), respectively. However, the high value of $\lambda$ needs a careful examination and further insights into the formation of the CDW phase at low temperatures for the hole-doped system which we adequately address in the following section.

To have a better estimate of $T_{c}$, we utilize a self-consistent solution of the anisotropic the Migdal-Eliashberg theory. The results are reported in Table. 2. Obviously, anisotropic effects alter $T_{c}$ at the first three hole-doped cases, where the Fermi surface has a more pronounced anisotropic character (see Fig. 1(b)), while a slight variation of $T_{c}$ is observed for other hole- and electron-doped cases when $T_{c}$s are extracted from Allen-Dynes formula ( Eq. 3) and self-consistent anisotropic Eliashberg equations. These results indicate that below the Lifshitz transition point, in comparison with the Allen-Dynes estimate, the $T_{c}$ is more pronounced in comparison with the cases above the Lifshitz transition point as well as the electron doped levels. For the +0.04 doping level, such an anisotropy can enhance $T_{c}$ from a range 42-55 K corresponding to the Allen-Dynes estimate to 62-75 K for different applied $\mu^{*}_{c}$.

More reduction in the electronic temperature to achieve $T_{CDW}$ is alongside the giant amplitude of the Kohn anomaly. To acquire an estimate of $T_{CDW}$, we extract the frequency of the most softened mode on the whole $q$-mesh, for different temperatures, then we fit the extracted frequencies to $\omega=a_{0}(T-T_{CDW})^{\delta}$Duong et al. (2015). In our calculations, $a_{0}$ is a constant close to 0.4 and $\delta$ yields values in the range 0.40-0.43 for all hole doping levels which are partly close to the value $\delta=0.5$ extracted from the mean-field approximation Duong et al. (2015); Gruner (1994). Figure 5 shows the variation of the phonon frequencies as a function of electronic temperature and related fitting curves (red dashed lines) for case +0.3 in both adiabatic and non-adiabatic regimes. The results indicate that the transition to the CDW region occurs in $T_{CDW}^{A}=476$ K and $T_{CDW}^{NA}=246$ K. The values of $T_{CDW}$ corresponding to other doping levels, for both adiabatic and non-adiabatic regimes are reported in Table 2.

Figure 6 depicts the amplitude of the Kohn anomaly as a function of the electronic Fermi-Dirac smearing for doping level +0.1. Typically decreasing the temperature leads to a more softening of the phonon energies and finally, the system suffers from a CDW instability at a smearing slightly lower than 416 K. For exploring the considerable variations of the phonon softening as a function of the Fermi-Dirac smearing, three upper temperatures, 420, 470 and 1580, in the adiabatic/static regime are depicted. The typical smearing 1580 K, as a starting point in the adiabatic regime, is large enough to wipe out the Kohn anomaly in the linear response calculations. In addition, this figure shows there are two $\textbf{q}_{CDW}$ which give rise to two different chiralities. One includes a $6\times 6$ commensurate supercell corresponding to the dip in the middle of the $\Gamma$-$K$ direction. The secondary point of the CDW instability is related to an incommensurate distortion precisely corresponding to another dip along the $\Gamma$-$M$ path. Our numerical calculations reveal that the dip in the middle of the $\Gamma$-K direction has a lower $\omega$ and we, therefore, refer to this point as $\textbf{q}_{CDW}$ in the reminder. Notice that for the other higher doped levels, i.e. $+0.2$ and $+0.3$, the CDW forms at the same q for the +0.1 doping level. On the other hand, in the adiabatic regime, low hole doping levels +0.01 and +0.04 show instability in a q marginally different from the high doped regime. However, it does not show any instability of the system even at extremely low temperatures by including non-adiabatic effects as illustrated in Table 2. Besides, in the comparison between low doped and high doped regimes in terms of phonon softening at $\textbf{q}_{CDW}$, we therefore report our results at $\textbf{q}_{CDW}$ for doping levels $+0.01$ and $+0.04$ as well.

Figure 7 shows different quantities associated with the CDW formation for various doping levels and temperatures. In particular, the average amounts of the electron-phonon interaction $\langle\textbf{g}^{2}\rangle_{\textbf{q}\nu}=\frac{\gamma_{\textbf{q}\nu}}{2\pi\omega_{\textbf{q}\nu}\xi_{\bf q}}$, where the nesting function is precisely defined as $\xi_{\bf{q}}={N}^{-1}_{{\bf k}}\sum_{mn,{\bf k}}\delta(\varepsilon_{n{\bf k}}-\varepsilon_{F})\delta(\varepsilon_{m{\bf{k}}+{\bf{q}}}-\varepsilon_{F})$, is properly used. The tilde symbol in Fig. 7 refers to the related calculations at the $\textbf{ q}_{CDW}$. Moreover, the depicted quantities are associated with the softened branch at $\textbf{q}_{CDW}$, therefore, the branch index $\nu$ is dropped.

The effects of phonon energy renormalization as a function of temperature within the adiabatic/static regime are shown in Fig. 7(a). These results reveal the tendency of the system to the CDW region for the three $+0.1,\;+0.2$, and $+0.3$ doping levels. On the contrary, the electron-doped and low hole doping levels, below the Lifshitz transition point, almost retain their constant behavior as a function of various temperatures. Figure 7(b) shows the bare susceptibility as a function of doped levels at the $\textbf{q}_{CDW}$ for the aforementioned temperatures. Notice that the $\langle{\tilde{\textbf{g}}}^{2}\rangle$ is the largest for doping level $+0.2$ (see Fig. 7(d)), in addition, the largest change of the $\chi_{0}$ basically belongs to the doping level $+0.2$. This leads to a further decline of $2\tilde{\omega}\tilde{\Pi}$ (from a temperature of 1580 K) for doping level $+0.2$ as shown in Fig. 7(c). Moreover, such a larger variation in the $\chi_{0}$ for doping levels $+0.1,\;+0.2$, and $+0.3$ leads to a giant Kohn anomaly and finally the appearance of the instability in monolayer InSe for smearing lower than 416, 539 and 476 K, respectively. A comparison for doping $+0.4$ implicitly expresses that though there is a reduction of the self-energy correction, having less temperature dependence on $\chi_{0}$ together with a smaller average of $\langle{\tilde{\textbf{g}}}^{2}\rangle$ (Fig. 7(d)) on the Fermi surface, results in less effective Kohn anomaly and therefore, the CDW is suppressed at $\textbf{q}_{CDW}$ for doping level $+0.4$.

Further analyses associated with the polarization of the softened mode at $\textbf{q}_{CDW}$ adequately explain the instability at this point mainly involves the in-plane displacements of the In atoms and the out-of-plane displacements of the Se atoms at the same time.

The notable absence of the Kohn anomaly for an electron doping is owing to the lack of a reduction of the $\chi_{0}$ with respect to the different temperatures alongside an extremely small $\langle{\tilde{\textbf{g}}}^{2}\rangle$ (Fig. 7(d)). In two low hole doping cases, $\langle{\tilde{\textbf{g}}}^{2}\rangle$ is smaller than that obtained for other hole-doped levels. For doping level $+0.01$ a specific combination of a small $\langle{\tilde{\textbf{g}}}^{2}\rangle$ and the lack of typically decreasing of $\chi_{0}$ as a function of temperature results in the absence of the Kohn anomaly at ${\bf q}_{CDW}$. In doping level $+0.04$, although there is a depletion in $\chi_{0}$ upon temperature reduction, due to a slight value of $\langle{\tilde{\textbf{g}}}^{2}\rangle$, it sufficiently shows a smaller softening.

Therefore, considering the adiabatic regime, competition and coexistence between $T_{c}$ and $T_{CDW}$, reveals that $T_{CDW}$ is exceedingly greater than $T_{c}$ and consequently, the CDW instability prevents access to the high-temperature superconductivity in the first five hole-doped cases +0.01, +0.04, +0.1, +0.2 and +0.3. On the other hand, in the intra-sheet scattering process, when $|\varepsilon_{\textbf{k+q}}-\varepsilon_{\textbf{k}}|\approx\omega$, the substantional difference of the non-adiabatic and adiabatic frequencies is $\Delta\omega$ which approximately specifies $\Delta\omega\simeq N(\varepsilon_{\rm F})\langle{\tilde{\textbf{g}}}^{2}\rangle$ at the Fermi surface Novko et al. (2019); Saitta et al. (2008); Lazzeri and Mauri (2006). Hence, this proper discrepancy is remarkable for the doping cases $+0.01,+0.04,+0.1,+0.2$ and $+0.3$ encompassing large amounts for both the $N(\varepsilon_{\rm F}$) and $\langle{\tilde{\textbf{g}}}^{2}\rangle$; essentially restating the considerable importance of the non-adiabatic effects for these hole-doped cases.

Figure 8 shows non-adiabatic effects on phonon modes in the case of $+0.1$ doping for two low temperatures ($T_{0}$ = 130 and 470 K) together with a high enough temperature ($T_{1}$ = 1580 K). In order to perceive the effect of the phonon softening on $T_{c}$, $T_{0}$ = 130 K is chosen such that it is slightly larger than $T_{CDW}^{NA}$ = 120 K. Employing non-adiabatic phonons at $T_{0}$ = 130 K for the calculation of $T_{c}$ results in a slight enhancement of $T_{c}$ = 57 K within anisotropic Eliashberg theory, which still is much smaller than $T_{CDW}^{NA}$ = 120 K. This lack of enhancement of $T_{c}$ could be understood based on Allen-Dynes estimation of $T_{c}$, as softening related to phonon modes is accompany with shift of $\alpha^{2}\textbf{F}$ to the lower frequencies, $T_{0}$ = 130 K, in particular in acoustic branches (see Fig.8(b)). This softening results in both remarkable enhancement of $\lambda$ and suppression of $\omega_{\text{log}}$ at the same time which finally leads to a little enhancement of $T_{c}$. Notice that the amplitude of the Kohn anomaly decreases in the presence of non-adiabatic effects as one may compare the phonon dispersion corresponding to electronic broadening at $470$ K in Figs. 6 and 8.

In addition, the same calculations are repeated for doping $+0.2$ and $+0.3$. Applying the non-adiabatic effects on the phonon modes in two cases $+0.2$ and $+0.3$ at temperatures slightly above their $T_{CDW}^{NA}$ reveal a negligible enhancement of the superconducting transition temperature, $T_{c}$ = 26, 15 K respectively. This slight enhancement of $T_{c}$ is simultaneous with a considerable suppression of $\omega_{\text{log}}$ = 36, 36 K respectively.

Consequently, non-adiabatic effects shift only the CDW region to lower temperatures 120, 191 and 246 K for elevated doping levels $+0.1,+0.2$ and $+0.3$, respectively, and are not capable of suppressing the formation of the CDW instability in these three cases. Therefore, it appears that the superconducting transition for the three mentioned hole doping levels is unlikely to be accessible as a CDW phase forms before a superconductive phase. On the other hand, Table 2 shows no dynamic instability at the remaining doped levels in the presence of non-adiabatic effects.

In Fig. 9 the high temperature phonon dispersion, $T_{1}$ = 1580 K, and non-adiabatic low temperature one with $T_{0}^{NA}=16$ K are plotted along with their corresponding $\alpha^{2}\textbf{F}$ for hole doping level +0.01. The system is stable even for temperatures considerably smaller than its $T_{c}\,\approx$ 54-73 K (see Table 2). Notice that the $\alpha^{2}\textbf{F}$ calculated based on non-adiabatic phonons gives marginally different $T_{c}$ as small as 2 K, owing to the slight softening at certain q points. Accordingly, the low hole-doped monolayer InSe likely shows a superconductive phase with maximum $T_{c}\sim 75$ K. The same analysis holds for hole doping level +0.04, where $T^{NA}_{CDW}$ is far below its $T_{c}$ as it is shown in Tables 1 and Table 2.

Note that the convergence of Eq. (13) for $\eta$ is carefully checked to adequately explain this equation becomes practically $\eta$-independent when $\eta$ was changed in the range of 0.0015-0.015 Ry. In addition, the desired results reported in Table 2 show that in the presence of the non-adiabatic effects, monolayer InSe is dynamically stable for all aforesaid doped levels at room temperature because all $T_{CDW}^{NA}$s are lower than room temperature.