These authors contributed equally to this work. \equalcontThese authors contributed equally to this work.
[1,5]\fnmErika \surKawakami
1]\orgdivRIKEN Center for Quantum Computing, \orgnameRIKEN, \orgaddress\street2-1 Hirosawa, \cityWako, \postcode351-0198, \stateSaitama, \countryJapan
2]\orgdivDepartment of Applied Sciences, \orgnameDelft University of Technology, \orgaddress\streetLorentzweg 1, \cityDelft, \postcode2628 CJ, \countryThe Netherlands
3]\orgdivPhysics of Quantum Fluids and Crystals, \orgnameB. Verkin Institute for Low Temperature Physics and Engineering of the National Academy of Sciences of Ukraine, \orgaddress\street47 Nauky Ave., \cityKharkiv, \postcode61103, \stateKharkiv, \countryUkraine
4]\orgdivInstitute of Physics, \orgnameKazan Federal University, \orgaddress\street16a Kremlyovskaya St., \cityKazan, \postcode420008, \stateRepublic of Tatarstan, \countryRussian Federation
5]\orgdivCluster for Pioneering Research, \orgnameRIKEN, \orgaddress\street2-1 Hirosawa, \cityWako, \postcode351-0198, \stateSaitama, \countryJapan
Characterization of Tunnel Diode Oscillator for Qubit Readout Applications
Abstract
We developed a tunnel diode oscillator and characterized its performance, highlighting its potential applications in the quantum state readout of electrons in semiconductors and electrons on liquid helium. This cryogenic microwave source demonstrates significant scalability potential for large-scale qubit readout systems due to its compact design and low power consumption of only 1 W, making it suitable for integration on the 10 mK stage of a dilution refrigerator. The tunnel diode oscillator exhibits superior amplitude stability compared to commercial microwave sources. The output frequency is centered around 140 MHz, commonly used for qubit readout of electrons in semiconductors, with a frequency tunability of 20 MHz achieved using a varactor diode. Furthermore, the phase noise was significantly improved by replacing the commercially available voltage source with a lead-acid battery, achieving a measured phase noise of -115 dBc/Hz at a 1 MHz offset.
keywords:
electrons, qubit readout, cryogenic electronics, tunnel diode1 Introduction
One of the key features required to realize a fault-tolerant scalable quantum computer is the integration of energy-efficient and reliable qubit control and readout electronics. Recently, qubit control electronics have been successfully integrated using cryogenic Complementary Metal-Oxide-Semiconductor (CMOS) technology [1, 2, 3, 4, 5] , and superconducting Josephson-junction [6]. Here, we focus on developing the readout electronics using tunnel-diode oscillator [7, 8] (TDO) circuits. TDO uses a tunnel diode as a negative resistance element [9], generating a microwave signal when connected to an LC circuit. Comparable to cryogenic CMOS devices (typical power consumption: 10 mW [2, 3, 4, 10, 11, 5]) and superconducting Josephson-junction circuits (100 W [6]), the TDO presented here exhibits significantly lower power dissipation, consuming only 1 W.
The motivation of this research is to develop a technique that enables scalable qubit read-out schemes for quantum computers operating at cryogenic temperatures. The conventional method, illustrated in Fig. 1(a), is to generate a microwave signal with a room-temperature (RT) microwave source and send it to a resonator dispersively coupled to the qubit at 10 mK. The amplitude and phase of the reflected microwave signal depend on the qubit state, allowing us to determine the qubit state through measurement. This method is commonly used for qubits made from electrons in semiconductors [12, 13, 14, 15, 16] and a similar method has been proposed for electrons on helium [17].

As the input signal is generated at RT, attenuators are placed at 4K to reduce thermal noise from RT reaching the qubit. To prevent the reflected output signal from being overwhelmed by thermal noise at RT, it must be amplified at cryogenic temperatures. Cryogenic amplifiers typically have a lower noise figure, resulting in a higher signal-to-noise ratio. The resonant frequency of the resonator is typically in the range of 100 MHz to 2 GHz [18, 19, 15], and such high-frequency signals are transmitted through coaxial cables. A major scalability issue arises as the number of qubits increases because each qubit requires its own coaxial cable, which are relatively thick (diameter 1 cm) with attenuators and amplifiers also taking up the limited space inside a cryogenic refrigerator (diameter 10-100 cm). Multiplexing can reduce the number of coaxial cables to some extent, but is limited by the resonator bandwidth [20].
To address this challenge, we propose placing the microwave source closer to the qubits. By integrating the microwave source and qubits on the same board, we can replace bulky coaxial cables with compact on-board transmission lines. This integration significantly reduces the circuit’s size, making it more suitable for scaling up the number of qubits. Since the qubits must be operated at cryogenic temperatures (typically 10 mK), the microwave source must also function at the same temperatures. In this regard, the TDO we developed operates at the same temperature as the qubit, which gives it an advantage over cryogenic CMOS devices which should be placed at 4 K due to its high power consumption [1, 2, 3, 4, 5]. CMOS technology offers the advantage of high output power; however, such high power is not necessary for qubit readout applications.
The TDO we developed is compact, with a size of approximately (Fig. 2(a)), and could be further miniaturized. It is powered by a DC voltage supplied through DC lines. For these scenarios, an analog-to-digital converter (ADC) at cryogenic temperatures [21] (Fig. 1(b)) can be placed to remove the need for co-axial cables on the resonator output lines as well. This approach would enable faster quantum error correction [22] feedback without the need to transmit signals to RT. Only the final computation results would need to be transmitted to RT. Placing the ADC at cryogenic temperatures also eliminates the need for amplifiers, as thermal noise at RT would no longer be a concern.
In this work, we first focus on the characterization of the TDO without utilizing an ADC or a resonator coupled to qubits (Fig. 1(c)). This initial step allows us to evaluate the performance and stability of the TDO as a standalone device under cryogenic conditions, providing a foundation for future integration with qubits.
2 Tunnel Diode Oscillator
We use the commercial BD-6 Ge-backward tunnel diode (General Electric) because it has the lowest power consumption among the commercially available options. TDOs with backward tunnel diodes demonstrate frequency stability of 0.001 ppm [8, 23]. Utilizing this precision, TDOs with backward tunnel diodes have been employed in the past to investigate various physical properties, such as paramagnetic susceptibility in salts [24], penetration depth in superconductors [25, 26], and the melting point of 3He [27]. These results were obtained with long integration times using a frequency counter, whereas qubit readout demands precise measurements within shorter durations. This emphasises the need to understand the frequency and amplitude stability achievable over shorter integration times. Furthermore, the oscillation frequencies, typically around 10 MHz [24, 28, 25, 26, 29, 30], are relatively low for qubit readout applications. In the early stages of testing qubit readout, it is also desirable to have the capability to externally tune the frequency. To address this issue, we developed a TDO operating at around 140 MHz utilizing a microfabricated superconducting spiral inductor, and by incorporating a varactor diode as a variable capacitor, we achieved a frequency tunability of 20 MHz without altering the amplitude.

We measured 62 different BD-6 diodes and observed a wide variation in parasitic capacitance, ranging from 1.3 pF to 29.4 pF, while the peak and valley points of their I-V characteristics remained relatively consistent. For high frequency oscillation, selecting a BD-6 with low parasitic capacitance is preferable. The tunnel diode used in this study has a parasitic capacitance of approximately 7 pF for the voltage applied to the tunnel diode (TD) V. Here, we use the microfabricated 15-turn Nb spiral coil as an inductor, which was separately measured to be 95 nH at 4 K. When a solenoid coil made of normal metal with a similar inductance value was used as the inductor, oscillation could not be observed. We deduce this was because the oscillation frequency approached the self-resonant frequency of the solenoid coil inductor. This is why we employed the micro-scale spiral inductor, as it reduces the parasitic capacitance and increases the self-resonant frequency to overcome this limitation. Furthermore, by employing a superconducting material, the Q-factor of the inductor was enhanced, enabling oscillation from the TDO at around 140 MHz. Relatively high frequencies, around 100 MHz, have been achieved using a different approach based on a toroidal LC resonator [31]. However, due to its bulky nature, this approach is unsuitable for scalable qubit applications.
Fig. 2(a,b) shows the details of the developed circuit. The part enclosed by the pink line represents the TDO, which consists of the Nb spiral inductor and a variable capacitance formed by a varactor diode (MA46H201, MACOM). The varactor diode allows tuning of the LC resonator’s capacitance, thereby varying the oscillation frequency of the TDO. The varactor diode is biased via DC port 2 using a DC voltage source (Yokogawa GS200). The oscillation signal is coupled to the pickup coil with a coupling ratio of 15:1.5. In previous work [24, 28, 25, 26, 29, 30], the signal was extracted capacitively from the same line used to provide the DC bias to the tunnel diode. Instead, in this work, the signal is extracted inductively. This approach is taken to dedicate the DC bias line solely to providing the DC bias, thereby avoiding interference with filters and other components further along the line. As a result, a more stable DC bias can be supplied to the tunnel diode. The tunnel diode is biased via DC port 1 using either the Yokogawa GS200 or a lead-acid battery. After the pickup coil, the signal is sent to AC port II and measured at RT. It is also routed through a directional coupler (ZEDC-15, Mini-Circuits). The coupling from the coupling port to the input/output port of the ZEDC-15 is 20 dB, as measured separately at 4 K. The signal from the coupler is amplified at 4 K with a cryogenic amplifier (CMT-BA1, Cosmic Microwave Technology) before being sent to RT.
The part enclosed by the green line in Fig. 2(a, c) represents the resonator, which can be coupled to a qubit. In this work, the resonator’s resonant frequency is set far outside the TDO’s operating range, allowing it to act as a high-impedance element and remain unused. The signal output from the coupler is sent to a cryogenic low-noise amplifier (CMT-BA1, Cosmic Microwave Technology) at 4 K and is measured at RT using a spectrum analyzer or a digital oscilloscope.
As shown in Fig. 2(c), the operating point of the tunnel diode BD-6, where it exhibits negative resistance and oscillates, is approximately and , resulting in a power consumption of about .
3 Frequency and power tunability
In this section, we demonstrate that the output power and frequency can be controlled by varying the voltage applied to the tunnel diode and that the frequency can be independently adjusted by varying the voltage applied to the varactor diode. The frequency variation due to the voltage applied to the tunnel diode (TD) is shown in Fig. 3(a). The capacitance of the TD, , is voltage-dependent because the distance of the depletion layer in the p-n junction changes as a function of . It is given by [7], where V is the diffusion potential (estimated from a measurement), and the equation has been fitted, as shown by the dashed lines, where represents the sum of the parasitic capacitance of the circuit board and the capacitance of the varactor diode. The fitting results give pF and pF at 11 mK, and pF and pF at 3.4 K. Fig. 3(b) demonstrates that the output power can be adjusted by approximately 20 dB through tuning because the operating point of the tunnel diode shifts along its I-V curve. The microwave power that would be delivered to the resonator is around -90 dBm, which is comparable to the optimized power range or qubit readout of electrons used as qubits in semiconductors [32].
Fig. 3(c) shows the frequency tunability as a function of . Considering the additional changes due to , we observe a total frequency tunability of 20 MHz. From this, we estimated that varies from 4.2 pF at V to 6.3 pF at V. Fig. 3(d) shows that for V, the output power remains unaffected by , indicating that the resistive component of the varactor remains unchanged (leakage current stays significantly small within this voltage range as seen in Fig. 6). Please note that we have observed a change in output power when is varied within the same voltage range at RT when using a similar circuit with a normal coil inductor. We attribute this difference to the fact that the leakage current becomes significantly suppressed at low temperatures.

4 Phase noise
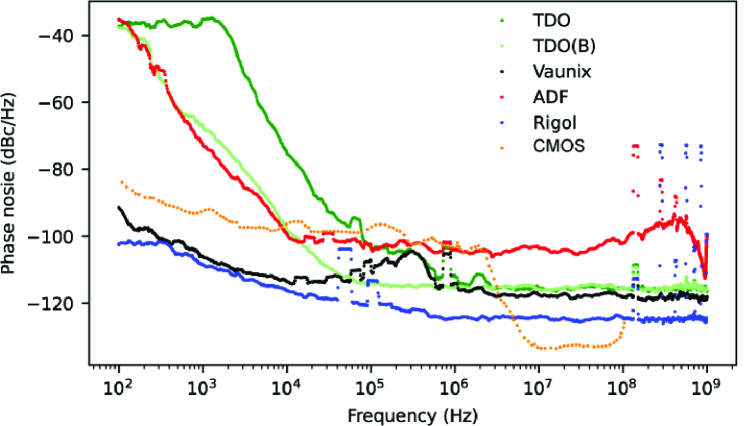
In this section, we report the phase noise of the signal from the TDO operating at 11 mK through port AC I using a spectrum analyzer (R&S FSV3030). Additionally, we sent the signal from the commercial microwave source through port AC II and measured the phase noise of the reflected signal through port AC I. The results are compared and shown in Fig. 4. Note that the phase noise of the commercial microwave source, measured directly on the spectrum analyzer without routing it to the device at low temperature, showed identical results. This indicates that the measured phase noise originates from the microwave sources and not from the device at low temperature.
We found that using a lead-acid battery to bias the TDO instead of the Yokogawa GS200 improves the phase noise as shown in Fig. 4 (see also Sec. C for details). The measured phase noise of the TDO, powered by a battery, was dBc/Hz at a 1 MHz offset, demonstrating comparable or superior performance to CMOS devices operating at 4 K in a similar carrier frequency range [33, 34, 11]. While CMOS devices achieve better phase noise in the lower- and higher-frequency ranges, the TDO provides better performance within the mid-frequency range. Moreover, with the battery as its power source, the TDO’s phase noise is either comparable to or outperforms that of a commercial microwave source (Vaunix Lab-Brick LMS-451D) across the entire measured frequency range.
5 Amplitude stability
In this section, we measured the amplitude of the signal from the TDO operating at 11 mK through port AC I. The TDO generated a signal at 141.8 MHz with V and V. The signal, recorded at a sampling rate of 20 GS/s for 1.6 ms, was passed through a digital bandpass filter centered at the carrier frequency with a 50 MHz bandwidth (see Appendix D). The amplitude was then extracted using a Hilbert transform and is plotted in Fig. 5(a) and its histogram is shown in Fig. 5(b). Similar to the phase noise measurement, the signal from a commercial microwave source was sent through port AC II, and the amplitude stability of the reflected signal measured through port AC I is also shown for comparison in Fig. 5. For validation of our analytical method, a synthetic signal at 141.8 MHz generated using a sine function is also plotted. Regardless of whether a lead-acid battery or the Yokogawa GS200 was used as the DC source, the amplitude stability of the TDO was superior to that of any commercial microwave source used in this study.
As with the phase noise measurements, the amplitude stability of the commercial microwave source, measured directly without routing it to the device at low temperature, showed identical results to those obtained when the signal was passed through the cryogenic device. This indicates that the observed amplitude stability is determined by the microwave sources themselves and not influenced by the device at low temperatures.

6 Discussion
We do not yet know the origin of the amplitude fluctuations, and identifying it will be the subject of future work. Since the oscilloscope used in this study has an 8-bit resolution, its resolution of is comparable to the observed fluctuations of . This suggests that the fluctuations might arise from the resolution limit of the oscilloscope rather than being intrinsic to the TDO. To investigate this further, improvements in the measurement setup, such as using higher-resolution ADCs, will be necessary. For qubit readout, particularly for electrons in semiconductors being used as qubits, where the qubit state is determined by observing the amplitude distribution [14, 15, 16], it is unlikely that the TDO we developed would result in worse readout fidelity compared to the commercial microwave sources used here. However, looking forward, it will be necessary to evaluate the level of amplitude stability required for qubit readout using actual qubits.
Although the current study focuses on qubit readout, the TDO could potentially be utilized for qubit operation although its phase noise is currently not superior to that of commercial sources and could become a limiting factor if used for qubit operation [35]. Further studies are needed to determine the phase noise requirements for qubit operation. Moreover, for qubit operation, the frequency of 140 MHz is too low. For operations involving electron spin states, GHz-range frequencies would be required. To achieve oscillation at higher frequencies, it is essential to reduce the parasitic capacitance of the tunnel diode and the circuit board. The parasitic capacitance of tunnel diodes exhibits significant variation, which is unlikely to be solely due to the pn-junction capacitance. Instead, this variation may originate from the diode packaging. Therefore, rather than relying on commercially available tunnel diodes, designing a tunnel diode specifically optimized for qubit readout or operation applications would be more effective. Minimizing the parasitic capacitance on the circuit board is also important. One possible approach is to fabricate the entire circuit board using microfabrication techniques. Another approach is to replace bulky varactor diodes with variable capacitors made from ferroelectric materials, such as strontium titanate (STO) [36]. Ferroelectric materials like STO not only allow for variable capacitance but also eliminate leakage currents, reducing circuit losses and providing a significant advantage over traditional varactor diodes.
Considering that the cooling power of a typical cryogenic refrigerator’s 4 K stage is approximately 200 mW, and its mixing chamber stage provides about at 100 mK, it is feasible to place up to 20,000 microwave sources on the 4 K stage and 400 on the mixing chamber stage. These numbers are promising for realizing a scalable quantum computer; nevertheless, further improvements are necessary. In principle, lower power consumption of tunnel diodes can be fabricated by making the surface area of the tunnel diode smaller. While this would also lead to a reduction in output power, it can be compensated by adjusting the ratio of the number of turns in the spiral inductor to the number of turns in the pickup coil. However, the impact of back action on the oscillator must be carefully considered to ensure reliable operation.
Considering the need to apply a magnetic field for electron spin qubits, improvements such as using magnetic field-resilient superconducting materials like NbTiN instead of Nb and designing spiral inductors with these materials could be explored.
7 Conclusion
In conclusion, we developed a 140 MHz tunnel diode oscillator with low power consumption of 1 W and characterized its performance at 11 mK. The achieved output power and frequency fall within the range typically used for qubit readout for electrons in semiconductors being used as qubits. The amplitude stability is better than that of the commercial microwave sources measured in this study, which is encouraging for its application in qubit readout.
Acknowledgements
This work was supported by the RIKEN-Hakubi program, RIKEN Center for Quantum Computing, JST-FOREST, and Yazaki Foundation. We thank Denis Konstantinov and Daimo Yoshikawa for useful discussions.
Data Availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Appendix A Temperature dependence
We conducted detailed measurements of the temperature dependence of the oscillation frequency using a similar circuit. This circuit utilized a BD-6 diode with a parasitic capacitance of 1.7 pF and a 50-turn Nb spiral inductor with an inductance of 1.28 H, and did not include a varactor diode. The resulting oscillation frequency was 107 MHz. The circuit described in this work exhibited a comparable temperature dependence based on preliminary measurements.
The sensitivity was found to be 0.3 kHz/mK in the temperature range of 60 mK to 120 mK, with no detectable dependence below 60 mK with a slight hysteresis. This result is significantly better than the temperature dependence reported in previous studies above 1 K [8].
The observed temperature dependence between 60 mK and 120 mK is unlikely to be due to changes in the tunnel diode’s I-V curve, as no significant variation in the I-V characteristics is observed in this temperature range, making it improbable that frequency shifts result from a change in the operating point.
In prior studies measuring above 1 K [8], temperature dependence was attributed to the surface impedance, thermal expansion, and magnetic susceptibility induced by iron impurities in the copper used in the inductor. In contrast, this work uses a superconducting material, Nb, with a critical temperature of 6 K, in the inductor. Given that the measured temperature range is significantly below , it is unlikely that the temperature dependence is primarily due to changes in the properties of Nb, though some contributions cannot be ruled out. Alternatively, the temperature dependence might arise from changes in the physical properties of the metals used in the PCB substrate.
Appendix B Varactor diode IV curve
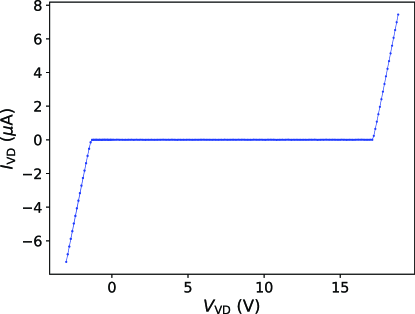
We measured the IV curve of the varactor diode at 11 mK. The range in which the leak current is suppressed matches the range in which the output power remains constant (Fig. 3).
Appendix C DC voltage source stability
We discovered that the DC voltage source (Yokogawa GS200) was significantly affected by strong electromagnetic interference from a nearby radio station broadcasting at 810 kHz. The impact of the 810 kHz signal was directly observed in the output voltage of the Yokogawa GS200 (Fig. 7) and also in the frequency stability of the TDO.
Despite attempts to mitigate the interference using ferrite coils, shielding the lines used for delivering the DC voltage, and shielding the laboratory where the experiment was conducted, the 810 kHz radio signal in the lab was too strong to be removed, likely due to the radio station being only 200 m away. As a result, we decided to switch to using a lead-acid battery, which is not affected by the 810 kHz radio signal. Consequently, as shown in Fig. 4, the phase noise of the TDO was significantly improved.

Appendix D Time-domain data
The time-domain data were sampled at 20 GS/s using an 8-bit oscilloscope over a duration of 1.6 ms. 100 ns segments are shown in Fig. 8. The signals from the ADF and Vaunix generators contain many harmonics, but their influence is eliminated after applying a digital filter (Fig. 8). Such harmonics could become an issue when generating signals for multiplexing using these generators. On the other hand, the signal from the TDO shows no observable harmonics, giving it an advantage in this regard.

Appendix E Power spectra
Fig. 9(a) shows the power spectra obtained from the time-domain signal in Fig. 8 with an integration time of 1.6 ms, while Fig. 9(b) shows the power spectra measured using a spectrum analyzer with an RBW of 5 Hz. In Fig. 9(a), little difference is observed between the TDO, commercial microwave sources, and even the synthetic signal. This is because the high-frequency phase noise (see Fig. 4) is low and relatively similar for all cases. The differences observed in Fig. 9(b) must originate from variations in low-frequency phase noise.

To obtain the power spectra shown in Fig. 9(a), the discrete Fourier transform with zero-padding was computed using the following formula:
| (1) |
where the time-domain data is shown in Fig. D(b) and represents the Fourier coefficients. The root-mean-square amplitude in volts was calculated as:
| (2) |
where is the magnitude of the Fourier coefficient and is the total number of samples. The power spectrum in dBm, assuming a 50 system, was computed using:
| (3) |
where represents the power in watts.
References
- \bibcommenthead
- van Dijk et al. [2019] Dijk, J.P.G., Kawakami, E., Schouten, R.N., Veldhorst, M., Vandersypen, L.M.K., Babaie, M., Charbon, E., Sebastiano, F.: Impact of classical control electronics on qubit fidelity. Phys. Rev. Appl. 12(4), 044054 (2019) https://doi.org/10.1103/PhysRevApplied.12.044054
- Bardin et al. [2019] Bardin, J.C., Jeffrey, E., Lucero, E., Huang, T., Naaman, O., Barends, R., White, T.: A 28nm bulk-cmos 4-to-8ghz ¡2mw cryogenic pulse modulator for scalable quantum computing. In: 2019 IEEE International Solid- State Circuits Conference - (ISSCC), pp. 456–458 (2019). https://doi.org/10.1109/ISSCC.2019.8662480
- Pauka et al. [2021] Pauka, S.J., Das, K., Kalra, R., Moini, A., Yang, Y., Trainer, M., Bousquet, A., Cantaloube, C., Dick, N., Gardner, G.C., Manfra, M.J., Reilly, D.J.: A cryogenic cmos chip for generating control signals for multiple qubits. Nature Electronics 4(1), 64–70 (2021) https://doi.org/10.1038/s41928-020-00528-y
- Peng et al. [2022] Peng, Y., Ruffino, A., Yang, T.-Y., Michniewicz, J., Gonzalez-Zalba, M.F., Charbon, E.: A cryo-cmos wideband quadrature receiver with frequency synthesizer for scalable multiplexed readout of silicon spin qubits. IEEE J. Solid-State Circuits 57(8), 2374–2389 (2022) https://doi.org/10.1109/JSSC.2022.3174605
- Pellerano et al. [2022] Pellerano, S., Subramanian, S., Park, J.-S., Patra, B., Mladenov, T., Xue, X., Vandersypen, L.M.K., Babaie, M., Charbon, E., Sebastiano, F.: Cryogenic cmos for qubit control and readout. In: 2022 IEEE Custom Integrated Circuits Conference (CICC), pp. 01–08 (2022). https://doi.org/10.1109/CICC53496.2022.9772841
- Howe et al. [2022] Howe, L., Castellanos-Beltran, M., Sirois, A.J., Olaya, D., Biesecker, J., Dresselhaus, P.D., Benz, S.P., Hopkins, P.F.: Digital control of a superconducting qubit using a josephson pulse generator at 3 k. PRX Quantum 3(1), 010350 (2022) https://doi.org/10.1103/PRXQuantum.3.010350
- Chow [1964] Chow, W.F.: Principles of Tunnel Diode Circuits, 1st edition edn. John Wiley & Sons, London and New York (1964)
- Van Degrift [1975] Van Degrift, C.T.: Tunnel diode oscillator for 0.001 ppm measurements at low temperatures. Rev. Sci. Instrum. 46(5), 599–607 (1975) https://doi.org/10.1063/1.1134272
- Ezaki and Kurose [1962] Ezaki, R., Kurose, Y.: Diode type semiconductor device. US Patent 3,033,714. Filed: August 14, 1959. Granted: May 8, 1962 (1962)
- Kang et al. [2022] Kang, K., Minn, D., Bae, S., Lee, J., Bae, S., Jung, G., Kang, S., Lee, M., Song, H.-J., Sim, J.-Y.: A cryo-cmos controller ic with fully integrated frequency generators for superconducting qubits. In: 2022 IEEE International Solid-State Circuits Conference (ISSCC), vol. 65, pp. 362–364 (2022). https://doi.org/10.1109/ISSCC42614.2022.9731574
- Lee et al. [2023] Lee, K., Jung, J., Kim, S., Oh, S., Lee, J., Park, S.M.: A 208-mhz, 0.75-mw self-calibrated reference frequency quadrupler for a 2-ghz fractional-n ring-pll in 4-nm finfet cmos. IEEE Trans. Circuits Syst. II Express Briefs 70(8), 2719–2723 (2023) https://doi.org/10.1109/TCSII.2022.3217756
- Hanson et al. [2007] Hanson, R., Petta, J.R., Tarucha, S., Vandersypen, L.M.K.: Spins in few-electron quantum dots. Reviews of Modern Physics 79(4), 1217–1265 (2007) https://doi.org/10.1103/RevModPhys.79.1217
- Zwanenburg et al. [2013] Zwanenburg, F.A., Dzurak, A.S., Morello, A., Simmons, M.Y., Hollenberg, L.C.L., Klimeck, G., Rogge, S., Coppersmith, S.N., Eriksson, M.A.: Silicon quantum electronics. Reviews of Modern Physics 85(3), 961–1019 (2013) https://doi.org/10.1103/RevModPhys.85.961
- Burkard et al. [2023] Burkard, G., Ladd, T.D., Pan, A., Nichol, J.M., Petta, J.R.: Semiconductor spin qubits. Rev. Mod. Phys. 95(2), 025003 (2023) https://doi.org/10.1103/RevModPhys.95.025003
- Vigneau et al. [2023] Vigneau, F., Fedele, F., Chatterjee, A., Reilly, D., Kuemmeth, F., Gonzalez-Zalba, M.F., Laird, E., Ares, N.: Probing quantum devices with radio-frequency reflectometry. Appl. Phys. Rev. 10(2) (2023) https://doi.org/10.1063/5.0088229
- Urdampilleta et al. [2019] Urdampilleta, M., Niegemann, D.J., Chanrion, E., Jadot, B., Spence, C., Mortemousque, P.-A., Bäuerle, C., Hutin, L., Bertrand, B., Barraud, S., Maurand, R., Sanquer, M., Jehl, X., De Franceschi, S., Vinet, M., Meunier, T.: Gate-based high fidelity spin readout in a cmos device. Nat. Nanotechnol. 14(8), 737–741 (2019) https://doi.org/10.1038/s41565-019-0443-9
- Kawakami et al. [2023] Kawakami, E., Chen, J., Benito, M., Konstantinov, D.: Blueprint for quantum computing using electrons on helium. Phys. Rev. Appl. 20(5), 054022 (2023) https://doi.org/10.1103/PhysRevApplied.20.054022
- Schoelkopf et al. [1998] Schoelkopf, R.J., Wahlgren, P., Kozhevnikov, A.A., Delsing, P., Prober, D.E.: The radio-frequency single-electron transistor (rf-set): A fast and ultrasensitive electrometer. Science 280(5367), 1238–1242 (1998) https://doi.org/10.1126/science.280.5367.1238
- Colless et al. [2013] Colless, J.I., Mahoney, A.C., Hornibrook, J.M., Doherty, A.C., Lu, H., Gossard, A.C., Reilly, D.J.: Dispersive readout of a few-electron double quantum dot with fast rf gate sensors. Phys. Rev. Lett. 110(4), 046805 (2013) https://doi.org/10.1103/PhysRevLett.110.046805
- Hornibrook et al. [2014] Hornibrook, J.M., Colless, J.I., Mahoney, A.C., Croot, X.G., Blanvillain, S., Lu, H., Gossard, A.C., Reilly, D.J.: Frequency multiplexing for readout of spin qubits. Appl. Phys. Lett. 104(10), 103108 (2014) https://doi.org/10.1063/1.4868107
- Braga et al. [2024] Braga, D., Das, K., Dick, N., Dyer, K., England, T., Fahim, F., Holm, S., Lu, P., Moini, A., Nolet, F., Rubinov, P., Sanderson, L., Thompson, B., Wang, X.: Design of a low-jitter 10 ghz pll for a 12-bit 10-gsps cryogenic adc for quantum readout in 22fdx (2024) https://doi.org/10.2172/2305629
- Fowler et al. [2012] Fowler, A.G., Mariantoni, M., Martinis, J.M., Cleland, A.N.: Surface codes: Towards practical large-scale quantum computation. Phys. Rev. A 86(3), 032324 (2012) https://doi.org/10.1103/PhysRevA.86.032324
- Van Degrift and Love [1981] Van Degrift, C.T., Love, D.P.: Modeling of tunnel diode oscillators. Rev. Sci. Instrum. 52(5), 712–723 (1981) https://doi.org/10.1063/1.1136656
- Clover and Wolf [1970] Clover, R.B., Wolf, W.P.: Magnetic susceptibility measurements with a tunnel diode oscillator. Rev. Sci. Instrum. 41(5), 617–621 (1970) https://doi.org/10.1063/1.1684598
- Hashimoto et al. [2010] Hashimoto, K., Serafin, A., Tonegawa, S., Katsumata, R., Okazaki, R., Saito, T., Fukazawa, H., Kohori, Y., Kihou, K., Lee, C.H., Iyo, A., Eisaki, H., Ikeda, H., Matsuda, Y., Carrington, A., Shibauchi, T.: Evidence for superconducting gap nodes in the zone-centered hole bands ofkfe2as2from magnetic penetration-depth measurements. Phys. Rev. B Condens. Matter Mater. Phys. 82(1), 014526 (2010) https://doi.org/10.1103/PhysRevB.82.014526
- Fletcher et al. [2009] Fletcher, J.D., Serafin, A., Malone, L., Analytis, J.G., Chu, J.-H., Erickson, A.S., Fisher, I.R., Carrington, A.: Evidence for a nodal-line superconducting state in lafepo. Phys. Rev. Lett. 102(14), 147001 (2009) https://doi.org/10.1103/PhysRevLett.102.147001
- Mikheev et al. [1989] Mikheev, V.A., Movsesyan, G.D., Babayan, K.Z., Mina, R.T., Maidanov, V.A., Mikhin, N.P., Chagovets, V.K., Sheshin, G.A.: Crystallization thermometer with tunnel-diode oscillator for measurement of ultralow temperatures. Instrum. Exp. Tech. 32(1 pt 2), 259–261 (1989)
- Al-Harthi and Sellai [2007] Al-Harthi, S., Sellai, A.: Features of a tunnel diode oscillator at different temperatures. Microelectronics J. 38(8), 817–822 (2007) https://doi.org/10.1016/j.mejo.2007.07.085
- Srikanth et al. [1999] Srikanth, H., Wiggins, J., Rees, H.: Radio-frequency impedance measurements using a tunnel-diode oscillator technique. Rev. Sci. Instrum. 70(7), 3097–3101 (1999) https://doi.org/10.1063/1.1149892
- El-Basit et al. [2020] El-Basit, W.A., Awad, Z.I.M., Kamh, S.A., Soliman, F.A.S.: Temperature dependence of backward tunnel diode oscillator circuit. Microelectronics J. 99, 104756 (2020) https://doi.org/10.1016/j.mejo.2020.104756
- Van Degrift [1974] Van Degrift, C.T.: A sensitive displacement transducer using an extremely reentrant 84 mhz cavity oscillator. Rev. Sci. Instrum. 45(9), 1171–1172 (1974) https://doi.org/10.1063/1.1686838
- Gonzalez-Zalba et al. [2015] Gonzalez-Zalba, M.F., Barraud, S., Ferguson, A.J., Betz, A.C., Delsing, P.: Probing the limits of gate-based charge sensing. Nat. Commun. 6, 6084 (2015) https://doi.org/10.1038/ncomms7084
- Xue et al. [2023] Xue, Q., Zhang, Y., Wen, M., Zhai, X., Chen, Y., Lu, T., Luo, C., Guo, G.: Cryo-cmos modeling and a 600 mhz cryogenic clock generator for quantum computing applications. Chip 2(4), 100065 (2023) https://doi.org/10.1016/j.chip.2023.100065
- Yang et al. [2019] Yang, P., Guo, Y., Jiang, H., Wang, Z.: A 360–456 mhz pll frequency synthesizer with digitally controlled charge pump leakage calibration. In: 2019 IEEE Asian Solid-State Circuits Conference (A-SSCC), pp. 285–286 (2019). https://doi.org/10.1109/A-SSCC47793.2019.9056900
- Ball et al. [2016] Ball, H., Oliver, W.D., Biercuk, M.J.: The role of master clock stability in quantum information processing. Npj Quantum Inf. 2(1), 1–8 (2016) https://doi.org/10.1038/npjqi.2016.33
- Apostolidis et al. [2024] Apostolidis, P., Villis, B.J., Chittock-Wood, J.F., Powell, J.M., Baumgartner, A., Vesterinen, V., Simbierowicz, S., Hassel, J., Buitelaar, M.R.: Quantum paraelectric varactors for radiofrequency measurements at millikelvin temperatures. Nat. Electron. 7(9), 760–767 (2024) https://doi.org/10.1038/s41928-024-01214-z