Characterization of the OU matrix of a braid diagram
Abstract
The OU matrix of a braid diagram is a square matrix that represents the number of over/under crossings of each pair of strands. In this paper, the OU matrix of a pure braid diagram is characterized for up to 5 strands. As an application, the crossing matrix of a positive pure braid is also characterized for up to 5 strands. Moreover, a standard form of the OU matrix is given and characterized for general braids of up to 5 strands.
1 Introduction
An -braid is an object in consisting of strands whose endpoints are fixed at horizontal bars at the top and bottom, where each strand runs from top to bottom without returning ([1]). We say that two -braids are equivalent (or same) if they are sent to each other by an ambient isotopy of fixing the top and bottom bars pointwise. In this paper, we call the equivalence class of a braid simply a braid. An -braid diagram is a regular projection of an -braid with horizontal bars in which each intersection point has the over/under information as shown in Figure 1.

Let be the strands of an -braid diagram with subscripts from the left-hand side to the right-hand side on the top of the braid diagram as shown in Figure 1. The OU matrix, , of is an matrix with zero diagonal such that the entry is the number of crossings between and where is over as shown in Figure 1. (For more precise definition, see [9] or Section 2.) The OU matrix was introduced in [9] to discuss the “warping degree” of a braid diagram ([8]), which estimates the unknotting number of the closure of a braid diagram (see [6, 7] for the warping degree of a link diagram). It was also found that the determinant of the OU matrix acts effectively on layered braid diagrams ([9]). In this paper, we characterize the OU matrix of a pure braid diagram of up to .
We call a matrix whose entries are all integers (resp. non-negative integers) an integer matrix (resp. non-negative integer matrix). We call a matrix whose entries are all non-negative even integers a non-negative even matrix. We say that a square matrix is a zero-diagonal matrix when has zero diagonal, namely all the entries on the main diagonal are zero. We denote the entry of a matrix by . The following properties of zero-diagonal matrices, T0 and T1, are introduced in [2].
Definition 1 ([2]).
A zero-diagonal matrix is said to be T0 if whenever , then implies . A zero-diagonal matrix is said to be T1 if whenever , then implies .
For example, the matrices
are not T0 since they do not meet the condition with and , and . In this paper, when we say that a matrix is T0, it means that is a T0 zero-diagonal matrix. Let denote the transpose of a matrix . In this paper, we prove the following theorem.
Theorem 1.
When , an matrix is the OU matrix of some pure -braid diagram if and only if is a non-negative even T0 matrix.
For an -braid diagram , the crossing matrix of is defined in [2] to be the zero-diagonal matrix whose entry is the algebraic number (positive minus negative) of crossings of where the strand is over the strand (see also [5]). If two braid diagrams and represent the same braid, then holds by definition, and therefore the crossing matrix is an invariant of equivalence classes of braids. This means that the crossing matrix of the equivalence class of is well defined. We denote by for simplicity. In [2], it is proved that the crossing matrix can completely characterize positive braids of canonical length at most 2 (in terms of the canonical form as explained in [3, 10]), whereas it is also proved that it is impossible for length 3 or more.
As for the OU matrices, the equation does not hold for the braid diagrams and that represent the same braid because the OU matrix changes when two consecutive crossings of two strands are produced or reduced, that is, it changes by a Reidemeister move of type II. This implies that the OU matrix is not an invariant of equivalence classes of braids but an invariant of (planner isotopy class of) braid diagrams. For positive braids, it is shown in [9] that the OU matrix is an invariant by taking any positive diagram.
In this paper, we show that the equality holds for any positive braid diagram (Proposition 7) and hence for any positive braids as well. In [2], a conjecture is proposed about a necessary and sufficient condition for a matrix to be the crossing matrix of a positive pure braid , and it was proved that the conjecture is true when . In this paper, we show that the conjecture is true when (Corollary 9) by discussing OU matrices. The conjecture is now open for , although an algorithm that exhibits all positive braids with a given crossing matrix, if any exist, or declares that there are none is known (see [5]).
The rest of the paper is organized as follows. In Section 2, we describe the definitions and properties of the OU matrix, CN matrix, and the crossing matrix. In Section 3, we investigate CN matrices whose entries are 0 or 2, introducing the BW-ladder diagram. In Section 4, we investigate the CN matrices of -pure braid diagrams for . In Section 5, we prove Theorem 1, namely, we characterize the OU matrices of pure braid diagrams up to . We also discuss the crossing matrices of positive pure braids and the OU matrices of braid diagrams that are not necessarily pure.
2 OU, CN and crossing matrices
This section includes an introductory overwiew of the OU, CN and crossing matrices. In Section 2.1, we review the definition of the OU matrix of a braid diagram which was defined in [9]. In Section 2.2, we define the CN matrix which will be used for the proof of the main theorem and see some properties. In Section 2.3, we review the definition of the crossing matrix of a braid which was defined in [2]. In Section 2.4, we discuss the relation between the OU matrices and the crossing matrices. In Section 2.5, we discuss matrices which realize such matrices.
2.1 OU matrix
In this subsection, we review the definition and some properties of the OU matrix defined in [9]. Let be an -braid diagram with the strands that are ordered from the left-hand side to the right-hand side on the top of . Let be a permutation on . The OU matrix of with is an zero-diagonal matrix such that is the number of crossings on the strand that are over the strand (), where the “ strand” stands for the strand , that is, the strand according to the order . In this paper, we also denote simply by for the identity permutation . In Figure 2, the OU matrices of a braid diagram with the permutations and are shown as and , respectively.

For -braid diagrams and , we define the product by the -braid diagram obtained by placing above so that the endpoints of on the bottom bar coincide with those of on the top bar. We call this product the braid product. We have the following proposition.
Proposition 1 ([9]).
Let , be -braid diagrams, and let be the braid permutation of . Then holds for any strand permutation . In particular, when is a pure braid, namely , we have .
2.2 CN matrix
In this subsection, we define the CN matrix. Let be an -braid diagram with the strands ordered from left to right on the top of . A crossing number matrix , or CN matrix, of an -braid diagram is an zero-diagonal matrix such that is the number of crossings between and (). By definition, is a symmetric matrix, and holds for any (see Figure 2). From Proposition 1, we have the following proposition.
Proposition 2.
The addition holds when is a pure braid diagram.
We also have the following proposition for pure braid diagrams.
Proposition 3.
All the entries of the CN matrix of a braid diagram are even numbers if and only if is a pure braid diagram.
Proof.
A braid diagram has the identity braid permutation if and only if each pair of strands has the same relative position on the top and bottom, and that is equivalent to that each pair of strands has an even number of crossings between them. ∎
Definition 2.
For a square matrix , the reverse of , denoted by , is the matrix obtained from by reversing the order of the row and column.
Proposition 4.
If a matrix is the CN matrix of a braid diagram, then the reverse is also the CN matrix of a braid diagram.
Proof.
Let be an -braid diagram such that . Take the vertical rotation . Then, the order of the strands is reversed, and we have . (See and in Figure 2, where and .) ∎
Proposition 5.
If is the CN matrix of a braid diagram, then is T0.
Proof.
Let be a braid diagram such that . If for a pair of and with , then has a crossing between the and strands by definition. Let be the upper-most crossing between the and strands. Let be the region bounded by the top horizontal bar, the and strands from the top to . Since is homeomorphic to the disc , each strand with has a positive even number of intersections with the boundary , and exactly one of them is on the top bar and the others are on the or strands. Hence, the strand has a crossing with the or strand, and we have or . ∎
2.3 Crossing matrix
As mentioned in Section 1, the crossing matrix is a matrix defined in [2] for braids. Let be an -braid diagram with strands with subscripts from left to right at the top of the braid diagram. The crossing matrix of is an zero-diagonal matrix such that each entry is the algebraic number of crossings, i.e., the number of positive crossings minus the number of negative crossings111The definition of positive/negative crossings in this paper is opposite to [2] and same to [5] or [9]., of where is over . For a braid diagram , we denote by the equivalent class of a braid that has as a diagram. We note that if two diagrams and represent the same braid in , i.e., , then (see [2, 5]). Therefore, for a braid that has a diagram , we can define the crossing matrix of by . In [2], the crossing matrices of -braids and pure -braids are completely characterized for all . More specifically, it is proved in [2] that an matrix is the crossing matrix of a pure braid if and only if is a zero-diagonal integer symmetric matrix. For positive pure braids, it is conjectured as follows.
Conjecture 1 ([2]).
An matrix is the crossing matrix of some positive pure braid if and only if is a non-negative integer T0 symmetric matrix.
It has been shown that the conjecture is true when in [2].
2.4 OU matrix and crossing matrix
In this subsection, we discuss the relation between the OU matrix and the crossing matrix. In [9], the following proposition was shown for positive pure braid diagrams.
Proposition 6 ([9]).
The OU matrix of a positive pure braid diagram is a symmetric matrix.
The OU matrix coincides with the crossing matrix for positive braid diagrams.
Proposition 7.
When is a positive braid diagram, the equality holds.
Proof.
Let be the number of crossings between a pair of strands and where is over . By the definition of the OU matrix, the enrty of the OU matrix is . The entry of the crossing matrix is also because all the crossings are positive crossings. ∎
Let be the set of planar isotopy classes of -braid diagrams. Then, forms a monoid under the braid product. Let be the submonoid of which consists of planar isotopy classes of pure braid diagrams and let be the submonoid of which consists of planar isotopy classes of positive pure braid diagrams. Let be the -braid group, that is, the set of equivalent classes of -braids with the group operation naturally induced by the braid product. Let be the subgroup of which consists of pure -braids and let be the monoid which consists of positive pure -braids.
Let be the set of zero-diagonal integer matrix and let be the set of matrices such that for any . We note that is a group whereas is a monoid. Let be the map defined by that is the crossing matrix of , let be the map defined by that is the OU matrix of and let be the map defined by is the CN matrix of .
For and a permutation , let be the matrix obtained by rearranging the rows and columns of according to , i.e. the row and column are row and column of the original , respectively. We easily see that for (resp. ), it holds that (resp. ), and we obtain a group (resp. monoid) right action of on . Thus, we have semi-direct products (as a group) and (as a monoid) using the above right action of on and .
For any two -braids and , it holds that (see [2, 5]). Thus, the map induces a group homomorphism defined by for , where is the braid permutation of . As noted in [5], , where is the comutator subgroup of . On the other hand, for two -braid diagrams , it holds that (see [9]). Then for each braid diagram of and each , the map induces a monoid homomorphism defined by . For each , it obviously holds that for , where is the zero matrix, if and only if is a “trivial braid diagram”, that is, there are no crossings in .
2.5 Realizable matrices
We say that a matrix is OU-realizable (resp. CN-realizable) if there exists a braid diagram such that (resp. ). We say that a matrix is C-realizable if there exists a braid such that . By Proposition 5, we have the following proposition.
Proposition 8.
A square matrix is not OU-realizable if is not T0.
Example 1.
For
the matrix is OU-realizable because in Figure 2, whereas is not OU-realizable since is not T0. In addition, and are not CN-realizable because they are not symmetric.
Proposition 9.
If an symmetric matrix is CN-realizable, then any non-negative integer matrix that satisfies is OU-realizable.
Proof.
Let be a CN-realizable matrix and let be an -braid diagram such that . Let be a matrix such that , that is, , and for any and . For each pair of strands and of , apply crossing changes if necessary so that is over at crossings and is under at crossings. Then we obtain a braid diagram such that . ∎
Since a crossing change does not change the braid permutation, we have the following corollary from the proof of Proposition 9.
Corollary 1.
If an symmetric matrix is CN-realizable by a pure -braid diagram, then any non-negative integer matrix that satisfies is OU-realizable by a pure -braid diagram.
The following proposition allows us to extend the size of CN-realizable matrices.
Proposition 10.
Let be a CN-realizable matrix. Let be an matrix such that for each and for each . Then is also CN-realizable.
Proof.
Let be an -braid diagram with . Let be an -braid diagram obtained from by adding a straight strand on the right-hand side. Then, . ∎
3 -CN matrix of pure braid diagram
From now on in Sections 3 and 4, we denote the CN matrices, which are zero-diagonal symmetric matrices, by strictly upper triangular matrices by replacing the entries below the main diagonal with , for simplicity. For example, we denote the CN matrix
Definition 3.
We call a matrix whose entries are or a -matrix. In particular, when a CN matrix is a -matrix, we call it a -CN matrix.
In this section, we explore -CN matrices. In Section 3.1, we see some properties of the -CN matrices. In Section 3.2, we introduce a tool to construct a braid diagram that realizes the -CN matrix for some -matrices.
3.1 Properties of -CN matrix
We have the following proposition from Proposition 3.
Proposition 11.
When the CN matrix of a braid diagram is a -matrix, is a pure braid diagram.
Then we have the following proposition.
Proposition 12.
If -matrices and are CN-realizable, then the sum is also CN-realizable.
Proof.
The following proposition implies that studying -CN matrices is essential for the study of CN matrices of pure braid diagram.
Proposition 13.
Let be an strictly upper triangular matrix whose entries are non-negative even numbers. Let be the -matrix obtained from by replacing all positive entries with 2. If is CN-realizable, then is also CN-realizable by a pure braid diagram.
Proof.
Let be an -braid diagram such that . We note that is a pure braid diagram by Proposition 11. For each entry , if , that is, , replace one of the crossings between and of by half twists on , as shown in Figure 3. We note that this replacememt does not change the braid permutation because is also an odd number. Thus, we obtain another pure braid diagram , which satisfies . ∎

3.2 BW-ladder diagram
In this subsection, we introduce the “BW-ladder diagram” to discuss the CN-realizablity for -matrices.
We call a filled vertex a black vertex and an open vertex a white vertex.
A BW-ladder diagram is a ladder-fashioned diagram consisting of some vertical segments and two types of horizontal edges, a black edge and a white edge which have black vertices and white vertices at the endpoints on vertical segments, respectively.
In particular, we call a BW-ladder diagram with only black (resp. white) edges a B-ladder diagram (resp. W-ladder diagram).
We consider white edges whose endpoints are on vertical segments which are next to each other only.
We denote a black edge that has black vertices at the and vertical segments () from the left-hand side by , as shown in Figure 4.
Similarly, we denote a white edge that has white vertices at the and vertical segments by .
Each BW-ladder diagram can be represented by a word of and .

For an strictly upper triangular -matrix , a B-ladder diagram of is a B-ladder diagram with vertical segments that has a black edge if . Considering as a hook of the two segments where has roots, as shown in the left-hand side in Figure 4, we can restore from the B-ladder diagram. Moreover, considering as a half-twist of the segments where has roots, as shown in Figure 4, we consider the following local moves.
Definition 4.
A ladder move is one of the following moves L1 to L9 on a BW-ladder diagram. (See Figure 5.)
-
(L1)
for any .
-
(L2)
for any .
-
(L3)
when or .
-
(L4)
for any .
-
(L5)
when , or .
-
(L6)
when .
-
(L7)
when .
-
(L8)
when .
-
(L9)
when .

The ladder move L1 means the replacement of a hook of two segments that are next to each other and a pair of half-twists between them. L2 means the change of the order of the black edges. L3 and L4 mean the transformations based on the braid relation. L5 means the change of the order of a black edge and a white edge whose endpoints are all different. L6 to L9 mean the transformation that a root of a hook moves along a half-twist, as shown in Figure 6.

Since a W-ladder diagram implies a braid diagram (without crossing information), we have the following proposition.
Proposition 14.
A strictly upper triangular -matrix is CN-realizable if a B-ladder diagram of can be transformed into a W-ladder diagram by a finite sequence of ladder moves.
Example 2.
The -matrix shown in the left-hand side in Figure 7 is CN-realizable because the B-ladder diagram can be transformed into a W-ladder diagram by ladder moves.

We have the following proposition.
Proposition 15.
The BW-ladder diagram can be transformed into by ladder moves.
Proof.
On , replace with by the ladder move L1.
Then is transformed into
by applying L9 repeatedly.
Replace with by L1.
Then we have by L9.
Repeat this procedure until is replaced with .
(See Figure 8.)
∎

From Proposition 15, we have the following corollary.
Corollary 2.
Let be an -matrix satisfying the following condition for some with :
Then is CN-realizable.
Proof.
The matrix has the B-ladder diagram of Proposition 15 with , which can be transformed into a W-ladder diagram by ladder moves. ∎
Corollary 3.
Let be a CN-realizable strictly upper triangular -matrix. Then, an matrix satisfying the following condition for some with is also CN-realizable.
Example 3.
We also have the following proposition.
Proposition 16.
Any T0 upper triangular -matrix with for is CN-realizable.
Proof.
Suppose the B-ladder diagram with the following order of black edges,
where we ignore if . By the ladder move L1, we have
Since is T0, if exists in the sequence, namely , then at least one of or exists in the sequence. Use the white edge, which is next to , to apply L7 or L8 and obtain or . By L1, then, we obtain a W-ladder diagram. ∎
We have the following corollary.
Corollary 4.
Any -matrix with for is CN-realizable.
Proof.
Since any matrix such that for is T0, it follows from Proposition 16. ∎
4 CN matrices of pure braid diagrams up to
4.1 -CN matrices of to
For and matrices, we have the following proposition.
Proposition 17.
Every or T0 upper triangular -matrix is CN-realizable.
Proof.
It follows from Proposition 16. ∎
For matrices, we have the following proposition.
Proposition 18.
Every T0 upper triangular -matrix is CN-realizable.
Proof.
By Corollary 3 and Proposition 17, if a T0 upper triangular -matrix has the fourth column as , , or , then is CN-realizable. Therefore, it is sufficient to check the following four cases, which is , Cases A, B, C, D that the fourth column is , , , , respectively.
-
Case A:
Since the entry is , it is CN-realizable by Proposition 16.
- Case B:
-
Case C:
By T0, the entry is . Divide the matrix as
where and are either or . The first matrix is CN-realizable regardless of the value of , as shown in Figure 9. The second matrix is also CN-realizable regardless of by Corollary 4. Hence, by Proposition 12, the sum of them is CN-realizable, too.

Figure 9: Cases A to D. For Case C, ignore the purple-colored broken black edge when the entry is . - Case D:
∎
4.2 -CN matrices of
In this subsection, we show the following proposition.
Proposition 19.
Every T0 upper triangular -matrix is CN-realizable.
To prove Proposition 19, we prepare three lemmas below.
Lemma 1.
Let be a T0 upper triangular -matrix such that when or for some with and . Then is CN-realizable.
Proof.
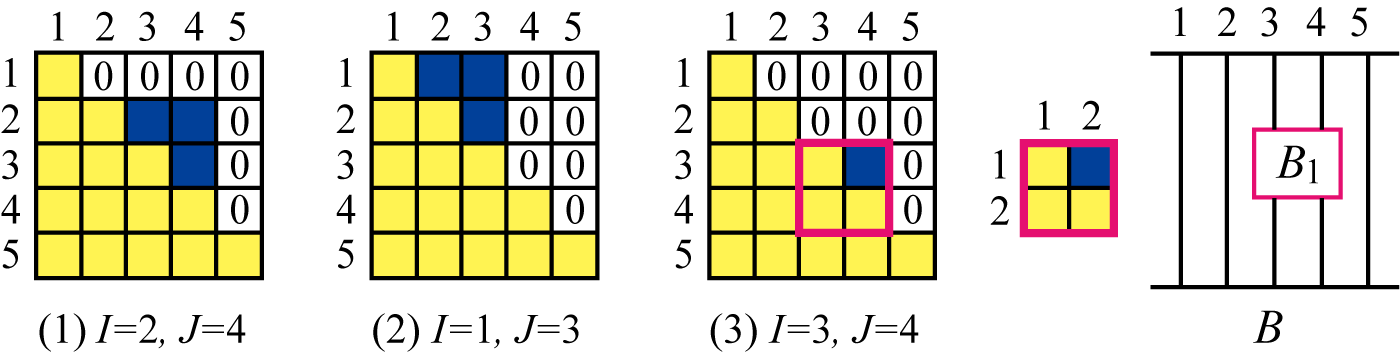
Consider the matrix such that . We note that is T0 because is T0. Since , is CN-realizable by Propositions 17 and 18. Let be a -braid diagram such that . Add and straight strands to on the left- and right-hand sides, respectively, as shown in Figure 10 (3). Thus, we obtain a -braid diagram such that . ∎
Lemma 2.
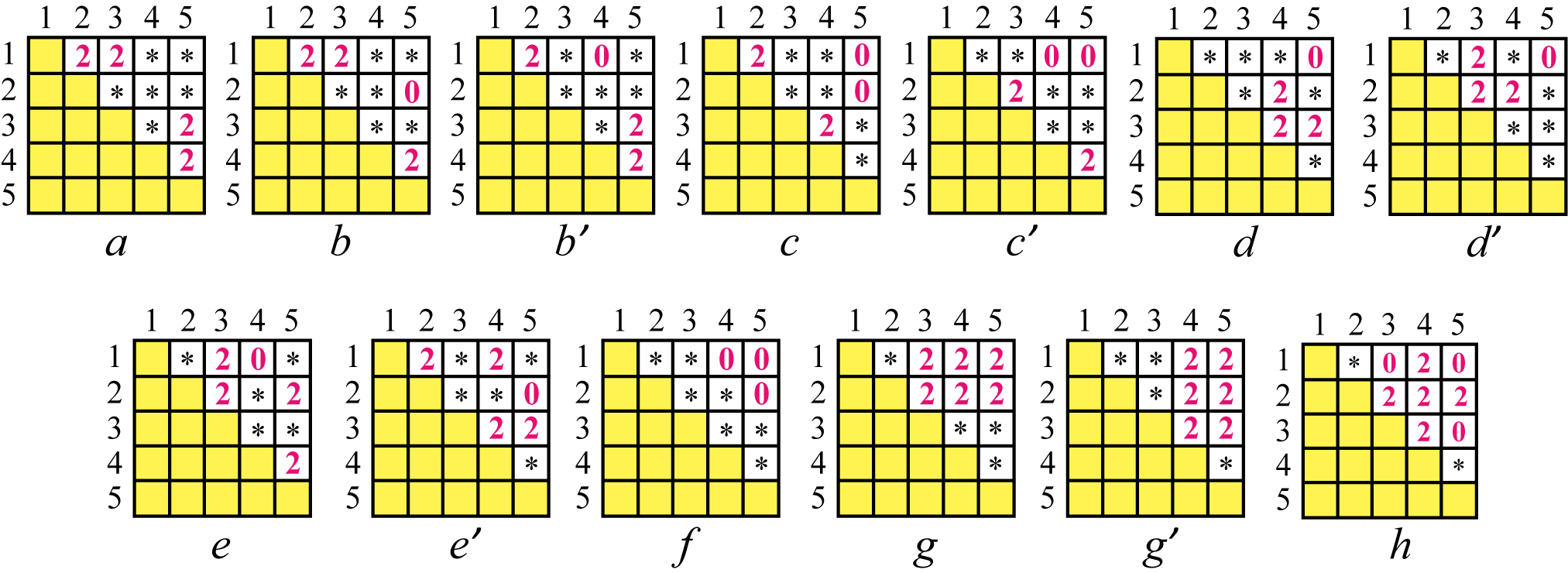
If a T0 upper triangular -matrix has the configuration of one of to in Figure 11, then is CN-realizable.
Proof.
We use Proposition 12 and Lemma 1. For the configuration , divide the matrix as
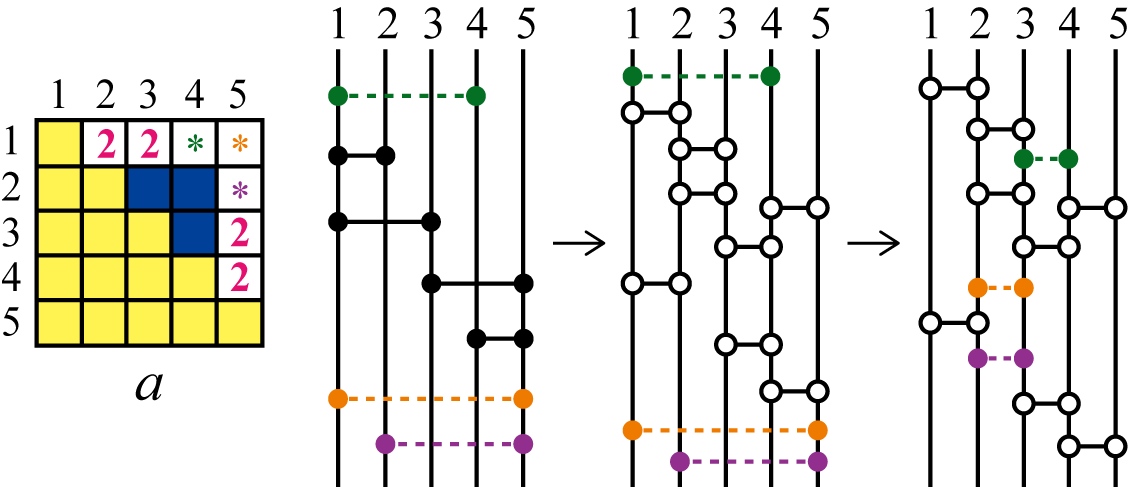
where and are either 0 or 2 (). The first matrix is CN-realizable as shown in Figure 12 regardless of the values of , and .
The second matrix is CN-realizable by Lemma 1. Hence, the sum is also CN-realizable by Proposition 12. In the same way, we can see the CN-realizability for the configurations to as shown in Figure 13. We note that we use Lemma 1 and Proposition 12 twice for the configurations .

The configuration realizes a CN matrix by Proposition 16. For the configurations and , the matrices
are CN-realizable as shown in Figure 14.

We note that the reverses to of the configurations to also realize a CN matrix by Proposition 4. We also have the following lemma.
Lemma 3.
If a T0 upper triangular -matrix has one of the configurations shown in Figure 15, which we call configuration , then is CN-realizable.

Now we prove Proposition 19.
Proof of Proposition 19. By Corollary 3, it is sufficient to check the eleven cases, which is , on the fifth column A to K in Figure 16. By T0, some of the entries in the first to fourth columns are automatically assigned, as shown in Figure 16.

-
Case A:
By the configuration , it is sufficient to suppose that the entry is . Then, by configuration , suppose that the entry is . By T0, then, the entry is , and observe that it has configuration . Hence, any matrix of Case A is CN-realizable.
-
Case B:
By the configuration , suppose that the entry is . By configuration , suppose that the entry is . This has the configuration .
-
Case C:
This has the configuration .
-
Case D:
By configuration , suppose that the entry is . Then, by configuration , suppose the three subcases shown in Figure 17. The first subcase has the configuration . The second subcase has the braid diagram as shown in the figure. (See Example 7 for the construction of the braid diagram.) The third has the configuration .
-
Case E:
By the configuration , suppose that the entry is . This has the configuration .
-
Case F:
This has the configuration .
-
Case G:
This has the configuration .
-
Case H:
This has the configuration .
-
Case I:
By the configuration , suppose that the entry is . By the configuration , suppose that the entry is . By T0, then, the entry is . This has the configuration .
-
Case J:
By the configuration , suppose that the entry is . By the configuration , suppose that the entry is . Then, it has the configuration .
-
Case K:
This has the configuration .

Hence, every T0 upper triangular -matrix is CN-realizable.
∎
Corollary 5.
When , any T0 upper triangular -matrix is CN-realizable.
Corollary 6.
When , any non-negative even T0 upper triangular matrix is CN-realizable by a pure -braid diagram.
5 Proof of Theorem 1 and applications
We prove Theorem 1 in Section 5.1 and then discuss the crossing matrices of positive pure braids in Section 5.2, the OU matrices of braid diagrams that are not necessarily pure in Section 5.3. In this section, we consider a CN matrix as a symmetric matrix as defined in Section 2, not a strictly upper triangular matrix as in Sections 3 and 4.
5.1 Proof of Theorem 1
In this subsection, we prove Theorem 1. We have the following proposition.
Proposition 20.
When , an matrix is the CN matrix of a pure -braid diagram if and only if is a non-negative even T0 symmetric matrix.
Proof.
We prove Theorem 1.
5.2 C-realizable matrix
In this subsection, we discuss the crossing matrices of positive pure braids. We have the following lemmas.
Lemma 4.
A zero-diagonal symmetric matrix is T0 if and only if is T0.
Proof.
When is symmetric, i.e., , if and only if . ∎
Lemma 5.
When , an matrix is the OU matrix of a pure -braid diagram such that each pair of strands and has the same number of crossings such that is over and is over if and only if is a non-negative integer T0 symmetric matrix.
Proof.
By Theorem 1, the OU matrix of a pure -braid satisfies that is a non-negative even T0 matrix. Moreover, is symmetric with the condition of the crossing number of and , i.e., . Hence itself is also T0 by Lemma 4.
On the other hand, let be an non-negative integer T0 symmetric matrix (). Then is also T0 by Lemma 4 and the entries of are all non-negative even numbers since is symmetric. Therefore, is CN-realizable by a pure -braid diagram by Proposition 20. Then is OU-realizable by a pure -braid diagram by Corollary 1. Moreover, is a braid diagram such that each pair of strands , of has the same number of crossings such that is over and is over because . ∎
We have the following corollaries.
Corollary 7.
When , the crossing matrix of any positive pure -braid diagram is an non-negative integer T0 symmetric matrix.
Corollary 8.
When , any non-negative integer T0 symmetric matrix is C-realizable by a positive pure -braid.
Proof.
For the pure -braid diagram in the proof of Lemma 5 with , apply crossing changes if necessary to obtain a positive braid diagram . We note that is still a pure -braid diagram such that each pair of strands and has the same number of crossings such that is over and is over . Then by Proposition 7 and Lemma 5. ∎
Corollary 9.
Conjecture 1 is true when .
5.3 OU matrix and CN matrix for a general braid type
A simple braid (or a permutation braid) is a braid that has a simple diagram, that is, each crossing is positive and each pair of strands has at most one crossing, which has been used in studies of the normal form of braids (see [3, 4, 10]). Let be the set of simple -braids. There is one-to-one correspondence from to by taking their braid permutations . Let be the set of zero-diagonal integer matrices. As explained in [2, 5], using Lemma 9.1.6 in [10] directly, we have the following lemma.
Lemma 6.
The map is injective and its image is the set of satisfying the following conditions:
-
(i)
if ,
-
(ii)
,
-
(iii)
is both T0 and T1, i.e., if whenever , then implies for .
We call a square matrix satisfying the conditions (i)-(iii) in Lemma 6 a simple matrix. Take a simple diagram of . If a pair of strands and of has a crossing, then passes under , and equivalently passes over at the crossing. Thus, for any simple diagram of any . We note that and for any . By Lemma 6, we have the following lemma.
Lemma 7.
The map is injective and its image is the set of satisfying the following conditions:
-
(I)
for any ,
-
(II)
,
-
(III)
is T0 and T1.
We call a matrix satisfying the conditions (I)-(III) in Lemma 7 a double simple matrix. We also remark that and , where is the set of matrices such that for any . In conclusion, we have the following corollary.
Corollary 10.
Let . For each braid ,
-
(1)
there exists a braid diagram of such that for some such that is non-negative even T0 and is simple.
-
(2)
There exists a braid diagram of such that for some such that is non-negative even T0 symmetric and is double simple.
Proof.
Let be the braid permutation of and let be the permutation -braid corresponding to . Let . It is easily seen that . Take a pure braid diagram of and take a simple diagram of . Let and . Then, by Proposition 1 and by Proposition 2. We can see that is non-negative even T0 by Theorem 1 and is non-negative even T0 symmetric by Proposition 20. We can also see that is simple by Lemma 6 and is double simple by Lemma 7. ∎
Acknowledgment
The work of the first author was partially supported by the JSPS KAKENHI Grant Number JP21K03263. The work of the second author was partially supported by the JSPS KAKENHI Grant Number JP19K03508.
References
- [1] E. Artin, Theory of braids, Ann. Math. 48 (1947), 101–126.
- [2] J. Burillo, M. Gutierrez, S. Krstić and Z. Nitecki, Crossing matrices and Thurston’s normal form for braids, Topl. Appl. 118 (2002), 293–308.
- [3] E. Elrifai, H. Morton, Algorithms for positive braids, Quart. J. Math. Oxford 45 (2)(1994), 479 497.
- [4] F. A. Garside, The braid group and other groups, Quart J. Math. Oxford Ser. 20 (1969), 235–254.
- [5] M. Gutierrez and Z. Nitecki, Crossing matrix of positive braids. (arXiv:1805.12189)
- [6] A. Kawauchi, Lectures on knot theory (in Japanese), Kyoritsu Shuppan Co. Ltd. (2007).
- [7] A. Shimizu, The warping degree of a link diagram, Osaka J. Math. 48 (2011), 209–231.
- [8] A. Shimizu, A. Gill and S. Joshi, A note on the unknotting number and the region nuknotting number of weaving knots, preprint. (arXiv:2408.14938)
- [9] A. Shimizu and Y. Yaguchi, Determinant of the OU matrix of a braid diagram, to appear in J. Knot Theory Ramifications.
- [10] W. Thurston, Braid groups, in: D. Epsteinetal. (Eds.), Word Processing in Groups, Jonesand Bartlett, Boston, MA, 1992, pp.181–209.