Characterization of saturated graphs related to pairs of disjoint matchings
Abstract.
For a finite graph , we study the maximum -edge colorable subgraph problem and a related ratio , where is the matching number of , and is the size of the largest matching in any pair of disjoint matchings maximizing (equivalently, forming a maximum -edge colorable subgraph). Previously, it was shown that , and the class of graphs achieving was completely characterized. In this paper, we first show that graph decompositions into paths and even cycles provide a new way to study these parameters. We then use this technique to characterize the graphs achieving among all graphs that can be covered by a certain choice of a maximum matching and , as above.
1. Introduction
We investigate the ratio of two parameters of a finite graph , , where is the size of a maximum matching in , and is the size of the largest matching in a pair of disjoint matchings whose union is as large as possible. More formally,
To place the mentioned parameters and the ratio in the context of what is commonly considered in graph theory, recall that for , a proper edge-coloring of a graph with colors is exactly a partition of the edge-set into disjoint matchings. Thus, determining is the case of the following well-known problem:
Maximum -edge colorable subgraph problem (-ECS).
For a given , what is the maximum number of edges of a given finite graph that can be covered with disjoint matchings?
We note here that and , so the case of this problem is the maximum matching problem, while the case is what we are concerned with here. Before describing our result, we overview what is known about -ECS concerning its computational complexity, numerical bounds, and structural aspects.
Computational complexity
The simple case of -ECS is completely solved as it admits a polynomial-time algorithm [Edmonds:1965]. On the other hand, -ECS is already -hard; in fact, the problem of determining whether is equal to the number of vertices of the graph is -complete even for cubic graphs. This follows immediately from Holyer’s work [Holyer] by the following argument. Holyer proves that determining whether a graph is -edge colorable is -complete even for cubic graphs. Letting be a cubic graph, any -edge-coloring gives disjoint perfect matchings, in particular, . Conversely, if , then for any pair of disjoint matchings with , and are both perfect matchings, and the remaining edges in form a third perfect matching, so , , is a 3-edge-coloring of . Thus, a cubic graph is -edge colorable if and only if .
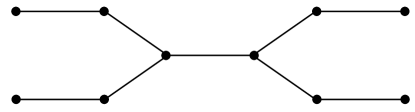
To give an intuitive idea why finding is hard, we illustrate how the greedy algorithm fails to find it. The algorithm would firstly take a maximum matching of the whole graph and then take a maximum matching of the remaining edges. However, this may not cover the maximum number of edges : see Fig. 1 for an example where , while the greedy algorithm yields . The ratio that we study in the present paper measures the failure of optimality of the greedy algorithm for -ECS; in particular, this ratio is for the graph in Fig. 1.
In the positive direction for computing , it is shown in [Agrawal+] that finding is fixed-parameter tractable.
More generally for all , it is known that -ECS is -hard [Feige+] and APX-hard [Kosowski:2009]. Related complexity bounds are shown in [A-M:2019].
Although finding is -hard, the complexity of finding is still unknown.
Question 1.
What is the computational complexity of finding ? In particular, is it also -hard?
Remark 2.
One may wonder whether there is an analogue for the Berge–Tutte formula [Berge, Tutte] [Lovasz-Plummer][Theorem 3.1.14], which relates to the number of odd connected components in subgraphs of , for . However, that formula provides a witness to for a fixed , hence implying that finding is both in and co-. Thus, since we already know that finding (-ECS) is -hard, it is unlikely that there is an analogue of the Berge–Tutte formula for in general. However, such a formula may exist for subclasses of graphs.
Numerical bounds
In [M-M-Ts:2008], V. Mkrtchyan, V. Musoyan, and A. Tserunyan proved that
for any graph , and more recently, in [IGL:2019], it was shown that for any rational with , there is a connected graph with and (an explicit construction is provided).
As shown in [A-M-P-V:2014], this lower bound can be improved for the case of cubic graphs. In this case, we have
for a cubic graph .
A related line of research studies the general , which is the most edges that can be colored by disjoint matchings (i.e. ). In this direction, [M-P-V:2010] shows that in cubic graphs,
Lastly, [K-M:2019] establishes the following family of inequalities for a bipartite graph and any :
Structural aspects and our result
Besides the relevance and naturalness of -ECS problem, our motivation for studying the parameters and , and the ratio is that they reveal interesting structural properties of the graph. Furthermore, we observe in Section 3 below that the parameters , , and are tied to decompositions of graphs into paths and even cycles, which provides a dual angle of interest for studying these parameters.
It was shown in [Tserunyan:2009] that the graphs minimizing the ratio (i.e. ) admit rigid structure; in fact, this paper provides a complete structural characterization of these graphs. Fig. 1 depicts the spanner — the unique minimal graph that achieves the ratio .
As for the graphs achieving the upper bound for the ratio , the question is still open:
Question 3.
Is there a structural characterization of all graphs with ?
This question has been considered previously. For example, Mkrtchyan in [Mkrtchyan] shows that trees whose every edge is in a maximum matching satisfy . A more general sufficient condition for achieving the upper bound is provided in [IGL:2019], where is it proven that any graph with must contain one of a special family of graphs as a subgraph.
In the present paper, we answer Question 3 for a core (with respect to the involved parameters) subclass of graphs, providing a complete structural characterization. To describe this class, we define a choice of maximally intersecting matchings , and in Definition 13, and we call a graph saturated if its edges are covered by some maximally intersecting matchings , , and , where is a maximum matching and are disjoint matchings with and . These maximally intersecting matchings feature the core structure of graphs with , as the edges not included in these matchings can appear in limited configurations and do not contribute to the parameters or . Among saturated graphs, we precisely characterize those with by equating this class with that of skeletons. Referring the reader to Definition 16 for the precise definition, we roughly define a -skeleton here as a disjoint union of -many odd leaf-to-leaf paths with some additional special odd paths intertwining them. Our main result is:
Theorem 4.
If a finite, connected graph is saturated and satisfies , then it is a -skeleton with . Furthermore, if is a -skeleton, then is saturated, and . In particular, for all -skeletons.
The precise statement of this result is given in Theorems 19 and 20.
In the proof of Theorem 4, we use an alternative characterization of the parameters , , , which is interesting in its own right. This characterization replaces the maximization on matchings used in our definitions to minimization on decompositions into paths and even cycles, which we call PEC decompositions (see Section 3).
As for unsaturated graphs, i.e. those with edges not covered with the mentioned three matchings, we provide in Section 6 a couple of structural restrictions on those extra edges and state a question. However, Question 3 remains open in general.
Organization
Section 2 provides the preliminaries and sets up notation. PEC decompositions are discussed in Section 3. In Section 4, we establish the basic theory of the maximally intersecting matchings studied in this paper and the alternating paths that they form. Our main results, Theorem 19 and Theorem 20, are proved in Section 5 using the techniques from the previous sections. We conclude in Section 6 with a discussion of those graphs that are not covered by these matchings.
Acknowledgements
We thank Vahan Mkrtchyan for his invaluable insight into this direction of research and for pointing out the relevant literature and context. We also thank Alexandr Kostochka for helpful suggestions and advice.
2. Definitions & notation
Throughout, we denote by a finite graph with vertex set and edge set . A matching in is a set of edges such that no two are adjacent. In particular, we will consider the following specific types of matchings.
-
•
A maximum matching is a matching of maximum size, i.e., for all matchings , . We let denote the size of a maximum matching.
-
•
A perfect matching is a matching such that for every vertex in , there exists an such that is incident to .
-
•
A near perfect matching is a matching such that for every vertex in except for one, there exists an such that is incident to .
In addition to sizes of maximum matchings, we will also pay special attention to the size of the union of two disjoint matchings whose union is of maximum size. More formally:
-
•
;
-
•
is the set of pairs of disjoint matchings satisfying ;
-
•
.
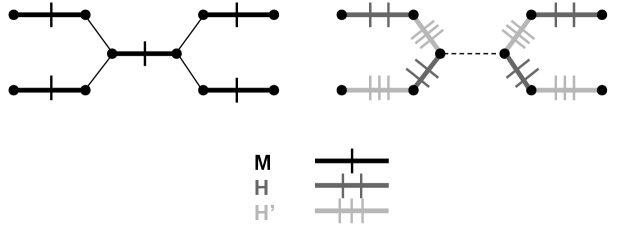
, , and are the main concern of this paper. We present an example with the spanner graph to illustrate our key parameters. The left spanner of Fig. 2 has the unique maximum matching, , highlighted. It has size 5, and so for the spanner. The largest matching disjoint from has size 2, for combined size of 7. However, if we choose a separate set of disjoint matchings, we can achieve . On the right of the same figure, our maximal disjoint matchings and are highlighted. They each have size , so for the spanner. Most graphs with share key structural properties with the spanner, as we will make clear in Section 5.
-
•
is the subset of of pairs with .
-
•
.
-
•
By a chain in , we mean a sequence , , where the are vertices and the are edges of such for all ; we also assume that our chains are simple, i.e. all edges are distinct. We refer to as the length of the chain and to and as its endpoints.
-
•
By an odd (resp. even) chain we mean that the length (i.e., the number of edges on it) is odd (resp. even).
-
•
By a path, we mean a simple path, i.e. a chain with distinct vertices, and by a cycle we mean a simple cycle, i.e. a chain whose endpoints are equal but all other vertices are distinct.
-
•
An edge on an odd path is called even (resp. odd) if is even (resp. odd). Note that this would not change if the path was written in the reverse order.
-
•
If , then an alternating chain is a chain such that edges of odd index are in and edges of even index are in , or vice versa. Note that if and are both matchings, then the chain must be either a path or a cycle, or else some vertex will be incident to two edges of the same matching.
-
•
If is a subset of the edges of the graph , then := is the complement in of .
The majority of the techniques used in Section 5 make use of the properties of the alternating paths of various matchings.
3. PEC decompositions
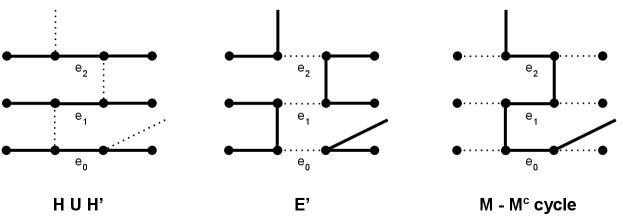
Now, we present a type of decomposition for graphs that highlights matching structure and gives an alternative way to compute the parameters , , and . Several of the following lemmas will be used in the proof of our main theorems. Throughout this section, let be a graph and .
-
•
A subgraph of is a graph with and . A subgraph of is spanning if .
-
•
A pec decomposition of is a spanning subgraph , each of whose (connected) components is a path or an even cycle. (Isolated vertices are treated as even paths.)
-
•
If is a subset of , then we use the notation to denote the spanning subgraph of with edge set . In particular, we use this notation in the case that is the union of certain matchings.
For a pec decomposition of , let
-
•
(resp., ) denote the number of components of that are paths (resp., even paths);
-
•
;
-
•
.
These last three parameters describe structural properties of the graph that can be assessed with matchings and alternating paths. They are a direct parallel to our original , and . For our first lemma, we show that and are directly related.
Lemma 5.
For any pec decomposition of , .
Proof.
Let be a maximum matching for . It is clear that is a perfect matching on each odd path and even cycle of and a near perfect matching for each even path. Thus, misses exactly one vertex from each even path and no other vertex. Hence, . ∎
Proposition 6.
. In fact:
-
(a)
For any maximum matching , is a pec decomposition with .
-
(b)
Conversely, for any pec decomposition with , .
Proof.
For , let be a maximum matching. Then is a pec decomposition and is the unique maximum matching in , so by Lemma 5, .
For , let be a pec decomposition with , so by Lemma 5, .
Thus, we have , so looking back, we see that the inequalities in the first two paragraphs are equalities, and hence and . ∎
We can find a similar correspondence between and if we consider the pairs of disjoint matchings in instead of the maximum matchings.
Lemma 7.
For any pec decomposition of , .
Proof.
Let be a pec decomposition and let be a pair of disjoint matchings of with . It is clear that because each component of can be taken as an -alternating path/cycle i.e. a path/cycle whose edges alternate between being in and .
It remains to show that . Since is pec, we have , where is the number of edges in paths of and is the number of edges in even cycles of . Since paths have one more vertex than they have edges and cycles have as many vertices as edges, and , where (resp., ) is the number of vertices on paths (resp., cycle) of . Thus, . ∎
Proposition 8.
. In fact:
-
(a)
For any , is a pec decomposition with .
-
(b)
Conversely, for any pec decomposition with , .
Proof.
For , let . Then every vertex in the spanning subgraph has degree at most 2 in . Additionally, there can be no odd cycles in because and are disjoint. is thus a pec decomposition, so by Lemma 7, .
For , let be a pec decomposition with . Then by Lemma 7, .
Thus, we have , so looking back, we see that the inequalities in the first two paragraphs are equalities, and hence and . ∎
Now, define
i.e. is the minimum number of even paths in a pec decomposition that minimizes the number of paths. If we now take instead of , we obtain a result for and .
Lemma 9.
. In fact:
-
(a)
For any , is a pec decomposition with and .
-
(b)
Conversely, for any pec decomposition with , .
Proof.
For , let . Then is a pec decomposition. By Lemmas 7 and 8, , so . Furthermore, is a maximum matching in , so by Lemma 5, .
For , let be a pec decomposition with and . Let . By Proposition 8, , so . Moreover, and is a maximum matching for , so by Lemma 5, .
Thus, we have , so looking back, we see that the inequalities in the first two paragraphs are equalities, and hence achieves and , and . ∎
These new and parameters provide as much information as our original , and . In fact, we can now restate theorems concerning the ratio in terms of our new pec parameters.
Corollary 10.
if and only if .
Proof.
Follows from Propositions 6 and 9. ∎
Example 11.
If is the spanner, and it is achieved by a pec decomposition into a path of length and two paths of length . Therefore, . On the other hand, and it is achieved by a unique pec decomposition into two paths of length . Thus, . Because such a is unique, it also witnesses , so .
We present one more brief result for pec decompositions that is useful in studying size differences of disjoint matchings.
Corollary 12.
. In particular, .
4. Basics tools
In this section we will state and prove several structural lemmas about alternating chains (i.e., paths or cycles) that will be used to prove our main theorems. Let be a finite connected graph. Among the maximum matchings and maximum disjoint matchings in , there are some that have maximal intersection, and this condition allows for sharper restrictions on the possible edge configurations. More specifically, we define maximally intersecting matchings:
Definition 13.
As we will demonstrate in the next section, these matchings capture the most important structural behavior of graphs. Throughout this section, let , , be maximally intersecting matchings. Here are a few basic facts about - alternating chains. Define an end-edge of a path to be an edge in the path incident to one of the path’s terminal vertices.
Lemma 14.
-
(a)
The maximal - alternating chains are odd paths with end-edges in .
-
(b)
The end-edges of - alternating paths are in .
-
(c)
All vertices on maximal - alternating paths are incident to .
Proof.
(a) Let be such a chain. Since these chains are alternating, cannot be an odd cycle. If is an even path or cycle, define . is a matching since is a matching and since is alternating. Furthermore, , and so is a maximum matching. However, since not all edges may have been in , and since , either of (c) or (d) must be violated, a contradiction. Now suppose that some end-edge of is not in . This edge, , is in , and is adjacent to exactly one edge in . But then if is removed from and is added to , is again increased, a contradiction.
(b) Consider an end-edge in . Again note that can be incident to on only one side. If is not in , then we can remove , the preceding edge, from , add to , and again increase .
(c) Suppose instead some interior vertex is not incident to , and note that this vertex is incident to no end-edges. This vertex is incident to exactly one edge in , which we call . is incident to at most once. Via a similar argument to above, if we take to be in instead of this adjacent edge, we increase . ∎
We now present similar structural lemmas about maximal - alternating paths.
Lemma 15.
-
(a)
If a maximal - alternating path is odd, then its end-edges are in .
-
(b)
The end-edges of maximal - alternating paths (which we know are in ) are end-edges of even - alternating paths.
-
(c)
All inner (not end) vertices of maximal - alternating paths are inner vertices of - alternating paths. In other words, each end-vertex of an - alternating path is either an end-vertex of a maximal - alternating path or is not on any - alternating path.
-
(d)
On every even maximal - alternating chain, the edges in are at least as many as those in .
-
(e)
Each end-edge of a maximal - alternating path that is in is also in .
Proof.
(a): Otherwise, we would switch and on that path, keeping the same, but increasing .
(b): Each such edge is adjacent to exactly on one side, so it is an end-edge of a maximal - alternating path, which hence must be even by (a).
5. Subclass of graphs with
We are now prepared to state and prove our main theorems. For , we call a vertex in a graph a -vertex if its degree is , and we say that a graph has degree if the degree of each vertex is at most . An edge incident to a leaf (a -vertex) is called a leaf-edge.
A path in a graph whose end-vertices are leaves is called leaf-to-leaf. Call an edge on an odd path odd (resp. even) if it is in an odd (resp. even) position in both obvious orderings of the edges, i.e. the end edges of are both odd. Similarly, call a vertex on an even path odd (resp. even) if its edge-distance from either end-edge of is odd (resp. even).
Our main theorems, Theorem 19 and Theorem 20, establish that the core structural properties of graphs with are due to a graph’s skeleton structure.
Definition 16.
A connected nonempty graph is called a skeleton if it is of degree and admits a (not necessarily spanning) subgraph satisfying the following conditions:
-
(a)
consists of vertex-disjoint odd leaf-to-leaf paths of length at least .
-
(b)
For each odd edge on a maximal path in , either both of its incident vertices have -degree (in which case, we call this odd edge rich) or neither of them do.
-
(c)
Each maximal path in contains a -vertex.
-
(d)
The vertices in have -degree at most .
-
(e)
The graph obtained from by removing consists of vertex-disjoint odd paths.
-
(f)
Let the subgraph of obtained by removing the rich edges. The -connected component of each end-vertex of a maximal path in is an even path and these are the only connected components that are even paths.
-
(g)
is bipartite.
-
(h)
Let be the matching containing each odd edge of and each even edge of . Then contains no alternating cycles.
Take note in particular of the final condition involving alternating cycles. Some of the following proofs are argued by contradiction to construct such a cycle. Call a skeleton a -skeleton if has -many connected components (odd paths). The spanner is an example of a -skeleton.
Remark 17.
It follows from (b) and (d) that removing the rich edges from results in a graph of degree , so each connected component of is a path or a cycle. Condition (f) demands that the connected components of the end-vertices of the maximal paths in are exactly those that are even paths (necessarily of length at least ). Condition (g) demands that there are no odd cycles in .
The main theorems of this paper, Theorem 19 and Theorem 20, make the following characterization. A connected graph is a -skeleton if and only iff and any satisfying conditions (a)–(d) cover all of , i.e., . This condition for an edge covering of is not arbitrary; the key structural properties in a graph that cause are included in the definition of skeleton, and there are very few ways that edges not in this choice of can be added to a skeleton without forcing . A brief discussion for these remaning unmatched edges appears in the last section.
We prove a proposition before proving our main theorems.
Proposition 18.
Every skeleton admits a unique perfect matching.
Proof.
Let be a skeleton graph and let be as in Definition 16. Because the connected components of and are odd paths and each odd path admits a perfect matching, the whole graph admits a perfect matching (the union of the matchings on each odd path). Call this matching .
It remains to show uniqueness. Suppose towards a contradiction that contains another perfect matching . Observe that if on each of the paths in then this forces on all of . Thus, some path of must contain an edge. Denote some direction along this path as the left, and take the leftmost edge on this path. We mark the following edges in Fig. 4. Observe that must be rich since must contain all edges left of and is perfect. Since must saturate the left vertex of , it must include another edge incident to this vertex. Observe that there exists an alternating path connecting this vertex to another rich edge elsewhere in , since if this path terminates in a leaf, would necessarily be in . Consider the edge on the other end of this path and call it . The vertex of not incident to this path must also be incident to some non- edge. One of these edges must be in since is perfect. If it is a edge, travel along the alternating path it is a part of, and if it is a edge, travel along this edge to the adjacent edge. Again, we end on an edge . Repeat this process for . This process can never end by travelling into some leaf of , since this would imply that one of the is in . This process can only terminate if some for some . But observe that the cycle we have created has alternating edges in and the remaining in , contradicting (h). ∎
This unique perfect matching is used in our first main theorem. Our proof uses structural properties derived from the pec parameters of Section 3. For a pair of disjoint matchings, call a vertex -saturated (or just saturated if is clear from the context) if , where .
Theorem 19.
For a -skeleton , .
Proof.
Let be as in Definition 16.
-
•
Let be the unique perfect matching of .
-
•
Put in all the even edges of the maximal odd paths of and all the odd edges of maximal odd paths of .
-
•
Put in all the non-rich odd edges of , all even edges of the maximal odd paths of , and all edges of that are not in and .
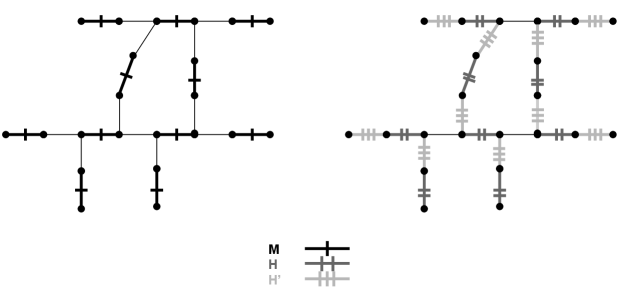
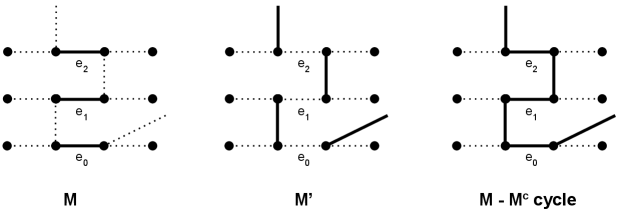
These matchings are illustrated in Fig. 5 on a 2-skeleton. Notice that covers the edges of and that and are disjoint. Observe also that all of the and edges must occur in . Then , as there is one more edge than edge along each path of . If we can show that , then we have . Note that every non-leaf vertex of is saturated by both and , and every leaf is saturated by either or . Hence, all vertices are saturated, so , and so by Proposition 8, the corresponding pec decomposition achieves . We will now show that the pec decomposition formed by is the unique pec decomposition achieving .
Suppose that there exists some other pec decomposition that achieves . Every leaf in must be a leaf of , and since achieves , these are the only leaves of . must have the same size as , and so there must exist an edge not in . Call this edge . We mark the following edges in Fig. 6. Each vertex of must be degree 3, since otherwise, the vertex would be a leaf in . Since is a cover, this vertex must be adjacent to a rich edge in . The opposite vertex of this edge must also be degree three. One of the adjacent edges in or must be in to prevent this vertex from being a leaf in . Call the edge not in . The other vertex of must be degree 3 to avoid making new leaves. The M rich edge adjacent to this vertex must be adjacent to another two and edges. Of these two, the one not in is . We may repeat this argument to deduce further . This process of following edges can only terminate if some . But then we have followed an even alternating cycle, which is forbidden by (h). Thus, the only pec decomposition of is the one formed by .
To complete the proof, we will show that the given maximizes the size of among the pairs in . Every shares the same pec decomposition, so we need only show that the end-edges of each maximal odd alternating path are in . Consider some edge that is the end-edge of a maximal alternating path. By definition, this must be an end-edge of a path in . But then the resulting alternating path is even length by (f). ∎
For our second main theorem, we now prove that the converse is true if is covered by a certain choice of .
Theorem 20.
Let be a connected graph with and suppose that any (equivalently, some) maximally intersecting cover all of , i.e., , then is a skeleton. In particular, is a -skeleton.
Proof.
Since each vertex is incident to each of and , and since , is a graph of degree 3. We will show that taking to be the set of edges in a nontrivial alternating path satisfies conditions (a)-(h).
(a): Paths being odd length follows from (a). If the length of some path were exactly three, then this path cannot be connected to the rest of the graph since the end vertices cannot be incident to and .
(c): If instead some path does not contain a 3-vertex, then every edge on this path is an edge. Swapping and along this path will keep the same but increase , a contradiction.
(d): The vertices in certainly have degree at most . But if some edge is incident to , this edge must also be in , as otherwise, the edge is part of some maximal alternating path in .
(e): The only edges that can be incident to are edges. Observe that any edge not in must be an edge or else it would be part of a maximal alternating path of length at least 3 and would be in . must then be degree 2. Observe also that any edge incident to on some side must be incident to on the other, or else the edge adjacent in could be moved onto the edge to increase . Similarly, for any edge not in , there must exist a alternating path connecting it to . Then this edge must be incident to on its other side, or else we could shift down this path, including the edge in , and increase intersection. is acyclic since there must be some path connecting these vertices to and is degree 2. The connected components of must then be odd alternating paths beginning and ending in .
(f): The rich edges with this are exactly the edges. Consider the maximal alternating path going through any such end-vertex. This path is even by (b). All edges in this path are in . The connected component of containing this path is the path itself since the internal vertices of this path cannot be incident to any edges in except for at most a single edge. To show these are the only even paths in , observe that every edge in must be in either or since and contains no edges. Then in fact every connected component of is an alternating path or cycle. Even length path implies some end is in . But these can only be the endpoints of the paths that are edges, since every other edge must be incident to on both sides.
(g): By above, every connected component must be an alternating path or cycle. can thus have no odd cycles, so it is bipartite.
(h): Suppose towards a contradiction that there was such an alternating cycle . Note that . But if we moved the edges of onto the edges of we would increase since must contain some edge.
Note that, following (a), every connected component of is an odd alternating path with end edges in , and that by construction, every edge appears in . Therefore, (paths in ), since there is exactly one more edge than edge along each of these paths. ∎
6. Possible edges in
Characterizing the graphs with ratio less than 1 and covered by our special choice of matchings was possible due to the restrictions on the configurations in which , , and edges can appear along alternating chains. The edges not appearing in these maximally intersecting matchings do not contribute to the overall structure of graphs with . In this section, we demonstrate that these remaining edges can only appear in specific configurations. There are many questions still open for the edges not in any of the maximally intersecting matchings. Fully understanding the ways in which these unmatched edges can appear in a graph would lead to a full characterization of graphs with .
Throughout, let be an arbitrary finite connected graph.
Lemma 21.
For any , no two -unsaturated vertices are adjacent (in ), unless they are the end-vertices of the same even maximal - alternating path.
Proof.
Let be unsaturated and assume . If both and are not incident to (resp. ), then adding to (resp. ) increases , a contradiction. Thus, say is incident to but not and is incident to but not . Then both and are end-vertices of maximal - alternating paths and . If these paths are different, then we can switch the and on , making incident to and reducing to the previous case, i.e. adding to and increasing . ∎
Lemma 22.
For any , no end-vertex of an even maximal - alternating path is adjacent to any inner vertex of an odd maximal - alternating path or any inner odd vertex of an even maximal - alternating path.
Proof.
Let be an even maximal - alternating path, be an end-vertex of , and be an inner vertex of an odd maximal - alternating path or an inner odd vertex of an even maximal - alternating path. Without loss of generality, by swapping and on , we may assume that is incident to .
If and were adjacent, we could remove the edge on incident to and instead add to , thus replacing both and with new chains and . Note that is an odd path. If , then is an even cycle; otherwise is an odd path. Either way, the number of paths in doesn’t increase, while the number of even paths definitely decreases, contradicting that achieves and . ∎
Perhaps the task of characterizing all unsaturated graphs with ratio in general is difficult and out of reach at the moment, but one can look at subclasses of graphs and try to find a characterization among those. We do not even know whether the following graphs have ratio .
Definition 23.
A graph is called tetris if it is a finite connected subgraph of the grid with no leaves or cutvertices111A cutvertex in a graph is a vertex whose removal increases the number of connected components..
The authors of [IGL:2019] have attempted to prove that tetris graphs have ratio , but unsuccessfully. We state it here as a question.
Question 24.
Is for all tetris graphs ?