CHARACTERIZATION OF DIM LIGHT RESPONSE IN DVS PIXEL: DISCONTINUITY OF EVENT TRIGGERING TIME

The typical DVS circuit of one pixel is illustrated in ${\rm{Fig.}\ref{fig:pixel_circuit}}$. When the light signal on the photodiode $\rm PD$ is static without change, there will be few events other than some noise induced by the junction leak current of diode DL. Assume that the last event triggers at the time $t_{1}$. After time $\Delta t$, the incident light on $\rm PD$ changes from $L(t_{1})$ to ${L(t_{1}+\Delta t)}$, and the source voltage of the metal-oxide-semiconductor (MOS) transistor $\rm{M_{fb}}$ varies from $V_{d}(t_{1})$ to ${V_{d}(t_{1}+\Delta t)}$. In case that the MOS comparators $(\rm{M_{ONp}}\quad and\quad\rm{M_{OFFp}})$ detect that ${V_{d}(t_{1}+\Delta t)}$ overcomes predefined ON threshold -$\Theta_{ON}$ or OFF threshold $\Theta_{OFF}$, an ON or OFF event is triggered, respectively. The process is formulated as follows:

The source voltage ${V_{d}}$ will be reset when the event triggers.

After the introduction of event triggering, we analyze the signal transduction from light signal $L(t)$ to electrical signal $V_{d}(t)$ in the DVS circuit. At time $t_{1}$, the photocurrent flowing across the photodiode $\rm PD$ is $I_{pd}(t_{1})$. After time $\Delta t$, the change of photocurrent is induced in the photodiode $\rm PD$ that satisfies:

The differential amplifier with capacitors $\rm C_{1}$ and $\rm C_{2}$ amplifies $V_{sf}$ that is buffered from $V_{p}$ and then drives the gate of MOS $\rm M_{dp}$ to control the source voltage $V_{d}$ [4]:

where $A=\frac{\rm C_{1}}{\rm C_{2}}$ is the gain of differential amplifier, $\kappa_{sf}$ and $\kappa_{fb}$ are the slope factors of MOS $\rm M_{sf}$ and $\rm M_{fb}$, respectively, and $V_{T}$ is the thermal voltage.

Actually, the photodiode voltage $V_{pd}$ changes with the light signal $L$, despite the clamping by the feedback loop and cascode. The cascode of $\rm M_{n}$ and $\rm M_{cas}$ senses the change of $V_{pd}$ with amplification. The amplified result $V_{p}$ is fed back by $\rm M_{fb}$ to accommodate the change of $I_{pd}$.

In the distributed diagram of photodiode $\rm PD$ given in ${\rm{Fig.}\ref{fig:distribute_photodiode}}$, the junction of $\rm PD$ consists of the parasitic capacitor $\rm C_{J}$. As the parallel resistance $\rm R_{SH}$ is extremely high and the series resistance $\rm R_{S}$ tends to be quite low [15], the charge and discharge of $\rm C_{J}$ is one of the main reasons for the delay and discontinuity of event triggering time.

Ideally, when there is a light intensity change in time $\Delta t$, an immediately stimulated current $\Delta I_{pd}=I_{pd}(t_{1}+\Delta t)-I_{pd}(t_{1})$ will flow across $\rm M_{fb}$. However, in fact this is not the case. In the distributed diagram of photodiode $\rm PD$ shown in ${\rm{Fig.}\ref{fig:distribute_photodiode}}$, $\Delta I_{pd}$ needs to charge or discharge the parasitic capacitor $\rm C_{J}$ of $\rm PD$, firstly. The process is not completed until the voltage of $\rm C_{J}$ reaches $V_{pd}(t_{1}+\Delta t)$ to accommodate the stimulated current $\Delta I_{pd}$.

The charge and discharge of parasitic capacitor $\rm C_{J}$ is time-consuming, leading to a time delay between triggering events. If we evaluate the triggering time of events, the distribution of triggering time is probably discontinuous because there are few events in the time delay region.

As the photodiode $\rm PD$ is reverse-biased, the barrier capacitance is dominant in $\rm C_{J}$. Compared with the built-in potential of photodiode $\rm PD$ (usually hundreds of mV) [16], the voltage change of $V_{pd}$ is much smaller (nearly a few mV) [17]. According to [16], the parasitic capacitance of $\rm C_{J}$ is almost unchanged.

The change of electric charge $\Delta Q$ stored in the capacitor $\rm C_{J}$ is:

Based on Eqs. 1 and 2.1, the change $\Delta V_{p}$ is fixed between two consecutive events. In the small-signal analysis of cascode,

where $-A_{cas}$ is the small-signal gain of cascode.

Therefore, $\Delta V_{pd}$ and $\Delta Q$ are invariable between two consecutive triggering events if we do not consider the influence by shot noise, dark current, and leak noise. Assuming that $\Delta Q_{e}$ is the fixed electric charge difference, there is a time delay between triggering events:

Note that: 1. $\Delta t_{e}$ is not proportional to $\frac{\Delta L}{L}$ ($\Delta\ln L$), which means that the time delay follows a non-first-order system rule of DVS; 2. As $\Delta I_{pd}$ is only related to the threshold ($\Theta_{ON}$ and $\Theta_{OFF}$), $\Delta t_{e}$ is invariant to current light intensity.

In fact, $\Delta I_{pd}$ needs some time to change because light intensity varies with time. DVS voltmeter [14] supposes that $\Delta I_{pd}$ and $\Delta L$ change linearly with time, which is a reasonable assumption in a short period. In that case, $\Delta t_{e}$ follows:

where $\mu=\frac{L(t_{1}+\Delta t)-L(t_{1})}{\Delta t}$ is the changing speed of light intensity and $T$ is the total time between the two triggering events. As can be seen, the time delay $\Delta t_{e}$ is inversely proportion to the changing speed of light intensity $\mu$.

The existence of $\Delta t_{e}$ delays the triggering of events, breaking the inverse Gaussian distribution that is followed by the event triggering time [14]. Because that there are few events triggering during the time delay $\Delta t_{e}$, the distribution of event triggering time fluctuates dramatically, appearing as the discontinuity in the histograms and probability density functions (PDF). As a result, the length of discontinuity in the histograms and PDFs of event triggering time is $\Delta t_{e}$.

In the dim light conditions, the difference of light intensity is generally small, leading to a slow changing speed of light. Therefore, the time delay $\Delta t_{e}$ is prominent.

A real public DAVIS dataset [10], captured by DAVIS240 event camera, is used. Inside the dataset, boxes  6dof scene including over 1.3 billion events is applied. To evaluate the time delay and discontinuity of event triggering time accurately, the frame-based videos are interpolated [18] by 10 times, as done in [14, 12, 19]. We use the ITU-R recommendation $BT.\ 709$ for linear conversion [20]. For the gray frame-based videos, the pixel value is treated as the luma value, in the changing speed $\mu$ and light intensity $L$.

In the following experiments, the histograms of event triggering time are collected under different light intensity $L$ and light changing speed $\mu$. Here $L$ is specified as the average pixel value between the two consecutive events.

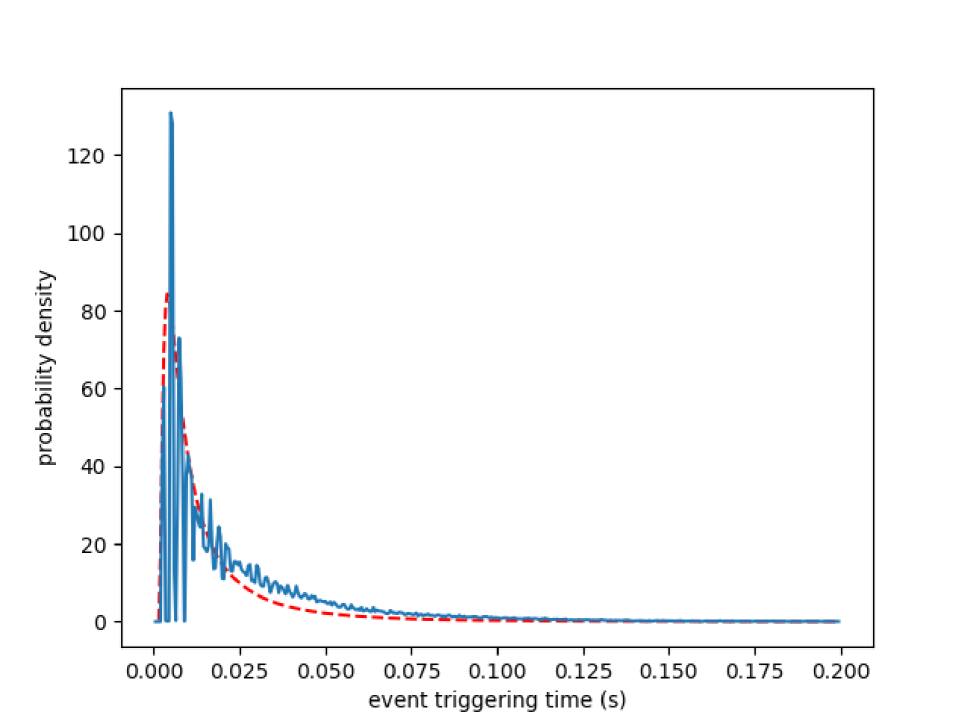
Fig. 3 shows the statistical distributions of event triggering time as the histograms with blue lines in different conditions. The fitting curves above the histograms, marked as red dashed lines, roughly follow the inverse Gaussian distribution. As is exemplified in Fig. 4, there exists significant discontinuity in the histograms, which is also shown in Fig. 3. It validates the existence of the time delay $\Delta t_{e}$ between consecutive triggering events caused by charge and discharge of parasitic capacitor of photodiode $\rm PD$.

In Fig. 3, the lengths of discontinuity remain the same in each row but vary in each column, which demonstrates that the time delay $\Delta t_{e}$ only depends on $\mu$ rather than current light intensity $L$. Therefore, the time delay $\Delta t_{e}$ follows a non-first-order behavior.

We also evaluate the discontinuity length quantitatively in Table 2. The time delay $\Delta t_{e}$ declines with the increasing of changing speed $\mu$, which can also be seen in Fig. 3. Furthermore, the product of $\Delta t_{e}$ and $\mu$ is almost unchanged with the light intensity $L$. It proves our analysis of the inversely proportional relation between them.

The time delay $\Delta t_{e}$ exists with a non-first-order behavior, unlike the usual manner of first-order system of DVS. In the dim light conditions, the changing speed of light is slow because the absolute difference of light is small. As a result, the time delay $\Delta t_{e}$ is more significant.