Chaotic resonance modes in dielectric cavities:
Product of conditionally invariant measure and universal fluctuations

Eigenfunctions in closed quantum systems with classically chaotic dynamics, e.g., in quantum billiards, are well understood based on quantum ergodicity, universal fluctuations, and scarring along unstable periodic orbits [1, 2]. Resonance modes in chaotic scattering systems with escape of particles [3, 4, 5], e.g., the paradigmatic three-disk scattering [6, 7, 8], have a fractal support on which they are distributed depending on their lifetime [9, 10, 11, 12, 13, 14, 15] and the spectrum follows a fractal Weyl law [16, 17, 18, 19].

Resonance modes in scattering systems with partial escape of probability [3] are less understood. The most relevant example are dielectric microcavities [20], see Fig. 1. The relation of cavity shape, ray dynamics, mode structure, and far-field emission pattern has been studied extensively experimentally and theoretically [21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39]. A multifractal probability distribution based on ray dynamics [24], a so-called natural conditionally invariant measure [40], gives a good description of modes with long lifetimes [24, 29, 30, 32, 33, 36, 38, 39].

However, resonance modes have various lifetimes, while the natural measure applies to precisely one lifetime. It is not understood how the multifractal structure of resonance modes depends on their lifetime, even in the simplest setting of a cavity shape with fully chaotic ray dynamics. Experimentally this is most relevant for modes with the longest lifetimes, which have longer lifetimes than the natural measure. Their enhanced scarring has been reported experimentally and numerically [23, 41, 42, 26, 27, 43, 44, 45, 46, 47], but the relation to periodic-orbit scarring is under investigation. On a fundamental level it is open, which features of a resonance mode are system specific with a ray-dynamical origin and which are universal wave phenomena.

In this Letter we answer these questions based on recent progress on quantum maps with partial escape [48, 49], leading to the following conjecture: Chaotic resonance modes in scattering systems are a product

of (i) conditionally invariant measures from classical dynamics with a smoothed spatial density $\varrho(\boldsymbol{r})$ depending on the mode’s lifetime and (ii) universal exponentially distributed fluctuations $\eta(\boldsymbol{r})$ with mean one. An immediate consequence is that the average intensity of modes with similar lifetime is determined by the first factor. We support this conjecture using a dielectric cavity with chaotic ray dynamics, by factorizing modes into an average of modes with similar lifetime and universal fluctuations. It is demonstrated that the multifractal structure of the average strongly depends on the lifetime. This is described by appropriate conditionally invariant measures based on ray dynamics. In particular, this holds for the experimentally relevant modes of optical microcavities with longest lifetime. We explain the scarring of the vast majority of modes along segments of rays based on multifractality and universal fluctuations. It conceptually differs from periodic-orbit scarring and becomes even more prominent in the semiclassical limit. Our computations are done at very small wavelengths.

Modes of dielectric cavity.—We study passive modes in a limaçon shaped cavity, given in polar coordinates by $\rho(\varphi)=R(1+\varepsilon\cos\varphi)$ [50, 30]. For $\varepsilon=0.6$ it is non-convex and shows chaotic ray dynamics practically everywhere in phase space, with possible regular regions [51] being negligibly small. We choose a refractive index $n=3.3$ typical for a semiconductor laser cavity [20] and outside the cavity $n=1$. Antisymmetric TM polarized modes $\psi(\boldsymbol{r})$ fulfilling the Helmholtz equation $[\Delta+n^{2}(\boldsymbol{r})k^{2}]\psi(\boldsymbol{r})=0$ with outgoing boundary conditions are computed for complex wave numbers with $\text{Re}(kR)\in[3100,3101]$ and $\text{Im}(kR)\in[-0.1,0]$. With $nkR\approx 10^{4}$ this is more than an order of magnitude further in the short wavelength limit than previous studies of dielectric cavities, see e.g., Refs. [20, 37, 38, 39]. This allows for numerical comparison to wave chaos experiments with large cavities [39].

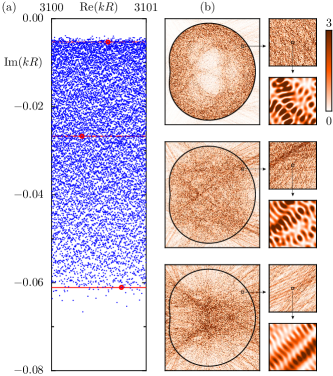
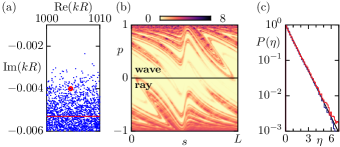
One observes a band of resonance poles with two spectral gaps, one near the real line and one further in the complex plane, see Fig. 1(a). The upper end of the spectrum, with long-lived modes of high quality factor $Q=-(1/2)\text{Re}(k)/\text{Im}(k)\approx 4\cdot 10^{5}$, occurs near the classical natural decay rate $\gamma_{\text{nat}}$ from ray dynamics, discussed below. The lower end of the spectrum, with short-lived modes and a gap towards external modes [52], occurs near the classical natural decay rate $\gamma_{\text{inv}}$ from the inverted ray dynamics, see below. The middle of the spectrum corresponds to the typical classical decay rate $\gamma_{\text{typ}}$ of an ergodic ray [53]. These classical decay rates are indicated in Fig. 1(a) by horizontal lines at $\text{Im}(kR)=-(\gamma/2)R/c$.

For exemplary modes with long, medium, and short lifetimes the intensity $|\psi(\boldsymbol{r})|^{2}$ is presented on a $500\times 560$ grid in Fig. 1(b), showing large-scale structures and fluctuations. Consecutive magnifications reveal finer structures and eventually a smooth wave function on the scale of the wavelength. As expected, one observes a drastic change of the overall structure from long-lived to short-lived modes, with strong intensities shifting from near the boundary to the center of the cavity and angles of reflection changing from total internal reflection to perpendicular to the boundary (see also Fig. 4(b) below). For modes with a similar lifetime one finds similar structures, see gallery of modes [54].

Numerically, we determine the modes using boundary integral equations [55, 56]. For analytic boundaries we use the approach of Ref. [57], which allows to use just slightly more than two discretization points per wavelength on the boundary, giving modes and spectrum with machine accuracy. Here we need $N_{b}=11500$ points on the desymmetrized boundary of length $L/2$ with $L=6.8627R$ at wavelength $\lambda=2\pi/\text{Re}(nk)$ giving $b=2N_{b}\lambda/L=2.06$ points per wavelength. We find all poles in a complex wave number region using a Taylor expansion of the matrix equation in $k$, extending an approach for quantum billiards [58, 59] to complex $k$. We increase the accuracy to machine precision by applying the method of Ref. [58] to every pole in a subspace and subsequent convergence steps. Further details about the numerical approach will be published elsewhere [60]. The high precision of this approach has been used for analyzing resonance assisted tunneling with a resolution of $\text{Im}(kR)=10^{-12}$ [61]. We expect to find all poles in the considered complex wave number region, namely 9964, which is supported by the leading order Weyl term of a dielectric cavity [62, 63] giving $N=\frac{A}{4\pi}n^{2}(3101^{2}-3100^{2})=9960.5$ poles, with area $A=(\pi/2)(1+\varepsilon^{2}/2)$ of the desymmetrized cavity. The next order boundary term for TM modes [62, 63] gives a contribution of less than one mode.

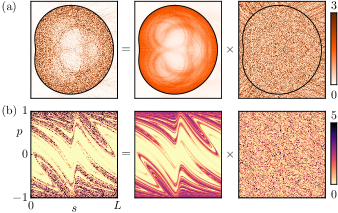
Factorization.—We numerically extract the two factors of Eq. (1) from the resonance modes. The average intensity $\varrho(\boldsymbol{r})=\langle|\psi(\boldsymbol{r})|^{2}\rangle$ is determined from the 200 modes nearest in lifetime. The fluctuations at every point of the grid are determined by $\eta(\boldsymbol{r})=|\psi(\boldsymbol{r})|^{2}/\langle|\psi(\boldsymbol{r})|^{2}\rangle$. For the long-lived mode of Fig. 1(b) this factorization in position space is visualized in Fig. 2(a).

Such a factorization also applies to the incident Husimi function $H(s,p)$ [64] on the boundary phase space $(s,p)$, where $s=0$ is the boundary point for $\varphi=0$ and $p$ is the normalized momentum parallel to the boundary. The average Husimi function $\varrho(s,p)=\langle H(s,p)\rangle$ is determined from the 200 modes nearest in lifetime. The fluctuations at every point $(s,p)$ are determined by $\eta(s,p)=H(s,p)/\langle H(s,p)\rangle$. This factorization is visualized in Fig. 2(b).

One observes that the fluctuations $\eta$ in position space are quite uniform and have almost no spatial structure within the cavity. The same is true for the fluctuations $\eta$ in the boundary phase space. This even holds for regions, where the intensity of the mode and the average are both close to zero. More generally, we expect that the same factorization holds in the full phase space restricted to the energy shell. In the following we will demonstrate that the two factors fulfill the conjecture.

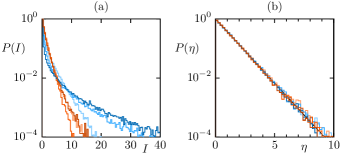
Universal fluctuations.—In Fig. 3(a) the non-universal distribution of the intensities $I$ in position space, $I=|\psi(\boldsymbol{r})|^{2}$, and phase space, $I=H(s,p)$, is shown for the three modes from Fig. 1(b). In contrast, in Fig. 3(b) the fluctuations $\eta$ follow a universal exponential distribution of mean one for more than three orders of magnitude in all cases. This has been conjectured for quantum maps with partial escape [49], corresponds to the properties of a normalized complex random vector [65, 66], and supports property (ii) of the conjecture. Accordingly, the complex amplitude fluctuations $\psi(\boldsymbol{r})/\sqrt{\langle|\psi(\boldsymbol{r})|^{2}\rangle}$ follow a complex Gaussian distribution of variance one (not shown). We stress, that the analysis of the fluctuations presented here is possible only, if the average is determined from sufficiently many and sufficiently nearby modes in lifetime. We mention that the fluctuations $\eta$ of the far-field intensities also agree with the universal exponential distribution (not shown). The correlations of $\eta(\boldsymbol{r})$ and $\eta(s,p)$ on the scale of the wavelength and under time evolution are expected to show similar behavior as for closed systems [67].

A factorization of chaotic modes into an average part and a fluctuating part is used for the explanation of single-mode lasing [68], however under the strong assumption of small fluctuations. For the analysis of single- versus multi-mode lasing the spatial overlap of two modes within the cavity, $C=\int|\psi_{1}(\boldsymbol{r})|\,|\psi_{2}(\boldsymbol{r})|\,\text{d}\boldsymbol{r}$, is important [37], with $\int|\psi_{1,2}(\boldsymbol{r})|^{2}\,\text{d}\boldsymbol{r}=1$. For long-lived modes of the stadium billiard the mean value is $C\approx 0.77$ [37]. From the above universal fluctuations and assuming independence from the average we find universally $C=\pi/4\approx 0.785$ for two chaotic modes with nearby lifetimes in any chaotic cavity. This is consistent with the findings in Ref. [37] and is numerically well confirmed in the present cavity. Thus the demonstrated factorization has a strong impact on the experimentally relevant question of single-mode lasing.

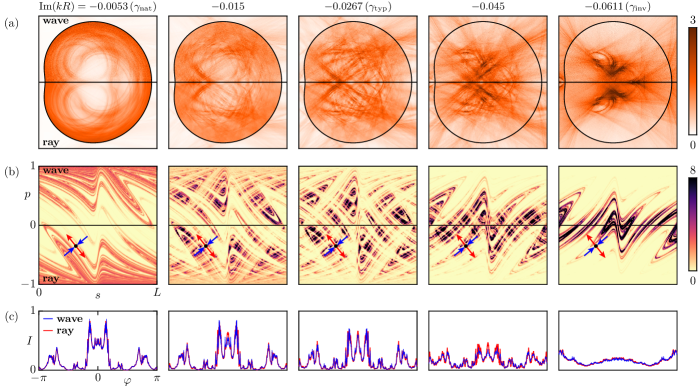
Average of modes and ray dynamics.—In the following we demonstrate that the average structure of chaotic modes with similar lifetime strongly depends on the lifetime and is described by appropriate conditionally invariant measures of ray dynamics, supporting property (i) of the conjecture. So far averages have been computed for long-lived modes [32, 36, 38, 39]. In Fig. 4 we show the strong dependence on $\text{Im}(kR)$ for the average intensity in position space, phase space, and in the far field. The averages are each over 200 nearby modes in $\text{Im}(kR)$ normalized within the cavity. They show very fine details compared to the individual modes in Fig. 1(b).

In Fig. 4(b) we show the corresponding incident Husimi functions. Their structure changes completely with $\text{Im}(kR)$. One observes fractal structures in both the stable and the unstable direction of the ray dynamics. The average far-field intensity is presented in Fig. 4(c). It shows strong directionality in agreement with Ref. [30].

These averaged modes are well explained by conditionally invariant measures based on ray dynamics and smoothed on the scale of a wave length, giving spatial densities $\varrho(\boldsymbol{r})$ and densities $\varrho(s,p)$ in the boundary phase space. The wave-ray comparison supports property (i) of the conjecture, see upper half (wave) and lower half (ray) in Fig. 4(a) and (b). We find perfect agreement at the natural decay rate $\gamma_{\text{nat}}$ and the inverse natural decay rate $\gamma_{\text{inv}}$, while for all other decay rates we use the approximate, but very good, description by product measures, as described in the following.

The natural conditionally invariant measure [40] with natural decay rate $\gamma_{\text{nat}}$ is determined from time evolution of a smooth initial density in phase space using ray dynamics and intensity changes at each reflection according to Fresnel’s laws. This approach has been established for microcavities by Soo-Young Lee et al. [24] and is confirmed for many chaotic cavities [24, 29, 30, 32, 33, 36, 38, 39]. We stress that this measure describes those long-lived modes only, which are close to the natural decay rate $\gamma_{\text{nat}}$. Note that at $\gamma_{\text{nat}}$ the phase-space distribution is smooth along the unstable direction, see Fig. 4(b, left).

A second natural measure is determined from the inverse dynamics, i.e. applying the inverse of Fresnel’s laws at each reflection [69, 70, 48]. The corresponding natural decay rate of the inverse dynamics, $\gamma_{\text{inv}}$, corresponds to short-lived modes, which again are perfectly described, see Fig. 4 right. Note that at $\gamma_{\text{inv}}$ the phase-space distribution is smooth along the stable direction.

For all other decay rates we use the product measures introduced for quantum maps [48]. They are based on the observation that locally in phase space the averaged modes have an (approximate) product structure along stable and unstable direction of ray dynamics. The product measures interpolate between the natural and the inverse natural measure (depending on a parameter $\xi\in\mathbb{R}$) and provide conditionally invariant measures for all decay rates, see Ref. [48] for their construction. These product measures show very good, but not perfect, agreement with the averaged modes, see the three intermediate examples in Fig. 4. Thus we have found wave-ray correspondence for the multifractal structures of the average of chaotic modes down to unprecedented fine details.

Modes with longest lifetime.—Experimentally, the most relevant modes for lasing are those with longest lifetime, i.e. closest to the real axis. Their spectral density decreases with smaller wavelength [71, 70]. In order to have enough modes for averaging, it is therefore numerically convenient to use larger wavelengths, see spectrum in Fig. 5(a). The average incident Husimi function near $\text{Im}(kR)=-0.004$ has structure along the unstable direction, see Fig. 5(b, upper half), and thus clearly differs from the one at $\gamma_{\text{nat}}$, which is smooth along the unstable direction, see Fig. 4(b, left). This structure is qualitatively well described by the corresponding conditionally invariant product measure, see Fig. 5(b, lower half). We analyze the relative fluctuations and find a universal exponential distribution over almost three orders of magnitude, see Fig. 5(c). Thus factorization into ray-dynamical average and universal fluctuations is essential for understanding the structure of these modes.

As an aside we mention that for the considered cavity shape there are whispering gallery-like modes for $\text{Re}(kR)\approx 1000$ and below, which are related to partial barriers. For larger $\text{Re}(kR)\approx 3000$ this ray-dynamical property does no longer affect the modes, as expected from universal scaling properties [72, 73].

Scarring.—The scarring of eigenfunctions in closed chaotic quantum billiards refers to an enhancement along short unstable periodic orbits [74, 75]. For chaotic modes in dielectric cavities and in corresponding quantum maps with escape enhanced scarring of modes has been reported [23, 41, 42, 26, 27, 43, 44, 45, 46, 47]. We observe at very small wavelengths that, in fact, the vast majority of modes show enhanced intensities along segments of rays. This is visible in Fig. 1(b) for examples with medium and short lifetime as well as in the gallery of modes [54] for modes with longest lifetime. It is best seen when the mode is shown with a resolution on the scale of the wavelength, see the first magnifications in Fig. 1(b) and also see Fig. S7 [54], which shows the mode in the middle of Fig. 1(b) with a tenfold finer resolution.

We explain this type of scarring in scattering systems based on multifractality and universal fluctuations and emphasize that it conceptually differs from periodic-orbit scarring. It has a combined ray and wave origin: Whenever the multifractal average structure (ray origin) shows strong intensity enhancements in phase space, then the additional universal fluctuations (wave origin) give rise to some phase-space points with extremely high intensities. For the examples in Fig. 3(a) there are even intensities that are more than a factor of 100 larger than the mean intensity. In position space this gives rise to enhancement of the mode along the corresponding ray in forward and backward direction, sometimes persisting for one or two reflections. Thus we call this phenomenon ray-segment scarring. The most likely directions are determined by the high intensities of the multifractal averaged structure in phase space. The specific direction of the ray segment varies from mode to mode, as the phase-space points with extreme intensities vary due to the universal fluctuations, see e.g. Fig. S3 [54].

The strongest intensity variation in the averaged modes occurs according to Fig. 4(b) for medium and short lifetime and according to Fig. 5(b) for modes with longest lifetime. Correspondingly, the most prominent scarring occurs in these cases, see gallery of modes [54].

For increasingly smaller wavelengths the averaged modes show finer multifractal structures with increasing intensity maxima. Thus we expect that ray-segment scarring becomes even more prominent and is visible for longer segments of a ray in the semiclassical limit.

Outlook.—A semiclassical theory that derives the perfect conditionally invariant measures for modes of all lifetimes remains a future challenge. A first step in this direction is based on a local random vector model applicable to the randomized baker map with partial escape [76]. Further support for the conjecture is expected in chaotic scattering systems with full escape, like the three-disk system.

We thank S. Bittner, E.-M. Graefe, T. Harayama, M. Hentschel, J. Kullig, J. Lötfering, M. Lebental, T. Prosen, J.R. Schmidt, M. Sieber, and J. Wiersig for valuable discussions as well as the organizers of the WOMA conference series. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 262765445.