Cesium + Rydberg molecules and their permanent electric dipole moments
Abstract
Cs2 Rydberg-ground molecules consisting of a Rydberg, (33 39), and a ground state atom, 63 or 4, are investigated by photo-association spectroscopy in a cold atomic gas. We observe vibrational spectra that correspond to triplet and mixed molecular states. We establish scaling laws for the energies of the lowest vibrational states vs principal quantum number and obtain zero-energy singlet and triplet -wave scattering lengths from experimental data and a Fermi model. Line broadening in electric fields reveals the permanent molecular electric-dipole moments; measured values agree well with calculations. We discuss the negative polarity of the dipole moments, which differs from previously reported cases.
pacs:
32.80.Ee, 33.20.-t, 34.20.CfRecently, molecules formed between a ground-state and a Rydberg atom have attracted considerable attention due to their rich vibrational level structure and permanent electric dipole moments, which are unique for homonuclear molecules. A Rydberg-ground molecule arises from low-energy scattering between the Rydberg electron and ground-state atoms located inside the Rydberg electron’s wavefunction. This interaction, initially investigated in Fermi ; Omont , has been predicted to lead to molecular binding in a novel type of Rydberg molecules, including the so-called trilobite Greene and butterfly molecule Hamilton ; Chibisov . The molecular bond length is on the order of the Rydberg-atom size (a thousand Bohr radii a0). Rydberg-ground molecules were first reported in experiments with Rb ( = 35-37) states V. Bendkowsky and later with Rb M. A. Bellos and D. A. Anderson ; A. T. Krupp ; Maclennan states, as well as with Cs J. Tallant ; Booth , HS and Shaffer2019 states. The permanent electric dipole moment of S-type Rydberg-ground molecules has been measured to be 1 Debye for Rb Li2011 and a few thousand Debye for Cs Booth . The large size and the permanent electric dipole moments of Rydberg-ground molecules make these molecules good candidates for the realization of certain strongly correlated many-body gases Weimer and for quantum information processing Lukin ; Demille ; Rabl , as well as for dipolar quantum gases and spin systems with long-range interactions Baranov ; Kadau .
Here we report on the measurement of long-range Cs2 () Rydberg-ground molecules for 33 39, or 5/2, and or 4. These molecules are deeply in the Hund’s case(c)-regime, which differs from Rb -type molecules at lower , which are Hund’s case(a) Maclennan or between Hund’s case(a) and (c) D. A. Anderson ; A. T. Krupp . Using a Fermi model, we calculate molecular potential energy curves (PECs), vibrational energies and permanent electric-dipole moments.
The scattering interaction between the Rydberg electron and the ground-state atom is, in the reference frame of the Rydberg ionic core Omont ,
| (1) | ||||
where r and are the positions of the Rydberg electron and the perturber atom, the scattering lengths, is the electron momentum, and the scattering partial-wave order (0 or 1 for -wave or -wave, respectively). The full Hamiltonian of the system is Anderson ,
| (2) |
where is the unperturbed Hamiltonian, which includes the spin-orbit interaction of the Rydberg atom. The second term sums over singlet ( = ) and triplet ( = ) scattering channels, using the projection operators , ( and are the electronic spins of the Rydberg and ground-state atom, respectively). The last term represents the hyperfine coupling of to the ground-state-atom nuclear spin , with hyperfine parameter . Numerical solutions of the Hamiltonian in Eq. (2) on a grid of -values yield sets of PECs. Figure 1(a) shows four PECs that are asymptotically connected with the atomic 36-state. The PECs for for =3 and =4 are practically identical, while the PECs for are 10 MHz deeper for =3 than for =4. A similar behavior was seen in Rb D. A. Anderson ; Maclennan and Cs HS .
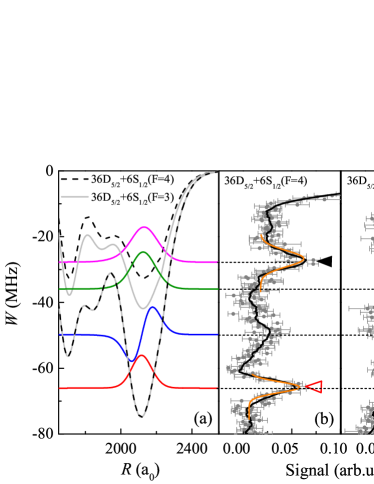
The experiment is performed in a crossed optical dipole trap (CODT) loaded from a magneto-optical trap (MOT). The CODT density, measured by absorption imaging, is cm-3. This is sufficiently dense to excite Rydberg-ground molecules with bond lengths m (our case). After switching off the trapping lasers, two counter-propagated 852- and 510-nm lasers (pulse duration 3 s) are applied to photo-associate the atoms into Rydberg-ground molecules. The lasers are both frequency-stabilized to the same high-finesse Fabry-Perot (FP) cavity to less than 500 kHz linewidth. The 852-nm laser is 360 MHz blue-detuned from the intermediate F’ level. The 510-nm laser is scanned from the atomic Rydberg line to 150 MHz below by scanning the radio-frequency signal (RF) applied to the electro-optic modulator used to lock the laser to the FP cavity. Rydberg molecules are formed when the detuning from the atomic line matches the binding energy of a molecular vibrational state. Rydberg atoms and molecules are detected using electric-field ionization and a microchannel plate (MCP) ion detector. Suitable timing of the MOT repumping laser allows us to prepare the atoms and molecules in either =4 or =3. The 510-nm laser can be tuned to excite either or molecules.
In Fig. 1 we show photo-association spectra of molecules for (Fig. 1(b)) and (Fig. 1(c)), respectively. To reduce uncertainties, the spectra are averaged over ten measurements. Both spectra display a pair of dominant molecular peaks, marked with triangles. They correspond to the vibrational ground () states in the outermost wells of the shallow () and deep () PECs shown in Fig. 1(a), which arise from -wave scatting. The deep, PEC corresponds with a triplet state of the Rydberg electron and the atom. The two PECs correspond with mixed singlet-triplet states and have a reduced depth, which roughly is in proportion with the amount of triplet character in the molecular states. The binding energies of the states are extracted from Gaussian fits to the measured molecular peaks, with statistical uncertainties on the order of 1 MHz. Systematic uncertainties in the molecular line positions are negligible because of the high signal-to-noise ratio of the atomic reference lines in the spectra (relative to which the binding energies are measured), and because the FP cavity and the RF used to lock and scan the lasers have no significant drift.
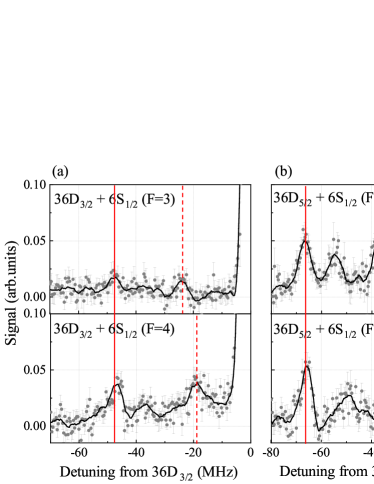
We have obtained the photo-association spectra for all combinations of and , for to 39. In Fig. 2 we show the results for the case . The and states are well-resolved and allow for accurate comparison of level energies between experiment and theory. The , levels, marked by solid vertical lines, do not depend on . Since the PECs for the measured states are largely due to -wave scattering, the ratio of the binding energies of the , levels between and is approximately given by the square of the ratio between the Clebsch-Gordan coefficients , with or , and with magnetic quantum numbers , and for the coupled, orbital and electron spins of the Rydberg electron, respectively. For -type Rydberg-ground molecules in Hund’s case (c), the binding-energy ratio is , which is close to the binding-energy ratio evident in Fig. 2. The vertical dashed lines of Fig. 2 mark the states, which are mixed singlet-triplet. These are about half as deeply bound as , whereby for is about 5 to 10 MHz more deeply bound than for .
For quantitative modeling of the singlet and triplet -wave scattering length functions and , we have measured the binding energies of the states and for molecules with , for both values of . The measured data, listed in detail in the Supplement, are fitted with functions , with effective quantum number and exponent (see Table I). The are concentrated around , with one exception. Calculated binding energies, listed in the Supplement, yield respective fitted exponents that are within the uncertainty of the (see Table I), with the exception of the case, where the binding energies are smallest. The -values generally have a magnitude that is significantly less than . A value of would be expected based on Rydberg wavefunction density. The deviation of from may be attributed to the fact that at lower the molecules are less deep in Hund’s case (c) than at higher . This may diminish the binding of the molecules at lower and lead to a reduction of the magnitude of . A modification of the scaling may also arise from -wave-scattering-induced configuration mixing at lower as well as from the zero-point energy of the vibrational states.
The measured binding-energy data are employed to determine -wave scattering lengths via comparison with model calculations similar to Maclennan . The calculations yield best-fitting -wave scattering-length functions for both singlet and triplet scattering, and , with zero-energy scattering lengths a0 and a0; a comparison with previous results is presented in the Supplement. In our calculation we have included -wave scattering and found that it has only a small effect on the lowest vibrational resonances in the outermost wells of the PECs suying2020 , within our -range of interest. This is because the outermost wells are separated fairly well from further-in wells and are therefore strongly dominated by -wave scattering, justifying our use of less accurate non-relativistic -wave scattering-length functions and Khuskivadze2002 .
| S/T(F=3) | T(F=3) | S/T(F=4) | T(F=4) | |
|---|---|---|---|---|
| -5.65 0.38 | -5.60 0.16 | -6.19 0.14 | -5.62 0.16 | |
| -5.68 0.01 | -5.62 0.01 | -5.55 0.01 | -5.62 0.01 |
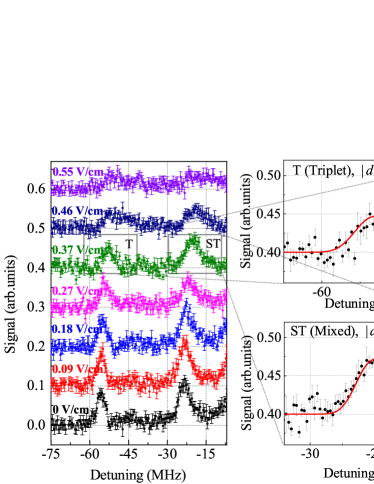
Homonuclear Rydberg-ground molecules are unusual, in part, because of their permanent electric dipole moment, , which are caused by configuration mixing. The values of are usually small in molecules with low- character, with the notable exception of Cs -type molecules, where the quantum defect allows strong mixing with trilobite states Booth . The values of , with index denoting the PEC and the vibrational state, can be measured via the broadening of the respective molecular line in an applied weak electric field, . For electric-dipole energies, , that are much smaller than the molecular binding energy, the line is inhomogeneously broadened about its center by a square function of full width in frequency. This model applies if the moment of inertia of Rydberg molecules is very large and rotational structure cannot be resolved (our case). The square function is convoluted with a Gaussian profile to account for laser line broadening, electric-field inhomogeneities, magnetic fields etc. The standard deviation of this Gaussian is experimentally determined by fitting field-free molecular lines. The overall line profile, , as a function of detuning from the line center then is
| (3) |
Since the field is accurately known from Rydberg Stark spectroscopy, the values of follow from comparing measured line shapes with profile functions calculated using Eq. (3) over a range of test values for .
In Fig. 3 we show line-broadening measurements for + Rydberg molecules in several electric fields, as well as fit results based on Eq. 3 for the vibrational ground states of (top) and (bottom) PECs for the case V/cm. The obtained dipole-moment magnitudes are 5.70 (6.34) for the triplet (mixed) states. Analysis of the spectra for 0.18, 0.27 and 0.37 V/cm yields averaged dipole-moment magnitudes of 4.79 0.78 for and 5.49 1.03 for .
For a comparison with theory, we first solve Eq. (2) to obtain the PECs and electronic adiabatic dipole moments along the internuclear axis, . We then find the vibrational energies and wavefunctions, , on the PECs Anderson . The dipole moments of the molecules, , are
| (4) |
For the states we find values ranging between -4.85 ea0 at and -4.60 ea0 at . For , the calculated dipole moment is -4.64 ea0, which is in good agreement with the measured result ( = 4.79 0.78 ).
We note that the molecular lines also exhibit a DC Stark shift due to the electric polarizability, , of the Rydberg atom. The atomic DC Stark shifts, , depend on the magnetic quantum number due to the tensor component of the polarizability. If the molecular Stark shift is less than the molecular binding, it can be calculated perturbatively as an average shift with weights , where is in the laboratory frame (defined by the direction of the applied electric field). Figure 3 further includes a hint that the molecular lines may split in stronger electric fields (top curve for 0.55 V/cm). The DC Stark shifts and possible splittings can result in an overestimate of the molecular dipole moment; this may explain the deviations between measured and calculated dipole moments.
While the current measurement method does not give the sign of , the calculations reveal that the of Cs -type Rydberg-ground molecules are negative, which differs from reports on other types of Rydberg-ground molecules J. Tallant ; Booth ; HS ; Markson . Physically, the sign of reflects the direction of the electronic charge shift along the axis of the Rydberg molecule relative to the location of the Cs 6 atom. The direction of the weak electric field applied to measure the dipole moment is not relevant, as long as the field is weak (our case). A negative corresponds with a deficiency of electron charge from the vicinity of the Cs 6 perturber atom. This situation can generally be described as destructive interference of the Rydberg electron wavefunction near the perturber or, equivalently, as a possible case of electronic configuration mixing near the perturber (LCAO picture).
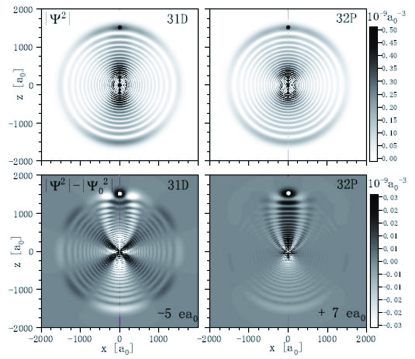
For further illustration, in Fig. 4 we show electronic wavefunctions of Cs -type and -type Rydberg-ground molecules in the outer well of the respective PECs (see Fig. 1 for typical PECs). Since the configuration mixing is weak, in the bottom panels in Fig. 4 we plot the difference of the wavefunction density relative to that of the unperturbed atomic state. An analysis of the electronic states by - and -quantum numbers shows that the -type molecule mostly mixes with orbitals and with a combination of high states similar to the trilobite state Greene , while the -type molecule mostly mixes with orbitals and the trilobite-like state. Admixtures from - and -states are smaller. The admixture probabilities , corresponding to a typical wavefunction density variation on the order of a few percent, as seen in Fig. 4, leading to -values much smaller than the wavefunction diameter. In Fig. 4 it is seen that the -state molecule exhibits predominantly constructive interference near the perturber, corresponding to a positive dipole moment. A similar mixing analysis was reported for Rb (+) molecules with a small positive dipole moment Li2011 . Interestingly, for the -state molecule in Cs the mixing near the perturber is predominantly destructive, corresponding to a negative dipole moment.
In summary, we have observed Cs Rydberg-ground molecules involving Rydberg-state fine structure and ground-state hyperfine structure. Measurements of the binding energies for and molecular vibrational states were modeled with calculations. We have measured permanent electric dipole moments with magnitudes of a few ea0. Calculations show that the dipole moment is negative. Future work may further elucidate this behavior, the exact shifts and splittings due to the tensor atomic polarizability, as well as the transition from weak to large electric-dipole energy shifts relative to the molecular binding.
The work was supported by the National Key RD Program of China (Grant No. 2017YFA0304203), the National Natural Science Foundation of China (Grants Nos. 11434007, 61835007, 61675123, 61775124 and 11804202), Changjiang Scholars and Innovative Research Team in University of Ministry of Education of China (Grant No. IRT_17R70) and 111 project (Grant No. D18001) and 1331KSC.
References
- (1) E. Fermi, Il Nuovo Cimento 11, 157 (1934).
- (2) A. Omont, J. Phys. France 38, 1343 (1977).
- (3) C. H. Greene, A. S. Dickinson, and H. R. Sadeghpour, Phys. Rev. Lett. 85, 2458 (2000).
- (4) E. L. Hamilton, C. H. Greene and H. R. Sadeghpour, J. phys. B: At. Mol. Opt. Phys. 35, L199 (2002).
- (5) M. I. Chibisov, A. A. Khuskivadze and I. I. Fabrikant, J. phys. B: At. Mol. Opt. Phys. 35, L193 (2002).
- (6) V. Bendkowsky, B. Butscher, J. Nipper, J. P. Shaffer, R. Löw, and T. Pfau, Nature 458, 1005 (2009).
- (7) M. A. Bellos, R. Carollo, J. Banerjee, E. E. Eyler, P. L. Gould, and W. C. Stwalley, Phys. Rev. Lett. 111, 053001 (2013).
- (8) D. A. Anderson, S. A. Miller, and G. Raithel, Phys. Rev. Lett. 112, 163201 (2014).
- (9) A. T. Krupp, A. Gaj, J. B. Balewski, P. Ilzhöfer, S. Hofferberth, R. Löw, T. Pfau, M. Kurz, and P. Schmelcher, Phys. Rev. Lett. 112, 143008 (2014).
- (10) J. L. MacLennan, Y. J.Chen, and G. Raithel, Phys. Rev. A 99, 033407 (2019).
- (11) J. Tallant, S. T. Rittenhouse, D. Booth, H. R. Sadeghpour, and J. P. Shaffer, Phys. Rev. Lett. 109, 173202 (2012).
- (12) D. Booth, S. T. Rittenhouse, J. Yang, H. R. Sadeghpour and J. P. Shaffer, Science 348, 6230 (2015).
- (13) H. Saßmannshausen, F. Merkt, and J. Deiglmayr, Phys. Rev. Lett. 114, 133201 (2015).
- (14) C. Fey, J. Yang, S. T. Rittenhouse, F. Munkes, M. Baluktsian, P. Schmelcher, H. R. Sadeghpour and J. P. Shaffer, Phys. Rev. Lett. 122, 103001 (2019).
- (15) W. Li, T. Pohl, J. M. Rost, Seth T. Rittenhouse, H. R. Sadeghpour, J. Nipper, B. Butscher, J. B. Balewski, V. Bendkowsky, R. Löw, T. Pfau, Science, 334, 1110 (2011).
- (16) H. Weimer, M. Müller, I. Lesanovsky, P. Zoller and H. P. Büchler. Nature Physics, 6, 382-388 (2010).
- (17) M. D. Lukin, M. Fleischhauer, R. Cote, L. M. Duan, D. Jaksch, J. I. Cirac and P. Zoller. Phys. Rev. Lett. 87, 037901 (2001).
- (18) D. DeMille, Phys. Rev. Lett. 88, 067901 (2002).
- (19) P. Rabl, D. DeMille, J. M. Doyle, , M. D. Lukin, R. J. Schoelkopf and P. Zoller, Phys. Rev. Lett. 97, 033003 (2006).
- (20) M. A. Baranov, M. Dalmonte, G. Pupillo, P. Zoller, Chem. Rev. 112, 5012-5061 (2012).
- (21) H. Kadau, M. Schmitt, M. Wenzel, C. Wink, T. Maier, I. Ferrier-Barbut and T. Pfau. Nature 530, 194-197 (2016).
- (22) S. Markson, S. T. Rittenhouse, R. Schmidt, J. P. Shaffer and H. R. Sadeghpour, Chem. Phys. Chem. 17, 3683-3691 (2016).
- (23) D. A. Anderson, S. A. Miller, and G. Raithel, Phys. Rev. A 90,062518 (2014).
- (24) S. Bai, X. Han, J. Bai, Y. Jiao, H. Wang, J. Zhao and S. Jia, J. Chem. Phys. 152, 084302 (2020);
- (25) A. A. Khuskivadze, M. I. Chibisov, and I. I. Fabrikant, Phys. Rev. A 66, 042709 (2002).