Certifying Some Distributional Fairness
with Subpopulation Decomposition

Now we are ready to define the fairness certification based on the optimized fairness constrained distribution. We define the certification under two data generation scenarios: general shifting and sensitive shifting. In particular, consider the data generative model $\Pr(X_{o},X_{s},Y)=\Pr(Y)\Pr(X_{s}|Y)\Pr(X_{o}|Y,X_{s})$, where $X_{o}$ and $X_{s}$ represent the non-sensitive and sensitive features, respectively. If all three random variables on the RHS are allowed to change, we call it general shifting; if both $\Pr(Y)$ and $\Pr(X_{s}|Y)$ are allowed to change to ensure the fair base rate (Def. 2) while $\Pr(X_{o}|Y,X_{s})$ is the same across different groups, we call it sensitive shifting. In Section 3 we will introduce our certification framework for both scenarios.

In the above definition, we define the fairness certificate as the upper bound of the model’s loss among all fair base rate distributions ${\mathcal{Q}}$ within a bounded distance from ${\mathcal{P}}$. Besides the bounded distance constraint $\mathrm{dist}({\mathcal{P}},{\mathcal{Q}})\leq\rho$, there is no other constraint between ${\mathcal{P}}$ and ${\mathcal{Q}}$ so this satisfies “general shifting”. This bounded distance constraint, parameterized by a tunable parameter $\rho$, ensures that the test distribution should not be too far away from the training. In practice, the model $h_{\theta}$ may represent a DNN whose complex analytical forms would pose challenges for solving Problem 1. As a result, as we will show in Equation 2 we can query some statistics of $h_{\theta}$ trained on ${\mathcal{P}}$ as constraints to characterize $h_{\theta}$, and thus compute the upper bound certificate.

The feasible region of optimization problem 1 might be empty if the distance bound $\rho$ is too small, and thus we cannot provide fairness certification in this scenario, indicating that there is no nearby fair distribution and thus the fairness of the model trained on the highly “unfaired" distribution is generally low. In other words, if the training distribution ${\mathcal{P}}$ is unfair (typical case) and there is no feasible fairness constrained distribution ${\mathcal{Q}}$ within a small distance to ${\mathcal{P}}$, fairness cannot be certified.

This definition follows the intuition of typical real-world scenarios: The real-world training dataset is usually biased due to the limitation in data curation and collection processes, which causes the model to be unfair. Thus, when the trained models are evaluated on the real-world fairness constrained test distribution or ideal fair distribution, we hope that the model does not encode the training bias which would lead to low test performance. That is to say, the model performance on fairness constrained distribution is indeed a witness of the model’s intrinsic fairness.

We can further constrain that the subpopulation of ${\mathcal{P}}$ and ${\mathcal{Q}}$ parameterized by $X_{s}$ and $Y$ does not change, which results in the following “sensitive shifting” fairness certification.

The definition adds an additional constraint between ${\mathcal{P}}$ and ${\mathcal{Q}}$ that each subpopulation, partitioned by the sensitive attribute $X_{s}$ and label $Y$, does not change. This constraint corresponds to the scenario where the distribution shifting between training and test distributions only happens on the proportions of different sensitive attributes and labels, and within each subpopulation the shifting is negligible.

In addition, to model the real-world test distribution, we may further request that the test distribution ${\mathcal{Q}}$ is not too skewed regarding the sensitive attribute $X_{s}$ by adding constraint (1). We will show that this constraint can also be integrated into our fairness certification framework flexibly in Section 4.3.

$$\small\forall i\in[S],\forall j\in[S],\left|\Pr_{(X,Y)\sim{\mathcal{Q}}}[X_{s}=i]-\Pr_{(X,Y)\sim{\mathcal{Q}}}[X_{s}=j]\right|\leq\Delta_{S}.$$

(1)

Connections to Other Fairness Measurements. Though not explicitly stated, our goal of certifying the performance on a fair distribution ${\mathcal{Q}}$ relates to certifying established fairness definitions in the literature. Consider the following example: Suppose Problem 2 is feasible and returns a classifier $h_{\theta}$ that achieves certified fairness per group and per label class $\bar{l}:=\Pr_{(X,Y)\sim{\mathcal{Q}}}[h_{\theta}(X)\neq Y|Y=y,X_{s}=i]\leq\epsilon$ on ${\mathcal{Q}}$. We will then have the following proposition:

The core idea in our framework is (finite) subpopulation decomposition. Consider a generic optimization problem for computing the loss upper bound on a constrained test distribution ${\mathcal{Q}}$, given training distribution ${\mathcal{P}}$ and trained model $h_{\theta}(\cdot)$, we first characterize model $h_{\theta}(\cdot)$ based on some statistics, e.g., mean and variance for loss of the model: $h_{\theta}(\cdot)$ satisfies $e_{j}({\mathcal{P}},h_{\theta})\leq v_{j}$, $1\leq j\leq L$. Then we characterize the properties (e.g., fair base rate) of the test distribution ${\mathcal{Q}}$: $g_{j}({\mathcal{Q}})\leq u_{j}$, $1\leq j\leq M$. As a result, we can upper bound the loss of $h_{\theta}(\cdot)$ on ${\mathcal{Q}}$ as the following optimization:

$$\small\max_{{\mathcal{Q}},\theta}\mathbb{E}_{(X,Y)\sim{\mathcal{Q}}}[\ell(h_{\theta}(X),Y)]\quad\mathrm{s.t.}\quad H({\mathcal{P}},{\mathcal{Q}})\leq\rho,\quad e_{j}({\mathcal{P}},h_{\theta})\leq v_{j}\,\forall j\in[L],\quad g_{j}({\mathcal{Q}})\leq u_{j}\,\forall j\in[M].$$

(2)

Now we decompose the space ${\mathcal{Z}}:={\mathcal{X}}\times{\mathcal{Y}}$ to $N$ partitions: ${\mathcal{Z}}:=\biguplus{\mathcal{Z}}_{i}$, where ${\mathcal{Z}}$ is the support of both ${\mathcal{P}}$ and ${\mathcal{Q}}$. Then, we denote ${\mathcal{P}}$ conditioned on ${\mathcal{Z}}_{i}$ by ${\mathcal{P}}_{i}$ and similarly ${\mathcal{Q}}$ conditioned on ${\mathcal{Z}}_{i}$ by ${\mathcal{Q}}_{i}$. As a result, we can write ${\mathcal{P}}=\sum_{i\in[N]}p_{i}{\mathcal{P}}_{i}$ and ${\mathcal{Q}}=\sum_{i\in[N]}q_{i}{\mathcal{Q}}_{i}$. Since ${\mathcal{P}}$ is known, $p_{i}$’s are known. In contrast, both ${\mathcal{Q}}_{i}$ and $q_{i}$’s are optimizable. Our key observation is that

$$\small H({\mathcal{P}},{\mathcal{Q}})\leq\rho\iff 1-\rho^{2}-\sum_{i=1}^{N}\sqrt{p_{i}q_{i}}(1-H({\mathcal{P}}_{i},{\mathcal{Q}}_{i})^{2})\leq 0$$

(3)

which leads to the following theorem.

In Problem 2, the challenge is to deal with the fair base rate constraint. Our core technique in Thm. 1 is subpopulation decomposition. At a high level, thanks to the disjoint support among different subpopulations, we get Equation 3. This equation gives us an equivalence relationship between distribution-level (namely, ${\mathcal{P}}$ and ${\mathcal{Q}}$) distance constraint and subpopulation-level (namely, ${\mathcal{P}}_{i}$’s and ${\mathcal{Q}}_{i}$’s) distance constraint. As a result, we can rewrite the original problem (2) using sub-population as decision variables as in Equation 4b and then imposing the unity constraint (Equation 4c) to get Thm. 1. We provide a detailed proof in Section C.2. Although the optimization problem (Equation 4) may look more complicated then the original Equation 2, this optimization simplifies the challenging fair base rate constraint, allows us to upper bound each subpopulation loss $\mathbb{E}_{(X,Y)\sim{\mathcal{Q}}_{i}}[\ell(h_{\theta}(X),Y)]$ individually, and hence makes the whole optimization tractable.

For the sensitive shifting case, we instantiate Thm. 1 and obtain the following fairness certificate.

As Thm. 2 suggests, we can exploit the expectation information $E_{s,y}=\mathbb{E}_{(X,Y)\sim{\mathcal{P}}_{s,y}}[\ell(h_{\theta}(X),Y)]$ and density information $p_{s,y}=\Pr_{(X,Y)\sim{\mathcal{P}}}[X_{s}=s,Y=y]$ of each ${\mathcal{P}}$’s subpopulation to provide a tight fairness certificate in sensitive shifting. The convex optimization problem with $(S+C)$ variables can be efficiently solved by off-the-shelf packages.

For the general shifting case, we leverage Thm. 1 and the parameterization trick $q_{s,y}:=k_{s}r_{y}$ used in Thm. 2 to reduce Problem 1 to the following constrained optimization.

Now the main obstacle is to solve the non-convex optimization in Problem 6. Here, as the first step, we upper bound the loss of $h_{\theta}(\cdot)$ within each shifted subpopulation ${\mathcal{Q}}_{s,y}$, i.e., upper bound $\mathbb{E}_{(X,Y)\sim{\mathcal{Q}}_{s,y}}[\ell(h_{\theta}(X),Y)]$ in Equation 6a, by Equation 12 in Section B.2 [47]. Then, we apply variable transformations to make some decision variables convex. For the remaining decision variables, we observe that they are non-convex but bounded. Hence, we propose the technique of grid-based sub-problem construction. Concretely, we divide the feasible region regarding non-convex variables into small grids and consider the optimization problem in each region individually. For each sub-problem, we relax the objective by pushing the values of non-convex variables to the boundary of the current grid and then solve the convex optimization sub-problems. Concretely, the following theorem states our computable certificate for Problem 1, with detailed proof in Section C.5.

In Section 3.2 and Section 3.3, we present Thm. 2 and Thm. 3 that provide computable fairness certificates for sensitive shifting and general shifting scenarios respectively. In these theorems, we need to know the quantities related to the training distribution and trained ${\mathcal{P}}$ and model $h_{\theta}(\cdot)$:

$$\small E_{s,y}=\underset{(X,Y)\sim{\mathcal{P}}_{s,y}}{\mathbb{E}}[\ell(h_{\theta}(X),Y)],V_{s,y}=\underset{(X,Y)\sim{\mathcal{P}}_{s,y}}{{\mathbb{V}}}[\ell(h_{\theta}(X),Y)],p_{s,y}=\Pr_{(X,Y)\sim{\mathcal{P}}}[X_{s}=s,Y=y].$$

(9)

Section 3.3 further requires $C_{s,y}$ and $\bar{\gamma}_{s,y}$ which are functions of $E_{s,y}$ and $V_{s,y}$. However, a practical challenge is that common training distributions do not have an analytical expression that allows us to precisely compute these quantities. Indeed, we only have access to a finite number of individually drawn samples, i.e., the training dataset, from ${\mathcal{P}}$. Thus, we will provide high-confidence bounds for $E_{s,y}$, $V_{s,y}$, and $p_{s,y}$ in Lemma D.1 (stated in Section D.1).

For Thm. 2, we can replace $E_{s,y}$ in the objective by the upper bounds of $E_{s,y}$ and replace the concrete quantities of $p_{s,y}$ by interval constraints and the unit constraint $\sum_{s}\sum_{y}p_{s,y}=1$, which again yields a convex optimization that can be effectively solved. For Thm. 3, we compute the confidence intervals of $C_{s,y}$ and $\rho_{s,y}$, then plug in either the lower bounds or the upper bounds to the objective (8a) based on the coefficient, and finally replace the concrete quantities of $p_{s,y}$ by interval constraints and the unit constraint $\sum_{s}\sum_{y}p_{s,y}=1$. The resulting optimization is proved to be convex and provides an upper bound for any possible values of $E_{s,y}$, $V_{s,y}$, and $p_{s,y}$ within the confidence intervals. We defer the statement of Thm. 2 and Thm. 3 considering finite sampling error to Section D.2. To this point, we have presented our framework for computing high-confidence fairness certificates given access to model $h_{\theta}(\cdot)$ and a finite number of samples drawn from ${\mathcal{P}}$.

In the general shifting scenario, we similarly randomly generate $30,000$ fair distributions ${\mathcal{Q}}$ shifted from ${\mathcal{P}}$. Different from sensitive shifting, the distribution conditioned on sensitive attribute $X_{s}$ and label $Y$ can also change in this scenario. Therefore, we construct another distribution ${\mathcal{Q}}^{\prime}$ disjoint with ${\mathcal{P}}$ on non-sensitive attributes and mix ${\mathcal{P}}$ and ${\mathcal{Q}}^{\prime}$ in each subpopulation individually guided by mixing parameters satisfying fair base rate constraint. Detailed generation steps are given in Section E.2. Since the fairness certification for general shifting requires bounded loss, we select classification error (Error) and Jensen-Shannon loss (JSD Loss) as the evaluation metric. Figure 2 illustrates the certified fairness with classification error metric under general shifting. Results of JSD loss and more results on two relatively small datasets (Crime, German) are in Section E.5.

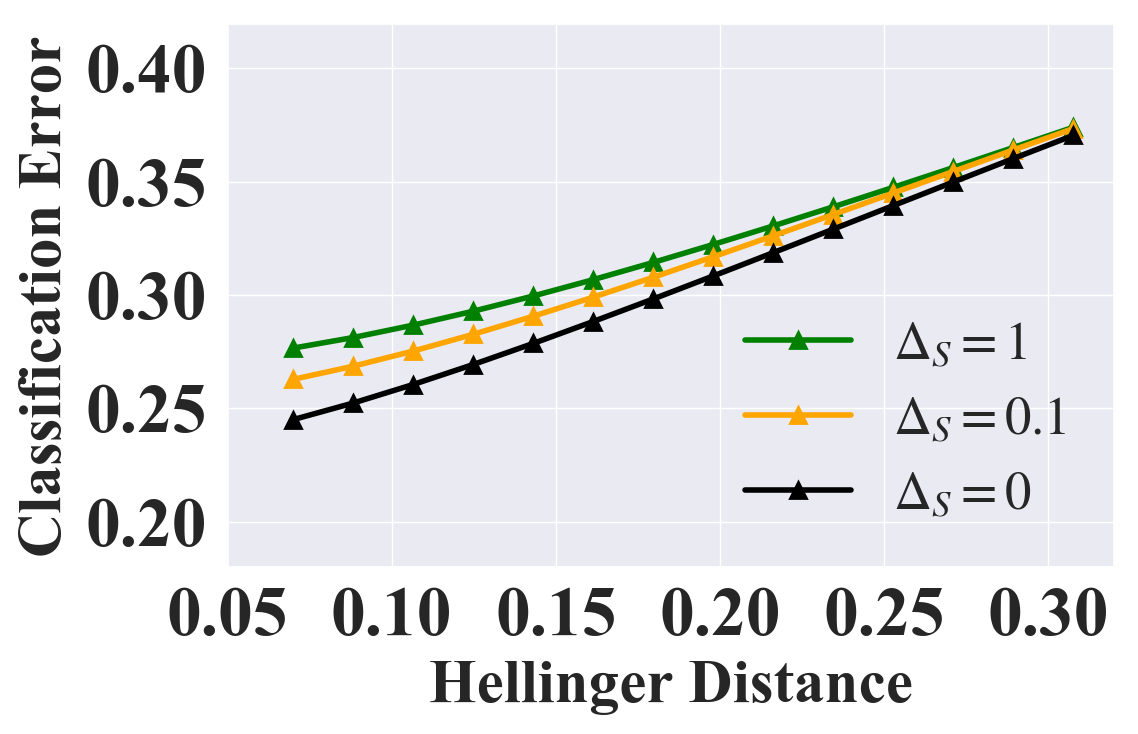
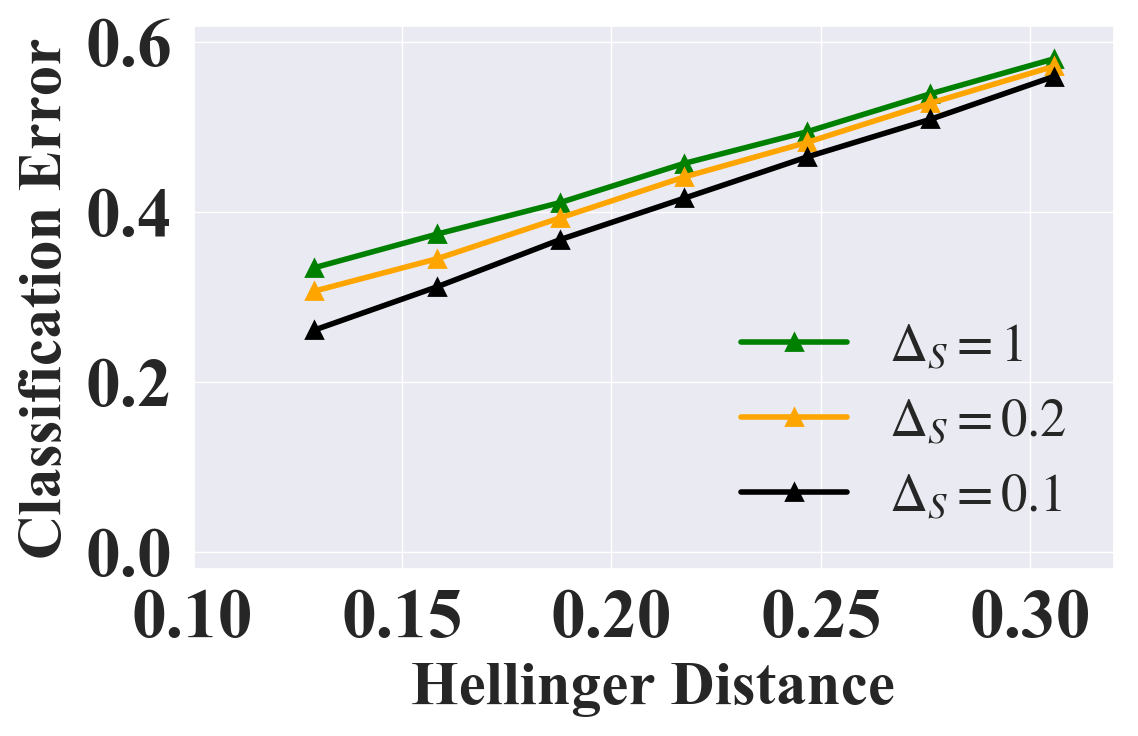
In Section 2.1, we discussed that to represent different real-world scenarios we can add more constraints such as Equation 1 to prevent the skewness of ${\mathcal{Q}}$, which can be flexibly incorporated into our certificate framework. Concretely, for sensitive shifting, we only need to add one more box constraint²²2Note that such modification is only viable when sentive attributes take binary values, which is the typical scenario in the literature of fairness evaluation [39, 38, 31, 42]. $0.5-\Delta_{s}/2\leq k_{s}\leq 0.5+\Delta_{s}/2$ where $\Delta_{s}$ is a parameter controlling the skewness of ${\mathcal{Q}}$, which still guarantees convexity. For general shifting, we only need to modify the region partition step2, where we split $[0.5-\Delta_{s}/2,0.5+\Delta_{s}/2]$ instead of $[0,1]$. The certification results with additional constraints are in Figures 3(a) and 3(b), which suggests that if the added constraints are strict (i.e., smaller $\Delta_{s}$), the bound is tighter. More constraints w.r.t. labels can also be handled by our framework and the corresponding results as well as results on more datasets are in Section E.6.

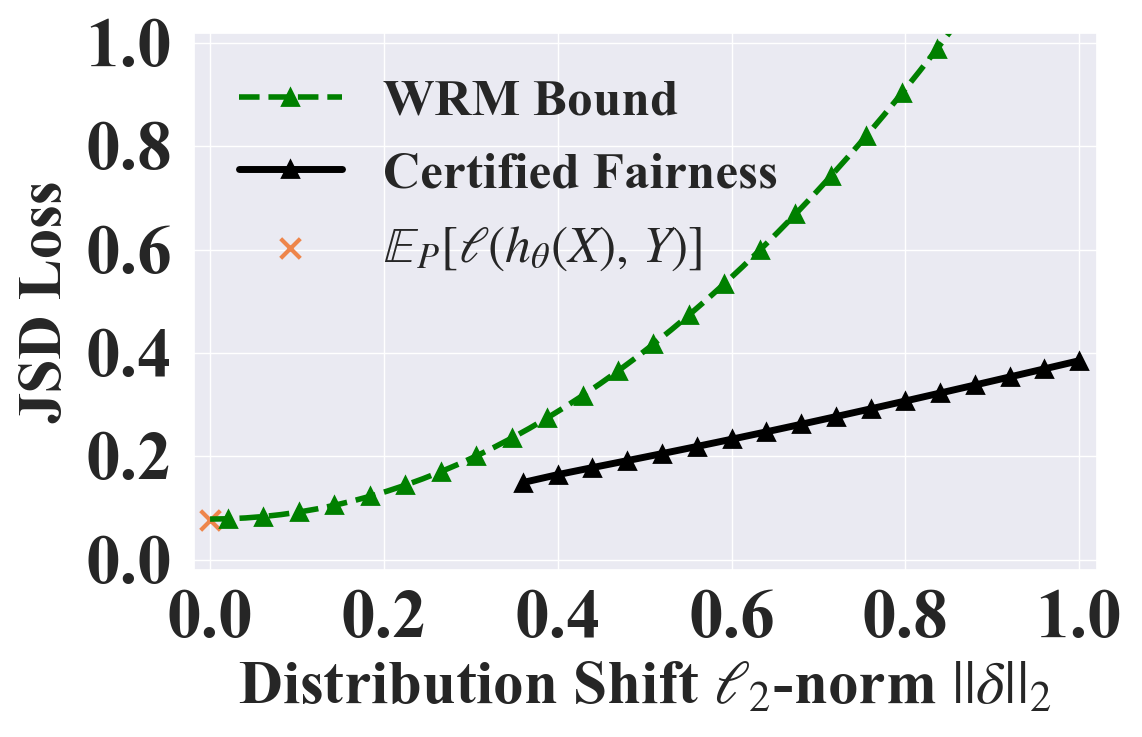
To the best of our knowledge, there is no existing work providing certified fairness on the end-to-end model performance. Thus, we try to compare our bound with the distributional robustness bound since both consider certain distribution shifts. However, it is challenging to directly integrate the fairness constraints into existing bounds. Therefore, we compare with the state-of-the-art distributional robustness certification WRM [43], which solves the similar optimization problem as ours except for the fairness constraint. For fair comparison, we construct a synthetic dataset following [43], on which there is a one-to-one correspondence between the Hellinger and Wasserstein distance used by WRM. We randomly select one dimension as the sensitive attribute. Since WRM has additional assumptions on smoothness of models and losses, we use JSD loss and a small ELU network with 2 hidden layers of size 4 and 2 following their setting. More implementation details are in Section E.4. Results in Figure 3(c) suggest that 1) our certified fairness bound is much tighter than WRM given the additional fairness distribution constraint and our optimization framework; 2) with additional fairness constraint, our certificate problem could be infeasible under very small distribution distances since the fairness constrained distribution ${\mathcal{Q}}$ does not exist near the skewed original distribution ${\mathcal{P}}$; 3) with the fairness constraint, we provide non-trivial fairness certification bound even when the distribution shift is large.