∎
22email: {aryo.jamshidpey, mostafa.wahby, mary.katherine.heinrich, michael.allwright, weixu.zhu,
marco.dorigo}@ulb.be
33institutetext: A. Jamshidpey 44institutetext: University of Ottawa, Ottawa, Canada
44email: [email protected]
Centralization vs. decentralization in multi-robot coverage: Ground robots under UAV supervision
Abstract
In swarm robotics, decentralized control is often proposed as a more scalable and fault-tolerant alternative to centralized control. However, centralized behaviors are often faster and more efficient than their decentralized counterparts. In any given application, the goals and constraints of the task being solved should guide the choice to use centralized control, decentralized control, or a combination of the two. Currently, the tradeoffs that exist between centralization and decentralization have not been thoroughly studied. In this paper, we investigate these tradeoffs for multi-robot coverage, and find that they are more nuanced than expected. For instance, our findings reinforce the expectation that more decentralized control will provide better scalability, but contradict the expectation that more decentralized control will perform better in environments with randomized obstacles. Beginning with a group of fully independent ground robots executing coverage, we add unmanned aerial vehicles as supervisors and progressively increase the degree to which the supervisors use centralized control, in terms of access to global information and a central coordinating entity. We compare, using the multi-robot physics-based simulation environment ARGoS, the following four control approaches: decentralized control, hybrid control, centralized control, and predetermined control. In comparing the ground robots performing the coverage task, we assess the speed and efficiency advantages of centralization—in terms of coverage completeness and coverage uniformity—and we assess the scalability and fault tolerance advantages of decentralization. We also assess the energy expenditure disadvantages of centralization due to different energy consumption rates of ground robots and unmanned aerial vehicles, according to the specifications of robots available off-the-shelf.
Keywords:
Swarm robotics Distributed control Hybrid control Hierarchical control Multi-robot systems Coverage control Area coverage Environment monitoring1 Introduction
In multi-robot systems, a fundamental design decision is whether to use centralized control, decentralized control, or some combination of the two. Fully centralized control approaches are often high performing and efficient, but can suffer from single points of failure and poor scalability, due to limitations such as communication bottlenecks. Fully decentralized approaches do not have these drawbacks, due to features such as redundancy and parallelization, but may have lower speed and efficiency. The relative advantages and disadvantages of centralized and decentralized control are somehow well-accepted common knowledge, but the precise trade-offs involved when considering specific tasks have not been fully characterized. Some research has studied the relationship between controller structure and controller performance—e.g., in network topology (Nedić et al., 2018) or controller architectures (Jovanović and Dhingra, 2016)—but these studies do not cover the full set of issues that can arise during robot deployment, such as fault tolerance of group performance after arbitrary robot failures, or physical interference when robots collide.
In this paper, we take a step towards comprehensive comparison between centralized and decentralized control in multi-robot systems, by studying the performance of these configurations in a coverage task, i.e., when an environment must be uniformly explored. We start by using a group of ground robots and then we compare it to the same group, but enlarged with unmanned aerial vehicle (UAV) supervisors, with progressively increased centralization.111All the experiments discussed in this paper have been run in simulation using the multi-robot physics-based simulation environment ARGoS (Pinciroli et al., 2012). In all methods, the coverage task is completed exclusively by the ground robots. The UAVs are strictly supervisors; they observe the environment and send motion instructions to ground robots. To make a fair comparison between methods, we only change the sensing and communication capabilities of the UAV supervisors, not of the ground robots. In this paper we consider multi-robot coverage that would take place in large outdoor environments (e.g., search and rescue, environment monitoring, or precision agriculture), and setup our simulation experiments accordingly. We use UAV supervisors to provide the ground robots with a mobile hub for communication, control, and position tracking. A similar approach could also be applicable to small indoor environments, using external infrastructure such as cameras and local area networks to add varying degrees of centralization.
We consider (de)centralization in terms of two key categories: control structure and access to information. The control structure includes the topology of the communication network, the distribution of control and decision-making roles, and the processes by which the network is formed and the control roles are allocated. Access to information includes the availability of information about the environment (size, shape, and locations of boundaries) and each robot (position and orientation) and the sensing process by which the information is obtained. We compare four example control approaches, ranging from fully reactive and decentralized to fully predetermined and centralized, and evaluate their performance in simulated experiments.

We define perfect coverage performance as the uniform and complete exploration of an environment, and therefore evaluate the performance of the four control approaches using two metrics: coverage uniformity and coverage completeness. We define a scalable system as one without a communication bottleneck, in which communication overhead increases linearly with the number of robots at a slow rate, interference between robots does not decrease task performance, and task performance increases linearly or better with the number of robots. We therefore evaluate scalability in terms of bottlenecks, inter-robot interference, communication, and the impact of scaling on coverage performance. We define a fault-tolerant system as one without a single point of failure, in which arbitrary robot failures do not disrupt connectivity between the remaining robots, and do not cause task performance to decrease worse than linearly. We therefore evaluate fault tolerance in terms of connectivity and performance after robot failures.
We also evaluate the limitations associated with increasing centralization by adding mobile external infrastructure in the form of UAVs. When adding UAV supervisors, energy consumption is a key metric to assess their added value, because UAVs and ground vehicles usually have different rates of energy consumption, and therefore different operating times and travel distances. We compare the coverage performance of the four example control methods under the limitations of maximum operating time and maximum distance traveled (which is proportional to the amount of used energy). We also compare them under the limitation of a maximum energy consumption budget for the whole multi-robot system. We conduct this analysis according to the listed specifications of a number of real ground robots and UAVs that are available off-the-shelf and suitable for experimentation in multi-robot systems (see the Appendix).
One would expect more centralized and predetermined control to perform well in terms of speed, accuracy, and efficiency, and not so well in terms of fault tolerance and scalability. For more reactive and decentralized control, one would expect the opposite. We would therefore anticipate that well-designed hybrid control could potentially achieve better task performance than fully reactive and decentralized control, and better fault tolerance and scalability than fully predetermined and centralized control. One would also expect approaches without UAV supervisors to perform better in terms of energy consumption. However, our experimental results and analysis indicate that the relative advantages and disadvantages of (de)centralization are much more nuanced than the assumed simple trade-offs (see Fig. 1).
For instance, our results show that the accuracy gap between centralized and hybrid control is quite small, suggesting that features such as a central coordinating entity do not necessarily deliver a substantial performance boost. Our results further suggest that the somewhat better efficiency of the predetermined approach is due to its a priori knowledge of the environment, rather than its central coordinating entity. As another example, one might expect decentralized approaches to be better suited to cluttered environments. However, our results indicate that more centralized approaches perform quite well with randomized obstacles, outperforming fully decentralized control. In terms of scalability and fault tolerance, our results show that hybrid control can have similar advantages to fully decentralized control. Some of the existing hybrid approaches (e.g., using a dynamically elected leader) still suffer from setbacks such as a bottleneck when scaling. It is therefore interesting to note that in the hybrid approach tested in this paper, communication scales linearly and no bottlenecks occur. Finally, in terms of energy consumption, one might expect the energy efficiency of UAV supervisors to be the most relevant limitation. However, our analysis indicates that the limited operating time of UAVs is more restrictive than their energy efficiency, and inefficient ground robots pose more of a problem than inefficient UAVs. Overall, our results contradict some expectations and progress towards a better understanding of the trade-offs between centralization and decentralization in multi-robot systems.
2 Related work
Ideally, when designing a multi-robot system, one would be able to guarantee that a selected control approach is the top performer for its objectives. Tools have been proposed in swarm robotics to assess general performance (Hamann, 2013) and specific aspects of performance (e.g., (Valentini et al., 2015)), and in self-organizing software and embedded systems to assess general performance (Kaddoum et al., 2010; Eberhardinger et al., 2017, 2018) and the degree of self-organization (Tomforde et al., 2017). Although these contributions progress towards general metrics for decentralization, they are not applicable to centralized multi-robot systems. Therefore, the choice to use centralized or decentralized control is often made intuitively and most of the time is discipline dependent (e.g., decentralized control in the swarm robotics community).
In this paper, we present for the first time a comprehensive comparison of control structures in multi-robot systems, which includes comparison of speed, accuracy, efficiency, scalability, fault tolerance, and energy consumption. As mentioned above, we are not aware of any published attempt to formalize comprehensive and systematic metrics to assess both centralized and decentralized control, which would enable their direct comparison.
Whether centralization or decentralization is better for a given application will evidently depend on the scenario. Decentralization can address limitations such as unavailability of global communication in search and rescue (Almadhoun et al., 2019), single points of failure in object transport (Tuci et al., 2018), and poor fault tolerance in task allocation (Khamis et al., 2015). However, downsides to decentralization are unavoidable—for instance, in collective decision making, accurate decisions tend to have long convergence times (Valentini et al., 2015). Recently proposed methods could enable a multi-robot system to switch between centralized and decentralized control on demand (e.g., mergeable nervous systems (Mathews et al., 2017; Zhu et al., 2020)), which is crucial for the future of swarm robotics (Dorigo et al., 2020). To be useful, autonomous reorganization would need to be based on a systematic understanding of the relationship between task performance and control structure.
In this paper, we study the task of coverage as an example case, and compare different control structures. This paper builds upon our previous work, in which we proposed mergeable nervous systems (MNS) (Mathews et al., 2017; Zhu et al., 2020) to be an appropriate hybrid control approach for multi-robot coverage (Jamshidpey et al., 2020).
2.1 Coverage control
Multi-robot coverage targets the systematic, uniform observation of an environment. It is part of environment monitoring, and any other application in which more uniform observation would improve performance. For instance, in adaptive sensor networks, more efficient coverage in the exploration phase could improve the positions chosen by mobile sensors (Luo and Sycara, 2018; Siligardi et al., 2019; Santos et al., 2019). In robot swarms and multi-robot systems, more efficient observation of the environment could improve performance during, e.g., task allocation (Jamshidpey and Afsharchi, 2015), collective decision making (Valentini et al., 2015; Strobel et al., 2018), collective perception (Schmickl et al., 2006), search and rescue (Baxter et al., 2007), or foraging (Lima and Oliveira, 2017). In short, developing better solutions to coverage could improve performance in many other tasks.
2.1.1 Centralized approaches
When using a single robot, the goal of coverage control is to quickly and efficiently collect information that comprehensively represents an environment (Galceran and Carreras, 2013; Juliá et al., 2012), for instance by sweeping the environment using boustrophedon (i.e., “back-and-forth”) motion (Almadhoun et al., 2019; Avellar et al., 2015). To speed up the process, multiple robots can be centrally organized into a formation such as a line (Liu and Bucknall, 2018) and sweep the environment together, or be assigned to different zones for single robots to sweep individually (e.g., Rekleitis et al., 2008; Scherer et al., 2015). When robots sweep individually, the environment is often decomposed into zones using centralized control. Coverage is then executed using offline or online path planning, depending on whether the environment is decomposed a priori or not (Almadhoun et al., 2019). In offline decomposition, results can be improved through multi-robot path planning strategies, e.g., using particle swarm optimization (Thabit and Mohades, 2018), genetic algorithms (Nazarahari et al., 2019), or graph-based heuristics (Yu and LaValle, 2016)). In this paper, for centralized and predetermined coverage, we use a priori decomposition and offline path planning.
In online decomposition, aspects of decentralization are often used, in combination with robots building a shared reference map of the environment (Almadhoun et al., 2019). The map is built either before coverage begins (Mirzaei et al., 2011), or during coverage using broadcasting (Miki et al., 2018; Ge and Fua, 2005). Shared reference maps are also used without strict decomposition into zones, with maps updated by single-broadcast (Marjovi et al., 2009) or somewhat less efficiently by multi-broadcast (Albani et al., 2017). All of the approaches using shared reference maps are mostly decentralized, but their centralized aspects are sufficient to hinder scalability, and perhaps also fault tolerance. In these hybrid approaches, efficient performance and system scalability are not necessarily balanced, and the trade-offs between centralization and decentralization are not studied directly.
2.1.2 Decentralized approaches
Fully decentralized coverage can be completed using independent randomized motion with simple obstacle and collision avoidance (Ichikawa and Hara, 1999; McGuire et al., 2019; Huang et al., 2019), but the approach is highly inefficient. Many studies have improved upon random walk strategies to increase overall coverage performance, e.g., by optimizing step lengths in Brownian motion and Lévy flight (Pang et al., 2021), improving the scalability of Lévy walk (Khaluf et al., 2018), or proposing a new style of random walk (Pang et al., 2019). These approaches can achieve very high coverage completeness in unknown environments (up to 97% reported, Pang et al., 2021), if the available time is long enough and the swarm is large enough (Ichikawa and Hara, 1999). Randomized motion is also expected to eventually reach high coverage completeness in environments cluttered with obstacles Almadhoun et al. (2019). However, inefficiency is very high, as robots often repeat coverage of areas already explored by their peers (Zia et al., 2017; Huang et al., 2019). In other words, there is a presumed trade-off in decentralized approaches between coverage efficiency and environment difficulty (Almadhoun et al., 2019), which has not yet been precisely characterized. In this paper, for basic decentralized coverage, we use simple diffusive motion based on random billiards (Comets et al., 2009)—where each agent has constant velocity until reflecting off a boundary in a random direction—combined with obstacle avoidance.
One fault-tolerant approach to improving coordination and efficiency in decentralized coverage is to leave ant-inspired artificial pheromones in the environment (Koenig and Liu, 2001). However, both randomized motion and pheromone-based approaches have shown poor scalability in terms of speedup (Huang et al., 2019; Koenig and Liu, 2001). As the swarm scales, new robots provide diminishing returns—i.e., each added robot provides increasingly less speedup in overall coverage. In Koenig and Liu (2001), adding a sixth robot to a swarm of five, for instance, barely reduces the total coverage time. Parameters of pheromone-based coverage approaches have been tuned for efficiency when using with Lévy flight (Schroeder et al., 2017) or a combination of Lévy flight and Brownian motion (Deshpande et al., 2017), but it is not clear if scalability in terms of speedup has been improved. Currently there are no studies directly comparing the coverage performance of pheromone-based approaches to simpler randomized motion approaches.
Some decentralized approaches include aspects of centralization by leaving robots in the environment to act as static beacons, either permanently before coverage begins (Maftuleac et al., 2015), or temporarily during coverage (Stirling et al., 2010). In the approach of Stirling et al. (2010), some robots temporarily park themselves while the swarm explores as a group. In a 5 x 5 analysis grid in a 15 m x 15 m environment with obstacles, the approach achieves mean coverage completeness of 99.7%, and also demonstrate scalability. Repeated coverage and fault tolerance are not directly measured. The approach of Stirling et al. (2010) is comparable to the formation approaches in this paper, in that some robots act as supervisors while others perform coverage by staying together in a group.
2.1.3 Formation approaches
If robots sweep the environment as a group, their coordination can be improved by using formation control strategies (Liu and Bucknall, 2018) to manage motion control and relative positions. Formation control is often cited as a good approach for coverage applications such as search and rescue (Liu and Bucknall, 2018; Campbell et al., 2012), but the coverage performance of the various strategies has not been directly compared. Of the common formation shape types (cf. Campbell et al., 2012), line formations are considered suitable for sweeping and mapping tasks (Liu and Bucknall, 2018). In the two formation approaches considered in this paper, we use a line formation. We offset the robot positions slightly, into a zigzag line (see Fig. 3, to better avoid inter-robot collisions during obstacle avoidance.
Formation control can be fully centralized, or can incorporate aspects of decentralized control, such as a potential field for local collision avoidance (Liu and Bucknall, 2018). In centralized approaches, robots share a common reference via broadcast, for instance a predetermined leader (Wang, 1991) or a dynamically selected navigator and virtual leader (Din et al., 2018). In this paper, we use basic leader-follower formation control with a predetermined leader for our centralized formation approach. Formation control can also be accomplished without centralized communication, by instead using a self-organized ad-hoc communication network (Zhu et al., 2020). In this paper, for our hybrid formation approach, we use a self-organized network and hierarchical control, based on mergeable nervous systems (Mathews et al., 2017; Zhu et al., 2020) and hierarchical frameworks (Zhang et al., 2023).
3 Methods
We investigate the advantages and limitations associated with varying degrees of (de)centralization in a group of ground robots that may be supervised by one or more UAVs. We assess four control approaches spanning from reactive and fully decentralized control (i.e., all robots are acting autonomously) to predetermined and fully centralized control (i.e., all robots are given fully predetermined instructions by a central entity). In this section, we describe the methods for our experiments. First, we define the coverage task. Then, we present the implementation details for the four coverage approaches: fully decentralized, hybrid formation, centralized formation, and predetermined. Finally, we describe the details of the simulation setup.
We define the coverage task as uniform and complete exploration of the environment. If an environment is partitioned, the robots should collectively visit all portions and should spend equal time visiting each portion. The experiment arena is a m2 enclosed square, overlaid with a grid. For complete coverage, each of the 256 grid cells must be visited by the ground robots. The difficulty of this task is increased by adding small cm3 obstacles to the environment (see Fig. 2). In each run of an experiment, the obstacle positions and orientations are defined randomly with uniform distribution. We test arenas with the following three obstacle difficulties: 100 obstacles for low difficulty (i.e., 1% of the environment surface occupied), 200 obstacles for medium difficulty, and 300 obstacles for high difficulty.




3.1 Coverage methods
We compare the following four types of coverage control, from most decentralized to most centralized (see Fig. 3).
-
1.
Decentralized. There are no UAV supervisors. The ground robots are fully independent; there is no explicit communication and each robot controls itself. The robots can locally detect objects in their environment. The motion control strategy is basic diffusion with obstacle avoidance.
-
2.
Hybrid formation control using mergeable nervous systems. UAVs are limited to local onboard sensing, through which they can observe the positions and orientations of ground robots and of environment boundaries, within a certain range. UAVs have a limited communication range and send motion control instructions to ground robots using a self-organized ad-hoc communication network (for details, see the mergeable nervous systems (MNS) approach described below). Motion control is based on a formation shape designed for sweeping.
-
3.
Centralized formation control. The single UAV has unlimited access to all ground robots’ positions and orientations and can sense the environment boundaries. The UAV has an unlimited communication range and directly sends motion control instructions to all ground robots over a predetermined star-graph communication network. Motion control is based on the same formation shape as in the hybrid formation approach.
-
4.
Predetermined control based on a priori knowledge. The UAV calculates instructions for the ground robots before the task begins, based on full a priori knowledge of the environment and the robots. The UAV has the same unlimited communication range and predetermined network topology as in the centralized formation approach. For motion control, the UAV decomposes the environment into zones and calculates motion trajectories offline, and then gives each ground robot its predetermined motion trajectory to sweep its predetermined zone.
In all approaches, the ground robots execute reactive obstacle avoidance using onboard sensing. The details of ground robot and UAV control for the four approaches are given below.
3.1.1 Decentralized
For fully decentralized coverage, we use motion control based on random billiards (Comets et al., 2009) and reactive obstacle avoidance. Each ground robot independently follows a constant velocity unless it reflects off a boundary in a random direction, or unless it turns to avoid an obstacle. The robots’ onboard sensing can distinguish a boundary from an obstacle or robot. When avoiding an obstacle, a robot turns in place until the obstacle is no longer near its heading. The pseudocode for boundary reflection and obstacle avoidance is given in Algorithm 1. The starting positions and headings of the robots are defined randomly with uniform distribution.
3.1.2 Hybrid formation control using Mergeable Nervous Systems (MNS)
We use hybrid formation control based on remote ‘mergeable nervous systems’ (MNS) (Zhu et al., 2020). In MNS formation control, a heterogeneous swarm can self-organize into a dynamic ad-hoc communication network with a hierarchical structure (for full implementation details, see (Zhu et al., 2020)). Using this hierarchy, robots report sensing events and cede their autonomy to a temporary ‘brain’ robot (see Fig. 3). The brain robot determines its own motion trajectory. As the brain moves, it acts as a motion reference for its children (i.e., the brain acts as a reference coordinate frame used to calculate the motion instructions sent to its children), which in turn act as motion references for their children. The robots in an MNS can self-reconfigure into a new communication network and control hierarchy on the fly, for instance, in case of task change or brain failure (Zhu et al., 2020).
In our MNS formation control setup, there are some targets guiding the self-organization of the network. The target communication network topology is a caterpillar tree—i.e., a tree in which all inner nodes are on one central path, to which each leaf node is connected. Ground robots try to become leaf nodes in the communication network. They complete the coverage task and perform independent obstacle avoidance. The pseudocode for the ground robots is given in Algorithm 2. UAV supervisors try to become inner nodes or the brain node and act as motion references for their children. The UAVs direct their ground robot children into a line-like formation, which is ideal for sweeping an environment. The target line formation has a slight zigzag, to reduce inter-robot collisions when ground robots perform obstacle avoidance. The UAV that becomes the brain (see Zhu et al. (2020)) uses a reactive perimeter-following behavior to sweep the environment counterclockwise, turning when it encounters a boundary. A behavior flowchart for all UAVs in the MNS hybrid formation is given in Figure 4(a).
In each experiment run, the starting positions and headings of the ground robots and UAVs are defined randomly with uniform distribution. When the experiment begins, the robots self-organize into an MNS, according to the approach defined in (Zhu et al., 2020). Once the MNS is formed, the brain begins its reactive sweeping behavior. The brain UAV moves at a constant speed, irrespective of the speed of the other robots. The formation is maintained because the other robots adjust their motion according to the motion of their parents. The perimeter-following behavior of the brain is deterministic, therefore each sweep of the environment by the robots takes the same amount of time. Given the dimensions of the line formation and the arena, this simple counter-clockwise path is sufficient to enable full coverage.



3.1.3 Centralized formation control
For centralized formation control, we use a basic leader–follower approach (Wang, 1991), in which all robots follow one global leader that broadcasts information. At the start of each experiment run, the starting positions and headings of the ground robots are defined randomly with uniform distribution. At initiation, they are already connected to a UAV hub in a star (i.e., spoke and hub) communication network. The UAV acts as a single coordinating entity, providing all ground robots with motion instructions. The ground robots perform independent obstacle avoidance (see pseudocode in Algorithm 2), but otherwise follow the UAV’s instructions. At initiation, the UAV immediately directs the ground robots into the target formation—a line with a slight zigzag, identical to the MNS formation—as shown in Fig. 3. Then, the UAV follows the same reactive perimeter-following behavior used by the brain in the MNS formation, sweeping the environment counterclockwise. A behavior flowchart for the UAV is given in Figure 4(b).
3.1.4 Predetermined control based on a priori knowledge
For predetermined coverage control, we decompose the environment offline into zones for robots to sweep individually (e.g., Rekleitis et al., 2008; Scherer et al., 2015). As in the centralized formation approach, ground robots receive instructions from one UAV over a predetermined central communication network. Unlike in the centralized formation approach, the UAV does not use reactive control to update ground robots’ motion instructions in real time—rather, the UAV uses a priori knowledge to decompose the environment and calculate predetermined motion trajectories for the ground robots before they begin the task. The motion trajectories for the ground robots are based on boustrophedon (i.e., “back-and-forth”) motion (cf. Avellar et al., 2015) to sweep their zones. Based on this trajectory, the ground robots are also given a predetermined path to circumnavigate obstacles (see pseudocode in Algorithm 3). The UAV supervisor in this approach has access to all information about the environment (shape, size, and boundaries) and robots (number of robots, positions, orientations), and at initialization is connected to all ground robots as the hub of a star network (the same as the centralized formation approach). The UAV decomposes the environment into lanes that are suitable for the number of ground robots, boustrophedon motion style, and the dimensions of the environment and the analysis grid (see Fig. 3). To sweep every cell of the analysis grid in its lane, a ground robot only needs to change direction once. At initialization, the starting positions and headings of the ground robots are defined randomly with uniform distribution. The UAV, which hovers in a stationary position during the experiment, immediately gives the ground robots predetermined trajectories to drive to the starting positions of their lanes and sweep them.
3.2 Simulation setup
The experiments are conducted in the ARGoS simulator (Pinciroli et al., 2012), with robot models implemented using a plugin for prototyping new robots (Allwright et al., 2018a, b). All four approaches complete the coverage task with nine ground robots. In addition, the predetermined control and centralized formation control approaches each have one UAV supervisor, whereas the MNS hybrid formation control approach has three UAV supervisors, one of which is the MNS ‘brain’ (see Fig. 3). The simulated ground robot is based on the e-puck ground robot. It uses differential wheeled drive, with an average speed of cm/sec, and is equipped with a ring of 12 short-range proximity sensors. The ground robots can detect obstacles, other ground robots, and the boundaries of the environment at a distance of 5 cm. The simulated UAV is a quadrotor restricted to a maximum speed of cm/sec (such that the ground robots are able to follow the UAVs at their avergae speed), and is equipped with a downward-facing camera. Obstacles cannot be detected by the UAVs, only by the ground robots. Both simulated ground robots and UAVs are represented by simple cm radius cylinders.
Fiducial markers encoding unique IDs sit atop the ground robots. The UAVs detect these markers, tracking the relative positions and orientations of the ground robots in order to give them motion instructions. UAVs can establish a communication link with ground robots that lie within their field of view. In centralized formation control and predetermined control, the UAV can view the full arena and communicate with all ground robots. In MNS hybrid formation control, the UAVs fly at a constant altitude and each UAV can view ground robots in an approx. m2 rectangular ground area (for details, see Zhu et al., 2020). Three UAVs are required in order to keep all ground robots in their collective view when in a line formation. In the MNS, two UAVs can establish a communication link when they can see the same ground robot (for details, see Zhu et al., 2020).
At the start of each experiment, the cm3 obstacles are distributed randomly throughout the m2 arena, with a cm buffer to the outer boundary and a cm buffer between separated obstacles. The buffers ensure that it is always possible for the ground robots to sweep the environment without becoming stuck. Also at the start, the robots are randomly distributed in a m2 rectangular area against the perimeter of the arena.
For the MNS hybrid formation, centralized formation, and predetermined control approaches, we define a round as one complete sweep of the environment. These experiments are terminated at the completion of the round. A round takes the same amount of time in the hybrid and centralized formation approaches, because the reactive controller that the UAVs use for perimeter following is deterministic. The decentralized approach does not perform a comparable sweep, therefore we define its round end to be at the same time step as the round ends of the hybrid and centralized approaches, to enable direct comparisons between the approaches. In the decentralized approach experiments, we continue to collect data after the round end, terminating the experiments at time step 11000.
4 Results
To assess the impact of (de)centralization on coverage control, we run experiments that test the coverage performance of all four approaches: fully decentralized, MNS hybrid formation control, centralized formation control, and predetermined control. Existing coverage approaches with high performance incorporate some degree of centralization, and most have not been tested for fault tolerance and scalability. We run experiments testing the fault tolerance and scalability of the MNS hybrid formation control approach, and conduct analysis to compare these results to the fault tolerance and scalability of the other approaches.
To assess the costs and limitations associated with adding UAV supervisors, we analyze the performance results of the four approaches according to energy consumption. We base our analysis on the energy consumption and efficiency of state-of-the-art mobile robots and drones. (See the Appendix for tables reporting the specifications of eleven autonomous ground vehicles and five UAVs currently available off-the-shelf.)
4.1 Performance
In high-performing and efficient multi-robot coverage, robots cover a high percentage of the environment with a low rate of repeated coverage. We assess the performance of the four approaches in terms of coverage completeness (i.e., the percentage of grid cells visited) and coverage uniformity (i.e., the variability of time that robots collectively spend visiting each cell). We complete 50 runs for each control approach, in each of the three obstacle setups (100, 200, and 300 obstacles), for a total of 600 runs.
4.1.1 Coverage completeness
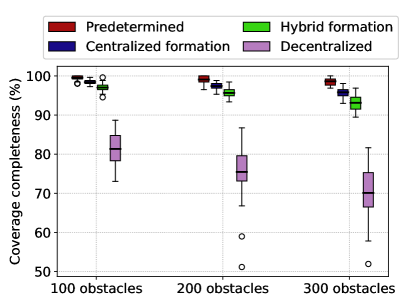
At the end of one round, the predetermined control approach outperforms all other approaches in terms of coverage completeness, for all obstacle difficulties (see Table 2 and Fig. 6). More in general, the higher the degree of centralization, the higher the coverage completeness. The predetermined control approach outperforms the centralized formation and hybrid formation approaches by a relatively small margin, compared to the decentralized approach. For example, in the setup with 100 obstacles, the centralized formation and hybrid formation approaches only omit an additional 1.1% and 2.5% of the arena, respectively, while the fully decentralized approach misses an additional 18.2%.
As the number of obstacles increases, the difference in average coverage completeness between the predetermined control approach and the other approaches grows larger (see Table 2). All four approaches are impeded by obstacles, and all four suffer a reduction in average coverage completeness as the number of obstacles increases. The lower the degree of centralization, the greater the suffered reduction.
The predetermined control approach takes less time to complete one round than the centralized formation and hybrid formation approaches (see Fig. 5). However, as the number of obstacles increases, the time advantage of the predetermined control approach decreases. In the setup with 100 obstacles, the predetermined control approach is approximately 1000 time steps faster (see Fig. 5-a), but in the setup with 300 obstacles, it is only approx. 280 time steps faster (see Fig. 5-b). If the decentralized approach continues past the completion of one round, it eventually reaches a coverage completeness comparable to that of the other approaches (see Fig. 5), but it takes more than twice the amount of time to reach that completeness.
| Hybrid | Centralized | |||
| Decentralized | formation | formation | Predetermined | |
| 100 | Completeness : 81.3% | Comp. : 97.0% | Comp. : 98.4% | Comp. : 99.5% |
| obstacles | Uniformity () : 9.56 | Unif. : 8.29 | Unif. : 7.93 | Unif. : 4.95 |
| 200 | Completeness : 75.5% | Comp. : 95.7% | Comp. : 97.4% | Comp. : 99.1% |
| obstacles | Uniformity () : 9.99 | Unif. : 8.47 | Unif. : 8.12 | Unif. : 6.17 |
| 300 | Completeness : 70.1% | Comp. : 93.1% | Comp. : 95.8% | Comp. : 98.6% |
| obstacles | Uniformity () : 10.23 | Unif. : 8.73 | Unif. : 8.37 | Unif. : 6.87 |
| Performance differences compared to the Predetermined approach | ||||
| 100 | Completeness : -18.2% | Comp. : -2.5% | Comp. : -1.1% | |
| obstacles | Uniformity () : 4.61 | Unif. : 3.34 | Unif. : 2.98 | |
| 200 | Completeness : -23.6% | Comp. : -3.4% | Comp. : -1.7% | |
| obstacles | Uniformity () : 3.82 | Unif. : 2.30 | Unif. : 1.95 | |
| 300 | Completeness : -28.5% | Comp. : -5.5% | Comp. : -2.8% | |
| obstacles | Uniformity () : 3.36 | Unif. : 1.86 | Unif. : 1.50 | |
| Hybrid | Centralized | |||
| Decentralized | formation | formation | Predetermined | |
| Change in | - 5.6% | - 2.0% | - 1.3% | - 0.5% |
| Completeness | ||||
| Change in | + 0.34 | + 0.22 | + 0.22 | + 0.96 |
| Uniformity () |


4.1.2 Coverage uniformity
We define coverage uniformity as a measure of the variability of cell visits. The best performing coverage approach would be one without any repeated coverage—there would be no variability in cell visits, so uniformity would be . For each run, is defined as the total time spent by all robots in cell . The coverage uniformity is the norm of , calculated as follows:
| (1) |
where is the median of , and is the number of cells. The smaller the value of , the more uniformity between cells; the most uniform case is .
At the end of one round, the predetermined control approach has a better coverage uniformity () than all other approaches, for all obstacle difficulties (see Table 2). The higher the degree of centralization, the better the coverage uniformity. However, as the obstacle difficulty increases, the coverage uniformity of the predetermined control approach worsens at a faster rate than the other approaches—approximately twice as fast as the fully decentralized approach and four times as fast as the formation approaches (see Table 2 and Fig. 7-a). In the 300 obstacle setup, the coverage uniformity of the centralized and hybrid formation approaches are worse than the predetermined control approach by margins of only 1.5 and 1.66, respectively (see Table 2).
Similar to coverage completeness, the fully decentralized approach has substantially worse uniformity than the other approaches (see Fig. 7-a). However, unlike coverage completeness, the uniformity of the decentralized approach does not improve if it continues past the end of a round (see Fig. 7-b). For instance, in the 300 obstacle setup, if the fully decentralized approach continues long enough to achieve coverage completeness that is comparable to the other approaches, its uniformity becomes worse by an additional margin of approximately 3.4.
In all approaches, at the end of one round, there is low variability of coverage uniformity between runs (see Fig. 7-a). The variability in the formation approaches is slightly lower than in the other two. However, after round completion, the variability of uniformity in the fully decentralized approach grows substantially (see Fig. 7-b).


4.2 Fault tolerance




We assess the fault tolerance of coverage control in terms of the impact that robot failures have on coverage completeness. For the MNS hybrid formation control approach, we test this experimentally. For the other approaches, we conduct analysis to assess the impact of failures.
A common vulnerability in multi-robot systems is the presence of single points of failure. The fully decentralized approach is not susceptible to this problem, because it does not have a central coordinating entity. By contrast, a failure of the UAV in either the predetermined or centralized formation approaches results in a system-wide failure—neither approach can autonomously replace the failed UAV in order to recover. The MNS hybrid formation approach also has a central coordinating entity—however, if the robot fulfilling this role fails, then another robot can substitute it on the fly, because the role is defined dynamically through self-organization. Previous work has already shown the fault tolerance of MNS formation control in terms of replacing a failed robot (even the brain) and reconfiguring the formation accordingly (Zhu et al., 2020). In short, the predetermined control and centralized formation control approaches suffer from a single point of failure, while the fully decentralized and MNS hybrid formation control approaches do not.
| Estimate for | Estimate for | |||
| Estimate for | Hybrid | Centralized | Fully | |
| Decentralized | formation | formation | centralized | |
| No failure | Total : 82.0% | T. : 96.9% | T. : 98.4% | T. : 99.6% |
| Per robot : 9.1% | P. : 10.8% | P. : 10.9% | P. : 11.1% | |
| 3 failures | Total : 65% | T. : 82.1% | T. : 83% | T. : 77% |
| Per robot : 11% | P. : 13.7% | P. : 14% | P. : 13% | |
| 5 failures | Total : 52% | T. : 69.5% | T. : 71% | T. : 55% |
| Per robot : 14% | P. : 17.4% | P. : 18% | P. : 14% | |
| 7 failures | Total : 36% | T. : 41.0% | T. : 46% | T. : 32% |
| Per robot : 18% | P. : 20.5% | P. : 23% | P. : 16% |
| Estimate for | Estimate for | |||
| Estimate for | Hybrid | Centralized | Fully | |
| Decentralized | formation | formation | centralized | |
| \nth4 robot | + 1.8% (per 1000 steps) | + 2.7% | + 2.8% | + 3.6% |
| \nth6 robot | + 1.5% (per 1000 steps) | + 1.4% | + 1.5% | + 3.6% |
| \nth8 robot | + 1.3% (per 1000 steps) | + 1.3% | + 1.3% | + 3.6% |
| Hybrid | Centralized | Fully | ||
|---|---|---|---|---|
| Decentralized | formation | formation | centralized | |
| Maximum | 0 | 10 | 2 per | 2 per |
| messages | ground robot | ground robot |
Another key possibility is failure of robots that are responsible for the task and that cannot be replaced during runtime. Here, we test the impact on coverage completeness when failures of ground robots reduce the size of the system. In the MNS hybrid formation control approach, performance depends in part on maintaining the ad-hoc communication network. We therefore evaluate the impact of failures on both coverage completeness and connectivity. We run the fault tolerance experiments in the setup with 100 obstacles and allow the MNS hybrid formation control approach to complete one round. At time step 400, we impose failure on either one, three, five, seven, or eight out of the nine total ground robots. We complete 10 runs for each number of failing robots.
The MNS hybrid formation results show that the performance drop per robot failure is fairly consistent for 1, 3, or 5 failures—coverage completeness drops at a rate of approximately 5% per robot failure (see Fig. 8-c). When there are more than 5 failures, the performance drop per robot failure approximately doubles (see Fig. 8-c). This pattern of performance occurs because the brain UAV is capable of maintaining connectivity with its children UAVs whenever there are 5 or fewer failures (i.e., 56% or less of ground robots fail), but sometimes experiences disconnections when there are more failures (see Fig. 8-d). When there are 7 or 8 failures, the brain UAV might additionally lose contact with some of the remaining ground robots, causing the observed increase in performance drop.
We compare the MNS hybrid formation results to the other approaches using analysis (see Table 5), based on the assumption that no approach is permitted to adapt its coverage strategy during runtime (e.g., the formation approaches cannot adapt their path planning and the predetermined control approach cannot adapt its environment decomposition). As in the MNS hybrid formation approach, the fully decentralized and centralized formation approaches both include some inter-robot redundancy and interference, so we calculate the impact of failures based on the results of the MNS approach, taking into account the respective differences in coverage uniformity.222For each failure rate, we scale the difference in performance recorded in the MNS hybrid formation experiments for fault tolerance, according to the difference between the MNS hybrid formation approach and the compared approach in terms of average absolute deviation, based on . By contrast, robots are confined to their own lanes in the predetermined control approach, so any variability in uniformity is due to self-redundant coverage. We calculate the impact of failures by simply subtracting the coverage achieved by the failed robots after time step 400. The predetermined control approach experiences the largest drop in overall coverage completeness due to robot failures (see Table 5), because the remaining robots have no opportunity to cover the zones assigned to the failed robots. In the other approaches, overall performance drops more slowly with fewer failures and more quickly with more failures. This change appears in the decentralized approach because robots have a higher chance of redundancy in a larger group, and it appears in the formation approaches because the redundancy between two robots depends on their positions in the formation. The decentralized approach experiences smaller performance drops overall, because it has more inter-robot redundancy. However, the decentralized approach never outperforms the formation approaches at the end of a round (see Table 5), because in the decentralized approach a robot has more self-redundant coverage. The centralized formation approach maintains a slight advantage over the MNS hybrid formation, up to 5 failures. With more failures, the centralized formation approach more substantially outperforms the MNS hybrid formation approach (see Table 5), because at these failure rates the MNS formation may lose contact with the remaining ground robots.
4.3 Scalability
We assess scalability in terms of the number of messages exchanged between the robots, the number of inter-robot collisions, and the performance speedup achieved by the addition of one robot. We test the MNS hybrid formation approach experimentally and conduct analysis to compare to the other approaches.
We assess the performance speedup associated with adding one ground robot, regardless of the number of UAV supervisors. For the MNS hybrid formation approach, we base our analysis on the data obtained in the fault tolerance experiments (i.e., in the 100 obstacle setup) after time step 400. Similar to the fault tolerance analysis, for the fully decentralized and centralized formation approaches we calculate the performance speedup based on the results of the MNS approach, taking into account the respective differences in coverage uniformity.333For each number of ground robots, we scale the difference in performance recorded after time step 400 in the MNS hybrid formation experiments for fault tolerance, according to the difference between the MNS hybrid formation approach and the compared approach in terms of average absolute deviation, based on . We calculate performance speedup for the predetermined control approach based on the assumption that before runtime the supervisor UAV calculates the environment decomposition according to the number of ground robots. In the predetermined control approach, the speedup in coverage completeness per time step is the same for each additional robot (see Table 5). In the predetermined control approach, the overall coverage completeness does not increase as the system scales—rather, the time required to complete a round decreases. In the other approaches, the speedup provided by one additional robot gets smaller as the system grows in size (see Table 5). Overall, the speedups in the fully decentralized approach are the lowest, because its inter-robot redundancy is highest and because its overall coverage completeness at the end of a round is lowest.
To test the scalability of communication and inter-robot collisions in the MNS hybrid formation approach, we run experiments without obstacles in the environment, with the following three heterogeneous system sizes: 1) two UAVs and four ground robots, 2) four UAVs and eight ground robots, and 3) six UAVs and twelve ground robots. We complete 10 runs per system size. For each system size, we keep the same type of communication topology and formation shape (i.e., caterpillar tree communication network, and linear formation with a slight zigzag).
In the MNS hybrid formation approach, the total number of messages exchanged is expected to scale linearly, because the robots communicate only with those they are connected to in the network. The experimental results confirm this expectation (see Fig. 8-a): at time step 5 000, the total messages passed is approximately in the 6-robot system, in the 12-robot system, and in the 18-robot system. Based on the field of view, the maximum number of children for one UAV is 5. We can therefore conclude that, in the MNS hybrid formation approach, the maximum number of messages passed by one robot in one time step is 10, no matter the size of the system. Just as in the fully decentralized approach, no communication bottleneck will appear in larger systems in the MNS formation approach (see Table 5). By contrast, in the centralized formation and predetermined control approaches, the maximum number of messages passed by one robot in one time step is dependent on the number of ground robots (i.e., the supervisor UAV passes 2 messages per ground robot). Therefore, the scalability limit of these approaches depends on the maximum communication load of the UAV.
In all four approaches, inter-robot collisions can occur due to obstacles in the environment. Here, we only assess interference between robots in terms of collisions caused by the control approach. In the MNS formation, it is expected that inter-robot collisions will only occur during the formation establishment phase, which is confirmed by the experiment results (see Fig. 8-b). In the fully decentralized approach, inter-robot collisions are not considered to be interference, because changes in direction help the robots cover the environment. In both the centralized formation and predetermined control approaches, robots start the experiment by moving to their target positions before proceeding with coverage. However, in these approaches, it is possible for the supervisor UAV to calculate paths for all robots that prevent collision.
5 Analysis of energy consumption
When UAV supervisors are added to a group of ground robots, any improvements in performance need to be assessed in the context of the new limitations they introduce to the system. We identify two primary limitations introduced by the addition of UAV supervisors:
-
1.
reduced operating time for the system during a single battery charge, due to the quicker energy exhaustion of the UAVs, and
-
2.
increased total energy consumption if UAVs are added to the system, and the number of ground robots remains unchanged.
Under these limitations, we determine the highest performing approach in terms of coverage completeness. We also compare the performance of the MNS hybrid formation and decentralized approaches even if they are not the highest performers, because they are more comparable in terms of scalability and fault tolerance, in that they do not have a single point of failure or a communication bottleneck.
First, we analyze coverage completeness under the constraint of energy exhaustion. Although the state of the art includes a few robots that charge themselves continuously (e.g., using solar power), the majority require their batteries to be recharged separately from operation. We consider the coverage completeness that would be possible before energy exhaustion, with a single charge of both ground robots and UAVs (cf. off-the-shelf robots listed in the Appendix). Second, we analyze coverage completeness under the constraint of total energy consumption. UAVs and ground robots can have substantially different rates of energy consumption, so we consider the coverage completeness that would be possible for certain energy budgets and energy consumption ratios (cf. off-the-shelf robots listed in the Appendix).
We base our analysis calculations on the coverage completeness results obtained in Sec. 4.1.1 (i.e., from experiments with nine ground robots in a square arena with obstacles, with three UAVs for the MNS hybrid formation approach, and one UAV for both the centralized formation and predetermined control approaches).
5.1 Energy exhaustion



| Area per robot (sqm) | ||||
|---|---|---|---|---|
| Ground robot | ||||
| distance | Top performer: | Top performer: | Top performer: | Hybrid form. |
| per charge, or | Decentralized | Centralized | Fully | outperforms |
| max. speed | formation | centralized | decentralized | |
| 2 km | 2,000 | 1,000–2,000 | 1,000 | 800 |
| 10 km | 10,000 | 6,000–10,000 | 6,000 | 4,000 |
| 25 km | 30,000 | 15,000–30,000 | 15,000 | 10,000 |
| 50 km | 60,000 | 30,000–60,000 | 30,000 | 20,000 |
| 0.15 m/s | 300 | 150–300 | 150 | 100 |
| 0.5 m/s | 1,000 | 500–1,000 | 500 | 350 |
| 1.0 m/s | 2,000 | 1,000–2,000 | 1,000 | 700 |
| 10.0 m/s | 20,000 | 10,000–20,000 | 10,000 | 7,000 |
We analyze the coverage completeness achieved by each method under the constraint of energy exhaustion (i.e., limited operation). Although the experiment results for coverage completeness show that the predetermined control approach is the highest performing overall, the other methods outperform it in the initial 1 000 time steps (see Fig. 5). We analyze the robot, UAV, and environment constraints under which a system would be limited to those initial performance results.
To analyze the constraint of robot distance traveled, Fig. 9 gives the average coverage completeness according to the total meters traveled by all ground robots, in one square meter of the environment. Fig. 9 shows that the decentralized method is the top performer until 0.87 m traveled per sqm, then the centralized formation method is the top performer until 1.64 m traveled per sqm, after which the predetermined control approach is the top performer. Fig. 9 also shows that the decentralized method outperforms the MNS method until 2.61 m traveled per sqm.
The point at which a robot’s energy is exhausted during a coverage task will depend on the power and efficiency of the robots, and on the size of the environment. These conditions can vary greatly, so it is relevant to better characterize performance according to energy exhaustion. To assess the limit imposed by ground robot exhaustion, we calculate the average coverage completeness depending on the maximum distance a ground robot can travel in one charge. To assess the limit imposed by typical UAV exhaustion (i.e., 30 minutes in one charge), we also calculate the average coverage completeness depending on the maximum speed of the ground robot. Because the maximum speed of the UAV will always be higher, it is not a limitation. We consider environment sizes of up to 100 000 square meters per ground robot. Such an environment is large enough to assess the performance shifts for ground robots with a maximum travel distance from 1.5 km to 100 km per robot per charge and a maximum speed from 0.1 m/s to 50 m/s (under the condition of 30 minutes of UAV flight time). These ranges are representative of ground robots available off-the-shelf (and the flight time is representative of the average UAV), as listed in the Appendix.
In general, the analysis results indicate that more centralization performs better if maximum distances or maximum speeds are higher, while more decentralization performs better if operating areas are larger (see Fig. 10). For indoor environments, even in the most limited robots available off-the-shelf (see the Appendix), the environment size in which the decentralized approach would be the best performer is somewhat large (see Table 6). For example, for e-puck2 or Thymio II robots designed for indoor research, for a group of nine ground robots, the decentralized approach would only be the top performer in environments larger than m2. However, for applications such as outdoor search and rescue, the environment could easily be large enough to make the decentralized approach the top performer (see Table 6). For example, for a group of nine Boston Dynamics Spot robots, the decentralized approach will be the top performer in any environment larger than m2.
5.2 Energy consumption: ratio of ground robots to UAVs






In some coverage applications, battery life could be increased or autonomous recharging could be implemented. The energy efficiency of ground robots might also be significantly different from the efficiency of UAVs. To characterize the impact of energy efficiency on performance, we analyze the coverage completeness achieved by each approach under an overall energy budget, regardless of battery life. Basing our analysis on the results obtained in Sec. 4.1.1, we assign the system a total energy consumption budget of either 200 or 300 kilojoules. The budget is shared among all ground robots and UAVs used in that method (i.e., nine ground robots for all methods, three UAVs for MNS hybrid formation, one UAV for both centralized formation and predetermined control, and no UAVs for decentralized). We consider ground robots with energy consumption rates from 3 joules/s to 70 j/s, and UAVs with energy consumption rates from 6 j/s to 60 j/s. These ranges represent robots available off-the-shelf (see the Appendix).
Under a constrained energy budget, in general, more centralization tends to perform better if the ground robots are more efficient, and more decentralization tends to perform better if the ground robots are less efficient (see Fig. 11). In most of the analyzed energy consumption scenarios, the decentralized approach is the top performer if the UAV has its highest possible energy consumption rate (i.e., 60 j/s). All the approaches that have UAV supervisors perform better if the UAVs are more efficient, but the MNS hybrid formation approach benefits the most from efficient UAVs, because it has more of them. As the energy budget increases, the performance of all approaches improves (see Fig. 11). If the budget is unlimited, the performance rankings of the four approaches will always be those seen at the end of a round in Sec. 4.1.1, regardless of the energy consumption ratio between ground robots and UAVs.
6 Discussion
It is generally expected that fully centralized and predetermined control approaches will have the highest possible performance, in terms of speed, efficiency, and accuracy. Decentralized approaches are often preferred only if the environment or other conditions cannot be known a priori (cf. Almadhoun et al., 2019; Liu and Bucknall, 2018). As expected, our results show that the predetermined control approach outperforms all other approaches, in terms of both coverage completeness and coverage uniformity (see Table 2). The performance gap between the predetermined control and fully decentralized approach is quite large—up to a 28.5% gap for coverage completeness. Also, as one would expect, the performance gap between the predetermined control and centralized formation control approaches is relatively small. However, perhaps more surprisingly, the performance gap between the predetermined control and hybrid formation control approaches is also relatively small—as small as 2.5%, and not more than 5.5%. Centralized and predetermined control approaches are sometimes criticized for being impractical to implement. Our results suggest that, beyond being impractical, some features commonly used in various centralized approaches—e.g., having unlimited a priori knowledge, unlimited communication ranges, and a central coordinating entity with unlimited field of view—may not always deliver as substantial a performance benefit as might be expected.
Decentralized approaches are expected to be much less efficient than other approaches and to decrease in efficiency with longer running times, because of inherent redundancy. This expectation is confirmed by our experimental results in coverage uniformity (see Fig. 7). Existing decentralized approaches often add more robots to speedup coverage completeness, but then repeated coverage also worsens (Koenig and Liu, 2001). Existing hybrid approaches that achieve high coverage completeness also suffer from high repeated coverage (e.g., Stirling et al., 2010), compared to their fully centralized counterparts. In our experimental results with the MNS hybrid formation approach, coverage uniformity is noticeably worse than in the predetermined control approach, but nearly the same as in the centralized formation control approach. This suggests that a priori knowledge of the environment, rather than broadcasting from a central coordinating entity, provides the benefit of decreased repeated coverage.
As obstacle difficulty increases, it causes more disruption for all approaches. The MNS hybrid formation approach also has the added risk that its brain could lose contact with robots if blockage by obstacles is significant. Although the MNS formation did not lose any robots in our performance experiments (i.e., not fault tolerance experiments), it still might lose robots in more challenging environments than those tested. This risk could be alleviated by upgrading the behavior of the brain UAV to be responsive to its ground robots, waiting for them if they temporarily get disconnected.
Existing literature suggests that although decentralized approaches are less efficient in open environments, they may be better suited to environments cluttered with unknown objects (cf. Almadhoun et al., 2019). However, in the tested obstacles difficulties, our results suggest that the predetermined control approach is the most resilient to obstacles in terms of coverage completeness (see Table 2). If the performance reduction rates for 100–300 obstacles are consistent at higher obstacle densities, then only the more centralized approaches would be tenable for coverage completeness. For example, if there were 1000 obstacles, the predetermined control approach would achieve coverage completeness of 94.2% in one round, while the fully decentralized approach would achieve only 32.5%. By contrast, at higher obstacle densities, the predetermined control approach’s starting advantage in terms of coverage uniformity would disappear (see Table 2). If there were 1000 obstacles, the MNS hybrid formation control approach would achieve a coverage uniformity of 10.7, while the predetermined control approach would achieve the much worse uniformity of 14.03. Similarly, the predetermined control approach’s speed advantage over the formation approaches begins to disappear at higher obstacle densities. In summary, our results suggest that there is not necessarily a simple trade-off between coverage efficiency and resilience to environment difficulty. Each of the trends suggested by the current results could be further investigated, in a variety of more challenging environments.
6.1 Fault tolerance and scalability
It is evident that the predetermined control and centralized formation control approaches suffer from a single point of failure and a communication bottleneck when scaling. As would be expected, our analysis also suggests that the predetermined control approach suffers much more from robot failures than the other approaches (see Table 5). Perhaps less expected, our analysis suggests that the MNS hybrid and centralized formation control approaches do not suffer much more from robot failures than the decentralized approach. These analysis results should be investigated further, in experimental setups with a variety of failure types.
Many existing hybrid approaches use a dynamically elected leader to increase fault tolerance and flexibility in an otherwise centralized approach (e.g., Din et al., 2018), but these approaches still suffer from a bottleneck when scaling. It might be expected that the MNS hybrid formation control approach would suffer from a similar bottleneck. However, our experimental results indicate that communication in the MNS hybrid formation approach scales linearly (see Fig. 8), and that the communication load on the MNS brain does not increase when scaling.
6.2 Energy consumption
In later time steps (e.g., after the first 1000 time steps in the main experiments, see Fig. 5), the relative performance rankings of the four methods remain consistent—in terms of coverage completeness, the ranking is: \nth1 predetermined, \nth2 centralized formation, \nth3 MNS hybrid formation, and \nth4 fully decentralized (see Fig. 5). However, these performance rankings are not representative of earlier time steps. Although the coverage completeness in these earlier steps is low (e.g., 10% or 40%), our experiments use a high-resolution analysis grid, where adjacent grid points are cm apart. This matches a real-world application in which, for instance, ground robots can sense a targeted condition within a cm radius. In scenarios where a ground robot’s sensing range is much higher, then a low coverage completeness in our experiments may be sufficient. For example, with a ground robot sensing range of cm radius, intuitively we would posit that a coverage completeness of 25% could be sufficient for a monitoring application. This should be further investigated experimentally, using different grid resolutions in a discrete environment or using different sensor ranges. Similarly, all the analysis results in Sec. 5 need to be further investigated to be confirmed as representative—for example, by running experiments in larger arenas, up to 100 000 m2. Such experiments would involve implementing new behaviors in some of the approaches. For instance, in a larger environment, the formation approaches would need to use a different path planning strategy such as boustrophedon motion (Almadhoun et al., 2019; Avellar et al., 2015).
In general, our energy analysis results indicate that overall operation time is a highly relevant constraint. In large environments or with tight energy budgets, fully decentralized control may be the only feasible approach. In order to achieve high coverage completeness in real applications, our results indicate that the development of autonomous recharging is essential. Autonomous recharging will likely be easier to implement in hybrid or predetermined control approaches, because localization and positioning is more challenging in fully decentralized approaches. From among our tested approaches, the MNS hybrid formation control approach may be the most suitable for autonomous recharging, because it is already able to replace robots on the fly (Zhu et al., 2020).
Future work could also investigate the implications of monetary costs. If many robots are added, the area per robot can be kept smaller, even in larger environments. However, in outdoor environments, suitable robots are expensive and the monetary cost of adding ground robots can be very high (see the Appendix). The cost of adding UAV supervisors is low in comparison, so adding UAV supervisors may sometimes be a more effective way to increase coverage completeness, depending on task conditions.
7 Conclusion
We have tested four approaches to multi-robot coverage with varying degrees of (de)centralization, and compared them using experiments and analysis. The predetermined control approach unsurprisingly achieves the highest performance. However, the performance of the hybrid approach is much closer to that of the centralized approaches than might be expected. Our results also indicate that the hybrid approach displays scalability and fault tolerance similar to the fully decentralized approach. In terms of resilience to challenging environments, our results indicate that more centralized approaches might perform better than expected in messy environments with randomized obstacles, outperforming the fully decentralized approach. In terms of the possible limitations associated with UAV supervisors, we find that the limited operating time of UAVs is more restrictive than their energy efficiency. Perhaps surprisingly, we also find that inefficient ground robots pose more of a problem than inefficient UAVs for the centralized approaches, and that in order for any approach to achieve coverage completeness in large outdoor environments, autonomous recharging will be necessary. These results provide a better understanding of the task conditions and constraints that are relevant when selecting the degree of (de)centralization for multi-robot coverage control. Although our ad-hoc comparisons are task-specific, they are an initial step towards better characterizing the assumed trade-offs between centralization and decentralization in multi-robot systems.
Acknowledgements
Funding: This work was partially supported by the Program of Concerted Research Actions (ARC) of the Université libre de Bruxelles; by the Ontario Trillium Scholarship Program through the University of Ottawa and the Government of Ontario, Canada; by the Office of Naval Research Global (Award N62909-19-1-2024); by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 846009; and by the China Scholarship Council (grant number 201706270186). Mary Katherine Heinrich and Marco Dorigo acknowledge support from the Belgian F.R.S.-FNRS, of which they are a Postdoctoral Researcher and a Research Director respectively.
Authors’ contributions: AJ, MW, MA, and MD conceived and planned the experiments. AJ, MA, and WZ developed the code used in the experiments. Code development was supervised by MW and MA. AJ conducted the experiments and collected the data. AJ, MW, and MKH led the interpretation of the experimental results and conducted the analysis. The manuscript was written by AJ, MKH, MW, and MD, led by MKH. All authors read and approved the final manuscript.
References
- Albani et al. (2017) Albani D, Nardi D, Trianni V (2017) Field coverage and weed mapping by UAV swarms. In: 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), IEEE, pp 4319–4325
- Allwright et al. (2018a) Allwright M, Bhalla N, Pinciroli C, Dorigo M (2018a) ARGoS plug-ins for experiments in autonomous construction. Tech. Rep. TR/IRIDIA/2018-007, IRIDIA, Université Libre de Bruxelles, Brussels, Belgium
- Allwright et al. (2018b) Allwright M, Bhalla N, Pinciroli C, Dorigo M (2018b) Simulating multi-robot construction in ARGoS. In: Swarm Intelligence – Proceedings of ANTS 2018 – Eleventh International Conference, Springer, Berlin, Germany, Lecture Notes in Computer Science, vol 11172, pp 188–200
- Almadhoun et al. (2019) Almadhoun R, Taha T, Seneviratne L, Zweiri Y (2019) A survey on multi-robot coverage path planning for model reconstruction and mapping. SN Applied Sciences 1(8):847
- Avellar et al. (2015) Avellar GS, Pereira GA, Pimenta LC, Iscold P (2015) Multi-uav routing for area coverage and remote sensing with minimum time. Sensors 15(11):27783–27803
- Baxter et al. (2007) Baxter JL, Burke E, Garibaldi JM, Norman M (2007) Multi-robot search and rescue: A potential field based approach. In: Autonomous robots and agents, Springer, pp 9–16
- Campbell et al. (2012) Campbell S, Naeem W, Irwin GW (2012) A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidance manoeuvres. Annual Reviews in Control 36(2):267–283
- Comets et al. (2009) Comets F, Popov S, Schütz GM, Vachkovskaia M (2009) Billiards in a general domain with random reflections. Archive for rational mechanics and analysis 191(3):497–537
- Deshpande et al. (2017) Deshpande A, Kumar M, Ramakrishnan S (2017) Robot swarm for efficient area coverage inspired by ant foraging: the case of adaptive switching between brownian motion and lévy flight. In: ASME 2017 dynamic systems and control conference, American Society of Mechanical Engineers Digital Collection
- Din et al. (2018) Din A, Jabeen M, Zia K, Khalid A, Saini DK (2018) Behavior-based swarm robotic search and rescue using fuzzy controller. Computers & Electrical Engineering 70:53–65
- Dorigo et al. (2020) Dorigo M, Theraulaz G, Trianni V (2020) Reflections on the future of swarm robotics. Science Robotics 5(49):eabe4385
- Eberhardinger et al. (2017) Eberhardinger B, Anders G, Seebach H, Siefert F, Knapp A, Reif W (2017) An approach for isolated testing of self-organization algorithms. In: Software Engineering for Self-Adaptive Systems III. Assurances, Springer, pp 188–222
- Eberhardinger et al. (2018) Eberhardinger B, Ponsar H, Klumpp D, Reif W (2018) Measuring and evaluating the performance of self-organization mechanisms within collective adaptive systems. In: International Symposium on Leveraging Applications of Formal Methods, Springer, pp 202–220
- Galceran and Carreras (2013) Galceran E, Carreras M (2013) A survey on coverage path planning for robotics. Robotics and Autonomous systems 61(12):1258–1276
- Ge and Fua (2005) Ge SS, Fua CH (2005) Complete multi-robot coverage of unknown environments with minimum repeated coverage. In: Proceedings of the 2005 IEEE International Conference on Robotics and Automation, IEEE, pp 715–720
- Hamann (2013) Hamann H (2013) Towards swarm calculus: Urn models of collective decisions and universal properties of swarm performance. Swarm Intelligence 7(2):145–172
- Huang et al. (2019) Huang X, Arvin F, West C, Watson S, Lennox B (2019) Exploration in extreme environments with swarm robotic system. In: 2019 IEEE International Conference on Mechatronics (ICM), IEEE, vol 1, pp 193–198
- Ichikawa and Hara (1999) Ichikawa S, Hara F (1999) Characteristics of object-searching and object-fetching behaviors of multi-robot system using local communication. In: Proceedings of 1999 IEEE International Conference on Systems, Man, and Cybernetics, IEEE, vol 4, pp 775–781
- Jamshidpey and Afsharchi (2015) Jamshidpey A, Afsharchi M (2015) Task allocation in robotic swarms: Explicit communication based approaches. In: Canadian Conference on Artificial Intelligence, Springer, pp 59–67
- Jamshidpey et al. (2020) Jamshidpey A, Zhu W, Wahby M, Allwright M, Heinrich MK, Dorigo M (2020) Multi-robot coverage using self-organized networks for central coordination. In: Swarm Intelligence – Proceedings of ANTS 2020 – Twelfth International Conference, Springer, Berlin, Germany, Lecture Notes in Computer Science, vol 12421, pp 216–228, DOI 10.1007/978-3-030-60376-2˙17
- Jovanović and Dhingra (2016) Jovanović MR, Dhingra NK (2016) Controller architectures: Tradeoffs between performance and structure. European Journal of Control 30:76–91
- Juliá et al. (2012) Juliá M, Gil A, Reinoso O (2012) A comparison of path planning strategies for autonomous exploration and mapping of unknown environments. Autonomous Robots 33(4):427–444
- Kaddoum et al. (2010) Kaddoum E, Raibulet C, Georgé JP, Picard G, Gleizes MP (2010) Criteria for the evaluation of self-* systems. In: Proceedings of the 2010 ICSE Workshop on Software Engineering for Adaptive and Self-Managing Systems, pp 29–38
- Khaluf et al. (2018) Khaluf Y, Van Havermaet S, Simoens P (2018) Collective lévy walk for efficient exploration in unknown environments. In: International Conference on Artificial Intelligence: Methodology, Systems, and Applications, Springer, pp 260–264
- Khamis et al. (2015) Khamis A, Hussein A, Elmogy A (2015) Multi-robot task allocation: A review of the state-of-the-art. Cooperative Robots and Sensor Networks 2015 pp 31–51
- Koenig and Liu (2001) Koenig S, Liu Y (2001) Terrain coverage with ant robots: a simulation study. In: Proceedings of the fifth international conference on Autonomous agents, Association for Computing Machinery, pp 600–607
- Lima and Oliveira (2017) Lima DA, Oliveira GM (2017) A cellular automata ant memory model of foraging in a swarm of robots. Applied Mathematical Modelling 47:551–572
- Liu and Bucknall (2018) Liu Y, Bucknall R (2018) A survey of formation control and motion planning of multiple unmanned vehicles. Robotica 36(7):1019–1047
- Luo and Sycara (2018) Luo W, Sycara K (2018) Adaptive sampling and online learning in multi-robot sensor coverage with mixture of gaussian processes. In: 2018 IEEE International Conference on Robotics and Automation (ICRA), IEEE, pp 6359–6364
- Maftuleac et al. (2015) Maftuleac D, Lee SK, Fekete SP, Akash AK, López-Ortiz A, McLurkin J (2015) Local policies for efficiently patrolling a triangulated region by a robot swarm. In: 2015 IEEE International Conference on Robotics and Automation (ICRA), IEEE, pp 1809–1815
- Marjovi et al. (2009) Marjovi A, Nunes JG, Marques L, De Almeida A (2009) Multi-robot exploration and fire searching. In: 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, IEEE, pp 1929–1934
- Mathews et al. (2017) Mathews N, Christensen AL, O’Grady R, Mondada F, Dorigo M (2017) Mergeable nervous systems for robots. Nature communications 8(439)
- McGuire et al. (2019) McGuire K, De Wagter C, Tuyls K, Kappen H, de Croon GC (2019) Minimal navigation solution for a swarm of tiny flying robots to explore an unknown environment. Science Robotics 4(35)
- Miki et al. (2018) Miki T, Popović M, Gawel A, Hitz G, Siegwart R (2018) Multi-agent time-based decision-making for the search and action problem. In: 2018 IEEE International Conference on Robotics and Automation (ICRA), IEEE, pp 2365–2372
- Mirzaei et al. (2011) Mirzaei M, Sharifi F, Gordon BW, Rabbath CA, Zhang Y (2011) Cooperative multi-vehicle search and coverage problem in uncertain environments. In: 2011 50th IEEE Conference on Decision and Control and European Control Conference, IEEE, pp 4140–4145
- Nazarahari et al. (2019) Nazarahari M, Khanmirza E, Doostie S (2019) Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm. Expert Systems with Applications 115:106–120
- Nedić et al. (2018) Nedić A, Olshevsky A, Rabbat MG (2018) Network topology and communication-computation tradeoffs in decentralized optimization. Proceedings of the IEEE 106(5):953–976
- Pang et al. (2019) Pang B, Song Y, Zhang C, Wang H, Yang R (2019) A swarm robotic exploration strategy based on an improved random walk method. Journal of Robotics 2019
- Pang et al. (2021) Pang B, Song Y, Zhang C, Yang R (2021) Effect of random walk methods on searching efficiency in swarm robots for area exploration. Applied Intelligence pp 1–11
- Pinciroli et al. (2012) Pinciroli C, Trianni V, O’Grady R, Pini G, Brutschy A, Brambilla M, Mathews N, Ferrante E, Di Caro G, Ducatelle F, Birattari M, Gambardella LM, Dorigo M (2012) ARGoS: a modular, parallel, multi-engine simulator for multi-robot systems. Swarm intelligence 6(4):271–295
- Rekleitis et al. (2008) Rekleitis I, New AP, Rankin ES, Choset H (2008) Efficient boustrophedon multi-robot coverage: an algorithmic approach. Annals of Mathematics and Artificial Intelligence 52(2):109–142
- Santos et al. (2019) Santos M, Mayya S, Notomista G, Egerstedt M (2019) Decentralized minimum-energy coverage control for time-varying density functions. In: 2019 International Symposium on Multi-Robot and Multi-Agent Systems (MRS), IEEE, pp 155–161
- Scherer et al. (2015) Scherer J, Yahyanejad S, Hayat S, Yanmaz E, Andre T, Khan A, Vukadinovic V, Bettstetter C, Hellwagner H, Rinner B (2015) An autonomous multi-uav system for search and rescue. In: Proceedings of the First Workshop on Micro Aerial Vehicle Networks, Systems, and Applications for Civilian Use, pp 33–38
- Schmickl et al. (2006) Schmickl T, Möslinger C, Crailsheim K (2006) Collective perception in a robot swarm. In: International Workshop on Swarm Robotics, Springer, pp 144–157
- Schroeder et al. (2017) Schroeder A, Ramakrishnan S, Manish K, Trease B (2017) Efficient spatial coverage by a robot swarm based on an ant foraging model and the lévy distribution. Swarm Intelligence 11(1):39–69
- Siligardi et al. (2019) Siligardi L, Panerati J, Kaufmann M, Minelli M, Ghedini C, Beltrame G, Sabattini L (2019) Robust area coverage with connectivity maintenance. In: 2019 International Conference on Robotics and Automation (ICRA), IEEE, pp 2202–2208
- Stirling et al. (2010) Stirling T, Wischmann S, Floreano D (2010) Energy-efficient indoor search by swarms of simulated flying robots without global information. Swarm Intelligence 4(2):117–143
- Strobel et al. (2018) Strobel V, Castelló Ferrer E, Dorigo M (2018) Managing byzantine robots via blockchain technology in a swarm robotics collective decision making scenario. In: Dastani M, Sukthankar G, André E, Koenig S (eds) Proceedings of the 17th International Conference on Autonomous Agents and Multiagent Systems, International Foundation for Autonomous Agents and Multiagent Systems, Richland, SC, AAMAS ’18, pp 541–549, DOI http://dl.acm.org/citation.cfm?id=3237383.3237464
- Thabit and Mohades (2018) Thabit S, Mohades A (2018) Multi-robot path planning based on multi-objective particle swarm optimization. IEEE Access 7:2138–2147
- Tomforde et al. (2017) Tomforde S, Kantert J, Sick B (2017) Measuring self-organisation at runtime-a quantification method based on divergence measures. In: International Conference on Agents and Artificial Intelligence, SciTePress, vol 2, pp 96–106
- Tuci et al. (2018) Tuci E, Alkilabi MH, Akanyeti O (2018) Cooperative object transport in multi-robot systems: A review of the state-of-the-art. Frontiers in Robotics and AI 5:59
- Valentini et al. (2015) Valentini G, Hamann H, Dorigo M (2015) Efficient decision-making in a self-organizing robot swarm: On the speed versus accuracy trade-off. In: Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems, pp 1305–1314
- Wang (1991) Wang PK (1991) Navigation strategies for multiple autonomous mobile robots moving in formation. Journal of Robotic Systems 8(2):177–195
- Yu and LaValle (2016) Yu J, LaValle SM (2016) Optimal multirobot path planning on graphs: Complete algorithms and effective heuristics. IEEE Transactions on Robotics 32(5):1163–1177
- Zhang et al. (2023) Zhang Y, Oğuz S, Wang S, Garone E, Wang X, Dorigo M, Heinrich MK (2023) Self-reconfigurable hierarchical frameworks for formation control of robot swarms. IEEE transactions on cybernetics 54(1):87–100
- Zhu et al. (2020) Zhu W, Allwright M, Heinrich MK, Oğuz S, Christensen AL, Dorigo M (2020) Formation control of UAVs and mobile robots using self-organized communication topologies. In: Swarm Intelligence – Proceedings of ANTS 2020 – Twelfth International Conference, Springer, Berlin, Germany, Lecture Notes in Computer Science, vol 12421, pp 306–314, DOI 10.1007/978-3-030-60376-2˙25
- Zia et al. (2017) Zia K, Din A, Shahzad K, Ferscha A (2017) A cognitive agent-based model for multi-robot coverage at a city scale. Complex Adaptive Systems Modeling 5(1):1–13
Appendix: Robots Available in Practice
Given that energy consumption is mostly a practical consideration, we catalog the performance and capabilities of several robot options that are currently available off-the-shelf444When the monetary cost is not listed by the manufacturer, the listed cost is from the distributor Generation Robots: generationrobots.com.. Although this catalog is an ad-hoc summary of available products, the spread of these products is one way to assess the scope of energy consumption and efficiency of mobile robots and drones at the technical state of the art.
For ground robots, we catalog the e-puck2555https://www.gctronic.com/doc/index.php/e-puck2, Thymio II666I.e., Thymio Wireless, http://wiki.thymio.org/en:thymiospecifications, TurtleBot3 Burger777https://emanual.robotis.com/docs/en/platform/turtlebot3/features/#specifications, iRobot Roomba e888https://www.irobot.com/roomba/e-series, Clearpath robotics Husky999https://clearpathrobotics.com/husky-unmanned-ground-vehicle-robot/, Clearpath robotics Warthog101010https://clearpathrobotics.com/warthog-unmanned-ground-vehicle-robot/, ECA Group Cameleon C111111https://www.ecagroup.com/en/solutions/cameleon-c-ugv-unmanned-ground-vehicle, Autonomous Solutions Inc. (ASI) Chaos121212https://asirobots.com/platforms/chaos/, SMP Robotics Rover S5 PTZ131313https://smprobotics.com/products_autonomous_ugv/area-and-perimeter-gas-monitoring-robot/, Mattro Rovo 2141414https://www.mattro.com/en/the-rovo/technical-specifications, and Boston Dynamics Sopt Explorer151515https://shop.bostondynamics.com/spot. The relevant product specifications listed by the manufacturer are given in Table 7. The approximate energy metrics, calculated from the product specifications in Table 7, are given in Table 9. We calculate the approximate energy metrics for ground robots according to energy consumption corresponding to distance traveled.
For drones, we consider those with cameras, LiDAR, or other imaging capabilities suitable for a supervisor role. We do not consider fixed-wing drones, as they are not suitable for slow speeds or hovering. We catalog the DJI Mini 2161616https://www.dji.com/be/mini-2 DJI Mavic 2 Pro171717https://store.dji.com/be/product/mavic-2, Force1 U49WF FPV Camera Drone181818https://force1rc.com/products/u49w-blue-heron-wifi-drone-with-camera-fpv-drone-w-live-video-altitude-hold, Skydio 2191919https://www.skydio.com/pages/skydio-2, and Autel Evo II202020https://auteldrones.com/pages/evo-ii-detail. The relevant product specifications listed by the manufacturer are given in Table 8. The approximate energy metrics, calculated from the product specifications in Table 8, are given in Table 10. We calculate the approximate energy metrics for drones according to energy consumption corresponding to flight time.
| Locomotion, | Estimated | Estimated | Listed | |
| Product | estimated | operating time, | hourly energy | monetary |
| name | max. speed | charging time | consumption | cost |
| e-puck2 | two-wheeled, | 3 h, | 600mAh | 850 CHF |
| 0.154 m/s | 2.5 h | 3.7V | ||
| Thymio II | two-wheeled, | 4 h, | 375mAh | 140 EUR |
| 0.14 m/s | 1.5 h | 3.7V | ||
| TurtleBot3 | two-wheeled, | 2.5 h, | 720mAh | 580 EUR |
| Burger | 0.22 m/s | 2.5 h | 11.1V | |
| iRobot | two-wheeled, | 1.5 h, | 1200mAh | 400 EUR |
| Roomba e | 0.5 m/s | 3 h | 14.4V | |
| Clearpath | four-wheeled, | 3 h, | 6500mAh | 22000 EUR |
| Husky | 1 m/s | 4 h | 24V | |
| Clearpath | four-wheeled, | 3 h, | 36500mAh | 90000 EUR |
| Warthog | 5 m/s | 4 h | 48V | |
| ECA Group | tracked, | 4 h, | - | - |
| Cameleon C | 1.7 m/s | - | - | |
| ASI Chaos | tracked, | 3 h, | - | - |
| 2.2 m/s | - | - | ||
| SMP Rover | four-wheeled, | 12 h, | 10000mAh | - |
| S5 PTZ | 1.8 m/s | 4 h | 12V | |
| Mattro | tracked, | 8 h, | 11000mAh | - |
| Rovo 2 | 8.3 m/s | 3.25 h | 100V | |
| Spot | quadruped, | 1.5 h, | 7000mAh | 75000 USD |
| Explorer | 1.6 m/s | 2 h | 58V |
| Locomotion, | Estimated | Estimated | Listed | |
| Product | estimated | flight time, | hourly energy | monetary |
| name | max. speed | charging time | consumption | cost |
| DJI | quadrotor, | 31 minutes, | 1160mAh | 1500 EUR |
| Mini 2 | 16 m/s | - | 7.7V | |
| DJI | quadrotor, | 31 minutes, | 1990mAh | 1500 EUR |
| Mavic 2 | 20 m/s | - | 15.4V | |
| U49WF | quadrotor, | 25 minutes, | 830mAh | 100 USD |
| FPV | - | - | 7.4V | |
| Skydio 2 | quadrotor, | 23 minutes, | 1640mAh | 1000 USD |
| 16.1 m/s | - | 11.4V | ||
| Autel | quadrotor, | 40 minutes, | 4730mAh | 1500 USD |
| Evo II | 20.1 m/s | 1.5 h | 11.55V |
| Approximate | Approximate | Approximate | Approximate | |
| maximum | energy | energy | robot cost | |
| Product | distance | consumption | consumption | by distance |
| name | per charge | (at 0.068 m/s) | by distance | per charge |
| e-puck2 | 1.7 km | 2.9 joules/s | 43 joules/m | 0.50 EUR/m |
| Thymio II | 2 km | 2.7 joules/s | 40 joules/m | 0.07 EUR/m |
| TurtleBot3 | 2 km | 6.2 joules/s | 91 joules/m | 0.29 EUR/m |
| Burger | ||||
| iRobot | 3 km | 3.5 joules/s | 52 joules/m | 0.15 EUR/m |
| Roomba e | ||||
| Clearpath | 11 km | 32.0 joules/s | 470 joules/m | 2.04 EUR/m |
| Husky | ||||
| Clearpath | 55 km | 71.4 joules/s | 1050 joules/m | 1.67 EUR/m |
| Warthog | ||||
| ECA Group | 25 km | - | - | - |
| Cameleon C | ||||
| ASI Chaos | 25 km | - | - | - |
| SMP Rover | 80 km | 54.4 joules/s | 800 joules/m | - |
| S5 PTZ | ||||
| Mattro | 240 km | 72.1 joules/s | 1060 joules/m | - |
| Rovo 2 | ||||
| Spot | 9 km | 25.8 joules/s | 380 joules/m | 7.26 EUR/m |
| Explorer |
| Approximate | Approximate | Approximate | Approximate | |
| maximum | energy | energy | robot cost | |
| Product | distance | consumption | consumption | by distance |
| name | per charge | during flight | by distance | per charge |
| (at 0.074 m/s) | (at 0.074 m/s) | (at 0.074 m/s) | ||
| DJI | 140 m | 8.9 joules/s | 120 joules/m | 10.71 EUR/m |
| Mini 2 | ||||
| DJI | 140 m | 30.6 joules/s | 410 joules/m | 10.71 EUR/m |
| Mavic 2 | ||||
| U49WF | 110 m | 6.1 joules/s | 82 joules/m | 0.76 EUR/m |
| FPV | ||||
| Skydio 2 | 100 m | 18.7 joules/s | 250 joules/m | 8.36 EUR/m |
| Autel | 180 m | 54.6 joules/s | 740 joules/m | 6.97 EUR/m |
| Evo II |