Cellular uptake of active nonspherical nanoparticles

The transport of nano-sized particles across cells or vesicles made of lipid-bilayer membranes is a ubiquitous phenomenon in biological processes with many applications in biomedical and biotechnology fields ranging from drug and gene delivery Panyam2003 ; Xu2018 ; Wang2019 ; N.Pardi2015 to biomedical imaging and sensing R.Weissleder2006 ; D.Peer2007 ; W.Kukulski2012 . Cellular uptake is a key pathway for transporting cargo into cell via being engulfed and internalized by cell membranes, a process related to the interaction between cell membranes and NPs. Such a wrapping process plays an integral role in a wide range of health related aspects B.Alberts2005 such as nutrient import, signal transduction, neurotransmission F.Frey2019PRE ; G.V.Meer2004 ; N.Walani2015PNAS , and cellular entry and exit of viruses, pathogens and parasites into host cells J.Mercer2010 ; S.Dasgupta2014BJ ; G.Bao2005 ; S.Zhang2015 . In addition, it is also important for designing diagnostic and therapeutic agents due to the rapid development of NPs for the delivery of, for example, anticancer agents M.E.Davis2008 . For example, specifically enveloped particles are utilized to serve as targeting drug delivered into tumor cells D.Peer2007 ; W.Rao2015 ; Y.Min2015 ; R.Imani2017 ; M.Wang2023 , based on the understanding of the interactions between cell membranes and NPs. Despite its biological importance, it is still not fully understood how the active force and the aspect ratio of NPs and membrane properties (adhesion energy density and membrane tension) affect the wrapping behaviors.

Investigations concerning the engulfment and internalization of passive particles by cell membranes have been extensively conducted experimentally, theoretically, and numerically. Among them, many studies are focused on the influence of physical parameters, including particle size Deserno2002 ; Deserno2003 ; M.Deserno2004 ; S.Zhang2009 ; B.D.Chithrani2006 ; J.Agudo2015 ; C.Contini2020 , shape J.Midya2023 ; F.Frey2019 ; K.Yang2010 ; Z.Shen2019 ; S.Dasgupta2014 ; S.Dasgupta2013 ; A.H.Bahrami2013 ; D.M.Richards2016 ; L.P.Chen2016 , elastic properties of invading particles J.Midya2023 ; X.Yi2011 ; J.C.Shillcock2005 ; X.Yi2014 ; A.Verma2010 ; X.Ma2021 , ligand and receptor density H.Yuan2010PRL ; H.Yuan2010 ; T.Wiegand2020 , as well as the mechanical properties of the membrane J.Agudo-Canalejo2015 ; H.T.Spanke2020 , based on adhesion-mediated wrapping mechanism. In recent years, there has been a growing research interest in the interactions between biological self-propelled bacterial pathogens (Rickettsia rickettsii or Listeria monocytogenes, Escherichia coli bacteria, and Bacillus subtilis bacteria, etc.) or synthetic self-propelled particles (synthetic Janus particles) and the cell membranes H.R.Vutukuri2020 ; S.C.Takatori2020 ; C.Wang2019 ; Y.Li2019 ; M.S.E.Peterson2021 ; L.LeNagarda2022 . One of the main features of these self-propelled bacterial pathogens or synthetic artificial particles is that they are able to generate mechanical forces by consuming energy from their environment, which often results in motion S.Ramaswamy2010 . For instance, it has been found that Rickettsia rickettsii are able to produce active force to facilitate their mobility by forming actin tails P.M.Colonne2016 , and Listeria monocytogenes can generate active force to push out a tube-like protuberance from the plasma membrane by hijacking the actin polymerization-depolymerization apparatus of their host J.A.Theriot1992 ; J.R.Robbins1999 ; T.Chakraborty1999 ; F.E.Ortega2019 ; G.C.Dowd2020 . Furthermore, the interplay of self-propelled particles with cell membranes also leads to rich intriguing dynamical behaviors and functions such as membrane fluctuations and large deformations H.R.Vutukuri2020 ; S.C.Takatori2020 , shape transformations C.Wang2019 ; Y.Li2019 ; M.S.E.Peterson2021 , and even deformation of lipid vesicles into flagellated swimmers L.LeNagarda2022 . The specific interactions between membranes and self-propelled bacterial pathogens or artificial self-propelled particles plays a key role in designing active matter systems A.T.Brownet2016 . How the active force of these self-propelled agents affects the wrapping behaviors remains to be elucidated.

Nevertheless, the studies mentioned above are confined within spherical NPs. In many biological systems, active NPs such as the wrapped pathogens or viruses, can be highly nonspherical S.Dasgupta2014 ; C.Hulo2011 , such as egg-shaped malaria parasite S.Dasgupta2014 and cylindrical Listeria monocytogenes. Moreover, the shape of the wrapped particles also affects the wrapping behaviors in cellular uptake, and scientists have been motivated to model the wrapping behaviors of artificial particles with various geometries such as ellipsoids, rod-like particles, and capped cylinders J.Midya2023 ; F.Frey2019 ; K.Yang2010 ; Z.Shen2019 ; S.Dasgupta2014 ; S.Dasgupta2013 ; A.H.Bahrami2013 ; D.M.Richards2016 ; J.A.Champion2006 ; N.Doshi2010 ; D.Paul2013 . However, in these studies, particle activity was not taken into account.

Theoretically, the interplay of a lipid membrane with an NP is typically governed by only a few physical parameters (membrane bending rigidity, membrane tension, and adhesion energy density), through which the membrane resists bending and stretching. The deformation of a membrane can also occur as a consequence of adhesive interactions between the membrane and the particle, characterized by an adhesion energy per unit area. A detailed and comprehensive investigation of how the wrapping behaviors depend on the active force, the particle’s aspect ratio, and the membrane properties (adhesion energy density and membrane tension) is needed.

To model the action of forces on a membrane, we adopted the spirit of continuum mechanics by treating the membrane as a smooth surface and incorporating the work done by the force into the total energy of the membrane Brochard2006 ; Derenyi2002 ; B.Bozic1997 . To determine the equilibrium shape of the membrane, the corresponding variational problem carried out here is mathematically equivalent to many of previous papers Derenyi2002 ; B.Bozic1997 ; B.Sabass2016 .

In this work, we use energy minimization to calculate and predict shapes and wrapping states for an ellipsoidal NP at an initially flat membrane. Our article is organized as follows. In Section II, we describe our theoretical model including the numerical method employed and the parameters we used. Section III is devoted to results and discussions, including the influence of the active force on the wrapping states of ellipsoid and its corresponding phase diagram, the effects of the particle’s aspect ratio and the membrane properties and its corresponding phase diagrams. Section IV is devoted to conclusion.

We consider an initially flat membrane pushed by an active self-propelled rigid ellipsoidal NP (prolate or oblate spheroid) with its principle rotational axis orthogonal to the membrane, as shown in Fig. 1. For simplicity, we assume that the active force is constant and always falls strictly along the $z$ direction in a way so that the system obeys rotational symmetry and the particle will not rotate during the wrapping process. Here it should be noted that for a passive particle, it may undergo orientational rotation, possibly due to stochastic thermal fluctuation of the membrane L.P.Chen2016 .

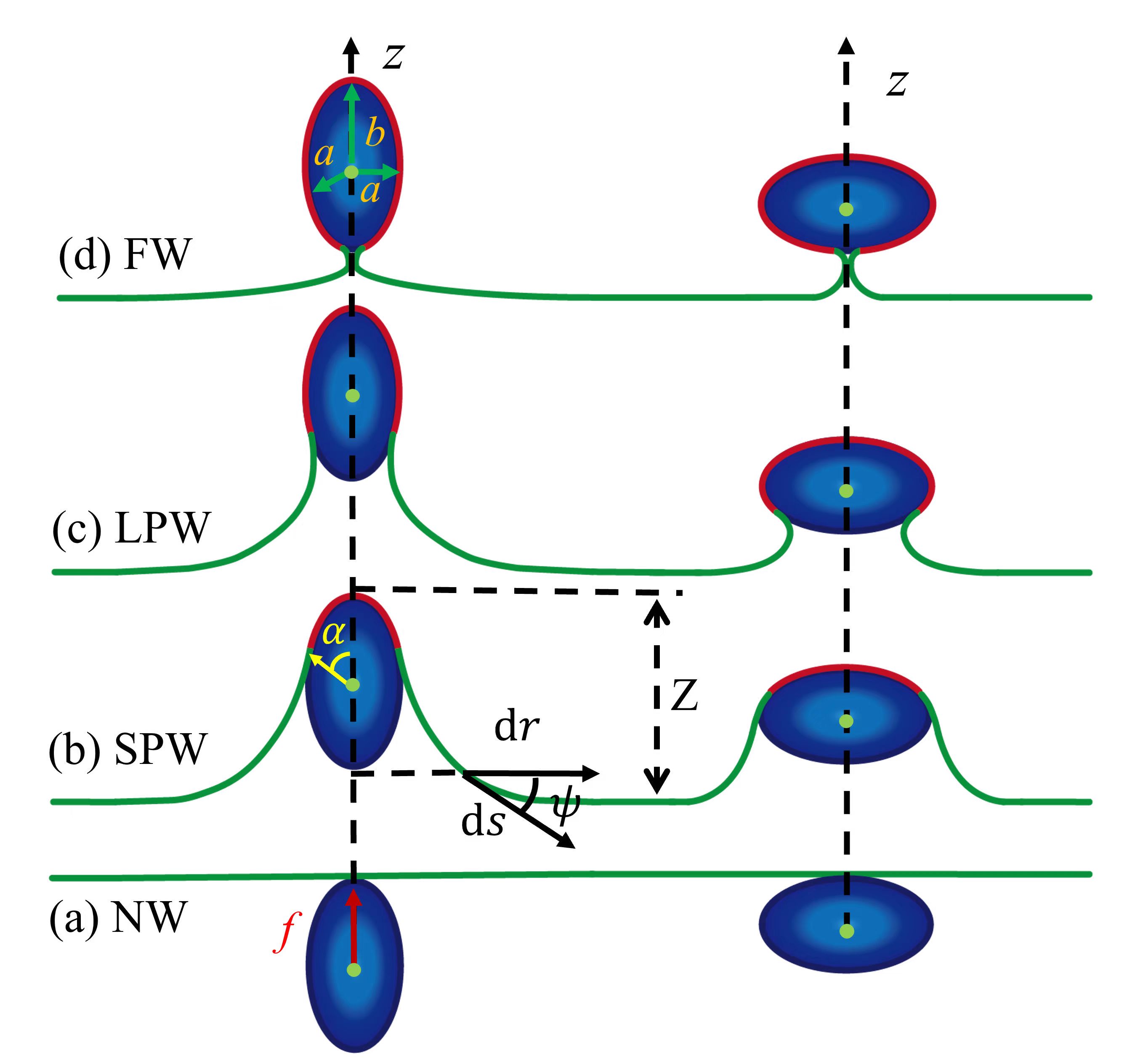
The shape of this ellipsoidal particle can be defined by the shape equation in Cartesian coordinates $x$, $y$, $z$,

$\displaystyle\frac{x^{2}+y^{2}}{a^{2}}+\frac{z^{2}}{b^{2}}=1,$

(1)

where $a$ and $b$ denote the semi-axes perpendicular to and along the principle rotational axis, respectively. The geometry of the particle is parameterized by the aspect ratio $e=b/a$, with $e<1$ for oblate ellipsoids, $e=1$ for spheres, and $e>1$ for prolate ellipsoids, respectively. Using the classical Canham-Helfrich continuum membrane model Helfrich1973 ; F.Julicher1994 ; M.Deserno2004 , the total free energy of such a system is given by

$\displaystyle E^{\mathrm{tot}}=\int_{A_{\rm mem}}\frac{\kappa}{2}(2H)^{2}dA+\sigma\Delta A-\int_{A_{\rm ad}}\omega\leavevmode\nobreak\ dA-fZ,$

(2)

where the first term is contributed by the bending energy of the membrane, with $\kappa$ the bending rigidity and $H$ the local mean curvature. The second term is the tension energy, with $\sigma$ being the membrane tension and $\Delta A$ being the excess area induced by wrapping. The third term represents the gain in adhesive energy, characterized by a negative adhesion energy per unit area $-\omega$. The deformation of the membrane can not only be induced by the adhesive interactions between the membrane and the particle, but also occurs as a consequence of the work done by the active force, as represented by the last therm of Eq. (2). Here the membrane is assumed to be pushed by the active force $f$ to a height of $Z$ [see Fig. 1].

An ellipsoidal NP-membrane system can be divided into two parts: the wrapped part and the free part of the membrane. In practice, it is convenient use the parametric equations $x=a\sin\theta\cos\phi$, $y=a\sin\theta\sin\phi$ and $z=b\cos\theta$, to describe the ellipsoidal NP surface. Given this, the area element can be obtained in terms of polar angle: $dA=2\pi a\sin\theta\sqrt{a^{2}\cos^{2}\theta+b^{2}\sin^{2}\theta}\leavevmode\nobreak\ d\theta$, and the energy generated by the particle-membrane adhesive interaction is written as

$\displaystyle E_{\rm ad}=-\int_{0}^{\alpha}2\pi\omega a\sin\theta\sqrt{a^{2}\cos^{2}\theta+b^{2}\sin^{2}\theta}\leavevmode\nobreak\ d\theta,$

(3)

where $\alpha$ is the wrapping angle. The mean curvature of the ellipsoidal particle can be calculated as

$\displaystyle H=\frac{c_{1}+c_{2}}{2}=\frac{b[2a^{2}+(b^{2}-a^{2})\sin^{2}\theta]}{2a[a^{2}+(b^{2}-a^{2})\sin^{2}\theta]^{3/2}},$

(4)

where $c_{1}$ and $c_{2}$ are the two principle curvatures. Hence, the bending energy of the adhesive (wrapping) part can be written as

	$\displaystyle E_{\rm bend}^{\rm ad}=$	$\displaystyle\int_{0}^{\alpha}\pi\kappa\sin\theta\frac{b^{2}[2a^{2}+(b^{2}-a^{2})\sin^{2}\theta]^{2}}{a[a^{2}+(b^{2}-a^{2})\sin^{2}\theta]^{3}}\times$
		$\displaystyle\sqrt{a^{2}\cos^{2}\theta+b^{2}\sin^{2}\theta}\leavevmode\nobreak\ d\theta.$		(5)

Similarly, the contribution made by the surface tension of the adhesive (wrapping) part can be given by

	$\displaystyle E_{\rm ten}^{\rm ad}=$	$\displaystyle\int_{0}^{\alpha}2\pi\sigma a\sin\theta\biggl{(}1-\frac{a\cos\theta}{\sqrt{a^{2}\cos^{2}\theta+b^{2}\sin^{2}\theta}}\biggr{)}\times$
		$\displaystyle\sqrt{a^{2}\cos^{2}\theta+b^{2}\sin^{2}\theta}\leavevmode\nobreak\ d\theta,$		(6)

which is proportional to the area difference between the contact area (red in Fig. 1) and the area of its projection. The work done by the active particle for the adhered part is calculated as $E_{f}^{\rm ad}=-fb(1-{\rm cos}\alpha)$. Given these and using $e=b/a$, the free energy of the wrapping part reads

	$\displaystyle\frac{E_{\rm ad}^{\rm tot}}{\kappa}=$	$\displaystyle\int_{0}^{\alpha}\pi\sin\theta\biggl{\{}e^{2}\frac{[2+(e^{2}-1)\sin^{2}\theta]^{2}}{[1+(e^{2}-1)\sin^{2}\theta]^{3}}+$
		$\displaystyle 2\frac{a^{2}}{\lambda^{2}}\biggl{(}1-\frac{\cos\theta}{\sqrt{\cos^{2}\theta+e^{2}\sin^{2}\theta}}\biggr{)}-2\frac{\omega a^{2}}{\sigma\lambda^{2}}\biggr{\}}\times$
		$\displaystyle\sqrt{\cos^{2}\theta+e^{2}\sin^{2}\theta}\leavevmode\nobreak\ d\theta-2\pi\frac{aef}{\lambda f_{0}}(1-\cos\alpha),$		(7)

where $\lambda=\sqrt{\kappa/\sigma}$ and $f_{\rm 0}=2\pi\sqrt{\kappa\sigma}$ feature a typical length scale and a force scale, respectively.

For the free part of the membrane, its elastic energy comes from the axisymmetrically curved membrane shape described by $r(s)$, $z(s)$ and $\psi(s)$ [see Fig. 1(b)], where $s$ is the arc length of the free membrane. The coordinates $r(s)$ and $z(s)$ depend on $\psi(s)$ through constraints $\dot{r}={\rm cos}\psi$ and $\dot{z}=-{\rm sin}\psi$, where the dots denote a derivative with respect to the arc length. The total energy of the free membrane, with the two principal curvatures given by $\dot{\psi}$ and $({\rm sin}\psi)/r$, can be written as F.Julicher1994 ; M.Deserno2004 ; U.Seifert1990

$\displaystyle\frac{E_{\rm free}^{\rm tot}}{\kappa}=\pi\int_{0}^{S}ds\leavevmode\nobreak\ \mathcal{L}(\psi,\dot{\psi},r,\dot{r},\dot{z},\eta,\xi,f),$

(8)

where $\mathcal{L}$ is a Lagrangian defined by

	$\displaystyle\mathcal{L}=\leavevmode\nobreak\$	$\displaystyle r\biggl{(}\dot{\psi}+\frac{{\rm sin}\psi}{r}\biggr{)}^{2}+2\frac{\sigma}{\kappa}r(1-{\rm cos}\psi)-\frac{f}{\pi\kappa}{\rm sin}\psi$
		$\displaystyle+\eta(\dot{r}-{\rm cos}\psi)+\xi(\dot{z}+{\rm sin}\psi).$		(9)

Here $\eta(s)$ and $\xi(s)$ are Lagrangian multipliers used to impose the geometric constraints between $r$, $z$ and $\psi$. The term associated with the active force $f$ is proportional to the membrane height of the free part $Z_{\mathrm{free}}=\int_{0}^{L}\sin\psi ds$. A variation of the energy functional Eq. (8) against the shape variables $r(s)$, $z(s)$ and $\psi(s)$ produces a set of shape equations, of which the details can be found in Appendix A. Here, we take the value of $\xi$ as a constant which equals to zero due to the fact that its first order derivative is zero, as well as the variation of the energy against $z(0)$ is zero (see Appendix A). With boundary conditions at the contact point between the particle and the membrane, $\psi(0)=\arctan(e\tan\alpha)$ for $\alpha\leq\pi/2$, $\psi(0)=\pi+\arctan(e\tan\alpha)$ for $\alpha>\pi/2$, and $r(0)=a\sin\alpha$, as well as $\psi(\infty)=0$ and $z(\infty)=0$ at the infinity, we numerically solve the shape equations for various $\alpha$ and obtain the total energy $E^{\mathrm{tot}}(\alpha)$ as a function of the wrapping angle $\alpha$. Based on the optimal wrapping angle $\alpha$ obtained via minimizing the total energy, we identify 4 types of wrapping states: nonwrapping (NW) when $\alpha=0$, small partial wrapping (SPW) when $0<\alpha\leq\pi/2$, large partial wrapping (LPW) when $\pi/2\leq\alpha<\pi$, and full wrapping (FW) when $\alpha=\pi$, as shown in Fig. 1. Here it should be noted that, in our theoretical model, we consider a special case when the pressure difference between the inside and outside of the plasma membrane, as well as the spontaneous curvature of the membrane, is neglected.

In summary, based on the total energy functional, we study the wrapping states of a self-propelled nonspherical particle when it is pushed against a membrane. It is found that the active force generated by the particle is able to trigger a first-order wrapping transition, accompanied with a hysteresis behavior. Such a transition provides a deeper insight into the wrapping behaviors induced by a self-propelled nonspherical particle. The wrapping states of the active particle are tunable by active force, aspect ratio, particle size, and membrane properties (including the adhesion energy density and the membrane tension), as demonstrated by the phase diagrams in the two-parameter space. It is also identified that the wrapping degree can be enhanced (for small particle, weak adhesion strength, and high membrane tension) or decreased (for large particle, strong adhesion strength, and low membrane tension) upon increasing the active force of the particle. Our results provide a useful guidance for engineering active particle-based therapeutics to promote biomedical applications.

We acknowledge financial support from National Natural Science Foundation of China under Grant Nos.12147142, 11974292, 12174323, and 1200040838, and 111 project B16029.

For axisymmetric surfaces, from the energy functional Eq. (8) in the main text and by variational methods one can derive the Euler-Lagrange equations

	$\displaystyle\ddot{\psi}=\leavevmode\nobreak\$	$\displaystyle-\frac{{\rm cos}\psi}{r}\dot{\psi}+\frac{{\rm sin}\psi{\rm cos}\psi}{r^{2}}+\frac{\sigma}{\kappa}{\rm sin}\psi-\frac{f}{2\pi\kappa r}{\rm cos}\psi$
		$\displaystyle+\frac{\eta}{2r}{\rm sin}\psi+\frac{\xi}{2r}{\rm cos}\psi,$		(10)

$\displaystyle\dot{\eta}=\dot{\psi}^{2}-\frac{{\rm sin}^{2}\psi}{r^{2}}+2\frac{\sigma}{\kappa}(1-{\rm cos}\psi),$

(11)

$\displaystyle\dot{\xi}=0,$

(12)

$\displaystyle\dot{r}={\rm cos}\psi,$

(13)

$\displaystyle\dot{z}=-{\rm sin}\psi.$

(14)

In order to numerically solve the above equations, we first map the region $s\in[0,\infty]$ to a finite region $s\in[0,S_{tot}]$ and introduce a parameter $u=s/S_{tot}$ which is defined on a fixed interval $[0,1]$. All the functions of $s$ are therefore transformed into functions of $u$. The derivative $\frac{d}{ds}$ are replaced with $\frac{1}{S_{tot}}\frac{d}{ds}$ and the five equations (10)-(14) are transformed into ordinary differential equations with respect to the parameter $u$. The equations are all first order except Eq. (10), which is second order of $\psi$. They are equivalent to 6 first order ordinary differential equations. In addition, with the unknown parameter $S_{tot}$, we need 7 boundary conditions to complete the problem. These boundary conditions include: $\psi(u=0)=\arctan(e\tan\alpha)$ for $\alpha\leq\pi/2$, $\psi(u=0)=\pi+\arctan(e\tan\alpha)$ for $\alpha>\pi/2$, $\psi(u=1)=0$, $r(u=0)=a\sin\alpha$, $r(u=1)=R_{b}$, $\xi(0)=0$, $z(u=1)=0$. In practice, we let $R_{b}$ to be a large enough number such that the results are not changed for values greater than $R_{b}$. Here we only have 6 boundary conditions and one more boundary condition still needed. To complete the boundary conditions, we consider a homogeneous membrane, so that the Lagrangian $\mathcal{L}$ is explicitly independent of the arc length $s$. As a result, the Hamiltonian $\mathcal{H}\equiv-\mathcal{L}+\dot{\psi}\partial\mathcal{L}/\partial\dot{\psi}+\dot{r}\partial\mathcal{L}/\partial\dot{r}+\dot{z}\partial\mathcal{L}/\partial\dot{z}$ is a conserved quantity F.Julicher1994 given by

	$\displaystyle\mathcal{H}=\leavevmode\nobreak\$	$\displaystyle r\biggl{(}\dot{\psi}^{2}-\frac{{\rm sin}^{2}\psi}{r^{2}}\biggr{)}-2\frac{\sigma}{\kappa}r(1-{\rm cos}\psi)+\frac{f}{\pi\kappa}{\rm sin}\psi$
		$\displaystyle+\eta{\rm cos}\psi-\xi{\rm sin}\psi.$		(15)

Due to that $\mathcal{H}$ is conserved along the arc length, i.e., $\mathcal{H}(s)=0$. We therefore impose the seventh boundary condition which is $\mathcal{H}(u=0)=0$. The 6 first order equations with an unknown parameter $S_{tot}$ plus 7 boundary conditions constitute a well-defined boundary value problem (BVP) that can be numerically solved by the Matlab solver ’bvp4c’.

By combining Eqs. (10) and (15), and letting $\xi=0$, one can derive the general shape equation

	$\displaystyle\ddot{\psi}r^{2}\cos\psi+\dot{\psi}r\cos^{2}\psi$	$\displaystyle+\frac{1}{2}\dot{\psi}^{2}r^{2}\sin\psi-\frac{1}{2}(\cos^{2}\psi+1)\sin\psi$
		$\displaystyle-\frac{\sigma}{\kappa}r^{2}\sin\psi+\frac{fr}{2\pi\kappa}=0.$		(16)

As mentioned in the main text, the total free energy of the system can be divided into two main parts: the wrapping part of the membrane in contact with the particle, and the free part of the membrane. At the NW-SPW transition, the wrapping angle is zero, $\alpha=0$. According to the local mean curvature on the contact point Eq. (4), we assume that the particle’s local effective radius at this point is

$\displaystyle R_{\rm eff}=\frac{1}{H\mid_{\theta=0}}=\frac{a^{2}}{b}=\frac{a}{e}.$

(17)

As a result, the contribution of the wrapping part to the total free energy can be rewritten as

$\displaystyle\frac{E_{\rm ad}^{\rm tot}}{\kappa}=\pi(1-{\rm cos}\alpha)\biggl{[}\frac{R_{\rm eff}^{2}}{\lambda^{2}}(1-{\rm cos}\alpha)-2\frac{\omega R_{\rm eff}^{2}}{\sigma\lambda^{2}}-\frac{2R_{\rm eff}f}{\lambda f_{\rm 0}}+4\biggr{]}.$

(18)

Here, it should be noted that we have assumed the wrapping part as part of a sphere of an effective radius $R_{\rm eff}$.

For weakly deformed membrane ($\psi\ll 1$) and small value of $\alpha$, Eq. (16) can be linearized as

$\displaystyle\ddot{\psi}r^{2}+\dot{\psi}r-(1+\lambda^{-2}r^{2})\psi=-\frac{fr}{2\pi\kappa}.$

(19)

The small value of function $\psi$ leads to an proper approximation that the radial coordinate $r$ equals to the arc length $s$ to the first order due to $dr=ds\cos\psi\approx ds+O(\psi^{2})$. Given this, the general solution to Eq. (19) reads

$\displaystyle\psi=\frac{f\lambda^{2}}{2\pi\kappa r}+A\textit{I}_{1}(r/\lambda)+B\textit{K}_{1}(r/\lambda),$

(20)

where $\textit{I}_{1}(x)$ and $\textit{K}_{1}(x)$ are first-order modified Bessel functions, and $A$ and $B$ are integration constants. According to the boundary conditions $\psi(r=R_{\rm eff}\sin\alpha)=\alpha$ and $\psi(r=+\infty)=0$, one can determine that $A=0$ and $B=[\alpha-f\lambda^{2}/(2\pi\kappa R_{\rm eff}\sin\alpha)]/K_{1}(R_{\rm eff}\sin\alpha/\lambda)$. Therefore, in the limit of $\alpha\ll 1$ and $\psi\ll 1$, we can calculate the work done by the active particle for the free part as

	$\displaystyle E_{\rm f}^{\rm free}$	$\displaystyle=-f\int_{R_{\rm eff}\alpha}^{R_{\rm b}}\psi{\rm d}r$
		$\displaystyle=-\frac{f\lambda(f\lambda^{2}-2\pi\kappa R_{\rm eff}\alpha^{2})}{2\pi\kappa R_{\rm eff}\alpha K_{1}(R_{\rm eff}\alpha/\lambda)}[K_{0}(R_{\rm b}/\lambda)-K_{0}(R_{\rm eff}\alpha/\lambda)]$
		$\displaystyle+\frac{f^{2}\lambda^{2}}{2\pi\kappa}{\rm ln}(\frac{R_{\rm eff}\alpha}{R_{\rm b}}).$		(21)

Here the lower limit for the integration variable $r$ is $R_{\rm eff}\sin\alpha\approx R_{\rm eff}\alpha$, as shown in the schematic Fig. 8. The upper limit $R_{\mathrm{b}}$ in practice is chosen to be a finite value so as to avoid the divergence of the integral Eq. (21) when $R_{\mathrm{b}}\rightarrow\infty$, but large enough (e.g. $R_{\mathrm{b}}/\lambda=1000$) so that further increasing $R_{\mathrm{b}}$ brings little change to the result when calculating the second derivative of the total energy, as discussed later in this subsection. The bending energy of the free part of the membrane reads

	$\displaystyle E_{\rm bend}^{\rm free}$	$\displaystyle=\pi\kappa\int_{R_{\rm eff}\alpha}^{R_{\rm b}}\biggl{(}\dot{\psi}+\frac{\psi}{r}\biggr{)}^{2}r{\rm d}r$
		$\displaystyle=\biggl{(}\frac{f\lambda^{2}-2\pi\kappa R_{\rm eff}\alpha^{2}}{2\sqrt{2\pi\kappa}R_{\rm eff}\alpha\lambda K_{1}(R_{\rm eff}\alpha/\lambda)}\biggr{)}^{2}\biggl{[}R_{\rm b}^{2}(K_{0}^{2}(R_{\rm b}/\lambda)$
		$\displaystyle-K_{1}^{2}(R_{\rm b}/\lambda))+R_{\rm eff}^{2}\alpha^{2}(K_{1}^{2}(R_{\rm eff}\alpha/\lambda)-K_{0}^{2}(R_{\rm eff}\alpha/\lambda))\biggr{]},$		(22)

and the tension energy is given by

	$\displaystyle E_{\rm tens}^{\rm free}$	$\displaystyle=\pi\sigma\int_{R_{\rm eff}\alpha}^{R_{\rm b}}r\psi^{2}{\rm d}r$
		$\displaystyle=\frac{\sigma}{8\pi\kappa^{2}\alpha^{2}R_{\rm eff}^{2}K_{1}^{2}(R_{\rm eff}\alpha/\lambda)}\biggl{\{}(f\lambda^{2}-2\pi\kappa R_{\rm eff}\alpha^{2})^{2}$
		$\displaystyle\biggl{[}R_{\rm b}^{2}\bigl{(}K_{1}^{2}(R_{\rm b}/\lambda)-K_{0}^{2}(R_{\rm b}/\lambda)\bigr{)}+R_{\rm eff}^{2}\alpha^{2}\bigl{(}K_{0}^{2}(R_{\rm eff}\alpha/\lambda)$
		$\displaystyle-K_{1}^{2}(R_{\rm eff}\alpha/\lambda)\bigr{)}\biggr{]}-2\lambda(2\pi\kappa R_{\rm eff}\alpha^{2}-f\lambda^{2})K_{0}(R_{\rm b}/\lambda)\cdot$
		$\displaystyle\biggl{[}R_{\rm b}(2\pi\kappa R_{\rm eff}\alpha^{2}-f\lambda^{2})K_{1}(R_{\rm b}/\lambda)+2fR_{\rm eff}\alpha\lambda^{2}K_{1}(R_{\rm eff}\alpha/\lambda)\biggr{]}$
		$\displaystyle+2R_{\rm eff}\alpha(4\pi^{2}\kappa^{2}R_{\rm eff}^{2}\alpha^{4}\lambda-f^{2}\lambda^{5})K_{0}(R_{\rm eff}\alpha/\lambda)K_{1}(R_{\rm eff}\alpha/\lambda)$
		$\displaystyle+2f^{2}R_{\rm eff}^{2}\alpha^{2}\lambda^{4}K_{1}^{2}(R_{\rm eff}\alpha/\lambda){\rm ln}\frac{R_{\rm b}}{R_{\rm eff}\alpha}\biggr{\}}.$		(23)

Summing these three terms and the total energy for the adhesion part, and doing a Taylor expansion with respect to $\alpha$ to the second order of $\alpha$, leads to

	$\displaystyle E_{\rm tot}/\kappa=$	$\displaystyle-\pi\left(\frac{f}{f_{0}}\right)^{2}\biggl{[}\frac{R_{\rm b}}{\lambda}K_{0}(R_{\rm b}/\lambda)K_{1}(R_{\rm b}/\lambda)+{\rm ln}(R_{\rm b}/\lambda)+\gamma-{\rm ln2}\biggr{]}$
		$\displaystyle+\frac{\pi}{2}\left(\frac{f}{f_{0}}\right)^{2}\left(\frac{R_{\rm eff}}{\lambda}\right)^{2}\alpha^{2}\biggl{[}\left({\rm ln\alpha}+\frac{R_{\rm b}}{\lambda}K_{0}(R_{\rm b}/\lambda)K_{1}(R_{\rm b}/\lambda)+\frac{2}{(f/f_{0})(R/\lambda)}+{\rm ln}(R_{\rm eff}/\lambda)+\gamma-{\rm ln2}-\frac{1}{2}\right)^{2}$
		$\displaystyle-\biggl{(}\frac{R_{\rm b}}{\lambda}K_{0}(R_{\rm b}/\lambda)K_{1}(R_{\rm b}/\lambda)\biggr{)}^{2}-2\frac{\omega/\sigma}{(f/f_{0})^{2}}+\frac{1}{4}\biggr{]},$		(24)

where $\gamma$ is the Euler Gamma function.

	$\displaystyle\frac{{\rm d}(E_{\rm tot}/\kappa)}{{\rm d}\alpha}=$	$\displaystyle\pi\left(\frac{f}{f_{0}}\right)^{2}\left(\frac{R_{\rm eff}}{\lambda}\right)^{2}\alpha\biggl{[}2\frac{R_{\rm b}}{\lambda}K_{0}(R_{\rm b}/\lambda)K_{1}(R_{\rm b}/\lambda)\left({\rm ln}\alpha+\frac{2}{(f/f_{0})(R_{\rm eff}/\lambda)}+{\rm ln}(R_{\rm eff}/\lambda)+\gamma-{\rm ln}2\right)-2\frac{\omega/\sigma}{(f/f_{0})^{2}}$
		$\displaystyle+\left(\frac{2}{(f/f_{0})(R_{\rm eff}/\lambda)}+\gamma\right)^{2}+\left({\rm ln}\alpha+\frac{4}{(f/f_{0})(R_{\rm eff}/\lambda)}+{\rm ln}(R_{\rm eff}/\lambda)+2\gamma-{\rm ln}2\right)\biggl{(}{\rm ln}\alpha+{\rm ln}(R_{\rm eff}/\lambda)-{\rm ln}2\biggr{)}\biggr{]},$		(25)

The second order derivative of the total energy with respect to $\alpha$ is obtained as

	$\displaystyle\frac{{\rm d^{2}}(E_{\rm tot}/\kappa)}{{\rm d}\alpha^{2}}=$	$\displaystyle\pi\left(\frac{f}{f_{0}}\right)^{2}\left(\frac{R_{\rm eff}}{\lambda}\right)^{2}\biggl{[}\left(\frac{2}{(f/f_{0})(R_{\rm eff}/\lambda)}+\gamma\right)\left(\frac{2}{(f/f_{0})(R_{\rm eff}/\lambda)}+\gamma+2\right)-2\frac{\omega/\sigma}{(f/f_{0})^{2}}$
		$\displaystyle+2\frac{R_{\rm b}}{\lambda}K_{0}(R_{\rm b}/\lambda)K_{1}(R_{\rm b}/\lambda)\left({\rm ln}\alpha+\frac{2}{(f/f_{0})(R_{\rm eff}/\lambda)}+{\rm ln}(R_{\rm eff}/\lambda)+\gamma+1-{\rm ln}2\right)$
		$\displaystyle+\biggl{(}{\rm ln}\alpha+{\rm ln}(R_{\rm eff}/\lambda)-{\rm ln}2\biggr{)}^{2}+2\biggl{(}{\rm ln}\alpha+{\rm ln}(R_{\rm eff}/\lambda)-{\rm ln}2\biggr{)}\biggl{(}\frac{2}{(f/f_{0})(R_{\rm eff}/\lambda)}+\gamma+1\biggr{)}\biggr{]}.$		(26)

By setting ${\rm d^{2}}(E_{\rm tot}/\kappa)/{\rm d}\alpha^{2}=0$, we can get the analytical solution corresponding to the critical transition line between NW and SPW, which is shown by the red dash line in Figs. 5 and  6 in the main text. A comparison between the analytical results and the exact numerical results indicates that the approximate expression is remarkably accurate.