This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

††thanks: Contributed equally to this work.††thanks: Contributed equally to this work.

Cavity Quantum Electrodynamics with Second-Order Topological Corner State

Xin Xie Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China CAS Center for Excellence in Topological Quantum Computation and School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China    Weixuan Zhang Key Laboratory of advanced optoelectronic quantum architecture and measurements of Ministry of Education, School of Physics, Beijing Institute of Technology, 100081, Beijing, China Beijing Key Laboratory of Nanophotonics &\& Ultrafine Optoelectronic Systems, Micro-nano Center, School of Physics, Beijing Institute of Technology, 100081, Beijing, China    Xiaowu He State Key Laboratory of Superlattices and Microstructures, Institute of Semiconductors Chinese Academy of Sciences, Beijing 100083, China    Shiyao Wu    Jianchen Dang    Kai Peng    Feilong Song    Longlong Yang Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China CAS Center for Excellence in Topological Quantum Computation and School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China    Haiqiao Ni State Key Laboratory of Superlattices and Microstructures, Institute of Semiconductors Chinese Academy of Sciences, Beijing 100083, China    Zhichuan Niu State Key Laboratory of Superlattices and Microstructures, Institute of Semiconductors Chinese Academy of Sciences, Beijing 100083, China    Can Wang    Kuijuan Jin Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China CAS Center for Excellence in Topological Quantum Computation and School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China Songshan Lake Materials Laboratory, Dongguan, Guangdong 523808, China    Xiangdong Zhang [email protected] Key Laboratory of advanced optoelectronic quantum architecture and measurements of Ministry of Education, School of Physics, Beijing Institute of Technology, 100081, Beijing, China Beijing Key Laboratory of Nanophotonics &\& Ultrafine Optoelectronic Systems, Micro-nano Center, School of Physics, Beijing Institute of Technology, 100081, Beijing, China    Xiulai Xu [email protected] Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China CAS Center for Excellence in Topological Quantum Computation and School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China Songshan Lake Materials Laboratory, Dongguan, Guangdong 523808, China
Abstract

Topological photonics provides a new paradigm in studying cavity quantum electrodynamics with robustness to disorder. In this work, we demonstrate the coupling between single quantum dots and the second-order topological corner state. Based on the second-order topological corner state, a topological photonic crystal cavity is designed and fabricated into GaAs slabs with quantum dots embedded. The coexistence of corner state and edge state with high quality factor close to 2000 is observed. The enhancement of photoluminescence intensity and emission rate are both observed when the quantum dot is on resonance with the corner state. This result enables the application of topology into cavity quantum electrodynamics, offering an approach to topological devices for quantum information processing.

I Introduction

Cavity quantum electrodynamics (CQED) studies the interaction between photons and quantum emitters, including the strong and weak coupling regime, which has widespread applications Vahala (2003); Khitrova et al. (2006); Lodahl et al. (2015). For instance, CQED systems are widely proposed for the realization of quantum information processing Imamoglu et al. (1999). Especially, the weak coupling can greatly enhance the spontaneous emission rate of quantum emitters Purcell (1995); Englund et al. (2005); Laucht et al. (2009), which can be used to optimize the photonic devices, such as high-efficiency single photon source Liu et al. (2018); Chang et al. (2006); Strauf et al. (2007), ultra-fast qubit gate Carter et al. (2013); Sweeney et al. (2014) and low-threshold laser Lončar et al. (2002). Up to now, solid-state CQED experiments have been implemented in a wide range of photonic nanocavities, including whispering gallery modes Srinivasan and Painter (2007), Anderson-localized modes Sapienza et al. (2010), and photonic crystal (PhC) cavities Yoshie et al. (2004); Hennessy et al. (2007); Brossard et al. (2010); Qian et al. (2018, 2019) with coupled two-level systems. These photonic nanocavities are optimized for high quality factor (Q) and small mode volume to enhance the coupling strength, and they are always strongly affected by defects and disorders introduced by fabrication imperfections, environment perturbations, etc. The emerging field of topological photonics provides a new paradigm to solve the problem, offering an approach to the development of photonic devices with robustness to defects and disorders.

So far, the application of topology in optics has been investigated in many areas Khanikaev and Shvets (2017); Ozawa et al. (2019); Lu et al. (2014); Wu and Hu (2015); Blanco-Redondo et al. (2016); Rechtsman et al. (2013a, b); Haldane and Raghu (2008); Wang et al. (2009, 2008); Fang et al. (2012); Hafezi et al. (2011); Khanikaev et al. (2013); Hafezi et al. (2013); Harari et al. (2018); Bandres et al. (2018); Zhao et al. (2018); Parto et al. (2018); Ota et al. (2018); Bahari et al. (2017); St-Jean et al. (2017); Ota et al. (2019a); Chen et al. (2014); Smirnova et al. (2019), such as one-way waveguide Wang et al. (2009, 2008); Haldane and Raghu (2008); Fang et al. (2012); Hafezi et al. (2011); Khanikaev et al. (2013); Hafezi et al. (2013), topological lasers Harari et al. (2018); Bandres et al. (2018); Zhao et al. (2018); Parto et al. (2018); Ota et al. (2018); Bahari et al. (2017); St-Jean et al. (2017); Ota et al. (2019a), which are mainly in the classical domain. The combination of topology with quantum regime will bring more interesting phenomena and physics Blanco-Redondo et al. (2018); Tambasco et al. (2018); Mittal et al. (2018); Wang et al. (2019a, b). Especially, the coupling between quantum emitters and topologically protected state will exhibit robust strong light-matter interaction, enabling a topological quantum optics interface Barik et al. (2018); Mehrabad et al. (2019). For example, the coupling to topological edge state enables the robust chiral emission of quantum dots (QDs) Barik et al. (2018). More importantly, the coupling to topological nanocavity will have more widespread applications in development of photonic devices and quantum optics devices for quantum information with built-in protection, which has not been demonstrated. To investigate CQED with topological state, both high-quality topological nanocavity and a good matching with quantum emitters are required. Recently, a new class of higher-order topological insulators have been proposed and experimentally demonstrated in different systems Xie et al. (2018, 2019); Ota et al. (2019b); Chen et al. (2019); Langbehn et al. (2017); Ezawa (2018); Ni et al. (2019a); Noh et al. (2018); Benalcazar et al. (2017a, b); Imhof et al. (2018); Peterson et al. (2018); Serra-Garcia et al. (2018); Mittal et al. (2019); Xue et al. (2019a); Zhang et al. (2019); Schindler et al. (2018); El Hassan et al. (2019); Zhang et al. (2020a); Bao et al. (2019); Xue et al. (2019b); Ni et al. (2019b); Zhang et al. (2020b), including 2D PhC slab where 0D topological corner state has been observed Ota et al. (2019b); Chen et al. (2019). This high-order topological state provides an ideal platform to design topological nanocavity for the investigation of CQED.

In this work, we report on the coupling between the second-order topological corner state and single QDs. Based on the generalised 2D Su-Schrieffer-Heeger (SSH) model, a topological PhC cavity is designed and fabricated into GaAs slab with QDs embedded. The Q is optimized by shifting the non-trivial PhC away from the corner. The existence of topological corner and edge states with high Q are observed by photoluminescence (PL) spectra. The emission intensity of single QD coupled to the corner state is enhanced by a factor of about 4, and the emission rate is enhanced by a factor of 1.3. Our results demonstrate the potential of the application of topology into CQED, enabling the development of quantum information processing.

II Design and optimization of topological corner state

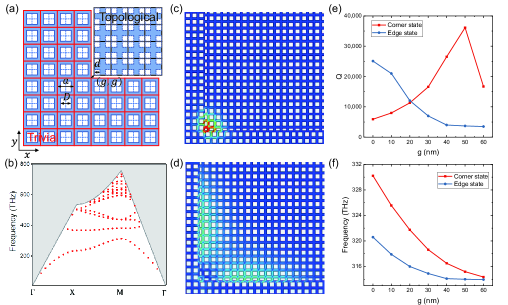
Refer to caption
Figure 1: (a) Schematic of the 2D topological PhC cavity in a square shape with square air holes with length of DD (d=D/2d=D/2). Unit cells with red (black) outline correspond to trivial (topological) PhC. The topological PhC is shifted away from the corner by (g,g)(g,g) to optimize Q of the corner state. (b) Bulk band structure of the 2D PhC slab with a=a= 280 nm, D=0.64​aD=0.64a and t=t= 150 nm. Electric field profile of (c) topological corner state at 321.11 THz and (d) topological edge state at 314.8 THz with g=g= 20 nm. (e) Q and (f) frequency of corner state and edge state with different gg.

Previous investigations have shown that the 0D corner state can exist in the 2D topological insulators protected by the quantized bulk quadrupole polarization Benalcazar et al. (2017b, a); Imhof et al. (2018); Peterson et al. (2018); Serra-Garcia et al. (2018); Mittal et al. (2019) or quantized edge dipole polarization Xie et al. (2018, 2019); Ota et al. (2019b); Chen et al. (2019), which is related to the 2D Zak phase, θZ​a​k=(θx,θy)\theta^{Zak}=(\theta_{x},\theta_{y}) defined as

θi\displaystyle\theta_{i} =\displaystyle= ∫dkx​dky​T​r​[Ai​(kx,ky)],\displaystyle\int\mathrm{d}k_{x}\mathrm{d}k_{y}Tr[A_{i}(k_{x},k_{y})], (1)

where i=xi=x or yy and Ai​(kx,ky)A_{i}(k_{x},k_{y}) is the Berry connection Zak (1989). Many recent works Ota et al. (2019b); Chen et al. (2019) have shown that the Wannier-type 0D corner state, which is induced by the non-trivial edge dipole polarization, can be easily realized in the optical system by combing two different photonic crystals with distinct topologies but identical band gap. In this case, we design a topological nanocavity in the 2D PhC slab based on such 0D corner state, as shown in Fig. 1(a). The cavity consists of two topologically distinct PhC slabs in square shape with the same period aa and thickness of tt, which are distinguished by different colors of the outline. It is clearly shown that the four sub-squares in unit cell with the black (red) outline are far away from (adjacent to) each other, corresponding to a topological (trivial) phase with the 2D Zak phase being θZ​a​k=(π,π)\theta^{Zak}=(\pi,\pi) ((0,0)(0,0)) Ota et al. (2019b); Chen et al. (2019). Additionally, due to the same period and size of the structures, these two PhC slabs share the common band structure, as presented in Fig. 1(b). By suitably combing the two topologically distinct PhC slabs, the quantized edge dipole polarizations along xx- and yy-axis can induce the 0D corner state in the band gap, and the related edge states get opened. Fig. 1(c) and (d) show the electric field profiles of the corner and edge states. Contrast to the dispersive distribution of 1D edge state, the corner state is tightly localized at the intersection of two types of PhC slab, which has a much smaller mode volume.

In addition to a small mode volume, the high Q is also important for the coupling between quantum emitters and nanocavity. The Q of corner state is optimized by slightly shifting the topological PhC away from the corner by (g,g)(g,g), as shown in Fig. 1(a). In that case, Q of corner state first increases and then decreases with increasing gg, while Q of edge states decrease monotonically, as shown in Fig. 1(e). When g=g= 20 nm, the Q of corner state and one of edge states are comparable with the magnitude of 10410^{4}. However, their mode volumes show a big difference, about 0.23​(λ/n)30.23(\lambda/n)^{3} for the corner state and 6.59​(λ/n)36.59(\lambda/n)^{3} for the edge state, where λ\lambda is the resonant wavelength of the cavity and nn is the refractive index of GaAs. Meanwhile, the corner state and edge state show redshift with increasing gg, as shown in Fig. 1(f). Detailed calculations and discussions about Q and mode volume are shown in the Supporting Information. Since the designed topological nanocavity has such high Q and small mode volume, it can be used for the investigation of CQED.

Refer to caption
Figure 2: (a) SEM image of a fabricated topological cavity with a scale bar of 2 μ​m\mu m. The inset shows an enlarged image of the blue area with a scale bar of 1 μ​m\mu m, indicating the location of the corner state. The different excitation positions are represented by green areas. (b) Schematics of measurement setup for PL measurement and time-resolved PL spectroscopy. (c) PL spectra collected from different positions of the cavity (a=a= 285 nm, D=0.61​aD=0.61a and g=g= 30 nm) with a pump power of 350 μ​W\mu W. The red (blue) line is the PL spectrum collected from the corner (bulk PhC). The two peaks are identified as corner state and edge state as the arrows indicated.

III Experimental results

We fabricate the designed topological PhC cavities with different geometric parameters into a 150 nm-thick GaAs slab using electron beam lithography followed by inductively coupled plasma and wet etching process. The GaAs slab is grown by molecular beam epitaxy and contains a single layer of InGaAs QDs at the center. The density of QDs is about 30 μ​m−2\mu m^{-2}, which is low enough to investigate the coupling between single QDs and topological cavity. The scanning electron microscope (SEM) image of a fabricated cavity is shown in Fig. 2(a). The inset is an enlarged SEM image around the location of the corner state. The fabricated square air holes are not perfect because of fabrication imperfection. However, the corner state can still exist with the slight shape perturbation, as long as there is no topological phase transition happens.

Then we perform the confocal micro-PL measurement at low temperature using a liquid helium flow cryostat as shown in Fig. 2(b). The topological cavity is excited by a continuous laser with wavelength of 532 nm. The PL signal is collected by a grating spectrometer and detected with a liquid-nitrogen-cooled charge coupled device camera with a spectral resolution of 60 μ​e​V\mu eV. Fig. 2(c) shows the collected PL spectra when the cavity with g=30g=30 nm is excited at different positions of the PhC slab with high excitation power, which are indicated in Fig. 2a. Two peaks are observed in the PL spectrum when excited around the corner (red line in Fig. 2(c)) while disappear in the bulk (blue line in Fig. 2(c)). According to the electric field profiles (Fig. 1(c) and (d)), the edge state will also be excited besides the corner state when the laser is focused at the corner. Furthermore, the energy difference between the edge state and corner state will decrease with increasing gg, enabling the observation of edge state close to the corner state in the spectrum. So the two peaks originate from the corner state and edge state. Thereinto the PL peak with short wavelength is identified as the corner state while the peak with long wavelength is the edge state. The Q of the corner state and the edge state are about 1900 and 1200, respectively. The coexistence of corner and edge state with high Q provides a new platform to integrate the waveguide and cavity on a single chip.

Refer to caption
Figure 3: (a) PL spectra collected when a topological cavity with a=a= 280 nm and g=g= 20 nm is excited at different positions. The corner state is identified. (b) PL spectra collected when the QDs are tuned across the corner state by temperature. The spectra are shifted for clarity. (c) Fitted intensity and wavelength of the QD indicated in (b). (d) Decay curves for QD tuned on resonance and off resonance with the corner state. Inset shows the normalized decay curves. The black (red) squares are the experimental results with a detuning Δ=1.1\Delta=1.1 m​e​VmeV (Δ=0\Delta=0 ). The fitted results are represented by the grey lines.

In order to resolve single QD lines and therefore investigate the interaction between QD and corner state, we pump the sample at low-excitation power about tens of μ​W\mu W. The stronger pump power compared with other CQED experiments Yoshie et al. (2004); Hennessy et al. (2007); Qian et al. (2018, 2019) may result from more defects in the samples. We tune the single QD lines across the corner state by temperature and the corner state with linewidth about 730 μ​e​V\mu eV is identified by the PL spectra (as shown in Fig. 3(a)). The absence of peak from the edge state may result from the low Q-factor induced by the fabrication imperfection. Fig. 3(b) shows the PL spectra while the QD is tuned across the corner state by temperature. A crossing behavior with an obvious enhancement is observed, suggesting the cavity-QD system is in the Purcell regime. The intensity and wavelength fitted with Lorentz lineshape are shown in Fig. 3(c). The intensity of the QD is enhanced by a factor of about 4 on resonance with the corner state.

The Purcell enhancement is further studied by means of time-resolved PL spectroscopy. The schematic of measurement setup is shown in Fig. 2(b). The pulsed laser centered at 750 nm with a repetition rate of 82.5 MHz is used. It is split to two beams by a beam splitter (BS). One is used for excitation of the QDs, the other is used as synchronization signal detected by a photodiode (PD). The PL signals are filtered by the grating monochrometer with a resolution less than 100 μ​e​V\mu eV then detected by a single-photon avalanche diode (SPAD). The time differences between photon detection events and synchronization pulses provided by the laser are transformed to electrical signals by a time-to-amplitude converter (TAC), which give the decay curve of the QD in topological cavity.

We measured the decay curves for the QD tuned on resonance (red points) and off resonance (black points) with the corner state, as shown in Fig. 3(d). From the inset, it can be clearly seen that the QD decays faster when on resonance. The curves can be well fitted by a biexponential decay function with fast and slow decay components. When the QD is off resonance (black), the fast and slow decay lifetime of QD are about 0.62 ns and 3.85 ns. On resonance (red), they are 0.48 ns and 3.00 ns, respectively. Both fast and slow decay components are changed, so they could be attributed to the two fine-structure components of neutral exciton Hohenester et al. (2009). The fast and slow decay rate are both enhanced by a factor of about 1.3, which are due to the Purcell effect. Here, limited by the weak enhancement, we didn’t take the lifetime of other QDs in positions without patterning the cavity as a reference. However, the Purcell enhancement can be extracted by comparison of the two decay curves with zero detuning and detuning that is much larger than the linewidth of cavity mode Sapienza et al. (2010); Laucht et al. (2009). In the coupling system between QD and cavity, the off-resonant coupling assisted by acoustic phonons generally exists and strongly depends on temperature and detuning Hohenester et al. (2009). Unfortunately, it is difficult to estimate its influence in our system since both temperature and detuning are changed during the measurement. Even though the effect of phonons is not taken into consideration, the enhancement of PL intensity and the emission rate sufficiently demonstrate the weak coupling between the QD and the corner state. The weak enhancement may result from spatial misalignment and polarization mismatch between QD and corner state. With better spatial and polarization matching, for example, with QDs embedded in the position with the strongest electric field which is around the smallest square at the corner (See Fig. S3 in Supporting Information), the coupling strength can be improved.

IV Conclusion

In conclusion, we have demonstrated a CQED system with second-order topological corner state. We designed and fabricated the topological PhC cavity based on 0D topological corner state. The coexistence of edge state and corner state with Q about 10310^{3} is observed. The Purcell enhancement of single QD on resonance with the corner state is demonstrated by means of PL spectra and time-resolved PL spectroscopy. The Q of corner state can be further optimized by changing the position and size of the air holes without changing the topology, therefore making the realization of the strong coupling regime in such a cavity-QD regime possible. Our results provide a new platform to investigate CQED combined with topology, offering an approach to topological devices for quantum information processing. Additionally, the coexistence of edge state and corner state with high Q may enable the integration of topological cavity and waveguide on a single chip, with potential applications in the realization of quantum photonic internet.

Acknowledgements.
X. Xie and W. Zhang contributed equally to this work. This work was supported by the National Natural Science Foundation of China (Grants No. 11934019, No.11721404, No. 51761145104, No. 61675228, and No. 11874419), the National key R&\&D Program of China (Grant No. 2017YFA0303800 and No. 2018YFA0306101), the Key R&\&D Program of Guangdong Province (Grant No. 2018B030329001), the Strategic Priority Research Program (Grant No. XDB28000000), the Instrument Developing Project (Grant No. YJKYYQ20180036) and the Interdisciplinary Innovation Team of the Chinese Academy of Sciences.

References

  • Vahala (2003) Kerry J Vahala, “Optical microcavities,” Nature 424, 839 (2003).
  • Khitrova et al. (2006) Galina Khitrova, HM Gibbs, M Kira, Stephan W Koch,  and Axel Scherer, “Vacuum rabi splitting in semiconductors,” Nat. Phys. 2, 81 (2006).
  • Lodahl et al. (2015) Peter Lodahl, Sahand Mahmoodian,  and Søren Stobbe, “Interfacing single photons and single quantum dots with photonic nanostructures,” Rev. Mod. Phys. 87, 347 (2015).
  • Imamoglu et al. (1999) A Imamoglu, David D Awschalom, Guido Burkard, David P DiVincenzo, Daniel Loss, M Sherwin, A Small, et al., “Quantum information processing using quantum dot spins and cavity qed,” Phys. Rev. Lett. 83, 4204 (1999).
  • Purcell (1995) Edward Mills Purcell, “Spontaneous emission probabilities at radio frequencies,” in Confined electrons and photons (Springer, 1995) pp. 839–839.
  • Englund et al. (2005) Dirk Englund, David Fattal, Edo Waks, Glenn Solomon, Bingyang Zhang, Toshihiro Nakaoka, Yasuhiko Arakawa, Yoshihisa Yamamoto,  and Jelena Vučković, “Controlling the spontaneous emission rate of single quantum dots in a two-dimensional photonic crystal,” Phys. Rev. Lett. 95, 013904 (2005).
  • Laucht et al. (2009) A Laucht, F Hofbauer, N Hauke, J Angele, S Stobbe, M Kaniber, G Böhm, P Lodahl, M-C Amann,  and J J Finley, “Electrical control of spontaneous emission and strong coupling for a single quantum dot,” New J. Phys. 11, 023034 (2009).
  • Liu et al. (2018) Feng Liu, Alistair J Brash, John O’Hara, Luis MPP Martins, Catherine L Phillips, Rikki J Coles, Benjamin Royall, Edmund Clarke, Christopher Bentham, Nikola Prtljaga, et al., “High purcell factor generation of indistinguishable on-chip single photons,” Nat. Nanotechnol. 13, 835 (2018).
  • Chang et al. (2006) WH Chang, WY Chen, HS Chang, TP Hsieh, JI Chyi,  and TM Hsu, “Efficient single-photon sources based on low-density quantum dots in photonic-crystal nanocavities,” Phys. Rev. Lett. 96, 117401 (2006).
  • Strauf et al. (2007) Stefan Strauf, Nick G Stoltz, Matthew T Rakher, Larry A Coldren, Pierre M Petroff,  and Dirk Bouwmeester, “High-frequency single-photon source with polarization control,” Nat. Photonics 1, 704 (2007).
  • Carter et al. (2013) Samuel G Carter, Timothy M Sweeney, Mijin Kim, Chul Soo Kim, Dmitry Solenov, Sophia E Economou, Thomas L Reinecke, Lily Yang, Allan S Bracker,  and Daniel Gammon, “Quantum control of a spin qubit coupled to a photonic crystal cavity,” Nat. Photonics 7, 329 (2013).
  • Sweeney et al. (2014) Timothy M Sweeney, Samuel G Carter, Allan S Bracker, Mijin Kim, Chul Soo Kim, Lily Yang, Patrick M Vora, Peter G Brereton, Erin R Cleveland,  and Daniel Gammon, “Cavity-stimulated raman emission from a single quantum dot spin,” Nat. Photonics 8, 442 (2014).
  • Lončar et al. (2002) Marko Lončar, Tomoyuki Yoshie, Axel Scherer, Pawan Gogna,  and Yueming Qiu, “Low-threshold photonic crystal laser,” Appl. Phys. Lett. 81, 2680–2682 (2002).
  • Srinivasan and Painter (2007) Kartik Srinivasan and Oskar Painter, “Linear and nonlinear optical spectroscopy of a strongly coupled microdisk–quantum dot system,” Nature 450, 862 (2007).
  • Sapienza et al. (2010) Luca Sapienza, Henri Thyrrestrup, Søren Stobbe, Pedro David Garcia, Stephan Smolka,  and Peter Lodahl, “Cavity quantum electrodynamics with anderson-localized modes,” Science 327, 1352–1355 (2010).
  • Yoshie et al. (2004) Tomoyuki Yoshie, Axel Scherer, J Hendrickson, Galina Khitrova, HM Gibbs, G Rupper, C Ell, OB Shchekin,  and DG Deppe, “Vacuum rabi splitting with a single quantum dot in a photonic crystal nanocavity,” Nature 432, 200 (2004).
  • Hennessy et al. (2007) Kevin Hennessy, Antonio Badolato, Martin Winger, D Gerace, Mete Atatüre, S Gulde, S Fält, Evelyn L Hu,  and A Imamoğlu, “Quantum nature of a strongly coupled single quantum dot–cavity system,” Nature 445, 896 (2007).
  • Brossard et al. (2010) FSF Brossard, XL Xu, DA Williams, M Hadjipanayi, M Hugues, M Hopkinson, X Wang,  and RA Taylor, “Strongly coupled single quantum dot in a photonic crystal waveguide cavity,” Appl. Phys. Lett. 97, 111101 (2010).
  • Qian et al. (2018) Chenjiang Qian, Shiyao Wu, Feilong Song, Kai Peng, Xin Xie, Jingnan Yang, Shan Xiao, Matthew J Steer, Iain G Thayne, Chengchun Tang, et al., “Two-photon rabi splitting in a coupled system of a nanocavity and exciton complexes,” Phys. Rev. Lett. 120, 213901 (2018).
  • Qian et al. (2019) Chenjiang Qian, Xin Xie, Jingnan Yang, Kai Peng, Shiyao Wu, Feilong Song, Sibai Sun, Jianchen Dang, Yang Yu, Matthew J Steer, et al., “Enhanced strong interaction between nanocavities and p-shell excitons beyond the dipole approximation,” Phys. Rev. Lett. 122, 087401 (2019).
  • Khanikaev and Shvets (2017) Alexander B Khanikaev and Gennady Shvets, “Two-dimensional topological photonics,” Nat. Photonics 11, 763 (2017).
  • Ozawa et al. (2019) Tomoki Ozawa, Hannah M Price, Alberto Amo, Nathan Goldman, Mohammad Hafezi, Ling Lu, Mikael C Rechtsman, David Schuster, Jonathan Simon, Oded Zilberberg, et al., “Topological photonics,” Rev. Mod. Phys. 91, 015006 (2019).
  • Lu et al. (2014) Ling Lu, John D Joannopoulos,  and Marin Soljačić, “Topological photonics,” Nat. Photonics 8, 821 (2014).
  • Wu and Hu (2015) Long-Hua Wu and Xiao Hu, “Scheme for achieving a topological photonic crystal by using dielectric material,” Phys. Rev. Lett. 114, 223901 (2015).
  • Blanco-Redondo et al. (2016) Andrea Blanco-Redondo, Imanol Andonegui, Matthew J Collins, Gal Harari, Yaakov Lumer, Mikael C Rechtsman, Benjamin J Eggleton,  and Mordechai Segev, “Topological optical waveguiding in silicon and the transition between topological and trivial defect states,” Phys. Rev. Lett. 116, 163901 (2016).
  • Rechtsman et al. (2013a) Mikael C Rechtsman, Julia M Zeuner, Yonatan Plotnik, Yaakov Lumer, Daniel Podolsky, Felix Dreisow, Stefan Nolte, Mordechai Segev,  and Alexander Szameit, “Photonic floquet topological insulators,” Nature 496, 196 (2013a).
  • Rechtsman et al. (2013b) Mikael C Rechtsman, Yonatan Plotnik, Julia M Zeuner, Daohong Song, Zhigang Chen, Alexander Szameit,  and Mordechai Segev, “Topological creation and destruction of edge states in photonic graphene,” Phys. Rev. Lett. 111, 103901 (2013b).
  • Haldane and Raghu (2008) FDM Haldane and S Raghu, “Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry,” Phys. Rev. Lett. 100, 013904 (2008).
  • Wang et al. (2009) Zheng Wang, Yidong Chong, John D Joannopoulos,  and Marin Soljačić, “Observation of unidirectional backscattering-immune topological electromagnetic states,” Nature 461, 772 (2009).
  • Wang et al. (2008) Zheng Wang, YD Chong, John D Joannopoulos,  and Marin Soljačić, “Reflection-free one-way edge modes in a gyromagnetic photonic crystal,” Phys. Rev. Lett. 100, 013905 (2008).
  • Fang et al. (2012) Kejie Fang, Zongfu Yu,  and Shanhui Fan, “Realizing effective magnetic field for photons by controlling the phase of dynamic modulation,” Nat. Photonics 6, 782 (2012).
  • Hafezi et al. (2011) Mohammad Hafezi, Eugene A Demler, Mikhail D Lukin,  and Jacob M Taylor, “Robust optical delay lines with topological protection,” Nat. Phys. 7, 907 (2011).
  • Khanikaev et al. (2013) Alexander B Khanikaev, S Hossein Mousavi, Wang-Kong Tse, Mehdi Kargarian, Allan H MacDonald,  and Gennady Shvets, “Photonic topological insulators,” Nat. Mater. 12, 233 (2013).
  • Hafezi et al. (2013) Mohammad Hafezi, S Mittal, J Fan, A Migdall,  and JM Taylor, “Imaging topological edge states in silicon photonics,” Nat. Photonics 7, 1001 (2013).
  • Harari et al. (2018) Gal Harari, Miguel A Bandres, Yaakov Lumer, Mikael C Rechtsman, Yi Dong Chong, Mercedeh Khajavikhan, Demetrios N Christodoulides,  and Mordechai Segev, “Topological insulator laser: theory,” Science 359, eaar4003 (2018).
  • Bandres et al. (2018) Miguel A Bandres, Steffen Wittek, Gal Harari, Midya Parto, Jinhan Ren, Mordechai Segev, Demetrios N Christodoulides,  and Mercedeh Khajavikhan, “Topological insulator laser: Experiments,” Science 359, eaar4005 (2018).
  • Zhao et al. (2018) Han Zhao, Pei Miao, Mohammad H Teimourpour, Simon Malzard, Ramy El-Ganainy, Henning Schomerus,  and Liang Feng, “Topological hybrid silicon microlasers,” Nat. Commun. 9, 981 (2018).
  • Parto et al. (2018) Midya Parto, Steffen Wittek, Hossein Hodaei, Gal Harari, Miguel A Bandres, Jinhan Ren, Mikael C Rechtsman, Mordechai Segev, Demetrios N Christodoulides,  and Mercedeh Khajavikhan, “Edge-mode lasing in 1d topological active arrays,” Phys. Rev. Lett. 120, 113901 (2018).
  • Ota et al. (2018) Yasutomo Ota, Ryota Katsumi, Katsuyuki Watanabe, Satoshi Iwamoto,  and Yasuhiko Arakawa, “Topological photonic crystal nanocavity laser,” Commun. Phys. 1, 86 (2018).
  • Bahari et al. (2017) Babak Bahari, Abdoulaye Ndao, Felipe Vallini, Abdelkrim El Amili, Yeshaiahu Fainman,  and Boubacar Kanté, “Nonreciprocal lasing in topological cavities of arbitrary geometries,” Science 358, 636–640 (2017).
  • St-Jean et al. (2017) P St-Jean, V Goblot, E Galopin, A Lemaître, T Ozawa, L Le Gratiet, I Sagnes, J Bloch,  and A Amo, “Lasing in topological edge states of a one-dimensional lattice,” Nat. Photonics 11, 651 (2017).
  • Ota et al. (2019a) Yasutomo Ota, Kenta Takaka, Tomoki Ozawa, Alberto Amo, Zhetao Jia, Boubacar Kante, Masaya Notomi, Yasuhiko Arakawa,  and Satoshi Iwamoto, “Active topological photonics,” arXiv preprint arXiv:1912.05126  (2019a).
  • Chen et al. (2014) Wen-Jie Chen, Shao-Ji Jiang, Xiao-Dong Chen, Baocheng Zhu, Lei Zhou, Jian-Wen Dong,  and Che Ting Chan, “Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide,” Nat. Commun. 5, 5782 (2014).
  • Smirnova et al. (2019) Daria Smirnova, Daniel Leykam, Yidong Chong,  and Yuri Kivshar, “Nonlinear topological photonics,” arXiv preprint arXiv:1912.01784  (2019).
  • Blanco-Redondo et al. (2018) Andrea Blanco-Redondo, Bryn Bell, Dikla Oren, Benjamin J Eggleton,  and Mordechai Segev, “Topological protection of biphoton states,” Science 362, 568–571 (2018).
  • Tambasco et al. (2018) Jean-Luc Tambasco, Giacomo Corrielli, Robert J Chapman, Andrea Crespi, Oded Zilberberg, Roberto Osellame,  and Alberto Peruzzo, “Quantum interference of topological states of light,” Sci.Adv. 4, eaat3187 (2018).
  • Mittal et al. (2018) Sunil Mittal, Elizabeth A Goldschmidt,  and Mohammad Hafezi, “A topological source of quantum light,” Nature 561, 502 (2018).
  • Wang et al. (2019a) Yao Wang, Xiao-Ling Pang, Yong-Heng Lu, Jun Gao, Yi-Jun Chang, Lu-Feng Qiao, Zhi-Qiang Jiao, Hao Tang,  and Xian-Min Jin, “Topological protection of two-photon quantum correlation on a photonic chip,” Optica 6, 955–960 (2019a).
  • Wang et al. (2019b) Yao Wang, Yong-Heng Lu, Feng Mei, Jun Gao, Zhan-Ming Li, Hao Tang, Shi-Liang Zhu, Suotang Jia,  and Xian-Min Jin, “Direct observation of topology from single-photon dynamics,” Phys. Rev. Lett. 122, 193903 (2019b).
  • Barik et al. (2018) Sabyasachi Barik, Aziz Karasahin, Christopher Flower, Tao Cai, Hirokazu Miyake, Wade DeGottardi, Mohammad Hafezi,  and Edo Waks, “A topological quantum optics interface,” Science 359, 666–668 (2018).
  • Mehrabad et al. (2019) Mahmoud Jalali Mehrabad, Andrew P Foster, René Dost, A Mark Fox, Maurice S Skolnick,  and Luke R Wilson, “Chiral topological photonics with an embedded quantum emitter,” arXiv preprint arXiv:1912.09943  (2019).
  • Xie et al. (2018) Bi-Ye Xie, Hong-Fei Wang, Hai-Xiao Wang, Xue-Yi Zhu, Jian-Hua Jiang, Ming-Hui Lu,  and Yan-Feng Chen, “Second-order photonic topological insulator with corner states,” Phys. Rev. B 98, 205147 (2018).
  • Xie et al. (2019) Bi-Ye Xie, Guang-Xu Su, Hong-Fei Wang, Hai Su, Xiao-Peng Shen, Peng Zhan, Ming-Hui Lu, Zhen-Lin Wang,  and Yan-Feng Chen, “Visualization of higher-order topological insulating phases in two-dimensional dielectric photonic crystals,” Phys. Rev. Lett. 122, 233903 (2019).
  • Ota et al. (2019b) Yasutomo Ota, Feng Liu, Ryota Katsumi, Katsuyuki Watanabe, Katsunori Wakabayashi, Yasuhiko Arakawa,  and Satoshi Iwamoto, “Photonic crystal nanocavity based on a topological corner state,” Optica 6, 786–789 (2019b).
  • Chen et al. (2019) Xiao-Dong Chen, Wei-Min Deng, Fu-Long Shi, Fu-Li Zhao, Min Chen,  and Jian-Wen Dong, “Direct observation of corner states in second-order topological photonic crystal slabs,” Phys. Rev. Lett. 122, 233902 (2019).
  • Langbehn et al. (2017) Josias Langbehn, Yang Peng, Luka Trifunovic, Felix von Oppen,  and Piet W Brouwer, “Reflection-symmetric second-order topological insulators and superconductors,” Phys. Rev. Lett. 119, 246401 (2017).
  • Ezawa (2018) Motohiko Ezawa, “Higher-order topological insulators and semimetals on the breathing kagome and pyrochlore lattices,” Phys. Rev. Lett. 120, 026801 (2018).
  • Ni et al. (2019a) Xiang Ni, Matthew Weiner, Andrea Alù,  and Alexander B Khanikaev, “Observation of higher-order topological acoustic states protected by generalized chiral symmetry,” Nat. Mater. 18, 113 (2019a).
  • Noh et al. (2018) Jiho Noh, Wladimir A Benalcazar, Sheng Huang, Matthew J Collins, Kevin P Chen, Taylor L Hughes,  and Mikael C Rechtsman, “Topological protection of photonic mid-gap defect modes,” Nat. Photonics 12, 408 (2018).
  • Benalcazar et al. (2017a) Wladimir A Benalcazar, B Andrei Bernevig,  and Taylor L Hughes, “Quantized electric multipole insulators,” Science 357, 61–66 (2017a).
  • Benalcazar et al. (2017b) Wladimir A Benalcazar, B Andrei Bernevig,  and Taylor L Hughes, “Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators,” Phys. Rev. B 96, 245115 (2017b).
  • Imhof et al. (2018) Stefan Imhof, Christian Berger, Florian Bayer, Johannes Brehm, Laurens W Molenkamp, Tobias Kiessling, Frank Schindler, Ching Hua Lee, Martin Greiter, Titus Neupert, et al., “Topolectrical-circuit realization of topological corner modes,” Nat. Phys. 14, 925 (2018).
  • Peterson et al. (2018) Christopher W Peterson, Wladimir A Benalcazar, Taylor L Hughes,  and Gaurav Bahl, “A quantized microwave quadrupole insulator with topologically protected corner states,” Nature 555, 346 (2018).
  • Serra-Garcia et al. (2018) Marc Serra-Garcia, Valerio Peri, Roman Süsstrunk, Osama R Bilal, Tom Larsen, Luis Guillermo Villanueva,  and Sebastian D Huber, “Observation of a phononic quadrupole topological insulator,” Nature 555, 342 (2018).
  • Mittal et al. (2019) Sunil Mittal, Venkata Vikram Orre, Guanyu Zhu, Maxim A Gorlach, Alexander Poddubny,  and Mohammad Hafezi, “Photonic quadrupole topological phases,” Nature Photonics 13, 692–696 (2019).
  • Xue et al. (2019a) Haoran Xue, Yahui Yang, Fei Gao, Yidong Chong,  and Baile Zhang, “Acoustic higher-order topological insulator on a kagome lattice,” Nat. Mater. 18, 108 (2019a).
  • Zhang et al. (2019) Xiujuan Zhang, Hai-Xiao Wang, Zhi-Kang Lin, Yuan Tian, Biye Xie, Ming-Hui Lu, Yan-Feng Chen,  and Jian-Hua Jiang, “Second-order topology and multidimensional topological transitions in sonic crystals,” Nat. Phys. 15, 582 (2019).
  • Schindler et al. (2018) Frank Schindler, Zhijun Wang, Maia G Vergniory, Ashley M Cook, Anil Murani, Shamashis Sengupta, Alik Yu Kasumov, Richard Deblock, Sangjun Jeon, Ilya Drozdov, et al., “Higher-order topology in bismuth,” Nat. Phys. 14, 918 (2018).
  • El Hassan et al. (2019) Ashraf El Hassan, Flore K Kunst, Alexander Moritz, Guillermo Andler, Emil J Bergholtz,  and Mohamed Bourennane, “Corner states of light in photonic waveguides,” Nature Photonics 13, 697–700 (2019).
  • Zhang et al. (2020a) Weixuan Zhang, Deyuan Zou, Wenjing He, Jiacheng Bao, Qingsong Pei, Houjun Sun,  and Xiangdong Zhang, “Topolectrical-circuit realization of 4d hexadecapole insulator,” arXiv preprint arXiv:2001.07931  (2020a).
  • Bao et al. (2019) Jiacheng Bao, Deyuan Zou, Weixuan Zhang, Wenjing He, Houjun Sun,  and Xiangdong Zhang, “Topoelectrical circuit octupole insulator with topologically protected corner states,” Phys. Rev. B 100, 201406 (2019).
  • Xue et al. (2019b) Haoran Xue, Yong Ge, Hong-Xiang Sun, Qiang Wang, Ding Jia, Yi-Jun Guan, Shou-Qi Yuan, Yidong Chong,  and Baile Zhang, “Quantized octupole acoustic topological insulator,” arXiv preprint arXiv:1911.06068  (2019b).
  • Ni et al. (2019b) Xiang Ni, Mengyao Li, Matthew Weiner, Andrea Alù,  and Alexander B Khanikaev, “Demonstration of a quantized acoustic octupole topological insulator,” arXiv preprint arXiv:1911.06469  (2019b).
  • Zhang et al. (2020b) Xiujuan Zhang, Zhi-Kang Lin, Hai-Xiao Wang, Zhan Xiong, Yuan Tian, Ming-Hui Lu, Yan-Feng Chen,  and Jian-Hua Jiang, “Symmetry-protected hierarchy of anomalous multipole topological band gaps in nonsymmorphic metacrystals,” Nat. Commun. 11, 1–9 (2020b).
  • Zak (1989) J Zak, “Berry’s phase for energy bands in solids,” Phys. Rev. Lett. 62, 2747 (1989).
  • Hohenester et al. (2009) Ulrich Hohenester, Arne Laucht, Michael Kaniber, Norman Hauke, Andre Neumann, Abbas Mohtashami, Marek Seliger, Max Bichler,  and Jonathan J. Finley, “Phonon-assisted transitions from quantum dot excitons to cavity photons,” Phys. Rev. B 80, 201311 (2009).