Cavity magnonics with easy-axis ferromagnet: critically enhanced magnon squeezing and light-matter interaction
Abstract
Generating and probing the magnon squeezing is an important challenge in the field of quantum magnonics. In this work, we propose a cavity magnonics setup with an easy-axis ferromagnet to address this challenge. To this end, we first establish a mechanism for the generation of magnon squeezing in the easy-axis ferromagnet and show that the magnon squeezing can be critically enhanced by tuning an external magnetic field near the Ising phase transition point. When the magnet is coupled to the cavity field, the effective cavity-magnon interaction becomes proportional to the magnon squeezing, allowing one to enhance the cavity-magnon coupling strength using a static field. We demonstrate that the magnon squeezing can be probed by measuring the frequency shift of the cavity field. Moreover, a magnonic superradiant phase transition can be observed in our setup by tuning the static magnetic field, overcoming the challenge that the magnetic interaction between the cavity and the magnet is typically too weak to drive the superradiant transition. Our work paves the way to develop unique capabilities of cavity magnonics that goes beyond the conventional cavity QED physics by harnessing the intrinsic property of a magnet.
Introduction.— The magnon is a quantized spin wave excitation of the spin ordering in magnets [1, 2, 3, 4, 5, 6] and has many virtues. Its long lifetime and negligible Joule heating make the magnon a potential candidate for spin-based computation and communication, which has led to the development of a new research field called magnonics [7, 8]. Various magnonic device components have been developed [9, 10, 11, 12]. The magnon can also have a non-trivial topological order and exhibit anomalous transport phenomena such as the magnon Hall effect and the magnon Nernst effect [13, 14, 15, 16, 17, 18, 19]. However, all these properties can be understood without quantizing the spin wave.
Recent studies unveiled various exotic properties of the magnon arising from its bosonic quantization. In particular, squeezing of a quantized magnon state [20] gives rise to various exotic properties such as the spin noise reduction below the standard quantum limit [21, 22], the magnon spin angular momentum enhancement beyond the standard value [23], the entanglement generation [24, 25, 26], and the macroscopic quantum state generation (cat state) [27, 28, 29]. Other interesting phenomena involving magnons such as anti-bunching [30, 31, 32, 33], the Bose-Einstein condensation [34, 35, 36, 37, 38, 39], the Casimir effect [40, 41, 42], and superradiant phase transitions (SPTs) [43, 44, 45, 46] are also reported. Unfortunately, very few of these exotic phenomena are experimentally verified [21, 22, 35]. Considering that they can be useful resources for quantum computation and communication, it is highly desired to bring those exotic theoretical possibilities into the realm of experimentally testable regimes.
In this Letter, we propose a cavity magnonics setup with an easy-axis ferromagnet as an experimentally promising platform to realize and probe the magnon squeezing and associated effects. The key feature of our setup is that simply applying an external static magnetic field to the magnet can critically enhance both magnon squeezing and cavity-magnon interaction. This enhancement creates opportunities in two directions. Firstly, since the magnon squeezing characteristics are imprinted on the cavity photons through the enhanced cavity-magnon interaction, the magnon squeezing and the enhanced spin angular momentum can be probed through the cavity photon measurement, which can be readily performed with quantum optical toolboxes available for cavity and circuit quantum electrodynamics (QED) systems [47, 48, 49, 50]. This probing scheme is expected to be more robust to the effects of noises than transport-based probing schemes of the magnon squeezing [23, 24]. Secondly, it allows one to induce an SPT by tuning the static field even though a bare cavity-magnon interaction is weak. Since our magnon-squeezing-based scheme to effectively enhance the interaction does not enhance the term, the term remains small, and does not significantly contribute to nor prevent the SPT. Moreover, our scheme is drastically different from existing schemes where the enhanced interaction is realized in a rotating frame [51, 52, 53] using time-dependent parametric driving. Our scheme utilizes the intrinsic property of the magnet without the parametric driving; therefore, it is free of unwanted processes due to the driving field that may limit the experimentally achievable coupling strength [54, 55], demonstrating unique capabilities of the cavity magnonics.
In the absence of the cavity, we first establish that the interplay between the static magnetic field and the magnetic anisotropy leads to the magnon squeezing of an easy-axis ferromagnet. As the field is tuned to drive the magnet close to the Ising transition, both the squeezing and the magnon spin angular momentum are critically enhanced with a power law. When the magnet is coupled to the magnetic field of the cavity photons in addition to the classical external field, the diverging spin angular momentum induces the diverging fluctuation of the cavity field, which in turn results in a ground-state superradiance where the symmetry associated with the mirror reflection symmetry is spontaneously broken. We study the critical behavior of the energy spectrum and the squeezing for the cavity magnon-polariton and identify its universality class to be that of fully connected systems.
Model Hamiltonian.— The cavity magnonics setup [Fig. 1(a)] consists of an easy-axis ferromagnetic insulator subject to an external static magnetic field, coupled to a cavity magnetic field. We model its low-energy excitations with the Hamiltonian,
| (1) |
with the spin Hamiltonian part of the ferromagnet,
| (2) |
where is the coupling strength, is the number of spins, denotes the dimensionless spin of magnitude at site , is a bosonic operator of the cavity field with the frequency and the strength , is the permeability, and is the static field. denotes the Heisenberg-type isotropic ferromagnetic exchange interaction between the neighboring sites, represents the easy-axis anisotropy along the axis, and is the gyromagnetic ratio for the Zeeman interaction. has the dominant energy scale responsible for the ferromagnetic spin ordering, whose direction is determined by the competition between , , and with weak characteristic energy scales. This competition gives rise to a phase transition with the diverging magnonic squeezing and the ground-state superradiance. For simplicity, we consider throughout the paper. The total Hamiltonian then has a symmetry corresponding to the following transformation
| (3) |
where is the mirror reflection operator along the axis. As we show below, upon modulating the static magnetic field , the spontaneous breaking of occurs, which leads to the superradiant phase.
Critically enhanced magnon squeezing.— We first investigate the spin Hamiltonian [Eq. (2)] in the absence of the cavity. In the ground state, spins are aligned along the axis for and tilted away from the axis toward the axis for finite . To determine the ground state, we regard as an -independent classical vector and minimize the mean-field energy with respect to the vector direction [56]. This calculation reveals that there is an Ising phase transition due to the spontaneous symmetry breaking of the symmetry at where . While the broken symmetry phase with a two-fold ground-state degeneracy appears in the weak-field regime (), the symmetric phase with a unique ground state is realized in the strong-field regime ().
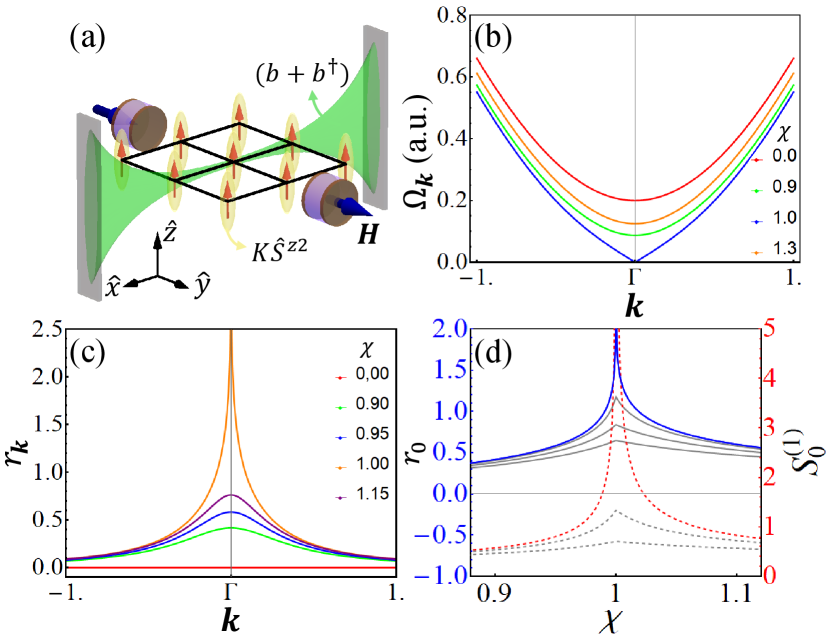
To study low-energy magnon excitations above the ground state in each regime, we describe the deviation from the mean-field ground state using magnon operators. The spin operator is rotated from the global coordinates to the local coordinates and transformed into the magnon operator using the conventional linear spin wave theory [57]. The resulting magnon Hamiltonian is given as follows in the Nambu basis [56],
| (4) |
where is the magnon operator. is the identity, and is the Pauli matrix in the Nambu space. and have different expressions depending on the regime:
| (5) |
where in the weak-field regime, and in the strong field regime. Here, is the coordination number, and is the displacement vector to the nearest neighbors. Note that contains squeezing terms, which create or annihilate two magnons simultaneously. Their magnitudes are proportional to and thus determined by and . can be diagonalized as with the energy by using the Bogoliubov transformation: where is the squeezed magnon operator and is the squeezing parameter with
| (6) |
The magnon energy is minimized at and the magnon energy gap vanishes at [Fig. 1(b)]. The squeezing parameter is maximized at for any value of [Fig. 1(c)].
We focus on the transition region. Near , the single-mode squeezing parameter diverges [Fig. 1(d)], implying the diverging magnonic quantum fluctuations at the energy gap closing. The energy gap and the magnon squeezing with exhibit power law scalings to zero and infinity, respectively, with an exponent , implying the universality class of fully connected systems [58, 59, 60]. Furthermore, large alludes to large spin angular momentum [23] of a squeezed single-magnon state , since exponentially enhances for large ,
| (7) |
Finally, we remark that this mechanism of the magnon squeezing enhancement is robust to the higher-order contribution of the magnetocrystalline anisotropy [56].
Enhanced cavity-magnon coupling.— Having established a mechanism for the generation of squeezing in the easy-axis ferromagnet, we now analyze the cavity magnonics Hamiltonian [Eq. (1)]. We first consider a symmetric (normal) phase where the spin is aligned along the direction due to the strong static magnetic field and the cavity exhibits no photon condensation so that the symmetry is conserved. In the normal phase, the effective Hamiltonian for the uniform magnonic mode , which coherently couples to the cavity field, reads [56]
| (8) |
where and
| (9) |
Remarkably, the effective cavity-magnon coupling strength is exponentially enhanced by the magnonic squeezing parameter . This is one of our main results. The enhancement stems from the competition between the easy-axis anisotropy and the Zeeman interaction in [Eq. (2)] and therefore can be tuned by the static magnetic field. We note that schemes to enhance the light-matter interaction have been proposed using squeezed cavity photons in time-dependent parametric driving setup [51, 53, 52]. However, in the rotating frame where the enhanced coupling is realized, unwanted fast oscillating processes always exist and may limit the range of coupling strength that can be synthesized. Our scheme eliminates this issue by the magnon squeezing, an intrinsic property of the magnet, as a resource to enhance by tuning the static field.
Moreover, the enhanced allows a quantum optical measurement of the squeezing and the large spin angular momentum of magnons. To this end, one can tune to realize the strong coupling regime where is larger than the cavity (magnon) decay rate, (), but is still smaller than the cavity (magnon) frequency (; namely, . On resonance, , an avoided crossing occurs giving rise to the vacuum Rabi splitting () that is determined by the magnon squeezing, i.e., . In a dispersive limit, , the cavity frequency is shifted by where is the detuning between the bare cavity and magnon frequencies. See Fig. 2(a) for the vacuum Rabi splitting and the dispersive shift of the cavity magnonics system. Therefore, by measuring the frequency shift of the cavity field, which is a standard experimental tool in the cavity and circuit QED [61], one can probe the degree of magnon squeezing. Note that the single excitation of magnon has successfully been probed using the same spectroscopic measurement [62, 63, 64] and therefore our scheme is feasible with current technology.
Going beyond the strong coupling regime, one can also synthesize the ultrastrong coupling regime where the coupling strength becomes a dominant energy scale; therefore, exotic quantum optical phenomena that have been predicted with the ultrastrong light-matter interaction can be explored in our setup [65, 66]. In particular, we find that there is a critical value of the squeezing parameter,
| (10) |
beyond which the normal phase Hamiltonian in Eq. (8) becomes unstable. This indicates a possibility where the enhanced cavity-magnon coupling strength drives an SPT [67, 68], which we examine in detail below.
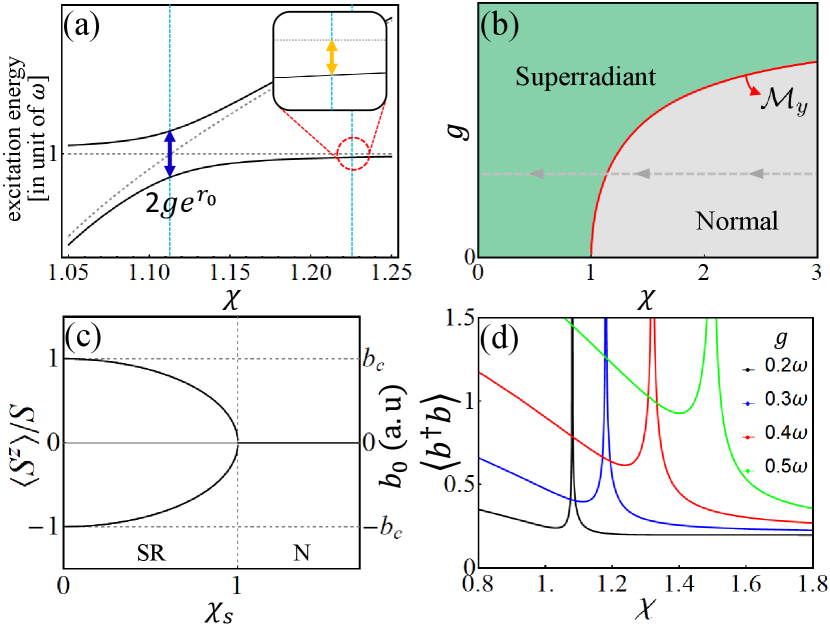
Magnonic superradiant phase transition.— In order to examine the emergence of superradiant and magnetic order, we perform a mean-field analysis for in Eq. (1) by considering as an -independent classical vector and as a complex variable . Our analysis [56] shows that the order parameters for the magnetic order or the magnon condensation and for the photon condensation indeed become non-zero when the dimensionless parameter becomes smaller than the critical value 1 [Fig. 2(b)]. In this superradiant phase, the symmetry is spontaneously broken for the ground state, which leads to the two-fold degeneracy [Fig. 2(c)]. Note that the critical line, , depends on both the bare coupling strength and [Fig. 2(b)]. Therefore, both and modulations can, in principle, induce the SPT, which we call the magnonic SPT.
Observing the -induced SPT in equilibrium is challenging since arising from the magnetic dipole coupling between the cavity and the magnet [62] is small and difficult to modulate in situ. On the other hand, the -induced magnonic SPT offers a promising and viable alternative to realize the SPT through simple static field adjustments. An additional advantage of the -induced SPT is its independence from the influence of the so-called term, whose role for the emergence of the SPT remains controversial [69, 70, 71, 72, 73, 74, 75], thanks to the relatively small bare coupling . Furthermore, in a weak magnetic field, the presence of a superradiant phase is robust and stable since the fluctuation due to the light-matter interaction is not strong enough to break the ordering and the magnon squeezing of the ferromagnet. This strong stability is absent in the standard cavity QED systems. Therefore, our cavity-magnonic system offers an exciting opportunity to observe the SPT.
In the superradiant phase, the fluctuation around the order parameter is governed by the following Hamiltonian [56],
| (11) |
where
| (12) |
is the energy of the squeezed magnon with the squeezing parameter ,
| (13) |
is the redefined cavity photon, and is the effective cavity-magnon coupling strength. Note that is also enhanced by the magnonic squeezing parameter in the superradiant phase.
We examine the critical properties near the magnonic SPT as (or ) is varied along the grey dashed line in Fig. 2(b). Both [Eq. (8)] and [Eq. (11)] have two eigenmodes. Among the two modes, the excitation energy of the magnon-like mode vanishes at the critical point, where both the magnon number and the photon number diverge due to the two-mode squeezing terms in and . For instance, diverges as , where is the critical value of [56]. The variation of with and is shown in Fig. 2(d). The divergence of both and follows power-law behaviors whose exponents are the same as those of the SPT in the Dicke model, indicating that the magnonic SPT belongs to the universality class of fully connected systems [58, 59, 60, 67]. The onset of the superradiant phase can be probed by the macroscopic occupation of the cavity photon due to the photon condensation, and the diverging fluctuation near the critical point can be probed by introducing a superconducting qubit dispersively coupled to the cavity field [49, 47, 62, 63, 61, 64].
Estimations.— The experimental parameters are estimated using the yttrium iron garnet as a specific example since it is a popular choice for cavity magnonics experiments. In its bulk crystal, it exhibits a weak uniaxial anisotropy of approximately 80 Oe [76, 77]. However, one can induce anisotropy by manipulating the sample geometry. For instance, its thin film can have an anisotropy field as Oe [78, 79, 80, 81]. This corresponds to an anisotropy coefficient GHz and the magnon frequency GHz in the absence of the external magnetic field. Assuming a nanoscale sample with spins, the expected magnon-photon coupling strength is GHz based on its unit coupling strength data [82, 83, 84]. Under these conditions, the critical field strength of the easy-axis magnet is estimated to be Oe and Oe with or without the cavity, respectively, demonstrating the feasibility of observing the -induced magnonic SPT. Moreover, we estimate that with a magnetic field of Oe, the cooperativity could increase about 20 times; therefore, it is feasible to synthesize both strong and ultrastrong coupling regimes of the cavity magnonics using our proposal.
Conclusion.— We have established the theory of magnon for the easy-axis ferromagnet and demonstrated that it endows the cavity-magnonics with a unique capability for enhancing the light-matter interaction using a static magnetic field in stark contrast to the traditional cavity or circuit QED systems based on an ensemble of two-level systems where a time-dependent parametric driving is typically needed. The proposed cavity-magnonics system based on the easy-axis ferromagnet allows one 1) to probe the large magnon spin using quantum optical measurement toolboxes that are, in general, more robust against the effects of noises than the transport measurement and 2) to realize the magnonic SPT simply by tuning the static magnetic field strength without modulating the bare cavity-magnon coupling strength that is not large enough to drive the SPT by itself.
Note added.— We became aware of a recent work [85] where a similar prediction on the divergence of magnon squeezing in the easy-axis ferromagnet is reported.
Acknowledgements.
J.M.L. and H.-W.L. acknowledge support from the Samsung Science and Technology Foundation (BA-1501-51). J.M.L. was supported by the POSCO Science Fellowship of the POSCO TJ Park Foundation. M.-J.H. was supported by the Startup Fund from Duke Kunshan University, and Innovation Program for Quantum Science and Technology 2021ZD0301602. J.M.L. thanks Min Ju Park and Ryan McKenzie for the fruitful discussions.References
- Kittel et al. [1996] C. Kittel, P. McEuen, and P. McEuen, Introduction to solid state physics, Vol. 8 (Wiley New York, 1996).
- Blundell [2003] S. Blundell, Magnetism in condensed matter (2003).
- Chumak et al. [2012] A. Chumak, A. Serga, M. Jungfleisch, R. Neb, D. Bozhko, V. Tiberkevich, and B. Hillebrands, Direct detection of magnon spin transport by the inverse spin hall effect, Applied Physics Letters 100, 082405 (2012).
- Cornelissen et al. [2015] L. Cornelissen, J. Liu, R. Duine, J. B. Youssef, and B. Van Wees, Long-distance transport of magnon spin information in a magnetic insulator at room temperature, Nature Physics 11, 1022 (2015).
- Xing et al. [2019] W. Xing, L. Qiu, X. Wang, Y. Yao, Y. Ma, R. Cai, S. Jia, X. Xie, and W. Han, Magnon transport in quasi-two-dimensional van der waals antiferromagnets, Physical Review X 9, 011026 (2019).
- Li et al. [2020] J. Li, C. B. Wilson, R. Cheng, M. Lohmann, M. Kavand, W. Yuan, M. Aldosary, N. Agladze, P. Wei, M. S. Sherwin, et al., Spin current from sub-terahertz-generated antiferromagnetic magnons, Nature 578, 70 (2020).
- Chumak et al. [2015] A. V. Chumak, V. I. Vasyuchka, A. A. Serga, and B. Hillebrands, Magnon spintronics, Nature physics 11, 453 (2015).
- Chumak et al. [2022] A. Chumak, P. Kabos, M. Wu, C. Abert, C. Adelmann, A. Adeyeye, J. Åkerman, F. Aliev, A. Anane, A. Awad, et al., Advances in magnetics roadmap on spin-wave computing, IEEE Transactions on Magnetics 58, 1 (2022).
- Chumak et al. [2017] A. Chumak, A. Serga, and B. Hillebrands, Magnonic crystals for data processing, Journal of Physics D: Applied Physics 50, 244001 (2017).
- Wang et al. [2020a] Q. Wang, M. Kewenig, M. Schneider, R. Verba, F. Kohl, B. Heinz, M. Geilen, M. Mohseni, B. Lägel, F. Ciubotaru, et al., A magnonic directional coupler for integrated magnonic half-adders, Nature Electronics 3, 765 (2020a).
- Wang et al. [2020b] Q. Wang, A. Hamadeh, R. Verba, V. Lomakin, M. Mohseni, B. Hillebrands, A. V. Chumak, and P. Pirro, A nonlinear magnonic nano-ring resonator, npj Computational Materials 6, 192 (2020b).
- Haldar and Adeyeye [2021] A. Haldar and A. O. Adeyeye, Functional magnetic waveguides for magnonics, Applied physics letters 119, 060501 (2021).
- Zhang et al. [2013] L. Zhang, J. Ren, J.-S. Wang, and B. Li, Topological magnon insulator in insulating ferromagnet, Physical Review B 87, 144101 (2013).
- Chisnell et al. [2015] R. Chisnell, J. Helton, D. Freedman, D. Singh, R. Bewley, D. Nocera, and Y. Lee, Topological magnon bands in a kagome lattice ferromagnet, Physical review letters 115, 147201 (2015).
- Owerre [2016] S. Owerre, A first theoretical realization of honeycomb topological magnon insulator, Journal of Physics: Condensed Matter 28, 386001 (2016).
- Nakata et al. [2017] K. Nakata, S. K. Kim, J. Klinovaja, and D. Loss, Magnonic topological insulators in antiferromagnets, Physical Review B 96, 224414 (2017).
- Chen et al. [2018] L. Chen, J.-H. Chung, B. Gao, T. Chen, M. B. Stone, A. I. Kolesnikov, Q. Huang, and P. Dai, Topological spin excitations in honeycomb ferromagnet cri 3, Physical Review X 8, 041028 (2018).
- Yao et al. [2018] W. Yao, C. Li, L. Wang, S. Xue, Y. Dan, K. Iida, K. Kamazawa, K. Li, C. Fang, and Y. Li, Topological spin excitations in a three-dimensional antiferromagnet, Nature Physics 14, 1011 (2018).
- Kim and Kim [2022] H. Kim and S. K. Kim, Topological phase transition in magnon bands in a honeycomb ferromagnet driven by sublattice symmetry breaking, Physical Review B 106, 104430 (2022).
- Kamra et al. [2020] A. Kamra, W. Belzig, and A. Brataas, Magnon-squeezing as a niche of quantum magnonics, Applied Physics Letters 117, 090501 (2020).
- Zhao et al. [2004] J. Zhao, A. V. Bragas, D. J. Lockwood, and R. Merlin, Magnon squeezing in an antiferromagnet: reducing the spin noise below the standard quantum limit, Physical review letters 93, 107203 (2004).
- Zhao et al. [2006] J. Zhao, A. V. Bragas, R. Merlin, and D. J. Lockwood, Magnon squeezing in antiferromagnetic and , Phys. Rev. B 73, 184434 (2006).
- Kamra and Belzig [2016] A. Kamra and W. Belzig, Super-poissonian shot noise of squeezed-magnon mediated spin transport, Phys. Rev. Lett. 116, 146601 (2016).
- Kamra et al. [2019] A. Kamra, E. Thingstad, G. Rastelli, R. A. Duine, A. Brataas, W. Belzig, and A. Sudbø, Antiferromagnetic magnons as highly squeezed fock states underlying quantum correlations, Phys. Rev. B 100, 174407 (2019).
- Zou et al. [2020] J. Zou, S. K. Kim, and Y. Tserkovnyak, Tuning entanglement by squeezing magnons in anisotropic magnets, Physical Review B 101, 014416 (2020).
- Mousolou et al. [2021] V. A. Mousolou, Y. Liu, A. Bergman, A. Delin, O. Eriksson, M. Pereiro, D. Thonig, and E. Sjöqvist, Magnon-magnon entanglement and its quantification via a microwave cavity, Physical Review B 104, 224302 (2021).
- Sharma et al. [2021] S. Sharma, V. A. Bittencourt, A. D. Karenowska, and S. V. Kusminskiy, Spin cat states in ferromagnetic insulators, Physical Review B 103, L100403 (2021).
- Sun et al. [2021] F.-X. Sun, S.-S. Zheng, Y. Xiao, Q. Gong, Q. He, and K. Xia, Remote generation of magnon schrödinger cat state via magnon-photon entanglement, Physical Review Letters 127, 087203 (2021).
- Kounalakis et al. [2022] M. Kounalakis, G. E. Bauer, and Y. M. Blanter, Analog quantum control of magnonic cat states on a chip by a superconducting qubit, Physical review letters 129, 037205 (2022).
- Xie et al. [2020] J.-k. Xie, S.-l. Ma, and F.-l. Li, Quantum-interference-enhanced magnon blockade in an yttrium-iron-garnet sphere coupled to superconducting circuits, Physical Review A 101, 042331 (2020).
- Yuan and Duine [2020] H. Yuan and R. A. Duine, Magnon antibunching in a nanomagnet, Physical Review B 102, 100402(R) (2020).
- Li et al. [2021] X. Li, X. Wang, Z. Wu, W.-X. Yang, and A. Chen, Tunable magnon antibunching in a hybrid ferromagnet-superconductor system with two qubits, Physical Review B 104, 224434 (2021).
- Li et al. [2022] X. Li, G.-L. Cheng, and W.-X. Yang, Tunable magnon antibunching via degenerate three-wave mixing in a hybrid ferromagnet–superconductor system, Applied Physics Letters 121, 122403 (2022).
- Nikuni et al. [2000] T. Nikuni, M. Oshikawa, A. Oosawa, and H. Tanaka, Bose-einstein condensation of dilute magnons in , Phys. Rev. Lett. 84, 5868 (2000).
- Demokritov et al. [2006] S. O. Demokritov, V. E. Demidov, O. Dzyapko, G. A. Melkov, A. A. Serga, B. Hillebrands, and A. N. Slavin, Bose–einstein condensation of quasi-equilibrium magnons at room temperature under pumping, Nature 443, 430 (2006).
- Giamarchi et al. [2008] T. Giamarchi, C. Rüegg, and O. Tchernyshyov, Bose–einstein condensation in magnetic insulators, Nature Physics 4, 198 (2008).
- Bunkov and Volovik [2010] Y. M. Bunkov and G. E. Volovik, Magnon bose-einstein condensation and spin superfluidity, Journal of Physics: Condensed Matter 22, 164210 (2010).
- Zapf et al. [2014] V. Zapf, M. Jaime, and C. Batista, Bose-einstein condensation in quantum magnets, Reviews of Modern Physics 86, 563 (2014).
- Serga et al. [2014] A. A. Serga, V. S. Tiberkevich, C. W. Sandweg, V. I. Vasyuchka, D. A. Bozhko, A. V. Chumak, T. Neumann, B. Obry, G. A. Melkov, A. N. Slavin, et al., Bose–einstein condensation in an ultra-hot gas of pumped magnons, Nature communications 5, 1 (2014).
- Neuberger and Ziman [1989] H. Neuberger and T. Ziman, Finite-size effects in heisenberg antiferromagnets, Physical Review B 39, 2608 (1989).
- Cheng et al. [2018] R. Cheng, D. Xiao, and J.-G. Zhu, Interlayer couplings mediated by antiferromagnetic magnons, Physical review letters 121, 207202 (2018).
- Nakata and Suzuki [2023] K. Nakata and K. Suzuki, Magnonic casimir effect in ferrimagnets, Physical Review Letters 130, 096702 (2023).
- Román-Roche et al. [2021] J. Román-Roche, F. Luis, and D. Zueco, Photon condensation and enhanced magnetism in cavity qed, Phys. Rev. Lett. 127, 167201 (2021).
- Bamba et al. [2022] M. Bamba, X. Li, N. Marquez Peraca, and J. Kono, Magnonic superradiant phase transition, Communications Physics 5, 1 (2022).
- McKenzie et al. [2022] R. McKenzie, M. Libersky, D. Silevitch, and T. Rosenbaum, Theory of magnon polaritons in quantum ising materials, Physical Review A 106, 043716 (2022).
- Liu et al. [2023] G. Liu, W. Xiong, and Z.-J. Ying, Switchable superradiant phase transition with kerr magnons (2023), arXiv:2302.07163 [quant-ph] .
- Schuster et al. [2007] D. Schuster, A. A. Houck, J. Schreier, A. Wallraff, J. Gambetta, A. Blais, L. Frunzio, J. Majer, B. Johnson, M. Devoret, et al., Resolving photon number states in a superconducting circuit, Nature 445, 515 (2007).
- Hofheinz et al. [2009] M. Hofheinz, H. Wang, M. Ansmann, R. C. Bialczak, E. Lucero, M. Neeley, A. D. O’Connell, D. Sank, J. Wenner, J. M. Martinis, and A. N. Cleland, Synthesizing arbitrary quantum states in a superconducting resonator, Nature 459, 546 (2009).
- Lolli et al. [2015] J. Lolli, A. Baksic, D. Nagy, V. E. Manucharyan, and C. Ciuti, Ancillary qubit spectroscopy of vacua in cavity and circuit quantum electrodynamics, Phys. Rev. Lett. 114, 183601 (2015).
- Blais et al. [2020] A. Blais, S. M. Girvin, and W. D. Oliver, Quantum information processing and quantum optics with circuit quantum electrodynamics, Nature Physics 16, 247 (2020).
- Leroux et al. [2018] C. Leroux, L. Govia, and A. Clerk, Enhancing cavity quantum electrodynamics via antisqueezing: Synthetic ultrastrong coupling, Physical review letters 120, 093602 (2018).
- Qin et al. [2018] W. Qin, A. Miranowicz, P.-B. Li, X.-Y. Lü, J. Q. You, and F. Nori, Exponentially enhanced light-matter interaction, cooperativities, and steady-state entanglement using parametric amplification, Phys. Rev. Lett. 120, 093601 (2018).
- Zhu et al. [2020] C. J. Zhu, L. L. Ping, Y. P. Yang, and G. S. Agarwal, Squeezed light induced symmetry breaking superradiant phase transition, Phys. Rev. Lett. 124, 073602 (2020).
- Braumüller et al. [2017] J. Braumüller, M. Marthaler, A. Schneider, A. Stehli, H. Rotzinger, M. Weides, and A. V. Ustinov, Analog quantum simulation of the Rabi model in the ultra-strong coupling regime, Nature Communications 8, 779 (2017).
- Langford et al. [2017] N. K. Langford, R. Sagastizabal, M. Kounalakis, C. Dickel, A. Bruno, F. Luthi, D. J. Thoen, A. Endo, and L. DiCarlo, Experimentally simulating the dynamics of quantum light and matter at deep-strong coupling, Nature Communications 8, 1715 (2017), 1610.10065 .
- [56] See supplemental material for further details that include Ref. [86] and Ref. [87].
- Holstein and Primakoff [1940] T. Holstein and H. Primakoff, Field dependence of the intrinsic domain magnetization of a ferromagnet, Physical Review 58, 1098 (1940).
- Sachdev [2011] S. Sachdev, Quantum Phase Transitions, 2nd ed. (Cambridge University Press, 2011).
- Dicke [1954] R. H. Dicke, Coherence in spontaneous radiation processes, Physical review 93, 99 (1954).
- Lipkin et al. [1965] H. J. Lipkin, N. Meshkov, and A. Glick, Validity of many-body approximation methods for a solvable model:(i). exact solutions and perturbation theory, Nuclear Physics 62, 188 (1965).
- Blais et al. [2021] A. Blais, A. L. Grimsmo, S. M. Girvin, and A. Wallraff, Circuit quantum electrodynamics, Reviews of Modern Physics 93, 025005 (2021).
- Lachance-Quirion et al. [2017] D. Lachance-Quirion, Y. Tabuchi, S. Ishino, A. Noguchi, T. Ishikawa, R. Yamazaki, and Y. Nakamura, Resolving quanta of collective spin excitations in a millimeter-sized ferromagnet, Science Advances 3, e1603150 (2017).
- Lachance-Quirion et al. [2020] D. Lachance-Quirion, S. P. Wolski, Y. Tabuchi, S. Kono, K. Usami, and Y. Nakamura, Entanglement-based single-shot detection of a single magnon with a superconducting qubit, Science 367, 425 (2020).
- Xu et al. [2023] D. Xu, X.-K. Gu, H.-K. Li, Y.-C. Weng, Y.-P. Wang, J. Li, H. Wang, S.-Y. Zhu, and J. Q. You, Quantum control of a single magnon in a macroscopic spin system, Phys. Rev. Lett. 130, 193603 (2023).
- Forn-Díaz et al. [2019] P. Forn-Díaz, L. Lamata, E. Rico, J. Kono, and E. Solano, Ultrastrong coupling regimes of light-matter interaction, Rev. Mod. Phys. 91, 025005 (2019).
- Frisk Kockum et al. [2019] A. Frisk Kockum, A. Miranowicz, S. De Liberato, S. Savasta, and F. Nori, Ultrastrong coupling between light and matter, Nature Reviews Physics 1, 19 (2019).
- Emary and Brandes [2003] C. Emary and T. Brandes, Quantum Chaos Triggered by Precursors of a Quantum Phase Transition: The Dicke Model, Phys. Rev. Lett. 90, 044101 (2003).
- Baumann et al. [2010] K. Baumann, C. Guerlin, F. Brennecke, and T. Esslinger, Dicke quantum phase transition with a superfluid gas in an optical cavity, Nature 464, 1301 (2010).
- Nataf and Ciuti [2010] P. Nataf and C. Ciuti, No-go theorem for superradiant quantum phase transitions in cavity QED and counter-example in circuit QED, Nature Communications 1, 72 (2010).
- Viehmann et al. [2011] O. Viehmann, J. von Delft, and F. Marquardt, Superradiant phase transitions and the standard description of circuit qed, Physical review letters 107, 113602 (2011).
- Vukics et al. [2014] A. Vukics, T. Grießer, and P. Domokos, Elimination of the -square problem from cavity qed, Phys. Rev. Lett. 112, 073601 (2014).
- Bamba and Ogawa [2014] M. Bamba and T. Ogawa, Stability of polarizable materials against superradiant phase transition, Phys. Rev. A 90, 063825 (2014).
- Di Stefano et al. [2019] O. Di Stefano, A. Settineri, V. Macrì, L. Garziano, R. Stassi, S. Savasta, and F. Nori, Resolution of gauge ambiguities in ultrastrong-coupling cavity quantum electrodynamics, Nature Physics 15, 803 (2019).
- Stokes and Nazir [2020] A. Stokes and A. Nazir, Uniqueness of the phase transition in many-dipole cavity quantum electrodynamical systems, Phys. Rev. Lett. 125, 143603 (2020).
- Andolina et al. [2020] G. Andolina, F. Pellegrino, V. Giovannetti, A. MacDonald, and M. Polini, Theory of photon condensation in a spatially varying electromagnetic field, Physical Review B 102, 125137 (2020).
- Gieniusz [1993] R. Gieniusz, Cubic and uniaxial anisotropy effects on magnetostatic modes in (111)-oriented yttrium iron garnet films, Journal of magnetism and magnetic materials 119, 187 (1993).
- Lee et al. [2016] S. Lee, S. Grudichak, J. Sklenar, C. Tsai, M. Jang, Q. Yang, H. Zhang, and J. B. Ketterson, Ferromagnetic resonance of a yig film in the low frequency regime, Journal of Applied Physics 120, 10.1063/1.4956435 (2016).
- Manuilov et al. [2009] S. A. Manuilov, S. Khartsev, and A. M. Grishin, Pulsed laser deposited y3fe5o12 films: Nature of magnetic anisotropy i, Journal of Applied Physics 106, 10.1063/1.3272731 (2009).
- Wang et al. [2014] H. Wang, C. Du, P. C. Hammel, and F. Yang, Strain-tunable magnetocrystalline anisotropy in epitaxial y 3 fe 5 o 12 thin films, Physical Review B 89, 134404 (2014).
- Bhoi et al. [2018] B. Bhoi, B. Kim, Y. Kim, M.-K. Kim, J.-H. Lee, and S.-K. Kim, Stress-induced magnetic properties of pld-grown high-quality ultrathin yig films, Journal of Applied Physics 123, 10.1063/1.5031198 (2018).
- Bhoi et al. [2019] B. Bhoi, N. Venkataramani, S. Prasad, R. Aiyar, G. Kumar, I. Samajdar, and M. Kostylev, Observation of enhanced magnetic anisotropy in pld yig thin film on ggg (1 1 1) substrate, Journal of Magnetism and Magnetic Materials 483, 191 (2019).
- Tabuchi et al. [2014] Y. Tabuchi, S. Ishino, T. Ishikawa, R. Yamazaki, K. Usami, and Y. Nakamura, Hybridizing ferromagnetic magnons and microwave photons in the quantum limit, Physical review letters 113, 083603 (2014).
- Zhang et al. [2014] X. Zhang, C.-L. Zou, L. Jiang, and H. X. Tang, Strongly coupled magnons and cavity microwave photons, Physical review letters 113, 156401 (2014).
- Bourhill et al. [2016] J. Bourhill, N. Kostylev, M. Goryachev, D. Creedon, and M. Tobar, Ultrahigh cooperativity interactions between magnons and resonant photons in a yig sphere, Physical Review B 93, 144420 (2016).
- Bauer et al. [2023] G. E. W. Bauer, P. Tang, M. Elyasi, Y. M. Blanter, and B. J. van Wees, Soft magnons in anisotropic ferromagnets (2023), arXiv:2304.10709 [cond-mat.mes-hall] .
- Cullity and Graham [2011] B. D. Cullity and C. D. Graham, Introduction to magnetic materials (John Wiley & Sons, 2011).
- Tolkunov and Solenov [2007] D. Tolkunov and D. Solenov, Quantum phase transition in the multimode dicke model, Physical Review B 75, 024402 (2007).