Causal inference in survival analysis using longitudinal observational data: Sequential trials and marginal structural models

Let us now assume a setting in which individuals are observed at regular ‘visits’ (data collection times) over a particular calendar period, reflecting the type of data that arise in our motivating example and in similar data sources. Let $t=0$ denote the start of follow-up, defined as the time at which a patient meets the eligibility criteria. We assume a ‘closed cohort’ such that all individuals in the study cohort were included at the same calendar time. In practice, some historical data are typically required to establish whether an individual meets the eligibility criteria at time $t=0$, e.g. past treatment status. The cohort is assumed to be followed up to (at least) the maximum time horizon of interest for the risk difference, $\tau_{\mathrm{max}}$. Information on treatment status and other covariates is observed at visits $k=0,1,\ldots,K$, and the time of visit $k$ is denoted $t_{k}$. Without loss of generality, we assume that $t_{k}=k$, for $k\geq 0$, and $K=\lfloor\tau_{\mathrm{max}}\rfloor$denotes the time of most recent visit before time $\tau_{\mathrm{max}}$ ($\lfloor\tau_{\mathrm{max}}\rfloor<\tau_{\mathrm{max}}$). At each visit $k$ we observe a binary treatment status $A_{k}$ and a set of time-dependent covariates $L_{k}$. To simplify the notation, each $L_{k}$ ($k=0,1,\ldots$) also includes any time-fixed covariates. A bar over a time-dependent variable indicates the history, that is $\bar{A}_{k}=\{A_{0},A_{1},\ldots,A_{k}\}$ and $\bar{L}_{k}=\{L_{0},L_{1},\ldots,L_{k}\}$. An underline indicates the future, so that $\underline{A}_{k}=\{A_{k},A_{k+1},\ldots\}$ denotes treatment status from time $k$ onwards.

The data set-up is illustrated in the directed acyclic graph (DAG) in Figure 1, using a discrete-time setting where $Y_{k}=I(t_{k-1}\leq T<t_{k})$ is an indicator of whether the event occurs between visits $k-1$ and $k$. One can imagine extending the DAG by adding a series of small time intervals between each visit, at which events are observed (but not $A$ or $L$, which are assumed constant between visits). As the time intervals become very small we approach the continuous time setting. From the DAG, we can see that $L_{k}$ are time-dependent confounders. Time-dependent confounding occurs when there are time-dependent covariates that predict subsequent treatment use, are affected by earlier treatment, and affect the outcome through pathways that are not just through subsequent treatment. The DAG also includes a variable $U$, which has direct effects on $L_{k}$ and $Y_{k}$ but not on $A_{k}$. $U$ is an unmeasured individual frailty and we include it because it is realistic that such individual frailty effects exist in practice. Because $U$ is not a confounder of the association between $A_{k}$ and $Y_{k}$ (after controlling for the observed confounders), the fact that it is unmeasured does not affect our ability to estimate causal effects of treatments. The DAG could be extended in various ways, for example, we could incorporate long term effects of $L$ on $A$ and vice versa by adding arrows from $L_{k}$ to $A_{k+1}$ and from $A_{k}$ to $L_{k+2}$. Long term effects of $A$ and $L$ on survival could also be added, for example by adding arrows from $L_{k}$ and $A_{k}$ to $Y_{k+2}$.

Next, we outline how the target trial outlined in Section 3 is emulated using the observational data described above. Each element of the target trial protocol should be considered. The eligibility criteria, treatment strategies, assignment strategies, and outcome in the emulated trial should be the same as far as possible as those in the target trial. An iterative process is appropriate when designing the target trial protocol, to take into consideration knowledge about the observational data. In some settings there may be some differences in eligibility criteria in the target trial and the emulated trial - for example, if the study pertains to individuals diagnosed with a particular infection, in the target trial a laboratory-confirmed diagnosis may be specified, whereas this may not possible in the emulated trial if diagnosis route is not recorded in the available observational data. There may also be differences in some aspects of treatment, for example the target trial may specify the dose of the treatment, whereas dose information may not be available in the observational data and so the emulated trial is pragmatic about dose. Making clear the differences between the target trial and the emulated trial can help us to understand possible sources of bias when we emulate the target trial using observational data.

The causal estimand of interest for the emulated trial is the same as that in the target trial. In our setting, the causal estimand compares marginal risks in a follow-up period $\tau$ under two treatment regimes: always treated ($\underline{a}_{0}=1$) or never treated ($\underline{a}_{0}=0$). In the observational data, individuals who are untreated initially can subsequently start treatment and vice versa. Treatment initiation and treatment switching may depend on time-dependent patient characteristics that also affect the outcome, as illustrated in the DAG in Figure 1. This must be addressed in the analysis, and the analysis stage is where we find the biggest differences between the emulated trial and target trial. However, we emphasise that the causal estimand in the emulated trial is the same as in the target trial. The time-dependent confounding is addressed in different ways in the MSM-IPTW approach and the sequential trials approach. We now describe how to estimate the causal risk difference (expression (1)) using these two approaches.

In the MSM-IPTW approach, a MSM is specified for the hazard. The counterfactual hazard under the possibly counter-to-fact treatment regime $\underline{a}_{0}$ is denoted $h_{T^{\underline{a}_{0}}}(t)$. In a slight abuse of standard notation we let $\lfloor t\rfloor$ denote the time of the most recent visit before time $t$ (so $\lfloor t\rfloor$ is always $<t$), and $\bar{a}_{\lfloor t\rfloor}$ denotes treatment pattern up to the most recent visit prior to $t$. The MSM is usually assumed to take the form of a Cox proportional hazards model ³⁸

$$h_{T^{\underline{a}_{0}}}(t)=h_{0}(t)e^{g(\bar{a}_{\lfloor t\rfloor};\beta_{A})},$$

(3)

where $h_{0}(t)$ is the baseline counterfactual hazard, and $g(\bar{a}_{\lfloor t\rfloor};\beta_{A})$ is a function of treatment pattern $\bar{a}_{\lfloor t\rfloor}$ to be specified, and $\beta_{A}$ is a vector of log hazard ratios. However, the hazards could take various other forms and we will also consider MSMs based on Aalen’s additive hazard model ³⁹, ⁴⁰, which has the form

$$h_{T^{\underline{a}_{0}}}(t)=\alpha_{0}(t)+g(\bar{a}_{\lfloor t\rfloor};\alpha_{A}(t)),$$

(4)

where $\alpha_{0}(t)$ is the baseline counterfactual hazard and $\alpha_{A}(t)$ is a vector of time-dependent coefficients. In both hazard models the $g(\cdot)$ function equals zero when $\bar{a}_{\lfloor t\rfloor}=0$. In a simple version of the MSM, the hazard at time $t$ is assumed to depend only on the current level of treatment: $g(\bar{a}_{\lfloor t\rfloor};\beta_{A})=\beta_{A}a_{\lfloor t\rfloor}$ or $g(\bar{a}_{\lfloor t\rfloor};\alpha_{A}(t))=\alpha_{A}(t)a_{\lfloor t\rfloor}$. Other options include that the hazard depends on duration of treatment, $g(\bar{a}_{\lfloor t\rfloor};\beta_{A})=\beta_{A}\sum_{k=0}^{\lfloor t\rfloor}a_{k}$ or $g(\bar{a}_{\lfloor t\rfloor};\alpha_{A}(t))=\alpha_{A}(t)\sum_{k=0}^{\lfloor t\rfloor}a_{k}$; or on the history of treatment in a more general way, $g(\bar{a}_{\lfloor t\rfloor};\beta_{A})=\sum_{k=0}^{\lfloor t\rfloor}\beta_{Ak}a_{k}$ or $g(\bar{a}_{\lfloor t\rfloor};\alpha_{A}(t))=\sum_{k=0}^{\lfloor t\rfloor}\alpha_{Ak}(t)a_{k}$.

The MSM cannot be estimated directly from the observed data because of time-dependent confounding by $L_{k}$. In the MSM-IPTW approach, individuals are assigned time-dependent weights and the MSM is fitted to the observed weighted data. The weight at time $t$ for a given individual is the inverse of the probability of their observed treatment pattern up to time $t$ given their time-dependent covariate history, $\bar{L}_{\lfloor t\rfloor}$. These weights can be large for some individuals, which induces large uncertainty in estimates from the MSM, and stabilized weights are typically used instead. The use of MSMs estimated using IPTW to estimate causal effects of joint treatments over time involves the four key assumptions of no interference, positivity, consistency, and conditional exchangeability (i.e. no unmeasured confounding) ¹, ⁴¹, ². Details on the weights and the assumptions are provided in the Supplementary Material (Sections A1 and A2). Weights are also discussed in detail in the context of the simulation study in Section 6.

The MSM can also be extended to include conditioning on baseline covariates $L_{0}$:

$$h_{T^{\underline{a}_{0}}}(t|L_{0})=h_{0}(t)e^{g(\bar{a}_{\lfloor t\rfloor};\beta_{A})+\beta_{L}L_{0}}$$

(5)

or

$$h_{T^{\underline{a}_{0}}}(t|L_{0})=\alpha_{0}(t)+g(\bar{a}_{\lfloor t\rfloor};\alpha_{A}(s))+\alpha_{L}(t)L_{0}.$$

(6)

When covariates $L_{0}$ are included in the MSM, they can also be included in the model in the numerator of the stabilized weights.

The survival probabilities required for the estimand in (1) can be estimated using the relation between the hazard and survivor functions. For the Cox MSM in (3) we have

$$\begin{split}\Pr(T^{\underline{a}_{0}}>\tau)&=\exp\left\{-e^{g(a_{0};\tilde{\beta}_{A})}\int_{0}^{1}h_{0}(s)ds-e^{g(\bar{a}_{1};\tilde{\beta}_{A})}\int_{1}^{2}h_{0}(s)ds\cdots-e^{g(\bar{a}_{\lfloor t\rfloor};\tilde{\beta}_{A})}\int_{\lfloor\tau\rfloor}^{\tau}h_{0}(s)ds\right\},\end{split}$$

(7)

where the integrated (cumulative) baseline hazards can be estimated using an IPTW Breslow’s estimator. Based on the Aalen MSM in (4) we have

$$\Pr(T^{\underline{a}_{0}}>\tau)=\exp\left(-\int_{0}^{t}\alpha_{0}(s)ds-\int_{0}^{1}g(a_{0};\alpha_{A}(s))ds-\int_{1}^{2}g(\bar{a}_{1};\alpha_{A}(s))ds\cdots-\int_{\lfloor\tau\rfloor}^{\tau}g(\bar{a}_{\lfloor\tau\rfloor};\alpha_{A}(s))ds\right),$$

(8)

where the integrals are obtained as the cumulative coefficients estimated in the Aalen additive hazard model fitting process. The probabilities of interest under the longitudinal treatment regimes of ‘always treated’ and ‘never treated’ ($\Pr(T^{\underline{a}_{0}=a}>\tau)$, $a=0,1$) are the obtained by setting $\underline{a}_{0}=a$ in (7) or (8). These probabilities are marginal and they refer to the population of $n$ individuals meeting the target trial eligibility criteria at $t=0$; we denote this population by $\mathcal{C}_{0}$. The MSMs including baseline covariates, as in (5) and (6), can be used to obtain the conditional probabilities $\Pr(T^{\underline{a}_{0}=a}\geq\tau|L_{0})$ for each individual in $\mathcal{C}_{0}$. Estimates of the marginal survival probabilities $\Pr(T^{\underline{a}_{0}}>\tau)$ can then be obtained using empirical standardization:

$$\begin{split}\widehat{\Pr}(T^{\underline{a}_{0}=a}\geq\tau)&=\frac{1}{n}\sum_{i\in\mathcal{C}_{0}}\widehat{\Pr}(T^{\underline{a}_{0}=a}_{i}\geq\tau|L_{0,i})\end{split}$$

(9)

where $\Pr(T^{\underline{a}_{0}=a}_{i}\geq\tau|L_{0,i})$ is estimated using the relation $\Pr(T^{\underline{a}_{0}=a}_{i}\geq\tau|L_{0,i})=\exp\left\{-\int_{0}^{\tau}h_{T^{\underline{a}_{0}=a}}(u|L_{0,i})du\right\}$, and where the integrals are estimated as outlined above for (7) or (8). In practice, the empirical standardization can be done by creating two copies of each individual in $\mathcal{C}_{0}$ and setting $A_{0}=A_{1}=\ldots=A_{\lfloor\tau\rfloor}=1$ for one copy and $A_{0}=A_{1}=\ldots=A_{\lfloor\tau\rfloor}=0$ for the other. The covariate values $L_{0,i}$ are the same for both copies. The estimated conditional survival probabilities are then obtained for each individual under both treatment regimes (i.e. for both copies), and then the average calculated across individuals under both treatment regimes.

If it is of interest to estimate the causal risk difference in (1) for several time horizons $\tau$, it is recommended to fit the MSM using all event times up to $\tau_{\mathrm{max}}$ and with administrative censoring at $\tau_{\mathrm{max}}$ to obtain risk difference estimates for all horizons $\tau\leq\tau_{\mathrm{max}}$, rather than fitting separate MSMs for different time horizons.

Confidence intervals for the estimated causal risk difference can be obtained by bootstrapping. The weights models and the MSM are fitted in each bootstrap sample, so that the bootstrap confidence intervals capture the uncertainty in the estimation of the weights as well as in the MSM.

In the MSM-IPTW approach each individual contributes to the emulated target trial from visit $k=0$, at which time they meet the eligibility criteria. However, individuals may in fact meet the eligibility criteria for the target trial at more than one visit during the study period. In the sequential trials approach an individual can contribute to an emulated trial starting from any visit $k=0,1,2,\ldots$ at which they meet the eligibility criteria. The emulated trial eligibility criteria are applied at each visit $k=0,1,\ldots$ to form a sequence of emulated trials. Recall that individuals who have previously used the treatment are not eligible and so all individuals eligible for the $k$th trial have $\bar{A}_{k-1}=0$. Those eligible for the $k$th trial therefore include ‘initiators’ who start treatment at visit $k$ ($A_{k}=1$) and ‘non-initiators’ who remain untreated at visit $k$ ($A_{k}=0$). Non-initiators in trial $k$ can appear as initiators in a later trial ($k+1,\ldots$). Individuals can therefore appear as initiators in only one trial, but as non-initiators in several trials.

In this paper we focus on a sequential trials approach in which the length of possible follow-up decreases for trials starting at later visits. An alternative would be to use a sequence of trials that all have equal length of follow-up. To explain this further, consider an example in which the observational cohort has visits at times $k=0,1,2,3,4$ and follow-up to time $5$ but our maximum time horizon of interest for the causal risk difference (1) is $\tau_{\mathrm{max}}=3$. We could have 5 trials starting at times $k=0,1,2,3,4$, with a decreasing length of follow-up from the start of each trial, such that the trials starting at times $k=0,1,2$ have follow-up of length 3 or longer (and administrative censoring would be applied after 3 time units of follow-up), and the trials starting at times $k=3,4$ only provide 2 and 1 time units of follow-up respectively. In the alternative we would only make use of trials starting at times $k=0,1,2$, with administrative censoring applied after 3 time units of follow-up.

The sequential trials approach focuses on comparing survival only under the two treatment regimes: ‘always treated’, in which eligible individuals initiate treatment and then always continue treatment, and ‘never treated’, in which eligible individuals do not initiate treatment at the time of meeting eligibility criteria and remain untreated at all later times. Previous descriptions of the sequential trials approach have described the analysis models used but have not been explicit about the causal interpretation of the model parameters. Here we begin by defining MSMs for populations meeting the emulated trial eligibility criteria at visits $k=0,1,2,\ldots,K$ and explain how these relate to the estimand of interest in (1). We then outline how the MSMs can be estimated using the observational data under certain assumptions, using the methods described by Hernan et al.⁴ and Gran et al.⁵.

Consider the trial starting at visit $k$. Let $T^{\underline{A}_{k}=a}$ denote the counterfactual event time under a treatment regime in which individuals follow their observed treatments up to and including visit $k-1$ and are then assigned to treatment $a$ ($a=0,1$) from visit $k$ onwards (if they survive to visit $k$). Let $h_{k,T^{\underline{A}_{k}=a}}(t-k|\bar{A}_{k-1}=0,\bar{L}_{k})$ denote the hazard at time $t-k$ after visit $k$ under this treatment regime, conditional on the baseline characteristics $L_{k}$ at the start of trial $k$. The time scale is time since the start of the trial. The conditioning on $\bar{A}_{k-1}=0$ indicates the restriction to individuals who have not initiated treatment prior to the start of the $k$th trial, which is part of the eligibility criteria. MSMs for this hazard using a Cox model and Aalen’s additive hazard model are

$$h_{k,T^{\underline{A}_{k}=a}}(t-k|\bar{A}_{k-1}=0,L_{k})=h_{0k}(t-k)\exp\left\{af(t-k;\beta_{Ak})+\beta_{Lk}L_{k}\right\}$$

(10)

and

$$h_{k,T^{\underline{A}_{k}=a}}(t-k|\bar{A}_{k-1}=0,L_{k})=\alpha_{0k}(t-k)+\alpha_{Ak}(t-k)a+\alpha_{Lk}(t-k)L_{k}.$$

(11)

Recall that $L_{k}$ includes any time fixed covariates. The conditioning on $L_{k}$ could be excluded, but we include it because conditioning on baseline variables is a feature of the previously-described sequential trials analysis methods, which we discuss below. In the Cox MSM (10) the hazards in the treated and untreated could be assumed proportional, $f(t-k;\beta_{Ak})=\beta_{Ak}$, or we could allow the hazard to depend on duration of treatment, e.g. $af(t-k;\beta_{Ak})=a\beta_{Ak,0}+a\beta_{Ak,1}(t-k)$. The additive hazards MSM (11) naturally incorporates a flexible time-dependent effect of treatment on the hazard. Both models could be extended to include interactions between $A_{k}$ and $L_{k}$. The above MSMs are conditional on $L_{k}$ rather than $\bar{L}_{k}$, which is an assumption. They could be written as conditional on $\bar{L}_{k}$, but it is likely to be appropriate that the hazard for each trial $k$ depends on the same amount of history of $L_{k}$. For example, if we wish to allow the hazard for each trial $k$ to depend on $L_{k}$ and $L_{k-1}$ then the first trial would need to start at time $k=1$ instead of $k=0$, unless data on the $L$ were available prior to time 0.

Conditional survival probabilities (conditional on $L_{k}$ and $T\geq k$) for the counterfactual event times are related to the hazard according to the formula

$$\begin{split}\Pr(T^{\underline{A}_{k}=a}>k+\tau|&T\geq k,\bar{A}_{k-1}=0,L_{k})\\ &=\exp\left\{-\int_{k}^{k+\tau}h_{k,T^{\underline{A}_{k}=a}}(u-k|\bar{A}_{k-1}=0,L_{k})du\right\},\quad\tau\leq\tau_{\mathrm{max}}-k.\end{split}$$

(12)

Below we discuss how marginal survival probabilities, and therefore the causal estimand of interest (marginal risk difference), can be obtained. First, however, we outline how the MSMs in (10) or (11), and hence the conditional survival probabilities in (12), can be estimated using the observed data. The MSMs in (10) and (11) cannot be estimated directly from the observational data because not all individuals meeting the eligibility criteria at visit $k$ are then ‘always treated’ ($\underline{A}_{k}=1$) or ‘never treated’ ($\underline{A}_{k}=0$). In the sequential trials approach as described by Hernan et al.⁴ and Gran et al.⁵ individuals are artificially censored at the visit at which they switch from their treatment group at the start of a given trial. In the $k$th trial individuals are censored at the earliest visit $m>k$ such that $A_{m}\neq A_{k}$. This results in a modified data set in which all individuals in the trial starting at time $k$ have either $\underline{A}_{k}=0$ or $\underline{A}_{k}=1$ up to the earliest of their event time, their censoring time, or their artificial censoring time due to treatment switch. The treatment switching is expected to depend on time-dependent covariates that are also associated with the outcome, meaning that the artificial censoring is informative. It is addressed using weights, which we refer to as inverse probability of artificial-censoring weights (IPACW). The IPACW at times $0<s<1$ after the start of trial $k$ are equal to 1. The IPACW at times $l\leq s<l+1$ ($l\geq 1$) after the start of trial $k$ is the inverse of the probability that the individual’s treatment status at time $l$ remained the same as their treatment status at the start of the trial, $A_{k}$, conditional on their observed covariates up to time $l$. The MSMs in (10) and (11) are then fitted using weighted regression using the time-dependent IPACW, with $a$ in the hazard model replaced by the observed treatment status $A_{k}$. The conditioning on baseline covariates $L_{k}$ in each trial controls for confounding of the association between treatment initiation at time $k$ and the hazard. Estimating the MSMs in this way is valid under the same assumptions of positivity, consistency and conditional exchangeability, as are required for the MSM-IPTW analysis. Further details on the IPACW are provided in the Supplementary Materials (Section A1). Hernan et al.⁴ used logistic regression to estimate the IPACW, whereas Gran et al.⁵ used Aalen’s additive hazard model. The IPACW could be fitted separately in each trial or combined across trials. After estimating the MSMs using this approach, the expression in (12) can be used to obtain estimates of conditional survival probabilities. The trial starting at $k=0$ provides estimates of $\Pr(T^{\underline{A}_{0}=a}>\tau|L_{0})$ ($\tau\leq\tau_{\mathrm{max}}$), and the trial starting at $k=1$ provides estimates of $\Pr(T^{\underline{A}_{1}=a}>\tau+1|A_{0}=0,L_{1},T\geq 1)$ ($\tau\leq\tau_{\mathrm{max}}-1$), ($a=0,1$), and so on for $k=2,\ldots,K$. These are conditional on covariates measured at the start of the trial, $L_{k}$.

After estimating the conditional survival probabilities in (12) estimates of marginal survival probabilities $\Pr(T^{\underline{A}_{k}=a}>\tau+k|\bar{A}_{k-1}=0,T\geq k)$ can be obtained via empirical standardization over the distribution of $L_{k}$ at the start of each trial, as described for the MSM-IPTW approach in Section 4.3. This enables estimation of marginal risk differences:

$$\Pr(T^{\underline{a}_{0}=1}>k+\tau|\bar{A}_{k-1}=0,T\geq k)-\Pr(T^{\underline{a}_{0}=0}>k+t|\bar{A}_{k-1}=0,T\geq k),\qquad\tau\leq\tau_{\mathrm{max}}-k.$$

(13)

The (true) marginal risk differences for the same time horizon $\tau$ after the start of the trial will differ in general for trials starting at different times $k=0,1,2,\ldots$ (for trials for which $\tau\leq\tau_{\mathrm{max}}-k$). Differences in the true value of the estimand for different trials arise when coefficients of the hazard model ((10) or (11)) depend on $k$, but also because the marginal risk differences for different $k$ refer to populations with different distributions of baseline characteristics, $L_{k}$. Marginal risk differences that have the same true value across trials starting at different times $k=0,1,\ldots$ can be estimated, using assumptions about the coefficients of the hazard models and standardisation to a common distribution of baseline covariates $L_{k}$.

Some or all parameters of the MSMs in (10) and (11) could be assumed common across trials (i.e. for all $k$). The common parameters can then be estimated by fitting the hazard models using the observed data combined across trials. It may be reasonable in many settings to assume that the impact of the treatment on the hazard at a given time post-initiation does not depend on the visit $k$ at which treatment was initiated, i.e. $\beta_{Ak}=\beta_{A}$ and $\alpha_{Ak}(t-k)=\alpha_{A}(t-k)$ for all $k$. Similarly the coefficients for $L_{k}$ could be assumed constant across trials. Often the underlying time scale $t$ will be in a sense arbitrary. For example, in some settings it will be calendar year, and in others the time since joining a cohort. Provided any elements of time (e.g. age, calendar year) that affect the hazard are included in the set of covariates $L_{k}$ then the baseline hazard may also be assumed common across trials, i.e. $h_{0k}(t-k)=h_{0}(t-k)$ or $\alpha_{0k}(t-k)=\alpha_{0}(t-k)$.

Suppose that all coefficients of the MSM in (10) and (11) are assumed to be the same across trials (i.e. for all $k$). The MSM would be fitted using the data combined across trials using a weighted regression with time-dependent IPACW, and with adjustment for baseline covariates in each trial, $L_{k}$. When estimating the marginal risk differences by empirical standardization it should be specified clearly which population the marginal probabilities refer to. We suggest that the population of interest for the marginal risk difference is not the population of individuals used in the combined analysis, since this population is not well defined and many individuals appear in it more than once. A better alternative is to estimate the risk difference for the population $\mathcal{C}_{0}$ of individuals meeting the target trial eligibility criteria at $t=0$ (visit $k=0$). This would make the marginal risk difference comparable with that estimated from the MSM-IPTW analysis. We note that the causal estimand in expression (1) is implicitly conditional on no prior treatment, which is part of the target trial eligibility criteria. Another possibility would be to estimate the risk difference for the population of individuals meeting the target trial eligibility criteria at the last visit time $K$, as this population might be expected to be the most similar to the patient population now in terms of their distribution of characteristics.

Suppose, instead, that we wish to allow the baseline hazard the differ across trials, but that the coefficients for treatment ($a$) and baseline covariates ($L_{k}$) are assumed the same across trials. The MSMs in(10) or (11) could be fitted using data combined across trials, but with a stratified baseline hazard. In this case, care should be taken over which baseline hazard is used to obtain the marginal risk difference estimates. For example, the baseline hazard corresponding to the trial starting at $k=0$ may be used to obtain the marginal risk difference estimates for all time horizons $\tau\leq\tau_{\mathrm{max}}$. This would make the marginal risk difference comparable with that estimated from the MSM-IPTW analysis. The baseline hazard from the trial starting at the penultimate visit $K-1$ can only be used to estimate marginal risk difference estimates for time horizons $\tau\leq\tau_{\mathrm{max}}-(K-1)$, and using baseline hazards corresponding to trials starting at visit $k\geq 1$ to estimate marginal risk differences would result in marginal risk differences that do not correspond to those estimated from the MSM-IPTW analysis.

In their descriptions of the sequential trials approach Gran et al.⁵ used the Cox proportional hazards model, and Hernan et al.⁴ used pooled logistic regression, which is equivalent as the times between visits gets smaller ⁴³. Røysland et al.⁴⁴ used an additive hazards model, though their aim was to estimate direct and indirect effects, which differs from our aims in this paper. Gran et al.⁵ assumed the hazard ratios for treatment in the Cox model to be common across the trials, but allowed a different baseline hazard in each trial. Hernan et al.⁴ allowed the odds ratio for treatment to differ across trials and also performed a test for heterogeneity, though it is unclear whether they allowed separate intercept parameters (baseline hazards) across trials. If the treatment effect is assumed the same across trials, it is recommended to assess this assumption using a formal test.

As in the MSM-IPTW approach, confidence intervals for the estimated causal risk difference can be obtained by bootstrapping. The formation of the sequential trials, estimation of the weights, fitting of the conditional MSMs, and obtaining the risk difference are all repeated in each bootstrap sample.

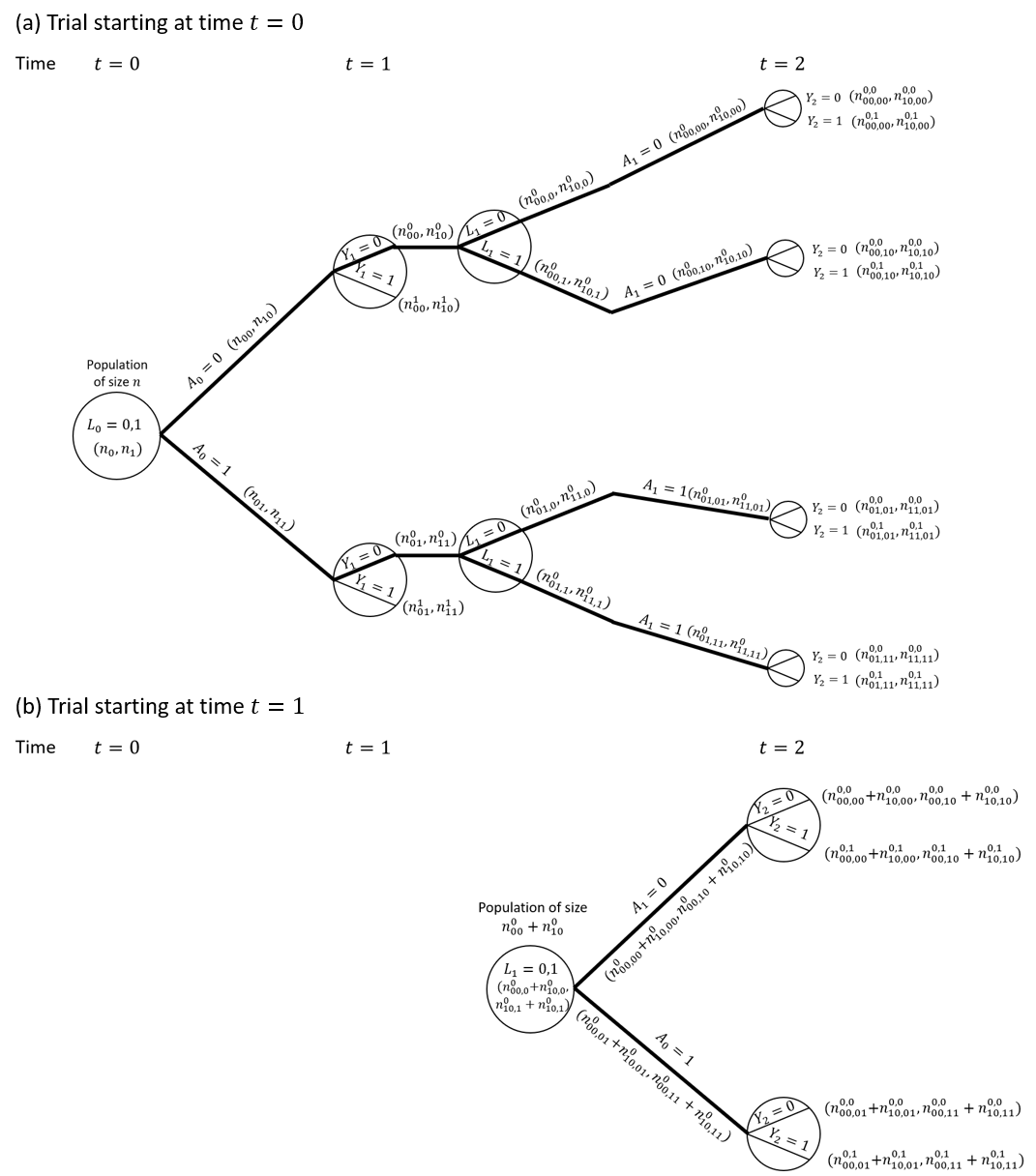
In this section we show how the MSM-IPTW and sequential trials approaches can estimate the same causal estimand using an illustrative example and non-parametric estimates. Our aim is to provide insight into how the two approaches use the data differently to estimate the same quantity.

Consider a situation as depicted in the DAG in Figure 1, but with treatment and covariate information only collected at up to two visits ($L_{0},A_{0}$ measured at time 0, and $L_{1},A_{1}$ measured at time 1) and survival status observed at times 1 ($Y_{1}=I(0\leq T<1)$) and 2 ($Y_{2}=I(1\leq T<2)$). We focus on a single binary time-dependent confounder $L$ and omit the unobserved variable $U$. Figure 2 shows a causal tree graph (see for example Richardson and Rotnitzky⁴⁵), representing the different possible combinations of the variables $L_{0},A_{0},Y_{1}$ up to time 1, and then the different combinations of $L_{1},A_{1},Y_{2}$ among individuals who survive to time 1 ($Y_{1}=0$). A total of $n$ individuals are observed at time 0. The numbers in brackets on the branches of the tree are the number of individuals who followed a given pathway up to that branch. The notation is as follows: $n_{l_{0}}$ denotes the number with $L_{0}=l_{0}$; $n_{l_{0},a_{0}}$ the number with $L_{0}=l_{0},A_{0}=a_{0}$; $n^{y_{1}}_{l_{0}a_{0}}$ the number with $L_{0}=l_{0},A_{0}=a_{0},Y_{1}=y_{1}$; $n^{0}_{l_{0}a_{0},l_{1}}$ the number with $L_{0}=l_{0},A_{0}=a_{0},Y_{1}=0,L_{1}=l_{1}$; $n^{0}_{l_{0}a_{0},l_{1}a_{1}}$ the number with $L_{0}=l_{0},A_{0}=a_{0},Y_{1}=0,L_{1}=l_{1},A_{1}=a_{1}$; and $n^{0y_{2}}_{l_{0}a_{0},l_{1}a_{1}}$ the number with $L_{0}=l_{0},A_{0}=a_{0},Y_{1}=0,L_{1}=l_{1},Y_{2}=y_{2}$.

Our interest is in comparing survival probabilities under two treatment regimes: always treated ($A_{0}=A_{1}=1$) and never treated ($A_{0}=A_{1}=0$). The branches representing these two treatment regimes are shown with thick lines in the causal tree diagram. The MSM analysis makes use of the causal tree diagram as depicted in Figure 2. Under the sequential trials approach, we create a trial starting at time 0 and a trial starting at time 1. In the trial starting at time 0 individuals who survive to time 1 are censored at time 1 if $A_{1}\neq A_{0}$, i.e. not all branches after time 1 are used. The trial starting at time 1 is restricted to individuals with $A_{0}=0$ and $Y_{1}=0$. The sections of the causal tree diagram for these two trials are shown in Figure 3.

Consider the probability of survival to time 1 with treatment $a$, $\Pr(Y_{1}^{A_{0}=a}=0)$. The MSM-IPTW approach estimates this using the results that (under the conditions of consistency, positivity and conditional exchangeability)

$$\Pr(Y_{1}^{A_{0}=a}=0)=E\left\{\frac{I(A_{0}=a)(1-Y_{1})}{\Pr(A_{0}=a|L_{0})}\right\}.$$

(14)

Based on the tree diagram, a non-parametric estimate of this is

$$\widehat{\Pr}(Y_{1}^{A_{0}=a}=0)=\frac{1}{n}\left\{n_{0a}^{0}\left(\frac{n_{0a}}{n_{0}}\right)^{-1}+n_{1a}^{0}\left(\frac{n_{1a}}{n_{1}}\right)^{-1}\right\},$$

(15)

where the two contributions come from individuals with $L_{0}=0$ and $L_{0}=1$. On the other hand, the sequential trial starting at time 0 estimates $\Pr(Y_{1}^{A_{0}=a}=0|L_{0})$. By consistency and conditional exchangeability we have $\Pr(Y_{1}^{A_{0}=a}=0|L_{0})=\Pr(Y_{1}=0|A_{0}=a,L_{0})$. Based on the tree diagram, a non-parametric estimate of this using the trial starting at time 0 is $\Pr(Y_{1}=0|A_{0}=a,L_{0}=l_{0})=\frac{n_{l_{0}a}^{0}}{n_{l_{0}a}},\quad l_{0}=0,1$. Using the result that $\Pr(Y_{1}^{A_{0}=a}=0)=\sum_{l_{0}}\Pr(Y_{1}=0|A_{0}=a,L_{0}=l_{0})\Pr(L_{0}=l_{0})$ (assuming consistency and conditional exchangeability) it follows that a non-parametric estimate of the marginal probability $\Pr(Y_{1}^{A_{0}=a}=0)$ based on the trial starting at time 0 is

$$\widehat{\Pr}(Y_{1}^{A_{0}=a}=0)=\frac{n_{0a}^{0}}{n_{0a}}\frac{n_{0}}{n}+\frac{n_{1a}^{0}}{n_{1a}}\frac{n_{1}}{n},$$

(16)

which is the same as the estimate using MSM-IPTW (i.e. equation (15)). Therefore the MSM-IPTW and sequential trials approaches give identical estimates of $\Pr(Y_{1}^{A_{0}=a}=0)$. The equivalence between inverse probability weighted estimates and standardized estimates obtained using the g-formula in the non-parametric setting is well established (see for example ^{2, 46}). In the sequential trials approach, the trial starting at time 1 can be used to estimate the probability of survival to time 2 after initiating the treatment strategy ($a=0,1$) conditional on survival to time 1 and on $A_{1}=0$. The non-parametric estimate is

$$\begin{split}\widehat{\Pr}(Y_{2}^{A_{1}=a}=0|Y_{1}=0,A_{1}=0)=&\left(\frac{n_{00,0a}^{0,0}+n_{10,0a}^{0,0}}{n_{00,0a}^{0}+n_{10,0a}^{0}}\right)\left(\frac{n_{00,0}^{0}+n_{10,0}^{0}}{n_{00}^{0}+n_{10}^{0}}\right)\\ &+\left(\frac{n_{00,1a}^{0,0}+n_{10,1a}^{0,0}}{n_{00,1a}^{0}+n_{10,1a}^{0}}\right)\left(\frac{n_{00,1}^{0}+n_{10,1}^{0}}{n_{00}^{0}+n_{10}^{0}}\right).\end{split}$$

(17)

The marginal probability estimate $\widehat{\Pr}(Y_{1}^{A_{0}=a}=0)$ refers to a population in which $\Pr(L_{0}=1)=n_{1}/n$, whereas the marginal probability estimate $\widehat{\Pr}(Y_{2}^{A_{1}=a}=0|Y_{1}=0,A_{1}=0)$ refers to a population with a different distribution of $L_{1}$. The estimate from the trial starting at time 1 could alternatively be standardized to the distribution of $L_{0}$ at time 0:

$$\widehat{\Pr}^{\mathrm{Std}}(Y_{2}^{A_{1}=a}=0|Y_{1}=0,A_{1}=0)=\left(\frac{n_{00,0a}^{0,0}+n_{10,0a}^{0,0}}{n_{00,0a}^{0}+n_{10,0a}^{0}}\right)\left(\frac{n_{0}}{n}\right)+\left(\frac{n_{00,1a}^{0,0}+n_{10,1a}^{0,0}}{n_{00,1a}^{0}+n_{10,1a}^{0}}\right)\left(\frac{n_{1}}{n}\right).$$

(18)

Under the assumption that $\Pr^{\mathrm{Std}}(Y_{2}^{A_{1}=a}=0|Y_{1}=0,A_{1}=0)=\Pr(Y_{1}^{A_{0}=a}=0)$, a combined estimate of $\Pr(Y_{1}^{A_{0}=a}=0)$ could be obtained from the two trials, for example using an inverse-variance-weighted combination of the estimates from the two trials.

We can also show that non-parametric estimates of $\Pr(Y_{2}^{\bar{A}_{1}=a}=0)$ from the two methods are the same. The MSM-IPTW approach uses

$$\Pr(Y_{2}^{\bar{A}_{1}=a}=0)=E\left\{\frac{I(A_{0}=a,A_{1}=a)(1-Y_{1})(1-Y_{2})}{\Pr(A_{0}=a|L_{0})\Pr(A_{1}=a|A_{0}=a,L_{0},L_{1})}\right\}.$$

(19)

Based on the tree diagram, a non-parametric estimate of this is

$$\begin{split}\widehat{\Pr}(Y_{2}^{\bar{A}_{1}=a}=0)=&\frac{1}{n}\left\{n_{0a,0a}^{0,0}\left(\frac{n_{0a}}{n_{0}}\right)^{-1}\left(\frac{n_{0a,0a}^{0}}{n_{0a,0}^{0}}\right)^{-1}+n_{0a,1a}^{0,0}\left(\frac{n_{0a}}{n_{0}}\right)^{-1}\left(\frac{n_{0a,1a}^{0}}{n_{0a,1}^{0}}\right)^{-1}\right.\\ &+\left.n_{1a,0a}^{0,0}\left(\frac{n_{1a}}{n_{1}}\right)^{-1}\left(\frac{n_{1a,0a}^{0}}{n_{1a,0}^{0}}\right)^{-1}+n_{1a,1a}^{0,0}\left(\frac{n_{1a}}{n_{1}}\right)^{-1}\left(\frac{n_{1a,1a}^{0}}{n_{1a,1}^{0}}\right)^{-1}\right\},\end{split}$$

(20)

where the four contributions come from individuals with the four possible combinations of $(L_{0},L_{1})$.

The sequential trials approach estimates $\Pr(Y_{2}^{\bar{A}_{1}=a}=0|L_{0})$, which can be written

$$\Pr(Y_{2}^{\bar{A}_{1}=a}=0|L_{0})=\Pr(Y_{2}^{\bar{A}_{1}=a}=0|Y_{1}^{A_{0}=a}=0,L_{0})\Pr(Y_{1}^{A_{0}=a}=0|L_{0}).$$

(21)

The term $\Pr(Y_{1}^{A_{0}=a}=0|L_{0})$ was considered above. The first term, $\Pr(Y_{2}^{\bar{A}_{1}=a}=0|Y_{1}^{A_{0}=a}=0,L_{0})$, is estimated by IPACW, because individuals with $A_{1}\neq A_{0}$ are censored at time 1, and the remaining individuals with $A_{1}=A_{0}$ weighted by $\Pr(A_{1}=a|A_{0}=a,L_{0},L_{1})^{-1}$. Under the assumptions of consistency, positivity and conditional exchangeability we can write

$$\Pr(Y_{2}^{\bar{A}_{1}=a}=0|Y_{1}^{A_{0}=a}=0,L_{0})=E\left\{\frac{I(A_{1}=a)(1-Y_{2})}{\Pr(A_{1}=a|A_{0}=a,L_{0},L_{1})}|Y_{1}^{A_{0}=a}=0,A_{0}=a,L_{0}\right\}.$$

(22)

Based on the tree diagram, a non-parametric estimate of this is

$$\begin{split}\widehat{\Pr}(Y_{2}^{\bar{A}_{1}=a}=0|Y_{1}^{A_{0}=a}=0,L_{0}=l_{0})&=\widehat{\Pr}(Y_{2}^{\bar{A}_{1}=a}=0|Y_{1}=0,A_{0}=a,L_{0}=l_{0})\\ &=\frac{1}{n_{l_{0}a}^{0}}\left\{n_{l_{0}a,0a}^{0,0}\left(\frac{n_{l_{0}a,0a}^{0}}{n_{l_{0}a,0}^{0}}\right)^{-1}+n_{l_{0}a,1a}^{0,0}\left(\frac{n_{l_{0}a,1a}^{0}}{n_{l_{0}a,1}^{0}}\right)^{-1}\right\}.\end{split}$$

(23)

Using this result along with the estimate $\widehat{\Pr}(Y_{1}^{A_{0}=a}=0|L_{0}=l_{0})=\widehat{\Pr}(Y_{1}=0|A_{0}=a,L_{0}=l_{0})=n_{l_{0}a}/n_{l_{0}}$, it can be shown that the sequential trials estimate of $\Pr(Y_{2}^{\bar{A}_{1}=a}=0)=\sum_{l_{0}=0,1}\Pr(Y_{2}^{\bar{A}_{1}=a}=0|L_{0}=l_{0})\Pr(L_{0}=l_{0})$ is the same as the MSM-IPTW estimate in (20). By comparing (20) and (23) we can see clearly the connection between the weights used in the MSM-IPTW approach and those used in the sequential trials approach (IPACW).

In practice, model-based estimates are typically required instead of non-parametric estimates, as we usually have multiple time-dependent confounders to consider, including continuous variables. In this section we compare in more detail the form of the MSMs used in the two approaches, and how they are estimated using inverse probability weights.

A key difference in the MSMs used in the two approaches is that in the MSM-IPTW the MSM for the hazard at time $t$ includes the history of treatment up to time $t$, $\bar{A}_{\lfloor t\rfloor}$, whereas the MSM used in the sequential trials approach involves only the treatment status assigned at the start of the trial. The MSM-IPTW approach therefore requires that the relation between treatment history $\bar{A}_{\lfloor t\rfloor}$ and the hazard is correctly specified, whereas in the sequential trials approach there are limited options for the form of the MSM because only two treatment patterns are considered, because after the artificial censoring all individuals used in the analysis are either always treated or never treated. In MSM-IPTW, when baseline covariates are excluded from the MSM, the MSM is a fully marginal model - the possibility of interaction between treatment and baseline covariates is not ruled out but does not have to be modelled. If the MSM used in the MSM-IPTW approach includes baseline covariates $L_{0}$ then any interactions that exist between treatment and $L_{0}$ must be included in the MSM and correctly specified. Similarly, in the sequential trials approach, if there are interactions between treatment and the baseline covariates at the start of each trial, $L_{k}$, then these must be included in the MSM and correctly specified. MSMs that condition on baseline covariates are therefore more susceptible to misspecification. The sequential trials approach could use weighting in the first time period instead of adjustment for baseline covariates, though that is not how the method has been described or used to date. Conditioning on baseline covariates in the sequential trials approach enables use of empirical standardization to obtain risk difference estimates for a population with any distribution of the baseline covariates. When combined with assumptions about the form of the MSM for the hazard in each trial, this enables us to estimate the same causal estimand in the sequential trials approach as in the MSM-IPTW approach.

If the sequential trials analysis makes the assumption that the effect of treatment on the hazard is the same in all trials, i.e. does not depend on the time of treatment initiation, then the sequential trials approach has information about the effect of treatment initiation from several time origins. If the assumptions are valid, this re-use of individuals from several time origins could lead to gains in efficiency in the marginal risk difference estimate at some time horizons $\tau$ relative to the MSM-IPTW approach. On the other hand, in the MSM-IPTW analysis individuals who switch their treatment status during follow-up continue to contribute information to the analysis, whereas in the sequential trials analysis individuals cease to contribute information when they deviate from their treatment group at the start of a given trial. This means that in the sequential trials analysis the number of individuals with longer term follow-up will be smaller than in the MSM-IPTW analysis.

To fit the MSMs, both approaches require time-updated weights, and hence the data should be formatted with multiple rows per individual (one for each visit for MSM-IPTW, and one for each visit within each trial for the sequential trials approach). In the MSM-IPTW approach (without conditioning on baseline covariates), the MSM is estimated by weighting individuals in the observed data using time-updated weights. In the sequential trials approach the MSM is instead estimated through adjustment in trial $k$ for baseline covariates $L_{k}$ and artificial censoring of individuals when they deviate from their initial treatment group at time $k$. The artificial censoring is addressed using IPACW. The weight up to time 1 after the start of a given trial is always equal to 1. In the MSM-IPTW approach with conditioning on baseline variables $L_{0}$ the IPTW weight at a given time is the same as the IPACW weight used in the sequential trials approach for the trial starting at time 0 for individuals following the ‘always treated’ or ‘never treated’ regimes. In the MSM-IPTW approach without conditioning on baseline variables the IPTW weights are proportional to the IPACW weights used in the sequential trials approach. Because the MSM-IPTW approach includes individuals following any treatment regime (not just ‘always treated’ or ‘never treated’), we may expect to see more extreme weights with increasing follow-up, compared with the weights used in the sequential trials approach.

Because the two approaches use the data differently and because the MSM-IPTW approach could make use of more extreme weights, it is of interest to investigate the relative efficiency of the two approaches for estimating the causal estimand. We note that it is only appropriate to consider the relative efficiency of the two approaches when they target the same causal estimand, which, as discussed in section 4.4, requires assumptions that some parameters of the MSM used in the sequential trials approach are common across trials.

In Sections 4.3 and 4.4 we considered MSMs based on Cox models or on additive hazard models. In this section we show that one can use an additive hazard model for the MSM for the sequential trials analysis (expression (11)) (with common parameters assumed across trials) and an additive hazard model for the MSM used in the MSM-IPTW approach (expression (4), without conditioning on $L_{0}$), and that both MSMs can be correctly specified. However, if we use a Cox model for the MSM for the sequential trials analysis (expression (10)) and a Cox model for the MSM used in the MSM-IPTW approach (expression (3), then both MSMs cannot simultaneously be correctly specified in general. This is because the parameters of additive hazard models are collapsible, whereas hazard ratios in the Cox model are non-collapsible. Martinussen and Vansteelandt (2013)¹⁹ explained the implications of collapsibility for the use of Aalen additive hazards models and Cox models in the context of estimating the causal effect of a point treatment on survival. Keogh et al. (2021)²³ extended to a longitudinal setting similar to that considered in this paper. Here we outline some key points in the context of the simple setting depicted in Figures 2 and 3.

For the MSM-IPTW analysis in this section we again focus on an MSM that is not conditional on $L_{0}$, as in (3),(4). The MSMs used in a MSM-IPTW analysis and in the sequential trials analysis may be considered to be consistent with each other if there exists an underlying fully conditional hazard model that implies both the MSM used in MSM-IPTW and the MSM used in the sequential trials approach, which is conditional on baseline covariates at the start of each trial. As above we consider estimating $\Pr(Y_{1}^{A_{0}=a}=0)$ (or $\Pr(T^{\underline{A}_{0}=a}>1)$) and $\Pr(Y_{2}^{\bar{A}_{1}=a}=0)$ (or $\Pr(T^{\underline{A}_{1}=a}>2)$). First consider a fully conditional additive hazard model of the form

$$h(t|\bar{A}_{\lfloor t\rfloor},\bar{L}_{\lfloor t\rfloor})=\alpha_{0}(t)+\alpha_{A}(t)A_{\lfloor t\rfloor}+\alpha_{L}(t)L_{\lfloor t\rfloor}.$$

(24)

Under this model the conditional survival probability at time 1 is

$$\Pr(Y_{1}=0|A_{0},L_{0})=\exp\left(-\int_{0}^{1}(\alpha_{0}(u)+\alpha_{A}(u)A_{0}+\alpha_{L}(u)L_{0})du\right)$$

(25)

and the marginal probability of survival to time 1 is

$$\begin{split}\Pr(Y_{1}^{A_{0}=a}=0)&=e^{-\int_{0}^{1}(\alpha_{0}(u)+\alpha_{A}(u)A_{0})du}\Pr(L_{0}=0)+e^{-\int_{0}^{1}(\alpha_{0}(u)+\alpha_{A}(u)A_{0}+\alpha_{L}(u))du}\Pr(L_{0}=1)\\ &=e^{-\int_{0}^{1}(\alpha_{0}^{*}(u)+\alpha_{A}(u)A_{0})du},\end{split}$$

(26)

where $\int_{0}^{1}\alpha_{0}^{*}(u)=\int_{0}^{1}\alpha_{0}(u)du+\log\{\Pr(L_{0}=0)+e^{-\int_{0}^{1}\alpha_{L}(u)du}\Pr(L_{0}=1)\}$. This expression is in the form of the survival probability from a marginal additive hazard model of the form

$$h_{T^{{}^{A_{0}=a}}}(t)=\alpha_{0}^{*}(t)+\alpha_{A}(t)a.$$

(27)

It follows that we could use an additive hazard model for $\Pr(Y_{1}^{A_{0}=a}=0|L_{0})$ in the sequential trials analysis and an additive hazard model for $\Pr(Y_{1}^{A_{0}=a}=0)$ in the MSM-IPTW analysis, and that both models can be correctly specified.