CatFedAvg: Optimising Communication-efficiency and
Classification Accuracy in Federated Learning
Abstract
Federated learning has allowed the training of statistical models over remote devices without the transfer of raw client data. In practice, training in heterogeneous and large networks introduce novel challenges in various aspects like network load, quality of client data, security and privacy. Recent works in FL have worked on improving communication efficiency and addressing uneven client data distribution independently, but none have provided a unified solution for both challenges. We introduce a new family of Federated Learning algorithms called CatFedAvg which not only improves the communication efficiency but improves the quality of learning using a category coverage maximization strategy.
We use the FedAvg framework and introduce a simple and efficient step every epoch to collect meta-data about the client’s training data structure which the central server uses to request a subset of weight updates. We explore two distinct variations which allow us to further explore the tradeoffs between communication efficiency and model accuracy. Our experiments based on a vision classification task have shown that an increase of 10% absolute points in accuracy using the MNIST dataset with 70% absolute points lower network transfer over FedAvg. We also run similar experiments with Fashion MNIST, KMNIST-10, KMNIST-49 and EMNIST-47. Further, under extreme data imbalance experiments for both globally and individual clients, we see the model performing better than FedAvg. The ablation study further explores its behaviour under varying data and client parameter conditions showcasing the robustness of the proposed approach.
In this era of computing, we have seen an explosion of connected personal devices and IoT (Lueth 2018). We see tremendous progress in Deep Learning (LeCun, Bengio, and Hinton 2015), which has partially been driven by the growth of data that we collect. This combination has lead to exciting research and applications in the area of distributed model training.
The conventional data processing approach has been centralized with all these devices, uploading their data into cloud servers or data centres (Li et al. 2017). This data is then processed to provide insights or training various inference models. Recently, consumers and business alike have questioned data centralization. Governments are responding by the enactment of legislation like GDPR (Custers et al. 2019) in the EU, and Consumer Privacy Bill of Rights (Gaff, Sussman, and Geetter 2014) in the US. These laws focus on limiting data collection and storage to what the consumer has consented for and required for processing. As data collection happens at scale, there are other technical issues like latency (Mao et al. 2017) for real-time use cases and network loads.
So, we see the emergence of Mobile Edge Computing (MEC) that use the storage and processing capabilities of the edge servers and edge devices to train models closer to the data generators (Shi et al. 2016). In this solution, we transmit data to the edge servers for training a few layers, and the cloud servers do more computationally heavy tasks. This approach has shown challenges with managing communication costs and models that require continuous training (Han et al. 2020). We see the application of Differential Privacy (DP) (Abadi et al. 2016) for privacy preservation, but many users are unwilling to expose their private data.
In this regard, we see the introduction of a decentralized ML approach called Federated Learning (McMahan et al. 2016). It guarantees that the data remains on the personal devices and allows collaborative machine learning of complex models. A high-level view of the approach is that we cooperatively train an ML model on a mobile device using its local data. We send the client trained model’s weight to the FL server for aggregation. We repeat the steps until to reach some target accuracy. This approach is network bandwidth-efficient as only model weights are sent instead of raw data. As the model is on the mobile device, it enables privacy and makes low inference latency.
We see its successful application in production with like the Federated Averaging Algorithm (FedAvg) (McMahan et al. 2016) used in Google’s GBoard (Hard et al. 2018) to improve next-word predictions. There are other examples like recommendations (Chen et al. 2018) and training of health diagnosis models which allows many hospitals and government agencies can collaborate without explicit data sharing (Brisimi et al. 2018).
The Federated learning problem has a few challenges; for example, with federated networks comprising of a massive number of devices, the network data transfer costs can be humongous. There is much variability in the device capabilities in the network that leads to uncertain client behaviour. The client also generates data in a non-identically distributed manner across the network. Finally, privacy is a concern even when model weights are shared as they can reveal sensitive information about the client data.
In this paper, we take on the dual challenge of communication efficiency and model training accuracy under client non-IID conditions. We see the use of two strategies for improving the communication efficiency, current work (McMahan et al. 2017) uses the static selection of a fraction of client models, and the other is the compression of the model updates (Alistarh et al. 2017). We further see that FedAvg performs badly when the client datasets are non-IID (Zhao et al. 2018) in the experiments performed. Our proposed approach improves model accuracy significantly. The contributions of the paper can be summarized as follows
-
•
We propose a new family of algorithms called CatFedAvg with two proposed variants that significantly improve communication efficiency by up to 70AP while boosting model accuracy by up to 22AP.
-
•
We build a framework that uses a simple and efficient client categorical coverage strategy identify the best client combinations for training. This allows us to tradeoff communication overheads for accuracy and vice-versa.
-
•
Our experiments show that we outperform the baseline FedAvg and VIRTUAL MTL algorithm. We solve an image classification problem using multiple image datasets under various client distribution conditions. We perform an ablation study to further show the robustness of our approach.
Related Works
Federated Learning
Federated learning (McMahan et al. 2016) is a decentralized machine learning method, which uses distributed training on clients without sending the raw data to the central server. We can split this into three categories of vertical federated learning, horizontal federated learning and federated transfer learning.
Communication Cost
In FL, there are several rounds of communication between the clients and the server during training. We have DL models that have millions of parameters. Thus, the larger size of the updates will lead to higher communication costs, which can be a training bottleneck. Further, unreliable network conditions and asymmetric net connection speeds will result in delays from the client.
We can use model compression (Wang et al. 2018) which is used widely in distributed learning where techniques like sparsification, quantization or subsampling (Stich, Cordonnier, and Jaggi 2018) are to reduce the model update size. However, our goal is to maintain the quality of the trained models (Caldas et al. 2018).
Alternatively, we can use selective communication where only relevant or essential updates are transmitted back (Tao and Li 2018). This technique saves communication costs and at times, improves the Global performance. We see the usage of random subsampling of clients in the sketched updating method (Konecný et al. 2016) to improve communication efficiency.
Statistical Heteroginity
Federated learning has a few statistical challenges. In traditional distributed ML, the central server has access to the complete dataset. Allowing the server to split it into subsets with similar distributions; we transfer these to the clients for distributed training. However, this approach is impractical for FL, as the dataset is local to the client.
In this setting, the clients may have datasets with variable distributions, i.e. the datasets are non-IID. We have cases (Zhao et al. 2018) where FedAvg is unable to achieve the desired accuracy in these conditions. When the dataset is highly skewed and non-IID, we have a solution where a common dataset is sent to the clients by the central server. However, this may not be possible in all cases.
We also see the challenge of global imbalance where the collection of data held across all the clients is class imbalanced, which leads to a decrease in model accuracy. We see the Astrea framework (Duan 2019) trying to solve this problem, where clients initially send their data distribution to the server. Then we have a rebalancing step where each client performs data augmentation on minority classes. There is a mediator that selects the best clients that contribute to the uniform distributions. This approach has shown accuracy improvements.
There have been solutions like FEDPER (Arivazhagan et al. 2019) using concepts from Multi-task learning to learn separate but structurally related models for each participant. We see the training of another set of personalization layers being trained by the client locally on its data. This has been used for building recommender systems, and testing on Flickr-AES dataset (Deng et al. 2017) has shown it to outperform FedAvg. Even though federated multi-task learning has been shown to be an effective paradigm for real-world datasets, it has been applied only to convex models. We compare our algorithm performance with VIRTUAL algorithm (32) with that has been designed for the federated multi-task learning with non-convex models in non-IID conditions.
CatFedAvg
We introduce the category maximization federated averaging algorithm (CatFedAvg) for classification models whose primary objective is to ensure the usage of model updates which have been trained with the most number of categories.
This is based on the FedAvg Algorithm as shown. Here C denotes fraction of selected clients, while K selected clients are indexed by k; B is the local minibatch size, E is the number of local epochs, and is the learning rate.
Our proposal is the introduction of a meta-data collection round that makes the central system aware of what is the data distribution at the client’s end. We then select a set of clients instead of the random strategy taken in FedAvg such that we maximize the coverage of categories.
We choose a classification problem that has categories, where is the total number of federated clients. In this, a random subset of is selected. This represents the larger subset whose meta-data we request. We use to denote a limiting parameter which is the maximum number of clients that we can sample.
All the clients share their , which is a client mask of bits, where a bit on denotes that a category is present in the new client dataset. The algorithm selects clients to maximize the coverage of at the central server level. Assuming that all categories are present in the system, if we set , we can guarantees coverage of all categories under both modes of operation.
These represent the updated client subset selection executed in line 1 of the Federated Averaging Algorithm.
We introduce the first client selection strategy, in which select a fixed number of clients. We collect the category bitmasks, sort them in decreasing order of set bits. We then try and cover each category with one client.
If then all categories will be covered. Further, it is possible that each category is covered more than once in the sampled model updates. This will lead to adequate data coverage for training and leads to better model accuracy.
In the cost strategy, we select a variable number of clients depending on the distribution. Similar to the first strategy, we pick a category and then select a client. However, we know that a client may have more than one category covered. That means we can skip those categories that have been covered and continue selection for the uncovered ones. We will select a maximum of C clients.
If we have then each category is covered at least once with the least probability of having a particular category covered more than once. It optimizes cost with maximum category coverage with the goal of minimizing the number of clients required to cover all categories.
Analysis
Federated Averaging
We have a federated system with clients with datasets with a central server . A fixed number of clients can be sampled from clients to participate in updating the global cloud model. The global loss function is related with participating clients with loss function for client as shown below.
| (1) |
Let denote loss contribution of class id from client. The loss contribution from client can be expressed in terms of losses of each category for a global problem with C categories, as shown below.
| (2) |
| (3) |
Ideally, should have loss contribution from all categories, but in real-world skewed Non-IID conditions, some classes may not be covered by the usual random sampling technique of FedAvg technique. Hence, there may exist cases where is not defined for any value of
Category coverage-based aggregation
We define a novel method of aggregation which is focused on maximizing category coverage. Let denote loss contribution of class from client and let denote the total loss of class id for all clients .
| (4) |
We select clients in such a way that is defined for atleast one client with id . This is ensured using bitmasking strategy. Hence, global loss function of server can be represented as shown below.
| (5) |
Understanding Tradeoffs
Communication Cost
Let be the cost of updating the global model, assuming extra cost introduced by each client while averaging the weights to be negligible. Let be the cost incurred at the server end while interacting with a single client. The total cost for one single round with K participating clients can be approximately expressed as shown below.
| (7) |
The total cost for R rounds of global updates can expressed as:
| (8) | |||
| (9) | |||
| (10) |
The cost per client interaction for R rounds can be obtained by differentiating eq (8) with respect to .
| (11) | |||
| (12) |
Dividing eq (13) by R yields cost incurred per client per round
| (13) |
Eq (14) depends directly on K. Hence, the cost incurred at the server end, increasing proportionately with the number of incorporating clients (K).
Model performance
Let the number of data samples with each of the participating client be . Let the total number of data samples seen by the server be D.
| (14) |
Hence, D increases with K. Increasing value of D help in generalizing the global model.
From eqs. (13,14) we can conclude that both cost and performance increases with number of participating clients K.
We see that a tradeoff between high model accuracy and low cost.
Experiments
| Total Samples | Samples per class | ||||||
|---|---|---|---|---|---|---|---|
| Dataset | Number of Classes | Training | Validation | Training | Validation | ||
| Mean | Std | Mean | Std | ||||
| MNIST | 10 | 60000 | 10000 | 6000 | 322 | 1000 | 59 |
| FMNIST | 10 | 60000 | 10000 | 6000 | 0 | 1000 | 0 |
| KMNIST-10 | 10 | 60000 | 10000 | 6000 | 0 | 1000 | 0 |
| FEMNIST | 47 | 112800 | 18800 | 2400 | 0 | 400 | 0 |
| KMNIST-49 | 49 | 232365 | 38547 | 4742 | 1839 | 786 | 309 |
We present a set of experiments that take compare our algorithms with FedAvg and Virtual MTL. We use five datasets and varying categories along with client data distribution. We further perform an ablation study to dissect the various parameters that show it as a clear improvement over FedAvg.
Datasets
We have primarily used vision datasets, and all details of the datasets used for our experiments have been summarized in Table 1.
-
•
MNIST: (Deng 2012) The dataset contains a total of 70,000 small square 28x28 pixels grayscale images of handwritten single digits between 0 and 9. The subdivision of dataset is 60,000 training samples and 10,000 testing samples. We federated the dataset amongst the clients to simulate client conditions.
-
•
FMNIST Fashion MNIST (Xiao, Rasul, and Vollgraf 2017) abbreviated as FMNIST is a dataset of Zalando’s article images consisting of a training set of 60,000 examples and a test set of 10,000 examples. Each example is a 28x28 grayscale image, associated with a label from 10 classes. It is relatively challenging dataset and simulates the everyday computer vision tasks. The classes consist of fashion objects T-shirt/top, Trouser, Pullover, Dress, Coat, Sandal, Shirt, Sneaker, Bag and Ankle Boot.
-
•
KMNIST-10: Kuzushiji-MNIST-10 (KMNIST-10) (Clanuwat et al. 2018)consists of 70,000 28x28 pixels grayscale images of handwritten Japanese characters of Hiragana. The subdivision of this dataset is 60,000 training samples and 10,000 testing samples. It is a well-balanced dataset across all classes and is relatively difficult to learn as compared to MNIST. We use this to simulate the federated settings.
-
•
FEMNIST: The FEMNIST dataset is the federated version of EMNIST dataset (Cohen et al. 2017). It is a set of handwritten character digits derived from the NIST Special Database 19 and converted to a 28x28 pixel image format and dataset structure that directly matches the MNIST dataset. We used the balanced version with ten single-digit classes between 0 and 9 inclusive, 26 uppercase alphabets and 11 lowercase alphabets. We federated this 47 classes dataset for the simulation of real-world federated settings.
-
•
KMNIST 49: Kuzushiji-MNIST 49 is a much larger, but imbalanced dataset containing 48 Hiragana characters and one Hiragana iteration mark. It is an excellent example to simulate the universal problem of an imbalanced class problem under federated settings. It consists of 49 classes 28x28 grayscale images. It is a comparatively much larger dataset.
Data distributions

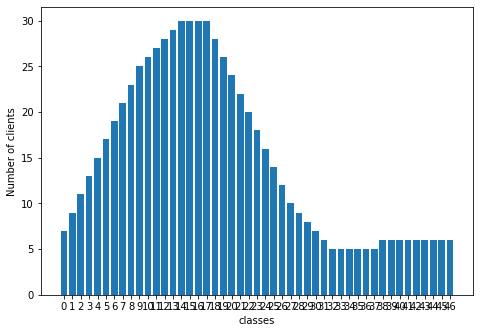
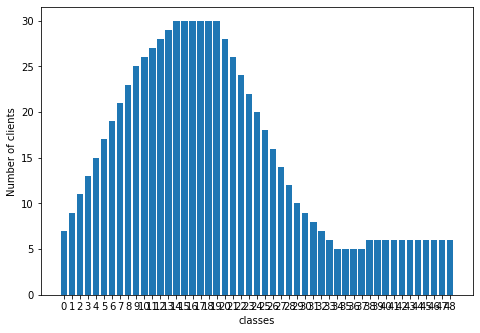


We simulate various client data distribution conditions to compare the algorithm. We take a total of 100 clients in the Federated system. We vary the number of clients having a particular category. In all of our experiments, all clients have a proper subset of categories varying from clients having a single category to clients having half the number of total categories. There are five distribution conditions (D1, D2, D3, D4, D5) which we use and have been shown in figure 1. We share specific details in the Appendix.
Settings

All networks employed are multilayer perceptrons (MLP) with two hidden dense Flipout layers with 100 units in case of MNIST, single hidden layer of 512 units in case of FMNIST and KMNIST-10 and a single hidden layer of 784 units in case of FEMNIST-47 and KMNIST-49. Activation function Rectified Linear Unit (ReLU) is employed between the hidden layers and input layers, while the softmax activation function is employed in the final output layer. The final output layer consists of 10 units in case of MNIST, FMNIST and KMNIST-10. In FEMNIST and KMNIST-49 number of final layer units are 47 and 49 respectively.
We define two modes of experiments per algorithm where we set the value of the maximum number of clients to sample. We define Mode A where N is kept at ten and Mode B, where we keep N as equal to the number of categories in the dataset. This allows us to explore conditions where we may want to sample as few clients as possible. We will denote the algorithms for performance strategy to be A1 and cost strategy to be A2.
Each client has 600 training samples, and batch size is 32 is used in the execution of subroutine of local refinements for all experiments. In the case of a random client selection method, which is the default FedAvg case, a total of 10 clients are selected for participation in global training.
For all cases, the learning rate is used as 0.003, and a total of 50 rounds of global refinements are performed using Stochastic Gradient Descent (SGD) with Federated Averaging (FedAvg) method of updating the global model.
Results
| Dataset | FedAvg | Mode A - A1 | Mode A - A2 | Mode B - A1 | Mode B - A2 | Virtual MTL |
|---|---|---|---|---|---|---|
| MNIST | 0.72850.0092 | 0.92020.0007 | 0.83430.0080 | 0.94450.004 | 0.83710.0060 | 0.57110.0060 |
| FMNIST | 0.56220.0230 | 0.79370.0020 | 0.70840.0050 | 0.80870.003 | 0.68290.0010 | 0.44320.0060 |
| KMNIST-10 | 0.57760.0070 | 0.80710.0004 | 0.75860.0030 | 0.81290.007 | 0.74980.0040 | 0.47210.0060 |
| Dataset | Distribution | FedAvg | Mode A - A1 | Mode A - A2 | Mode B - A1 | Mode B - A2 |
|---|---|---|---|---|---|---|
| FEMNIST | D2 | 0.55730.0130 | 0.41230.0005 | 0.69030.006 | 0.75370.002 | 0.69210.002 |
| D4 | 0.41230.023 | 0.27120.0007 | 0.58180.008 | 0.70230.001 | 0.64460.002 | |
| KMNIST-49 | D3 | 0.52110.0150 | 0.39720.0050 | 0.62130.004 | 0.67530.001 | 0.62860.001 |
| D5 | 0.42360.0270 | 0.26530.0080 | 0.53250.008 | 0.61570.005 | 0.57950.005 |
| Distribution/(Classes) | Mode A-A1 | Mode A-A2 | Mode B-A1 | Mode B-A2 | ||||
|---|---|---|---|---|---|---|---|---|
| Selected | Covered | Selected | Covered | Selected | Covered | Selected | Covered | |
| D1 (10) | 10 | 10 | 3 | 10 | 10 | 10 | 3 | 10 |
| D2 (47) | 10 | 24 | 6 | 47 | 47 | 47 | 6 | 47 |
| D3 (49) | 10 | 24 | 6 | 49 | 49 | 49 | 6 | 49 |
| D4 (47) | 10 | 14 | 10 | 39 | 47 | 47 | 19 | 47 |
| D5 (49) | 10 | 14 | 10 | 39 | 49 | 49 | 19 | 49 |
Here we describe the various insights about the experimental results as presented in Tables 2 and 3.
We discuss the number of clients selected, as that reflects the communication efficiency along with the model accuracy numbers under various conditions. We further performed an ablation study which has been shared in the Appendix.
FedAvg
We pick a subset of 10 clients is selected randomly for global refinement. It performs well when the distribution of classes is not skewed. However, for the skewed environments of D1 with ten categories, we see a dip in performance as depicted in Table 2. The deterioration is pronounced when a large number of categories (47 and 49) are there as seen in distributions D2 and D3. The primary reason is the lack of data coverage of all categories in the simulated skewed environment is not guaranteed. The dataset conditions D4 and D5 show the worst performance.
CatFedAvg - performance strategy
Here we primarily discuss the algorithm A1 which implements the model performance strategy.
Mode A : We limit the total number of clients selected to . In this scenario, all ten categories were covered in case of MNIST, FMNIST and KMNIST-10 under distribution D. In case of distribution D2, and D3 using FEMNIST and KMNIST-49 only 24 categories out of 47 and 49 respectively were covered while in D4 and D5 only 14 categories were covered as described in 4. This results in poor performance of this strategy as the category coverage is not enough.
Mode B: We don’t limit the number of clients selected in this mode. Hence, coverage of all categories is guaranteed by this algorithm. We see that clients are specifically selected for each category which leads to the selection of 10 clients in distribution D1, 47 clients in distributions D2 and D4 and 49 clients in distributions D3 and D5. This performs the best in comparison to other algorithms as evident from Tables 2 and 3.
CatFedAvg - cost strategy
Here we primarily discuss the algorithm A2 which implements the communication efficiency strategy.
Mode A: We limit the total number of clients selected to . It is seen that only three clients are selected in case of distribution D1 while six clients are selected in case of D2 and D3. In D4 and D total clients, selected are ten which is the maximum limit (N=10). Hence the coverage of all categories is not guaranteed here, and only 39 categories were covered in each round, but it performs better than the performance strategy variant in the same mode.
Mode B: We don’t limit the number of clients selected in this mode. All categories are covered with minimal probability of a category being selected more than once. In this case, three clients are selected in distribution D1 while six clients are selected in distributions D2 and D3. In the extremely skewed distributions D4 and D5, selected of 19 clients is sufficient for complete coverage.
Observations
Model Accuracy
As described in 2 and 3, the performance of Algorithm 1 under mode B is the best across the entire spectrum under all conditions.
If we denote the number of categories in global problem begin solved as C, the relative performance of proposed algorithms is as below.
If NC: Mode A-A1 Mode A-A2 Mode B-A1 Mode B-A2
If NC: Mode B-A1 Mode B-A2 Mode A-A2 Mode A-A1
Communication Cost
Communication cost is related to the efficiency of a particular algorithm when it comes to deployment, and the cost of refining the global model increases with the number of clients participating in the training round. 4 describes the number of clients selected in various distributions.
Considering all distributions, , we can see that number of clients participating is least in case of Mode A-A2. We limit the clients participating in mode A-A1 to N. In contrast; Mode B-A2 has a comparatively higher number of participating clients when the number of global categories is less than N in mode A-A2.
Let C be the number of global categories. The following is the relative order of algorithms in terms of communication cost expense.
If NC: Mode A-A1 Mode B-A1 Mode A-A2 Mode B-A2
If NC: Mode B-A1 Mode B-A2 Mode A-A1 Mode A-A2
Trade Off : Accuracy versus Communication
We can see that the better performance of mode B-A1 comes at a higher communication cost. If we want the best performance, we need to compromise with communication cost. Alternatively, if we desire a communication efficiency, then Mode A-A2 is desirable. A better compromise is achieved with both performance and communication cost may suggest Mode B-A2 as the best one.
Conclusions & Future Work
In this work, we have proposed an approach that can help tradeoff communication overheads with model accuracy with the usage of a simple and efficient technique. This family of algorithm CatFedAvg has been shown to perform better by 10AP in some cases than existing well-proven methods like FedAvg and VIRTUAL MTL. The communication efficiency has seen a jump of 70AP in some cases. We show a formal analysis that gives a framework to understand how to work with the critical parameters for the tradeoff between communication efficiency and model accuracy.
We have also shown the robustness of the approach with various statistical heterogeneous conditions like global class imbalance and client distribution variations. We believe that existing techniques that involve data augmentation may not be feasible in production conditions. We would see this approach combined with compression to deliver even more communication efficiency. It would be interesting to use latency to be factored in when the initial larger set of random clients are selected. We offer a technique that can possibly work easily with Differential Privacy due to its inherent simplicity offering privacy as well.
References
- Abadi et al. (2016) Abadi, M.; Chu, A.; Goodfellow, I. J.; McMahan, H. B.; Mironov, I.; Talwar, K.; and Zhang, L. 2016. Deep Learning with Differential Privacy. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security .
- Alistarh et al. (2017) Alistarh, D.; Grubic, D.; Li, J.; Tomioka, R.; and Vojnovic, M. 2017. QSGD: Communication-Efficient SGD via Gradient Quantization and Encoding. In Guyon, I.; Luxburg, U. V.; Bengio, S.; Wallach, H.; Fergus, R.; Vishwanathan, S.; and Garnett, R., eds., Advances in Neural Information Processing Systems 30, 1709–1720. Curran Associates, Inc. URL http://papers.nips.cc/paper/6768-qsgd-communication-efficient-sgd-via-gradient-quantization-and-encoding.pdf.
- Arivazhagan et al. (2019) Arivazhagan, M. G.; Aggarwal, V.; Singh, A.; and Choudhary, S. 2019. Federated Learning with Personalization Layers. ArXiv abs/1912.00818.
- Auger et al. (2018) Auger, N.; Jugé, V.; Nicaud, C.; and Pivoteau, C. 2018. On the Worst-Case Complexity of TimSort. ArXiv abs/1805.08612.
- Brisimi et al. (2018) Brisimi, T. S.; Chen, R.; Mela, T.; Olshevsky, A.; Paschalidia, I. C.; ; and Shi, W. 2018. Federated learning of predictive models from federated electronic health records. International journal of medical informatics vol. 112, pp. 59–67.
- Caldas et al. (2018) Caldas, S.; Konecný, J.; McMahan, H.; and Talwalkar, A. 2018. Expanding the Reach of Federated Learning by Reducing Client Resource Requirements. ArXiv abs/1812.07210.
- Chen et al. (2018) Chen, F.; Luo, M.; Dong, Z.; Li, Z.; and He, X. 2018. Federated Meta-Learning with Fast Convergence and Efficient Communication. arXiv: Learning .
- Clanuwat et al. (2018) Clanuwat, T.; Bober-Irizar, M.; Kitamoto, A.; Lamb, A.; Yamamoto, K.; and Ha, D. 2018. Deep Learning for Classical Japanese Literature. ArXiv abs/1812.01718.
- Cohen et al. (2017) Cohen, G.; Afshar, S.; Tapson, J.; and Schaik, A. 2017. EMNIST: an extension of MNIST to handwritten letters. ArXiv abs/1702.05373.
- Custers et al. (2019) Custers, B.; Sears, A.; Dechesne, F.; Georgieva, I.; Tani, T.; and van der Hof, S. 2019. EU Personal Data Protection in Policy and Practice .
- Deng (2012) Deng, L. 2012. The MNIST Database of Handwritten Digit Images for Machine Learning Research [Best of the Web]. IEEE Signal Processing Magazine 29: 141–142.
- Deng et al. (2017) Deng, X.; Cui, C.; Fang, H.; Nie, X.; and Yin, Y. 2017. Personalized Image Aesthetics Assessment. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, CIKM ’17, 2043–2046. New York, NY, USA: Association for Computing Machinery. ISBN 9781450349185. doi:10.1145/3132847.3133052. URL https://doi.org/10.1145/3132847.3133052.
- Duan (2019) Duan, M. 2019. Astraea: Self-Balancing Federated Learning for Improving Classification Accuracy of Mobile Deep Learning Applications. 2019 IEEE 37th International Conference on Computer Design (ICCD) 246–254.
- Gaff, Sussman, and Geetter (2014) Gaff, B. M.; Sussman, H. E.; and Geetter, J. 2014. Federated Learning of Deep Networks using Model Averaging. Privacy and big data Computer, vol. 47, no. 6, pp. 7–9.
- Han et al. (2020) Han, Y.; Wang, X.; Leung, V. C. M.; Niyato, D.; Yan, X.; and Chen, X. 2020. Convergence of Edge Computing and Deep Learning: A Comprehensive Survey. IEEE Communications Surveys & Tutorials 22: 869–904.
- Hard et al. (2018) Hard, A.; Rao, K.; Mathews, R.; Beaufays, F.; Augenstein, S.; Eichner, H.; Kiddon, C.; and Ramage, D. 2018. Federated Learning for Mobile Keyboard Prediction. ArXiv abs/1811.03604.
- Konecný et al. (2016) Konecný, J.; McMahan, H.; Yu, F.; Richtárik, P.; Suresh, A. T.; and Bacon, D. 2016. Federated Learning: Strategies for Improving Communication Efficiency. ArXiv abs/1610.05492.
- LeCun, Bengio, and Hinton (2015) LeCun, Y.; Bengio, Y.; and Hinton, G. 2015. Deep learning. nature 521(7553): 436–444.
- Li et al. (2017) Li, P.; Li, J.; Huang, Z.; Li, T.; Gao, C.-Z.; Yiu, S.-M.; and Chen, K. 2017. Multi-key privacy-preserving deep learning in cloud computing. Future Generation Computer Systems 74: 76 – 85. ISSN 0167-739X. doi:https://doi.org/10.1016/j.future.2017.02.006. URL http://www.sciencedirect.com/science/article/pii/S0167739X17302005.
- Lueth (2018) Lueth, K. L. 2018. State of the iot 2018: Number of iot devices now at 7b market accelerating .
- Mao et al. (2017) Mao, Y.; C.You; J.Zhang; K.Huang; and B.Letaief, K. 2017. A Survey on Mobile Edge Computing: The Communication Perspective. IEEE Communications Surveys Tutorials 19(4): 2322–2358.
- McMahan et al. (2017) McMahan, H.; Moore, E.; Ramage, D.; Hampson, S.; and y Arcas, B. A. 2017. Communication-Efficient Learning of Deep Networks from Decentralized Data. In AISTATS.
- McMahan et al. (2016) McMahan, H.; Moore, E.; Ramage, D.; and y Arcas, B. A. 2016. Federated Learning of Deep Networks using Model Averaging. ArXiv abs/1602.05629.
- Mohri, Sivek, and Suresh (2019) Mohri, M.; Sivek, G.; and Suresh, A. T. 2019. Agnostic Federated Learning. In ICML.
- Shi et al. (2016) Shi, W.; J.Cao; Q.Zhang; Y.Li; and L.Xu. 2016. Edge Computing: Vision and Challenges. IEEE Internet of Things Journal 3(5): 637–646.
- Stich, Cordonnier, and Jaggi (2018) Stich, S.; Cordonnier, J.-B.; and Jaggi, M. 2018. Sparsified SGD with Memory. In NeurIPS.
- Tao and Li (2018) Tao, Z.; and Li, Q. 2018. eSGD: Communication Efficient Distributed Deep Learning on the Edge. In USENIX Workshop on Hot Topics in Edge Computing (HotEdge 18). Boston, MA: USENIX Association. URL https://www.usenix.org/conference/hotedge18/presentation/tao.
- Wang et al. (2018) Wang, H.; Sievert, S.; Liu, S.; Charles, Z. B.; Papailiopoulos, D.; and Wright, S. 2018. ATOMO: Communication-efficient Learning via Atomic Sparsification. ArXiv abs/1806.04090.
- Xiao, Rasul, and Vollgraf (2017) Xiao, H.; Rasul, K.; and Vollgraf, R. 2017. Fashion-MNIST: a Novel Image Dataset for Benchmarking Machine Learning Algorithms. ArXiv abs/1708.07747.
- Zhao et al. (2018) Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; and Chandra, V. 2018. Federated Learning with Non-IID Data. ArXiv abs/1806.00582.