Categorical enumerative invariants of the ground field
Abstract
Abstract: For an -framed modular operad , we introduce its “Feynman compactification” denoted by which is a modular operad. Let be the -framed modular operad defined using moduli spaces of smooth curves with framings along punctures. We prove that the homology operad of is isomorphic to , the homology operad of the Deligne-Mumford operad. Using this isomorphism, we obtain an explicit formula of the fundamental class of in terms of Sen-Zwiebach’s string vertices. As an immediate application, we prove Costello’s categorical enumerative invariants of the ground field match with the Gromov-Witten invariants of a point.
1 Introduction
CEI of the algebra .
Categorical enumerative invariants (CEI) were introduced by Costello [5] and recently made explicit in [2] and [3]. These are invariants associated with a pair where
-
•
is a cyclic algebra of dimension over a field (of characteristic zero) that is proper, smooth and satisfies the Hodge-to-de-Rham degeneration.
-
•
is a choice of splitting of the non-commutative Hodge filtration of .
Explicitly, CEI take the following form
with in the -shifted Hochschild homology of adjoining a formal variable of homological degree . It was proved in [3] that CEI is only possibly non-zero if
| (1) |
In the cohomological degree convention, this is precisely the dimension axiom in Gromov-Witten theory. Indeed, the original motivation to define and study such invariants came from mirror symmetry following Kontsevich’s proposal [14]. It is expected that these invariants, when applied to Fukaya categories, should recover Gromov-Witten invariants at all genera.
At first glance, comparing these categorical invariants with Gromov-Witten invariants may look rather difficult since CEI are defined purely algebraically while the GW invariants involves moduli spaces of stable maps. The purpose of this paper is to demonstrate otherwise. We begin with the case when the ground field and the algebra is also . In this case, the dimension is zero, and the algebra has a unique homogeneous splitting of the Hodge filtration which we still denote by . Furthermore, its Hochschild homology group is and so the insertions lie in the space .
Theorem A. The categorical enumerative invariants of the algebra (the field of rationals) matches the Gromov-Witten invariants of a point, i.e. we have
where ’s are the -classes on the Deligne-Mumford moduli space . By the dimension formula (1), these invariants are only non-zero when .
Basic constructions and notations.
In order to prove the above theorem, it is necessary to have a better understanding of Sen-Zwiebach’s string vertices [18], since they play a central role in the construction of CEI.
We need to introduce some notations. For a topological space , denote by its normalized singular chain complex with coefficients in . For each pair such that , denote by the moduli space of tuples where is a Riemann surface of genus ; are marked points in ; and for each , is a holomorphic chart such that it extends to an open neighborhood of the unit disk in . We also require that the pair-wise intersections of the closures of the framed disks be empty, i.e. . As in Segal [17], sewing along the coordinate charts defines two types of composition maps:
We shall denote both of them by , as no confusion can arise in this way. The collection of topological spaces together with the two sewing operations form a modular operad defined by Getzler-Kapranov [10] in the category of topological spaces.
Applying the normalized singular chain functor yields a differential graded modular operad . For the first type composition, note that the functor is lax monoidal, i.e. for two topological spaces and , we have a naturally defined map , the Alexander-Whitney map. This enables us to define a composition map still denoted by
Denote this differential graded modular operad by , with .
The modular operad is in fact an -framed modular operad with the circle actions given by rotations of the local coordinate charts. Explicitly, the circle actions on are given by degree one operators
We refer to Section 2 for more details on the definition of -framed modular operad and examples. Denote the homotopy quotient complex of the -action by
with circle parameters of homological degree . Observe that the symmetric group still acts on . Denote its further quotient space by .
String vertices.
With these preparations, we are ready to introduce one of the main constructions in defining CEI: Sen-Zwiebach’s differential graded Lie algebra (DGLA) [2, Section 3]. As a graded vector space, this DGLA is given by
where , are two formal variables both of homological degree . The differential of is of the form with the operator defined by all possible ways of “twisted sewing”:
The Lie bracket of is defined in a similar way:
Observe that the circle operator has homological degree one. This explains the shift by in the definition of : to make the Lie bracket of homological degree zero. We refer to [2, Section 3] for more details of the construction of .
By definition, the string vertex is a Maurer-Cartan element of the form
in the DGLA satisfying an initial condition of . The Maurer-Cartan equation satisfied by is equivalent to the following system of equations usually known as the quantum master equation:
| (2) |
Costello proves that the above equations together with the initial condition of characterize up to homotopy ( [5, Theorem 1]).
In the homological convention, a Maurer-Cartan element has degree , which implies that is of degree inside the equivariant chain complex . Thus explicitly, the string vertex at position is of the form
with the coefficient chains
By definition, it is also symmetric under permutations of the indices. Then, after unwinding the definition of CEI in [2, 3], in the case of Theorem A we have
Here in the second case, note that is a zero chain, hence it is a linear combination of points. The notation stands for the sum of its coefficients.
Feynman compactification of .
To prove Theorem A, it remains to relate these numbers with integrals of -classes on the Deligne-Mumford compactification . It is natural to do this on the level of operads.
In Section 2 we define the Feynman compactification of the -framed modular operad . Denote the resulting operad by . Intuitively speaking, this is an ordinary modular operad such that the circle actions on the composition maps of have been universally trivialized. More precisely, an element of is given by a stable graph together with decorations:
-
•
At a vertex , the decoration is by an element in the homotopy quotient .
-
•
At an edge , it is decorated by a homological degree element .
We think of the edge decoration as giving a universal trivialization of the circle action on the composition map, by setting its boundary to be exactly the twisted sewing operation along the edge , see Equation (6) for a precise definition.
Theorem B. There is an isomorphism of modular operads
where is the Deligne-Mumford modular operad [10, Section 6.2].
Remark 1.1.
This result may be viewed as a higher genus extension of the beautiful works by Dotsenko-Shadrin-Vallette [7] [8], Drummond-Cole [9] and Khoroshkin-Markarian-Shadrin [12] in genus zero. Indeed, we prove in Section 2 that a -algebra together with a trivialization of the circle action induces a -algebra structure on the homotopy quotient (see Proposition 2 for details). Together with the theorem above, this implies that the homology carries a -algebra structure. However, the approach taken here which uses the Feynman compactification is different even in genus zero. It is worthwhile to explore the comparison with the previous works.
Remark 1.2.
To this point, we say a word about the proof of Theorem B. The idea is to exhibit a sequence of quasi-isomorphisms:
Here is a simplicial resolution of which we refer to as Mondello’s resolution as it’s first constructed by Mondello [15]. The hatted version is given by the normalized singular chain complex of the space constructed in [13]. Basically, this is the framed version of the oriented real blowup of along its boundary divisors, see Section 2 for more details. The first map is constructed explicitly in Section 3, see Equation (13). Our main construction is the second map defined in Section 4. The natural inclusion map , being a homotopy equivalence, does not respect the operad structures in the strict sense. The map is precisely to interpolate between the two operadic compositions using higher coherent homotopies. The last map is a canonical projection map, see Paragraph 4. We prove in Section 4 that the composition induces an isomorphism in homology that also respect the operadic composition on both sides.
Geometric understanding of string vertices.
Using Theorem B, we can finally unlock the mystery of string vertices and the quantum master equation (2). In Section 5, we obtain a simple formula expressing the orbifold fundamental class of the symmetric Deligne-Mumford space in terms “disk bundles” over string vertices :
| (3) |
where the summation is over isomorphism classes of stable graphs of type , is a degree element associated to an edge of , and the superscript denotes the symmetrization map. Note that the closedness of the right hand side follows from the quantum master equation (2). Note that the above equation makes sense under the isomorphism in Theorem B: the fundamental cycle lies in the -invariants of , while the expression on the right hand side of Equation (3) lies inside the -invariants of .
Using the above identity of the fundamental classes, Theorem follows immediately after unwinding the definitions of CEI.
Geometrically, Equation (3) may be viewed as a decomposition of the fundamental class of the symmetric Deligne-Mumford space according to its boundary strata labeled by stable graphs. String vertices are simply a coherent choice of the complement of a tubular neighborhood of the boundary divisor in the ambient space for all such that . The coherence equation is precisely the quantum master equation in the Sen-Zwiebach DGLA. Once such a coherent choice is made, Equation (3) simply corresponds to the decomposition of the fundamental class in terms disk bundles over products of string vertices.
We illustrate this point of view in the following figures. The left figure corresponds to the cases when or . For example, the symmetric quotient is topologically a sphere. In it there is a point (denoted by ) representing a nodal sphere with marked points. Thus the fundamental class is decomposed into a (closed) disk bundle over the point and which is the closure of . The same decomposition holds in the case of with the point given by the once punctured nodal elliptic curve. The figure on the right illustrates the situation when two boundary divisors cross, producing a codimension strata in the moduli space. For example, the symmetric quotient is decomposed into , disk bundles and double disk bundles.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b886645b-0cf9-4c62-9987-6624992a72ec/M04.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b886645b-0cf9-4c62-9987-6624992a72ec/codim2.png)
This geometric point of view was already implicit in the original work of Sen-Zwiebach [18] and more recently the work of Costello-Zwiebach [6]. From this perspective, it is appropriate to think of the CEI at as a way of decomposing an integral over into integrals over poly-disk bundles on each degenerate strata whose combinatorial types are given by stable graphs in .
Organization of the paper.
In Section 2 we define Feynman compactifications of -framed modular operads. In Section 3 we introduce a simplicial resolution of the Feynman compactification , which is a minor modification of the one constructed by Mondello [15]. In Section 4, we prove Theorem B. Section 5 is devoted to prove the main identity (3). In Section 6 we obtain Theorem A, as well as clarify some technicalities in generalizing it to Fukaya categories with semi-simple cohomology.
Notations and Conventions.
Throughout the paper, we work with chain complexes and homological degree convention. Unless otherwise stated, we take the ground field to be , the field of rationals. For a topological space , the notation stands for its normalized singular chain complex, with coefficients in .
When working with graphs, we follow notations in [10, Section2]. By a labeled graph, we shall mean a graph that is endowed with a genus labeling on its set of vertices . The genus of a labeled graph is defined by
If is a labeled graph, denote by
-
•
: the set of vertices of .
-
•
: the set of edges of .
-
•
: the set of half-edges at a vertex .
-
•
: the set of all half-edges of .
-
•
: the set of leaves of .
Denote by the set of isomorphism classes of labeled graphs of genus and with leaves. For a vertex of a graph, its valency is denoted by . A graph is called stable if holds at every vertex . The set of isomorphism classes of stable graphs is denoted by . If is a morphism of graphs, denote by the set of edges that are contracted by , and denote by the complement.
Acknowledgments.
The author is grateful for Lino Amorim, Andrei Caldararu, and Kevin Costello for discussions around the topic.
2 Feynman compactifications of -framed modular operads
In this section, we introduce the notion of Feynman compactifications of -framed modular operads. Intuitively speaking, the construction yields an ordinary modular operad such that the circle actions on the composition maps of the original operad have been universally trivialized.
-framed modular operads.
Recall from [10] the notion of a stable -module given by a collection of chain complexes with an action of the symmetric group on . For a finite set of cardinality , we set
with the direct sum taken over all bijections from to . For each stable graph , denote by
A modular operad structure on the stable -module is given by an extension of to a functor on the category of stable graphs, that is, for each we have a morphism such that whenever and are two composable morphisms of stable graphs.
We shall work with a -framed version of modular operads. First, we introduce some terminologies. Let be a chain complex. By an -action on , we mean a homological degree one operator such that and . Let , by an -action, we mean mutually commuting circle actions , i.e. for all . Its homotopy quotient is defined as the chain complex
with the ’s of homological degree . The -module structure is given by the quotient of by the subspace . Observe that the inclusion map
is a map of chain complexes, which we refer to as the canonical quotient map.
With this preparation, an -framed modular operad is given by a modular operad together with the following additional data:
-
•
There is an action of on each , extending the -action.
-
•
The morphism associated with a morphism with is -equivariant. Here we implicitly identified as a subset of using the morphism (see [10, Section 2.13]).
-
•
The morphism is invariant under simultaneous rotation at the two ends of an edge. More precisley, we require that
Here is of the form and and are the two circle actions at the two half edges of a contracted edge .
A first example.
For each , let be the oriented real blowup along the boundary divisors in the Deligne-Mumford space . An element in is given by a stable curve together with a decoration at each nodal point by a unit tangent vector :
where is the normalization of and is the preimage of a nodal point labeled by . We also consider a framed version of it denoted by . An element of this moduli space consists of a decorated stable Riemann surface , together with a framing around each marked point. That is, for each , a local coordinate system such that the biholomorphic maps ’s extend to an open neighborhood of . We also require that the pair-wise intersection of the closures of the framed disks be empty, i.e. . The circle acts on a local coordinate system by rotation: . This action is clearly a free action. It is also well-known that the set of local coordinate systems around any point is homotopy equivalent to . Thus, the forgetful map
is a homotopy -bundle.
We define a -equivariant modular operad by setting
Let be a morphism of stable graphs, the composition morphism is defined as follows. The map on the underlying stable curve is the product of inclusions
We keep the same framings at marked points, and the same decorations of tangent vectors at nodes corresponding to the edges of . For the decoration at a node corresponding to a contracted edge , we decorate by the unit tangent direction of the vector
where and are the two framings at the two legs of the edge . This defines a map
which, by taking normalized singular chain functor, induces the desired map .
A second example.
We define another example of -equivariant modular operad by setting
given by the moduli space of smooth curves of type together with a framing at each marked point. The composition morphism
associated to a contraction map is defined as follows. Again we keep the same framing at the leaves of and . For a contracted edge , we sew the Riemann surfaces at the two ends of using the two framings and . More precisely, we cut out and from the two surfaces, then identify a neighborhood of the boundary circle by the equation . This defines a map
which induces the desired map .
It is a general fact of the oriented real blowup construction that the natural inclusion map is a homotopy equivalence, which induces a homotopy equivalence of chain complexes for each :
However, observe that the operad structure of does not restrict to that of since when composing, the former is by forming a nodal curve while the latter is by sewing using framings.
Twisted sewing operations.
Let be an -equivariant modular operad. We may form the homotopy quotients: for each pair we set
This collection of stable -module does not form a modular operad. This is evident in the previous two examples: for instance in the case of , the sewing operation of two Riemann surfaces is ambiguously defined if we first quotient out the circle actions on the framings.
Nevertheless, there does exist a degree one composition by allowing a full -twist of the composition map of . There are two types of compositions depending on whether we compose along a loop edge or a non-loop edge. We begin with the loop edge case as illustrated in Figure .

Indeed, we write down by setting
| (4) |
The case of a non-loop edge contraction is similar, see Figure . Explicitly we define a map of chain complexes for each by
| (5) | ||||
where is the composition map of is the graph map that contracts the edge connecting and .

Generalizing the above, for each stable graph , we put
to be the homotopy quotient version of , i.e. on each vertex of we put the homotopy quotient by the circle action. Furthermore, associated to an edge we also have the corresponding twisted composition map defined using ’s constructed above:
Note that is of homological degree one.
Feynman compactifications of -equivariant modular operads.
We now proceed to define the Feynman compactification of an -framed modular operad . The underlying stable -module of is given by
where is the ”cocycle” (see [10, Section 4]) defined by
The notation stands for the one-dimensional vector space generated by at homological degree . Hence is also one-dimensional, at homological degree , generated by the tensor product
The differential on is the given by with the differential of , while the extra map is given by
| (6) |
Observe that since has degree one while each has degree two, the degree of is as required. The idea behind this definition of is that each should be thought of as a universal trivialization of the twisted sewing operation along .
Composition maps of .
Associated with a morphism of stable graphs, we shall define a composition map so that the stable -module forms a modular operad. By the structure of modular operads [10, Section 3], it suffices to construct for an edge contraction map as in Figure and Figure . In the case of Figure , by definition of , we have
For a stable graph , we denote by the stable graph obtained from by forming a loop using the two legs labeled by and . Observe that since both graph have isomorphic set of edges. Then we set the composition map as
| (7) | ||||
The composition map is a chain map.
Proof 2.1.
For simplicity, we shall suppress the ’s to only and as other circle parameters are not relevant in the calculation. We need to verify that . When the input is of the form , one has
The modular operad structure is a chain map, which shows that the two computations indeed give the same answer. When the input is of the form we compute the two compositions as
The case of is similar. In the general case when the input is with , the computation is easier and is left as an exercise.
The second type composition corresponding to Figure is defined similarly:
The verification that this defines a chain map is analogous to the previous lemma.
Trivializations of circle actions.
By a cyclic -algebra structure on a chain complex we mean the following data:
-
•
A circle action on the chain complex .
-
•
An -equivariant action map
-
•
A graded symmetric inner product such that is graded anti-self-adjoint and is graded self-adjoint.
The compatibility condition between and the inner product should be self-evident: for an elementary contraction , it corresponds to contracting two copies of at the half-edges labeled by and using the inner product.
A trivialization of the circle action (see [7, 12]) is given by a chain map
of the form with of homological degree .
Let be a cyclic -algebra and let be a trivialization of the circle action. Then this data induces a natural cyclic -algebra structure on .
Proof 2.2.
Taking -quotients of the action map
yields an action of on , i.e. an action map still denoted by
To extend this action to it suffices to define the action of associated with an edge of a stable graph . Observe that the inverse operator of is another operator of the form
Here the operator ’s are defined by the following identity
Solving the above recursively yields formulas of in terms ’s. For example, we have
Using the ’s and ’s, we define a contraction map
with component maps given by formula
Here we set . Then we define the action of on by the symmetrization of , i.e. acts by
The verification that is compatible with the boundary map in Equation (6) is a calculation, and is done in [3, Proposition 4.5].
3 Mondello’s resolution
Let and be the two -framed modular operads as defined in Paragraphs 2 and 2. In this section, we introduce a simplicial resolution denoted by of the Feynman compactification . We call it Mondello’s resolution since its construction is a minor modification of Mondello’s construction in [15]. Similarly, we also have the resolution of the Feynman compactification . The main result of the section is the existence of the following quasi-isomorphisms:
We shall mainly deal with the hatted version, the un-hatted version is completely parallel.
Mondello’s construction [15].
Let be a smooth algebraic variety with a simple 222Simplicity is not necessary for this construction, as was remarked by Mondello [15, Footnote 1]. normal crossing divisor
i.e. we assume that each is a smooth irreducible divisor, and pair-wise intersect transversally. For a subset , denote by . Denote by the manifold with corners obtained by performing a real oriented blow-up of along a divisor . Note that the natural inclusion is a homotopy equivalence. For a chain of inclusions of subsets of , define . Observe that the space
| (8) |
is given by the -bundle where is the circle bundle associated to the normal bundle of in , the map is the natural projection, and . In loc. cit. the author constructs a simplicial topological space with
such that its geometric realization is homotopy equivalent to .
Application to .
We apply the previous construction to the case with equals the Deligne-Mumford compactification , and the divisor corresponding to nodal curves. Instead of working with an index set labeling the irreducible components of , it is most natural in this setup to work with stable graphs in . That is, for each , let us write for the image of the map
| (9) |
Denote by the locus of such that at each vertex of we have a smooth curve in . The oriented real blowup of along boundary divisors is denoted by . A general fact of oriented real blowup is that the natural inclusion map is a homotopy equivalence. Let be a graph contraction map. It induces a corresponding inclusion map
In dimension , we describe the set of non-degenerate -simplices of Mondello’s construction applied to in terms of stable graphs. For each -step graph contraction, we set
Explicitly, an element of consists of
-
•
A stable curve with marked points . By definition, its dual graph admits a contraction map .
-
•
For each edge that got contracted by the composition map , the corresponding node is decorated by a unit tangent vector in the tensor product where is the normalization of the nodal curve , and is the pre-image of the nodal point .
Then the set of non-degenerate -simplices is given by
where the colimit is taken over the category of isomorphisms of -step stable graph contractions.
Next, we describe the boundary maps of . There are three types of boundary maps in :
-
•
The first type boundary map is a map of the form
(10) given by the natural projection map which forgets the decorations at nodes that got contracted in the map .
-
•
The second type boundary map is given by
(11) simply the inclusion map induced by the inclusion .
-
•
The third type boundary map is defined in the case and for each , and is given by the identity map
(12)
Circle/Disk bundles.
For each stable graph contraction , we shall work with a modified but homotopy equivalent version of . Let be a graph contraction. Denote by the normal bundle associated with the embedding . Its rank is equal to , the number of contracted edges in . Moreover, we denote by the associated -bundle, and the associated -bundle. For with the unique stable graph in with one vertex, we write and for the corresponding circle/disk bundles. As observed by Mondello [15] (see Equation 8), we have
where is the canonical projection map by definition of the oriented real blowup construction.
We shall make two modifications to the above space, both of which are homotopy equivalent to it by construction:
-
•
The first modification is to add a disk bundle in the normal direction of inside . More precisely, we use
Since disks are contractible, it is clear that this is homotopy equivalent to .
-
•
The second modification is to put framings on the marked points, then realizing the above space as its -quotient. Since the circle action on framings is a free action, the resulting space is also homotopy equivalent to .
More formally, for each , we define
where an element of consists of a stable curve with marked points together with framings . This stable curve’s dual graph admits a contraction map . For each edge that got contracted by the composition map , we decorate the corresponding node by a unit tangent vector in the tensor product . For each of the remaining node of , we decorate it by a tangent vector in the unit disk of .
Analogous to , there are three types of simplicial boundary maps on so that it is compatible with the boundary map of defined in Equations (10) (11) (12). We shall abuse the notations for the three types of boundary maps.
-
•
For the first type boundary map, we set
to be the natural map induced by the inclusion map at the nodes that are contracted by the morphism .
-
•
The boundary map of the second type
is again induced by the inclusion while keeping decorations at nodes and framings at marked points.
-
•
The third type boundary map is again the identity map:
Note that by construction we have a homotopy equivalence of simplicial spaces between and . By Mondello’s theorem, we obtain a quasi-isomophism of chain complexes
Simplicial resolution of the Feynman compactification.
To link the simplicial complex with the Feynman compactification we observe that there is a discrepancy at nodes. Indeed, let us consider a node corresponding to a contracted edge in the dual graph of a surface . In the case of , a node is decorated by elements in the tensor product , while for the two circle actions on and has already been quotiented out. The two constructions are related by the following {Lemma} Let and be two complexes with a circle action. Then there is a canonical homotopy equivalence
where on the left hand side we take the homotopy quotient of the off-diagonal action, i.e. with circle operator , and on the right hand side, the differential is given by .
Proof 3.1.
This is standard Koszul duality between and its Koszul dual coalgebra . Thus for any -module , there is a chain equivalence
Apply this formula to our setting to obtain
where in the second equivalence we split the product -action using and .
We proceed to define a simplicial resolution of . Let be a -step contraction. Define
That is,
-
•
For each vertex we decorate it by homotopy -quotient of .
-
•
For each contracted edge , we decorate by the cellular chain complex of circle:
with of homological degree .
-
•
For each of the remaining edges in , we decorate by the cellular chain complex of the disk
with of homological degree . The differential acts on the -cell by .
The differential of is not simply the tensor product differential. The extra differential comes from Lemma 3. Indeed, for every edge (no matter if it’s contracted by or not), the extra differential is given by
with and the two circle parameters acting on chains and on the two ends of . For each , we define the set of -simplices by setting
to obtain a simplicial chain complex . Again, just like and , it has three types of simplicial boundary maps:
-
•
The first type boundary map
is defined via the inclusion at the edges that are contracted by .
-
•
The second type boundary map
is defined by applying Lemma 3 at the edges that are contracted by the map .
-
•
The third simplicial boundary map
is again the identity map.
In conclusion, for each pair such that , we have defined a simplicial chain complex . Denote its total complex by
Mondello [15]’s simplicial resolution construction implies the following
There is a homotopy equivalence of chain complexes
Homotopy colimit of .
When , we have
On the other hand the Feynman compactification is given by
The latter space is clearly a subspace of the former. However, observe that neither the canonical inclusion map nor the canonical projection map is a map of complexes.
In the following proposition, we prove that the homotopy colimit of the simplicial chain complex is given by the Feynman compactification .
There exists a quasi-isomorphism of chain complexes
depicted as
Proof 3.2.
Let us fix a stable graph and consider the subspace of the total complex given by
which is endowed with the differential . The natural inclusion map
which decorates each edge by the disk cell splits the projection map
induced by the projection map at every edges of . We first construct a homotopy operator
such that it satisfies the deformation retract identity . To construct such an , consider an element
Let be edges in such that in its decoration is in . Then we set
where is obtained from by contracting the edges . Let us check the identity . Indeed, if the set is not empty, we have and . While in the other direction, we have
This shows that if . Since if , we have , thus the previous identity is equivalent to the homotopy retract identity. In the case , we have , and that
This also implies the desired identity .
Finally, we evoke the differential and use homological perturbation formula to compute the induced differential on the Feynman compactification which matches the definition given in Paragraph 2. Indeed, the perturbed differential turns out to have two terms:
The first term corresponds to the boundary map on vertices of stable graphs in the Feynman compactification . The extra differential of (defined in Equation 6) applied to edges of stable graphs is precisely the second term, i.e.
This is a calculation which we illustrate in the case when the underlying stable graph has only one edge joining two vertices decorated by and :
This agrees with the formula of in Equation 6, which finishes the proof.
W
e write down the perturbed inclusion and projection maps which will be used later in the paper.
| (13) | ||||
Completely parallel to the construction of , one may also define a simplicial resolution for the Feynman compactification . We also have the quasi-isomorphisms:
4 Comparison with the Deligne-Mumford operad
In this section, we prove the following theorem.
There is an isomorphism of modular operads
where is the Deligne-Mumford modular operad [10, Section 6.2].
The proof of this theorem occupies the rest of the section. We briefly outline the main idea here. By results of the previous section, we have isomorphisms:
Thus in order to relate the first line with the second line, we shall construct a quasi-isomorphism
Combining with the previous isomorphisms yields the isomorphism in Theorem 4. One then checks the compatibility of the modular operad structures.
Comparison between and .
As was pointed in Paragraph 2, the inclusion map
does not respect the operadic composition map. This implies that the induced inclusion map between and does not respect the simplicial structure. More precisely, the simplicial boundary map is not compatible with the inclusion map. However, the failure of this compatibility is actually homotopically trivial. Consider the simplest situation with with a stable graph with two vertices , and an unique edge . Consider the following (non-commutative) diagram:
The above diagram is commutative up to homotopy. Indeed, let and be the two framings to be sewed. Fix , we may scale the two framings by setting
The scaled framings are given by and . Using the scaled framings we obtain a -dependent sewing map
It is clear that .
Let the notations be as above. Then we have
Proof 4.1.
It is clear that on the underlying stable curve, as the limiting curve becomes a nodal curve with the node given by the image of and . The limiting decoration at this node is then given by the unit tangent direction vector of
Thus the unit tangent direction is independent of , and thus have a limiting vector given by the unit tangent direction vector of , which is precisely the definition of .
Using the geometric homotopy , we obtain a homotopy operator of homological degree one:
The lemma above implies that .
In general, for each -step contraction, consider the following diagram:
We may apply the previous construction to all the edges in with the same parameter to yield a homotopy operator still denoted by
of homological degree one such that . Using these homotopy operators and its higher extensions (introduced in the proof below), we prove the following
There exists a quasi-isomorphism of chain complexes
Proof 4.2.
We inductively construct a morphism of chain complexes of the form
with . Recall that the total differential on both total complexes is of the form with the internal differential, and the simplicial boundary maps. From the definition, it is easy to verify that . But the boundary map is not compatible with . Its commutator is precisely bounded by the homotopy defined in the previous paragraph.
In general, for each , we shall define a map of homological degree of the form
such that
| (14) | ||||
Indeed, associated with a -step stable graph contraction we have a family of sewing maps depending on -variables
where we use the -variable to scale the sewing operation at an edge that got contracted by . See Figure (3) for illustrations of this homotopy maps.
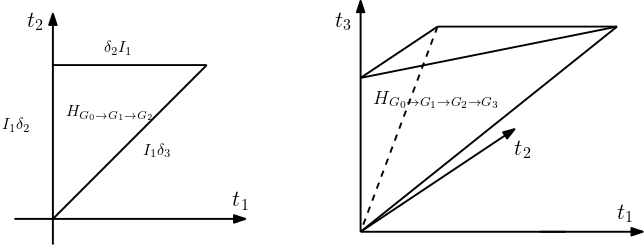
We use this -parameter family to induce a higher homotopy operator:
To see the above identities (14) hold, observe that the facets defined by and corresponds to , the intermediate facets defined by are . Here we used that since the image of lies in the index while vanishes on such type of component. Putting the maps together, we obtain a map of chain complexes
To argue that is a quasi-isomorphism, we consider the increasing filtration on both sides defined by that the -th filtration consists of elements of simplicial degree less than or equal to . Observe that preserves the filtration. Thus it induces a morphism of the associated spectral sequences on the two total complexes. But we already have an isomorphism in the -page since the map is induced by the natural inclusion maps which are homotopy equivalences.
Operadic compositions.
To summarize the previous discussions, we have the following diagram
where all the arrows are quasi-isomorphisms. To prove analyze the operadic compositions in Theorem 4, we shall define a canonical projection map
This map is only non-zero at simplicial degree zero, in which case we need to define a map
for each stable graph . Let with its underlying stable graph . Explicitly, such an element is of the form
At a vertex , its vertex decoration is of the form
with the constant term in . Let us denote by
the map obtained by first projection onto the constant term, followed by the forgetful map which forgets both the framings and the nodal decorations. For each edge , denote by
the projection map onto . Then the map is defined by
where is the sewing map in Equation (9). Using the map , we consider the composition
The induced map on homology
is a morphism of modular operads.
Proof 4.3.
We shall only deal with the first type composition corresponding to a loop contraction . The case of non-loop contraction is analogous. In the loop case, we want to prove that the following diagram is commutative up to homotopy:
Let be an element with its underlying stable graph . Let us explicitly write down the composition
using Equations of , and Equation (13). We have
Since vanishes on , we have
where the summation is over orderings of the edge set , and . Observe that in the definition of , we required the sewing parameters be ordered as . Summing over ordering of the edges gets rid of this ordering condition. Thus, the above expression can be rewritten as
| (15) |
with
the sewing map depending on parameters as in the proof of Theorem 4. Intuitively speaking, for each , we act on the chain by the circle action and also sewing with the radius parameter . The forgetful map precisely collapses the circle at , which forms a disk over each edge .
To this end, we shall finish the proof using the explicit formula of above. Indeed, let be such that at the half-edges labeled by and the -powers are and . If either or is strictly positive, the resulting composition is trivial in homology. In the interesting case when , denote by the graph obtained from by sewing the two leaves indexed by and . Then we see that the two compositions and are related by the homotopy
This finishes the proof of proposition, which combined with Theorem 4 yields Theorem 4.
5 String vertices and fundamental classes
In this section, we use the Feynman compactification construction to provide a geometric extension of the algebraic trivialization of circle actions in [3]. Roughly speaking, we construct a compactified version denoted by of Sen-Zwiebach’s DGLA (reviewed in the beginning of the section) so that we have an inclusion of DGLA’s
Then we construct an quasi-isomorphism where the DGLA has the same underlying space as , but its BV differential and the Lie bracket are both zero. We prove the identity (3) stated in the introduction that the push-forward of the string vertex consists of the fundamental class of .
DGLA’s.
Recall the construction of Sen-Zwiebach’s DGLA:
with two formal variables and both of homological degree . By construction, its differential is with defined using the twisted self-sewing map (4), and its Lie bracket is defined using the twisted sewing map (5). We refer to [2, Section 3] for more details of this construction.
Similar to the definition of , one may define a “compactified” version of by putting
with the differential (with as in Equation (6)) and the Lie bracket defined in the same way as . Observe that there is an inclusion map
of DGLA’s onto the -component of each .
We also define a trivialized version of , denoted by which has the same underlying graded vector space as , but is endowed with differential and zero Lie bracket.
There exists an quasi-isomorphism of DGLA’s:
This theorem is the geometric “lift” of the algebraic version proved in [3, Theorem 4.2]. The proof is in complete parallel as well. In the following, we describe the construction of . Roughly speaking, the map is simply inserting elements of on vertices of stable graphs, as illustrated in Figure (4).
Construction of .
We proceed to construct an -morphism . First, we introduce more notations about graphs. Denote by (respectively ) the set of labeled (respectively stable) graphs with vertices. For a labeled graph , a marking of is a bijection
An isomorphism between two marked and labeled graphs is an isomorphism of the underlying labeled graphs that also preserves the marking map. Denote by (respectively ) the set of isomorphism classes of marked (respectively stable) graphs.
For each integer , we shall define a degree zero linear map
The shift by one of is given by
For each marked labeled graph with a marking on the vertices of , denote by and . Define a -linear map

For each , let
be an element of , with its underlying stable graph given by . In order to insert the graphs ’s into , we need to make identification of leaves of with . There is no canonical choice for such an identification, thus we take the symmetrization of the ’s. We set
where the notation is the same element as , but labeled by an isomorphism . Fixing the identifications on vertices of , denote by
the stable graph obtained by inserting at vertex through the isomorphism . With this preparation, we define
This makes sense because
-
•
There is a natural isomorphism
-
•
We have .
-
•
This map descends to coinvariants by graph automorphisms. Indeed, given an automorphism , it induces an isomorphism
where is the identification given by first applying then followed by the automorphism acting on leaves of .
-
•
This map is of homological degree zero after the shift by . To see this, observe that at vertices the degrees are simply that in ’s, but since the term has degree . Putting this together with the shift by and the powers of , we have
Finally, extending by -linearity, we define for each a linear (in both and variables) by setting
| (16) |
Proof of Equation (3).
In this subsection, we prove the main identity (3) that the push-forward of the String vertex via the composition map
gives exactly the fundamental classes .
Under the isomorphism in Theorem 4, we have the following formula expressing the fundamental class of in terms of String vertices:
Proof 5.1.
Define a filtration on the chain complex by the setting to be chains that are supported on the locus such that the underlying stable Riemann surfaces have at least nodes. Similarly, we also have the nodal filtration on the homotopy quotient , and further -quotient . Following Costello [5, Theorem 9.0.7], one may form a DGLA on the homology of the associated graded
Its differential and Lie bracket are denoted by and respectively. The boundary map is the boundary map induced by the sequence
The two operations and are both defined using the twisted sewing operations. Observe that when we have
The last isomorphism is induced by the canonical map that forgets the decoration at all nodes. The orbifold fundamental class , under this isomorphism, corresponds to the fundamental class . It was shown in Loc. Cit. that the element
of the DGLA satisfies the Maurer-Cartan equation and is uniquely determined by the equation after fixing the initial condition at .
To this end, let us consider the following commutative diagram
where the downward arrow is the projection map onto the component, the upward arrow is the map that forgets the nodal decoration, and the bottom horizontal arrow is the canonical quotient map followed by forgetting framings at punctures. Recall from Paragraph 4 the isomorphism in Theorem 4 is induced by the chain map . By the previous discussion, it suffices to prove that
satisfies the Maurer-Cartan equation in . Using the identity (15) we have
To finish the proof, we show that the Maurer-Cartan equation satisfied by ’s implies the desired Maurer-Cartan equation of ’s. Indeed, the leading coefficients of string vertices satisfies the equation:
| (17) |
The boundary of the expression consists of three types of terms:
-
(i)
For an edge , the corresponding parameter (with a minus sign).
-
(ii)
For an edge , the corresponding parameter (with a plus sign).
-
(iii)
At a vertex , there is .
We observe that using Equation (17), the and type terms cancel each other. Moreover, the term is precisely the twisted sewing operations used in defining the DGLA structure of . Hence depending on whether is a separating or a non-separating edge, the term can be rewritten as
This finishes the proof.
6 CEI of the ground field
In this section, we use Equation (3) to prove Theorem A. Throughout the section, let be a cyclic algebra of dimension over a field (of characteristic zero) that is proper, smooth and satisfies the Hodge-to-de-Rham degeneration.
A sketch of the definition of CEI.
CEI defined in [3]) takes a roundabout route due to the fact that the -dimensional Topological Conformal Field Theory (TCFT) structure on the reduced Hochschild chain complex has to have strictly positive number of inputs. This separation of inputs and outputs is the source of main difficulties in making Costello’s original definition [5] of categorical enumerative invariants explicit. Indeed, in [2] and [3], a Koszul type resolution is constructed for the Sen-Zwiebach Lie algebra (see Paragraph 5), giving a quasi-isomorphism of DGLA’s:
where the right hand side DGLA consists of Riemann surfaces with strictly positive number of inputs. The precise definition of is not so much relevant to this paper: we shall see that in the particular case when the algebra is the ground field there is no need to use the Koszul resolution.
Similar to the construction of the Sen-Zwiebach Lie algebra , associated with the Hochschild chain complex and the Connes operator , we may form a DGLA
In [2], we also introduced its Koszul resolution , and a canonical quasi-isomorphism of DGLA’s:
Again we omit the definition of and refer the details to [2].
In an ideal situation, the TCFT structure on would give us a commutative diagram
with and the TCFT structure maps. In reality, the left vertical map is not there, which prevents us to obtain the push-forward of the string vertex in order to define categorical enumerative invariants. In [3], we took the roundabout route:
-
(1.)
We find string vertices in .
-
(2.)
Then push-forward to obtain a Maurer-Cartan element
of the DGLA .
-
(3.)
The bottom map is a quasi-isomorphism of DGLA’s when is smooth, proper, and satisfies the Hodge-to-de-Rham degeneration property. Hence, by homotopy invariance of the Maurer-Cartan moduli space, we obtain the desired Maurer-Cartan element with its defining property that is gauge-equivalent to .
Categorical enumerative invariants of the ground field.
When is the ground field , the above roundabout route is not necessary: we can actually define a map
to obtain the commutative diagram in the previous paragraph. Thus when computing the CEI, we may simply take the Maurer-Cartan element in . Explicitly, the map is just the augmentation map: at degree , the map sends any point class in to , and is zero otherwise.
For the splitting of the Hodge filtration, observe that the Connes operator acts on by zero on . Thus, we may choose the splitting to be
Since is of degree , such a splitting is characterized by the homogeneity condition. By Proposition 2, a splitting induces an extension of the TCFT to give a map
In summary, we obtain a commutative diagram of morphisms between DGLA’s:
| (18) |
The construction of is done in Section 5 while is done in [3].
The CEI of agrees with the Gromov-Witten invariants of a point, i.e. we have
Proof 6.1.
The string vertex is of the form
with . The bracket is to indicate the quotient map by the action. In characteristic zero, we may assume that the chains are invariant under the action of . Then we have
In the above formula, the right hand side takes value in , and the variable corresponds the basis . The combinatorial number is the size of the set of -permutations that fixes the sequence . The extension formula in Proposition 2 of the splitting yields the zero map for the action of on the edges of a stable graph. This implies that the bottom algebra map is the identity map, which shows that
By definition of CEI, we have
On the other hand, by Theorem 5 we have
This implies that
This proves the theorem.
References
- [1] Amorim, L.; Tu, J., Categorical primitive forms of Calabi-Yau -categories with semi-simple cohomology. arXiv:1909.05319
- [2] Caldararu, A.; Costello, K.; Tu, J., Categorical Enumerative Invariants, I: String vertices, arXiv:2009.06673.
- [3] Caldararu, A.; Tu, J., Categorical Enumerative Invariants, II: Givental formula, arXiv:2009.06659.
- [4] Costello, K., Topological conformal field theories and Calabi-Yau categories, Advances in Mathematics, Volume 210, Issue 1, 20 March 2007, 165-214.
- [5] Costello, K., The partition function of a topological field theory, J. Topol. 2 (2009), no. 4, 779-822.
- [6] Costello, K.; Zwiebach B. Hyperbolic String Vertices, preprint, arXiv:1909.0003.
- [7] Dotsenko, V.; Shadrin, S.; Vallette, B., Givental group action on topological field theories and homotopy Batalin-Vilkovisky algebras. Adv. Math. 236 (2013), 224-256.
- [8] Dotsenko, V.; Shadrin, S.; Vallette, B., Givental action and trivialisation of circle action. J. Ec. polytech. Math. 2 (2015), 213-246.
- [9] Drummond-Cole, G. Homotopically trivializing the circle in the framed little disks. J. Topol. 7 (2014), no. 3, 641-676.
- [10] Getzler, E.; Kapranov, M., Modular operads. Volume 110, Issue 1 January 1998 , pp. 65-125.
- [11] Givental, A., Gromov-Witten invariants and quantization of quadratic Hamiltonians, Mosc. Math. J. 1 (2001), 551-568.
- [12] Khoroshkin, A.; Markarian, N.; Shadrin, S., Hypercommutative operad as a homotopy quotient of BV. Comm. Math. Phys. 322 (2013), no. 3, 697-729.
- [13] Kimura, T.; Stasheff, J.; Voronov, A., On operad structures of moduli spaces and string theory, Comm. Math. Phys. 171(1), 1-25 (1995).
- [14] Kontsevich, M., Homological algebra of mirror symmetry, Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Zürich, 1994), 120-139, Birkhäuser, Basel, 1995.
- [15] Mondello, G. A remark on the virtual homotopical dimension of some moduli spaces of stable Riemann surfaces, Journal of the European Mathematical Society, vol.10 (1) 2008, pp.231-241.
- [16] Pandharipande, R.; Pixton, A.; Zvonkine, D., Relations on via -spin structures, J. Amer. Math. Soc. 28 (2015), 279-309.
- [17] Segal, G. The Definition of Conformal Field Theory. Differential Geometrical Methods in Theoretical Physics. NATO ASI Series (Series C: Mathematical and Physical Sciences), vol 250 (1988). Springer, Dordrecht.
- [18] Sen, A., Zwiebach, B., Quantum background independence of closed-string field theory, Nuclear Phys. B 423(2-3), (1994), 580-630
- [19] Teleman, C., The structure of 2D semi-simple field theories, Invent. Math. 188 (2012), 525-588.