Catalysis by Dark States in Vibropolaritonic Chemistry

The past decade has seen much interest in the control of chemical phenomena via the strong coupling of matter to confined electromagnetic modes [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]. An exciting prospect in this direction is vibropolaritonic chemistry, that is, the use of collective vibrational strong coupling (VSC) [19, 20, 21] to modify thermally-activated chemical reactivity without external pumping (e.g., laser excitation) [22]. While collective VSC involves a large number of molecules per photon mode, it has been observed to substantially alter the kinetics of organic substitution [23, 24], cycloaddition [25], hydrolysis [26], enzyme catalysis [27, 28], and crystallization [29], among other electronic ground-state chemical processes.

However, such modified reactivity under VSC is still not well understood. Studies [30, 31, 32, 33] show that the observed kinetics cannot be explained with transition state theory (TST) [34], the most commonly used framework to predict and interpret reaction rates. Breakdowns of TST, including recrossing the activation barrier [35], deviation from thermal equilibrium [32, 36], and quantum/nonadiabatic phenomena [37, 38, 32, 36, 39], have also been considered. The aforementioned works regard all $N$ vibrations coupled to the cavity mode to be identical. Under this assumption, VSC forms two polaritons and $N-1$ optically dark vibrational modes, where the latter remain unchanged from the cavity-free system. It follows that VSC-induced changes to thermally-activated reactivity must arise from the polaritons. In fact, one study from our group highlighted the molecular parameter space where polaritons dominate the kinetics [37] with respect to dark modes; however, this hypothesis has been questioned as entropically unlikely [40].

Disorder, despite its ubiquity in molecular systems, has often been ignored when modeling molecules under strong light-matter coupling. Only recently has it been shown that the strong coupling of disordered chromophores to an optical cavity mode can produce dark states which are delocalized on multiple molecules [41, 42] (hereafter, referred as semilocalized). This semilocalization is predicted to improve or even enable coherent energy transport [41, 43]. Other findings hint at adding sample impurities to help strong coupling modify local molecular properties [44].

In this Letter, we demonstrate that the VSC of a disordered molecular ensemble (Fig. 1) can significantly modify the kinetics of a thermally-activated chemical reaction. The altered reactivity is attributed to the semilocalized dark modes. The semilocalization affects the reaction rate by changing the efficiency with which a reactive mode dissipates energy.

Consider a disordered ensemble of $N$ molecular vibrations, respectively corresponding to $N$ independent molecules, inside an optical cavity (Fig. 1). The system is described by the Hamiltonian $H=\hbar\omega_{c}a_{0}^{\dagger}a_{0}+\hbar\sum_{i=1}^{N}\omega_{i}a_{i}^{\dagger}a_{i}+\hbar\sum_{i=1}^{N}g_{i}(a_{i}^{\dagger}a_{0}+\text{h.c.})$. Vibrational mode $i$ is represented by annihilation operator $a_{i}$ and has frequency $\omega_{i}=\overline{\omega}_{v}+\delta\omega_{i}$, where $\overline{\omega}_{v}$ is the mean vibrational frequency and $\delta\omega_{i}$ is the frequency offset of mode $i$. Reflecting inhomogeneous broadening (static diagonal disorder), $\delta\omega_{i}$ is a normally distributed random variable with mean zero and standard deviation $\sigma_{v}$. The cavity mode is represented by annihilation operator $a_{0}$, has frequency $\omega_{c}$, and couples to vibration $i$ with strength $g_{i}$. For simplicity, we hereafter take $g_{i}=g$ for all $i$.

Using $H$, we investigate the physicochemical properties of a disordered molecular system under VSC. Unless otherwise noted, calculations assume that the cavity is resonant with the average vibration, $\omega_{c}=\overline{\omega}_{v}$, and couples to the vibrations with collective strength $g\sqrt{N}=8\sigma_{v}$ (for all $N$). Numerical values reported below are obtained by averaging over 5000 disorder realizations, i.e., sets $\{\omega_{i}\}_{i=1}^{N}$. In plots versus the $H$ eigenfrequencies, each data point is an average over the $H$ eigenmodes—from all disorder realizations—whose frequency lies in the bin $\left(\Delta\omega(l-\frac{1}{2}),\Delta\omega(l+\frac{1}{2})\right]$ for $\Delta\omega=10^{-1}\sigma_{v}$ and $l\in\mathbb{Z}$.

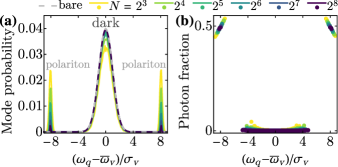
We first study the eigenmodes of $H$. Formally, mode $q=1,\dots,N+1$ is represented by operator $\alpha_{q}=\sum_{i=0}^{N}c_{qi}a_{i}$ and has frequency $\omega_{q}$. Figs. 2(a) and 2(b) show the probability distribution and photon fraction ($|c_{q0}|^{2}$), respectively, of the eigenmodes with respect to eigenfrequency. The majority of modes form a broad distribution in frequency around $\overline{\omega}_{v}$ and are optically dark. A minority of modes are polaritons, which have frequency $\overline{\omega}_{v}\pm 8\sigma_{v}$, photon fraction $\approx 0.5$, and a lineshape minimally affected by inhomogeneous broadening [45]. As $N$ rises, the eigenmodes become increasingly composed of dark modes, whose probability distribution approaches that of the bare vibrational modes [Fig. 2(a), gray dashed line].

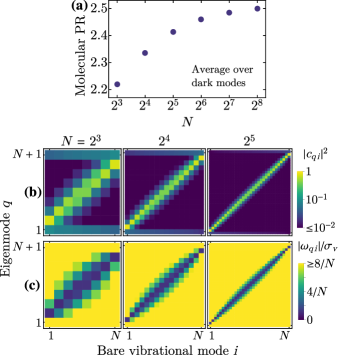
Next, we examine the delocalization of the dark modes. For the purpose of studying chemical reactions, it is useful to compute the molecular participation ratio (PR) [46, 42]. This measure, defined as

$$\text{molecular PR}=1/\sum_{i=1}^{N}\left|\frac{c_{qi}}{\sqrt{\sum_{i=1}^{N}|c_{qi}|^{2}}}\right|^{4}$$

(1)

and analogous to the usual PR [47], estimates the number of molecules over which eigenmode $q$ is delocalized. According to Fig. 3(a), the average dark mode has molecular PR $\sim$2-3, and this semilocalization persists as $N$ increases. These phenomena were first noted independently by Scholes [42] and Schachenmayer and co-workers [41]. For additional insight, we plot the squared overlap [$|c_{qi}|^{2}$, Fig. 3(b)] and frequency difference [$|\omega_{qi}|$, where $\omega_{qi}=\omega_{q}-\omega_{i}$; Fig. 3(c)] between each dark mode and each bare vibrational mode. The typical dark mode has sizable overlap with the bare modes that are nearest to it in frequency. The frequency difference between the dark mode and any of its major constituents is $O(\sigma_{v}/N)$, i.e., negligible for large $N$.

We now explore how VSC influences the kinetics of a thermally-activated chemical reaction. Consider a reactive molecule under collective VSC (Fig. 1). The molecule undergoes nonadiabatic intramolecular electron transfer, and a cavity mode interacts collectively with a reactive vibrational mode and $N-1$ nonreactive vibrational modes. The model here considered is general enough that it should also be applicable to the case of “solvent-assisted VSC” [48, 49, 50, 51].

To model the reaction of one molecule in the ensemble, we employ the Hamiltonian $H_{\text{rxn}}=H+\sum_{X=R,P}|X\rangle\langle X|\{E_{X}+\hbar\omega_{r}[\lambda_{X}(a_{r}+a_{r}^{\dagger})+\lambda_{X}^{2}]\}+V+H_{s}^{(l)}$. Note that vibrational and cavity modes are still described by $H$. In writing $H_{\text{rxn}}$, we have changed the numerical index of the bare vibrational mode ($i=1$) involved in the reaction to the letter $r$ (i.e., $\omega_{1}\rightarrow\omega_{r}$, $a_{1}\rightarrow a_{r}$); hereafter, we refer to this mode as $v_{r}$. The electronic subspace consists of reactant $|R\rangle$ and product $|P\rangle$ states. Electronic state $|X\rangle$ has energy $E_{X}$ and couples to $v_{r}$ with dimensionless strength $\lambda_{X}$. As a result of the vibronic coupling, $v_{r}$ experiences a displacement in its equilibrium position upon electron transfer. The interaction between $|R\rangle$ and $|P\rangle$ is represented by $V=J_{RP}(|P\rangle\langle R|+\text{h.c.})$, where $J_{RP}$ is the interaction strength. Through $H_{s}^{(l)}$ [52], Hamiltonian $H_{\text{rxn}}$ also accounts for low-frequency vibrational modes of the solvent that help mediate electron transfer. There is no direct coupling, though, of the cavity mode to the $|R\rangle\rightleftharpoons|P\rangle$ electronic transitions, which we assume are dipole-forbidden.

Since we are considering a nonadiabatic reaction, we treat $V$ perturbatively and calculate rates of reactive transitions between the zeroth-order electronic-vibrational-cavity eigenstates of $H_{\text{rxn}}$. These states take the form $|X,\chi\rangle=|X\rangle\otimes|\tilde{\chi}_{(X)}\rangle$. Belonging to the subspace of vibrational and cavity modes, $|\tilde{\chi}_{(X)}\rangle=\left(\prod_{q=1}^{N+1}D_{q}^{\dagger}(\lambda_{Xq})\right)|\chi\rangle$ is a displaced Fock state with $m_{q}^{(\chi)}$ excitations in $H$ eigenmode $q$. The undisplaced Fock state $|\chi\rangle$ is an eigenstate of $H$, and $D_{q}(\lambda)=\exp(\lambda\alpha_{q}^{\dagger}-\lambda^{*}\alpha_{q})$ is a displacement operator. Mode $q$ has equilibrium (dimensionless) position $\lambda_{Xq}=\lambda_{X}c_{qr}(\omega_{r}/\omega_{q})$ when the system is in electronic state $|X\rangle$. Returning to the electronic-vibrational-cavity state $|X,\chi\rangle$, we can write its energy as $E_{(X,\chi)}=E_{X}+\sum_{q=1}^{N+1}m_{q}^{(\chi)}\hbar\omega_{q}+\Delta_{X}$, where $\Delta_{X}=\lambda_{X}^{2}\hbar\omega_{r}-\hbar\sum_{q=1}^{N+1}|\lambda_{Xq}|^{2}\omega_{q}$ is the difference in reorganization energy—namely, that due to vibronic coupling between $v_{r}$ and $|X\rangle$—with and without VSC.

Following extensions [37, 38, 36] of Marcus-Levich-Jortner theory [53, 54, 55] to electron transfer under VSC, the rate of the reactive transition from $|R,\chi\rangle$ to $|P,\chi^{\prime}\rangle$ can be expressed as

$\displaystyle k_{(R,\chi)\rightarrow(P,\chi^{\prime})}$

$\displaystyle=\mathcal{A}F_{\chi,\chi^{\prime}}\exp\left(-\beta E_{a}^{\chi,\chi^{\prime}}\right),$

(2)

where $\mathcal{A}=\sqrt{\pi\beta/\lambda_{s}}|J_{RP}|^{2}/\hbar$, $\lambda_{s}$ is the reorganization energy associated with low-frequency solvent modes [52], and $\beta$ is the inverse temperature For this transition, the activation energy is $E_{a}^{\chi,\chi^{\prime}}=(E_{(P,\chi^{\prime})}-E_{(R,\chi)}+\lambda_{s})^{2}/(4\lambda_{s})$. Through the Franck-Condon (FC) factor $F_{\chi,\chi^{\prime}}=|\langle\tilde{\chi}_{(R)}|\tilde{\chi}^{\prime}_{(P)}\rangle|^{2}$, the transition rate depends on the overlap between initial and final vibrational-cavity states $|\tilde{\chi}_{(R)}\rangle$ and $|\tilde{\chi}^{\prime}_{(P)}\rangle$, respectively. It can be shown that the rate $k_{(P,\chi^{\prime})\rightarrow(R,\chi)}$ corresponding to the backward transition, $|P,\chi^{\prime}\rangle\rightarrow|R,\chi\rangle$, is related to Eq. (2) by detailed balance [56].

We specifically study a reaction where, in the absence of light-matter coupling, reactive transitions occur on the same timescale as internal thermalization (i.e., thermalization of states having the same electronic component). In such cases, internal thermal equilibrium is not maintained throughout the reaction, and the reaction rate (i.e., net rate of reactant depletion) may not be approximated by a thermal average of reactant-to-product transition rates. Instead, the reaction rate can also depend on, e.g., backward reactive transitions (from product to reactant) or vibrational relaxation.

With this in mind, we numerically simulate the bare ($g=0$) and VSC reactions using a kinetic model [52, 36], which includes forward and backward reactive transitions [Eq. (2)], vibrational and cavity decay, and energy exchange among dark and polariton states [57, 58, 59]. The third set of processes results from vibrational dephasing interactions (i.e., homogeneous broadening) of the molecular system [57, 52]. The reaction parameters [52]—in particular $\overline{\omega}_{v}=2000$ cm^-1, $\sigma_{v}=10$ cm^-1, $N\leq 32$, $g\sqrt{N}=8\sigma_{v}$ (for all $N$), $E_{P}-E_{R}=-0.6\overline{\omega}_{v}$, and the chosen temperature values—are such that the population dynamics proceeds almost completely through states $|X,\chi\rangle$ with zero or one excitation in the vibrational-cavity modes. To reduce computational cost, the kinetic model includes only these states, which are denoted by $\chi=0$ and $\chi=1_{q}$, respectively, where $q$ is an eigenmode of the vibrational-cavity subspace. The kinetic master equation [52] is numerically solved with the initial population being a thermal distribution of reactant states ($|R,\chi\rangle$). Then, the apparent reaction rate is obtained by fitting the reactant population as a function of time [52]. Note that, for large enough $N$ (we estimate $N>72$ for the chosen parameters), the energy spacing between dark modes becomes smaller than their decay linewidths; under this condition, our kinetic model is not valid [52]. Interestingly, such invalidation suggests that, within our model, VSC-modified chemistry might not occur in the weak light-matter coupling regime, where the polaritons and dark modes cannot be spectrally resolved.

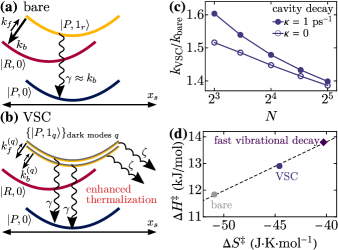
Even though we run the full numerical simulations as explained above, we now introduce approximate models that shed conceptual intuition on the calculated kinetics. First, the bare reaction can be essentially captured by Fig. 4(a), described as follows. Starting from its vibrational ground state, the reactant converts to product mainly by a $0\rightarrow 1$ vibronic transition, which excites the reactive mode and has rate $k_{f}\equiv k_{(R,0)\rightarrow(P,1_{r})}$, where

$\displaystyle k_{f}$

$\displaystyle=\mathcal{A}F_{0,1_{r}}\exp\left(-\beta E_{a}\right),$

(3)

$E_{a}\equiv E_{a}^{0,1_{r}}$. The vibrationally hot product either reverts to the reactant at rate $k_{b}\equiv k_{(P,1_{r})\rightarrow(R,0)}\gg k_{f}$, where

$\displaystyle k_{b}$

$\displaystyle=k_{f}\exp\left[\beta(E_{P}+\hbar\omega_{r}-E_{R})\right],$

(4)

or decays to its vibrational ground state at rate $\gamma\approx k_{b}$. Once the product reaches its vibrational ground state, it effectively stops reacting due to the high reverse activation energy. This kinetic scheme leads to a bare reaction rate [52]

$$k_{\text{bare}}^{(\text{analytical})}=k_{f}\left(\frac{\gamma}{\gamma+k_{b}}\right).$$

(5)

Second, under VSC, the primary reaction pathway of the bare case is split into multiple pathways, each involving the (de)excitation of a dark or polariton eigenmode $q$. For the VSC reaction channels, the forward and backward rates take the form

	$\displaystyle k_{f}^{(q)}$	$\displaystyle=\mathcal{A}F_{0,1_{q}}\exp\left(-\beta E_{a}^{(q)}\right),$		(6)
	$\displaystyle k_{b}^{(q)}$	$\displaystyle=k_{f}^{(q)}\exp\left\{\beta\left[E_{P}+\hbar\omega_{q}+\Delta_{P}-(E_{R}+\Delta_{R})\right]\right\},$		(7)

respectively, where $k_{f}^{(q)}\equiv k_{(R,0)\rightarrow(P,1_{q})}$, $k_{b}^{(q)}\equiv k_{(P,1_{q})\rightarrow(R,0)}$, and $E_{a}^{(q)}\equiv E_{a}^{0,1_{q}}$. Now, consider the following argument, which holds strictly for large $N$. As $N$ increases, the average bare mode becomes localized on dark modes that have essentially the same frequency as it [Figs. 3(b)-3(c)], and its overlap with the polariton modes vanishes [i.e., $c_{qr}\propto\frac{1}{\sqrt{N}}\to 0$ for $q=1,N+1$; see Fig. 3(b)]. These observations suggest that $c_{qr}\not\approx 0$ only for modes $q$ that are dark and have frequency $\omega_{q}\approx\omega_{r}$. It is then straightforward to show that $\left.E_{a}^{(q)}\right|_{c_{qr}\not\approx 0}\approx E_{a}$, $F_{0,1_{q}}\approx|c_{qr}|^{2}F_{0,1_{r}}$, and

$\displaystyle k_{f/b}^{(q)}$

$\displaystyle\approx|c_{qr}|^{2}k_{f/b}.$

(8)

Thus, VSC leads to reaction channels that have lower rates of reactive transitions, due to changes not in activation energies but in FC factors, which are smaller as a result of the semilocalization of dark modes. From Eq. (8), it is evident that the total forward rate is approximately that of the bare reaction ($\sum_{q=1}^{N+1}k_{f}^{(q)}\approx k_{f}$, since $\sum_{q=1}^{N+1}|c_{qr}|^{2}=1$). However, once a forward reactive transition happens—and a dark mode is excited—the product either returns to the reactant at a reduced rate ($k_{b}^{(q)}<k_{b}$) or, due to the almost fully vibrational nature of the dark modes, vibrationally decays to its stable form ($|P,0\rangle$) at essentially the same bare rate ($\gamma$). In other words, VSC suppresses reverse reactive transitions by promoting the cooling of the reactive mode upon product formation. In analogy to Eq. (5), we determine an effective rate for the VSC reaction [52]:

$\displaystyle k_{\text{VSC}}^{(\text{analytical})}$

$\displaystyle=k_{f}\left\langle\frac{\gamma}{\gamma+|c_{qr}|^{2}k_{b}}\right\rangle_{\text{dark modes }q},$

(9)

where $\langle\cdot\rangle_{\text{dark modes }q}$ is a weighted average over all dark modes $q$, each with weight $|c_{qr}|^{2}$. Since $|c_{qr}|^{2}<1$ for all $q$, then $k_{\text{VSC}}^{(\text{analytical)}}>k_{\text{bare}}^{(\text{analytical})}$. We emphasize that the major contributions to the average in Eq. (9) come from dark modes which are closest in frequency to the bare reactive mode (see above). Further enhancement of the VSC reaction, beyond that given by $k_{\text{VSC}}^{(\text{analytical})}$, occurs via dissipative scattering from these dark modes to those with $c_{qr}\approx 0$. Said differently, the product is protected from reversion to reactant when dark modes with relatively more reactive character lose their energy to those with relatively less. Importantly, this scattering requires dark modes to be delocalized. The VSC reaction kinetics, as described above, is summarized in Fig. 4(b).

Fig. 4(c) shows the ratio of VSC reaction rate to bare reaction rate, as determined from numerical kinetic simulations. As we have shown analytically, VSC significantly accelerates the reaction compared to the bare case. For $8\leq N\leq 32$ (and $g\sqrt{N}$ held constant), the rate enhancement is roughly 50%. Notably, the effect of cavity decay on the reaction is minor and diminishes with $N$ [Fig. 4(c)]. This behavior supports that the reaction proceeds mainly through the dark modes. The present scenario is quite generic and contrasts with our previous model where extreme geometric parameters are needed for polaritons to dominate the VSC kinetics [37].

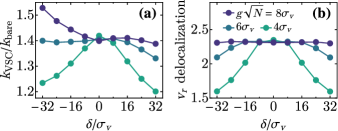
We next look at the dependence on cavity detuning, $\delta=\omega_{c}-\overline{\omega}_{v}$, of the reaction rate and reactive-mode delocalization. The lattermost quantity is defined as $1/\sum_{q=1}^{N+1}|c_{qr}|^{4}$ (the PR of $v_{r}$ when the mode is expressed in the eigenbasis of $H$). We find, for various light-matter coupling strengths, that the reactive-mode delocalization is maximum close to resonance and eventually decreases with detuning [Fig. 5(a)]. The rate enhancement due to VSC mostly follows the same trend [Fig. 5(b)]. Deviation from this trend at large negative detunings and collective light-matter couplings is attributed to polariton contributions to the rate which, as discussed in [37], decrease as N increases [52]. The observed correlation between reactivity under VSC and delocalization of the reactive mode corroborates that the reaction is sped up by dark-mode semilocalization. This mechanism is robust to moderate increases in inhomogeneous broadening [52].

For additional mechanistic insight into VSC catalysis and following the procedures in [23, 48, 25], we plot in Fig. 4(d) the activation enthalpy ($\Delta H^{\ddagger}$) versus activation entropy ($\Delta S^{\ddagger}$) for multiple cases of VSC and bare reactions. The thermodynamic parameters of activation are computed by calculating the apparent reaction rate for additional temperatures and fitting the obtained values to the Eyring-Polanyi equation [52]. This fit indicates that changes in effective parameters $\Delta H^{\ddagger}$ and $\Delta S^{\ddagger}$ can result from dynamical effects such as accelerated vibrational decay, rather than from potential energy changes.

In conclusion, we show that, by forming semilocalized dark modes, the VSC of a disordered molecular ensemble can modify the kinetics of a thermally-activated chemical reaction. For a reactive molecule under collective VSC, we find that the electron transfer rate is significantly increased. The spreading of reactive character across dark modes, as well as the dissipative scattering among these modes, allows the reactive mode to thermalize more efficiently once the product is formed, suppressing dynamical effects, such as reversion to reactant. Although experimental characterization of dark states remains a challenge, the phenomena proposed here might be verified using nonlinear infrared spectroscopy to measure populations [58, 60] and spatially resolved energy transport measurements to detect delocalization [41]. The main mechanisms operating in our model do not seem to be limited to nonadiabatic reactions and might have generalizations in adiabatic reactions; these will be explored in future work. Given that these mechanisms only rely on collective VSC, they should also be operative in the cavity-free polaritonic architectures [61], although experiments along this front have so far not been reported. More broadly, our work highlights that the previously overlooked dark states are the entropically likely channels through which collective light-matter interaction can control chemistry.