Cascades of Global Bifurcations and Chaos
near a Homoclinic Flip Bifurcation: A Case Study

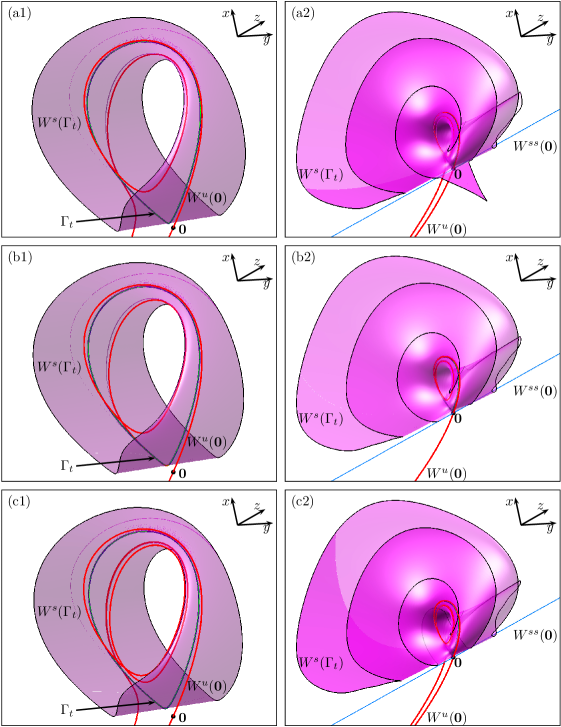
Figure 1 shows phase portraits of system eq. 1 at three different points along the homoclinic bifurcation curve given by $\mu=0$ in the $(\alpha,\mu)$-plane. The individual panels show the homoclinic orbit together with the associated stable and unstable manifolds of 0, where the stable manifold $W^{s}(\mathbf{0})$ is rendered in two shades of blue to illustrate its orientability; here, every trajectory that forms $W^{s}(\mathbf{0})$ has arclength four. The homoclinic orbit $\mathbf{\Gamma_{\rm hom}}$ is the branch of $W^{u}(\mathbf{0})$ (red curves) that lies in $W^{s}(\mathbf{0})$. The homoclinic bifurcations in panels (a) and (b) in fig. 1 are of codimension one, because they fullfil the following genericity conditions [15, 18]:

• (G1)

  (Non-resonance) $|\lambda^{s}|\not=\lambda^{u}$;

• (G2)

  (Principal homoclinic orbit) In positive time the homoclinic trajectory approaches the equilibrium tangent to the eigenvector $e^{s}$ associated with $\lambda^{s}$;

• (G3)

  (Strong inclination) The tangent space ${\rm{T}}W^{s}(\mathbf{0})$ of the stable manifold $W^{s}(\mathbf{0})$, when followed along $\mathbf{\Gamma_{\rm hom}}$ backward in time, converges to the plane spanned by the eigenvectors associated with $\lambda^{ss}$ and $\lambda^{u}$.

These three properties ensure that a portion of $W^{s}(\mathbf{0})$ close to $\mathbf{\Gamma}_{\rm hom}$ folds over and closes along a trajectory of $W^{s}(\mathbf{0})$ tangent to the strongest stable eigenvector of $\mathbf{0}$, that is, along the strong stable manifold $W^{ss}(\mathbf{0})$ (blue curve); hence, locally near $\mathbf{\Gamma_{\rm hom}}$, the stable manifold $W^{s}(\mathbf{0})$ is topologically equivalent to a cylinder, in fig. 1 (a), or a Möbius band, in fig. 1 (b); see [1] for more details. Recall that, for $\mu=0$, system eq. 1 always exhibits a homoclinic bifurcation; hence, it seems that one can transition between panels (a) and (b) by varying $\alpha$ continuously. However, a cylinder and a Möbius band are not homeomorphic surfaces, so there must exist a transition point, where $W^{s}(\mathbf{0})$ does not close in either of the two ways depicted in panels (a) and (b). This transition case is shown in panel (c) of fig. 1 for $\alpha\approx 0.3694818$, where a homoclinic flip bifurcation takes place, which is called an inclination flip (IF). At this bifurcation point genericity condition (G3) is not fulfilled and $W^{s}(\mathbf{0})$ does not close along $W^{ss}(\mathbf{0})$; see fig. 1 (c). It was proven in [9, 15, 18] that the inclination flip bifurcation is one mechanism by which one can transition between the orientable and nonorientable case of a homoclinic bifurcation of codimension one. It is not the only known mechanism: a transition in orientability of the homoclinic bifurcation may also occur via a so called orbit flip bifurcation, which corresponds to a homoclinic bifurcation that does not fulfill condition (G2). Both inclination and orbit flip are codimension-two homoclinic flip bifurcations whose unfolding can be of cases A, B and C.

For the purpose of this paper, we only consider the inclination flip bifurcation of case C, which occurs if one of the following eigenvalue conditions are satisfied [17]:

$$|\lambda^{ss}|<\lambda^{u}\quad\text{or}\quad 2|\lambda^{s}|<\lambda^{u},$$

(2)

and the following geometric conditions are met:

1. (i)

   $|\lambda^{s}|\neq|\lambda^{ss}|/2$

2. (ii)

   If $|\lambda^{s}|<|\lambda^{ss}|/2$, the homoclinic orbit converges to $\mathbf{0}$ tangent to $e^{s}$ in a typical way. Geometrically, this means that the homoclinic orbit is not contained in the one-dimensional leading (weak) stable manifold tangent to $\mathbf{0}$, which exists uniquely as a smooth manifold under these eigenvalue conditions; for further details see [17].

3. (iii)

   If $|\lambda^{s}|>|\lambda^{ss}|/2$, the invariant manifold of the homoclinic orbit, which is tangent to the span$\{e^{s},e^{u}\}$ backward in time, has a nondegenerate quadratic tangency with $W^{s}(\mathbf{0})$ along the homoclinic orbit.

The literature distinguishes between two different unfoldings of a homoclinic flip bifurcation of case C [15]. These are given by global conditions regarding the geometry of the stable manifold $W^{s}(\mathbf{0})$ during the creation of the Smale–horseshoe, and they are called an outward twist $\mathbf{C_{\rm out}}$ and an inward twist $\mathbf{C_{\rm in}}$ in the literature [9, 15]. Both twist cases contain the same codimension-one bifurcation curves but their relative positions differ. In particular, we find that the homoclinic flip bifurcation point $\mathbf{C_{I}}$ found for system eq. 1 corresponds to the outward twist case.

Figure 2 shows a sketch of what is known theoretically about the unfolding of a homoclinic flip bifurcation of case C for an outward twist $\mathbf{C_{out}}$ [15, 16]. The unfolding consists of an orientable homoclinic bifurcation curve $H_{o}^{1}$ that becomes nonorientable (twisted) $H_{t}^{1}$ after transitioning through the codimension-two flip bifurcation point $\mathbf{C_{out}}$. Furthermore, the following bifurcation curves emanate from $\mathbf{C_{out}}$: a saddle-node bifurcation $SN^{1}$ of periodic orbits, an infinite sequence of period-doubling bifurcations labeled $PD^{n}$, $n=1,2,4,8,...$, and an infinite sequence of $n$-homoclinic bifurcations labeled $H_{t}^{n}$, $n=2,4,8,...$, where $t$ indicates that these are codimension-one nonorientable (twisted) homoclinic bifurcations. The value of $n$ indicates the number of loops made by the homoclinic orbit before it connects back to the equilibrium point. As each homoclinic bifurcation occurs, a saddle periodic orbit with $n$ loops is created. The Smale–horseshoe region lies in between the period-doubling and homoclinic cascades; however, the boundaries of this region are not identified in the sketch. Note that the orientability of the saddle periodic orbits, labeled $1^{u}$ and $2^{u}$, is not explicitly stated in fig. 2, meaning that labels are not unique to each saddle periodic orbit.

To explain the overall structure of the unfolding, we start with the orientable saddle periodic orbit $1^{u}$ that bifurcates from the orientable homoclinic bifurcation $H_{o}^{1}$. This same label $1^{u}$ is also used for the nonorientable saddle periodic orbit that bifurcates from $H_{t}^{1}$. Note in the sketch that the orientable and nonorientable saddle periodic orbits persist throughout the cascades of period-doubling and homoclinic bifurcations, and they disappear in the saddle-node bifurcation $SN^{1}$, after the nonorientable saddle periodic orbit becomes an attracting periodic orbit, labeled $1^{s}$, in the period-doubling bifurcation $PD^{1}$. Even though it is not illustrated in fig. 2, the unfolding is known to have infinitely many saddle-node bifurcation curves that also emanate from $\mathbf{C_{out}}$ and occur along the period-doubling cascade [17].

Most of the literature on case C does not delve into details about bifurcations related to interactions of manifolds of saddle periodic orbits. This is also the case in fig. 2 where the bifurcation diagram only shows local bifurcations of saddle periodic orbits and homoclinic bifurcations of the real saddle. For ease of exposition and in contrast to fig. 2, we label the orientable saddle periodic orbit that bifurcates from $H_{o}^{1}$ as $\Gamma_{o}$, and the nonorientable saddle periodic orbit that bifurcates from $H_{t}^{1}$ as $\Gamma_{t}$ throughout this paper.

By computing the interaction of the manifolds of these saddle periodic orbits with other objects, we are able to present what is known about the unfolding of case C in a new light, namely, as part of the bifurcation diagram in the $(\alpha,\mu)$-plane of system eq. 1. Throughout this paper, we center our attention on the saddle periodic orbits $\Gamma_{o}$ and $\Gamma_{t}$, and their corresponding global manifolds. As a starting point, we show in fig. 3 the bifurcation diagram for system eq. 1 in the $(\alpha,\mu)$-plane near the homoclinic flip point $\mathbf{C_{I}}$ of case C. Note that we changed the orientation of the $\mu$-axis from top to bottom in the bifurcation diagram for ease of comparison. Figure 3 shows the principal homoclinic branch (brown curve) together with representative period-doubling $\mathbf{PD}$ (red curves) and saddle-node $\mathbf{SNP}$ (green curves) bifurcations of periodic orbits. To exemplify the relevance of the global bifurcations concerning saddle periodic orbits, we also compute representative codimension-one heteroclinic and homoclinic bifurcations in system eq. 1 of the saddle periodic orbits $\Gamma_{o}$ and $\Gamma_{t}$, labeled $\mathbf{C}_{\mathbf{0}}^{\Gamma_{o}}$ and $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{t}}\!\left[m\Gamma_{o}\right]$ for $m=1,2,3,4$. At first glance, the period-doubling and saddle-node bifurcation curves are indiscernible near the inclination flip point $\mathbf{C_{I}}$ in fig. 3. To visualize these curves, the inset shows an enlargement of a region of the bifurcation diagram that distinguishes the first three computed period-doubling bifurcation $\mathbf{PD}_{\Gamma_{t}}$, $\mathbf{PD}_{{}^{2}\Gamma_{t}}$ and $\mathbf{PD}_{{}^{4}\Gamma_{t}}$ of a period-doubling cascade. Furthermore, it shows the saddle-node bifurcation curves $\mathbf{SNP}_{\Gamma_{o}}$, $\mathbf{SNP}_{{}^{3}\Gamma_{o}}$, $\mathbf{SNP}_{{}^{4}\Gamma_{o}}$ and $\mathbf{SNP}_{{}^{5}\Gamma_{o}}$ which are responsible for the disappearance of the orientable saddle periodic orbits created during the homoclinic cascade, as will be discussed in detail in section 5. In fact, by computing representative codimension-one homoclinic bifurcations close to $\mathbf{C_{I}}$, with an implementation of Lin’s method in Auto [8], we are able to obtain the bifurcating saddle periodic orbits; this allow us to find the subsequent saddle-node bifurcation curves presented in fig. 3. For the remainder of this paper, the subindices in the label of each saddle-node bifurcation $\mathbf{SNP}$ of periodic orbits refers to the orientable saddle period orbit involved. The same applies to the period-doubling bifurcations $\mathbf{PD}$, where the subindices refer to the corresponding nonorientable saddle periodic orbit involved. Note how the saddle-node bifurcation curves accumulate onto the codimension-one homoclinic bifurcation $\mathbf{Tan}_{\Gamma_{o}}$ (violet curve) of $\Gamma_{o}$ where the stable and unstable manifolds of $\Gamma_{o}$ have a tangency. We identify the curve $\mathbf{Tan}_{\Gamma_{o}}$ as one of the boundaries of the Smale–horseshoe region $\mathbf{SH}$ (gray region), as it delimits the region in the bifurcation diagram where there exist structurally stable homoclinic orbits of $\Gamma_{o}$.

Overall, the computed fig. 3 agrees well with the sketch in fig. 2; however, one of the most apparent differences are the curves $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{t}}\!\left[m\Gamma_{o}\right]$, with $m=1,2,3,4$, of heteroclinic connecting orbits between $\mathbf{0}$ and $\Gamma_{t}$ (magenta curves). For each of these heteroclinic bifurcation curves, we find many homoclinic and heteroclinic bifurcation curves accumulating on it; these are not shown in fig. 3 because they lie very close to the curves $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{t}}\!\left[m\Gamma_{o}\right]$. We describe in more detail these accumulation cascades in section 5. Notice in fig. 3 how the sequence of heteroclinic bifurcation curves $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{t}}\!\left[m\Gamma_{o}\right]$ accumulates onto the heteroclinic bifurcation $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{o}}$ (purple curve) of a heteroclinic connecting orbit between $\mathbf{0}$ and $\Gamma_{o}$, which corresponds to the other boundary of the Smale–horseshoe region $\mathbf{SH}$ in the bifurcation diagram. Both boundary curves, $\mathbf{Tan}_{\Gamma_{o}}$ and $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{o}}$, were not included or studied in the theoretical unfolding as shown in fig. 2. Furthermore, the bifurcation $\mathbf{Tan}_{\Gamma_{o}}$ acts as mechanism to destroy a strange attractor, which was conjectured to exist close to the inclination flip point due to the cascades of period-doubling and saddle-node bifurcation [26, 27]; this will be discussed in more detail in section 7.

The main purpose of this paper is to perform a detailed study of the role of representative invariant manifolds in the reorganization of phase space at different codimension-one bifurcations in the bifurcation diagram of system eq. 1 near the point $\mathbf{C_{I}}$. In this way, we obtain new insights into the bifurcation structures that must be expected as part of the unfolding of the inclination flip bifurcation of case C. Of particular interest is to understand the nature and roles of the infinitely many cascades of codimension-one homoclinic and heteroclinic bifurcations, the boundaries in parameter plane of the Smale–horseshoe regions, and the existence and annihilation of strange attractors, etc. To present our results, we choose parameter values in $(\alpha,\mu)$-plane close to $\mathbf{C_{I}}$ and provide representative figures of the relevant objects in phase space, as well as their intersection sets with a suitable sphere. This allows us to show the consequences of different codimension-one bifurcations for the organization of phase space, and to present an overall picture of the unfolding through the bifurcation diagram of $\mathbf{C_{I}}$ in the $(\alpha,\mu)$-plane. Motivated by the existence of infinitely many homoclinic and heteroclinic bifurcations, we define a winding number $\zeta$ as a topological invariant for system eq. 1. We compute the value of $\zeta$ for system eq. 1 as $\alpha$ and $\mu$ vary over a grid. Such a two-parameter sweep allows us to identify open regions in the $(\alpha,\mu)$-plane with constant winding number, both near $\mathbf{C_{I}}$ and even further away from this central codimension-two point. The respective boundaries of these regions correspond to codimension-one homoclinic bifurcation curves. Hence, this parameter sweep contributes to obtaining a clearer picture of how the infinitely many homoclinic bifurcation are organized and accumulate onto heteroclinic bifurcations curves of the saddle periodic orbit $\Gamma_{t}$. Furthermore, by considering a larger parameter range in the $(\alpha,\mu)$-plane, we are able to identify and characterize a phenomenon where two different homoclinic bifurcation curves emanating from $\mathbf{C_{I}}$ meet and create a structure referred to as a homoclinic bubble [16]. Such homoclinic bubbles do not arise as part of the unfolding in a small neighborhood of a codimension-two homoclinic flip bifurcation; however, they have been shown to be part of the unfolding of a codimension-three resonant homoclinic flip bifurcation, where they constitute a mechanism of transition between cases B and C [16, 28].

The organization of this paper is as follows. In section 2 we introduce some notation; here, we also present the parameter values used, and give the definition of the winding number $\zeta$. We present, in section 3, the bifurcation diagram of system eq. 1 near $\mathbf{C_{I}}$. Section 4 then focusses on the transition through the main codimension-one homoclinic bifurcation curve, section 5 on the homoclinic and heteroclinic cascades, section 6 on the Smale–horseshoe region, and section 7 on the period-doubling cascade and the existence of a strange attractor that resembles the Rössler attractor. Finally, we characterize, in section 8, the bubble phenomenon arising in the bifurcation diagram of $\mathbf{C_{I}}$. We end in section 9 with a discussion and an outlook on future research.

The computations in this paper are performed with the pseudo-arclength continuation package Auto [10, 11] and its extension HomCont [8]. More specifically, global manifolds are computed with a two-point boundary value problem set-up [6, 20] and the heteroclinic orbits are obtained with Lin’s method [21, 44]. The parameter sweeping of $\zeta$ in parameter plane, visualization and post-processing of the data are performed with Matlab^®.

System eq. 1 was constructed specifically to study different homoclinic flip bifurcations in three-dimensional vector fields [34]. It is a very convenient vector field, because its parameter can be chosen in such a way that either one of the cases A, B and C occur for both inclination and orbit flip bifurcations. System eq. 1 has been used extensively, particularly to study numerically transitions between the three cases as codimension-three phenomena due to resonance [28], and to investigate the unfoldings of homoclinic flip bifurcations of cases A and B [1, 13].

Note that $\mathbf{0}$ is an equilibrium of $X^{s}$ for all parameter values. We use the parameter ranges found in [28] as a reference to study case C in the $(\alpha,\mu)$-plane and fix parameters as given in table 1. Since $\delta=0$, the $z$-axis is invariant under the flow of system eq. 1 and the eigenvalues of $\mathbf{0}$ are given by

$$\lambda_{1,2}=a\pm\sqrt{b^{2}+4\tilde{\mu}^{2}}\text{ and }\lambda_{3}=c.$$

The inclination flip bifurcation point $\mathbf{C_{I}}$ of case C unfolds with respect to $\alpha$ and $\mu$. At $\mathbf{C_{I}}$, the equilibrium $\mathbf{0}$ has eigenvalues $\lambda_{1}=1.7$, $\lambda_{2}=-0.3$ and $\lambda_{3}=-2$, which confirms that $2|\lambda^{s}|<\lambda^{u}$ as required for case C. Note that the strong stable manifold $W^{ss}(\mathbf{0})$ is the $z$-axis.

For our chosen parameters, there exists a stable equilibrium $\mathbf{q}$, which is the same equilibrium that appears in the discussion of cases A and B in [1, 13]. However, unlike for these two cases, the stability of $\mathbf{q}$ is not of relevance in our study of case C. More specifically, we find that the orientable saddle periodic orbit $\Gamma_{o}$ takes on the role of q; in particular it is responsible for the creation of a fold bifurcation F in case C. For the case C considered in this paper, the equilibrium $\mathbf{q}$ is attracting and identifying its basin of attraction is critical for understanding the reorganization of phase space close to $\mathbf{C_{I}}$; see section 3.

The unfolding of an inclination flip bifurcation of case C is characterized by the existence of $k$-homoclinic orbits for any $k\in\mathbb{N}$ [15]. In [28], these codimension-one homoclinic bifurcations in the parameter plane are studied via the continuation of solutions to a suitable two-point boundary value problem (2PBVP) during the transition between cases B and C. A drawback of this technique is the limitation of sampling only a small number of these bifurcation curves, which increases the risk of missing subtle interactions in the parameter plane. We define a winding number $\zeta$ for system eq. 1 and run a two-parameter sweep in the $(\alpha,\mu)$-plane to complement the 2PBVP approach of finding bifurcation curves. Parameter sweeping techniques have been used in part to understand the nature of cascades of homoclinic bifurcation close to Bykov T-points in the Lorenz system [5] and Shimizu-Morioka system [5, 42]. It is also useful to illustrate spike adding in neuron models; for example, see [3, 4]. By combining continuation and parameter sweeping, we are able to characterize different phenomena not only in the vicinity of the homoclinic flip bifurcation point of case C, but also far away from it.

The value of $\zeta$ encodes the number of rotations that $W^{u}(\mathbf{0})$ makes around a tubular neighborhood of the homoclinic orbit that exists at the central singularity. In the present setting, $\zeta$ can be defined conveniently as the number of rotations around the one-dimensional manifold $W^{ss}(\mathbf{q})$, which always goes through ‘the hole’ of any such tubular neighborhood. To define the quantity $\zeta$ formally, let $V:=\{p=(x,y,z)\in\mathbb{R}^{3}\;|\;x\leq 0\text{ and }y\leq 0\}$ and let $\partial V$ be its boundary. Since we set $b=1>0$ and $\delta=0$ in table 1, we have $\dot{x}<0$ on $\{x=0\}\cap V\setminus\{y=0\}$ and $\dot{y}<0$ on $\{y=0\}\cap V\setminus\{x=0\}$. Furthermore, the $z$-axis, $\{x=0\}\cap\{y=0\}$, is a subset of $V$ and it is invariant. Hence, $V$ is a positively invariant set for system eq. 1, i.e., $\phi^{t}(V)\subset V$ for all $t\geq 0$ where $\phi^{t}$ is the flow defined by system eq. 1. Therefore, any intersection of $W^{u}(\mathbf{0})$ with $\partial V$ must be transversal and $W^{ss}(\mathbf{q})$ cannot intersect $\partial V$. We view $\zeta$, that is, the number of rotations that $W^{u}(\mathbf{0})$ makes around $W^{ss}(\mathbf{q})$, as a kind of linking number, which can only vary through bifurcation. Indeed, $W^{ss}(\mathbf{q})$ never intersects $\partial V$, and $W^{u}(\mathbf{0})$ cannot follow $W^{ss}(\mathbf{q})$ to undo itself by restriction of the flow of system eq. 1; therefore, we may view these orbits segments as closed curves by identifying their endpoints.

Homoclinic bifurcations are a mechanism for $\zeta$ to change, as is illustrated in fig. 4 for system eq. 1 with $\alpha=0.5$ and three different values of $\mu$. In panel (a) the manifold $W^{u}(\mathbf{0})$ loops once around $W^{ss}(\mathbf{q})$ before reaching $\partial V$, that is, $\zeta=1$. As $\mu$ decreases, system eq. 1 goes through a homoclinic bifurcation at $\mu=0$ in panel (b), after which $W^{u}(\mathbf{0})$ makes an extra turn around $W^{ss}(\mathbf{0})$ before intersecting $\partial V$, as shown in panel (c); hence, $\zeta$ increases to 2.

In practice, we calculate $\zeta$ by counting the number of intersections of $W^{u}(\mathbf{0})$ with $\Sigma:=\left\{(x,y,z)\in\mathbb{R}^{3}:x=\mathbf{q}_{x}\right\}$, where $\mathbf{q}_{x}$ is the $x$-component of $\mathbf{q}$, and dividing this number by two; see fig. 4. The parameter sweeps of $\zeta$ shown in figs. 5, LABEL:, 22, LABEL: and 23 are performed on a $1000\times 1000$ grid over the corresponding parameter ranges.

We study now the intersection sets of the stable manifolds with the sphere $\mathbb{S}^{*}:=\{x\in\mathbb{R}^{3}:\mid\!\mid\!x-c\!\mid\!\mid=R\}$, where $c:=(c_{x},c_{y},c_{z})=(0.5,0,0)$ and $R=0.6$. Since $\mathbb{S}^{*}$ is a compact set, all intersections of the stable manifolds with $\mathbb{S}^{*}$ are bounded. In particular, two-dimensional manifolds (in general position) lead to curves on $\mathbb{S}^{*}$, while one-dimensional stable manifolds intersect $\mathbb{S}^{*}$ in points. This is illustrated in fig. 8 for the invariant manifolds in region ${\color[rgb]{0,0,1}\mathbf{1_{t}}}$.

Next, we stereographically project these intersection sets onto one of the tangent planes of $\mathbb{S}^{*}$ to present them as two-dimensional pictures. More precisely, we first apply the transformation

$$\pi=\left(\frac{u}{\mid\!\mid\!u\!\mid\!\mid},\frac{v}{\mid\!\mid\!v\!\mid\!\mid},\frac{w}{\mid\!\mid\!w\!\mid\!\mid}\right),$$

formed by the vectors

$$u=(0.5706,0.1854,0)^{T},v=(1,-(u_{x}+u_{z})/u_{y},1)^{T}\text{ and }w=u\times v.$$

We rotate and translate points $(x,y,z)\in\mathbb{S}^{*}$ to points $(x^{\prime},y^{\prime},z^{\prime})$ on the sphere of radius $R=0.6$ centered at the origin, that is, $(x^{\prime},y^{\prime},z^{\prime})=\pi(x-c)$. This transformation rotates the stereographic point, the red dot in fig. 8, so that it corresponds to the south pole of the transformed sphere. We then use stereographic projection from the south pole onto the tangent plane at the north pole, via the transformation

$$(x^{\prime},y^{\prime},z^{\prime})\mapsto\left(\frac{Rx^{\prime}}{R+z^{\prime}},\frac{Ry^{\prime}}{R+z^{\prime}}\right).$$

(3)

This particular stereographic projection was chosen to improve the visibility of certain features of the intersection sets specific to case C.

Figure 9 shows the same series of phase portraits from fig. 7 in terms of their intersection sets of stable manifolds with $\mathbb{S}^{*}$. The left column of fig. 9 illustrates the transition through $\mathbf{H_{o}}$ and the right column through $\mathbf{H_{t}}$. Starting from panel  $\mathbf{1_{o}}$ in fig. 9, note how the intersection set $\widehat{W}^{s}(\Gamma_{o})$ (cyan curve) is made up of two topological circles that bound the disconnected basin $\widehat{\mathcal{B}}(\mathbf{q})$, that is, $\partial\widehat{\mathcal{B}}(\mathbf{q})=\widehat{W}^{s}(\Gamma_{o})$. The intersection $\widehat{W}^{s}(\mathbf{0})$ (blue curve) is a single curve that accumulates in a spiralling manner backward in time onto $\widehat{W}^{s}(\Gamma_{o})$. The accumulation is as expected: the $\lambda$-lemma implies that the transversal heteroclinic orbit from $\Gamma_{o}$ to $\mathbf{0}$ causes $\widehat{W}^{s}(\textbf{0})$ to spiral around $\widehat{W}^{s}(\Gamma_{o})$. Note that these phenomena are only observed if the sphere $\mathbb{S}^{*}$ is chosen small enough. At the moment of the bifurcation, shown in panel $\mathbf{H_{o}}$, the curve $\widehat{W}^{s}(\textbf{0})$ closes back on itself along $\widehat{W}^{ss}(\textbf{0})$ and $\widehat{W}^{s}(\Gamma_{o})$ disappears as $\Gamma_{o}$ becomes the homoclinic orbit $\Gamma_{\rm hom}$; the basin $\widehat{\mathcal{B}}(\mathbf{q})$ is now bounded by a subset of $\widehat{W}^{s}(\mathbf{0})$, that is, $\partial\widehat{\mathcal{B}}(\mathbf{q})\subset\widehat{W}^{s}(\mathbf{0})$. Hence, at $\mathbf{H_{o}}$, the boundary of the basin of attraction of $\mathbf{q}$ is contained in $W^{s}(\mathbf{0})$. As soon as we enter region  $\mathbf{2}$, the entire intersection set $\widehat{W}^{s}(\mathbf{0})$ becomes the boundary of $\widehat{\mathcal{B}}(\mathbf{q})$, which is now a connected region that is topologically equivalent to an open disk; see panel  $\mathbf{2}$.

In panel  $\mathbf{1_{t}}$ of fig. 9, one sees the same topological configuration as in panel  $\mathbf{1_{o}}$, because both phase portraits are from the same region; however, note how only one end of $\widehat{W}^{s}(\mathbf{0})$ gets close to both points in $\widehat{W}^{ss}(\mathbf{0})$ in panel  $\mathbf{1_{t}}$. At the nonorientable homoclinic bifurcation $\mathbf{H_{t}}$, the intersection set $\widehat{W}^{s}(\mathbf{0})$ connects back on itself at $\widehat{W}^{ss}(\mathbf{0})$ in a different way, as is illustrated in panel $\mathbf{H_{t}}$ of fig. 9. Here, $\widehat{W}^{s}(\mathbf{0})$ does not bound two open regions as in panel $\mathbf{H_{o}}$. Instead, at $\mathbf{H_{t}}$ the two segments that form $\widehat{W}^{s}(\mathbf{0})$ accumulate onto the two topological circles $\widehat{W}^{s}(\Gamma_{o})$ due to the persistence of the heteroclinic orbit from $\Gamma_{o}$ to $\mathbf{0}$. The nature of $\widehat{\mathcal{B}}(\mathbf{q})$ and its boundary is unchanged from panel  $\mathbf{1_{o}}$. As one transitions to region  $\mathbf{3}$, the homoclinic orbit $\mathbf{\Gamma_{\rm hom}}$ becomes the periodic orbit $\Gamma_{t}$ and the intersection set $\widehat{W}^{s}(\Gamma_{t})$ (purple curve) is a single curve that accumulates at both ends onto $\widehat{W}^{s}(\Gamma_{o})$ backward in time, due to the existence of a heteroclinic orbit from $\Gamma_{o}$ to $\Gamma_{t}$. As mentioned before, there are infinitely many heteroclinic orbits from $\Gamma_{o}$ to $\mathbf{0}$ in region $\mathbf{3}$. Since $\mathbb{S}^{*}$ is a sufficiently small sphere that is transverse to $\widehat{W}^{s}(\mathbf{0})$, there exist infinitely many curves in $\widehat{W}^{s}(\mathbf{0})$. One curve in $\widehat{W}^{s}(\mathbf{0})$ accumulates onto a single topological circle of $\widehat{W}^{s}(\Gamma_{o})$, and all other cuves accumulate onto both topological circles of $\widehat{W}^{s}(\Gamma_{o})$. These sets of curves get arbitrary close to $\widehat{W}^{s}(\Gamma_{t})$ from both sides; we say that $\widehat{W}^{s}(\Gamma_{t})$ is a geometric accumulation curve of $\widehat{W}^{s}(\mathbf{0})$. In panel  $\mathbf{3}$ of fig. 9 we only show three of these infinitely many intersection curves of $\widehat{W}^{s}(\mathbf{0})$, namely, the outer curve that accumulates onto the single topological circle of $\widehat{W}^{s}(\Gamma_{o})$, and two other curves that track $\widehat{W}^{s}(\Gamma_{t})$ on both sides. We remark that the intersection sets shown in fig. 9 are homotopic to the intersection sets shown in [13] for the transition through $\mathbf{H_{o}}$ and $\mathbf{H_{t}}$ in case B, provided one contracts $\widehat{W}^{ss}(\Gamma^{a}_{o})$ to $\widehat{W}^{s}(\mathbf{q})$ through $\mathbf{H_{o}}$ and blows up $\widehat{W}^{s}(\mathbf{q})$ to a closed curve through $\mathbf{H_{t}}$ in case B.

The fact that $\Gamma_{o}\rightarrow\Gamma_{t}\rightarrow\mathbf{0}$ implies the existence of infinitely many structurally stable heteroclinic orbits from $\Gamma_{o}$ to $\mathbf{0}$ is going to be a recurrent phenomenon for different equilibria and saddle periodic orbits. For ease of exposition, we summarize the consequences in general terms:

Starting from region  $\mathbf{3}$, we first encounter the codimension-one nonorientable homoclinic bifurcation ${}^{2}\mathbf{H_{t}}$ which is shown in fig. 10 as a stereographic projection of the stable invariant objects on $\mathbb{S}^{*}$ that exist in phase space. Panel (a) shows a sketch of the intersection sets in region  $\mathbf{3}$ shown in fig. 9. The pink region indicates the relative location of the infinitely many curves in $\widehat{W}^{s}(\mathbf{0})$ that accumulate geometrically onto $\widehat{W}^{s}(\Gamma_{t})$. At the moment of the codimension-one homoclinic bifurcation ${}^{2}\mathbf{H_{t}}$, the outer-most curve in $\widehat{W}^{s}(\mathbf{0})$ that connects both topological circles of $\widehat{W}^{s}(\Gamma_{o})$ splits into two curves that close on $\widehat{W}^{s}(\mathbf{0})$ at the two points $\widehat{W}^{ss}(\mathbf{0})$; see the sketch in panel (b1) of fig. 10 and the associated computed phase portrait on $\mathbb{S}^{*}$ in panel (b2). The bifurcation ${}^{2}\mathbf{H_{t}}$ gives rise to the saddle periodic orbit ${}^{2}\Gamma_{t}$, and we find the following transversal connections: $\Gamma_{o}\rightarrow{{}^{2}\Gamma_{t}}\rightarrow\mathbf{0}$, $\Gamma_{o}\rightarrow{\Gamma_{t}}\rightarrow{{}^{2}\Gamma_{t}}$ and $\Gamma_{o}\rightarrow{{}^{2}\Gamma_{t}}\rightarrow\Gamma_{t}$. Panel (c) illustrates the situation by way of a representative sketch. Note how the two curves of $\widehat{W}^{s}(\mathbf{0})$ that end at $\widehat{W}^{ss}(\mathbf{0})$ in panel (b1) give rise to the two light-green regions, which represent the accumulation onto $\widehat{W}^{s}(^{2}\Gamma_{t})$ (dark-cyan curves) of infinitely many curves in $\widehat{W}^{s}(\mathbf{0})$ and $\widehat{W}^{s}(\Gamma_{t})$ due to the existence of $\Gamma_{o}\rightarrow{{}^{2}\Gamma_{t}}\rightarrow\mathbf{0}$ and $\Gamma_{o}\rightarrow{{}^{2}\Gamma_{t}}\rightarrow{\Gamma_{t}}$; we refer to 4.2. Both circles in $\widehat{W}^{s}(\Gamma_{o})$ bound one of these two regions, but only one circle in $\widehat{W}^{s}(\Gamma_{o})$ bounds the other region. Furthermore, since $\Gamma_{o}\rightarrow{\Gamma_{t}}\rightarrow{\mathbf{0}}$ and $\Gamma_{o}\rightarrow{\Gamma_{t}}\rightarrow{{}^{2}\Gamma_{t}}$, the pink region must contain infinitely many curves of $\widehat{W}^{s}(^{2}\Gamma_{t})$, and infinitely many curves in $\widehat{W}^{s}(\mathbf{0})$ also accumulate geometrically onto these curves. The existence of both pink and light-green regions is important. As $\mu$ decreases, the outer-most curve from the region that is closest to $\widehat{W}^{ss}(\mathbf{0})$ will meet $\widehat{W}^{ss}(\mathbf{0})$ at a certain value $\mu^{*}$; depending on whether this is a curve from $\widehat{W}^{s}(\mathbf{0})$, $\widehat{W}^{s}(\Gamma_{t})$ or $\widehat{W}^{s}(^{2}\Gamma_{t})$, system eq. 1 exhibits a particular corresponding codimension-one homoclinic or heteroclinic bifurcation. Furthermore, as the infinitely many curves in $\widehat{W}^{s}(\mathbf{0})$ accumulate onto either $\widehat{W}^{s}(\Gamma_{t})$ or $\widehat{W}^{s}(^{2}\Gamma_{t})$, infinitely many homoclinic bifurcations must occur before a codimension-one heteroclinic bifurcation can take place. Whenever a homoclinic bifurcation occurs, the above sequence of different kinds of bifurcations occurs again; that is, an additional saddle periodic orbit is created, accompanied by two regions of accumulation with respect to the stable manifold of the new saddle periodic orbit. Moreover, an accumulation of intersection curves from this stable manifold is created inside the already existing regions. In addition, the closer $\widehat{W}^{s}(\mathbf{0})$ lies to $\widehat{W}^{s}(\Gamma_{t})$ or $\widehat{W}^{s}(^{2}\Gamma_{t})$, the higher the number of rotations are for both the homoclinic orbit and the bifurcating saddle periodic orbit.

We illustrate in fig. 11 the transition through the codimension-one heteroclinic bifurcation $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{t}}\!\left[\Gamma_{o}\right]$ and its effect on the reorganization of the stable manifold $W^{s}(\Gamma_{t})$ (purple surface) in phase space. The left column shows $W^{s}(\Gamma_{t})$ in a tubular neighborhood of $\Gamma_{t}$, showing that $W^{s}(\Gamma_{t})$ is topologically a Möbius band. The right column (2) shows a larger part of $W^{s}(\Gamma_{t})$. Panels (a1) and (a2) show $W^{s}(\Gamma_{t})$, at $\mu=-0.002$, before the bifurcation $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{t}}\!\left[\Gamma_{o}\right]$ and the associated first homoclinic cascade; panels (b1) and (b2) are at the moment of the bifurcation, when $\mu\approx-0.002880324$; and panels (a3) and (b3) are for $\mu=-0.0035$, in region  $\mathbf{4}$ past the first cascade; see fig. 5.

We first focus on the local behavior in a tubular neighborhood. In panel (a1), the unstable manifold $W^{u}(\mathbf{0})$ (red curve) makes one rotation close to $\Gamma_{o}$ and one close to $\Gamma_{t}$ and then escapes to infinity. As discussed before, a sequence of homoclinic bifurcations must occur before the bifurcation $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{t}}\!\left[\Gamma_{o}\right]$ is exhibited by system eq. 1. During this sequence, the unstable manifold $W^{u}(\mathbf{0})$ gains turns around $W^{s}(\Gamma_{t})$, thus increasing $\zeta$, until its limiting case at the bifurcation $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{t}}\!\left[\Gamma_{o}\right]$. However, note how the first loop of $W^{u}(\mathbf{0})$ is still close to $\Gamma_{o}$ before accumulating onto $\Gamma_{t}$; this situation is the same as in panel (a1) of fig. 6. After $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{t}}\!\left[\Gamma_{o}\right]$, a sequence of homoclinic bifurcations occur which decreases the winding number of $W^{u}(\mathbf{0})$ around $W^{s}(\Gamma_{t})$, thus decreasing $\zeta$. Finally in region  $\mathbf{4}$, the unstable manifold $W^{u}(\mathbf{0})$ makes two rotation close to $\Gamma_{o}$ and one again close to $\Gamma_{t}$ before escaping to infinity; see panel (c1). In particular, the orientation of the homoclinic bifurcation of $\mathbf{0}$ that follows, depends on how $W^{u}(\mathbf{0})$ passes near $\Gamma_{o}$ and $\Gamma_{t}$.

We gain a deeper understanding by studying a larger portion of $W^{s}(\Gamma_{t})$ as shown in the right column of fig. 11. Panel (a2) illustrates how $W^{s}(\Gamma_{t})$ spirals around $W^{s}(\Gamma_{o})$ due to the presence of heteroclinic orbits from $\Gamma_{o}$ to $\Gamma_{t}$; the outer rim of the computed part of $W^{s}(\Gamma_{t})$ is highlighted as the black curve. Note how part of $W^{s}(\Gamma_{t})$ gets close to $W^{ss}(\mathbf{0})$ before starting to spiral again. In panel (b2), this part of $W^{s}(\Gamma_{t})$ has disappeared, and the existence of the heteroclinic orbit $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{t}}\!\left[\Gamma_{o}\right]$ forces $W^{s}(\Gamma_{t})$ to accumulate onto $W^{ss}(\mathbf{0})$ backward in time. After the bifurcation $\mathbf{Q}_{\mathbf{0}}^{\Gamma_{t}}\!\left[\Gamma_{o}\right]$, the manifold $W^{s}(\Gamma_{t})$ no longer accumulates onto $W^{ss}(\mathbf{0})$; see panel (c2). Observe that $W^{s}(\Gamma_{t})$ in panel (c2) seems identical to $W^{s}(\Gamma_{t})$ in panel (b2), but it exhibits one additional loop. This extra loop would spread out if a much larger portion of $W^{s}(\Gamma_{t})$ were computed, and it would get close to $W^{ss}(\mathbf{0})$ in the same way as in panel (a2).