CaPhy: Capturing Physical Properties for Animatable Human Avatars
Abstract
We present CaPhy, a novel method for reconstructing animatable human avatars with realistic dynamic properties for clothing. Specifically, we aim for capturing the geometric and physical properties of the clothing from real observations. This allows us to apply novel poses to the human avatar with physically correct deformations and wrinkles of the clothing. To this end, we combine unsupervised training with physics-based losses and 3D-supervised training using scanned data to reconstruct a dynamic model of clothing that is physically realistic and conforms to the human scans. We also optimize the physical parameters of the underlying physical model from the scans by introducing gradient constraints of the physics-based losses. In contrast to previous work on 3D avatar reconstruction, our method is able to generalize to novel poses with realistic dynamic cloth deformations. Experiments on several subjects demonstrate that our method can estimate the physical properties of the garments, resulting in superior quantitative and qualitative results compared with previous methods.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/f3ee85b3-c663-4458-a113-7eff3d10bd9b/caphy.png)
1 Introduction
Digital human avatars are the backbone of numerous applications in the entertainment industry (e.g., special effects in movies, characters in video games), in e-commerce (virtual try-on), as well as in immersive telecommunication applications in virtual or augmented reality. Digital human avatars not only have to reassemble the real human in shape, appearance, and motion, but also have to conform to physics. Clothing must move consistently with the underlying body and its pose. In the past years, we have seen immense progress in digitizing humans to retrieve such digital human avatars by using neural rendering techniques [45, 46] or other 3D representations. Especially, recent methods [38, 24, 4, 51, 20, 27, 31] that rely on deep neural networks to represent appearance and geometry information show promising results. These data-driven methods store the body and clothing in a unified representation and can be animated using the underlying body prior that exhibits a kinematic deformation tree. While the methods aim at generalized animation of the captured human, the results often lack realistic deformations of the garment as they reproduce the deformation states seen during training. This is due to limited training data, as not all possible poses can be captured as well as occlusions during the scanning procedure. In contrast to data-driven methods, recent works [2, 40] have focused on incorporating physical constraints into dynamic clothing simulation and generating realistic simulation results of clothing under various complex human poses using unsupervised training. However, most of these methods rely on a fixed virtual physical model for formulating dynamic clothing, which prevents them from representing the physical properties of real-world clothing from real captures.
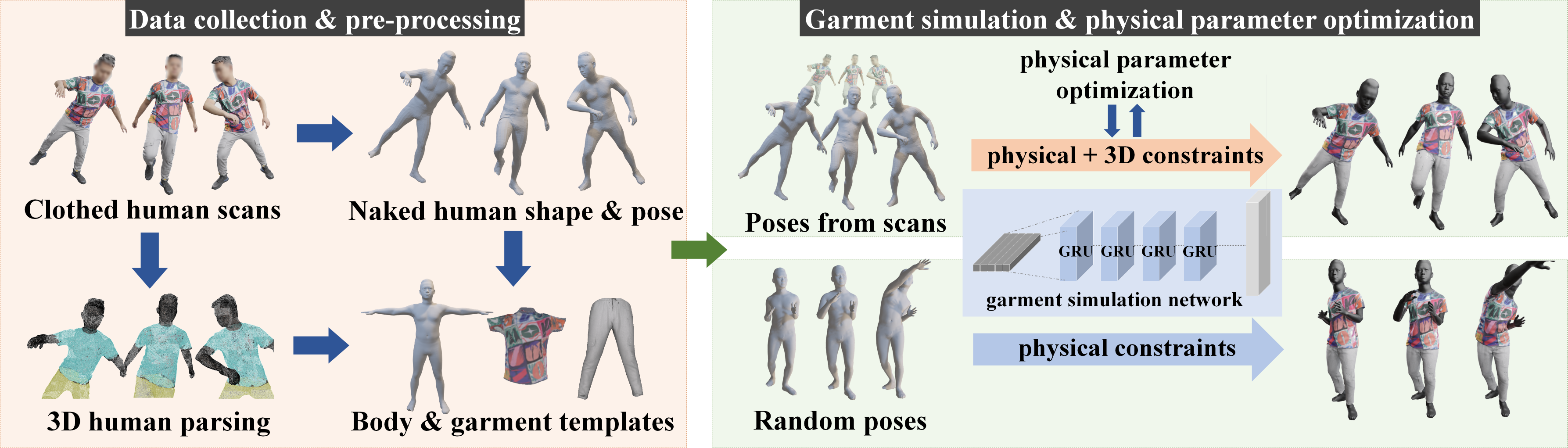
In this paper, we propose CaPhy, a clothing simulation and digital human avatar reconstruction method based on an optimizable cloth physical model. Our goal is to learn realistic garment simulations that can be effectively generalized to untrained human poses using a limited set of 3D human scans. First, unlike most existing digital human construction works [38, 24, 4], we model the human body and clothing separately to retain their different dynamic physical properties. We train a neural garment deformation model conditioned on the human pose that can produce realistic dynamic garment animation results by combining supervised 3D losses and unsupervised physical losses built upon existing real-world fabric measurements. This allows our network to generate simulated clothing results in various human poses even when insufficient scan data is available. In contrast to SNUG [40], we do not assume fixed physical garment properties and optimize the fabric’s physical parameters from human scans, thus, capturing its physical characteristics. By combining the optimization of clothing physical parameters and dynamic clothing training with both physical and 3D constraints, our method can generate highly realistic human body and clothing modeling results.
To summarize, we reconstruct dynamic clothing models from real-world observations that conform to the physical constraints of the input by combining unsupervised training with physics-based losses and supervised training. The contributions of this work are as follows:
-
•
For garment reconstruction, we introduce a physical model formulation based on real-world fabric measurement results, to better represent the physical properties of real-captured garments (see Sec. 3.2).
-
•
Using this physics prior and supervised 3D losses, we reconstruct an animatable avatar composed of body and garment layers including a neural garment deformation model which allows us to generalize to unseen poses (see Sec. 3.3).
-
•
Instead of using the given fixed physical parameters of the fabric, we propose to optimize the parameters of the prior to obtain better physical properties of the 3D scans (see Sec. 3.4).
2 Related Work
Animatable Human Avatar.
Animatable human avatar reconstruction aims to generate a pose-dependent human model based on observations from 3D scans or videos of a particular human object. Some works focus on building dynamic geometry of human models from scanned data [23, 38, 24, 56, 20, 48, 36]. Ma et al. [23] use local patches to represent the 3D human models, which encode local deformations of different clothing and body parts. Saito et al. [38] employ a reverse skinning network to learn the mapping of the posed space to the canonical space, enabling them to learn the dynamic geometry of clothing in various poses. Some methods reconstruct human avatars from a small number of 3D scans [19] or a monocular self-rotating human video [12], which can be driven by given monocular RGB inputs of the same subject. To achieve a more flexible representation and avatar learning, some works utilize point clouds to represent digital humans [24, 56, 20], while some works leverage SDF (signed distance function) or part-based SDF to represent human avatars [48, 36]. Some works learn the body surface deformation field in the posed space by utilizing single-view RGBD images or depth point clouds, enabling them to describe the dynamic geometry of the body surface [4, 27]. These data-driven methods aim to learn the mapping from human pose space to dynamic clothed human models using 3D data. However, these methods rely on large-scale 3D training data, posing a challenge for generalization to poses beyond the dataset if insufficient data is available.
More recently, with implicit shape rendering and volume rendering techniques [25, 26], some works focus on generating animatable human avatars with neural rendering methods, which supports dynamic human avatar reconstruction from RGB inputs. Some methods use neural texture or neural voxel representations [37, 32] to perform neural rendering-based avatars from single- or multi-view images. Some methods leverage Nerf representation [22, 31, 51, 42, 53, 58, 18] for generating articulated human Nerf models, which propose pose-deformable neural radiance fields for representing human dynamics. Grigorev et al. [8] integrate neural texture synthesis, mesh rendering, and neural rendering into the joint generation process through adversarial network training. Feng et al. [7] use the mesh-based human model and Nerf-based garment model to better represent different dynamic properties of the human avatar. These methods mainly focus on the rendering part without optimizing the dynamic geometry of the clothing. Therefore, this type of method has limited abilities in capturing detailed wrinkles and physical properties of clothing.
Clothing Capture.
Clothing capture aims to capture the geometric properties of the separate clothing layers. Pons-Moll et al. [34] and Tiwari et al. [47] fit the garment templates to the 3D human scans from the dataset. Jiang et al. [13] and Chen et al. [5] propose a method for capturing the body and garment model separately from a single image. Zhu et al. [59] generate a dataset containing 3D garment models of different styles and learn to reconstruct the 3D shape from 2D images of a garment. Su et al. [43] propose a multi-layer human and garment reconstruction method from a monocular RGB video, which recovers the basic garment 3D shapes and captures dynamic garment wrinkle details from the RGB inputs. By learning the 3D semantic field from the pixel-aligned implicit fields, Zhu et al. [60] extract the detailed garment geometry from a single image containing a clothed human. With a single RGBD camera, Yu et al. [54] reconstruct the dynamic clothed human model in real-time. Based on this technique, Yu et al. [55] separately capture the dynamic human and garment models by combining physical simulations into the garment tracking pipeline. Xiang et al. [52] utilize a multi-view capture system consisting of about 140 cameras to collect high-resolution videos for reconstructing the human body in clothing. In addition, some researchers focus on establishing correspondence between deformed garments [21]. Some researchers focus on more flexible garment shape and style representation and capture using UV-based methods [44, 1, 15] or deep unsigned distance functions [6]. These clothing capture methods focus on capturing the static or dynamic geometric features of clothing while disregarding the extraction of physical properties of garments and the application of physically realistic garment animation with the captured garments.
Physical-based Garment Simulation.
Physics-based simulation methods are widely used in dynamic garment reconstruction. Traditional physics-based garment simulation methods [35, 3, 14] rely on force and collision modeling or explicit time integration. Thus, applying these methods to clothing geometry inference using neural networks or integrating them with data-driven methods can be challenging, making them difficult to incorporate into a human avatar generation framework. Typical neural network-based methods for garment simulation [29, 39, 49, 28] rely on pre-generated virtual clothing simulation data using pre-defined simulators, without incorporating physical models into the deep learning framework. Recent research has made breakthroughs in developing physical constraints for clothing using neural networks. Bertiche et al. [2] incorporate physical constraints into the loss function by imposing both edge distance constraints and bending constraints, which achieves the first unsupervised training of a physical simulation model for clothing using neural networks. Santesteban et al. [40] employ the StVK (Saint Venant-Kirchhoff) model to build the neural physical model of clothing, which further improves the realism of the animated garments. However, these methods rely on fixed physical parameters of the fabric during training as well as require a fixed template mesh, with limited ability to represent the geometrical and physical properties of real captured garments.
3 Method
Our goal is to extract the geometrical and physical characteristics of specific garments from a limited set of 3D scans, typically consisting of 50 to 120 scans of a clothed human in various poses. We propose to learn a neural deformation model which imitates a garment simulation, to extrapolate to novel poses of the digital human avatar. In the first step, we extract the naked human and garment templates from the static scans, leveraging 2D semantic segmentations (see Sec. 3.1). Furthermore, by combining supervised 3D losses and unsupervised physical losses built upon existing real-world fabric measurements, we train a garment simulation model that can produce realistic dynamic garment animation results, which also shows 3D consistency with the scans (see Secs. 3.2 and 3.3). Based on such a model, we propose a method for optimizing the physical parameters of the cloth prior, such that the animated garment has consistent physical characteristics with the scanned data (see Sec. 3.4). To alleviate the collision between the upper and lower body garments, we fine-tune the model constrained by a collision loss (see Sec. 3.5).
3.1 Data Pre-processing
Given 3D scans of a clothed human in various poses, we extract the naked human model and the basic garment templates. Specifically, we use the SMPL-X [30] model to represent our human body. SMPL-X is a parametric model that represents the body, face, and hands jointly with the pose () and shape () parameters. By applying deformations to the base SMPL-X model, we can represent human faces and other surface details:
| (1) |
where is a standard linear blend skinning function, is the base SMPL-X template mesh in T-pose parameterized by , and adds corrective vertex displacements on the template mesh. outputs 3D joint locations from the human mesh. are the blend weights of the skeleton .
Human Body Shapes and Poses.
To obtain the naked human shape and pose of the human scan , we leverage 2D semantic information of the scans to solve the “naked body underneath the clothing” problem. Specifically, for a 3D human scan , we first render it with 32 uniformly distributed viewing angles to obtain color images and depth images . The color images are used for obtaining 2D semantic segmentation results, while the depth images are used for determining the visibility of each scan vertex at each viewing angle. We apply [17] to color images to obtain 2D semantic segmentation values. For each vertex , we project it to each view to get its corresponding projected depth. We consider a vertex to be visible in view if its projected depth approximates the corresponding depth value in the depth image . We then assign the 3D semantic segmentation value of the vertex , by applying a majority rule based on the 2D semantic segmentation values extracted from all visible viewing angles, where , and denote body and different garment labels, respectively. As shown in Fig. 3(b), we obtain accurate 3D human semantic segmentation results for the scan.
To incorporate this 3D semantic segmentation information for solving the naked human body underneath clothing, for each deformed SMPL-X vertex , we modify the vertex fitting energy term in both the ICP (iterative closest point) solver for calculating shape and pose and in the non-rigid ICP solver for vertex displacements , by constraining the deformed vertices to align the uncovered skin areas while being underneath the clothing areas. As shown in Fig. 3(c)(d), the mesh of the body closely conforms to the original scan.



Static Garment Templates.
Our goal is to generate static garment templates consistent with the scans containing less dynamic garment geometry information such as folds, which can be used in our physics-based training. To this end, we use TailorNet [29] for generating our garment template model in a standard pose. For the upper and lower garment (e.g., shirts and pants), we use the same procedure. In the following, we will describe it for the upper garment generation. We first select one scan that is closest to the standard T-pose or A-pose from our scanned data, and then extract the upper body garment vertices by leveraging the fused 3D semantics. We sample 300 garment shape parameters from the garment style space in [29] to generate 300 upper body garments .After calculating the 3D Chamfer distance between and for all 300 samples, we select the generated garment with the smallest Chamfer distance and set it to the static garment template .
3.2 Garment Simulation Network
After obtaining the human and garment templates, we train a garment simulation network from the scans. Our deformation model for the clothing is defined as:
| (2) |
where is the skinning weights of the static garment template . on each garment vertex is determined by the nearest-neighbor body vertex. Other symbols remain the same as defined in Eq. 1. represents the garment deformation in the canonical space. We aim to learn the garment deformation as a function of the human body poses . The garment deformation is predicted in the canonical space as in SCANimate [38] and SNUG [40].
We construct the garment simulation network as in SNUG [40], which proposes an unsupervised garment dynamic learning pipeline. Specifically, the garment simulation network structure consists of a 4-layer GRU network and a fully connected layer, which inputs 5 continuous human poses and outputs the dynamic garment deformations . The model also supports inputs from static poses.
Similar to Santesteban et al. [40], we use unsupervised physical losses, but additionally we add 3D matching losses to the network training to match the physics of the real observations. Santesteban et al. [40] propose the physics-based losses using the Saint Venant Kirchhoff (StVK) model, where the strain energy is formulated as:
| (3) |
where is the volume of each triangle. and are the Lamé constants, and is the Green strain tensor:
| (4) |
where is the local deformation metric of a triangle. However, we find that the StVK model with constant and does not accurately capture the strain behavior of real fabrics under tensile deformation. On the other hand, Wang et al. [50] measures and for 10 different cloth materials and find that they are related to the principal strains and strain angles, thus related to Green strain tensor . Therefore, we follow [50] and rewrite Eq. 3 to establish a real-measured anisotropic strain model as follows:
| (5) |
where and are obtained by interpolating the results measured by [50] under several conditions. represent 10 different cloth materials. We then define our physics-based losses similar to [40] as:
| (6) |
where models the bending energy determined by the angle of two adjacent triangles. Here we also adjust the bending term according to ARCSim [50, 33] as follows:
| (7) |
where is the bending stiffness coefficient of the cloth material [50], and denote the angles of two adjacent triangles under animation and static, respectively. and denote the adjacent edge length and the sum of the adjacent triangle areas. Other terms in Eq. 6 are formulated similarly to [40].
3.3 Training with physics and 3D constraints
In order to make our simulated garments both have physical realism and conform to our 3D scans, we introduce the combined training for garment simulation with both unsupervised physical loss and supervised 3D loss, which establishes the connection between physical-based simulated virtual garments and garments from real-world captures.
For the training using the physics-based loss, we randomly sample human poses from the CMU Mocap dataset. Specifically, we use 10000 sets of 5 consecutive frames of human poses . Here, we select the appropriate fabric material parameters according to the material descriptions in [50] and the type of clothing in the data. To ensure that our model can also conform to our 3D scanned data, we also train the garment simulation network for the human poses of the 3D scans generated in Sec. 3.1 by minimizing the following loss function:
| (8) |
where is the physics-based loss defined in Eq. 6, and is the supervised 3D matching loss defined as:
| (9) | |||
which computes the 3D Chamfer distance between the generated garments and the ground truth garment point cloud extracted from scan .
During training, in order to balance the unsupervised training for random poses and the supervised training for scan poses, we introduce a 1:4 training strategy, where we train our network for 1 epoch with random poses and 4 epochs with scan poses, repeatedly. In our experiments, we find that such a training strategy leads to natural and physically realistic garment dynamic results for both scan data and randomly sampled poses.

3.4 Cloth Physical Parameter Optimization
As mentioned in Sec. 3.2, for training a physically realistic garment simulation model, we select appropriate fabric material parameters to build our unsupervised physical losses. However, these preselected fabric parameters may not reflect the actual physical properties of the scan data.
Thus, our goal is to optimize the fabric’s physical parameters using the scanned data as ground truth. We observe that after training, the generated garments under scan pose converge to the global minimum of the sum of physical constraint energy and 3D constraint energy. As a result, we hypothesize that the gradients of the physical constraint energy and the 3D constraint energy of are opposite for each vertex. And ideally, if the physical model matches the real garments, the gradients of the two energies should approximate zero when the generated garments coincide with scans. Under such assumptions, we iteratively train the garment simulation network and optimize the fabric’s physical parameters. We first fix the generated garments generated by our pre-trained garment simulation model, and then optimize the physical parameters. The optimized physics-based loss term for dynamic garments is denoted as . Then we use Eq. 8 to train the garment network and obtain , etc. After the iterative training, the model can generate dynamic garments that are geometrically and physically consistent with the scan data.
In our pipeline, we denote the fabric’s physical parameters as , which correspond to the measured parameters in [50] used for calculating and , and , as mentioned in Sec. 3.2. The loss function of the physical parameters optimization is defined as follows:
| (10) |
where represents the gradient constraint of the physical energy constraint on the outputs of the garment dynamic network after iterations. is the physical parameter update of each iteration, which is constrained by the regularization coefficient . We adjust term for different parameters and reparametrize for balancing the order of magnitude between different parameters. We perform physical parameter optimization with the scan poses, and then train our garment simulation network with both random poses and scan poses with the optimized physics-based losses. Fig. 4 shows that the animation results of the garments more closely resemble the physical wrinkle details of the ground truth after optimization of the fabric’s physical parameters.

3.5 Collision Fine-tuning
After the physical parameter optimization and garment simulation training step, we can generate vivid animation results for each garment of the scanned person. However, we have not considered the penetration of different garments. Therefore, we perform a collision fine-tuning training step to address the collision between the upper and lower garments, as shown in Fig. 5. See more results in the supplementary.
Specifically, after training for each garment, we fine-tune the dynamic networks of the upper and lower garments using random pose data with the loss function:
| (11) |
For the scanned data, we add and accordingly. The collision term is defined similarly to the garment-body collision term in Eq. 6:
| (12) |
where is the nearest lower garment vertex of each upper garment vertex . is the corresponding normal. We only add constraints to the upper garment region near the lower garment, and fine-tune the network alternately on the random pose and scanned pose data for 10 epochs.

4 Experiments
In our experiments, we employ a multi-camera system to capture 3D scans of clothed human bodies, which is used to evaluate the effectiveness of our proposed method. For each collected human subject, we use 80% of the collected data as the training set and the remaining 20% as the test set. In addition, we show dynamic animations of the reconstructed digital human models based on monocular video tracking.
Training: In addition to data preparation and template reconstruction for the human and garments, each garment requires approximately 6-11 hours for the optimization of the fabric’s physical parameter described in Sec. 3.4, 8-14 hours for dynamic garment network training (Sec. 3.3), and 1 hour for collision fine-tuning (Sec. 3.5), using a single NVIDIA RTX 3090 GPU. The inference module takes about 3-6 ms per garment per pose (depending on the size of the garment template) which in principle could allow interactive control of the reconstructed human avatar.
4.1 Dynamic Animation Results
To evaluate our method, we reconstruct different digital humans from collected human scans with different styles of clothing. As shown in Fig. 6, the generated digital human models accurately replicate the physical characteristics of the scanned human subjects’ clothing on the test set, including wrinkles. Note that our results are visually more similar to the ground-truth observations in our test set than previous methods. The reconstructed digital human models can also be driven by a monocular RGB video with the human poses estimated by PyMAF [57]. As shown in Fig. 7, we generate digital human animation results based on a single-view video, similar to LiveCap [9] and DeepCap [10]. Unlike their static digital human reconstruction, the reconstruction results of our method have realistic dynamic characteristics for garments. Although texture reconstruction is not the focus of this work, we present some texture reconstruction results of the reconstructed digital human in Fig. 8 using the method of Ji et al. [11].


4.2 Comparison and Validation
We compare the proposed method with the typical data-driven digital human reconstruction method POP [24] and the unsupervised garment simulation method SNUG [40] (see Fig. 6). For a fair comparison, we apply Poisson Reconstruction to point clouds directly outputted by POP [24] and use the same rendering conditions to generate the results. As SNUG [40] can not obtain garment templates from real-world scans, we use our estimated template as input.
Limited by the size of our training set (consisting of 50 to 120 scans of a human body), the data-driven method POP [24] has difficulties learning the dynamic characteristics of clothing for poses beyond the pose space of the training set. SNUG [40] and our method generate realistic clothing wrinkles. However, since SNUG does not use 3D scanned data as constraints, the resulting clothing geometry is different from the clothing characteristics of the scanned data.
As shown in Tab. 1, we also present a quantitative comparison of the different methods for the generated garments. We use two sets of upper garments of human subjects for comparison. Based on a 3D chamfer distance [24] we evaluate the clothing geometry. Note that POP [24] does not explicitly reconstruct the clothing, so we calculate the 3D chamfer distance from the nearest-neighbor point of the ground truth garment. To ablate our method, we compare to our method only based on the unsupervised learning using our optimized garment physics model as described in Sec. 3.2, which we denote as Ours (-real data). Our method outperforms both the data-driven method POP and the unsupervised method SNUG [40] and Ours (-real data). We also perform ablation experiments on the optimization of the fabric’s physical parameter (denoted as Ours (-optim. phys.)), and find that the 3D chamfer distance remains almost unchanged before and after the optimization process. Note that the 3D chamfer distance mainly evaluates the overall fitting accuracy between the generated garment models and the ground truth. Therefore, we also introduce a 2D perceptual metric [16] to measure the geometric details of renderings of animated garments. The 2D perceptual loss is calculated through a pre-trained VGG-16 architecture [41]. Tab. 1 shows that our method achieves the best or equivalent results across all metrics, in comparison with POP [24], SNUG [40], and other ablation studies.
| Error metric (Case 1) | 3D-CD (mm) | 2D-Perceptual |
| POP [24] | ||
| SNUG [40] | ||
| Ours (-real data) | ||
| Ours (-optim. phys.) | ||
| Ours | ||
| Error metric (Case 2) | 3D-CD (mm) | 2D-Perceptual |
| POP [24] | ||
| SNUG [40] | ||
| Ours (-real data) | ||
| Ours (-optim. phys.) | ||
| Ours |
4.3 Limitations
For garment modeling, the proposed method utilizes clothing templates with clear topological structures to establish reasonable physical constraints for clothing. Therefore, it may face challenges when dealing with clothing that has complex geometric structures such as pockets. In addition, the proposed method relies on the human template of SMPL-X [30] to generate dynamic animations for clothing, making it difficult to handle garments that are relatively independent of the human body model, such as long dresses.
For training part, by incorporating other constraints like 2D perceptual losses during training, we may achieve results with higher fidelity in future work. Also, when performing physical parameter optimization, we fix some basic parameters (e.g. density) to avoid parameter degeneracy, future works may explore a more decent method to perform better physical optimization. In addition, with our collision fine-tune step, the garment-garment intersection problem is not fully solved and needs further improvement.
5 Conclusion
We introduced CaPhy, a digital human avatar reconstruction method that is based on an optimizable physics model to learn a neural garment deformation model which extrapolates to novel poses not seen in the input 3D scans. Specifically, we combine unsupervised physics-based constraints and 3D supervision to reproduce the physical characteristics of the real garments from observations. We demonstrate that this method, allows us to reconstruct an avatar with clothing that extrapolates to novel poses with realistic product of wrinkles. We believe that CaPhy is a stepping stone towards generalizable avatar animation that combines physics with sparse observations.
Acknowledgements. This paper is supported by National Key R&D Program of China (2022YFF0902200), the NSFC project No.62125107 and No.61827805.
References
- [1] Thiemo Alldieck, Gerard Pons-Moll, Christian Theobalt, and Marcus Magnor. Tex2shape: Detailed full human body geometry from a single image. In IEEE/CVF International Conference on Computer Vision (ICCV), pages 2293–2303, 2019.
- [2] Hugo Bertiche, Meysam Madadi, and Sergio Escalera. Pbns: physically based neural simulation for unsupervised garment pose space deformation. ACM Transactions on Graphics (TOG), 40(6):1–14, 2021.
- [3] Javier Bonet and Richard D Wood. Nonlinear continuum mechanics for finite element analysis. Cambridge university press, 1997.
- [4] Andrei Burov, Matthias Nießner, and Justus Thies. Dynamic surface function networks for clothed human bodies. In IEEE/CVF International Conference on Computer Vision (ICCV), pages 10754–10764, 2021.
- [5] Xin Chen, Anqi Pang, Wei Yang, Peihao Wang, Lan Xu, and Jingyi Yu. Tightcap: 3d human shape capture with clothing tightness field. ACM Transactions on Graphics (TOG), 41(1):1–17, 2021.
- [6] Enric Corona, Albert Pumarola, Guillem Alenya, Gerard Pons-Moll, and Francesc Moreno-Noguer. Smplicit: Topology-aware generative model for clothed people. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 11875–11885, 2021.
- [7] Yao Feng, Jinlong Yang, Marc Pollefeys, Michael J Black, and Timo Bolkart. Capturing and animation of body and clothing from monocular video. In SIGGRAPH Asia 2022 Conference Papers, pages 1–9, 2022.
- [8] Artur Grigorev, Karim Iskakov, Anastasia Ianina, Renat Bashirov, Ilya Zakharkin, Alexander Vakhitov, and Victor Lempitsky. Stylepeople: A generative model of fullbody human avatars. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 5151–5160, 2021.
- [9] Marc Habermann, Weipeng Xu, Michael Zollhoefer, Gerard Pons-Moll, and Christian Theobalt. Livecap: Real-time human performance capture from monocular video. ACM Transactions on Graphics (TOG), 38(2):1–17, 2019.
- [10] Marc Habermann, Weipeng Xu, Michael Zollhofer, Gerard Pons-Moll, and Christian Theobalt. Deepcap: Monocular human performance capture using weak supervision. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 5052–5063, 2020.
- [11] Chaonan Ji, Tao Yu, Kaiwen Guo, Jingxin Liu, and Yebin Liu. Geometry-aware single-image full-body human relighting. In European Conference on Computer Vision (ECCV), pages 388–405, 2022.
- [12] Boyi Jiang, Yang Hong, Hujun Bao, and Juyong Zhang. Selfrecon: Self reconstruction your digital avatar from monocular video. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 5605–5615, 2022.
- [13] Boyi Jiang, Juyong Zhang, Yang Hong, Jinhao Luo, Ligang Liu, and Hujun Bao. Bcnet: Learning body and cloth shape from a single image. In European Conference on Computer Vision (ECCV), pages 18–35, 2020.
- [14] Chenfanfu Jiang, Theodore Gast, and Joseph Teran. Anisotropic elastoplasticity for cloth, knit and hair frictional contact. ACM Transactions on Graphics (TOG), 36(4):1–14, 2017.
- [15] Ning Jin, Yilin Zhu, Zhenglin Geng, and Ronald Fedkiw. A pixel-based framework for data-driven clothing. In Computer Graphics Forum, volume 39, pages 135–144. Wiley Online Library, 2020.
- [16] Justin Johnson, Alexandre Alahi, and Li Fei-Fei. Perceptual losses for real-time style transfer and super-resolution. In European Conference on Computer Vision (ECCV), pages 694–711, 2016.
- [17] Peike Li, Yunqiu Xu, Yunchao Wei, and Yi Yang. Self-correction for human parsing. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), 44(6):3260–3271, 2020.
- [18] Zhe Li, Zerong Zheng, Yuxiao Liu, Boyao Zhou, and Yebin Liu. Posevocab: Learning joint-structured pose embeddings for human avatar modeling. In ACM SIGGRAPH Conference Proceedings, 2023.
- [19] Zhe Li, Zerong Zheng, Hongwen Zhang, Chaonan Ji, and Yebin Liu. Avatarcap: Animatable avatar conditioned monocular human volumetric capture. In European Conference on Computer Vision (ECCV), pages 322–341, 2022.
- [20] Siyou Lin, Hongwen Zhang, Zerong Zheng, Ruizhi Shao, and Yebin Liu. Learning implicit templates for point-based clothed human modeling. In European Conference on Computer Vision (ECCV), pages 210–228, 2022.
- [21] Siyou Lin, Boyao Zhou, Zerong Zheng, Hongwen Zhang, and Yebin Liu. Leveraging intrinsic properties for non-rigid garment alignment. In IEEE/CVF International Conference on Computer Vision (ICCV), 2023.
- [22] Lingjie Liu, Marc Habermann, Viktor Rudnev, Kripasindhu Sarkar, Jiatao Gu, and Christian Theobalt. Neural actor: Neural free-view synthesis of human actors with pose control. ACM Transactions on Graphics (TOG), 40(6):1–16, 2021.
- [23] Qianli Ma, Shunsuke Saito, Jinlong Yang, Siyu Tang, and Michael J Black. Scale: Modeling clothed humans with a surface codec of articulated local elements. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 16082–16093, 2021.
- [24] Qianli Ma, Jinlong Yang, Siyu Tang, and Michael J Black. The power of points for modeling humans in clothing. In IEEE/CVF International Conference on Computer Vision (ICCV), pages 10974–10984, 2021.
- [25] Ben Mildenhall, Pratul P Srinivasan, Matthew Tancik, Jonathan T Barron, Ravi Ramamoorthi, and Ren Ng. Nerf: Representing scenes as neural radiance fields for view synthesis. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part I 16, pages 405–421. Springer, 2020.
- [26] Michael Niemeyer, Lars Mescheder, Michael Oechsle, and Andreas Geiger. Differentiable volumetric rendering: Learning implicit 3d representations without 3d supervision. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 3504–3515, 2020.
- [27] Pablo Palafox, Aljaž Božič, Justus Thies, Matthias Nießner, and Angela Dai. Npms: Neural parametric models for 3d deformable shapes. In IEEE/CVF International Conference on Computer Vision (ICCV), pages 12695–12705, 2021.
- [28] Xiaoyu Pan, Jiaming Mai, Xinwei Jiang, Dongxue Tang, Jingxiang Li, Tianjia Shao, Kun Zhou, Xiaogang Jin, and Dinesh Manocha. Predicting loose-fitting garment deformations using bone-driven motion networks. In ACM SIGGRAPH 2022 Conference Proceedings, pages 1–10, 2022.
- [29] Chaitanya Patel, Zhouyingcheng Liao, and Gerard Pons-Moll. Tailornet: Predicting clothing in 3d as a function of human pose, shape and garment style. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 7365–7375, 2020.
- [30] Georgios Pavlakos, Vasileios Choutas, Nima Ghorbani, Timo Bolkart, Ahmed AA Osman, Dimitrios Tzionas, and Michael J Black. Expressive body capture: 3d hands, face, and body from a single image. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 10975–10985, 2019.
- [31] Sida Peng, Junting Dong, Qianqian Wang, Shangzhan Zhang, Qing Shuai, Xiaowei Zhou, and Hujun Bao. Animatable neural radiance fields for modeling dynamic human bodies. In IEEE/CVF International Conference on Computer Vision (ICCV), pages 14314–14323, 2021.
- [32] Sida Peng, Yuanqing Zhang, Yinghao Xu, Qianqian Wang, Qing Shuai, Hujun Bao, and Xiaowei Zhou. Neural body: Implicit neural representations with structured latent codes for novel view synthesis of dynamic humans. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 9054–9063, 2021.
- [33] Tobias Pfaff, Rahul Narain, Juan Miguel De Joya, and James F O’Brien. Adaptive tearing and cracking of thin sheets. ACM Transactions on Graphics (TOG), 33(4):1–9, 2014.
- [34] Gerard Pons-Moll, Sergi Pujades, Sonny Hu, and Michael J Black. Clothcap: Seamless 4d clothing capture and retargeting. ACM Transactions on Graphics (TOG), 36(4):1–15, 2017.
- [35] Xavier Provot et al. Deformation constraints in a mass-spring model to describe rigid cloth behaviour. In Graphics Interface (GI), pages 147–147. Canadian Information Processing Society, 1995.
- [36] Shenhan Qian, Jiale Xu, Ziwei Liu, Liqian Ma, and Shenghua Gao. Unif: United neural implicit functions for clothed human reconstruction and animation. In European Conference on Computer Vision (ECCV), pages 121–137, 2022.
- [37] Amit Raj, Julian Tanke, James Hays, Minh Vo, Carsten Stoll, and Christoph Lassner. Anr: Articulated neural rendering for virtual avatars. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 3722–3731, 2021.
- [38] Shunsuke Saito, Jinlong Yang, Qianli Ma, and Michael J Black. Scanimate: Weakly supervised learning of skinned clothed avatar networks. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 2886–2897, 2021.
- [39] Igor Santesteban, Miguel A Otaduy, and Dan Casas. Learning-based animation of clothing for virtual try-on. In Computer Graphics Forum, volume 38, pages 355–366. Wiley Online Library, 2019.
- [40] Igor Santesteban, Miguel A Otaduy, and Dan Casas. Snug: Self-supervised neural dynamic garments. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 8140–8150, 2022.
- [41] Karen Simonyan and Andrew Zisserman. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014.
- [42] Shih-Yang Su, Frank Yu, Michael Zollhöfer, and Helge Rhodin. A-nerf: Articulated neural radiance fields for learning human shape, appearance, and pose. Advances in Neural Information Processing Systems, 34:12278–12291, 2021.
- [43] Zhaoqi Su, Weilin Wan, Tao Yu, Lingjie Liu, Lu Fang, Wenping Wang, and Yebin Liu. Mulaycap: Multi-layer human performance capture using a monocular video camera. IEEE Transactions on Visualization and Computer Graphics (TVCG), 28(4):1862–1879, 2020.
- [44] Zhaoqi Su, Tao Yu, Yangang Wang, and Yebin Liu. Deepcloth: Neural garment representation for shape and style editing. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), 45(2):1581–1593, 2022.
- [45] Ayush Tewari, Ohad Fried, Justus Thies, Vincent Sitzmann, Stephen Lombardi, Kalyan Sunkavalli, Ricardo Martin-Brualla, Tomas Simon, Jason Saragih, Matthias Nießner, et al. State of the art on neural rendering. In Computer Graphics Forum, volume 39, pages 701–727. Wiley Online Library, 2020.
- [46] Ayush Tewari, Justus Thies, Ben Mildenhall, Pratul Srinivasan, Edgar Tretschk, Wang Yifan, Christoph Lassner, Vincent Sitzmann, Ricardo Martin-Brualla, Stephen Lombardi, et al. Advances in neural rendering. In Computer Graphics Forum, volume 41, pages 703–735. Wiley Online Library, 2022.
- [47] Garvita Tiwari, Bharat Lal Bhatnagar, Tony Tung, and Gerard Pons-Moll. Sizer: A dataset and model for parsing 3d clothing and learning size sensitive 3d clothing. In European Conference on Computer Vision (ECCV), pages 1–18, 2020.
- [48] Garvita Tiwari, Nikolaos Sarafianos, Tony Tung, and Gerard Pons-Moll. Neural-gif: Neural generalized implicit functions for animating people in clothing. In IEEE/CVF International Conference on Computer Vision (ICCV), pages 11708–11718, 2021.
- [49] Raquel Vidaurre, Igor Santesteban, Elena Garces, and Dan Casas. Fully convolutional graph neural networks for parametric virtual try-on. In Computer Graphics Forum, volume 39, pages 145–156. Wiley Online Library, 2020.
- [50] Huamin Wang, James F O’Brien, and Ravi Ramamoorthi. Data-driven elastic models for cloth: modeling and measurement. ACM Transactions on Graphics (TOG), 30(4):1–12, 2011.
- [51] Chung-Yi Weng, Brian Curless, Pratul P Srinivasan, Jonathan T Barron, and Ira Kemelmacher-Shlizerman. Humannerf: Free-viewpoint rendering of moving people from monocular video. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 16210–16220, 2022.
- [52] Donglai Xiang, Fabian Prada, Timur Bagautdinov, Weipeng Xu, Yuan Dong, He Wen, Jessica Hodgins, and Chenglei Wu. Modeling clothing as a separate layer for an animatable human avatar. ACM Transactions on Graphics (TOG), 40(6):1–15, 2021.
- [53] Hongyi Xu, Thiemo Alldieck, and Cristian Sminchisescu. H-nerf: Neural radiance fields for rendering and temporal reconstruction of humans in motion. Advances in Neural Information Processing Systems, 34:14955–14966, 2021.
- [54] Tao Yu, Zerong Zheng, Kaiwen Guo, Jianhui Zhao, Qionghai Dai, Hao Li, Gerard Pons-Moll, and Yebin Liu. Doublefusion: Real-time capture of human performances with inner body shapes from a single depth sensor. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 7287–7296, 2018.
- [55] Tao Yu, Zerong Zheng, Yuan Zhong, Jianhui Zhao, Qionghai Dai, Gerard Pons-Moll, and Yebin Liu. Simulcap: Single-view human performance capture with cloth simulation. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 5504–5514, 2019.
- [56] Ilya Zakharkin, Kirill Mazur, Artur Grigorev, and Victor Lempitsky. Point-based modeling of human clothing. In IEEE/CVF International Conference on Computer Vision (ICCV), pages 14718–14727, 2021.
- [57] Hongwen Zhang, Yating Tian, Xinchi Zhou, Wanli Ouyang, Yebin Liu, Limin Wang, and Zhenan Sun. Pymaf: 3d human pose and shape regression with pyramidal mesh alignment feedback loop. In IEEE/CVF International Conference on Computer Vision (ICCV), pages 11446–11456, 2021.
- [58] Zerong Zheng, Xiaochen Zhao, Hongwen Zhang, Boning Liu, and Yebin Liu. Avatarrex: Real-time expressive full-body avatars. ACM Transactions on Graphics (TOG), 42(4), 2023.
- [59] Heming Zhu, Yu Cao, Hang Jin, Weikai Chen, Dong Du, Zhangye Wang, Shuguang Cui, and Xiaoguang Han. Deep fashion3d: A dataset and benchmark for 3d garment reconstruction from single images. In European Conference on Computer Vision (ECCV), pages 512–530, 2020.
- [60] Heming Zhu, Lingteng Qiu, Yuda Qiu, and Xiaoguang Han. Registering explicit to implicit: Towards high-fidelity garment mesh reconstruction from single images. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 3845–3854, 2022.