Can a conventional optical camera realize turbulence-free imaging?

One of the most surprising consequences of quantum mechanics is the nonlocal correlation of a multiparticle system observable in the joint detection of distant particle detectors. Turbulence-free imaging is one such phenomena. Turbulence-free imaging was first realized with a dual light path ghost imaging framework [1,2]. Dual light path ghost imaging uses a correlation measurement between two spatially correlated beams to reconstruct the ghost image of an original object (Fig. 1a) [3,4]. One of the beams is called the reference arm, which never illuminates the object and is directly measured by a charged-coupled device (CCD). The other beam is the signal arm, which after illuminating the object is measured by a detector without spatial resolution. By a coincidence measurement of the signals from the two detectors, the ghost image is restructured. Different from ghost imaging, traditional optical imaging, which needs only one optical arm and one spatial resolution detector, directly measures the intensity distribution of the light field (Fig. 1b). Because of this, ghost imaging has some unique advantages that are important for scientific research [5-7], medical imaging [8-10], remote sensing [11], and night vision [12-14].

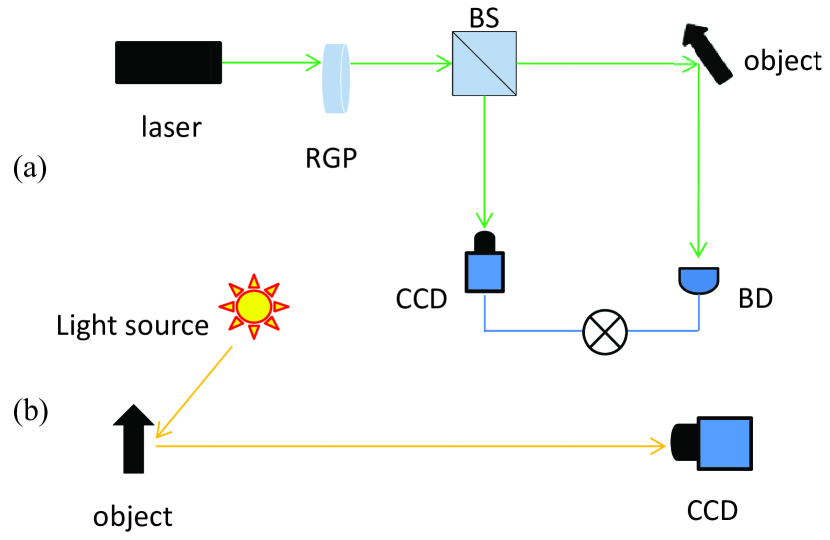
Although ghost imaging technology has many advantages, there is no property comparable to the incredible turbulence-free imaging property [1,2,15]. This practical property is an important milestone for optical imaging because any fluctuation index disturbance introduced in the optical path will not affect the image quality. However, conventional optical imaging cannot overcome the influence of atmospheric turbulence without image processing technology (see Appendix I for details). Previous works show that turbulence-free ghost imaging requires certain conditions [16,17]. For example, turbulence-free imaging requires that the two optical paths need to go through the same turbulence. Consequently, turbulence-free images cannot be obtained by conventional computational ghost imaging or single-pixel imaging [18]. Another condition requires that the transverse coherence size of the illumination light be less than that of the turbulence. Fortunately, the coherence size of sunlight is sufficiently small. For example, the coherence size of sunlight with a central wavelength of 550 nm on the ground is 0.08 mm. Consequently, sunlight is an ideal light source for turbulence-free imaging. Previous works show that ghost imaging can be realized by measuring the accumulation of the fluctuation intensity of sunlight at a certain time [17,19], which makes this problem solveable by ghost imaging.

The intensity correlation of the light field is a critical resource to realize turbulence-free imaging. However, conventional optical cameras cannot directly measure the intensity correlation of the light field [20]. Consequently, traditional optical imaging was affected by interference of atmospheric turbulence until the introduction of image processing. Now, satellite remote sensing images (e.g., Google Earth: 104.96E, 26.59N) still have distortions caused by atmospheric turbulence. Can turbulence-free imaging be achieved with only a conventional cameras and sunlight? In this article, we give an affirmative answer to this challenging question; i.e., a turbulence-free image can be obtained by processing the data collected by a conventional optical camera with a photon number fluctuation autocorrelation algorithm. Furthermore, we show that almost all conventional optical cameras, including mobile phones, can realize turbulence-free imaging by only adding this software and without changing their structures.

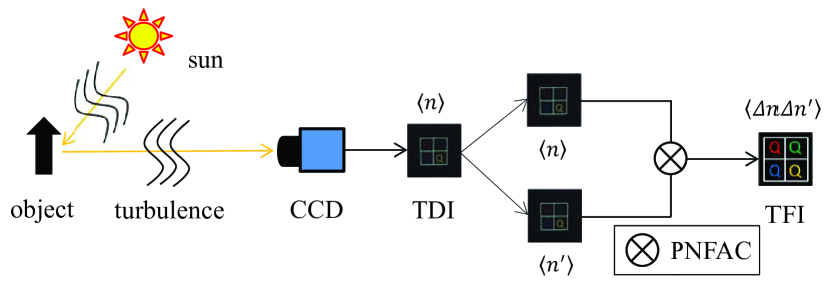
The conceptual arrangement of our method based on a conventional optical camera and sunlight is illustrated in Fig. 2. A beam of sunlight illuminates an object, and then its reflected light is directly received by a conventional optical CCD camera. Generally, we assume that atmospheric turbulence exists in the light path between the sun and the object and between the object and the camera. According to the imaging principle of optical cameras, the light field received by a camera can be expressed as

$$E\left(x\right)=\int\int dx_{i}dx_{o}E_{i}\left(x_{i}\right)g_{o}e^{\phi_{1}}T\left(x_{o}\right)g_{i}e^{\phi_{2}},$$

(1)

where $x_{o}$ and $x_{i}$ are the transverse coordinates in the object and image planes, respectively. $g_{o}$ is the Green’s function that propagates the light from the light source (coordinate $x_{i}$) to point $x_{o}$ on the object plane. $T(x)$ is the object. $g_{i}$ is the Green’s function that propagates the light field from $x_{o}$ to $x_{i}$ on the camera plane. $e^{\phi_{1}}$ and $e^{\phi_{2}}$ represent the atmospheric turbulence between the sun and the object and between the object and the camera, respectively [13-19,21,22]. The data are processed by the photon number fluctuation autocorrelation algorithm, and the reconstructed image can be expressed as

$$G^{\left(2\right)}=\left\langle\Delta n\Delta n^{{}^{\prime}}\right\rangle=\frac{1}{m}\left|\sum_{m}E_{m}^{\ast}\left(x\right)E_{m}^{{}^{\prime}}\left(x\right)\right|^{2},$$

(2)

where $m$ represents the number of measurements and $\Delta n$ and $\Delta n^{{}^{\prime}}$ represent the photon number fluctuations of $E$ and $E^{\prime}$, respectively. Equation 2 shows that a turbulence-free image can be obtained by our method (see Appendix II for details).

The photon number fluctuation autocorrelation algorithm is briefly described below (see Appendix III for details). The software first calculates the average counting numbers per each short time window $\overline{n}$. Two virtual logic circuits (post-neg identifiers) classify the counting numbers per window as positive and negative fluctuations based on $\overline{n}$. Thus, we have

	$\displaystyle\Delta n_{\alpha}^{(+)}$	$\displaystyle=\left\{\begin{array}[c]{c}n_{\alpha}-\overline{n},if,n_{\alpha}>\overline{n}\\ 0,otherwise\end{array}\right.$		(5)
	$\displaystyle\Delta n_{\alpha}^{(-)}$	$\displaystyle=\left\{\begin{array}[c]{c}n_{\alpha}-\overline{n},if,n_{\alpha}<\overline{n}\\ 0,otherwise,\end{array}\right.$		(8)

where $\alpha=1$ to $m$ and is used to label the $\alpha$th short time window. $m$ is the total number of time windows. Then, we define the following quantities for the statistical correlation calculations of

	$\displaystyle\left(\Delta n\Delta n^{\prime}\right)_{\alpha}^{\left(++\right)}$	$\displaystyle=\left|\Delta n_{\alpha}^{(+)}\Delta n_{\alpha}^{{}^{\prime}(+)}\right|,$
	$\displaystyle\left(\Delta n\Delta n^{\prime}\right)_{\alpha}^{\left(--\right)}$	$\displaystyle=\left|\Delta n_{\alpha}^{(-)}\Delta n_{\alpha}^{{}^{\prime}(-)}\right|,$
	$\displaystyle\left(\Delta n\Delta n^{{}^{\prime}}\right)_{\alpha}^{\left(+-\right)}$	$\displaystyle=\left|\left(\overline{n}-\Delta n_{\alpha}^{(+)}\right)\left(\overline{n}-\Delta n_{\alpha}^{{}^{\prime}(-)}\right)\right|,$
	$\displaystyle\left(\Delta n\Delta n^{{}^{\prime}}\right)_{\alpha}^{\left(-+\right)}$	$\displaystyle=\left|\left(\overline{n}-\Delta n_{\alpha}^{(-)}\right)\left(\overline{n}-\Delta n_{\alpha}^{{}^{\prime}(+)}\right)\right|.$		(9)

Thus, the corresponding statistical average of $\left\langle\Delta n\Delta n^{{}^{\prime}}\right\rangle$ is

	$\displaystyle\left\langle\Delta n\Delta n^{{}^{\prime}}\right\rangle$	$\displaystyle=\frac{1}{m}\left[\sum_{\alpha=1}^{m}\left(\Delta n\Delta n^{{}^{\prime}}\right)_{\alpha}^{\left(++\right)}+\sum_{\alpha=1}^{m}\left(\Delta n\Delta n^{{}^{\prime}}\right)_{\alpha}^{\left(--\right)}\right.$
		$\displaystyle+\left.\sum_{\alpha=1}^{m}\left(\Delta n\Delta n^{{}^{\prime}}\right)_{\alpha}^{\left(+-\right)}+\sum_{\alpha=1}^{m}\left(\Delta n\Delta n^{{}^{\prime}}\right)_{\alpha}^{\left(-+\right)}\right].$		(10)

A schematic of the experimental setup is shown in Fig. 2. It is a typical and traditional optical imaging schematic, except for the addition of data processing software. In this experiment, atmospheric turbulence is introduced by adding heating elements underneath any or all optical paths, as illustrated in Fig. 2. Heating of the air causes temporal and spatial fluctuations in the index of refraction and makes the traditional image of the object jitter about randomly on the image plane causing the image to become distorted. The sunlight illuminates the object (the letter “Q”) located at $x_{o}$. The photons reflected from the object are collected and counted by a conventional industrial camera (The Imaging Source DFK23U618). The path from the object to the detector over heating elements is 0.4 m. The CCD camera is controlled by software to collect data. A photon number fluctuation autocorrelation algorithm program is used to process the data.

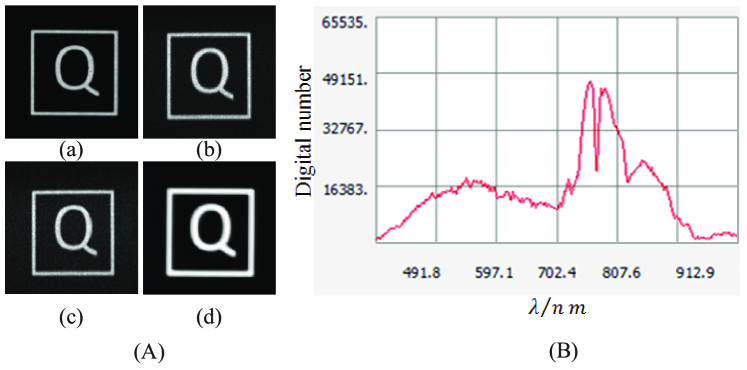
Fig. 3 shows a set of typical experimental results. Fig. 3A(a) and Fig. 3B(a) show two traditional optical images without turbulence, i.e., $\left\langle n\right\rangle$. Figs. 3A(b-e) show four distorted traditional images caused by atmospheric turbulence. Correspondingly, Figs. 3B(b-e) show four turbulence-free images reconstructed by the photon number fluctuation autocorrelation algorithm; i.e., $\left\langle\Delta n\Delta n^{{}^{\prime}}\right\rangle$. To quantitatively analyse the quality of the reconstructed image, the structural similarity index (SSIM) is used as an evaluation index. Table 3C shows that the image reconstructed by this method can indeed be regarded as a turbulence-free image.

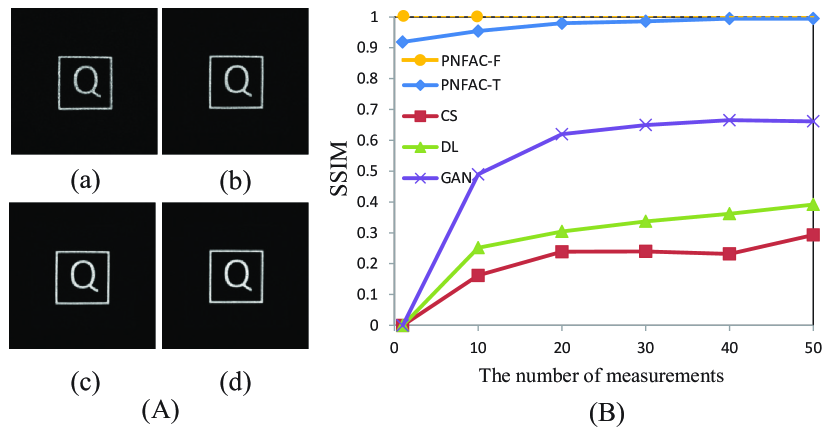
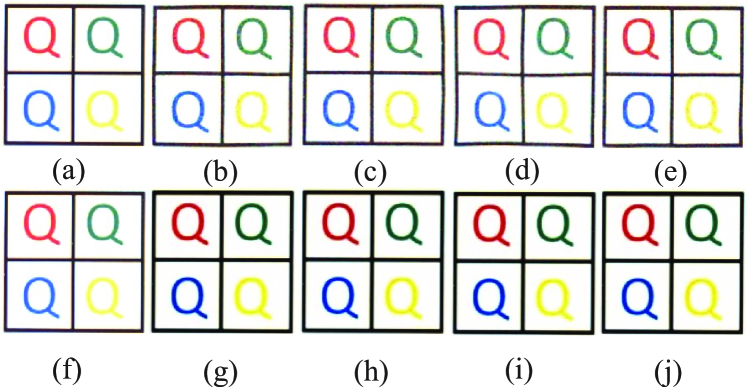
Due to the novel imaging mode, another significant advantage of this method is that it has a fast imaging speed and can meet the requirements of practical applications. The imaging speed of this method in a turbulent environment is almost comparable to that of traditional optical imaging in an environment without turbulence. The imaging speed of this method in turbulent environments is significantly better than that of conventional ghost imaging with optimization schemes in environments without turbulence [23-29]. Fig. 4A presents a set of experimental results. The experimental results show that a turbulence-free image with quality comparable to that of traditional optical imaging can be obtained with only 1 measurement, which is an almost impossible challenge for ghost imaging frameworks. The results of several other typical ghost imaging methods without turbulence and this method are presented and compared in Fig. 4B. Surprisingly, the image obtained by this method is completely consistent with the traditional optical image after 1 measurement in the environment without atmospheric turbulence. Moreover, a traditional optical imaging video and a video obtained with this method are shown and compared in the appendix. Fig. 5 is a set of colour turbulence-free images reconstructed by this method. The results show that this method can be directly applied to existing colour optical cameras. Another traditional optical imaging video and a video obtained with this method are shown in the appendix.

To demonstrate the feasibility of this method on a variety of cameras, we selected several typical cameras for experiments. The results are shown in Fig. 6. Here, we present the black-and-white image results because some cameras, such as infrared cameras, can only directly output black-and-white images. Fig. 6 shows that even a conventional mobile phone camera can realize turbulence-free imaging.

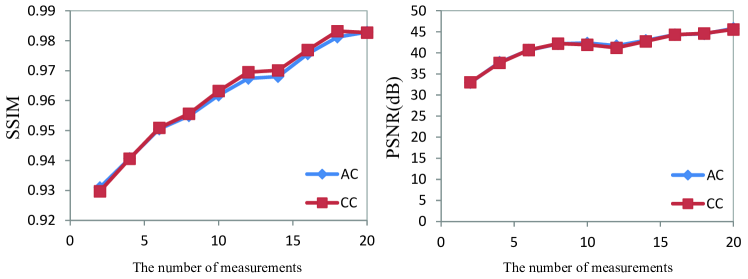
It should be emphasized that the photon number fluctuation autocorrelation algorithm can be used when the camera collects only one data. However, the results obtained by the photon number fluctuation autocorrelation algorithm and the photon number fluctuation crosscorrelation algorithm are consistent when the camera collects two or more data. See Appendix III for theoretical demonstration. To quantitatively demonstrate this property, we use the structural similarity (SSIM) and PSNR to measure the experimental results (Fig. 7).

These experiments represent the first demonstration of turbulence-free imaging realized on a conventional optical camera. Using the accumulation of intensity fluctuations of the light field at a certain time and the photon number fluctuation autocorrelation algorithm, our results illustrate how a conventional optical camera without any structural changes can produce a turbulence-free colour image. Moreover, we demonstrate that the imaging speed of this method is the same as that of traditional optical imaging in environments without atmospheric turbulence and is comparable to that of traditional optical imaging in environments with atmospheric turbulence. This imaging speed meets the practical application requirements of existing cameras. This technique provides a promising solution to images affected by atmospheric turbulence. More importantly, this technique can be applied quickly.

This project was supported by the National Natural Science Foundation (China) under grant nos. 11704221, 11574178 and 61675115 and the Taishan Scholar Project of Shandong Province (China) under grant no. tsqn201812059.

The authors declare that there are no conflicts of interest related to this article.