Camera-Space Hand Mesh Recovery via Semantic Aggregation
and Adaptive 2D-1D Registration
Abstract
Recent years have witnessed significant progress in 3D hand mesh recovery. Nevertheless, because of the intrinsic 2D-to-3D ambiguity, recovering camera-space 3D information from a single RGB image remains challenging. To tackle this problem, we divide camera-space mesh recovery into two sub-tasks, i.e., root-relative mesh recovery and root recovery. First, joint landmarks and silhouette are extracted from a single input image to provide 2D cues for the 3D tasks. In the root-relative mesh recovery task, we exploit semantic relations among joints to generate a 3D mesh from the extracted 2D cues. Such generated 3D mesh coordinates are expressed relative to a root position, i.e., wrist of the hand. In the root recovery task, the root position is registered to the camera space by aligning the generated 3D mesh back to 2D cues, thereby completing camera-space 3D mesh recovery. Our pipeline is novel in that (1) it explicitly makes use of known semantic relations among joints and (2) it exploits 1D projections of the silhouette and mesh to achieve robust registration. Extensive experiments on popular datasets such as FreiHAND, RHD, and Human3.6M demonstrate that our approach achieves state-of-the-art performance on both root-relative mesh recovery and root recovery. Our code is publicly available at https://github.com/SeanChenxy/HandMesh.
1 Introduction
Monocular 3D mesh recovery has attracted tremendous attention due to its extensive applications in AR/VR, human–machine interaction, etc. The task is to estimate 3D locations of mesh vertices from a single RGB image. It is particularly challenging owing to highly articulated structures, 2D-to-3D ambiguity, and self-occlusion. Significant efforts have been made recently for accurate 2D-to-3D reconstruction, including [16, 17, 20, 21, 23, 27, 30, 31, 32, 33, 36, 39], to name a few.
Most of the aforementioned methods [6, 9, 16, 20, 21, 22, 27, 40, 43] have difficulty in predicting absolute camera-space coordinates. Instead, they define a root (i.e., wrist of the hand) and estimate root-relative coordinates of the 3D mesh. In this aspect, these methods cannot be applied to many high-level tasks, e.g., hand-object interaction, that requires camera-space mesh information. To this end, we propose to jointly solve root-relative mesh recovery and root recovery by integrating these two sub-tasks into a unified framework, thereby bridging the gap between root-relative predictions and camera-space estimation.
RGB images consist of 2D patterns that are indirect cues of the underlying 3D structure. Therefore, 2D cues have long been leveraged to assist 3D tasks. For example, 2D pose and silhouette have been used to facilitate 3D pose regression [9, 20, 27, 33, 42, 43, 44].
However, the relationship between 2D cues and 3D structure remains unclear. We observe that 2D joint landmarks together with their semantic relations describe the 2D pose, while the silhouette indicates the holistic 3D-to-2D projection of the hand. They have different 2D properties and should be treated in different manners in the 3D task. Inspired by these observations, we set to explore the following aspects of the 2D-to-3D task: (1) different roles of 2D cues, (2) the reason for their different effects, and (3) how to construct more effective 2D cues.
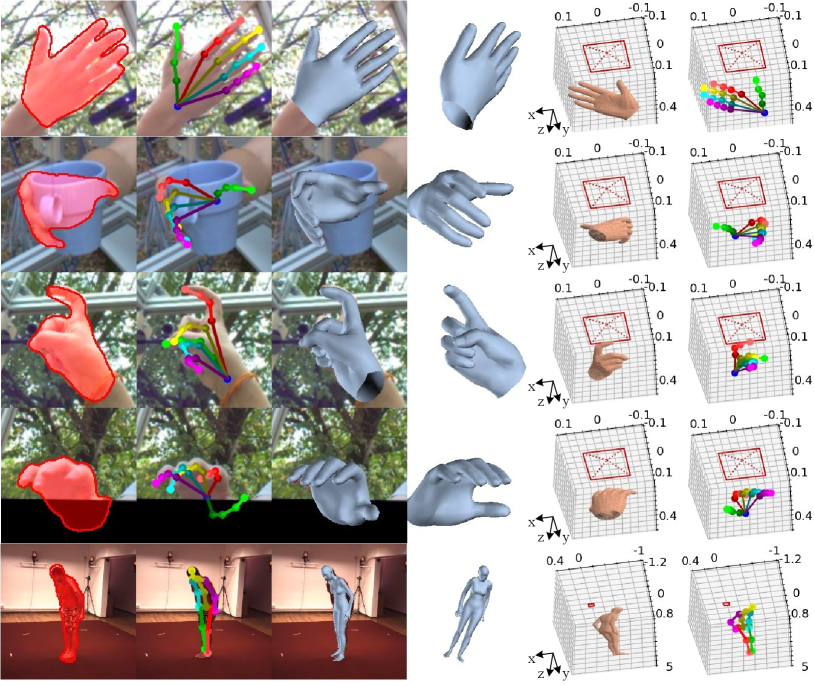
In this paper, we propose a camera-space mesh recovery (CMR) framework to integrate the tasks of 3D hand mesh and root recovery into a unified framework. CMR consists of three phases, i.e., 2D cue extraction, 3D mesh recovery, and global mesh registration. For 2D cue extraction, we predict joint landmarks and silhouette from a single RGB image. For mesh recovery, we introduce an Inception Spiral Module for robust 3D decoding. Moreover, an aggregation method is designed for composing more effective 2D cues. Specifically, instead of implicitly learning the relations among joints, we exploit their known relations by aggregating landmark heatmaps in groups, which proves to be effective for the subsequent 3D task. Finally, camera-space root location is obtained by a global mesh registration step that aligns the generated 3D mesh with the extracted 2D landmarks and silhouette. This step is carried out via an adaptive 2D-1D registration method that achieves robustness by leveraging matching objectives in different dimensions. Our full pipeline surpasses state-of-the-art methods in the 3D mesh and root recovery tasks. While our approach is mainly described for hand mesh, it can be readily applied to full-body mesh as shown in the experiments. Figure 1 demonstrates several example results of our CMR for camera-space mesh recovery.
Our main contributions are summarized as follows:
-
•
We propose a novel aggregation method to collect effective 2D cues and exploit high-level semantic relations for root-relative mesh recovery.
-
•
We design an adaptive 2D-1D registration method to sufficiently leverage both joint landmarks and silhouette in different dimensions for robust root recovery.
-
•
We present a unified pipeline CMR for camera-space mesh recovery and demonstrate state-of-the-art performance on both mesh and root recovery tasks via extensive experiments on FreiHAND, RHD, and Human3.6M.
2 Related Work
Root-relative mesh/pose recovery.
According to different output property, we categorize methods for single-view RGB-based mesh recovery into three types, i.e., RGBMANO/SMPL [16, 40, 42, 44], RGBVoxel [15, 27, 32, 39], and RGBCoord (coordinate) [8, 9, 21, 22].
MANO [35] and SMPL [25] are parameterized 3D models of hand and human body, factorizing 3D human mesh into coefficients of shape and pose. Tremendous literature attempts to predict these coefficients for human/hand mesh recovery. For example, Zhou et al. [44] estimated MANO coefficients based on the kinematic chain and developed an inverse kinematics network to improve prediction accuracy on pose coefficients. MANO/SMPL can reconstruct 3D mesh, but they embed 3D information into a parametrized space (e.g., PCA space), where the 3D structure is less straightforward (compared to 3D vertices).
Voxel is one type of Euclidean 3D representation, to which the canonical convolutional operator can be directly applied [28]. Thereby, the mesh recovery task can be explored in voxels. For example, Moon et al. [27] proposed an I2L-MeshNet by dividing voxels into three lixel spaces, where a 2.5D representation is leveraged for human mesh. The voxel/2.5D-based paradigm has impressive performance in terms of human mesh recovery because the merits of Euclidean space are fully leveraged. However, voxel/2.5D representations are not efficient enough in capturing 3D details (compared to 3D vertices).
Defferrard et al. [7] proposed a graph convolution network (GCN) based on spectral filtering to process 3D vertices in the non-Euclidean space. Based on GCN, Kolotouros et al. [21] developed a graph convolutional mesh regressor to directly estimate the 3D coordinates of mesh vertices. Ge et al. [9] also developed a graph-based method for hand mesh recovery by learning from mixed real and synthetic data. Instead of spectral filtering, Lim et al. [24] proposed spiral convolution (SpiralConv) to process mesh data in the spatial domain. Based on SpiralConv, Kulon et al. [22] developed an encoder-decoder structure for efficient hand mesh recovery. We follow the RGBCoord paradigm and explore versatile aggregation of 2D cues.
Root recovery.
In analogy to root recovery, estimation of external camera parameters has been widely studied [3, 16, 42]. For instance, Zhang et al. [42] designed an iterative regression method to simultaneously estimate external camera parameters and MANO coefficients. However, camera parameter estimation from RGB data is an ill-posed problem, leading to relatively low generalization performance. Moon et al. [26] proposed RootNet to predict the absolute 3D human root. RootNet essentially modeled object size in images, but the pixel-level object area has a relatively low correlation with 3D root. Rogez et al. [34] predicted both 2D and 3D pose so that the 3D root location can be obtained by aligning predicted 2D pose with projected 3D pose. We argue that this 2D-3D alignment cannot sufficiently leverage 2D information and propose an adaptive 2D-1D registration method for root recovery.
2D cues in 3D shape/pose recovery.
Researchers have long exploited 2D cues in recovering 3D human shape and body parts. Pavlakos et al. [33] utilized 2D pose to regress pose coefficients and used silhouette to estimate shape coefficients. Varol et al. [39] first predicted 2D joint landmarks and body part segmentation, both of which were then combined to predict 3D pose. In this work, we aim to investigate how 2D cues work in 3D tasks and to leverage them effectively for hand mesh and root recovery.
3 Our Method
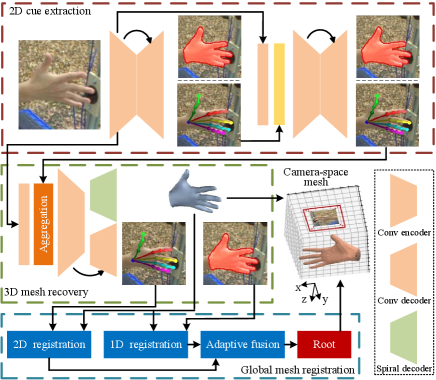
To represent a 3D mesh in camera-space, we divide it into the root-relative mesh and the camera-space root location. As shown in Figure 2, CMR includes three phases, i.e., 2D cue extraction, 3D mesh recovery, and global mesh registration. In the step of 2D cue extraction, we predict 2D pose and silhouette, which are used later for both mesh and root recovery. In the step of 3D mesh recovery, we generate a root-relative mesh which is then registered to the camera space in the final phase of the pipeline.
3.1 Mesh Recovery by Semantic Aggregation
2D cues for 3D mesh recovery.
The first phase of our pipeline extracts 2D pose and silhouette. Both 2D pose and silhouette are represented by heatmaps. To refine the 2D cues gradually, we use a multi-stack hourglass network [29].
The 3D mesh is defined by its shape and pose [35]. The silhouette is a holistic 3D-to-2D projection so it captures important shape cues. However, it can hardly describe the pose accurately. On the other hand, joint landmark locations are very informative for the pose. Given their different roles, how to better combine them becomes an interesting question. Therefore, we have an insight that to improve accuracy of the subsequent 3D tasks, it is essential not only to improve the accuracy of the 2D tasks respectively, but also to better aggregate them according to their semantic relations. Specifically, we propose to aggregate a series of 2D cues denoted as follows:

-
•
: heatmaps of 2D poses. Each heatmap corresponds to a joint landmark.
-
•
: a single heatmap of the silhouette.
-
•
cat(): concatenating heatmaps of and to aggregate 2D pose and silhouette.
-
•
sum(): combining all the joint landmarks as a single heatmap to aggregate joint locations.
-
•
group(): concatenating and tip-, part- , or level-grouped landmarks to aggregate joint semantics for high-level semantic relations.
2D silhouette and joint landmarks represent pixel-level locations in different aspects. A straightforward way of combining them is cat(). Another simple baseline, sum(), would discard semantics of individual joints by encoding their locations in a single heatmap. Thus, comparing and sum() would reveal the effect of joint semantics. These simple baselines, as we will show, are inferior to more semantically meaningful ways of aggregation: group(). That is, we sum the joint heatmaps in groups. As shown in Figure 3, three ways of grouping are introduced, i.e., by part, by level, and by tip grouping. Part grouping integrates joint landmarks on a finger, leg, arm, or torso, while level grouping integrates joint landmarks at the kinematic level [44]. Tip grouping integrates pairwise part tips. As a result, group() forms sub-poses that exploit high-level semantic relation of 2D joints.
Spiral decoder.
The second phase of our pipeline generates the root-relative 3D mesh from the aggregated 2D cues using an improved spiral convolution decoder.
A 3D mesh contains vertices and faces . Convolution methods for essentially process vertex features . SpiralConv [24] is a graph-based convolution operator, which processes vertex features in the spatial domain. By explicitly formulating the order of aggregating neighboring vertices, SpiralConv++ [10] presents an efficient version of SpiralConv. SpiralConv++ depends on a spiral manner of neighbor selection and adopts a fully-connected layer for feature fusion:
| (1) | ||||
where represents vertex neighborhood, and are weights and bias shared for .
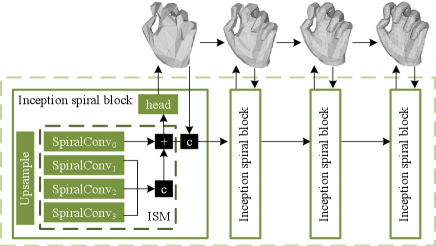
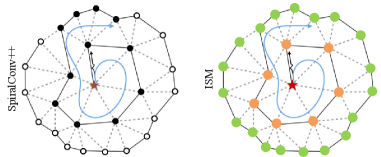
As shown in Figure 4(left), SpiralConv++ collects vertex neighbors (black dots) of the cell (red star) in a spiral manner. Then these neighbors are treated indiscriminately by a fully connected layer. Inspired by Inception and residual models [13, 38], we design an Inception Spiral Module (ISM) to enhance the receptive field of SpiralConv. Specifically, as shown in Figure 4(right), we distinguish neighbors according to the spiral hierarchy (red, orange, and green dots) and adopt parallel layers with diverse receptive field for 3D decoding. The ISM can be described as
| (2) | ||||
where denotes concatenating. In ISM we keep the number of parameters manageable by controlling the channel size of . Note that the for each vertex may contain different number of elements. Similar to SpiralConv++, we truncate it to obtain a fixed-length sequence so that and can be shared for all the vertices.
The overall architecture of our 3D mesh decoder is shown in Figure 5. Our design improves the spiral decoder in three aspects: (1) we replace SpiralConv with ISM; (2) we leverage multi-scale prediction and coarse-to-fine fusion; and (3) we introduce a self-regression mechanism by concatenating scale-level predictions with the same-scale feature. Meanwhile, we use a convolutional decoder which runs in parallel with the spiral decoder to refine the estimation of 2D pose and silhouette.
3.2 Root Recovery by Global Mesh Registration
1D projections.
The silhouette reflects holistic 3D-to-2D projection and contains strong geometric information for root recovery. Given the intrinsic matrix of the camera, predicted 3D vertices can be projected into the 2D space by , resulting in a 2D mesh which consists of 2D vertices with the original connectivity. Ideally, the 2D mesh should align well with the silhouette. However, they cannot be directly aligned because (1) the large number of 2D points leads to prohibitive computational cost, i.e., the silhouette contains thousands of pixels while the 2D mesh has 778 (for hand) or 6,890 (for human body) vertices; (2) 2D mesh vertices have no explicit correspondence with respect to the silhouette.
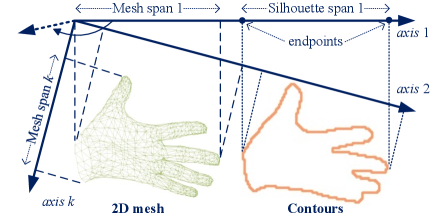
To overcome these difficulties, we design a group of 1D projections to align the silhouette with the 2D mesh. First, the silhouette is converted into contours by edge detection [5]. We define a set of 1D axes . These axes have unit length and are uniformly distributed, i.e., the angle difference between neighboring axes is . As shown in Figure 6, we project contours and 2D vertices onto , resulting in their 1D span, i.e., and .
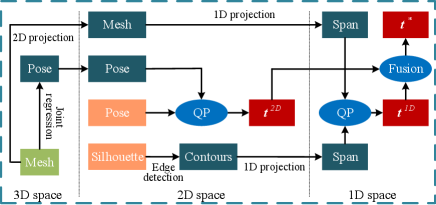
Adaptive 2D-1D registration.
We denote the camera-space root by and 2D joint landmark predictions by . Given and joint regressor defined by MANO [35] or SMPL [25], the camera-space 3D vertices can be converted into 2D joints by . Since and have intrinsic correspondence, we define the energy function for 2D matching as
| (3) |
whose solution is denoted as . Further, we use to implement the aforementioned 3D-2D-1D projection. Camera-space is thereby produced. Then the 1D correspondence is obtained using two endpoints of the 1D span. The energy function for alignment of 1D spans is defined as
| (4) |
In 1D space, . Both 2D and 1D optimizations are based on quadratic programming [2]. With and , we develop an adaptive method for the final root with their distance :
| (5) |
where , both of which are robust hyper-parameters according to 3D scale. Without wide search, we empirically use for the hand and for the body. This design attempts to sufficiently leverage the merits of 2D-1D registration. It is known that 2D pose is more fragile than silhouette. Hence, 2D pose is prone to be erroneous when there is a huge 2D-1D discrepancy, and silhouette is more dependable if . From another perspective, joint correspondence is more explicit than that of 1D projection. Thereby, the 2D process is more reliable if 2D and 1D results are similar (). The whole process of adaptive 2D-1D registration is presented in Figure 7, from which we can see that geometrical information is sufficiently exploited from 3D to 1D spaces for root recovery.
3.3 Loss Functions
We use L1 norm for loss terms of 3D mesh/pose , and our 2D pose/silhouette losses are based on binary cross entropy (BCE). We adopt normal loss and edge length loss for smoother reconstruction [9]. Formally, we have
| (6) | ||||
where are faces and vertices of a mesh; are the pose regressor and 3D joints; indicates unit normal vector of face ; are heatmaps of 2D pose and silhouette; and denotes the ground truth. Following [27], is constructed with Gaussian distribution.
Our overall loss function is , where are used to balance different terms.
4 Experiments
4.1 Experimental Setup
We conduct experiments on several commonly-used benchmarks as listed below.
- FreiHAND
-
[46] is a 3D hand dataset with 130,240 training images and 3,960 evaluation samples. The annotations of the evaluation set are not available, so we submit our predictions to the official server for online evaluation.
- Rendered Hand Pose Dataset (RHD)
-
[45] consists of 41,258 and 2,728 virtually rendered samples for training and testing on hand pose estimation, respectively.
- Human3.6M
-
[14] is a large-scale 3D body pose benchmark containing 3.6 million video frames with annotations of 3D joint coordinates. SMPLify-X [30] is used to obtain ground-truth SMPL coefficients. We follow existing methods [6, 16, 27, 32] to use subjects S1, S5, S6, S7, S8 for training and subjects S9, S11 for testing.
- COCO
We use the following metrics in quantitative evaluations.
- MPJPE/MPVPE
-
measures the mean per joint/vertex position error in terms of Euclidean distance (mm) between the root-relative prediction and ground-truth coordinates.
- PA-MPJPE/MPVPE
-
is the MPJPE/MPVPE based on procrustes analysis [11] with global variation being ignored.
- CS-MPJPE/MPVPE
-
measures MPJPE/MPVPE in the camera space for evaluation of the root recovery task.
- AUC
-
is the area under the curve of PCK (percentage of correct keypoints) vs. error thresholds.
Implementation details.
Our backbone is based on ResNet [13] and we use the Adam optimizer [19] to train the network with a mini-batch size of . Serving as network inputs, image patches are cropped and resized to resolutions of (for the hand) or (for the body). Because of different data amounts, the total number of iterations is set as 38 and 25 epochs for tasks on hand and body. The initial learning rate is , which is divided by at the 20th or 30th epoch. Data augmentation includes random box scaling/rotation, color jitter, etc.
4.2 Ablation Study
Baseline.
Our ablation studies are based on ResNet18. YoutubeHand [22] serves as the baseline, but its code and models are inaccessible. Our re-implemented model obtains mm PA-MPVPE (see Table 1). With our spiral decoder, mm PA-MPVPE is achieved. Thus, our designs can strengthen the robustness of 2D-to-3D decoding.
| Method | PA-MPJPE | PA-MPVPE |
|---|---|---|
| YoutubeHand [22] | 8.82 | 9.06 |
| + Our spiral decoder | 8.46 | 8.54 |
| Stack 1 | Stack 2 | PA-MPJPE | PA-MPVPE |
|---|---|---|---|
| 8.46 | 8.54 | ||
| 8.05 | 8.10 | ||
| 7.71 | 7.77 | ||
| cat() | 7.83 | 7.95 | |
| sum() | 7.89 | 7.94 | |
| group() | 7.55 | 7.60 | |
| group() | 7.47 | 7.55 | |
| group() | 7.39 | 7.46 |
Effects of various 2D cues.
This paper explores cues of 2D pose and silhouette for 3D mesh recovery, and a two-stack network is leveraged. At first, discarding the second stack, we only use one encoder-decoder structure for exposing details of 2D-cue effects. As shown in Table 2, leads to mm PA-MPVPE while sum() reduces PA-MPVPE to mm. Both and sum() are heatmaps that contain location information, so the locations of joint landmarks are more instructive than that of a holistic shape. This phenomenon is evident, because pose is more difficult to estimate than shape, and joint locations can directly provide cues on poses. Furthermore, leads to an improved PA-MPVPE of mm by providing both joint locations and semantics. Compared to sum(), it is seen that joint semantics is also important. In addition, the effect of cat() is worse than that of . Therefore, there is no complementary benefit from 2D pose and silhouette.
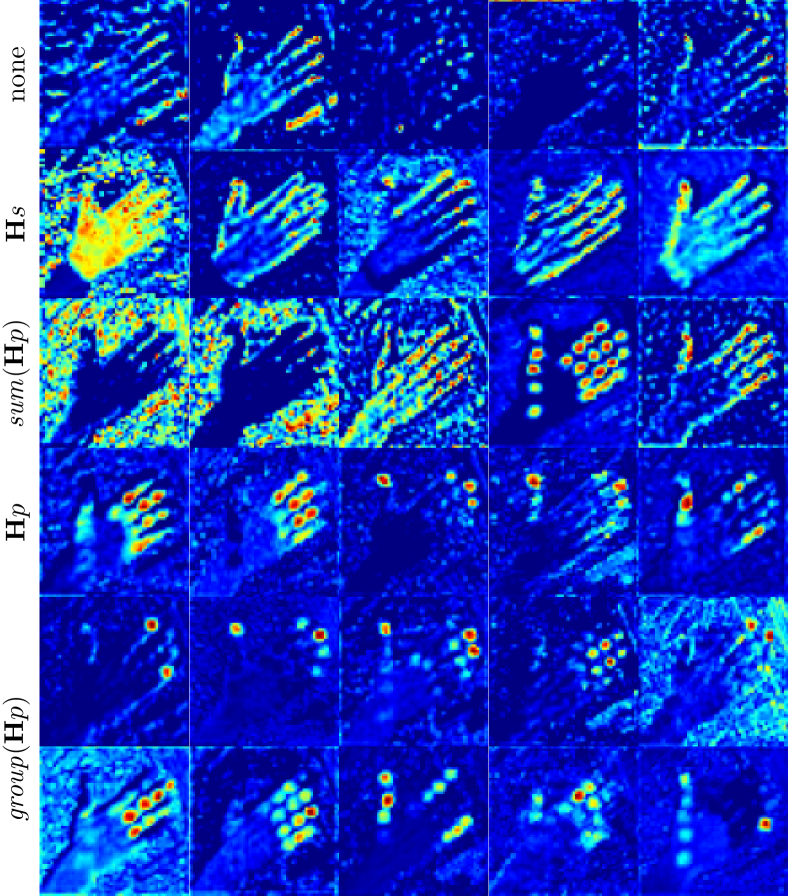
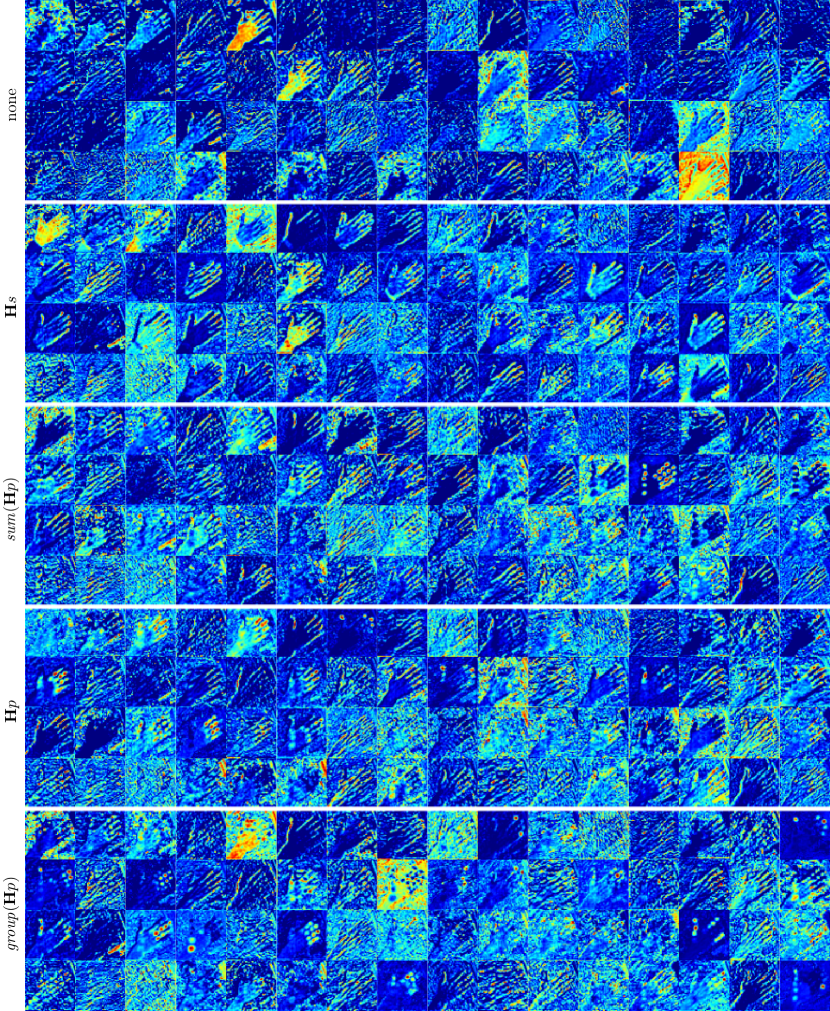
To reveal potential reasons for different effects of 2D cues, we dissect feature representation acted by them. It is known that channel-specific feature usually embeds semantics, so we focus on typical channels in the first encoding block in the 3D mesh recovery phase. As shown in Figure 8, this block tends to describe trivial properties such as edges (see “none”). If is employed, holistic 2D shapes emerge, but pose cues are ignored. With sum(), holistic 2D shapes still can be learned based on joint landmark locations. Thus, this phenomenon can be the reason why there exists no complementary benefit in joint landmarks and silhouette. Moreover, holistic joint locations can also be captured with sum(). As for , although joint information is provided in separate heatmaps, the features after have a tendency that multiple joints are simultaneously activated. Features shown in of Figure 8 imply semantic relation of joints, which can have significant impact on 3D tasks. However, relation representation invited by is not exhaustive enough. Specifically, the left two representations have similar patterns while both the 3rd and 4th representations mainly focus on the tips of thumb and middle finger.
| Parts | Levels | Tips | PA-MPJPE | PA-MPVPE |
|---|---|---|---|---|
| 7.71 | 7.77 | |||
| ✓ | 7.58 | 7.65 | ||
| ✓ | 7.63 | 7.69 | ||
| ✓ | 7.58 | 7.65 | ||
| ✓ | ✓ | 7.55 | 7.60 | |
| ✓ | ✓ | ✓ | 7.62 | 7.70 |
| Model | Root recovery | CJ | CV |
| Absolute coordinate prediction | 77.6 | 77.4 | |
| CMR-P (2D AUC=0.762, mIoU=0.824) | PnP | 98.9 | 99.0 |
| RootNet | 63.0 | 62.9 | |
| 2D (ours) | 53.7 | 53.7 | |
| 1D (ours,=2) | 55.8 | 55.8 | |
| 2D+1D (ours,=2) | 52.7 | 52.7 | |
| 2D+1D (ours,=12) | 52.1 | 52.1 | |
| CMR-PG (2D AUC=0.798, mIoU=0.826) | RootNet | 62.7 | 62.7 |
| 2D (ours) | 51.5 | 51.5 | |
| 1D (ours,=2) | 54.3 | 54.3 | |
| 2D+1D (ours,=2) | 51.1 | 51.1 | |
| 2D+1D (ours,=12) | 50.6 | 50.6 | |
| CMR-SG (2D AUC=0.790, mIoU=0.832) | RootNet | 62.8 | 62.7 |
| 2D (ours) | 52.0 | 52.0 | |
| 1D (ours,=2) | 52.6 | 52.6 | |
| 2D+1D (ours,=2) | 50.4 | 50.4 | |
| 2D+1D (ours,=12) | 49.7 | 49.8 | |
Effects of semantic aggregation.
Instead of implied relation learning, group() aims to aggregate joint semantics for explicit semantic relation. Referring to Table 3, part-, level-, and tip-based relations have instructive effects, and the integration of part- and tip-based relations leads to better performance on mesh recovery. Part-based aggregation provides within-part relations while tip-based aggregation models pairwise cross-part relations, so they are complementary for creating robust semantic relations. As a result, group() surpasses by mm on PA-MPVPE, i.e., mm. Referring to Figure 8, compared to , group() captures more exhaustive semantic relation, e.g., finger parts and various combinations of fingertips.
Besides, the two-stack network can provide more effective 2D cues, leading to better PA-MPVPE (see Table 2). Let CMR-P, CMR-SG, and CMR-PG be models shown in the 3rd, 7th, and 8th rows of Table 2 for later analysis.
Effects of adaptive 2D-1D registration.
We train a model that directly predicts absolute camera-space coordinates for comparison. Although this operation easily suffers from overfitting, it can handle the single-dataset task, obtaining mm CS-MPVPE (see Table 4.2). Perspective-n-Point (PnP) is a standard approach that solves external parameters of a camera based on pairwise 2D-3D points [18]. Based on 2D joint landmarks and root-relative 3D joints from CMR-P, the PnP method can predict absolute root coordinates. However, it obtains mm CS-MPVPE, lagging considerably behind the baseline. With our 2D or 1D registration, CMR-P achieves mm or mm CS-MPVPE, so both our 2D and 1D designs are valid. In detail, 2D registration is better because of unambiguous 2D-3D correspondence. Furthermore, based on our proposed adaptive fusion, the adaptive 2D-1D registration achieves mm CS-MPVPE. When , the 2D-1D process can induce a better CS-MPVPE of mm. Thus, our adaptive 2D-1D registration can sufficiently leverage 2D cues from joint landmarks and silhouette for root recovery.
| Method | PJ | PV | CJ | CV |
| Boukhayma et al.[3] | 35.0 | 13.2 | ||
| ObMan [12] | 13.3 | 13.3 | 85.2 | 85.4 |
| MANO CNN [46] | 11.0 | 10.9 | 71.3 | 71.5 |
| YotubeHand [22] | 8.4 | 8.6 | ||
| Pose2Mesh [6] | 7.7 | 7.8 | ||
| I2L-MeshNet[27] | 7.4 | 7.6 | 60.3 | 60.4 |
| CMR-SG (ResNet18) | 7.5 | 7.6 | 49.7 | 49.8 |
| CMR-PG (ResNet18) | 7.4 | 7.5 | 50.6 | 50.6 |
| CMR-SG (ResNet50) | 7.0 | 7.1 | 48.8 | 48.9 |
| CMR-PG (ResNet50) | 6.9 | 7.0 | 48.9 | 49.0 |
| Human3.6M | Human3.6M+COCO | ||||||
| Method | Type | MPJPE | PA-MPJPE | MPJPE | PA-MPJPE | FPS | GPU Mem. |
| HMR [16] | RGBSMPL | 184.7 | 88.4 | 153.2 | 85.5 | ||
| SPIN [20] | RGBSMPL | 85.6 | 55.6 | 72.9 | 51.9 | ||
| Pose2Mesh [6] | PoseCoord | 64.9 | 48.7 | 67.9 | 49.9 | 4 | 6G |
| I2L-MeshNet [27] | RGBVoxel | 82.6 | 59.8 | 55.7 | 41.7 | 25 | 4.6G |
| GraphCMR [21] | RGBCoord | 148.0 | 104.6 | 78.3 | 59.5 | ||
| CMR-PG (ours, ResNet18) | RGBCoord | 67.9 | 49.9 | 59.0 | 44.7 | 59 | 1.5G |
| CMR-PG (ours, ResNet50) | RGBCoord | 69.8 | 47.9 | 57.3 | 42.6 | 30 | 1.9G |
With CMR-PG and CMR-SG, the same tendency emerges, which also validates the effectiveness of our designs. Note that CMR-PG induces better 2D pose (i.e., AUC) while CMR-SG invites better silhouette (i.e., mIoU), so their 2D and 1D performances are distinct. Overall, CMR-SG achieves the best performance on root recovery and camera-space mesh recovery.
4.3 Comparisons with Existing Methods
We perform a comprehensive comparison on the FreiHAND dataset. As shown in Table 5, our proposed CMR outperforms other methods in terms of all the aforementioned metrics. Specifically, ResNet50-based CMR-PG achieves the best performance on root-relative mesh recovery, i.e., mm PA-MPVPE and mm PA-MPJPE.
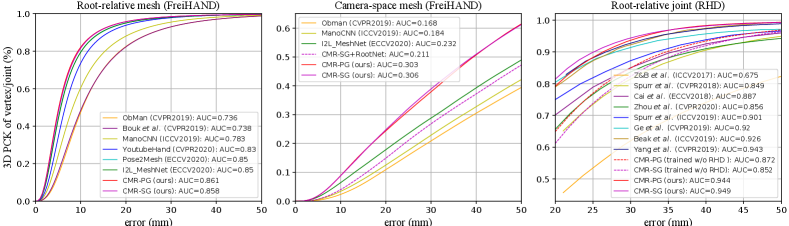
In Table 5, we evaluate the root recovery performance of camera-space mesh on the FreiHAND dataset. Our CMR outmatches ObMan [12] and I2L-MeshNet [27] by mm and mm on CS-MPVPE. To the best of our knowledge, CMR achieves state-of-the-art performance on camera-space mesh recovery, i.e., mm CS-MPVPE and mm CS-MPJPE. From Figure 9, we can see that the proposed CMR outperforms all the compared methods on 3D PCK by a large margin. With the root-relative mesh from CMR, we demonstrate that our adaptive 2D-1D registration consistently outperforms RootNet [26] as shown in Table 4.2.
Referring to CMR-PG’s PA-MPJPE and CS-MPJPE in Table 5, only an error of mm is incurred by relative pose with an error larger than mm from global translation, rotation, and scaling. Thus, compared with root-relative information, camera-space 3D reconstruction is more essential to improve the practicability of hand mesh recovery, and we advocate studying the camera-space problem.
In Figure 9, we compare our CMR with several pose estimation methods [1, 4, 9, 37, 41, 42, 44, 45] on the RHD dataset. Following the criterion of PA-MPJPE, the predicted 3D pose are processed with procrustes analysis. The AUC of CMR-PG and CMR-SG is and , respectively, surpassing all the other methods. In addition, we directly use the FreiHAND models for RHD test, inducing comparable AUC of and . Hence, the cross-domain generalization ability of CMR is verified.
In Table 6, we compare our method with several state-of-the-art approaches on body mesh recovery task using the Human3.6M and COCO datasets. Pose2Mesh [6] uses joint coordinates as the input and its performance downgrades slightly if the COCO dataset is added. As an RGB-to-voxel method, I2L-MeshNet performs better when both the Human3.6M and COCO datasets are used. By contrast, our CMR is more robust to different choices of training data and we achieve comparable or even better numbers of MPJPE and PA-MPJPE. Moreover, our approach has faster inference speed and consumes less GPU memory.
In Figure 1, we show several qualitative evaluation results on the FreiHAND and Human3.6M datasets. As demonstrated in this figure, our CMR can deal with a variety of complex situations for camera-space mesh recovery, e.g., challenging poses, object occlusion, and truncation.
5 Conclusions and Future Work
In this work, we aim to recover 3D hand and human mesh in camera-centered space and we present CMR to unify tasks of root-relative mesh recovery and root recovery. We first investigate 2D cues including 2D joint landmarks and silhouette for 3D tasks. Then, an aggregation method is proposed to collect effective 2D cues. Through aggregation of joint semantics, high-level semantic relations are explicitly captured, which is instructive for root-relative mesh recovery. We also explore 2D information for root recovery and design an adaptive 2D-1D registration to sufficiently leverage 2D pose and silhouette to estimate absolute camera-space information. Our CMR achieves state-of-the-art performance on both mesh and root recovery tasks when evaluated on FreiHAND, RHD, and Human3.6M datasets.
In the future, we plan to integrate 2D semantic information together with biomechanical relationship for more robust monocular 3D representation. We are also interested in extending our CMR with a human/hand detector in a top-down manner for multi-person tasks.
References
- [1] Seungryul Baek, Kwang In Kim, and Tae-Kyun Kim. Pushing the envelope for RGB-based dense 3D hand pose estimation via neural rendering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019.
- [2] Paul T Boggs and Jon W Tolle. Sequential quadratic programming. Acta Numerica, 4(1):1–51, 1995.
- [3] Adnane Boukhayma, Rodrigo de Bem, and Philip HS Torr. 3D hand shape and pose from images in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019.
- [4] Yujun Cai, Liuhao Ge, Jianfei Cai, and Junsong Yuan. Weakly-supervised 3D hand pose estimation from monocular RGB images. In Proceedings of the European Conference on Computer Vision (ECCV), 2018.
- [5] John Canny. A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), PAMI-8(6):679–698, 1986.
- [6] Hongsuk Choi, Gyeongsik Moon, and Kyoung Mu Lee. Pose2Mesh: Graph convolutional network for 3D human pose and mesh recovery from a 2D human pose. In Proceedings of the European Conference on Computer Vision (ECCV), 2020.
- [7] Michaël Defferrard, Xavier Bresson, and Pierre Vandergheynst. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of Advances in Neural Information Processing Systems (NeurIPS), 2016.
- [8] Bardia Doosti, Shujon Naha, Majid Mirbagheri, and David J Crandall. HOPE-Net: A graph-based model for hand-object pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020.
- [9] Liuhao Ge, Zhou Ren, Yuncheng Li, Zehao Xue, Yingying Wang, Jianfei Cai, and Junsong Yuan. 3D hand shape and pose estimation from a single RGB image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019.
- [10] Shunwang Gong, Lei Chen, Michael Bronstein, and Stefanos Zafeiriou. SpiralNet++: A fast and highly efficient mesh convolution operator. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) Workshops, 2019.
- [11] John C Gower. Generalized procrustes analysis. Psychometrika, 40(1):33–51, 1975.
- [12] Yana Hasson, Gul Varol, Dimitrios Tzionas, Igor Kalevatykh, Michael J Black, Ivan Laptev, and Cordelia Schmid. Learning joint reconstruction of hands and manipulated objects. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019.
- [13] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2016.
- [14] Catalin Ionescu, Dragos Papava, Vlad Olaru, and Cristian Sminchisescu. Human3.6M: Large scale datasets and predictive methods for 3D human sensing in natural environments. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), 36(7):1325–1339, 2013.
- [15] Umar Iqbal, Pavlo Molchanov, Thomas Breuel Juergen Gall, and Jan Kautz. Hand pose estimation via latent 2.5D heatmap regression. In Proceedings of the European Conference on Computer Vision (ECCV), 2018.
- [16] Angjoo Kanazawa, Michael J Black, David W Jacobs, and Jitendra Malik. End-to-end recovery of human shape and pose. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2018.
- [17] Angjoo Kanazawa, Jason Y Zhang, Panna Felsen, and Jitendra Malik. Learning 3D human dynamics from video. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019.
- [18] Tong Ke and Stergios I Roumeliotis. An efficient algebraic solution to the perspective-three-point problem. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2017.
- [19] Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), 2014.
- [20] Nikos Kolotouros, Georgios Pavlakos, Michael J Black, and Kostas Daniilidis. Learning to reconstruct 3D human pose and shape via model-fitting in the loop. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2019.
- [21] Nikos Kolotouros, Georgios Pavlakos, and Kostas Daniilidis. Convolutional mesh regression for single-image human shape reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019.
- [22] Dominik Kulon, Riza Alp Guler, Iasonas Kokkinos, Michael M Bronstein, and Stefanos Zafeiriou. Weakly-supervised mesh-convolutional hand reconstruction in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020.
- [23] Dominik Kulon, Haoyang Wang, Riza Alp Güler, Michael Bronstein, and Stefanos Zafeiriou. Single image 3D hand reconstruction with mesh convolutions. In Proceedings of the British Machine Vision Conference (BMVC), 2019.
- [24] Isaak Lim, Alexander Dielen, Marcel Campen, and Leif Kobbelt. A simple approach to intrinsic correspondence learning on unstructured 3D meshes. In Proceedings of the European Conference on Computer Vision (ECCV), 2018.
- [25] Matthew Loper, Naureen Mahmood, Javier Romero, Gerard Pons-Moll, and Michael J Black. SMPL: A skinned multi-person linear model. ACM Transactions on Graphics (TOG), 34(6):1–16, 2015.
- [26] Gyeongsik Moon, Ju Yong Chang, and Kyoung Mu Lee. Camera distance-aware top-down approach for 3D multi-person pose estimation from a single RGB image. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2019.
- [27] Gyeongsik Moon and Kyoung Mu Lee. I2L-MeshNet: Image-to-lixel prediction network for accurate 3D human pose and mesh estimation from a single RGB image. In Proceedings of the European Conference on Computer Vision (ECCV), 2020.
- [28] Gyeongsik Moon, Ju Yong Chang, and Kyoung Mu Lee. V2V-PoseNet: Voxel-to-voxel prediction network for accurate 3D hand and human pose estimation from a single depth map. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2018.
- [29] Alejandro Newell, Kaiyu Yang, and Jia Deng. Stacked hourglass networks for human pose estimation. In Proceedings of the European Conference on Computer Vision (ECCV), 2016.
- [30] Georgios Pavlakos, Vasileios Choutas, Nima Ghorbani, Timo Bolkart, Ahmed AA Osman, Dimitrios Tzionas, and Michael J Black. Expressive body capture: 3D hands, face, and body from a single image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019.
- [31] Georgios Pavlakos, Nikos Kolotouros, and Kostas Daniilidis. Texture-Pose: Supervising human mesh estimation with texture consistency. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2019.
- [32] Georgios Pavlakos, Xiaowei Zhou, Konstantinos G Derpanis, and Kostas Daniilidis. Coarse-to-fine volumetric prediction for single-image 3D human pose. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2017.
- [33] Georgios Pavlakos, Luyang Zhu, Xiaowei Zhou, and Kostas Daniilidis. Learning to estimate 3D human pose and shape from a single color image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2018.
- [34] Gregory Rogez, Philippe Weinzaepfel, and Cordelia Schmid. LCR-Net: Localization-classification-regression for human pose. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2017.
- [35] Javier Romero, Dimitrios Tzionas, and Michael J Black. Embodied hands: Modeling and capturing hands and bodies together. ACM Transactions on Graphics (TOG), 36(6):245:1–245:17, 2017.
- [36] Adrian Spurr, Umar Iqbal, Pavlo Molchanov, Otmar Hilliges, and Jan Kautz. Weakly supervised 3D hand pose estimation via biomechanical constraints. In Proceedings of the European Conference on Computer Vision (ECCV), 2020.
- [37] Adrian Spurr, Jie Song, Seonwook Park, and Otmar Hilliges. Cross-modal deep variational hand pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2018.
- [38] Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke, and Andrew Rabinovich. Going deeper with convolutions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2015.
- [39] Gul Varol, Duygu Ceylan, Bryan Russell, Jimei Yang, Ersin Yumer, Ivan Laptev, and Cordelia Schmid. Bodynet: Volumetric inference of 3D human body shapes. In Proceedings of the European Conference on Computer Vision (ECCV), 2018.
- [40] Lixin Yang, Jiasen Li, Wenqiang Xu, Yiqun Diao, and Cewu Lu. Bihand: Recovering hand mesh with multi-stage bisected hourglass networks. In Proceedings of the British Machine Vision Conference (BMVC), 2020.
- [41] Linlin Yang, Shile Li, Dongheui Lee, and Angela Yao. Aligning latent spaces for 3D hand pose estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2019.
- [42] Xiong Zhang, Qiang Li, Hong Mo, Wenbo Zhang, and Wen Zheng. End-to-end hand mesh recovery from a monocular RGB image. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2019.
- [43] Xingyi Zhou, Qixing Huang, Xiao Sun, Xiangyang Xue, and Yichen Wei. Towards 3D human pose estimation in the wild: A weakly-supervised approach. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2017.
- [44] Yuxiao Zhou, Marc Habermann, Weipeng Xu, Ikhsanul Habibie, Christian Theobalt, and Feng Xu. Monocular real-time hand shape and motion capture using multi-modal data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020.
- [45] Christian Zimmermann and Thomas Brox. Learning to estimate 3D hand pose from single RGB images. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2017.
- [46] Christian Zimmermann, Duygu Ceylan, Jimei Yang, Bryan Russell, Max Argus, and Thomas Brox. FreiHAND: A dataset for markerless capture of hand pose and shape from single RGB images. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2019.
Supplementary Materials
Visualization of 2D/1D registration.
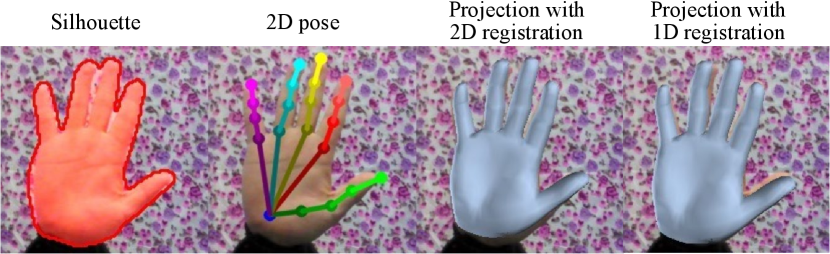
As shown in Figure 10, the 2D registration is instructive for finger alignment while the 1D process is beneficial to holistic shape alignment. Thus, joint landmarks and silhouette have different effects on the task of root recovery, and both of them can be effectively leveraged by our adaptive 2D-1D registration scheme.
Effects of our designs for spiral decoder.
We improve the spiral decoder with ISM, multi-scale mechanism, and self-regression. As shown in Table 7, all of these three design choices are beneficial to 2D-to-3D decoding, where ISM and multi-scale mechanism has relatively more significant impact.
| ISM | Multi-scale | Self-regression | PA-MPJPE | PA-MPJPE |
|---|---|---|---|---|
| 8.82 | 9.06 | |||
| ✓ | 8.73 | 8.89 | ||
| ✓ | ✓ | 8.47 | 8.56 | |
| ✓ | ✓ | ✓ | 8.46 | 8.54 |
| Method | Backbone | PA-MPJPE | J-AUC | PA-MPVPE | V-AUC | F@5 mm | F@15 mm |
|---|---|---|---|---|---|---|---|
| Boukhayma et al.(CVPR2019) [3] | ResNet50 | 35.0 | 0.351 | 13.2 | 0.738 | 0.427 | 0.895 |
| ObMan (CVPR2019) [12] | ResNet18 | 13.3 | 0.737 | 13.3 | 0.736 | 0.429 | 0.907 |
| MANO CNN (ICCV2019) [46] | ResNet50 | 11.0 | 0.783 | 10.9 | 0.783 | 0.516 | 0.934 |
| YotubeHand (CVPR2020) [22] | ResNet50 | 8.4 | 0.834 | 8.6 | 0.830 | 0.614 | 0.966 |
| Pose2Mesh (ECCV2020) [6] | 7.7 | 0.852 | 7.8 | 0.850 | 0.674 | 0.969 | |
| I2L-MeshNet (ECCV2020) [27] | ResNet50 | 7.4 | 0.854 | 7.6 | 0.850 | 0.681 | 0.973 |
| CMR-SG | ResNet18 | 7.5 | 0.851 | 7.6 | 0.850 | 0.685 | 0.971 |
| CMR-PG | ResNet18 | 7.4 | 0.853 | 7.5 | 0.851 | 0.687 | 0.973 |
| CMR-SG | ResNet50 | 7.0 | 0.860 | 7.1 | 0.858 | 0.706 | 0.976 |
| CMR-PG | ResNet50 | 6.9 | 0.863 | 7.0 | 0.861 | 0.715 | 0.977 |
| Method | Backbone | CS-MPJPE | J-AUC | CS-MPVPE | V-AUC | F@5 mm | F@15 mm |
| ObMan (CVPR2019) [12] | ResNet18 | 85.2 | 0.168 | 85.4 | 0.167 | 0.087 | 0.305 |
| ManoCNN (ICCV2019) [46] | ResNet50 | 71.3 | 0.185 | 71.5 | 0.184 | 0.102 | 0.345 |
| I2L-MeshNet (ECCV2020) [27] | ResNet50 | 60.3 | 0.233 | 60.4 | 0.232 | 0.132 | 0.394 |
| CMR-PG | ResNet18 | 50.6 | 0.290 | 50.6 | 0.289 | 0.155 | 0.474 |
| CMR-SG | ResNet18 | 49.7 | 0.295 | 49.8 | 0.294 | 0.159 | 0.481 |
| CMR-PG | ResNet50 | 48.9 | 0.304 | 49.0 | 0.303 | 0.163 | 0.488 |
| CMR-SG | ResNet50 | 48.8 | 0.307 | 48.9 | 0.306 | 0.166 | 0.492 |
Full result comparison on FreiHAND dataset.
Full-feature representation after 2D cues.
Figure 13 serves as a complement of Figure 8 in the main text. hs and sum(hp) induce holistic shape and pose. In contrast, hp invites simultaneously activated joint representation that essentially implies semantic relation. However, this relation representation is not comprehensive enough. We design group(hp) for explicitly exploring known high-level semantics so that more comprehensive joint relations can be captured.
More qualitative results.
Figure 14 and 15 illustrate comprehensive qualitative results of our predicted silhouette, 2D pose, projection of mesh, side-view mesh, camera-space mesh and pose in meter. Different from most methods, 3D roots required by image-mesh alignment are provided by CMR itself rather than ground truth, so CMR can handle images in the wild.
Referring to Figure 14, FreiHAND’s challenges include hard poses, object interactions, and truncation. Overcoming these difficulties, CMR can generate accurate silhouette, 2D pose, and camera-space 3D information.
Referring to Figure 15, samples of RHD, STB, and real-world dataset released by [9] are illustrated. We directly use the FreiHAND model for these datasets, and equally accurate predictions are obtained. Thus, CMR demonstrates superior capability of cross-domain generalization. Figure 15 also shows examples on Human3.6M and COCO. It can be seen that our CMR achieves reasonable results in the task of human body recovery.
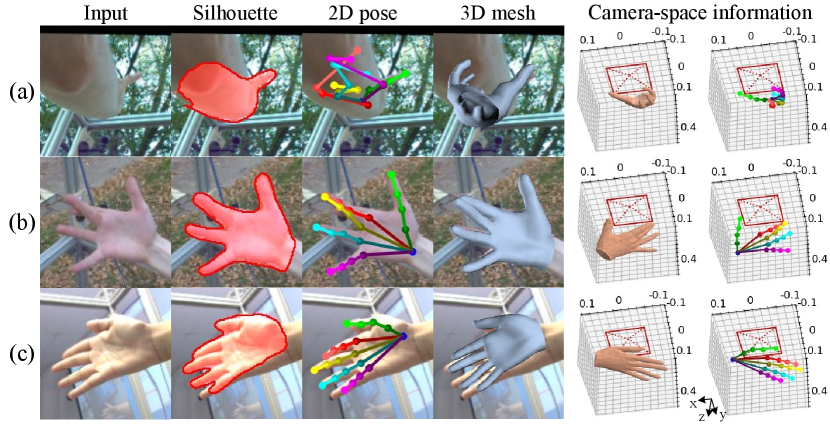
Failure case analysis.
Figure 12 shows three typical failure cases of CMR-SG. When only a small portion of the hand is visible in the input (Figure 12(a)), CMR-SG predicts wrong silhouette and 2D pose. Consequently, the camera-space information is not accurate. For cases of occlusion (e.g., Figure 12(b), in which the forefinger is completely occluded by the middle finger), although 2D pose and silhouette prediction results are still reasonable, it is difficult to obtain accurate 3D mesh since self-occlusion is challenging for the mesh recovery stage. Referring to Figure 12(c), strong contrast and extreme illumination change in the RGB input leads to large but consistent errors in silhouette, 2D pose, and 3D mesh prediction results.